Abstract
Sammon mapping is a widely used visualization technique to display complex data from high- to low-dimensional space. However, its extensive computational cost may pose potential computational challenges to big data visualization. This paper proposes a computationally-enhanced Sammon mapping (ESammon) by leveraging the characteristics of spatial data density. Unlike the conventional Sammon, ESammon preserves critical pairwise distances between data points in the process of projection, instead of all distances. Specifically, we integrated the Directed-Acyclic-Graph (DAG) based data density characterization method to select the critical distances. The numerical results demonstrated that our ESammon can achieve comparable projection results as the conventional Sammon mapping while reducing the computational cost from O(N2) to O(N).
Index Terms: Sammon mapping, data density, Multidimensional scaling (MDS)
I. Introduction
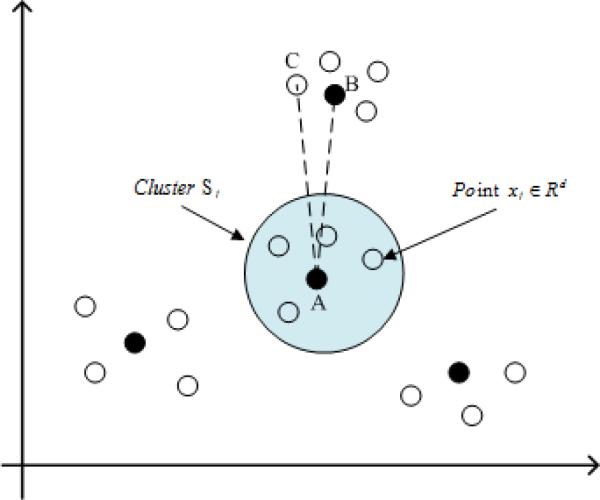
Dimension reduction plays an integral role in high-dimensional data mining, especially for big data [1]. The cognitive capabilities of humans enable us to rapidly identify data structures such as clusters, homogeneous regions, or outliers. Multi-dimensional scaling (MDS) is one of the most widely used tools for dimension reduction [2], [3]. It builds upon the pairwise relations between individual data points, and can help characterize the structure of high-dimensional data. Sammon mapping is a typical MDS technique to map complex data from high- to low-dimensional space and has been widely applied in health and medical data analyses [4], [5]. However, preserving all pair-wise data distances in dimension reduction can cause significant computational complexity especially for big data. Besides, optimization based on all pairwise distance could be redundant. As shown in Fig. 1, xj ∈ Rd denotes a d-dimension data point, Cj ∈ Rd as a Cluster centroid Sj. The solid dots A and B are two local cluster centroids, and the hollow dot C is near B. d(·) denotes the Euclidean distance. The distance d(A, B) between two local Cluster Centroids A and B represents a critical part of the global cluster structure. Additionally, the hollow dot C is close to B, and the distance d(B, C) represents the local cluster structure. However, compared with d(A, B) and d(B, C), d(A, C) is less important in characterizing the cluster structure. In fact, the structural information described by d(A, C) can be approximated by d(A, B) and d(B, C), and therefore redundant. Since dimension reduction aims at describing the cluster structure, it would be sufficient to preserve critical distances, e.g., d(A, B) and d(B, C) instead of all distances.
Fig. 1.
Demonstration of redundant pairwise distance in Sammon mapping
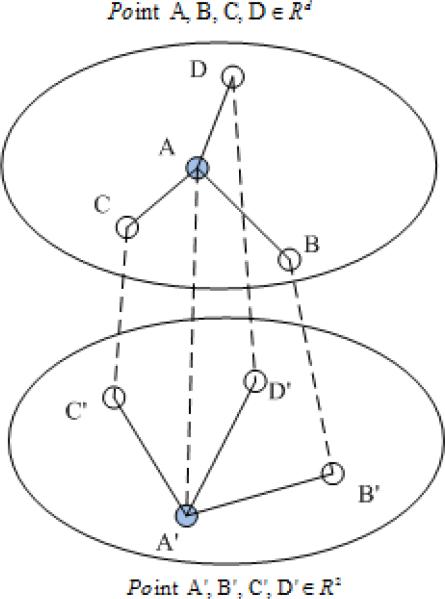
Besides, the typical gradient decent optimization algorithm used by Sammon mapping may lead to a local optimum, thus affecting the entire data structure. For example, as shown in Fig. 2, in the original high-dimensional space, point A is located near data points B, C, and D; on the low-dimensional plane, A′,B′, C′, and D′ are corresponding to A, B, C, and D, respectively. A′ is initialized outside the corresponding center of the three other points, and the distance between A′ and D′ is much greater than its original distance d(A, D). Then, when A′ moves close to D′ during the gradient decent optimization, d(A′, B′) and d(A′, C′) will also become shorter than the corresponding original distances, and easily cause the overall Sammon stress converging to a local optimum. If we ignore some pair-wise distances, we may reduce the possibility of trapping into local optimum.
Fig. 2.
Demonstration of local convergence of Sammon mapping
To solve these problems, this paper revises the Sammon mapping while achieving similar projection performance. We argue that it is sufficient to keep the spatial data structure by preserving some critical distances during Sammon projection, instead of all pairwise distances. Specifically, we propose a new method for critical distance selection based on data density, and then launch the Sammon mapping based on these selected critical distances. Overall, the main contribution of this paper is to reduce the computational complexity of Sammon mapping from O(N2) to O(N) while achieving a comparable projection quality.
The remainder of this paper is organized as follows: Section II describes the background of conventional Sammon mapping, Section III demonstrates the design of our ESammon mapping, Section IV evaluates the performance of this new algorithm, and Section V concludes our work.
II. Background of Sammon Mapping
Sammon mapping aims at mapping complex data from high-to low-dimensional space (e.g., 2 dimensions). Specifically, for a N × n dataset , where N is the number of points, ans n is the number of attributes of each data, Sammon mapping implements the corresponding low-dimensional projection of X by finding N data points in the q-dimension data space (q << n). The pairwise distances d* (yi, yj), yi, yj ∈ Y in the q-dimension space approximate its corresponding high-dimensional inter-data point distances d(xi, xj), xi, xj ∈ X. To achieve this data projection process, Sammon mapping defines the error criterion (a.k.a Sammon stress) E as Eq. 1, and solves the minimization problem Yoptimal = argminY E.
| (1) |
where , and d(·) and d* (·) denotes the Euclidean distance in high and low-dimensional space, respectively.
Sammon mapping typically applies the steepest decent method to minimize the stress E, and obtain the optimal solutions consisting of N × q variables yil, i = 1, 2, ··· , N, l = 1, 2, . . . , q on the projected space.
Assuming the t-th iteration of yil as yil(t), the update of yil can be achieved by Eq. 2-4.
| (2) |
where α is a nonnegative scalar constant, representing the step size for the gradient search. Some other searching related parameters can be computed as follows:
| (3) |
| (4) |
III. Algorithm Design of ESammon
The core idea of ESammon is to preserve critical pairwise distances, instead of all distances. First, we design a data density-based critical distance selection method, and then provide an optimal projection algorithm based on these critical distances.
A. How to select critical distances?
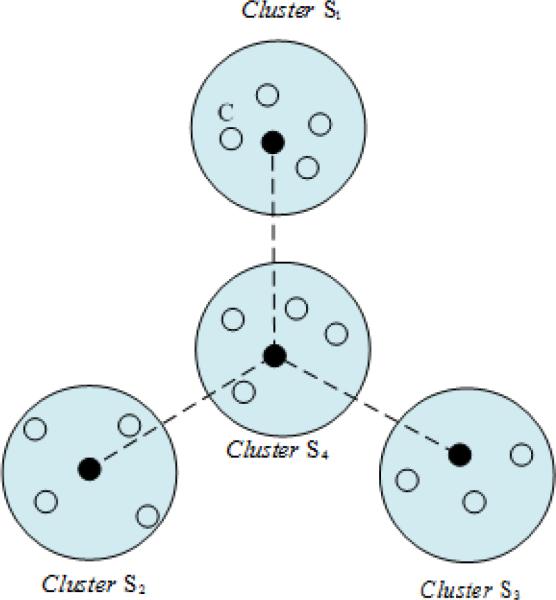
We define critical distances as the one that can characterize the profile of spatial data structures. For example, as demonstrated in Fig. 3, the solid dots represent the cluster centroids of corresponding clusters represented by the blue shadowed circles, and the hollow dots represent the data points in the clusters. The critical distances includes global and local critical distances. As shown in the graph. The pairwise distances between the solid dots are defined as the global critical distances, which characterize the global data structure. The distances between the hollow dots to its corresponding centroids in the same shadowed circle is the local critical distance, which characterizes the local data structure.
Fig. 3.
Illustration of critical distances
In order to select the critical distances, we adapted data density definition defined by Rodriguez et al. [6]. They [6] characterized the data distribution with local density and the minimum distance between the data point and any other data points with higher local density as Eq. 5 and 6.
Assuming the dataset X = {x1, x2, ··· , xN}, for any data point where n denotes the number of the attributes. Rodriguez et al. [6] computes the local data density ρi with Gaussian kernel function as Eq. 5.
| (5) |
Where ∥xi – xj∥ denotes the Euclidean distance, and dc as the cut-off distance.
The minimum distance between the point i and any other point with higher local density δi is defined as Eq. 6. In this paper, we call δi as the critical distance of data point i.
| (6) |
In particular, local density represents the compactness of spatial data structure. Large local density means more data points are distributed nearby, and may form a cluster. The critical distances describe the relationship between low-density data points and the nearest high-density data point. More generally, the local density and critical distance can describe the spatial data structure.
Based on the above data density characteristics, we further integrated our newly developed directed neighbor and Directed-Acyclic-Graph (DAG) method [7] to maintain the spatial data structure. Below we briefly show the definition of directed neighbor.
Definition 1
The directed neighbor of point xi is point xj = argminj:ρ(xj)>ρ(xi)d(xi, xj), where d(xi, xj) denotes the Euclidean distance of data xi and xj .
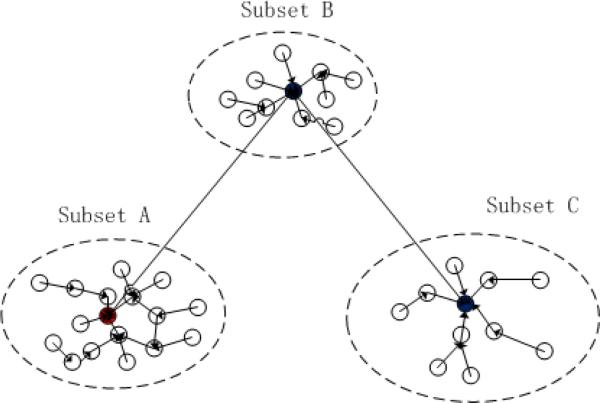
In particular, the data point with the highest density of the dataset has no directed neighbors. Hence, we set its critical distances δ = 0. The other three properties of directed neighbors are as follows: (1) assuming the directed neighbor of data point p as q, then ρp < ρq; (2) each data point has only one directed neighbor except the data point having the largest local density; (3) the directed neighbor relation is not reversible. If the directed neighbor of Point p is point q, then point p is not the directed neighbor of point q. Fig. 4 shows the construction of our DAG method, where the vertices denote the data points, and the directed edge denotes the directed neighbor relationship. The critical distance is used to define the weight of directed edge. For example, the data point with the largest local density is treated as the global anchor of other data points. Once it is initialized in the low-dimensional space, we can find the low-dimensional coordinates for the other data points based on their critical distances.
Fig. 4.
Demonstration of the DAG-based data density graph
B. Design of ESammon based on data density graph
Assuming the original dataset X = {x1, x2, . . . , xN}, for any data point where n denotes the number of the attributes, and the corresponding low-dimensional as Y = {y1, y2, . . . , yN}, , q << n, q = 2. We denote the directed neighbor of xi as neig(xi), and the original critical distance of xi as , and . Thus, our ESammon stress is expressed as follows:
| (7) |
where . Since the data point with the highest density of the dataset has no directed neighbors, and its critical distance δ = 0, its low-dimensional position does not distort the structural information of the final projection. Our ESammon does not update it in the low-dimensional space. Thus, the minimization of E is an optimization problem with 2*(N-1) variables yil, i = 1, 2, . . . , N, l = 1, 2. We also adopt the steepest decent method to minimize E, and the update of yil at the t-th iteration is expressed as Eq. 2. Particularly, we solve the parameters in the steepest decent method based on our ESammon stress as shown below.
| (8) |
| (9) |
where k = neig(xi).
Moreover, our ESammon preserves the main structural information of special data density. As demonstrated in Fig. 4, the data points located near the center of high-density areas usually have much larger critical distances than other data points, and thus influence the ESammon stress E more than other data points. In other words, these larger critical distances would be preserved more than any other data points in one cluster during our ESammon projection.
IV. ESammon Performance Evaluation
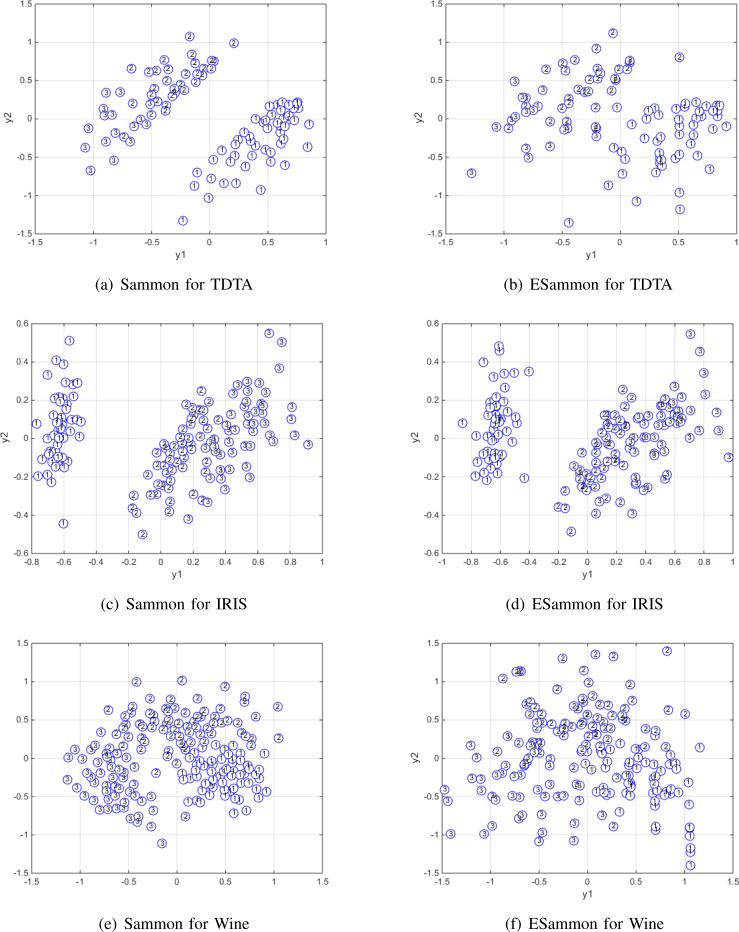
We evaluated ESammon with some real datasets as shown in Tab. I. Particularly, TDTA [8] is a longitudinal dataset with missing values less than 25%. We used multiple imputation-based method to deal with this incomplete data [9], [10]. The other datasets are from UCI [11]. IRIS includes three classes (three IRIS species: Setosa, Versicolor, and Virginica) with 50 samples each and four features (the length and the width of sepal and petal). Wine consists of 3 classes (3 types of wines grown in the same region in Italy but derived from three different cultivars); each class is characterized by 12 continuous-valued features, such as Malic acid, Ash, Alcalinity of ash, Magnesium, Total phenols, Flavanoids, Nonflavanoid phenols, Proanthocyanins, Color intensity, Hue, OD280/OD315 of diluted wines, Proline. The evaluation was performed on Windows 7 platform with Intel(R) Core(TM) i7-3520M 2.9 GHz CPU and 8 G memory. Fig. 5 demonstrates the numerical results. To visualize the comparison between conventional Sammon and ESammon, we denote different clusters with numbers 1, 2 and 3. For TDTA, it consists of 3 clusters. Cluster 1 is perfectly separated, yet the other 2 clusters are overlapped. Compared with the conventional Sammon mapping, although our ESammon has several data points overlapped between Cluster 1 and 2, we can still clearly detect the difference between Cluster 1 and 2. For IRIS, its spatial data structure is similar to TDTA, where one cluster is perfectly separated and the other two are overlapped. As demonstrated by the experimental results, our ESammon achieved almost the same projection as the conventional Sammon for IRIS. The clusters of the WINE dataset are more overlapped, where both Sammon mappings seem to project the three clusters close to each other.
TABLE I.
DESCRIPTION OF REAL DATASET
| Num. clusters | Size | Num. of Attributes | |
|---|---|---|---|
| TDTA | 3 | 97 | 9 |
| IRIS | 3 | 150 | 4 |
| Wine | 3 | 178 | 12 |
Fig. 5.
Sammon mapping vs. ESammon mapping for a) TDTA, b) IRIS, c) Wine
V. Conclusions and Future Work
Aiming at reducing the computational cost of the conventional Sammon Mapping, this paper proposed a newly designed Sammon mapping algorithm (ESammon). ESammon integrates the Directed-Acyclic-Graph (DAG) and Rodriguez's data density characterization methods to select the critical distances in order to reduce the computational complexity from O(N2) to O(N). As the numerical results demonstrated, our ESammon achieved comparable projection performance as the conventional Sammon mapping.
However, for highly overlapped datasets, both Sammon and ESammon might not project data well. In the future, we could consider more sophisticated dimension-reduction techniques such as subspace clustering [12].
Acknowledgment
This research was supported by NIH grant R01 DA033323-01A1, 1UL1RR031982-01 Pilot Project to Dr. Fang.
REFERENCES
- 1.Fang H, Zhang Z, et al. A survey on big data research. IEEE Network Magazine. 2015;29(5):6–9. doi: 10.1109/MNET.2015.7293298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Borg L, Groenen P. Modern Multidimensional Scaling. Springer; New York: 1997. [Google Scholar]
- 3.Cox T, Cox M. Multidimensional Scaling. London. Chapman & Hall; 1994. [Google Scholar]
- 4.Fang H, Zhang Z, et al. Using visualization-aided trajectory pattern validation in a longitudinal dietary data. 36th Annual Meeting & Scientific Sessions; San Antonio, TX, USA. 2015.pp. 22–25. [Google Scholar]
- 5.Fang H, Kim S, et al. Visualization-aided trajectory pattern recognition approach to smoking and depression among asian americans. Society for Research on Nicotine and Tobacco 2015; Philadelphia, PA. 2015.pp. 25–28. [Google Scholar]
- 6.Rodriguez A, Laio A. Clustering by fast search and find of density peaks. Science. 2014 Jun;344(6191):226–231. doi: 10.1126/science.1242072. [DOI] [PubMed] [Google Scholar]
- 7.Wang CJ, Fang JH, et al. Dag-searched and density-based initial centroid location method for fuzzy clustering of big biomedical data. Proc. International Conference on Bio-inspired Information and Communications Technologies ’14; Boston, USA. Dec. 1–3, 2014.pp. 290–293. [Google Scholar]
- 8.Kim SS, Kim SH, et al. A culturally adapted smoking cessation intervention for korean americans: A mediating effect of perceived family norm toward quitting. J. Immigr. Minor Health. 2015;17(4):1120–11. 129. doi: 10.1007/s10903-014-0045-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fang H, Johnson C, et al. A new look at quantifying tobacco exposure during pregnancy using fuzzy clustering. Neurotoxicol Teratol. 2011 Jan-Feb;33(1):155–165. doi: 10.1016/j.ntt.2010.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fang H, Dukic V, et al. Detecting graded exposure effects: a report on an east boston pregnancy cohort. Nicotine Tob. 2012 Apr;14(9):1115–1120. doi: 10.1093/ntr/ntr272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. [Online]. Available: http://archive.ics.uci.edu/ml/
- 12.Muller E, Assent I, et al. Relevant subspace clustering: Mining the most interesting non-redundant concepts in high dimensional data. Proc. International Conference on Data Mining (ICDM) ’14; Shenzhen, China. Dec. 14–17, 2014. [Google Scholar]