Partial linear varying multi-index coefficient model for integrative gene-environment interactions

Abstract

Gene-environment (G×E) interactions play key roles in many complex diseases. An increasing number of epidemiological studies have shown the combined effect of multiple environmental exposures on disease risk. However, no appropriate statistical models have been developed to conduct a rigorous assessment of such combined effects when G×E interactions are considered. In this paper, we propose a partial linear varying multi-index coefficient model (PLVMICM) to assess how multiple environmental factors act jointly to modify individual genetic risk on complex disease. Our model includes the varying-index coefficient model as a special case, where discrete variables are admitted as the linear part. Thus PLVMICM allows one to study nonlinear interaction effects between genes and continuous environments as well as linear interactions between genes and discrete environments, simultaneously. We derive a profile method to estimate parametric parameters and a B-spline backfitted kernel method to estimate nonlinear interaction functions. Consistency and asymptotic normality of the parametric and nonparametric estimates are established under some regularity conditions. Hypothesis testing for the parametric coefficients and nonparametric functions are conducted. Results show that the statistics for testing the parametric coefficients and the non-parametric functions asymptotically follow a χ²-distribution with different degrees of freedom. The utility of the method is demonstrated through extensive simulations and a case study.

1. Introduction

There has been great interest in identifying gene-environment (G×E) interaction in the scientific literature. G×E interaction is defined as how genotypes influence phenotypes differently under different environmental conditions (Falconer (1952)), a phenomenon also termed as genetic sensitivity to environmental stimulus. A growing number of reports have confirmed the role of G×E interaction in many diseases, such as Parkinson disease (Ross and Smith (2007)) and type 2 diabetes (Zimmet et al. (2001)). G×E interaction has traditionally been pursued based on a single environment exposure model. Evidence from epidemiological studies has clearly indicated that disease risk can be modified by simultaneous exposure to multiple environmental factors, higher than what would be expected from simple addition of the effects of factors acting alone (Carpenter et al. (2002); Sexton and Hattis (2007)). Thus, assessing the combined effect of environmental mixtures and the mechanism in which they, as a whole, interact with genes to affect disease risk could shed novel insight into disease etiology. Suppose that Y is the trait response of primary interest. In many genetic studies, one collects a p-dimensional continuous covariate vector X, and a q-dimensional discrete covariate vector Z. Motivated by an empirical analysis to study G×E interaction, see Section 5, we propose a partial linear varying multi-index coefficient model (PLVMICM):

$$Y=m_0({\beta }_0^T\mathbf{X})+{\mathit{\alpha }}_0^T\mathbf{Z}+\sum _{l=1}^L\{m_l({\mathit{\beta }}_l^T\mathbf{X})G_l+{\mathit{\alpha }}_l^T\mathbf{Z}{G}_l\}+\epsilon ,$$ (1.1)

where G_l, l = 1, ⋯,L are genetic variables (e.g., single nucleotide polymorphisms (SNPs)) of interest, ε is an error term with mean 0 and finite variance; m_l(·), l = 0, 1, ⋯,L are unknown index functions; α₀, ⋯, α_L and β₀, ⋯, β_L are parameters of interest, where the index coefficients β_l are the index loadings or the loading parameters. The SNP variable G_l can be coded as 2, 1, and 0 for genotype AA, Aa, and aa, assuming an additive model. Note that the main genetic effect for each G_l is captured by the function $m_l({\mathit{\beta }}_l^T\mathbf{X})(l=1,\cdots ,L)$. Thus we do not need to have a separate term to model the main genetic effect for each SNP. Model (1.1) provides a unified model framework for many existing models used for studying G × E interaction. Specifically, the model proposed in Ma et al. (2011) can be viewed as a special case with p = 1 (the dimension of β_l), q = 0 (the dimension of α_l), and L = 1. Model (1.1) also include the semiparametric varying-index coefficient model proposed by Ma and Xu (2015), studying G×E interaction, as a special case with β₀ = β_l = β, l = 1, ⋯,L, i.e., assuming the same index loading parameter. Our empirical analysis in the data example in Section 5 clearly shows that this assumption is not realistic, making it necessary to allow different loading parameters in the model.

Model (1.1) also includes many other existing models as special cases. It reduces to the partial linear single-index model (Carroll et al. (1997); Xia and Li (1999); Xia and Hardle (2006); Liang et al. (2010); Cui et al. (2011)), in which the discrete variable in the linear part is admitted if all G_l = 0; it reduces to VICM proposed by Ma and Song (2015) if Z = 0.

This paper aims to develop a set of statistical estimation and hypothesis procedures for model (1.1). We employ a B-spline backfitted kernel smoothing (BSBK) procedure to estimate the parametric parameters and the nonparametric functions (Wang and Yang (2007)). We first develop a profile least squares method to estimate the index coefficients β_l and the linear coefficients α_l by approximating unknown function m_l(·) with B-spline basis functions. The parametric estimates can be shown to be n^1/2-consistent and asymptotically normal. We also obtain uniformly consistent estimators of the nonparametric functions. Given the n^1/2-consistent parametric estimators and the consistent estimators of the nonparametric functions, the kernel estimators of nonparametric functions can be obtained from which we establish the asymptotic normality.

Under model (1.1), it is natural to ask whether there is an interaction between discrete/continuous environments and genes, and whether the interaction with the combined environmental exposures is linear or nonlinear. Cai et al. (2000) studied the nonparametric testing problem for varying coefficient models based on the generalized likelihood ratio test. Nonparametric inferences for additive models were previously discussed by employing the generalized likelihood ratio (GLR) statistic (Fan and Jiang (2005)). We propose a parametric likelihood ratio test to test for the linear interaction term and a nonparametric GLR test to test for the nonparametric interaction functions (Fan et al. (2001)). We further show that the proposed nonparametric GLR statistic is asymptotically χ². We conduct rigorous theoretical evaluation of the proposed estimators and test statistics and show the utility of the model through extensive simulations and a case study.

The paper is organized as follows. In Section 2.2, we formulate the model and describe the BSBK procedure and the parametric estimators for the continuous and discrete parts based on a profile least squares method. The nonparametric kernel estimators for index functions are given in Section 2.3. The consistency and normality of parametric and nonparametric estimators are given in Section 2.4. Section 3 gives the parametric likelihood ratio statistic and several nonparametric GLR statistics, as well as their theoretical properties. In Section 4, we report on simulation studies that illustrate the finite sample performance of the proposed estimators and test statistics. In Section 5 we show the utility of the method by applying it to a baby birthweight data set. Some concluding remarks are given in Section 6. The proofs of the main results are relegated to the Appendix.

2. Estimation Procedures

2.1. Estimation Procedures

We focus on the situation with L = 1 for ease of presentation, and rewrite (1.1) as

$$Y=m_0({\mathit{\beta }}_0^T\mathbf{X})+{\mathit{\alpha }}_0^T\mathbf{Z}+m_1({\mathit{\beta }}_1^T\mathbf{X})G+{\mathit{\alpha }}_1^T\mathbf{Z}G+\epsilon .$$ (2.1)

The proposed procedure for model (2.1) can be easily extend to model (1.1) with multiple G’s (i.e., multiple SNPs), and it is still more general than the existing ones used for G×E interaction. It is motivated by a recent genome-wide association study to identify genetic risk factors interacting with maternal uterine environments to increase the risk of low and high birth weight (HAPO Study Cooperative Research Group (2009)). The underlying hypothesis is that the variation of birth weight can be explained by complex G×E interactions in the context of the maternal-fetal unit. As a fetus resides inside its mother’s womb, there is intensive signalling and chemical exchanges between the two. The effects of fetal genes could be modified by simultaneous exposure to multiple stimuli from the mother’s side such as mother’s glucose level and blood pressure. For continuously measured environmental variables, we propose to model the joint effect of environment variables as a whole through an unknown index function m(·). The index function can be linear or nonlinear. That is determined by the data, with flexibility to capture the underlying mechanism of environmental mixtures modifying genetic influences on disease risk. For such discrete environmental variables as smoking status and family disease history, their interaction effects with genes can be modeled through a parametric function.

The motivation for assessing nonlinear G×E interaction in complex disease has been discussed extensively in Ma et al. (2011) and Wu and Cui (2013). The model for testing nonlinear G×E interactions in Ma et al. (2011) can be viewed as a special case of (2.1) with p = 1 (the dimension of β_l) and q = 0 (the dimension of α_l). We assume the index loading parameters β₀ and β₁ to be different; this differs from the single index model assuming common loading parameters for different index functions proposed by Xia and Li (1999). Li et al. (2010) studied the generalized functional linear models with semi-parametric single index interaction, but did not allow dissimilar loading parameters in different index functions. Although the varying-index coefficient model (VICM) proposed by Ma and Song (2015) could consider the joint interaction of multiple environments with genes, it does not admit discrete variables Z. Such discrete environmental variables are common in G×E studies and the inclusion of these variables is crucial to assess the discrete G×E interactions, as implemented in most partial linear single index models (Carroll et al. (1997); Xia and Li (1999); Xia and Hardle (2006);Liang et al. (2010)). Nevertheless, including both parametric and nonparametric terms into the same model poses computational and theoretical challenges. As discussed earlier, our model differs from that proposed by Ma and Xu (2015) in which they assumed the same loading parameters for different index functions. This assumption is too strong in reality, the modulation effect of environmental variables may differ from gene to gene. Our data analysis results in Section 5 indicate that such an assumption is invalid there. Theoretical and practical considerations thus motivate us to consider a more flexible model that can incorporate both linear and nonlinear interactions, and without too many assumptions on the model parameters, as in (2.1).

2.2. Parameter estimation

Consider the PLVMICM model given in (2.1). Let θ = (α^T, β^T)^T, where $\mathit{\alpha }={({\mathit{\alpha }}_0^T,{\mathit{\alpha }}_1^T)}^T$ and $\mathit{\beta }={({\mathit{\beta }}_0^T,{\mathit{\beta }}_1^T)}^T$. Let V_i = (X_i,Z_i,G_i), i = 1, ⋯, n, be the observations, and Θ_α and Θ_β be the parameter spaces for α and β, respectively. In this section, we derive the detailed estimation procedure employing the BSBK method proposed by Wang and Yang (2007). Let ℱ_n be the space of B-spline basis functions of order r (r ≥ 2) (de Boor (2001)) with the B-spline basis B_r(u) = (B_s,r(u) : 1 ≤ s ≤ J_n)^T, u ∈ [a, b], where J_n = N + r and N = N_n is the number of interior knots for a knot sequence ξ₁ = ⋯= 0 = ξ_r < ξ_r+1 < ⋯< ξ_r+Nn < 1 = ξ_r+Nn+1 = ⋯= ξ_Nn+2r in which N_n increases along with the sample size n. Then m_l(u_l) with $u_l=u_l({\mathit{\beta }}_l)={\mathit{\beta }}_l^T\mathbf{X}$, l = 0, 1, can be approximated by a spline function,

$${\stackrel{\sim }{m}}_l(u_l)\equiv {\stackrel{\sim }{m}}_l(u_l,\mathit{\beta })\approx \sum _{s=1}^{J_n}{B}_{s,r}(u_l){\lambda }_{s,l}(\mathit{\beta })={\mathbf{B}}_r^T(u_l){\lambda }_l(\mathit{\beta }),$$

where λ_l(β) = (λ_s,l(β), 1 ≤ s ≤ J_n)^T and λ(β) = (λ₀(β)^T, λ₁(β)^T). For given β, the B-spline coefficients λ(β) and α can be estimated as

$${({\widehat{\mathit{\alpha }}}^T,\widehat{\lambda }{(\mathit{\beta })}^T)}^T=\underset{\mathit{\alpha }\in {\mathbf{\Theta }}_{\alpha },\lambda (\mathit{\beta })\in {ℝ}^{2J_n}}{argmin}\stackrel{\sim }{R}({({\mathit{\alpha }}^T,{\mathit{\beta }}^T)}^T,\lambda (\mathit{\beta })),$$

where $\stackrel{\sim }{R}({({\mathit{\alpha }}^T,{\mathit{\beta }}^T)}^T,\lambda (\mathit{\beta }))={\sum }_{i=1}^n{[Y_i-{\stackrel{\sim }{m}}_0({\mathit{\beta }}_0^T{\mathbf{X}}_i)-{\mathit{\alpha }}_0^T{\mathbf{Z}}_i-({\stackrel{\sim }{m}}_1({\mathit{\beta }}_1^T{\mathbf{X}}_i)-{\mathit{\alpha }}_1^T{\mathbf{Z}}_i)G_i]}^2$. Let $D_i({\stackrel{\sim }{\mathbf{Z}}}_i,\mathit{\beta })={\left[{\stackrel{\sim }{\mathbf{Z}}}_i^T,{(D_{i,sl}({\mathit{\beta }}_l),1\le s\le J_n,l=0,1)}^T\right]}^T$, where ${\stackrel{\sim }{\mathbf{Z}}}_i={({\mathbf{Z}}_i^T,{\mathbf{Z}}_i^T{G}_i)}^T,D_{i,s0}({\mathit{\beta }}_0)=B_{s,r}({\mathit{\beta }}_0^T{\mathbf{X}}_i)$ and $D_{i,s1}({\mathit{\beta }}_1)=B_{s,r}({\mathit{\beta }}_1^T{\mathbf{X}}_i)G_i$. Let D(Z̃, β) = (D₁(Z̃₁, β), ⋯, D_n(Z̃_n, β))^T, an n × 2(q + J_n) matrix, and Y = (Y₁, ⋯, Y_n)^T, where Z̃ = (Z̃₁, ⋯, Z̃_n)^T is an n × 2q matrix. Then the least squares estimators of α and λ(β) is

$${({\widehat{\mathit{\alpha }}}^T,\widehat{\lambda }{(\mathit{\beta })}^T)}^T={(\mathbf{D}{(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta })}^T\mathbf{D}(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta }))}^{-1}\mathbf{D}{(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta })}^{T}Y.$$ (2.2)

Once the B-spline coefficients λ(β) are estimated, we can obtain the first derivative of the spline approximation of the nonparametric function as ${\stackrel{\sim }{m}}_l^{\prime }(u_l)\equiv {\stackrel{\sim }{m}}_l^{\prime }(u_l,\mathit{\beta })\approx {\mathbf{B}}_r^{\prime }{(u_l)}^T{\widehat{\lambda }}_l(\mathit{\beta })$, where ${\mathbf{B}}_r^{\prime }{(u_l)}^T$ is the first derivative of B_r(u_l). Given the estimator λ̂_l(β) in (2.2), we can estimate the loading parameters β by

$$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }\in {\mathbf{\Theta }}_{\beta }}{argmin}\stackrel{\sim }{R}\left({({\widehat{\mathit{\alpha }}}^T,{\mathit{\beta }}^T)}^T,\widehat{\lambda }(\mathit{\beta })\right),$$

Let λ̂_l(β̂) be the estimators of the spline coefficients obtained by replacing D(Z̃, β) with D(Z̃, β̂) in (2.2). Based on the parametric estimator θ̂, it is easy to obtain the estimator of the nonparametric function m_l(u_l) as

$${\stackrel{\sim }{m}}_l(u_l,\widehat{\mathit{\beta }})={\mathbf{B}}_r{(u_l)}^T{\widehat{\lambda }}_l(\widehat{\mathit{\beta }}),l=0,1.$$ (2.3)

A detailed estimation algorithm is given in Supplementary Materials.

2.3. Kernel estimator of nonparametric functions

To obtain the asymptotic normality of the spline estimators for the nonparametric functions m_l(u_l), l = 0, 1, as in Wang and Yang (2007), we use the BSBK estimator to establish their asymptotic normality. Define Ỹ_l = (Ỹ_1l, ⋯, Ỹ_nl)^T as the new pseudo-responses, and their corresponding “oracle” responses as $Y_l^O={(Y_{1l}^O,\cdots ,Y_{nl}^O)}^T$, l = 0, 1. By using the B-spline estimators m̃_l(·) and the parametric estimators $\widehat{\mathit{\theta }}={({\widehat{\mathit{\alpha }}}_0^T,{\widehat{\mathit{\alpha }}}_1^T,{\widehat{\mathit{\beta }}}_0^T,{\widehat{\mathit{\beta }}}_1^T)}^T$ of Section 2.2, we have

$${\stackrel{\sim }{Y}}_{i1}=Y_i-{\widehat{\mathit{\alpha }}}_0^T{\mathbf{Z}}_i-{\stackrel{\sim }{m}}_0({\widehat{\mathit{\beta }}}_0^T{\mathbf{X}}_i,\widehat{\mathit{\beta }})-{\widehat{\mathit{\alpha }}}_1^T{\mathbf{Z}}_i{G}_i,\text{and}{Y}_{i1}^O=Y_i-{\widehat{\mathit{\alpha }}}_0^T{\mathbf{Z}}_i-m_0({\widehat{\mathit{\beta }}}_0^T{\mathbf{X}}_i)-{\widehat{\mathit{\alpha }}}_1^T{\mathbf{Z}}_i{G}_i,$$

Similarly, Ỹ_i0 and $Y_{i0}^O$ can be defined. In the “oracle” responses, the functions m_l(·) are assumed to be known.

Based on the new responses Ỹ₁, we can obtain the BSBK estimator of m₁(u₁) as m̂₁(u₁, β̂) = â +b̂u₁ by local linear fitting, in which

$$(\widehat{a},\widehat{b})=\underset{a,b}{argmin}\sum _{i=1}^n{\left\{{\stackrel{\sim }{Y}}_{i1}-a{G}_i-b({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_i-u_1)G_i\right\}}^2{K}_{h_1}({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_i-u_1),$$

where K_h(t) = K(t/h)/h and K(·) is a kernel function and h is a bandwidth. By minimizing the weighted least squares, the estimator m̂₁(u₁, β̂) has a closed form

$${\widehat{m}}_1(u_1,\widehat{\mathit{\beta }})=(1,0){[{\stackrel{\sim }{\mathbf{X}}}^T\mathbf{W}\stackrel{\sim }{\mathbf{X}}]}^{-1}{\stackrel{\sim }{\mathbf{X}}}^T\mathbf{W}{\stackrel{\sim }{Y}}_1,$$ (2.4)

where

$$\begin{array}{ll}\hfill \stackrel{\sim }{\mathbf{X}}& \equiv \stackrel{\sim }{\mathbf{X}}(u_1,{\widehat{\mathit{\beta }}}_1)={\left(\begin{array}{ccc}{G}_1& \cdots & G_n\\ ({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_1-u_1)G_i/h_1& \cdots & ({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_n-u_1)G_n/h_1\end{array}\right)}^T,\hfill \\ \hfill \mathbf{W}& \equiv \mathbf{W}(u_1,{\widehat{\mathit{\beta }}}_1)=\text{diag}\left\{K_{h_1}({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_1-u_1),\cdots ,K_{h_1}({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_n-u_1)\right\}.\hfill \end{array}$$

Similarly, we can also obtain the “oracle” kernel estimator of m₁(u₁) as ${\widehat{m}}_1^O(u_1,{\widehat{\beta }}_1)$ based on new data $Y_1^O$ by local linear fitting

$${\widehat{m}}_1^O(u_1,\widehat{\mathit{\beta }})=(1,0){[{\stackrel{\sim }{\mathbf{X}}}^T\mathbf{W}\stackrel{\sim }{\mathbf{X}}]}^{-1}{\stackrel{\sim }{\mathbf{X}}}^T\mathbf{W}{Y}_1^O.$$ (2.5)

An outline of the algorithm can be found in Supplementary Materials. We use the BIC criterion to select the number of interior knots, while fixing the order of basis function as cubic to approximate the unknown functions, as described in Ma and Song (2015). The positions of interior knots are chosen as the uniform quantiles of $u_l^{(k)}={\mathbf{X}}^T{\widehat{\mathit{\beta }}}_l^{(k)}$ in the (k + 1)-th step (l = 0, 1, ⋯,L). Thus they change at each step while the number of knots remain fixed. This, however, does not affect the convergence of the algorithm in practice. To prove convergence of the algorithm with changes in knots is beyond the scope of this work. The BSBK estimator m̂_l(u_l, θ̂) is sensitive to the choice of bandwidth h_l, l = 0, 1. Bandwidth selection has been intensively studied, see Sepanski et al. (1994) and Ruppert et al. (1995) for good discussions. To avoid the estimation of high order derivatives, we employ a bandwidth selector based on the mean squared error (MSE) criterion, called empirical bias bandwidth selection (EBBS) (Ruppert (1997); Carroll et al. (1998); Liu et al. (2014)). The details of EBBS are provided in Supplementary Materials.

Remark 1

Cui et al. (2011) and Ma and Song (2015) relaxed the constraints ||β_l||₂ = 1 to ||β_l,−1|| < 1 with β _l,−1 = (β_l2, ⋯, β_lp)^T, l = 0, 1. We work directly on the equality constraints ||β_l||₂ = 1 which allows us to easily develop a Newton-Raphson algorithm. We can then test H₀ : β_lk = 0 for all k = 1, ⋯, p (see Section 5 for a demonstration). In addition, the Newton-Raphson algorithm is faster than the nonlinear optimization method adopted in Ma and Song (2015), especially under nonlinear constraints.

2.4. Theoretical results

We need some additional notation to show the asymptotic normality of the estimator. Let θ⁰ = ((α⁰)^T, (β⁰)^T)^T be the true parameter θ, where ${\mathit{\alpha }}^0={({({\mathit{\alpha }}_0^0)}^T,{({\mathit{\alpha }}_1^0)}^T)}^T$ and ${\mathit{\beta }}^0={({({\mathit{\beta }}_0^0)}^T,{({\mathit{\beta }}_1^0)}^T)}^T$. Let the space ℳ be a collection of functions with finite L₂ norm on [a₀, b₀]×[a₁, b₁]×ℛ with ℳ= {g(u) = g₀(u₀) + g₁(u₁)G, E_gl(u_l)² ≤ ∞}, where u = (u₀, u₁)^T. For 1 ≤ k ≤ q, let $g_{Z_k}^0(\mathbf{u})$ be a maximizer in ℳ for the optimization problem,

$$g_{Z_k}^0(U({\mathit{\beta }}^0))=g_0^0({\mathbf{X}}^T{\mathit{\beta }}_0^0)+g_1^0({\mathbf{X}}^T{\mathit{\beta }}_1^0)G=\underset{g\in \mathcal{M}}{argmin}E{\{Z_k-g(U({\mathit{\beta }}^0))\}}^2,$$

where $U({\mathit{\beta }}^0)={({\mathbf{X}}^T{\mathit{\beta }}_0^0,{\mathbf{X}}^T{\mathit{\beta }}_1^0)}^T$. Let $P_k(Z_k)=g_{Z_k}^0(U({\mathit{\beta }}^0))$ and P(Z) = (P₁(Z₁), ⋯, P_q(Z_q))^T. We take P(X) = (P₁(X₁), ⋯, P_p(X_p))^T with $P_k(X_k)=g_{X_k}^0(U({\mathit{\beta }}^0))$. Let Ẑ = Z − P(Z), X̂ = X − P(X) and ϕ(V,β⁰) = (ϕ₁(V,β⁰)^T,ϕ₂(V,β⁰)^T)^T, where ϕ₁(V,β⁰) = (Ẑ^T, Ẑ^T G)^T and ${\mathit{\varphi }}_2(\mathbf{V},{\mathit{\beta }}^0)={\left({[m_0^{\prime }({\mathbf{X}}^T{\mathit{\beta }}^0)\widehat{\mathbf{X}}]}^T,{[m_1^{\prime }({\mathbf{X}}^T{\mathit{\beta }}^0)\widehat{\mathbf{X}}G]}^T\right)}^T$. Define the covariance matrix of θ⁰ as

$$\mathrm{\sum }={\{E[\mathit{\varphi }{(\mathbf{V},{\mathit{\beta }}^0)}^{\otimes 2}]\}}^{-1}\{E[\sigma {(\mathbf{V})}^2\mathit{\varphi }{(\mathbf{V},{\mathit{\beta }}^0)}^{\otimes 2}]\}{\{E[\mathit{\varphi }{(\mathbf{V},{\mathit{\beta }}^0)}^{\otimes 2}]\}}^{-1},$$

where ζ^⊗2 = ζζ^T for any vector ζ. Σ can be simplified as $\mathrm{\sum }={\sigma }_0^2{\{E[\mathit{\varphi }{(\mathbf{V},{\mathit{\beta }}^0)}^{\otimes 2}]\}}^{-1}$ if the error variance σ(V) is a constant ${\sigma }_0^2$.

Theorem 1

If assumptions (A.1)–(A.4) in the Appendix hold, and nN⁴ → ∞ and nN^−2r−2 → 0, then ||θ̂−θ⁰||₂ = O_p(n^−1/2), and as n → ∞, $n^{1/2}\left(\widehat{\mathit{\theta }}-{\mathit{\theta }}^0\right)\stackrel{\mathcal{L}}{\to }N(\mathbf{0},\mathrm{\sum })$.

Theorem 2

If assumptions (A.1)–(A.4) in the Appendix hold, and nN⁴ → ∞ and nN^−2r−2 → 0, then for l = 0, 1,

$$\underset{u_l\in [a_l,b_l]}{sup}\mid {\stackrel{\sim }{m}}_l(u_l,\widehat{\mathit{\beta }})-m_l(u_l)\mid =O_p({(N/n)}^{1/2}+N^{-r}),$$

where m̃_l(u_l, β̂) is given in (2.3), and m_l(·) is the true function.

Next we show that the order of the asymptotic uniform magnitude of the difference between the BSBK estimator m̂_l(u_l, β̂) and its “oracle” version ${\widehat{m}}_l^O(u_l,\widehat{\mathit{\beta }})$ is o_p(n^−2/5), so m̂_l(u_l, β̂) and ${\widehat{m}}_l^O(u_l,\widehat{\mathit{\beta }})$ share the same asymptotic distribution.

Theorem 3

If assumptions (A.1)–(A.6) in the Appendix hold, and nN⁴ → ∞ and nN^−δ → 0 with δ = min(2r + 2, 5r/2), then for l = 0, 1,

$$\underset{u_l\in [a_l,b_l]}{sup}\mid {\widehat{m}}_l(u_l,\widehat{\mathit{\beta }})-{\widehat{m}}_l^O(u_l,\widehat{\mathit{\beta }})\mid =o_p(n^{-2/5}).$$

Set μ_k = ∫t^kK(t)dt, ν_k = ∫t^kK²(t)dt. The consistency and asymptotic normality of the unknown functions m₀(·) and m₁(·) now follow.

Theorem 4

If assumptions (A.1)–(A.6) in the Appendix hold, and nN⁴ → ∞ and nN^−2r−2 → 0, then, for l = 0, 1,

$${(n{h}_l)}^{1/2}\left\{{\widehat{m}}_l(u_l,\widehat{\mathit{\beta }})-m_l(u_l)-b_l(u_l)h_l^2\right\}\stackrel{\mathcal{L}}{\to }N(\mathbf{0},v_l(u_l)),asn\to \infty ,$$

where $b_l(u_l)={\mu }_1{m}_1^{″}(u_l)/2$, l = 0, 1, $v_0(u_0)=f_0{(u_0)}^{-1}{\nu }_{0}E[{\sigma }^2(\mathbf{V})\mid {\mathbf{X}}^T{\mathit{\beta }}_0^0=u_0]$, and $v_1(u_1)=f_1{(u_1)}^{-1}{\nu }_{0}E[G^2{\sigma }^2(\mathbf{V})\mid {\mathbf{X}}^T{\mathit{\beta }}_1^0=u_1]/{(E[G^2\mid {\mathbf{X}}^T{\mathit{\beta }}_1^0=u_1])}^2$.

If Equation ${\sigma }^2(\mathbf{V})={\sigma }_0^2$, the variance v_l(u_l) can be simplified as $f_l{(u_l)}^{-1}{\nu }_0{\sigma }_0^2$ for l = 0, 1.

3. Hypothesis tests

3.1. Testing for nonparametric components

Our model can assess the interaction of the combined effect of multiple environmental exposures with genes. This can be achieved by testing the nonparametric component m₁(·) to discover the change trend of the interaction of the combined environmental effect. We consider a test to detect whether m₁(u₁) is a linear function $m_1^0(u_1)={\delta }_0+{\delta }_1{u}_1$,

$$H_0:m_1(·)=m_1^0(·)\text{v.s.}{H}_1:m_1(·)\ne m_1^0(·),$$ (3.1)

via a generalized likelihood ratio (GLR) test (Fan et al. (2001); Liang et al. (2010); Ma and Song (2015)). Rejecting H₀ indicates statistical evidence of nonlinear interaction between G and multiple environmental mixtures. If we fail to reject H₀, we can further assess whether there exists a genetic effect as well as linear interaction effect between a gene and multiple environmental exposures by fitting a parametric linear interaction model.

Remark 2

In addition to the linear hypothesis, we are interested in testing H₀ : m₁(·) = 0 or H₀ : m₁(·) = c where c is a constant. Testing for zero or constant effect can be done under the varying-coefficient model proposed in Ma et al. (2011), this cannot be done in the current model setup due to the fact that the loading parameters β₁ are not identifiable under the above nulls. If we fail to reject the null in hypotheses (3.1), we can fit a linear interaction model as $Y=m_0({\mathit{\beta }}_0^T\mathbf{X})+{\mathit{\alpha }}_0^T\mathbf{Z}+({\delta }_0+{\mathit{\beta }}_1^T\mathbf{X}+{\mathit{\alpha }}_1^T\mathbf{Z})G+\epsilon$, where no constraints on β₁ are imposed. Then one can proceed to test $H_0^L:{\delta }_0={\mathit{\beta }}_1={\mathit{\alpha }}_1=0$ to assess the overall effect of G on Y. One can continue to assess the marginal effect of G on Y and the interaction effect between G and X or Z if $H_0^L$ is rejected.

Consider (3.1). Let θ̂ be the BSBK estimate of θ proposed in Section 2.2. Let m̂_l,H0(u_l) and m̂_l,H1 (u_l) be the estimators under H₀ and H₁, respectively. Let the residual sums of squares under H₀ and H₁ in (3.1) be ${\text{RSS}}_1(H_0)={\sum }_{i=1}^n{\left\{{\widehat{Y}}_i-{\widehat{m}}_{0,H_0}({\widehat{\mathit{\beta }}}_0^T{\mathbf{X}}_i)-{\widehat{m}}_{1,H_0}({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_i)G_i\right\}}^2$ and ${\text{RSS}}_1(H_1)={\sum }_{i=1}^n{\left\{{\widehat{Y}}_i-{\widehat{m}}_{0,H_1}({\widehat{\mathit{\beta }}}_0^T{\mathbf{X}}_i)-{\widehat{m}}_{1,H_1}({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_i)G_i\right\}}^2$, where Ŷ_i = Y_i − α̂^TZ̃_i. We define the generalized likelihood ratio (GLR) test statistic as

$$T_1=\frac{n}{2}\frac{{\text{RSS}}_1(H_0)-{\text{RSS}}_1(H_1)}{{\text{RSS}}_1(H_1)},$$ (3.2)

Let a_K = {K(0) − 1/2 ∫ K²(u)du} [∫{K(u) − 1/2K * K(u)}du]⁻¹, where K * K(u) denotes the convolution of K. Denote by Ω_l the support of ${\mathit{\beta }}_l^T\mathbf{x}$, and by |Ω_l| the length of Ω_l, l = 0, 1.

Theorem 5

If assumptions (A.1)–(A.6) in the Appendix hold, and nN⁴ → ∞ and nN^−2r−2 → 0, then under H₀ in (3.1), when $m_1^0(u_1)$ is a linear function of u₁,

$${\sigma }_{1n}^{-1}(T_1-{\mu }_{1n})\stackrel{\mathcal{L}}{\to }N(0,1),$$

where ${\sigma }_{1n}^2=\frac{2}{h_1}\mid {\mathrm{\Omega }}_1\mid \int {\{K(u)-1/2K\ast K(u)\}}^{2}du$, and ${\mu }_{1n}=\frac{1}{h_1}\mid {\mathrm{\Omega }}_1\mid \{K(0)-1/2\int K^2(u)du\}$. Furthermore, $a_K{T}_1\stackrel{a}{\sim }{\chi }_{d_1}^2$, where d₁ = a_Kμ_1n.

When assessing the linear form of the function, RSS₁(H₀) and RSS₁(H₁) can be calculated by first getting the estimators of m₀(·) and m₁(·) using the B-spline method under the null and alternative hypotheses. The B-spline estimators under H₀ are given by ${\stackrel{\sim }{m}}_{0,H_0}(u_0)={\mathbf{B}}_r^T(u_0){\widehat{\lambda }}_0$ and m̂_1,H0(u₁) = δ̂₀ +δ̂₁u₁, where δ̂₀, δ̂₁, and λ̂₀ are the ordinary least squares estimators of δ₀, δ₁, and λ₀. Then, we can obtain the kernel estimator m̂_0,H0(u₀) based on the new data (Ŷ_H0,X,Z,G) and ${\widehat{u}}_0={\widehat{\mathit{\beta }}}_0^T\mathbf{X}$, using the arguments in Section 2.3, where Ŷ_H0 = (Ŷ_1,H0, ⋯, Ŷ_n,H0)^T and ${\widehat{Y}}_{i,H_0}=Y_i-{\mathit{\alpha }}^T{\stackrel{\sim }{\mathbf{Z}}}_i-{\widehat{m}}_{1,H_0}({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_i)$. Here m̂_0,H1(·) and m̂_1,H1(.) are the BSBK estimators which can be obtained as in (2.4).

To illustrate the testing for the case with l > 1, we consider a model with two genetic variables G₁ and G₂,

$$Y=m_0({\mathit{\beta }}_0^T\mathbf{X})+{\mathit{\alpha }}_0^T\mathbf{Z}+\{m_1({\mathit{\beta }}_1^T\mathbf{X})+{\mathit{\alpha }}_1^T\mathbf{Z}\}{G}_1+\{m_2({\mathit{\beta }}_2^T\mathbf{X})+{\mathit{\alpha }}_2^T\mathbf{Z}\}{G}_2+\epsilon .$$ (3.3)

One can simultaneously test m₁(·) and m₂(·), for example, testing

$$H_0:m_1(·)=m_1^0(·),m_2(·)=m_2^0(·)\text{v.s.}{H}_1:m_1(·)\ne m_1^0(·)\text{or}{m}_2(·)\ne m_2^0(·),$$ (3.4)

where $m_1^0(·)$ and $m_2^0(·)$ are linear functions. Similarly, we can construct the corresponding GLR test statistic

$$T_2=\frac{n}{2}\{{\text{RSS}}_2(H_0)-{\text{RSS}}_2(H_1)\}/{\text{RSS}}_2(H_1),$$ (3.5)

where ${\text{RSS}}_2(H_0)={\sum }_{i=1}^n{\left\{{\widehat{Y}}_i-{\widehat{m}}_{0,H_0}({\widehat{\mathit{\beta }}}_0^T{\mathbf{X}}_i)-{\widehat{m}}_{1,H_0}({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_i)G_{i1}-{\widehat{m}}_{2,H_0}({\widehat{\mathit{\beta }}}_2^T{\mathbf{X}}_i)G_{i2}\right\}}^2,{\text{RSS}}_2(H_1)={\sum }_{i=1}^n{\left\{{\widehat{Y}}_i-{\widehat{m}}_{0,H_1}({\widehat{\mathit{\beta }}}_0^T{\mathbf{X}}_i)-{\widehat{m}}_{1,H_1}({\widehat{\mathit{\beta }}}_1^T{\mathbf{X}}_i)G_{i1}-{\widehat{m}}_{2,H_1}({\widehat{\mathit{\beta }}}_2^T{\mathbf{X}}_i)G_{i2}\right\}}^2,$, and ${\widehat{Y}}_i=Y_i-{\widehat{\mathit{\alpha }}}_0^T{\mathbf{Z}}_i-{\widehat{\mathit{\alpha }}}_1^T{\mathbf{Z}}_i{G}_{i1}-{\widehat{\mathit{\alpha }}}_2^T{\mathbf{Z}}_i{G}_{i2}$. Note that ${\widehat{m}}_{l,H_0}({\widehat{\mathit{\beta }}}_l^T{\mathbf{X}}_i)$, l = 0, 1, 2, are different from those in T₁, but the estimation is similar.

Theorem 6

If assumptions (A.1)–(A.6) in the Appendix hold, nN⁴ → ∞ and nN^−2r−2 → 0, then under H₀ in (3.4), when $m_1^0(u_1)$ and $m_2^0(u_2)$ are linear functions,

$${\sigma }_{2n}^{-1}(T_2-{\mu }_{2n})\stackrel{\mathcal{L}}{\to }N(0,1),$$

where ${\sigma }_{2n}^2=2b_n\int {\{K(u)-1/2K\ast K(u)\}}^{2}du$, μ_2n = b_n{K(0) − 1/2 ∫ K²(u)du} and b_n = Σ_l=1,2 |Ω_l|/h_l. Furthermore, $a_K^{\ast }{T}_2\stackrel{a}{\sim }{\chi }_{d_2}^2$, where $d_2=a_K^{\ast }{\mu }_{2n}$ with $a_K^{\ast }=2{\mu }_{2n}/{\sigma }_{2n}^2$.

Remark 3

The formulation of asymptotic normality in Theorem 6 is that in Fan and Jiang (2005). Theorem 6 can be generalized to cases where three or more genetic variables can be fitted and tested (l ≥ 3). One can apply Theorem 6 for simultaneous inference on the functions of some components of varying index coefficients. While the asymptotic results for T₁ and T₂ are available, they may not perform well when sample sizes are small. We recommend the conditional bootstrap method (Cai et al. (2000); Fan et al. (2001)) in applications.

3.2. Testing parametric components

We are also interested in assessing the interaction effects of genes with discrete environments. This can be addressed via parametric hypothesis testing. Furthermore, if there is G×E interaction, one may be interested in testing which index coefficients contribute to the joint effect. This results in another parametric hypothesis testing problem. We consider a class of general hypothesis testing problems with

$$H_0:\mathbf{A}\mathit{\zeta }=\gamma \text{v.s.}{H}_1:\mathbf{A}\mathit{\zeta }\ne \gamma ,$$ (3.6)

where A is a known k × (q + s) full-rank matrix, s is the number of elements in S ⊂ {1, ⋯, p}, $\mathit{\zeta }={({\mathit{\alpha }}_1^T,{\mathit{\beta }}_S^T)}^T$ with β_S = (β_j1, ⋯, β_js)^T, j_l ∈ S, and γ is a k-dimensional vector. For a special case, we can detect whether α₁ and β_S are zeros by taking

$$H_0:{\mathit{\alpha }}_1=\mathbf{0},{\mathit{\beta }}_S=\mathbf{0}\text{v.s.}{H}_1:{\mathit{\alpha }}_1\ne \mathbf{0}\text{or}{\mathit{\beta }}_S\ne \mathbf{0}.$$ (3.7)

Let ${\mathit{\theta }}_{H_0}={({\mathit{\alpha }}_{0,H_0}^T,{\mathit{\alpha }}_{1,H_0}^T,{\mathit{\beta }}_{0,H_0}^T,{\mathit{\beta }}_{1,H_0}^T)}^T$ be the parameters corresponding to θ under H₀ in (3.7) and ${\mathit{\theta }}_{H_1}={({\mathit{\alpha }}_{0,H_1}^T,{\mathit{\alpha }}_{1,H_1}^T,{\mathit{\beta }}_{0,H_1}^T,{\mathit{\beta }}_{1,H_1}^T)}^T$ be the counterparts under H₁. Define the residual sums of squares under H₀ and H₁ as

$$\begin{array}{ll}\hfill R_{H_0}& =\sum _{i=1}^n{\left\{Y_i-{\widehat{m}}_{0,H_0}({\widehat{\mathit{\beta }}}_{0,H_0}^T{\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_0})-{\widehat{\mathit{\alpha }}}_{0,H_0}^T{\mathbf{Z}}_i-({\widehat{m}}_{1,H_0}({\widehat{\mathit{\beta }}}_{1,H_0}^T{\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_0})-{\widehat{\mathit{\alpha }}}_{1,H_0}^T{\mathbf{Z}}_i)G_i\right\}}^2\hfill \\ \hfill R_{H_1}& =\sum _{i=1}^n{\left\{Y_i-{\widehat{m}}_{0,H_1}({\widehat{\mathit{\beta }}}_{0,H_1}^T{\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_1})-{\widehat{\mathit{\alpha }}}_{0,H_1}^T{\mathbf{Z}}_i-({\widehat{m}}_{1,H_1}({\widehat{\mathit{\beta }}}_{1,H_1}^T{\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_1})-{\widehat{\mathit{\alpha }}}_{1,H_1}^T{\mathbf{Z}}_i)G_i\right\}}^2,\hfill \end{array}$$

where θ̂_H0 and θ̂_H1 are the estimators of θ under H₀ and H₁ proposed in Section 2.2, and m̂_l,H0(·) and m̂_l,H1 are estimators of m_l(·) proposed in (2.4) under H₀ and H₁, l = 0, 1, respectively. We take the test statistic

$$T_3=\frac{n\{R_{H_0}-R_{H_1}\}}{R_{H_1}}.$$ (3.8)

Theorem 7

If assumptions (A.1)–(A.6) in the Appendix hold, nN⁴ → ∞ and nN^−2r−2 → 0, then when σ(V) is a constant ${\sigma }_0^2$,

1. under H₀ in (3.6), $T_3\stackrel{\mathcal{L}}{\to }{\chi }_k^2$;

2. under H₁ in (3.6), T₃ converges to a noncentral χ² distribution with k degrees of freedom with noncentrality parameter ϕ = lim_n→∞ nσ²(Aζ − γ)^T (AΣ⁻¹A)⁻¹(Aζ − γ), where Σ is defined as in Theorem 1.

4. Monte Carlo simulation

The finite sample performance of the proposed method was evaluated by simulation studies. Under model (2.1), we generated continuous X variables X₁, X₂, X₃ as independent uniform U(0, 1) and discrete Z variables Z₁, Z₂ as independent Bernoulli Ber(1, 0.5). The genetic variable G was coded as (2, 1, 0) corresponding to genotypes (AA, Aa, aa). We set the minor allele frequency (MAF) p_A = (0.1, 0.3, 0.5) and assumed Hardy-Weinberg equilibrium. SNP genotypes AA, Aa, and aa were simulated from a multinomial distribution with frequencies $p_A^2$, 2p_A(1 − p_A) and (1 − p_A)², respectively. The error term ε was normal N(0, 0.1).

We set m₀(u) = cos(πu) and m₁(u) = sin{π(u − A)/(B − A)} with $A=\sqrt{3}/2-1.645/\sqrt{12}$ and $B=\sqrt{3}/2+1.645/\sqrt{12}$, and ${\mathit{\beta }}_0=(\sqrt{5},\sqrt{4},\sqrt{4})/\sqrt{13},{\mathit{\beta }}_1=(1,1,1)/\sqrt{3}$, α₀ = (0.5, 0.5)^T, and α₁ = (0.3, 0.3)^T. We drew 1000 data sets with sample size n = 200, 500. The Epanechnikov kernel K(t) = 0.75(1 − t²)₊ was chosen to localize the unknown functions m₀(·) and m₁(·). The suitable smoothing bandwidths for estimating both functions were selected using the EBBS method described in Section 2.3. The number of interior knots N_k was selected by the BIC method.

4.1. Performance of estimation

Table 1 summarizes the average bias of the estimators (Bias), the standard deviation of the 1000 estimators (SD), the average of the estimated standard errors (SE) based on the theoretical calculation, and the estimated coverage probability (CP) at the nominal 95% confidence level for the parameters. In general, the coverage probability for all the parameters was close to 95% and reasonably controlled. As the sample size increased, the performance of the parameter estimators improved. We observed consistently smaller SD and SE when n increased from 200 to 500. The same trend was observed when n increased to 1000 (see Supplementary Materials for more details). The parameter estimators for the interaction effects (β₁, α₁) improved as MAF increased. For example, the SD of β̂₁₁ went from 0.028 to 0.012 when MAF increased from 0.1 to 0.5 under a fixed sample size n = 200. However, the estimators for the main effects (β₀,α₀) showed an opposite direction due to limited data information to estimate these parameters when MAF increased. This is due to the fact that the amount of data used to estimate these parameters is proportional to (1 − p_A)².

Table 1.

Simulation results for p_A = 0.1, 0.3, 0.5 with sample size n = 200, 500.

n	Param	True	pA = 0.1				pA = 0.3				pA = 0.5
			Bias	SD	SE	CP	Bias	SD	SE	CP	Bias	SD	SE	CP
200	α01	0.500	4.4E-04	0.016	0.016	95.2	3.1E-04	0.020	0.020	95.2	9.9E-04	0.026	0.026	95.1
	α02	0.500	−1.6E-04	0.016	0.016	95.3	4.1E-04	0.020	0.020	95.3	5.6E-04	0.026	0.026	95.8
	α11	0.300	9.4E-05	0.040	0.039	94.1	6.0E-04	0.024	0.024	94.1	6.7E-05	0.022	0.022	95.2
	α12	0.300	−1.1E-03	0.040	0.039	95.0	−1.1E-03	0.023	0.024	95.9	−4.4E-04	0.021	0.022	96.3
	β01	0.620	−3.7E-04	0.011	0.011	94.7	−1.7E-03	0.012	0.013	94.8	−2.1E-03	0.014	0.014	94.5
	β02	0.555	3.3E-04	0.012	0.012	95.3	1.0E-03	0.013	0.013	96.4	1.5E-03	0.014	0.015	96.6
	β03	0.555	−2.7E-04	0.012	0.012	94.0	4.2E-04	0.013	0.013	95.3	3.1E-04	0.015	0.015	95.4
	β11	0.577	1.4E-03	0.028	0.027	92.9	−4.0E-04	0.015	0.015	95.5	−7.5E-05	0.012	0.012	95.1
	β12	0.577	−3.4E-04	0.029	0.028	93.5	9.5E-05	0.015	0.015	95.3	2.9E-04	0.011	0.012	96.2
	β13	0.577	−3.2E-03	0.028	0.027	94.3	−2.6E-04	0.015	0.015	96.1	−5.7E-04	0.012	0.012	96.0
500	α01	0.500	−3.2E-04	0.010	0.010	95.8	−5.5E-04	0.012	0.012	95.2	−4.0E-04	0.016	0.016	96.1
	α02	0.500	1.9E-04	0.010	0.010	94.1	2.0E-04	0.013	0.012	94.2	3.8E-04	0.016	0.016	94.6
	α11	0.300	5.6E-04	0.023	0.022	93.7	9.9E-04	0.015	0.014	93.8	6.5E-04	0.013	0.013	94.5
	α12	0.300	1.2E-05	0.023	0.022	94.0	2.6E-04	0.015	0.014	93.8	2.0E-04	0.013	0.013	94.1
	β01	0.620	−4.6E-04	0.007	0.007	95.2	−1.0E-03	0.008	0.008	95.7	−1.2E-03	0.009	0.009	94.9
	β02	0.555	1.2E-04	0.007	0.007	95.5	4.3E-04	0.008	0.008	95.1	5.5E-04	0.009	0.009	95.1
	β03	0.555	2.6E-04	0.007	0.007	94.2	5.2E-04	0.008	0.008	94.1	5.2E-04	0.009	0.009	94.4
	β11	0.577	5.2E-04	0.015	0.016	95.0	3.0E-05	0.009	0.009	96.6	−8.5E-06	0.007	0.007	95.9
	β12	0.577	−3.4E-04	0.016	0.016	94.0	−8.0E-06	0.009	0.009	95.6	1.0E-04	0.007	0.007	96.3
	β13	0.577	−8.3E-04	0.016	0.016	94.5	−2.3E-04	0.009	0.009	95.2	−2.3E-04	0.007	0.007	94.8

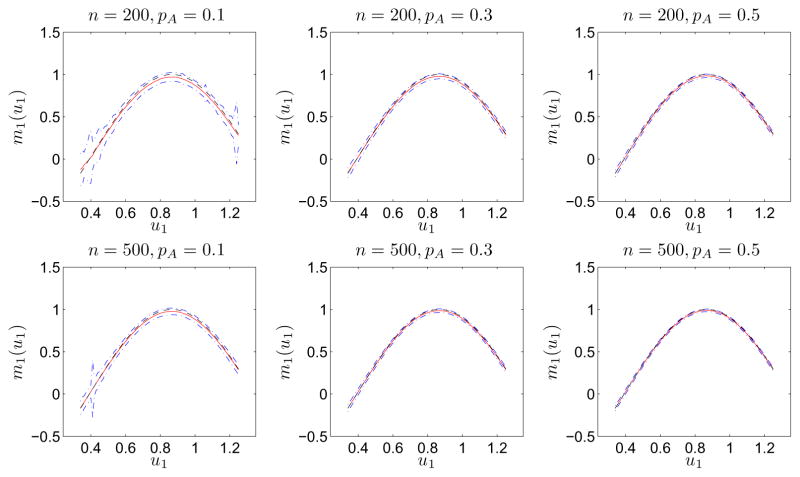
Figure 1 shows the plot of the estimators of m₁(u₁), and its corresponding confidence bands under different sample sizes and MAFs in the interval of u₁ from 0.25 to 1.25. It can be there seen that the estimated curves almost overlap with the corresponding true curves, and the confidence bands are very tight, especially under large MAF and sample size. We also plotted the estimate of m₀(·), see the Supplementary Materials.

Figure 1.

The estimation of function m₁(·) under different MAFs and sample sizes. The estimated and true functions are denoted by the solid and dashed lines, respectively. The 95% confidence band is denoted by the dotted-dash line.

4.2. Performance of hypothesis tests

We first evaluated the performance of the test for the nonparametric function under the hypothesis $H_0:m_1(·)=m_1^0(·)$, where $m_1^0(u_1)={\delta }_0+{\delta }_1{u}_1$, and δ₀ and δ₁ are some constants. Power was evaluated under a sequence of alternative models indexed by τ, $H_1^{\tau }:m_1^{\tau }(·)=m_1^0(·)+\tau \{m_1(·)-m_1^0(·)\}$. When τ = 0, the test results provide the false positive rates. The null model corresponds to a linear G×E effect.

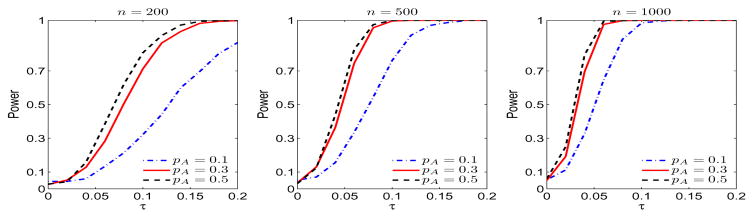
Figure 2 shows the size (τ = 0) and power function (τ > 0) at significance level 0.05 based on 500 Monte Carlo simulations each with 500 bootstrap samples under sample sizes n = 200, 500, 1000. The empirical type I errors under the three scenarios are very close to the nominal level 0.05. We observed dramatic power increase when MAF increased from 0.1 to 0.3 in all scenarios. The results indicate that our method can reasonably control the false positives and has appropriate power to detect genetic difference. We also considered the PLVMICM model in (3.3) with two genetic components and tested if both m₁(·) and m₂(·) are simultaneously linear, following Theorem 6. The results are in the Supplemental Materials.

Figure 2.

The empirical size and power function of testing nonparametric function m₁(·) under different sample sizes and MAFs.

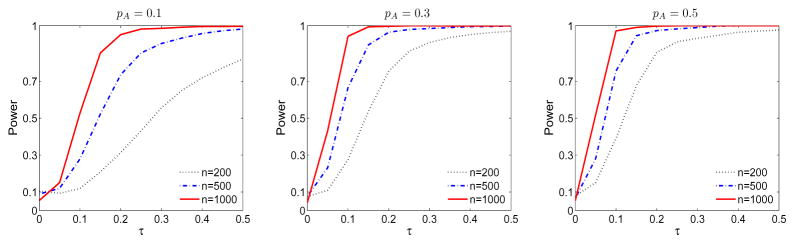
To check the performance of the interaction test between G and discrete variable Z, under model (2.1), we considered the hypothesis H₀ : α₁ = 0. The power of the test was evaluated under a sequence of alternatives indexed by τ, $H_1^{\tau }:{\mathit{\alpha }}_1^{\tau }=\tau {\mathit{\alpha }}_1$. Data were simulated as in the previous section. Figure 3 depicts the empirical size (τ = 0) and power functions (τ > 0) under different sample sizes and MAFs at the 0.05 significance level. As expected, the power and size improve as MAF and sample size increase. Under low MAF (p_A = 0.1), the size is a little inflated when n is small (200 and 500), but is well controlled when n increases to 1000. As tith the nonparametric test, dramatic power improvement is observed when MAF increases from 0.1 to 0.3. The power difference between MAF=0.3 and MAF=0.5 is small indicating good performance of the test.

Figure 3.

The empirical size and power functions of testing H₀ : α₁ = 0 under differen sample sizes and MAFs.

5. A case study

We applied the proposed PLVMICM model to a data set from the Gene Environment Association Studies initiative (GENEVA, http://www.genevastudy.org) funded by the trans-NIH Genes, Environment, and Health Initiative (GEI), to show the utility of the method. Low and high birth weights are not only the major causes of neonatal morbidity and mortality, but are also related to increased risk of metabolic diseases later in life. Fetal growth is determined by fetal genes as well as complex interactions between fetal genes and the maternal uterine environment. We focused on the Thai population with 1126 subjects genotyped with the Omni1-Quad v1-0 B platform after removing outliers. After regressing the baby’s body weight on twelve environmental variables, including nine continuous and three discrete variables, five continuous variables and one discrete variable remained significant at the 0.0001 significance level. Three of the five continuous variables were chosen, including mother’s mean OGTT diastolic blood pressure (denoted as X₁), mother’s one hour OGTT glucose level (denoted as X₂), and mother’s mean OGTT systolic blood pressure (denoted as X₃). The discrete variable, denoted as Z, is baby’s gender. To show the utility of the method, we picked one candidate gene CDKAL1 for a demonstration. The gene is located on chromosome 6 and contains 192 SNPs after removing those with MAF< 0.05. Low birth weight has been shown to be associated with high risk in type 2 diabetes later in life. Evidence of genetic studies on type 2 diabetes loci suggests that this gene is associated with reduced birth weight in Caucasian populations (Zhao et al. (2009); Andersson et al. (2010)). Our goal is to evaluate whether this gene also functions in the Thai population and, if so, how SNPs in the gene interact with mother’s condition (considered as environment) to affect birth weight and further determine the interaction mechanism.

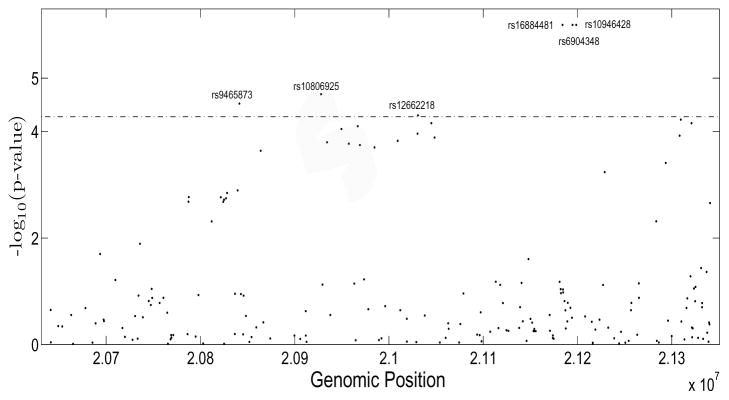
We first tested whether any SNP is associated with birth weight based on the nonparametric test of H₀ : m₁(u₁) = δ₀ + δ₁u₁ with p-value denoted by p_m1. Since we tested each SNP individually, we applied a simple multiple testing correction method. We first calculated the effective number of tests E₀ by using the Cheverud estimation method, given by $E_0=1+L^{-1}{\sum }_{i,j=1}^L(1-r_{ij}^2)$, where L = 192 is the total number of SNPs and r_ij are the pairwise correlation coefficients of SNPs (Cheverud (2001)). The estimated E₀ = 188.09, which yields a gene-wide significance level of α = 0.01/E₀ = 5.3 × 10⁻⁵. Figure 4 depicts the −log₁₀(p-values). Clearly, six SNPs rs16884481 rs10946428, rs6904348, rs10806925, rs9465873, and rs12662218 passed the significance level based on 10⁵ bootstrap samples.

Figure 4.

Plot of −log₁₀(p-value) for SNPs within gene CDKAL1.

The testing results for the six SNPs are reported in Table 2. We report SNP ID, MAF, allele information with bold font letter as the minor allele, p-values for the nonparametric test (described in Section 4.2). We also report the p-value of the test H₀ : β₀ = β₁ v.s. H₁ : β₀ ≠ β₁ in the column labeled by p_β as opposed to the model by Ma and Xu (2015) based on the generalized likelihood ratio test in Section 3.2. The p-value of the parametric test H₀ : α₁ = 0 is reported in the column labeled by p_α1 following the procedure described in Section 4.2. To compare the goodness of fit for PLVMICM with an additive varying-coefficient model (AVCM), $E(Y\mid \mathbf{X},\mathbf{Z},G)={\sum }_{j=1}^3{m}_{0j}(X_j)+{\mathit{\alpha }}_0^T\mathbf{Z}+{\sum }_{j=1}^3{m}_{1j}(X_j)G+{\mathit{\alpha }}_1^T\mathbf{Z}G$, and to see the relative gain by the integrative analysis, we calculated the MSEs of both models; they are given in the last two columns of Table 2. The p-values for testing H₀ : m₁₁(X₁) = m₁₂(X₂) = m₁₃(X₃) = 0 when fitting the AVCM model are reported in the column labeled by p_AVCM.

Table 2.

List of SNPs with MAF, allele, p-values under different hypothesis testing and MSE

SNP ID	MAF	Alleles	p-value				MSE
			pm1	pβ	pα1	pAVCM	PLVMICM	AVCM
rs16884481	0.1960	C/T	≤1.0E-05	5.1E-04	0.2517	0.1799	0.1342	0.1402
rs10946428	0.2744	A/G	≤1.0E-05	1.5E-05	0.0960	0.1227	0.1333	0.1399
rs6904348	0.2766	A/C	≤1.0E-05	1.9E-05	0.0869	0.1358	0.1334	0.1399
rs10806925	0.4761	C/T	2.0E-05	2.2E-06	0.3671	0.2733	0.1340	0.1405
rs9465873	0.4503	A/G	3.0E-05	6.5E-06	0.4911	0.2562	0.1340	0.1403
rs12662218	0.2719	A/G	5.0E-05	5.4E-06	0.2802	0.4616	0.1345	0.1408

The p-values in column p_β for the comparison of different model assumptions clearly show that the loading parameters are different for different index functions, indicating the necessity of the proposed model vs the one proposed by Ma and Xu (2015). The p-values in column p_α1 indicate that SNP×gender interactions are not significant for these six SNPs. The goodness of fit measure in the last two columns shows that the PLVMICM model fits the data better than the AVCM model, indicating the potential benefit of integrative G×E analysis. Furthermore, the testing p-values for the AVCM model do not show significance. The results imply that the genetic effects of these six SNPs are modified by the mixture effect of the three X variables, rather than separately, which further indicate the power of the integrative analysis.

For the 186 SNPs that were rejected, we fitted the model assuming m₁(u₁) = δ₀ + δ₁u₁, assuming linear G×E interaction, then testing H₀ : δ₀ = δ₁ = 0. No SNPs showed signs of significance at the 5.3E-05 significant level. The most significant SNP was rs12209806 with a p-value of 6.72E-05. This indicates that there is no linear interaction between these SNPs and the three environmental variables. However, there are four SNPs, rs12196595, rs6908425, rs6917599, and rs7773189 showing interactions with gender based on p_α1 for the 186 SNPs; the p-values were 6.12E-08, 1.89E-07, 3.69E-07, and 1.61E-05, respectively.

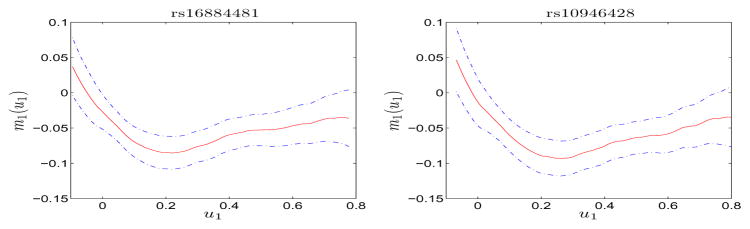
We tested the significance of the individual X variable that contributes to the joint effect following the procedure given in Section 3.2. The results showed that X₁ and X₂ contribute significantly to the joint effect in these six SNPs, but not X₃ (see Table S2 in Supplementary Materials). The estimators of the nonparametric function m₁(u₁) for the first two SNPs, rs16884481 and rs10946428 along with their 95% confidence band are given in Figure 5. The estimators for the other four SNPs are shown in Section 3 in Supplementary Materials due to space limit. The estimated function shows a decreasing pattern then slightly increases as the index value u₁ increases. Our model clearly reveals the nonlinear modulating effect of environmental mixtures on genetic effect of birth weight. Such dynamic effects can be helpful in designing prevention strategy when the model is applied to other complex diseases such as diabetes.

Figure 5.

Plot of the estimate (solid curve) of the nonparametric function m₁(u₁) for SNPs rs16884481 and rs10946428 along with their 95% confidence band (dash-dotted line).

6. Discussion

G×E interaction has been studied intensively in the literature and many statistical methods have been proposed. In this paper, we developed a partially linear varying multi-index coefficient model (PLVMICM) to conduct a rigorous assessment of the combined effect of multiple environmental exposures on the risk of disease under the paradigm of G×E interaction. Our model can be interpreted as a systems genetics approach to modeling the joint effect of environmental mixtures as a whole, then assessing how the integrative effect modifies genetic influence on disease risk. Our model is biologically attractive in that it addresses a long-term question on G×E interaction from a systems genetics perspective and is well supported by epidemiological studies (Carpenter et al. (2002); Monosson (2005); Powers et al. (2008)); and it has the flexibility to detect nonlinear interactions, and therefore, is more powerful when genetic effects are nonlinearly modified by simultaneous exposure to multiple environments.

From a statistical point of view, the index coefficient function treats multiple environmental variables X as a single index variable, and therefore can reduce multiple testing burden when interactions between the X variables and G are modelled separately. In addition, when there exist interactions between the X variables, our model has the flexibility to incorporate such interactions by adding interaction terms to the index function. PLVMICM is flexible and includes several existing models as special cases, for example, the partially linear single-index model (Carroll et al. (1997); Xia and Li (1999); Xia and Hardle (2006); Liang et al. (2010); Cui et al. (2011)) and the nonparametric additive model discussed by Fan and Jiang (2005).

In a typical G×E study, there are usually a large number of genetic variables (e.g., SNPs), and it is important to fit multiple SNPs in a single model and to select important players that interact with environmental mixtures to affect disease risk in a high dimensional model setup. In addition, many human diseases are measured on a binary scale. It is natural to extend the current PLVMICM model to a generalized PLVMICM model framework. This will be considered in a future investigation.

Appendix: Proofs

Notations

For any vector ξ = (ξ₁, ⋯, ξ_s)^T ∈ ℛ^s, let ||ξ||_∞ = max_1≤l≤s |ξ_l|. For any nonzero matrix A_s×s, denotes its L_r norm as ${\Vert \mathbf{A}\Vert }_r={max}_{\mathit{\xi }\in {ℝ}^s,\mathit{\xi }\ne 0}{\Vert \mathbf{A}\Vert }_r{\Vert \mathit{\xi }\Vert }_r^{-1}$. For any matrix $\mathbf{A}={(A_{ij})}_{i,j=1}^{s,t}$, let ${\Vert \mathbf{A}\Vert }_{\infty }={max}_{i\le i\le s}{\sum }_{j=1}^t\mid A_{ij}$. Let C^(p)[a, b] = {ψ : ψ^(p) ∈ C[a, b]} be the space of the pth-order smooth functions. Denote the space of Lipschitz continuous functions for any fixed constant c₀ as Lib([a, b], c₀) = {ψ : | ψ(x₁) − ψ(x₂)| ≤ c₀|x₁−x₂|, ∀x₁, x₂ ∈ [a, b]}. The following assumptions are required.

• A.1For each l = 0, 1, the density function f_U(βl)(·) of random variable $U({\mathit{\beta }}_l)={\mathit{\beta }}_l^T\mathbf{X}$ is bounded away from 0 on Ω_l, and there exists a constant 0 < c₀ < ∞ such that f_U(βl)(·) ∈ Lib([a, b], c₀) for β_l in the neighborhood of ${\mathit{\beta }}_l^0$, where ${\mathrm{\Omega }}_l=\{{\mathit{\beta }}_l^T\mathbf{X},\mathbf{X}\in \mathcal{X}\}$ and 𝒳 is a compact support of X.
• A.2The nonparametric function m_l ∈ C^(r)[a_l, b_l], l = 0, 1.
• A.3The noise ε satisfies E(ε|V) = 0, E(|ε|⁴) < ∞ and σ(v) = var(ε|V = v) < c₁ for some 0 < c₁ < ∞.
• A.4There exist constants 0 < c_z ≤ C_z < ∞ such that c_z ≤ Q(x) = E(Z̃Z̃^T |X = x) ≤ C_z for all x ∈ 𝒳.
• A.5The kernel function K(·) is a symmetric density function with compact support [−1, 1] and K ∈ Lib([a, b], c_K) for some constant c_K. The bandwidth h_l = O(n^−1/5), l = 0, 1.
• A.6The function u³K(u) and u³K′(u) are bounded and ∫ u⁴K(u)du < ∞.

Let $Y_{z,i}=Y_i-{\mathbf{Z}}_i^T{\mathit{\alpha }}_0^0-{\mathbf{Z}}_i^T{\mathit{\alpha }}_1^0{G}_i$, Y_z = (Y_z,1, ⋯, Y_z,n)^T, e = (ε₁, ⋯, ε_n)^T, 𝕏 = (X₁, ⋯, X_n)^T, ℤ = (Z₁, ⋯, Z_n)^T, ℤ̃ = (1_n, ℤ), and G = (G₁, ⋯, G_n)^T. Define

$$\begin{array}{r}\mathbf{U}(\mathit{\beta })=E[D_i(\mathit{\beta })D_i{(\mathit{\beta })}^T],\widehat{\mathbf{U}}(\mathit{\beta })=\frac{1}{n}\mathbf{D}{(\mathit{\beta })}^T\mathbf{D}(\mathit{\beta }),\\ \mathbf{U}(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta })=E[D_i(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta })D_i{(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta })}^T],\widehat{\mathbf{U}}(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta })=\frac{1}{n}\mathbf{D}{(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta })}^T\mathbf{D}(\stackrel{\sim }{\mathbf{Z}},\mathit{\beta }),\end{array}$$ (A.1)

where D_i(β) = (D_i,sl(β_l), 1 ≤ s ≤ J_n, l = 0, 1)^T and D(β) = (D₁(β), ⋯, D_n(β))^T, an n × 2J_n matrix.

Proof of Theorem 1

This is a straightforward result of Lemma S.6 in the Supplementary Materials.

Proof of Theorem 2

For simplicity, we assume [a_l, b_l] = [a, b] for l = 0, 1. Since for any u_l ∈ [a_l, b_l], B_s,l(u_l), s = 1, ⋯, J_n, l = 0, 1, have bounded first derivatives, by Lemmas S.4 and S.5 in the Supplementary Materials and Theorem 1, we have for any u_l ∈ [a, b],

$$\begin{array}{l}\mid {\stackrel{\sim }{m}}_l(u_l,\widehat{\mathit{\beta }})-{\stackrel{\sim }{m}}_l(u_l,{\mathit{\beta }}^0)\mid =\mid \mathbf{D}{(\widehat{\mathit{\beta }})}^T\widehat{\lambda }(\widehat{\mathit{\beta }})-\mathbf{D}{({\mathit{\beta }}^0)}^T\lambda ({\mathit{\beta }}^0)\mid \\ \le \mid \mathbf{D}{({\mathit{\beta }}^0)}^T\{\widehat{\lambda }(\widehat{\mathit{\beta }})-\lambda ({\mathit{\beta }}^0)\}\mid +\mid {\{\mathbf{D}(\widehat{\mathit{\beta }})-\mathbf{D}({\mathit{\beta }}^0)\}}^T\widehat{\lambda }(\widehat{\mathit{\beta }})\mid \\ \le \mid n^{-1}\mathbf{D}{({\mathit{\beta }}^0)}^T\widehat{\mathbf{U}}{({\mathit{\beta }}^0)}^{-1}\mathbf{D}{({\mathit{\beta }}^0)}^T\mathbf{e}\mid +O_p(n^{-1/2})\\ =O_p\left({(N/n)}^{1/2}\right).\end{array}$$

Then, combined with Lemma S.4, we have

$$\begin{array}{l}\underset{u_l\in [a,b]}{sup}\mid {\stackrel{\sim }{m}}_l(u_l,\widehat{\mathit{\beta }})-m_l(u_l)\mid \le \underset{u_l\in [a,b]}{sup}\mid {\stackrel{\sim }{m}}_l(u_l,\widehat{\mathit{\beta }})-{\stackrel{\sim }{m}}_l(u_l,{\mathit{\beta }}^0)\mid +\underset{u_l\in [a,b]}{sup}\mid {\stackrel{\sim }{m}}_l(u_l,{\mathit{\beta }}^0)-m_l(u_l)\mid \\ =O_p\left({(N/n)}^{1/2}+N^{-r}\right).\end{array}$$

This completes the proof of Theorem 2.

Proof of Theorem 4

As nh⁵ = O(1), we have (nh_l)^1/2n^−2/5 = o(1). By Theorem 3, we have

$${(n{h}_l)}^{1/2}\left\{{\widehat{m}}_l(u_l,\widehat{\mathit{\beta }})-m_l(u_l)-b_l(u_l)h_l^2\right\}={(n{h}_l)}^{1/2}\left\{{\widehat{m}}_l^O(u_l,\widehat{\mathit{\beta }})-m_l(u_l)-b_l(u_l)h_l^2\right\}+o_p(1).$$

Thus Theorem 4 can be shown straightforwardly following Lemma S.7 in the Supplementary Materials.

Proof of Theorem 7

This proof is similar to that of Liang et al. (2010). Accordingly, we only provide a sketch of the proof here, more details can be found in the Supplementary Materials. We first prove n⁻¹R(H₁) = E{σ(V)}+o_p(1). Let m̂(X, β) = m̂₀(X^Tβ₀, β) + m̂₁(X^Tβ₁, β)G and, correspondingly, ${\widehat{m}}^O(\mathbf{X},\mathit{\theta })={\widehat{m}}_0^O({\mathbf{X}}^T{\mathit{\beta }}_0,\mathit{\beta })+{\widehat{m}}_1^O({\mathbf{X}}^T{\mathit{\beta }}_1,\mathit{\beta })G$. By Theorem 3 and Lemma S.7 in the Supplementary Materials, n⁻¹R(H₁) can be decomposed as

$$\begin{array}{l}{n}^{-1}R(H_1)=\frac{1}{n}\sum _{i=1}^n{\left\{y_i-{\stackrel{\sim }{\mathbf{Z}}}^T\widehat{\mathit{\alpha }}-\widehat{m}({\mathbf{X}}_i,\widehat{\mathit{\beta }})\right\}}^2\\ =\frac{1}{n}\sum _{i=1}^n{\left\{y_i-{\stackrel{\sim }{\mathbf{Z}}}^T{\mathit{\alpha }}^0-{\widehat{m}}^O({\mathbf{X}}_i,{\mathit{\beta }}^0)\right\}}^2+o_p(n^{-2/5})+O_p(n^{-1/2})\\ =\frac{1}{n}\sum _{i=1}^n{\{{\epsilon }_i-({\widehat{m}}^O({\mathbf{X}}_i,{\mathit{\beta }}^0)-m({\mathbf{X}}_i,{\mathit{\beta }}^0)\}}^2+o_p(n^{-2/5})\\ \equiv {\mathbb{I}}_1+{\mathbb{I}}_2+{\mathbb{I}}_3+o_p(n^{-2/5}),\end{array}$$

where ${\mathbb{I}}_3=\frac{1}{n}{\sum }_{i=1}^n{\{{\widehat{m}}^O({\mathbf{X}}_i,{\mathit{\beta }}^0)-m({\mathbf{X}}_i,{\mathit{\beta }}^0)\}}^2,{\mathbb{I}}_2=-2\frac{1}{n}{\sum }_{i=1}^n\{{\widehat{m}}^O({\mathbf{X}}_i,{\mathit{\beta }}^0)-m({\mathbf{X}}_i,{\mathit{\beta }}^0)\}{\epsilon }_i$, and ${\mathbb{I}}_1=\frac{1}{n}{\sum }_{i=1}^n{\epsilon }_i^2$. It is easy to see by the Law of Large Numbers that 𝕀₁ = E{σ(V)} + O_p(n^−1/2). By Theorem 2.6 in Li and Racine (2007), we have max_i | m̂^O(X_i, β⁰) − m(X_i, β⁰)| = O_p((log(n)/(nh))^1/2), which results in 𝕀₂ = O_p((log(n)/(n²h))^1/2) and 𝕀₃ = O_p(log(n)/(nh)). This leads to n⁻¹R(H₁) = E{σ(V)} + o_p(1).

The difference R(H₀) − R(H₁) can be decomposed as

$$\begin{array}{l}R(H_0)-R(H_1)=\sum _{i=1}^n{\left\{{\stackrel{\sim }{\mathbf{Z}}}^T({\widehat{\mathit{\alpha }}}_{H_0}-{\widehat{\mathit{\alpha }}}_{H_1})+(\widehat{m}({\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_0})-\widehat{m}({\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_1}))\right\}}^2\\ +2\sum _{i=1}^n\left\{{\stackrel{\sim }{\mathbf{Z}}}^T({\widehat{\mathit{\alpha }}}_{H_0}-{\widehat{\mathit{\alpha }}}_{H_1})+(\widehat{m}({\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_0})-\widehat{m}({\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_1}))\right\}\\ \times \left\{y_i-{\stackrel{\sim }{\mathbf{Z}}}^T{\widehat{\mathit{\alpha }}}_{H_1}-\widehat{m}({\mathbf{X}}_i,{\widehat{\mathit{\beta }}}_{H_1})\right\}\equiv {\mathbb{I}}_4+{\mathbb{I}}_5.\end{array}$$

Under the null, we have ${\sigma }^{-2}{\mathbb{I}}_4\stackrel{\mathcal{L}}{\to }{\chi }_k^2$, and under the alternative σ⁻²𝕀₄ asymptotically follows a noncentral Chi-squared distribution with k degrees of freedom and noncentrality parameter ϕ. It remains to show that 𝕀₅ = o_p(1). This can be shown along the same lines as 𝕀₄. This completes the proof of Theorem 7.

The proofs of Theorem 3, 5, and 6 are in the Supplementary Materials.