Investigating the Transformations of Polyoxoanions Using Mass Spectrometry and Molecular Dynamics

Abstract

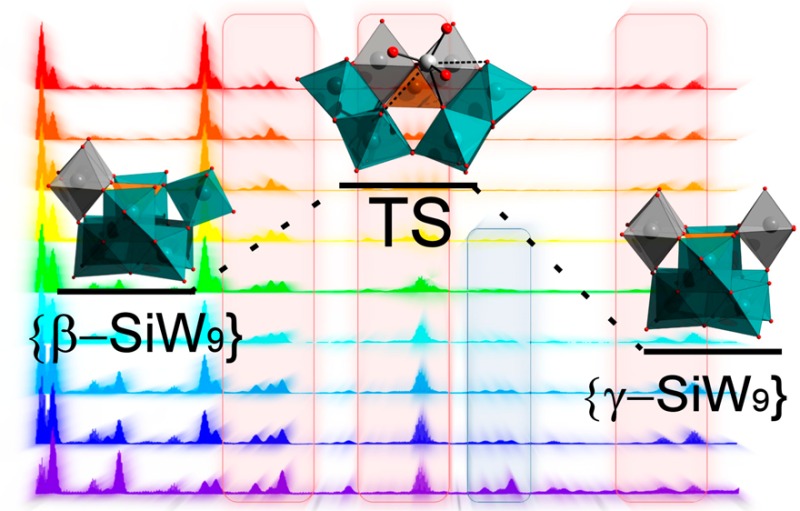
The reactions of [γ-SiW₁₀O₃₆]^8– represent one of the most important synthetic gateways into a vast array of polyoxotungstate chemistry. Herein, we set about exploring the transformation of the lacunary polyoxoanion [β₂-SiW₁₁O₃₉]^8– into [γ-SiW₁₀O₃₆]^8– using high-resolution electrospray mass spectrometry, density functional theory, and molecular dynamics. We show that the reaction proceeds through an unexpected {SiW₉} precursor capable of undertaking a direct β → γ isomerization via a rotational transformation. The remarkably low-energy transition state of this transformation could be identified through theoretical calculations. Moreover, we explore the significant role of the countercations for the first time in such studies. This combination of experimental and the theoretical studies can now be used to understand the complex chemical transformations of oxoanions, leading to the design of reactivity by structural control.

Introduction

The chemistry of polyoxometalates (POMs) has been the subject of considerable interest since the 1960s.^1,2 However, the true understanding of the processes by which these discrete metal-oxide nanoclusters speciate and assemble remains one of the most challenging analytical problems in the field. Compared to other well-known self-assembling inorganic, supramolecular, and coordination clusters,³⁻⁶ a rigorous mechanistic interpretation of the means by which POMs can assemble—and more specifically, how this can be exploited—has yet to be achieved. Such information would both aid in the design of new syntheses and inform our understanding of their rich chemical properties. This is still a somewhat distant goal and has attracted substantially less attention in recent years than the often loosely targeted synthesis of new and increasingly complex transition-metal-substituted POM clusters.⁷⁻⁹ Largely, this problem can be attributed to the lack of appropriate analytical “handles” in these systems or the availability of techniques possessing both the appropriate resolution (i.e., those capable of discerning clearly between similar species in solution) and time scale (i.e., seconds to minutes) to follow these dynamic processes as they occur.

One approach which has emerged in recent years as a promising tool to probe the assembly of POM species is the use of electrospray (ESI-MS) and cryospray (CSI-MS) mass spectrometry.^10,11 These “soft-ionization” approaches are unique in that they allow for well-defined resolution of multiple closely related species (as opposed to other common spectroscopic techniques such as UV–vis or IR) and can provide clear, well-resolved “snapshots” of a given system on a time scale down to within tens of seconds if necessary.¹²⁻¹⁶ POMs, in particular, are especially well-suited for ESI-MS analysis owing to their high charge and generally good solubility, and recent years have seen a more concerted effort to apply these methods toward unravelling some of the complex solution behavior, stability, and self-assembly of these species.¹⁷⁻¹⁹ It is nevertheless important to note that previous successful studies have relied on the judicious use of complementary techniques such as single-crystal X-ray diffraction to achieve the greatest impact.

However, while a detailed structural understanding undeniably underpins the majority of ESI-MS studies on POMs (as it does herein also), one of the more effective strategies to have recently emerged is the combined use of mass spectrometry and computational approaches to help both identify and rationalize the behavior of these fascinating cluster species.²⁰ To date, this dual approach has been especially instrumental in helping to understand the early stage aggregation and assembly of POM clusters,²¹⁻²³ though it is noteworthy that the majority of these pioneering studies employed a somewhat postfactual, fragmentation-based analysis rather than a true, bottom-up or experimentally directed approach. This has, however, hindered the study of more subtle or complex transformations between distinct cluster species in solution—fundamental processes which are becoming increasingly important as the application of POMs in areas as diverse as biochemistry, energy storage, and electronic engineering continues to grow.²⁴⁻²⁶ Exploring the speciation and transformation of these species is therefore neither trivial nor a niche pursuit and should represent an important goal in the continued development of this chemistry well into the 21st century.

While there is, therefore, a wide array of potentially functional polyoxometalate species to target for study, one key system which has long been exploited for its unusually rich structural diversity and speciation behavior is that of the lacunary silicotungstates based on the parent [SiW₁₂O₄₀]^4– Keggin-type anion (Scheme 1). In particular, the dilacunary [γ-SiW₁₀O₃₆]^8– cluster has long been employed as a structurally flexible precursor in the synthesis of an ever increasing library of metal-functionalized POM clusters and possesses the richest speciation chemistry of all lacunary polyoxoanions,²⁷ with products regularly including {SiW₆},²⁸ {SiW₈},²⁹⁻³¹ {SiW₉},^19,32 {SiW₁₀},^33,34 and {SiW₁₁} fragments having been previously reported.³⁵ This structural flexibility has also been adopted in the synthesis of an array of structurally unique, high nuclearity transition-metal-substituted polyoxometalates (TMSPs).³⁶⁻⁴⁰ Indeed, this precursor has been key in the development of several state-of-the-art functional materials including the {Ru₄(SiW₁₀)₂} water oxidation catalyst (WOC),⁴¹ which has been studied in great detail as one of the most promising Ru-based WOCs developed thus far.⁴² This is in addition to the use of {γ-SiW₁₀} for the direct epoxidation of olefins⁴³ or as a platform for the synthesis of single-molecule magnets,⁴⁴ while recent work has also demonstrated the formation of self-assembled monolayers of silicotungstate derivatives on Ag(111)⁴⁵ and the synthesis of catalytically active Pt-incorporating derivatives.⁴⁶ Understanding the fundamental behavior of these metal-oxide building blocks, particularly in the solution state (where POMs are increasingly exploited as homogeneous catalysts for instance), will therefore only increase in importance as applications for these materials continue to grow.

Scheme 1. Diagram Showing the Rich Structural Diversity, Applications, and Speciation Behavior of the Dilacunary {γ-SiW₁₀O₃₆}.

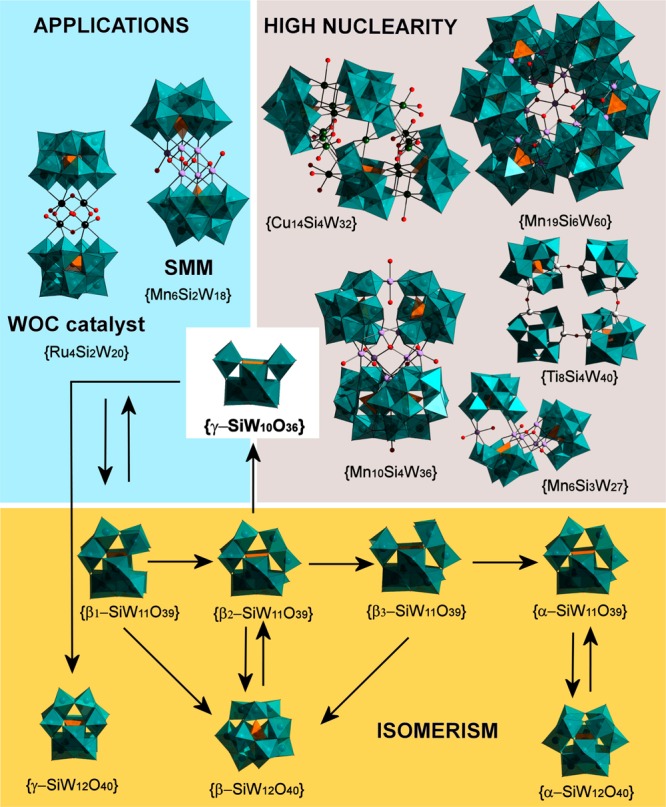
Top left: Ru-derived {Ru₄Si₂W₂₀} is a highly promising water oxidation catalyst, and Mn-derived compound {Mn₆Si₂W₁₈} is a Mn^II/III-based single-molecule magnet. Top right: several examples of high-nuclearity transition-metal-substituted polyoxometalate clusters. Bottom: Remarkable isomerism of tungstosilicate species showing the relationships between different known structures. Color code for polyhedra: W = teal, Si = orange; ball-and-stick: O = red, Ru = black, Mn = lavender, Cu = green, Ti = white.

Similarly, the synthesis of [γ-SiW₁₀O₃₆]^8– is in itself interesting,⁴⁷ specifically in that the synthetically simple one-pot transformation from the [β₂-SiW₁₁O₃₉]^8– (see Scheme 1, bottom) precursor involves both a change in nuclearity and an ill-defined β to γ isomerization step, which formally involves the rotation of one {W₃} triad unit in the cluster shell (see Figure S1 for more information). Despite the ubiquity of the [γ-SiW₁₀O₃₆]^8– anion as a precursor in POM chemistry, however, the formation of this cluster—and more significantly, the fundamental processes and structural transformations by which it occurs—remains remarkably understudied, and to the best of our knowledge, only one attempt has thus far been made to rationalize this previously.⁴⁸

Herein, we present a comprehensive, bottom-up study of the synthesis of [γ-SiW₁₀O₃₆]^8– from the parent [β₂-SiW₁₁O₃₉]^8– anion by employing time-resolved ESI-MS as a means to direct a complementary and detailed theoretical analysis. In this way, we aim to unravel the mechanism by which this important precursor species is formed in solution and, furthermore, discern new information about the diverse chemistry of this anion.

Results and Discussion

Initial Screening and Time-Resolved ESI-MS Studies

Time-resolved electrospray ionization mass spectrometry (ESI-MS) was employed to measure the transformation of K₈[β₂-SiW₁₁O₃₉] into K₈[γ-SiW₁₀O₃₆] over the course of 20 min upon addition of aqueous K₂CO₃ (following the method previously reported by Canny et al. performed at one-quarter scale).⁴⁷ In order to ensure that the results of these measurements were broadly comparable, a generalized procedure for the sampling and analysis of the reaction was created. Twenty microliter aliquots of the reaction mixture were collected at predetermined time intervals, diluted in an additional 1.0 mL of H₂O, and immediately transferred to the spectrometer for subsequent measurement under uniform instrument parameters. It is important to note at this point that the ESI-MS data presented here are, at best, pseudoquantitative in the strictest sense and should not be taken to give a precise overview of the true solution composition. That said, however, the genuine qualitative trends which emerge from these gas-phase measurements are highly significant in helping to reveal the solution behavior of these compounds and thus direct the additional computational studies discussed below. Similarly, while absolute structural information cannot be obtained by ESI-MS measurements alone, the stoichiometry of the observed fragments is particularly useful in helping to infer which possible isomeric configuration (i.e., β or γ) the anionic fragments may possess.

Prior to screening of the reaction mixture, we performed initial control measurements in the m/z range of 1000–1500 in order to account for both the in-source fragmentation of the {β₂-SiW₁₁} starting material under our chosen source settings and any initial solution-phase speciation at the reaction start point in order to provide a useful “baseline” for comparison (Figure S2). Interestingly, we were surprised to note the extensive fragmentation/speciation of this cluster across multiple cone voltages (see Table S1), even prior to the addition of base (i.e., the notional start point of the reaction), and several key observations can be made from this alone. In particular, the very high abundance of those envelopes falling in the range of m/z 1120–1180, which correspond to various mixed salts of [SiW₉O₃₄]^10– fragments (see Table 1).⁴⁹ This is in contrast to the very low initial abundance of stoichiometrically correct [γ-SiW₁₀O₃₆]^8– species in the mass spectrum, which, while detectable in the range of m/z 1315–1345 (indicating that a small amount of product is present even before addition of base), are far superseded by similarly stoichiometrically correct [β-SiW₁₀O₃₇]^10– fragments (in the range of m/z 1240–1300).

Table 1. Assignment of the Key Species Identified during the Course of the Time-Resolved ESI-MS Measurements^a.

anion	m/z (obs)	z	assignment	m/z (calcd)
{SiW9}	1128.6	2–	{NaH7[SiW9O34]}	1128.7
	1148.7	2–	{Na2H6[SiW9O34]·H2O}	1148.7
	1156.6	2–	{KNaH6[SiW9O34]·H2O}	1156.7
	1158.6	2–	{KNa2H5[SiW9O34]}	1158.7
	1167.6	2–	{KNa2H5[SiW9O34]·H2O}	1167.7
	1175.6	2–	{K2NaH5[SiW9O34]·H2O}	1175.7
{β-SiW10}	1244.6	2–	{NaH7[SiW10O37]}	1244.7
	1254.1	2–	{NaH7[SiW10O37]·H2O}	1253.7
	1264.6	2–	{Na2H6[SiW10O37]·H2O}	1264.7
	1273.1	2–	{KNaH6[SiW10O37]·H2O}	1272.7
	1283.5	2–	{KNa2H5[SiW10O37]·H2O}	1283.6
	1291.5	2–	{K2NaH5[SiW10O37]·H2O}	1291.6
{γ-SiW10}	1319.5	2–	{K5H[SiW10O36]}	1319.6
	1330.5	2–	{K5Na[SiW10O36]}	1330.6
	1338.5	2–	{K6[SiW10O36]}	1338.5
{β-SiW11}	1399.5	2–	{KNa2H3[SiW11O39]·2H2O}	1399.6
	1408.5	2–	{K3NaH2[SiW11O39]}	1408.6
	1419.5	2–	{K3Na2H[SiW11O39]}	1419.6
	1427.5	2–	{K4NaH[SiW11O39]}	1427.5

^aBoth calculated and observed m/z values refer to the most intense, or monoisotopic, peaks in the isotopic envelope.

From this initial screening, four key anion species can therefore be identified in the higher m/z range of the spectrum, which correspond to the {β-SiW₁₁} precursor, {γ-SiW₁₀} product, and two possible intermediate species, {β-SiW₁₀} and {SiW₉}. Interestingly, in the only previous discussion regarding the formation of the {γ-SiW₁₀} anion, Kortz et al. proposed a stoichiometrically identical {β-SiW₁₀} species as the key intermediate based on the isolation of a disubstituted {β-Ni₂SiW₁₀} fragment from the reaction of {γ-SiW₁₀} with Ni²⁺ cations.³⁷ While this interesting hypothesis certainly follows logically, based on these previous findings, the relative rarity of such fragments (suggesting possible instability in solution) certainly does not preclude an alternative mechanism. The relative overabundance of {SiW₉} fragments in our initial ESI-MS experiments is therefore of considerable interest, and indeed, a plausible case can also be constructed for the formation of {γ-SiW₁₀} via a {SiW₉} intermediate. While this may at first-principles appear to be somewhat less favorable owing to the necessity for the initial loss of two tungsten centers rather than one (though we note that overall loss of a ditungstate fragment in the reorganization of silicotungstate species has been experimentally observed before),^19,31 the key isomerization step between the β- and γ-conformations during the reaction can, in fact, be postulated to occur by the breaking and re-forming of a single W–O bond when proceeding through a {SiW₉} intermediate. This is in contrast to the rather more convoluted β to γ isomerization associated with a possible {SiW₁₀} intermediate, which would require the breaking and re-forming of two separate groups of W–O bonds in tandem with the loss of an additional O atom (Figure S3). We are therefore presented with two possible mechanistic pathways (Scheme 2) whereby the likelihood of each can be interrogated by exploring the behavior of these key species under a time-resolved ESI-MS approach.

Scheme 2. Hypothesized Mechanisms for the Transformation of [β₂-SiW₁₁O₃₉]^8– into [γ-SiW₁₀O₃₆]^8–

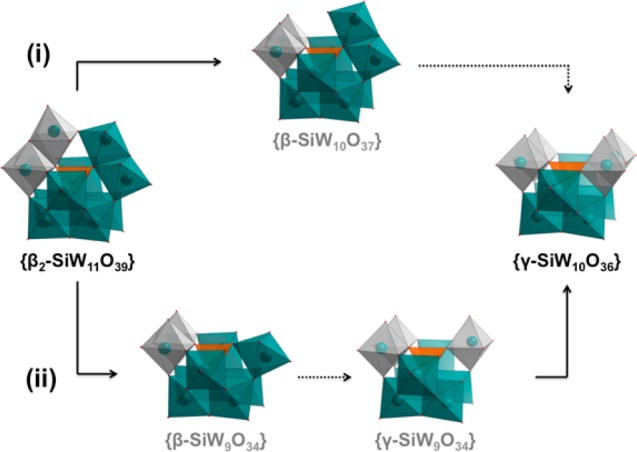
Details: (i) The two-step mechanism first proposed by Kortz et al., which proceeds through a single {β-SiW₁₀} intermediate and (ii) an alternative three-step mechanism which involves an isomerization event between two {SiW₉} intermediate species. Solid lines highlight speciation/nucleation events, whereas dotted lines represent isomerization steps. Color code: W = teal, Si = orange, O = red. Gray polyhedra are used to differentiate W centers belonging to rotated {W₃} triads.

A number of ESI-MS spectra were thus obtained which allowed for the construction of a series of pseudo-real-time “snapshots” of the reaction progress over the course of 20 min from the first addition of base to the precipitation of the product by addition of KCl, that is, the notional start and end points of the reaction (Figure 1). In this way, the unique power of mass spectrometry to yield discrete signals for mixtures of species with otherwise highly similar chemical/physical properties allowed us to easily track the fate of each of the key species independently. Indeed, since these are primarily delineated by the loss/gain of heavy W atoms and, therefore, enjoy relatively broad separation in the corresponding mass spectra, this allowed clusters of individual peak envelopes to be grouped, in the main, by the identity of the anion itself. Note that our analysis focused exclusively on the region of the spectra in which intact, doubly charged cluster species could be identified (see Table 1 and Figure 1) as this gave, by far, the clearest picture of the key cluster species in the reaction. Several triply charged species can be identified in the lower m/z region of the spectra; however, these were often badly obscured by overlapping singly and doubly charged fragements and thus presented a considerable analytical challenge. Several interesting observations arise from these time-resolved measurements. First, we are able to demonstrate the formation of {γ-SiW₁₀} from the {β₂-SiW₁₁} precursor directly as a function of time. Our results show that, while {γ-SiW₁₀} appears to be present in low amounts even when the starting material is simply dissolved in water, addition of base rapidly causes conversion of {β₂-SiW₁₁} into {γ-SiW₁₀}, and this process appears to effectively reach completion/equilibrium after ca. 10 min at pH 9.1 (Figure 2), at which point the combined ion count (CIC)⁵⁰ of both species is shown to essentially plateau for the remaining reaction time.

Figure 1.

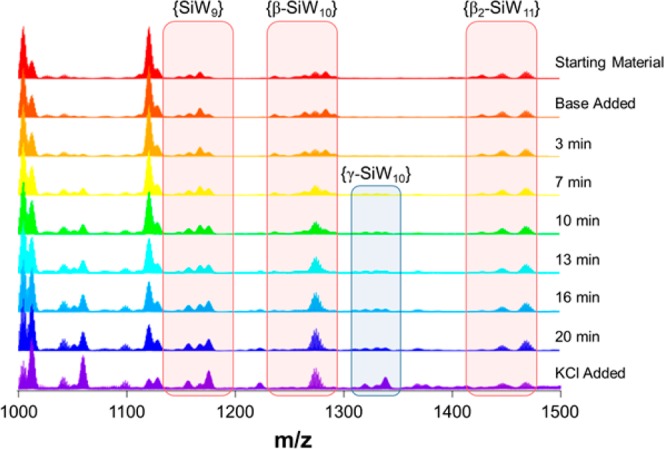
Time-resolved ESI-MS spectra pertaining to aliquots of the reaction mixture during the formation of {γ-SiW₁₀}.

Figure 2.

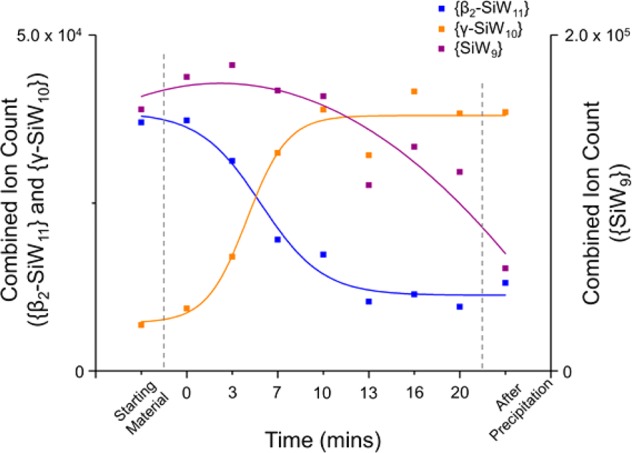
Plot of combined ion count values for the {β-SiW₁₁} starting material vs the {γ-SiW₁₀} product and the proposed {SiW₉} intermediate. The dashed vertical lines on the plot indicate the point in the reaction coordinate at which either base (left) or KCl (right) is added. The lines of best fit are provided primarily as a guide for the eye.

More interestingly, a plot of the CIC values for the group of related envelopes identified as {SiW₉} fragments (see Table 1) shows markedly different behavior when compared to both the precursor and product clusters (Figure 2). In this case, the relative abundance of {SiW₉} actually slightly increases over the first few minutes of the reaction (up to t ≈ 3 min) before gradually decreasing (though only by less than 10% total) up to t = 10 min. This is in marked contrast to both the {β₂-SiW₁₁} and {γ-SiW₁₀} envelopes, which change dramatically in intensity over this time frame (by a factor of more than 3 and 4, respectively), indicating that the observed {SiW₉} species must be playing some other role in this system and cannot be explained merely as a direct fragment of either the starting material or product (Figure 2 and Figure S4). Furthermore, from t = 10 min onward, the CIC of these {SiW₉} species then decreases significantly, though only once the abundance of both {β₂-SiW₁₁} and {γ-SiW₁₀} appears to have plateaued. Note that this is also in direct contrast to the behavior of the other most significant fragment in the mass spectra, {β-SiW₁₀}, which decreases sharply and tracks well with the same overall decrease in the parent anion {β₂-SiW₁₁} (see Figure S5).

It is important to emphasize that we cannot say with absolute certainty whether these fragments are simply ionization products or genuinely reflective of the solution composition (or, as appears more likely, arise as a combination of both effects), even at the relatively mild ionization parameters used in these experiments. That said, the qualitative trends in their abundance when viewed relative to each other are often indicative of their origins. We can therefore reasonably propose that the {β-SiW₁₀} species is most likely attributed to the direct fragmentation of the {β₂-SiW₁₁} precursor within the spectrometer and is thus significantly less likely to be mechanistically relevant in the formation of the final product, {γ-SiW₁₀}. This would also suggest that any {β-SiW₁₀} species formed by the hydrolysis/fragmentation of {β₂-SiW₁₁}—in which one of the W atoms notionally has three terminal oxygen ligands—should not be especially favorable or long-lived, and this appears to be borne out in both our measurements and in the literature, where the only known examples of {β-SiW₁₀} moieties to date have been found in transition-metal-substituted clusters in which coordination of additional metal cations has stabilized the POM.

This further strengthens the case for the hypothesis that the reaction may be proceeding through a trilacunary {SiW₉} intermediate rather than more directly through the dilacunary {β-SiW₁₀} species (though we would note that it cannot clearly be ascertained through these data alone whether the hydrolysis of {β₂-SiW₁₁} proceeds via {β-SiW₁₀} as a short-lived intermediate or forms the {β-SiW₉} species directly). Additionally, it is worth remarking that, in a purely qualitative sense at least, this behavior is not too far removed from the kinetic model one might expect of a classic first-order consecutive reaction. Of course, additional in-source fragmentation complicates this picture and must be taken into account to explain the significantly higher abundance of intermediate {SiW₉} species and the deviation these additional phenomena might cause from a more realistic or quantitative model, which for these reasons cannot be employed herein.

It can therefore be argued that the time-resolved ESI-MS measurements reported herein suggest that a mechanism centered on a {SiW₉} intermediate appears to be the most plausible; however, it also highlights the limitations of the technique. Unfortunately, given the identical stoichiometry of the potentially key {β-SiW₉} and {γ-SiW₉} intermediates involved in the crucial isomerization step, no further information can be gained by ESI-MS study alone. It does, however, allow us to perform a highly targeted, complementary computational study which might otherwise involve a potentially intractable (or at best highly time-consuming) search through a large computational parameter space.

Theoretical Validation of the Hypothetical Reaction Mechanism

To further demonstrate the viability of the trilacunary {SiW₉} intermediate and gain insight in the isomerization mechanism, we have performed theoretical calculations using both standard density functional theory (DFT) and molecular dynamics (MD) (classical and Car–Parrinello) approaches. As described above, the overall reaction [β₂-SiW₁₁O₃₉]^8– → [γ-SiW₁₀O₃₆]^8– can be formally separated into three distinct steps: (1) removal of the formal fragment [W₂O₅]²⁺ from the monolacunary species,⁵¹ (2) β to γ isomerization of the trilacunary {SiW₉} species, and (3) formal addition of the [WO₂]²⁺ unit to [γ-SiW₉O₃₄]^10– to give the final anion [γ-SiW₁₀O₃₆]^8– (Scheme 1). As we have already shown in previous studies,^21,22,52 the coordination number of metal ions in mononuclear and binuclear tungstates and molybdates is highly variable, with many isomers coexisting in solution. In fact, a unit such as [WO₂]²⁺ cannot exist as-is in aqueous solution, and coordination of W is completed via bonding to water and/or hydroxyl groups depending on the pH of the solution. The complete characterization of these species in solution is underway but is outside the present scope of this work. Here, we have focused primarily on identifying and analyzing the energy barrier of the isomerization between the two hypothesized {SiW₉} intermediates.

Once the possible isomerization path for the proposed {SiW₉} intermediate was analyzed, we realized that it was also necessary to obtain a better understanding of the interplay between the associated cations and the anionic clusters. The role of the countercation is often neglected when performing mechanistic studies, especially when heavy atoms are involved and, in this case, the interaction of the cations with the main silicotungstate anions is shown to be of significant importance.

Indeed, early work on these clusters has shown how the precise nature of the cation cannot be overlooked, and that, for instance, in the presence of monovalent cations smaller than K⁺, {γ-SiW₁₀} will spontaneously revert to a mixture of {β-SiW₁₁} clusters in solution.⁵² We therefore chose to first study the behavior of the key K₁₀[β-SiW₉O₃₄] and K₁₀[γ-SiW₉O₃₄] systems in explicit water in order to evaluate the potential effect of the counterions in the structural and electronic properties of the highly charged trilacunary species. Idealized structures for [β-SiW₉O₃₄]^10– and [γ-SiW₉O₃₄]^10– were optimized using the BP86 functional (+Grimme correction) and a Slater TZP basis set. In these calculations, the stabilizing effects of the solvent and counterions were considered with the COSMO approach (see Figure S6 and Table S2 for the most characteristic structural and electronic parameters). Then, the distribution of countercations around each of the anions was analyzed using classical MD simulations in a water box with dimensions of 20 × 20 × 20 ų and containing 247 water molecules. Figure 3 plots the 10 K⁺···Si distances between the K⁺ ions and the Si atom of the trilacunary {SiW₉} anions for 0.5 ns long trajectories. The Si atom can be generalized as occupying the notional center of the polyoxometalate so that the plot provides an idea of the motion of the counterions around the POM. In the two anions, it is interesting to remark that once one of the free K⁺ cations reaches the lacuna, it becomes trapped by the electrostatic attraction of the anion, displaying a rather restricted mobility, at least at room temperature. The reader can observe in Figure S7 that once the attractive forces of the lacuna capture the cation, it hardly abandons the area, and if another cation arrives to the region, the previous one quickly moves away from the basin. This agrees well with what we might expect given the observations of previous studies and may help to explain why the size of the cation plays an important role in stabilizing both the products and, presumably, based on the results presented here, the key intermediate species involved in the transformation of lacunary clusters such as these.

Figure 3.

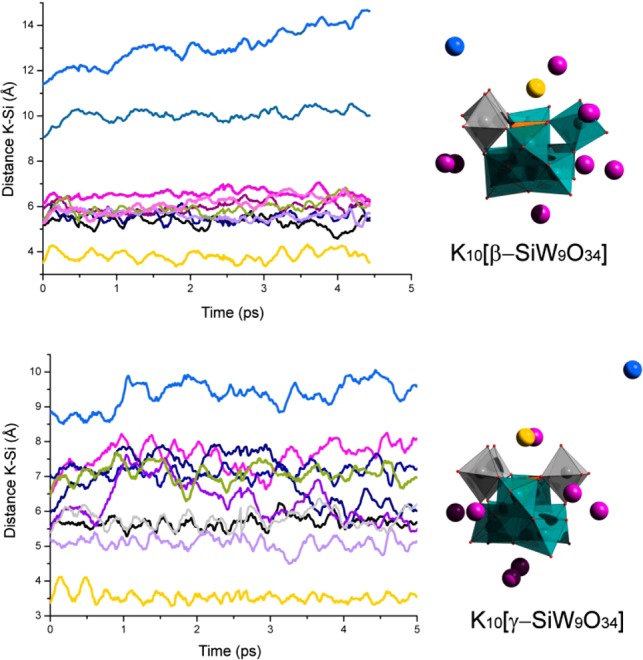
Left: K–Si distances for the 10 K⁺ ions for the trivacant K₁₀[β-SiW₉O₃₄] (top) and K₁₀[γ-SiW₉O₃₄] (bottom) systems along 5 ps of Car–Parrinello MD trajectories. Right: Polyhedral representation of a snapshot at t = 2.5 ps for both K₁₀[β-SiW₉O₃₄] and K₁₀[γ-SiW₉O₃₄]. Color code: W = teal, Si = orange, O = red. Gray polyhedra are used to differentiate W centers belonging to rotated {W₃} triads. Colored spheres are used for the 10 K⁺ ions: yellow, d_K–Si = ∼4 Å; purple, d_K–Si = ∼5–7 Å; blue, d_K–Si > 8 Å.

In order to obtain a deeper understanding of the dynamic processes surrounding the lacunary species as might occur in solution, Car–Parrinello MD simulations were also performed. Interestingly, though we are analyzing a rather short time frame in comparison to the classical MD simulations, we observe a similar distribution of K⁺ cations around the POM. Due to the quite high q/M ratio for {SiW₉} compared to that for other POMs,⁵³ we also explored if the POM could capture a proton from solvent in order to compensate the high negative charge on the anion. Despite the short time-scale simulation of the present calculations (5 ps), we were able to successfully observe hydrolysis of water in the case of the β-isomer. For the larger and less charged {β₂-SiW₁₁} parent anion, hydrolysis of the solvent was not observed even in somewhat larger simulations (see Supporting Information). The Car–Parrinello simulations also show that (i) the W atoms near the lacuna are more flexible; and (ii) the lacuna O atoms are more effectively solvated than the rest of the oxygens in the POM. The reader can find a deeper analysis of these results in the Supporting Information (Figure S9 and S10). Similar results are found for the mono- {β₂-SiW₁₁} and dilacunary {β-SiW₁₀} systems, which will be analyzed in detail elsewhere. In Figure S11, we have summarized the motion of the K⁺ closer to the lacuna site for both K₁₀[β-SiW₉O₃₄] and K₁₀[γ-SiW₉O₃₄].

With the knowledge obtained about the anions in solution, we subsequently attempted to directly analyze the isomerization of the {SiW₉} intermediates. Given that the anions are synthesized in basic media, our initial assumption was that the isomerization could be activated by the coordination of an OH^– ion to the polyoxometalate framework. However, after an extensive exploration of the potential energy surface at the DFT level (BP86/TZP) in implicit solvent (COSMO), we were unable to characterize a transition state corresponding to the β to γ transformation. Since our previous characterization demonstrates that the K⁺ remains firmly in the vicinity of the lacuna, we subsequently checked the potential influence of the presence of the cation under the same simulation conditions; however, we again failed to locate a transition state for the isomerization process. We therefore decided to explore the transformation without the presence of the hydroxyl group and with the incorporation of K⁺ in the lacuna. In this case, we were able to locate a stationary point that could be characterized as a transition state linking the β- and γ-isomers of the [SiW₉O₃₄]^10– anion. As shown in Figure 4, the two isomers are found to have similar energies (ΔE = 1.8 kcal mol^–1) and are connected by a remarkably low-energy barrier of 3.5 kcal·mol^–1. This result clearly indicates that these two open species are indeed present in solution and that it should be possible to effect a rapid transformation between them, strongly validating our initial hypothesis from the time-resolved ESI-MS data that a {SiW₉} intermediate may play a crucial role during the formation of {γ-SiW₁₀}. Car–Parrinello metadynamics simulations were also conducted to further characterize the free-energy barrier of the β to γ isomerization process in explicit solvent (water). The W–O distance that is being broken in the β-isomer (between W1 and W2 in Figure S3) and the W–O distance that is being formed in the γ-isomer (between W2 and W3 in Figure S3) were chosen as the variables to describe the reaction path (collective variables, CVs). A rather long trajectory (90 ps) and conservative parameters were used (for more details about the settings of the metadynamics, see the computational details). In this instance, the free-energy barrier for the isomerization is estimated to be ∼14 kcal mol^–1 (Figure 5), a value that is greater than the value predicted using the standard static methodology (i.e., the difference between the TS and reactants, 3.6 kcal mol^–1), including implicit solvent effects. The difference might be attributed to a combined effect of two factors, the somewhat different computational method and the influence that explicit solvent might exert in the transformation.

Figure 4.

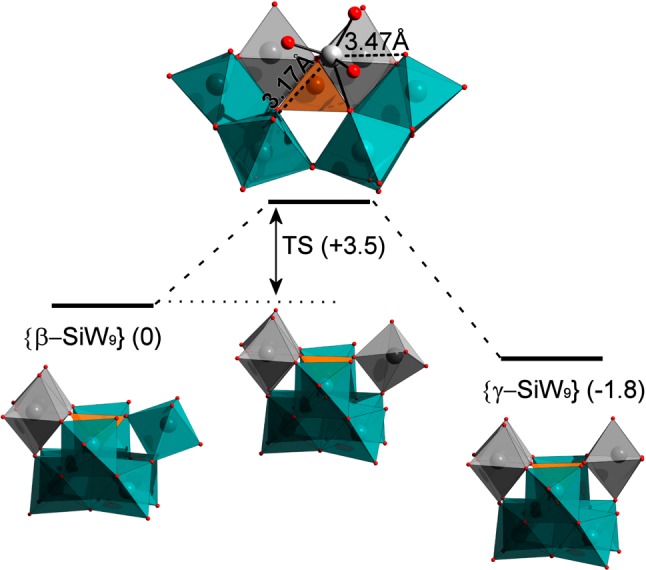
Schematic energy profile (in kcal·mol^–1) for the {β-SiW₉} to {γ-SiW₉} transformation, showing two perspectives of the transition state (TS) structure. Color code: W = teal, Si = orange, O = red. Gray polyhedra are used to differentiate W centers belonging to rotated {W₃} triads.

Figure 5.

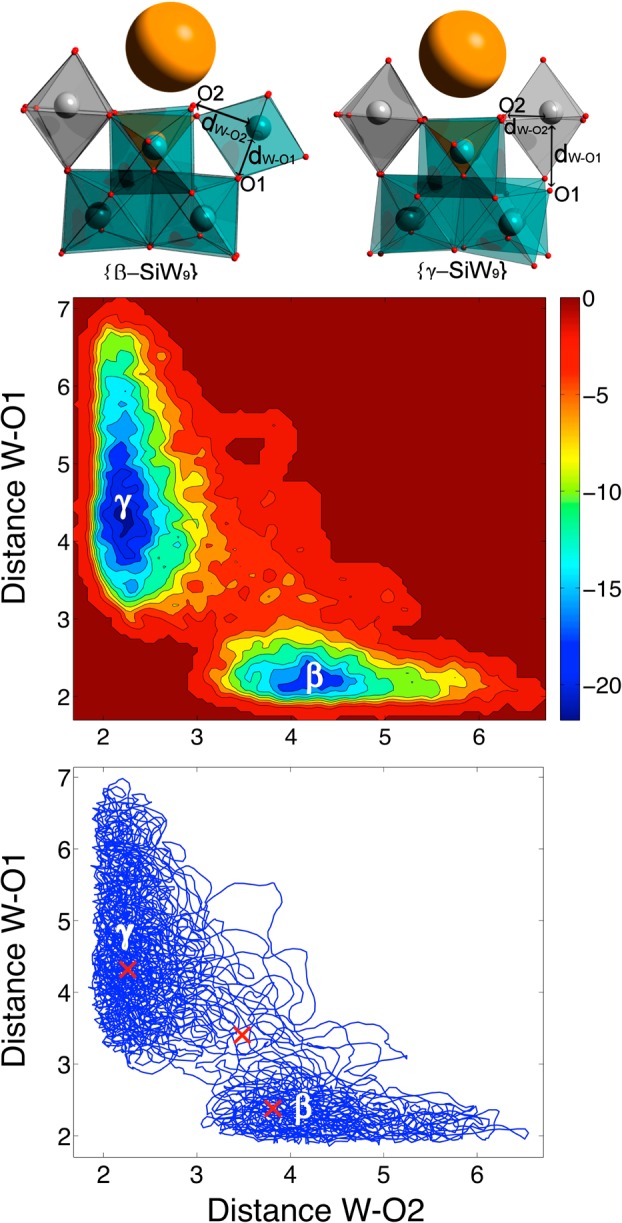
Top: Structures for the {β-SiW₉} starting and {γ-SiW₉} end points of the metadynamics calculation, with the structures showing the distances W–O1 and W–O2 corresponding to the collective variables. Middle: Free-energy surface obtained from Car–Parrinello metadynamics for the [β-SiW₉O₃₄]^10– to [γ-SiW₉O₃₄]^10– transformation as a function of the two selected CVs. Bottom: Detail of the trajectory of the two CVs during the metadynamics; the red crosses represent the position of the minima and transition structure at 0 K in the CV space. Energies are in kcal·mol^–1 and distances in Å. Color code: W = teal, Si = orange, O = red, K= yellow. Gray polyhedra are used to differentiate W centers belonging to rotated {W₃} triads.

Indeed, the O atoms involved in the isomerization (O1 and O2; see Figure 5) are efficiently solvated by nearby water molecules, thus enhancing somewhat the barrier for the transformation. In any case, the predicted barrier remains remarkably small and therefore easily surmountable at ambient temperature. Since the metadynamics was stopped when the system was back to reactants, the reconstructed free-energy surface (Figure 5, middle) allows us to estimate the free-energy difference between the β- and the {γ-SiW₉} isomer, which is 4 kcal mol^–1 (γ lower than β). This result indicates that the effect of the explicit solvent in the relative free energies between isomers is not as important as that for the isomerization barrier. The free-energy surface and the trajectory followed by the two CVs during the metadynamics simulations show that initially, while in the basin of the {β-SiW₉} isomer, the W–O1 bond (the bond to be broken) oscilates between 2 and 2.5 Å; meanwhile, the W···O2 distance (the bond to be formed) oscillates between 3.0 and 6.5 Å. At a given point, the W–O1 bond distance increases significantly until arriving to a value near 3.5 Å, and then the new tungsten–oxygen bond (W–O2) begins to form as the trajectory proceeds toward the basin of the {γ-SiW₉} isomer. This asynchronous representation slightly differs with the more synchronous picture suggested by the structure of the TS obtained from the static DFT calculations (represented as a red cross in Figure 5). The relative flatness of the energy surface around the points near the TS structure makes the paths followed at 300 K more asynchronous than at 0 K. These detailed calculations thus strongly support our initial, experimentally led hypothesis and suggest that a three-step mechanism involving the loss and subsequent gain of tungstate fragments, occurring either side of a remarkably low-energy isomerization event, which occurs explicitly on a previously unforeseen {SiW₉} intermediate species, is responsible for the formation of the {γ-SiW₁₀} anion.

Conclusions

In conclusion, we have demonstrated the use of time-resolved ESI-MS measurements as a means to help unravel the assembly of the ubiquitous polyoxometalate precursor species, [γ-SiW₁₀O₃₆]^8–, at a level of detail unobtainable by other analytical techniques. This study has thus allowed us to shed light on the fundamental processes by which POM clusters speciate, isomerize, and reassemble. Furthermore, the careful application of ESI-MS has allowed us to clearly define a complex computational problem based on the most likely hypothesis derived from our experiment: that a hitherto unconsidered [SiW₉O₃₄]^10– anion was acting as a “hidden” intermediate in the synthesis of {γ-SiW₁₀} from the parent [β₂-SiW₁₁O₃₉]^8– anion. Computational studies are used to model the four key intermediate species in a {SiW₉}-derived mechanism and, crucially, identify a remarkably low-energy transition state corresponding to the key isomerism step. Furthermore, in the course of identifying this transition state, we have also performed a comprehensive evaluation of the counterion distribution in lacunary POM species for the first time.

Though this study has clear significance from a purely fundamental standpoint, the somewhat unexpected conclusions we are able to draw from our results can also be shown to be more widely applicable to POM chemistry as a whole. While it has long been accepted that silicotungstate species (and heteropolyoxometalate clusters more generally) are capable of undergoing a remarkable (and often facile) array of speciation, isomerization, and reassembly events in solution—processes which have been the fundamental driving force behind a significant body of the research published in this area over the past few decades—the underlying mechanisms by which these processes occur are still somewhat overlooked. In that regard, while the work we report here is presently limited to a single well-known transformation, the counterintuitive nature of the mechanism we propose herein (occurring via several steps of disassembly and reassembly) does not appear to be inherently unique to this reaction and, in fact, may also help to explain a plethora of previously published results. Considering the attention that the {γ-SiW₁₀} anion receives is largely as a precursor to new cluster species, due to its ability to readily reorganize into a series of different lacuna, it is especially interesting to note that among the most common products of such rearrangements are {β-SiW₉}, {β-SiW₁₀}, and {β-SiW₁₁} fragments. All of these clusters may feasibly be accessed due to the principle of microscopic reversibility and the remarkably low barrier to the β/γ isomerization of the key {SiW₉} intermediate identified above.

This “rotational” pathway to the isolation of new isomeric fragments derived from the {γ-SiW₁₀} precursor, which explicitly occurs through a nonatungstate intermediate cluster, can be contrasted against some recently reported results which hint at contrasting, possibly transition-metal-driven, “speciation and reassembly” pathways.^19,31 These, in turn, may be progressing primarily through lower nuclearity octatungstate or hexatungstate intermediates. This only further serves to highlight the quite remarkable structural chemistry associated with just one small subsection of the wider class of POM materials as a whole. We therefore hope that these results can form the basis of a new predictive approach to the selection of reactive intermediates capable of forming nanoscale clusters which can be both predicted from this work and whose assembly can be followed by mass spectrometry.

Experimental Section

Materials

K₈[β₂-SiW₁₁O₃₉]·12H₂O was synthesized according to the previously reported literature procedure.⁵⁴ K₈[γ-SiW₁₀O₃₆]·12H₂O was synthesized according to the previously reported literature procedure,⁴⁶ though on a one-quarter scale (see Supporting Information for full details).

ESI-MS Analysis

All ESI-MS measurements were conducted on a Waters Synapt G2 HDMS spectrometer operating in sensitivity mode, equipped with a quadrupole time-of-flight (Q/ToF) module for MS analysis. All samples were prepared as described in the following and injected directly at a flow rate of 5 μL using a Harvard syringe pump. All spectra were collected in negative mode and analyzed using the MassLynx v4.1 software suite provided by Waters. Detailed instrument parameters are provided in the accompanying Supporting Information. Time-resolved electrospray measurements were conducted on 20 μL aliquots of the stirred reaction solution, taken at predetermined time intervals, and immediately diluted in an additional 1 mL of H₂O before subsequent filtration using 200 μm syringe filters to ensure removal of any precipitated material, if necessary, prior to injection into the spectrometer. Each sample was measured within no more than 15 min of their initial collection; however, control experiments performed on aged solutions showed minor changes in the peak composition, indicating that minimal sample evolution should occur over a realistic time frame corresponding to the measurement. Note that while neat reaction solutions are generally incompatible with ESI-MS analysis, the trends which hold true under diluted conditions appear to conform to what we might expect of the concentrated reaction (starting material consumption, product formation, and identification of possible intermediates) and so are treated as representative herein. This is also in excellent agreement with measurements performed by us in a related previous work.¹⁹

Computational Analysis

The static calculations were carried out using DFT methodology with the ADF program.⁵⁵ The gradient-corrected functionals of Becke and Perdew for the exchange and correlation energies, respectively, were used to improve the description of the electronic density provided by the local density approximation (X-alpha functional for the exchange part and Vosko–Wilk–Nusair functional for the correlation part).⁵⁶ A set of Slater-type basis functions of triple-ζ + polarization quality was employed to describe the valence electrons of all the atoms. Scalar relativistic corrections were included by means of the zeroth-order regular approximation formalism. All computed stationary points have a closed-shell electronic structure. All the structures discussed through this work were fully optimized in the presence of a continuous model solvent by means of the conductor-like screening model (COSMO) implemented in the ADF code.⁵⁷ The dielectric constant (ε) was set to 78 to model water as a solvent.

The classical MD simulations were performed by means of the DL_POLY program package. DL_POLY is a package of subroutines, programs, and data files designed to facilitate MD simulations of macromolecules, polymers, ionic systems, solutions, and other molecular systems.⁵⁸ The Car–Parrinello MD simulations were performed at the DFT level by means of the CPMD program package.⁵⁹ The description of the electronic structure is based on the expansion of the valence electronic wave functions into a plane wave basis set, which is limited by an energy cutoff of 70 Ry. The interaction between the valence electrons and the ionic cores is treated through the pseudopotential (PP) approximation. Norm-conserving Martins–Troullier PPs are employed, and nonlinear core corrections are included in the W PP.⁶⁰ We adopted the generalized gradient-corrected Becke–Lee–Yang–Parr (BLYP) exchange-correlation functional.⁶¹ The validity of these computational settings for the study of isopolyanions has been checked previously.⁵² In the Car–Parrinello MD simulations, the wave functions are propagated by integrating the equations of motion derived from the extended Car–Parrinello Lagrangian.⁶² We use a time step of 0.144 fs and a fictitious electronic mass of 700 au. The Nosé–Hoover thermostat for the nuclear degrees of freedom was used to maintain the temperature constant around 300 K.⁶⁴ The cell boxes for all dynamics contain the POM, the 10 K⁺ cations, and 247 H₂O molecules for classical and Car–Parrinello simulations. The size of the boxes are a = b = c = 20 Å and are repeated periodically in space by the standard periodic boundary conditions. The limited simulation time afforded by standard Car–Parrinello MD runs does not allow the observation of rare events like thermally activated chemical reactions. For this reason, we use the metadynamics technique, which is capable of efficiently reconstructing complex reaction mechanisms and provides the free-energy profile, as demonstrated in previous applications.^21,52,63 Two collective variables were considered, the W–O1 and W–O2 distances shown in Figure 5. For metadynamics, the cell boxes (a = b = c = 15 Å) contain the POM, one K⁺ cation, 91 H₂O molecules, and one OH^– anion to simulate the basic medium of the system. The parameters used in the extended Lagrangian scheme for these metadynamics were as follows: k₁ = k₂ = 1 au, M₁ = M₂ = 10 amu. The height of the hills was 0.63 kcal mol^–1; their perpendicular width was 0.1 au, and the deposition rate was 0.0144 ps. The metadynamics simulations were stopped once the system was back to reactants so that we could estimate the relative free energies between the two isomers (total time = 90 fs).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b02245.

• Additional experimental details, figures, and tables (PDF)

The authors declare no competing financial interest.