Skip to main content
PMC home page
Health Services Research logoLink to Health Services Research
. 2016 Feb 3;51(5):1960–1980. doi: 10.1111/1475-6773.12452

The Comparison of Matching Methods Using Different Measures of Balance: Benefits and Risks Exemplified within a Study to Evaluate the Effects of German Disease Management Programs on Long‐Term Outcomes of Patients with Type 2 Diabetes

Birgit Fullerton 1,✉, Boris Pöhlmann 2, Robert Krohn 2, John L Adams 3, Ferdinand M Gerlach 1, Antje Erler 1
PMCID: PMC5034215  PMID: 26841379

Abstract

Objective

To present a case study on how to compare various matching methods applying different measures of balance and to point out some pitfalls involved in relying on such measures.

Data Sources

Administrative claims data from a German statutory health insurance fund covering the years 2004–2008.

Study Design

We applied three different covariance balance diagnostics to a choice of 12 different matching methods used to evaluate the effectiveness of the German disease management program for type 2 diabetes (DMPDM2). We further compared the effect estimates resulting from applying these different matching techniques in the evaluation of the DMPDM2.

Principal Findings

The choice of balance measure leads to different results on the performance of the applied matching methods. Exact matching methods performed well across all measures of balance, but resulted in the exclusion of many observations, leading to a change of the baseline characteristics of the study sample and also the effect estimate of the DMPDM2. All PS‐based methods showed similar effect estimates. Applying a higher matching ratio and using a larger variable set generally resulted in better balance. Using a generalized boosted instead of a logistic regression model showed slightly better performance for balance diagnostics taking into account imbalances at higher moments.

Conclusion

Best practice should include the application of several matching methods and thorough balance diagnostics. Applying matching techniques can provide a useful preprocessing step to reveal areas of the data that lack common support. The use of different balance diagnostics can be helpful for the interpretation of different effect estimates found with different matching methods.

Keywords: Disease management, matching, propensity scores, measures of balance, chronic care, diabetes

Disease management programs (DMPs) as well as other health care delivery interventions were often introduced without prior testing in randomized controlled trials (RCTs) (Siering 2008; Nolte et al. 2012). Therefore, program evaluation has to rely on observational data. Due to the uncontrolled nature of treatment assignment, observational studies face various threats to validity when trying to determine the causal link between the treatment and the outcome. There are various observational methods (e.g., matching, instrumental variables, differences‐in‐differences, or regression discontinuity analyses) available to address different threats to validity, but all these methods rely on certain, not testable, assumptions about the nature of the data at hand. Especially matching methods have become increasingly popular in health services research (Ali et al. 2015). The key assumption of these methods is that treatment assignment is ignorable given the measured pretreatment variables (Rosenbaum and Rubin 1983).

In Germany, population‐wide DMPs have been introduced in 2003, where participation is voluntary. The largest program is the DMP for type 2 diabetes (DMPDM2) with about 3.6 million patients enrolled (Bundesversicherungsamt 2012). Recently, several studies have been published regarding the effectiveness of this program (Miksch et al. 2010; Stock et al. 2010; Windt and Glaeske 2010; Linder et al. 2011; Drabik et al. 2012). All studies have applied matching techniques, either using direct covariate (Miksch et al. 2010) or propensity score matching (PSM) (Stock et al. 2010; Windt and Glaeske 2010; Linder et al. 2011; Drabik et al. 2012) with some authors suggesting that using PSM is superior to previous approaches (Linder et al. 2011; Drabik et al. 2012). PSM was always used with a 1:1 matching ratio, a logistic regression model to estimate the PS and covariate balance checks using standardized mean differences. As has been shown in the literature, PSM is not necessarily the gold standard. Other matching approaches can, depending on the circumstances, achieve better balance, and furthermore, the performance of PSM can highly depend on the exact specification of the PS model, the matching algorithm used, and the choice of covariates (Rosenbaum and Rubin 1984; Dehejia and Wahba 2002; Harder, Stuart, and Anthony 2010; King et al. 2011). While there are several simulation studies that compare the performance of different matching methods, it cannot be taken for granted that their results are transferrable to another data situation (Franklin et al. 2014). Furthermore, the abundance of methods and their variations is too large to be all compared in one study. Therefore, it is advisable to check how sensitive the results of an analysis are to the choice of matching method (Oakes and Johnson 2006). Such sensitivity analyses are rarely carried out. Furthermore, while recent studies usually provide checks of covariate balance of the matched groups, it is usually done by reporting p‐values (Ali et al. 2015), which is problematic as a measure of balance because it is dependent on sample size.

The aim of this article was to provide guidance on how to carefully evaluate the choice of matching method in an observational study using the example of the German DMPDM2. We demonstrate how to compare various matching methods applying different measures of covariate balance and point out some pitfalls involved in relying on such measures. We further demonstrate how a careful investigation of the matched samples can provide insight regarding different effect estimates seen with different matching methods.

Methods

Data

We used anonymized routine data from a large statutory health insurance (SHI) fund (Techniker Krankenkasse) from three regions in Germany (North Rhine, Hesse, and North Wurttemberg) covering the years 2004–2008. These contain sociodemographic information of SHI members (e.g., age, gender, insurance status, region), alongside administrative data collected from different health care providers, other social insurance agencies and employers (e.g., diagnoses [ICD‐10 codes], medication [ATC codes], procedures, and costs). We further processed the diagnoses to obtain diagnostic groups (DXGs), where each DXG combines several ICD codes (Bundesversicherungsamt 2008).

Study Population

The study population (N = 44,005) consisted of type 2 diabetic patients who were 18 years or older in 2004 and either joined the DMPDM2 in 2005 (intervention group) or were not enrolled in the DMPDM2 for any period of time through 2008 (control group). Patients who died in 2005 were excluded. Outcomes were assessed from 2006 through 2008. Patients were identified as having type 2 diabetes based on ambulatory care, hospital, and/or prescription data (see Appendix S5).

Matching Techniques

Overall, we applied 12 different techniques. We first chose the two matching methods that had been applied in previous studies on German DMPs (1:1 PSM and direct covariate matching) and then added variations of these techniques. For PSM, we varied (1) the matching variable set (sel var and all var), (2) the regression model used for the estimation of the PS (general boosted regression [GBR] or logistic regression [LogR]), and (3) the matching ratio (1:1 or 1:3), resulting in eight different PSM variations:

  1. PSM LogR sel var 1:1

  2. PSM LogR sel var 1:3

  3. PSM LogR all var 1:1

  4. PSM LogR all var 1:3

  5. PSM GBR sel var 1:1

  6. PSM GBR sel var 1:3

  7. PSM GBR all var 1:1

  8. PSM GBR all var 1:3.

  1. The two variable sets were defined as
    1. Sel var: This variable set was created with the aim of applying an automatic variable selection procedure independent of a priori knowledge about relevant covariates. Using backward selection (with a p‐value >.1) in a logistic regression with DMPDM2 participation as the response variable, the variable set was chosen from all diagnosis (as DXGs) and prescription data (as two‐digit ATC codes) alongside age, gender, and region, resulting in 87 variables.
    2. All var: The second variable set consists of all variables included in “sel var” plus an additional 37 variables chosen based on what we considered potential confounders from the literature. These variables include more specifically coded diabetes‐related diagnoses and additional variables such as number of HbA1c measurements per year, annual ophthalmological exam by an eye specialist, as well as different utilization and cost measures. Overall, this dataset consisted of 4 categorical, 14 continuous, and 106 binary variables (see Appendix S2).

  2. In addition to the commonly used logistic regression, we also applied GBR, a multivariate nonparametric regression technique. It has the advantage that it can flexibly include nonlinear relationships between the PS and a large number of covariates (McCaffrey, Ridgeway, and Morral 2004). For the logistic PS models, all interactions or higher order terms would have to be explicitly specified as functional terms, which is rarely done for a large number of covariates. We therefore also only applied the (on the log odds scale) linear additive logistic model.

  3. To make better use of the large number of control patients, we used a matching ratio of 1:3 in addition to the previously used 1:1 matching.

PS were estimated in R (version 2.11.1) using the MatchIt (Ho et al. 2007a,b) and the TWANG (Ridgeway et al. 2013) packages for applying the LogR and GBR models, respectively. All PSM procedures were performed using the nearest neighbor matching algorithm of the MatchIt package in R. We chose nearest neighbor matching as it is widely used and produces similarly well balanced samples as optimized matching (Gu and Rosenbaum 1993). Subjects were matched on the logit of the PS using a caliper of 0.2 (Rosenbaum and Rubin 1985; Austin 2011).

The remaining four techniques did not use a summary distance measure, but matched on the covariates directly:

  • ELSID matching

  • Modified ELSID matching

  • Exact matching

  • Coarsened exact matching (CEM)

The method, referred to here as “ELSID matching,” was used in the ELSID (“Evaluation of a Large Scale Implementation of DMPs for patients with type 2 diabetes”) study (Miksch et al. 2010; Riens et al. 2010) and uses coarsened continuous and categorical variables to match one control group member to each DMPDM2 participant. Variables are divided into mandatory and optional: all mandatory variables must coincide between matching partners, while optional variables only have an effect on which of several potential matching partners is preferred but do not result in the exclusion of patients if they cannot be matched. The ELSID matching attempts to capture morbidity according to a slight modification of a model used in the Dutch risk adjustment scheme (Lamers 1998, 1999). It groups inpatient diagnoses into diagnostic cost groups (DCGs) and outpatient prescription information into pharmacy costs groups (PCGs). Mandatory matching variables of the ELSID matching are region, age group (5‐year bins), gender, most expensive PCG, number of PCGs, and number of DCGs. Optional variables are number of sick days (0, 1–5, 6–10, 11–15, 16–30, 31–60, 61–90, 91+), insurance status (full member, family member, retired), and domiciliary care allowance level (this variable was missing in our dataset and could not be used here).

In a modified version of the ELSID matching, we changed the variables to be matched to the 10 most important factors identified by the GBR model used for the PS methods on the full variable set (all var). These variables, all used as mandatory matching criteria, were as follows: diabetes medication (none, oral, insulin, oral and insulin), age group (5‐year bins), region, number of quarters with at least one HbA1C measurement, overall costs, number of outpatient consultations, diabetes diagnosis without complications, prescription costs, number of sick days, costs for home health care, therapeutic aids, and appliances. Continuous variables were binned into a maximum of four bins, based on distribution quartiles. The ELSID and modified ELSID matching were carried out in a Java‐based database.

Finally, we added two further direct matching methods: first, in “exact matching” (implemented using the MatchIt package in R) each DMPDM2 patient was matched to all control units with exactly the same values on all covariates (variable set “all var”); second, we applied CEM, which was implemented using the CEM package in R (Iacus, King, and Porro 2012). In CEM, the number of matching dimensions is reduced by creating intervals for continuous variables and possibly redefining categorical variables. We only coarsened the 14 continuous variables, where the definition of the intervals was based on the quartiles of variable distributions in the raw data, except for age, where the intervals were defined as <41, 41–60, 61–80, >80 years.

Balance Measures

We measured balance between the DMPDM2 and control group using three different approaches. First, balance was measured using the mean and maximum mean standardized differences. The mean standardized difference for one covariate is calculated using the formula, (μ DMP − μ C)/σ DMP, whereby μ DMP and μ C are the covariate means in the DMPDM2 and control group, respectively, and σ DMP is the standard deviation in the DMPDM2 group (Stuart 2010). Second, we compared the distributions of each covariate in the two groups using the Kolmogorov–Smirnov (KS) statistic and used the mean and maximum KS values as summary measures of balance. In the third approach, we measured how well the two groups' multidimensional distributions of all variables were matched by using the multivariate balance measure, L1(f,g,H) = ½*∑l1…lk є H(X)|fl1…lk – gl1…lk|, which was developed by Iacus, King, and Porro (2011). H(X) = H(X1)…H(Xk) denotes the multidimensional histogram of all covariates X1 to Xk, whereby each covariate Xi can take on a distinct set of values H(Xi) determined by the coarsening bins chosen. f and g are the relative empirical frequency distributions for the DMPDM2 and control group, respectively, with fl1…k and gl1…k being the relative frequencies of the observations falling within the cells with coordinates l1…k and g1…k of the two k‐dimensional tables. L1 can take on values between 0 and 1. L1 = 0, if there was no overlap between the multivariate distributions of the DMPDM2 and control group; L1 = 1, if the two distributions were perfectly matched.

The cut‐points chosen to coarsen the variables were different from those used for CEM matching. As recommended by Iacus, King, and Porro (2011), we chose the set of bins that corresponded to the median L1 of 100 randomly drawn bin definitions applied to measure balance on the raw data.

Regression Analyses

Regression analyses on the effect of DMPDM2 participation on the outcomes mortality, macrovascular endpoint (myocardial infarction or stroke), and microvascular endpoint (lower limb amputation or renal failure requiring dialysis), during a 3‐year (2006–2008) follow‐up, were performed using Cox proportional hazard models. Regression analyses were carried out in SAS 9.2 (SAS Inc., Cary, NC, USA). For matched data, we employed Cox models stratified on the matched units. We compared the hazard ratio (HR) of a multiple regression model including the full covariate set (all var) calculated for the full study sample with the HRs of the analyses on the subsamples resulting from the different matching techniques.

Results

Figure 1 compares the matching methods using three different approaches to measure balance. As would be expected, all three balance measures showed perfect balance with exact matching. CEM showed the best balance with the mean standardized mean difference or the multivariate balance measure L1. Using standardized mean differences as a balance measure including all variables generally resulted in better balance than using the reduced variable set (Figure 1a). Also, matching three controls for each DMPDM2 patient instead of matching 1:1 was generally beneficial when using standardized mean differences. It has been suggested that all standardized differences should be lower than 0.1 (D'Agostino 1998), which was achieved by all PS methods including the full variable set as well as CEM and exact matching. While all methods led to an improvement of the mean and maximum standardized mean difference, it should be noted that balance was not improved on all variables: for all but exact matching, imbalance on some variables was increased (see Appendix S3).

Figure 1.

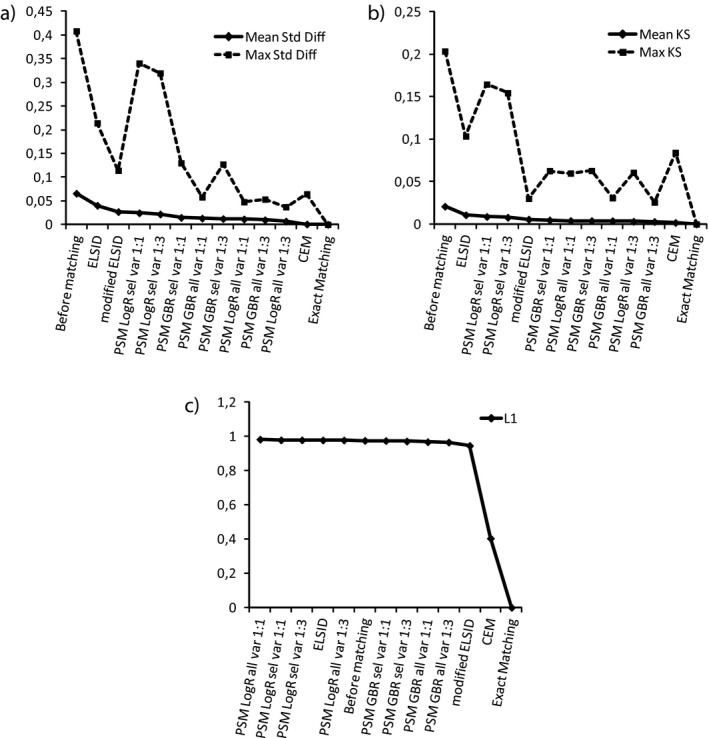
Figure 1

Open in a new tab

Balance Measures: (a) Mean and Maximum Standardized Mean Differences; (b) Mean and Maximum Kolmogorov–Smirnov (KS) Statistics; (c) The Multivariate Balance Measure, L1

Notes. (a) The measures for the different methods are presented in the order of decreasing mean standardized mean differences; a lower standardized mean difference implies better balance. (b) These are presented in the order of decreasing mean KS; a lower KS implies better balance. (c) A lower L1 implies better balance. A table corresponding to these plots can be found in Appendix S4.

The choice of regression model made a slight difference when using the KS statistic. If all other matching characteristics were held equal, using a GBR model resulted in slightly better balance based on KS balance measures (Figure 1b). Figure 2a shows that, for example, the variable “Age” was differently distributed in the treatment and control group before matching: the DMPDM2 group consisted of relatively less young, but also less very old patients compared to the control group. Figure 2b–e shows that GBR‐based matching methods managed to substantially reduce this difference in the age distribution, while LogR‐based methods only changed the shape of the QQ plot slightly. The figure shows results for the matching methods using the full variable set, but the same difference can be seen with the reduced set.

Figure 2.

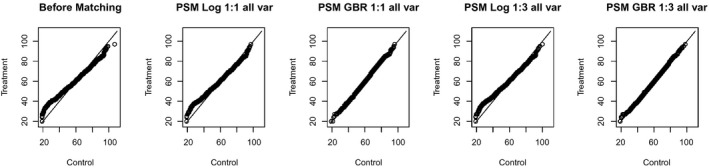
Figure 2

Open in a new tab

QQ Plots for the Variable Age before Matching and after Applying Different PSM Techniques Using the Full Variable Set. (The solid line indicates the diagonal; the variable age would be distributed equally before and after matching if all points were located on the diagonal)

When using the multivariate balance measure L1, we even observed a decrease in balance for all LogR‐based PS methods as well as the ELSID matching (Figure 1c). For GBR‐based PS methods, L1 was only marginally improved. The modified ELSID matching performed slightly better, possibly because 6 of the 10 matching variables were continuous variables, which were coarsened and then directly matched on. Only CEM (apart from exact matching of course) achieved a substantial improvement in multivariate balance.

Overall, relying only on these balance measures, exact matching, followed by CEM, would be the methods of choice as they performed well across all measures of balance.

However, using these methods excludes many observations. Usually, evaluation studies aim to estimate the average treatment effect on the treated (ATT) (Linden and Adams 2010). If matching causes a large number of patients to be excluded from the treatment group, there is the risk that the effect estimate might not be representative of this population anymore. Table 1 shows the number of patients remaining in the study sample after applying the different matching methods. When we tried to exactly match DMPDM2 and control patients using all of our covariates, the vast majority of patients had to be excluded, reducing our total sample size from 44,005 to 274 and the DMPDM2 group from 6,663 to 101. Defining intervals for continuous variables instead of trying to match exact values, as done in CEM, excluded about 95 percent of the DMPDM2 group and 97 percent of the total sample. Modified ELSID matching (basically a type of CEM using only 10 covariates) resulted in 7,376 patients in the total sample, and the original matching method used in the ELSID study led to a sample size of 12,744. This method achieves more matches by only including a few required matching variables while defining other variables as optional. In general, it is easier to maintain the intervention group by applying a PS‐based method. All of the PS‐based methods we applied kept more than 98 percent of the patients in the DMPDM2 group.

Table 1.

Number of Matched Patients

Method DMPDM2 Control Total
Before matching 6,663 37,342 44,005
ELSID matching 6,372 6,372 12,744
Modified ELSID matching 3,688 3,688 7,376
Exact matching 103 171 274
CEM 313 975 1,288
PSM LogR sel var 1:1 6,663 6,663 13,326
PSM LogR all var 1:1 6,663 6,663 13,326
PSM LogR sel var 1:3 6,662 19,037 25,699
PSM LogR all var 1:3 6,663 18,131 24,794
PSM GBR sel var 1:1 6,583 6,583 13,166
PSM GBR all var 1:1 6,572 6,572 13,144
PSM GBR sel var 1:3 6,578 16,999 23,577
PSM GBR all var 1:3 6,568 16,320 22,888
Open in a new tab

To check how representative the reduced DMPDM2 group was, we looked at a subset of the baseline variables for the DMPDM2 group before and after matching. Table 2 shows these baseline variables for those matching methods that resulted in the exclusion of more than 1 percent of the DMPDM2 group: ELSID matching, modified ELSID matching, CEM, and exact matching. For ELSID matching, the loss of DMPDM2 patients was only 4.4 percent and the baseline characteristics of the group remained similar to the original group with a slight trend toward lower utilization of the medical system. However, for the other three methods, pruning patients from the DMPDM2 group resulted in a clear change of baseline characteristics. Interestingly, different methods changed the DMPDM2 group in different directions. While modified ELSID matching resulted in a sample including a higher percentage of old and retired, but generally healthier patients, CEM and exact matching showed a much higher percentage of young patients who were not yet retired. For these two matching methods, the sample was substantially healthier than the original DMPDM2 group—basically only patients could be matched who hardly utilized the medical system and therefore did not have any diagnoses or costs associated with them. Clearly, any effect resulting from the analysis of these groups would not be representative of the original population and probably not of much interest.

Table 2.

Baseline Characteristics of the DMPDM2 Group before and after Matching

Baseline Variable Before Matching (N = 6,663) ELSID (N = 6,372) Modified ELSID (N = 3,688) CEM (N = 313) Exact (N = 103)
Age (years), Mean (SD) 63.4 (10.1) 63.5 (10.0) 64.2 (9.5) 56.4 (9.9) 56.2 (8.7)
Gender (% female) 31.2 30.5 31.5 18.5 5.8
Region (%)
HE 28.5 28.5 27.7 20.4 17.5
NR 59.9 60.0 63.0 67.4 69.9
NW 11.7 11.5 9.3 12.7 12.6
Number of doctor visits, Mean (SD) 28.6 (21.4) 27.9 (20.9) 26.2 (22.8) 2.6 (4.5) 0.1 (0.4)
At least one hospital admission (%) 23.3 22.0 18.0 0.0 0.0
Costs (Euros), Mean (SD) 2,335 (4,636) 2,191 (4,469) 2,092 (4,669) 51 (438) 0 (0)
Diabetes medication (%)
None 46.0 46.9 58.0 95.8 100.0
Oral 37.2 36.9 29.9 4.2 0.0
Insulin 8.6 8.6 7.8 0.0 0.0
Oral + Insulin 8.2 7.6 4.3 0.0 0.0
Neuropathy (%) 9.5 9.4 7.5 0.0 0.0
Retinopathy (%) 22.9 22.6 19.7 1.0 0.0
Cardiovascular complications (%) 23.3 23.2 22.9 0.6 0.0
Cerebrovascular complications (%) 10.0 10.0 10.0 0.0 0.0
Kidney disease (%) 5.4 5.2 4.6 0.0 0.0
Adipositas (%) 26.7 26.1 23.9 3.2 0.0
Hypertension (%) 66.7 66.2 65.3 10.9 0.0
Cancer (%) 15.8 15.8 15.7 0.6 0.0
Asthma (%) 19.5 19.1 18.8 1.3 0.0
Depression (%) 12.5 11.9 11.0 0.0 0.0
Dementia (%) 1.2 1.2 1.2 0.0 0.0
Open in a new tab

Figure 3 compares the effect measures on the outcomes mortality, macrovascular endpoint, and microvascular endpoint, using different matching methods. Without any adjustment for confounding, the HR of nonparticipation over participation in the DMPDM2 was 1.79 (CI: 1.57–2.04) for mortality, 0.92 (CI: 0.82–1.02) for macrovascular endpoint, and 0.87 (CI: 0.71–1.08) for microvascular endpoint. Apart from CEM and exact matching, the choice of matching method did not have a large impact on the outcomes of the analyses. For mortality, all other methods show a significant effect (Figure 3a). For the PS‐based methods, the hazard ratio (HR) varies between 1.40 (PSM GBR 1:1 sel var) and 1.74 (PSM LogR 1:1 sel var). The ELSID and modified ELSID matching not only show slightly higher HRs but also have larger confidence intervals. The HR of all PS‐based methods show similar estimation errors, although using a 1:3 matching ratio always resulted in slightly narrower confidence intervals compared to the equivalent method with a 1:1 ratio. Using a multiple regression model including the full set of covariates shows comparable results to the PS analyses. With CEM or exact matching the HRs are close to one with very large confidence intervals due to the low number of observations. Overall, a similar pattern of results can be seen for the other two outcomes, macro‐ and microvascular endpoints (Figure 3b and c). Again, most matching methods led to similar HRs. Aside from a just significant effect for the macrovascular outcome with modified ELSID matching, none of the methods show a significant effect of DMP participation on micro‐ or macrovascular outcomes. For the microvascular endpoint, we do not show the HRs for CEM and exact matching, as, during the whole follow‐up period, only five and two microvascular incidents occurred within the respective matched samples.

Figure 3.

Figure 3

Open in a new tab

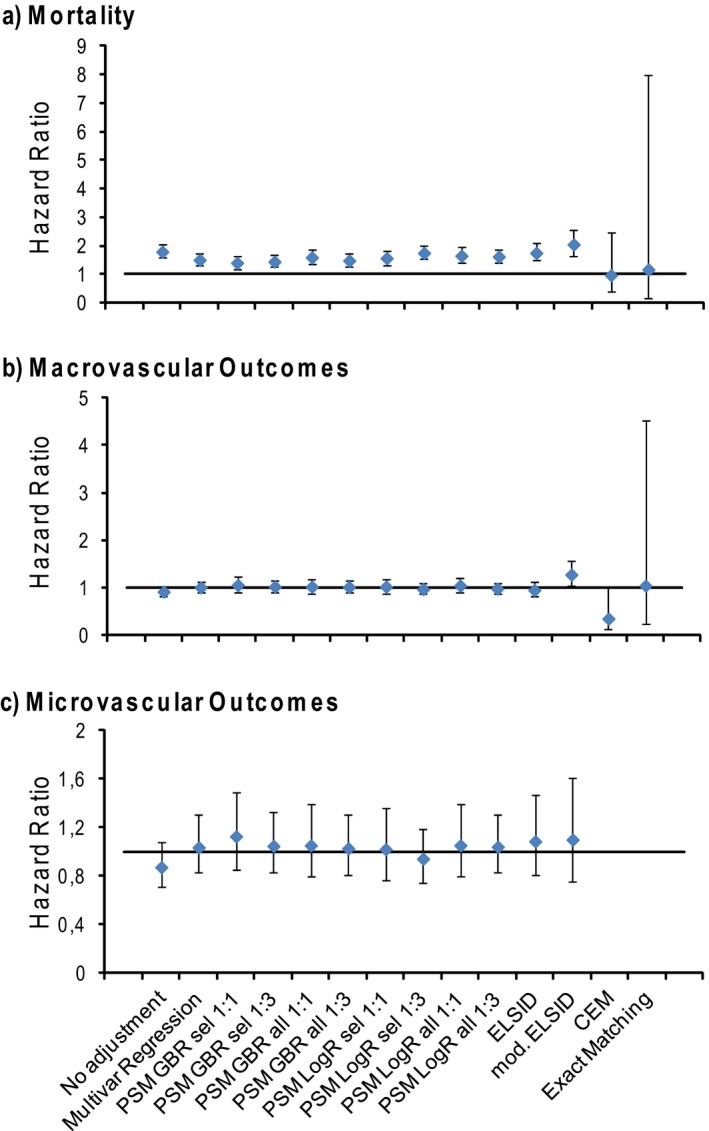
Outcome Analysis. The Hazard Ratios of Nonparticipation over Participation in the DMPDM2, for (a) the Outcomes Mortality, (b) Macrovascular Endpoint, and (c) Microvascular Endpoint after no Covariate Adjustment, Covariate Adjustment within a Multiple Regression Model, or after Applying Different Matching Techniques. (Error bars indicate 95 percent confidence intervals)

Discussion

All different PS methods applied in our study would lead to comparable conclusions regarding the effect of the German DMPDM2 on mortality, macrovascular, and microvascular complications. However, in a different setting, for example, if the effect size for mortality had been smaller, the variations between the estimated hazard ratios could have led to statistically significant effects with some methods but not others. Furthermore, we showed that the choice of the method could affect the different measures of balance. Compared to the ELSID matching, PS‐based methods generally achieved better balance, except for the multivariate balance measure L1, where PS methods using a logistic regression model were not superior to ELSID matching.

We further showed that from the perspective of balance, matching on covariates directly, either using exact values or coarsened variables, leads to the best results. However, especially with many covariates that have to be adjusted for, these methods lead to a substantial loss of observations. Here, using exact matching or CEM with all covariates, the only patients remaining had hardly used the medical system. They could be matched because their common characteristics were that they had no diagnoses, medication, or cost information associated with them. Obviously, this subsample is not representative of the DMPDM2 population of interest. This result illustrates the trade‐off between inexact matching and number of observations excluded. With CEM, researchers can define the variable bins based on a priori knowledge of what values of a variable should be equivalent regarding the research question. For example, looking at the number of days spent in the hospital per year, distinguishing between three categories, no stay, short stay, and long stay, might be sufficient. Iacus, King, and Porro (2012) argue that researchers should have enough knowledge of their field to define the amount of imbalance that should be allowed for each variable. Frequently, evaluation studies aim to estimate the ATT, where a substantial exclusion of subjects from the treatment group would be problematic. Iacus, King, and Porro (2011) list the following choices for a researcher in that case: (1) decide that the data are not suitable for this research question, (2) allow inferences for parts of the data without common support based on extrapolation, being aware that the effect measure estimate is model‐dependent, and (3) only estimate the effect estimate for the well‐matched subsample and basically change the quantity of interest from what Iacus, King, and Porro (2011) call the population average treatment effect on the treated (PATT) to the sample population average treatment effect on the treated (SATT). Furthermore, they describe a way of splitting up the effect estimate into a component based on well‐matched data and a model‐dependent component, so that at least the amount of model dependency is made explicit.

Compared to using a multiple regression model, in which case extrapolation automatically happens and easily hides the amount of model dependency of the effect measure, all matching approaches combined with thorough balance checking provide an approach to highlight regions of the data lacking common support between treatment and control groups.

It could be argued that CEM was bound to fail with the high‐dimensional covariate space used in our study. As the majority of the variables were binary, CEM in our case was not very different from exact matching. We did not pursue the alternative of applying CEM with a reduced set of especially important covariates as this would have been similar to the ELSID and modified ELSID matching.

All studies evaluating German DMPDM2 s using matching reported on balance either using standardized mean differences (Stock et al. 2010; Windt and Glaeske 2010; Linder et al. 2011) or statistical tests (Miksch et al. 2010). Statistical testing is not appropriate for assessing balance after matching, as the p‐value changes with a change in sample size, which might be mistaken as a change in balance. Using standardized mean differences is a good start, but to accurately measure covariate balance between the DMPDM2 and control group, not only the means of the variables but also ideally the multidimensional distributions of all covariates should be considered (Ho et al. 2007a; Iacus, King, and Porro 2011). Accordingly, we used two additional balance measures, the KS statistic to compare the distributions of individual covariates, and the multivariate balance measure L1. Our results show that depending on the balance measure used, comparing different matching methods can lead to different conclusions. While ideally one would only rely on the multivariate balance measure L1, our case with many binary variables illustrates that using this measure under any circumstances can be problematic. Also, only using summary balance measures can fail to detect imbalances of only a few important covariates. Therefore, complimentary individual balance diagnostics on key covariates using graphical displays can be helpful (Linden 2014). In general, there is still a lack of suitable comparisons for matching methods regarding their balance, taking into consideration the number of observations excluded. King et al. (2011) provide a graphical tool that considers both aspects and allows the user to choose a method with maximal levels of balance given different sample sizes.

Another problem using balance measures of covariate balance is that only some of the variables considered might be true confounders, while the balance measure depends on all of them. Ideally, only true confounder variables should be included in the matching (Pearl 2000). PSM usually uses variables that are associated with DMPDM2 enrollment, but to be a true confounder this variable also needs to be associated with the outcome variable (and not be on the causal path between treatment and outcome). It has been shown that including covariates strongly associated with exposure but unrelated to the outcome can increase bias (Patrick et al. 2011). Even more important than the inclusion of too many variables is the missing of unobserved confounders. It is rarely the case that all confounding variables are known and measured accurately. Any matching technique only adjusts for confounding variables that are assessed or are at least correlated with the assessed variables, so that unmeasured confounders always have to be considered as a potential threat to validity of any matching analysis. Additionally, Brooks and Ohsfeldt (2013) showed that improving balance on observed covariates in PS matching can further increase the imbalance of unobserved covariates.

Alternative methods such as instrumental variables, regression discontinuity, and interrupted time series analysis (McDowall 1980; Angrist, Imbens, and Rubin 1996; Imbens and Lemieux 2008) can provide an alternative approach to avoid confounding due to unmeasured confounders. However, in a lot of situations the requirements for these methods (e.g., availability of appropriate instrumental or threshold variables or enough observations over time) are not fulfilled.

Strengths and Limitations

The comparison of matching methods in this study is based on one empirical example. Applying these methods to a different dataset or a different research question might result in a very different picture regarding the performance of different matching techniques. The aim of this paper was to exemplify the issues that need to be addressed when comparing different techniques for one research question. As we used routine sickness fund data, we had a large sample of subjects and also many potential variables to include in the matching process. This situation might be different in studies that collect primary data, where the number of collected covariates is likely smaller and the variables are purposefully collected and coded with the research question in mind. We believe, however, that our study provides a typical example for the kind of data available when evaluating complex health care interventions.

The choice of methods presented is not exhaustive. There are other methods available that could provide suitable results. The methods used in this study were motivated by which matching methods had been applied in previous studies of the German DMPDM2. Furthermore, no combinations of techniques were applied. For example, combining exact matching or coarsened exact matching for a few important confounder variables and PSM for the rest might provide superior results to using either method alone.

Our paper did not evaluate different methods for automatic variable selection in large datasets. The high‐dimensional PS algorithm automatically identifies covariates for PS adjustment from different data dimensions in health care claims data. It selects covariates based on their prevalence among treated and control subjects and their association with the outcome while excluding surrogate variables (Schneeweiss et al. 2009). Recent studies have shown that this approach results in improved point‐estimates compared to traditional PSM analyses (Garbe et al. 2013; Franklin et al. 2014).

Due to the fact that covariate balance does not necessarily relate to bias of the effect estimate, it could be argued that choosing matching methods based on their performance on balance measures is not appropriate and that alternatively Monte Carlo simulations should be used to find the method that achieves the most precise and least biased effect estimate. However, as we usually never know the true causal model for the research question at hand, we cannot know whether we did not miss a crucial feature of the simulation dataset that might have affected the performance of the matching methods. Therefore, the results of such simulation studies might not be transferrable to other datasets.

The strength of balance measures is that they can be quickly applied by any researcher wanting to use matching in their own research project. Notwithstanding the various issues addressed in this paper, they can provide useful information regarding potential problems with common support and lack of balance regarding confounder variables when interpreted with due caution.

Conclusion

A single best matching method is probably not available but highly dependent on the research question. Best practice should therefore include the application of several matching methods and balance diagnostics. Comparing the effect measures resulting from the application of different matching methods can provide a useful sensitivity analysis. However, the choice of matching method might be less important than having good‐quality data and the correct confounder model.

Matching can be a very useful preprocessing step that, if applied correctly, can reveal for which part of the data there is common support so that a comparison between the control and treatment condition is possible without extrapolation and for which part the results are highly model‐dependent.

Supporting information

Appendix SA1: Author Matrix.

Click here for additional data file. (1.3MB, pdf)

Appendix SA2: List of Variables Included in Different Matching Methods.

Appendix SA3: Standardized Mean Differences of All Covariates Before and After Matching.

Appendix SA4: Table of Balance Measures Before and After the Application of Different Matching Techniques.

Appendix SA5: Patient Selection.

Click here for additional data file. (673.4KB, pdf)

Acknowledgments

Joint Acknowledgment/Disclosure Statement: The work was carried out as part of the European Union Framework 7 research programme‐funded project: “Developing and validating disease management evaluation methods for European health care systems” (DISMEVAL). We thank the Techniker Krankenkasse for providing the data and Mary J. Pitzer and Matthew Fullerton for copy‐editing.

Disclosures: None.

Disclaimers: None.

References

  1. Ali, M. S. , Groenwold R. H., Belitser S. V., Pestman W. R., Hoes A. W., Roes K. C., de Boer A., and Klungel O. H.. 2015. “Reporting of Covariate Selection and Balance Assessment in Propensity Score Analysis Is Suboptimal: A Systematic Review.” Journal of Clinical Epidemiology 68 (2): 112–21. [DOI] [PubMed] [Google Scholar]
  2. Angrist, J. D. , Imbens G. W., and Rubin D. B.. 1996. “Identification of Causal Effects Using Instrumental Variables.” Journal of the American Statistical Association 91 (434): 444–55. [Google Scholar]
  3. Austin, P. C. 2011. “Optimal Caliper Widths for Propensity‐Score Matching When Estimating Differences in Means and Differences in Proportions in Observational Studies.” Pharmaceutical Statistics 10 (2): 150–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brooks, J. M. , and Ohsfeldt R. L.. 2013. “Squeezing the Balloon: Propensity Scores and Unmeasured Covariate Balance.” Health services research 48 (4): 1487–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bundesversicherungsamt . 2008. “Festlegung der Morbiditätsgruppen, des Zuordnungsalgorithmus, des Regressions‐ sowie des Berechnungsverfahrens” [accessed on October 23, 2013]. Available at http://www.bundesversicherungsamt.de/fileadmin/redaktion/Risikostrukturausgleich/Festlegungen/AJ_2009/Festlegungen_Klassifikationsmodell.zip
  6. Bundesversicherungsamt . 2012. “Zulassung der Disease Management Programme (DMP) durch das Bundesversicherungsamt (BVA). Zulassungsstand” [accessed on August 27, 2013]. Available at http://www.bundesversicherungsamt.de/druckversion/weitere-themen/disease-management-programme/zulassung-disease-management-programme-dmp.html
  7. D'Agostino R. B. Jr 1998. “Propensity Score Methods for Bias Reduction in the Comparison of a Treatment to a Non‐Randomized Control Group.” Statistics in Medicine 17: 2265–81. [DOI] [PubMed] [Google Scholar]
  8. Dehejia, R. H. , and Wahba S.. 2002. “Propensity Score Matching Methods for Non‐Experimental Causal Studies.” Review of Economics and Statistics 84: 151–61. [Google Scholar]
  9. Drabik, A. , Büscher G., Karsten T., Graf C., Müller D., and Stock S.. 2012. “Patients with Type 2 Diabetes Benefit from Primary Care‐Based Disease Management: A Propensity Score Matched Survival Time Analysis.” Population Health Management 15 (4): 241–7. [DOI] [PubMed] [Google Scholar]
  10. Franklin, J. A. , Schneeweiss S., Polinski J. M., and Rassen J. A.. 2014. “Plasmode Simulation for the Evaluation of Pharmacoepidemiologic Methods in Complex Healthcare Databases.” Computational Statistics & Data Analysis 72 (2): 219–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Garbe, E. , Kloss S., Suling M., Pigeot I., and Schneeweiss S.. 2013. “High‐Dimensional versus Conventional Propensity Scores in a Comparative Effectiveness Study of Coxibs and Reduced Upper Gastrointestinal Complications.” European Journal of Clinical Pharmacology 69 (3): 549–57. [DOI] [PubMed] [Google Scholar]
  12. Gu, X. S. , and Rosenbaum P. R.. 1993. “Comparison of Multivariate Matching Methods: Structures, Distances, and Algorithms.” Journal of Computational and Graphical Statistics 2: 405–20. [Google Scholar]
  13. Harder, V. S. , Stuart E. A., and Anthony J. C.. 2010. “Propensity Score Techniques and the Assessment of Measured Covariate Balance to Test Causal Associations in Psychological Research.” Psychological Methods 15 (3): 234–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ho, D. , Imai K., King G., and Stuart E.. 2007a. “Matching as Nonparametric Preprocessing for Reducing Model Dependence in Parametric Causal Inference.” Political Analysis 15 (3): 199–236. [Google Scholar]
  15. Ho, D. , Imai K., King G., and Stuart E.. 2007b. “Matchit: Nonparametric Preprocessing for Parametric Causal Inference.” Journal of Statistical Software 42 (8): 1–28. [Google Scholar]
  16. Iacus, S. M. , King G., and Porro G.. 2011. “Multivariate Matching Methods That Are Monotonic Imbalance Bounding.” Journal of the American Statistical Association 106 (493): 345–61. [Google Scholar]
  17. Iacus, S. M. , King G., and Porro G.. 2012. “Causal Inference without Balance Checking: Coarsened Exact Matching.” Political Analysis 20 (1): 1–24. [Google Scholar]
  18. Imbens, G. W. , and Lemieux T.. 2008. “Regression Discontinuity Designs: A Guide to Practice.” Journal of Econometrics 142 (2): 615–35. [Google Scholar]
  19. King, G. , Nielsen R., Coberley C., Pope J. E., and Wells A.. 2011. “Comparative Effectiveness of Matching Methods for Causal Inference” [accessed on October 21, 2013]. Available at http://gking.harvard.edu/files/gking/files/psparadox.pdf
  20. Lamers, L. M. 1998. “Risk‐Adjusted Capitation Payments: Developing a Diagnostic Cost Groups Classification for the Dutch Situation.” Health Policy 45 (1): 15–32. [DOI] [PubMed] [Google Scholar]
  21. Lamers, L. M. 1999. “Pharmacy Costs Groups: A Risk‐Adjuster for Capitation Payments Based on the Use of Prescribed Drugs.” Medical Care 37 (8): 824–30. [DOI] [PubMed] [Google Scholar]
  22. Linden, A. 2014. “Graphical Displays for Assessing Covariate Balance in Matching Studies.” Journal of Evaluation in Clinical Practice. doi:10.1111/jep.12297. [DOI] [PubMed] [Google Scholar]
  23. Linden, A. , and Adams J. L.. 2010. “Using Propensity Score‐Based Weighting in the Evaluation of Health Management Programme Effectiveness.” Journal of Evaluation in Clinical Practice 16: 175–9. [DOI] [PubMed] [Google Scholar]
  24. Linder, R. , Ahrens S., Köppel D., Heilmann D., and Verheyen F.. 2011. “Nutzen und Effizienz des Disease‐Managment‐Programms Diabetes Mellitus Type 2.” Deutsches Ärzteblatt 108: 155–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. McCaffrey, D. F. , Ridgeway G., and Morral A. R.. 2004. “Propensity Score Estimation with Boosted Regression for Evaluating Causal Effects in Observational Studies.” Psychological Methods 9 (4): 403–25. [DOI] [PubMed] [Google Scholar]
  26. McDowall D. (Ed.). 1980. Interrupted Time Series Analysis (Vol. 21). Beverly Hills, CA: Sage. [Google Scholar]
  27. Miksch, A. , Laux G., Ose D., Joos S., Campbell S., Riens B., and Szecsenyi J.. 2010. “Is There a Survival Benefit Within a German Primary Care‐Based Disease Management Program?” American Journal of Managed Care 16 (1): 49–54. [PubMed] [Google Scholar]
  28. Nolte, E. , Knai C., Hofmacher M., Conklin A., Erler A., Elissen A., Flamm M., Fullerton B., Sönnichsen A., and Vrijhoef H. J. M.. 2012. “Overcoming Fragmentation in Healthcare: Chronic Care in Austria, Germany and the Netherlands.” Health Economics Policy and Law 7: 125–46. [DOI] [PubMed] [Google Scholar]
  29. Oakes, J. M. , and Johnson P. J.. 2006. “Propensity Score Matching for Social Epidemiology.” Methods in Social Epidemiology 1: 370–93. [Google Scholar]
  30. Patrick, A. R. , Schneeweis S., Brookhart M. A., Glynn R. J., Rothman K. J., Avorn J., and Stürmer T.. 2011. “The Implications of Propensity Score Variable Selection Strategies in Pharmacoepidemiology: An Empirical Illustration.” Pharmacoepidemiology and Drug Safety 20 (6): 551–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Pearl, J. 2000. Causality: Models, Reasoning, and Inference. Cambridge, England: Cambridge University Press. [Google Scholar]
  32. Ridgeway, G. , McCaffrey D. F., Morral A., Burgette L., and Griffin B. A.. 2013. “Toolkit for Weighting Analysis of Nonequivalent Groups: A Tutorial for the Twang Package” [accessed on October 23, 2013]. Available at http://cran.r-project.org/web/packages/twang/vignettes/twang.pdf
  33. Riens, B. , Broge B., Kaufmann‐Kolle P., Pöhlmann B., Grün B., Ose D., and Szecsenyi J.. 2010. “Creation of a Control Group by Matched Pairs with GKV Routine Data for the Evaluation of Enrolment Models.” Gesundheitswesen 72: 363–70. [DOI] [PubMed] [Google Scholar]
  34. Rosenbaum, P. R. , and Rubin D. B.. 1983. “The Central Role of the Propensity Score in Observational Studies for Causal Effects.” Biometrika 70: 41–55. [Google Scholar]
  35. Rosenbaum, P. R. , and Rubin D. B.. 1984. “Reducing Bias in Observational Studies Using Subclassification on the Propensity Score.” Journal of the American Statistical Association 79: 515–24. [Google Scholar]
  36. Rosenbaum, P. R. , and Rubin D. B.. 1985. “Constructing a Control Group Using Multivariate Matched Sampling Methods That Incorporate the Propensity Score.” The American Statistician 39: 33–8. [Google Scholar]
  37. Schneeweiss, S. , Rassen J. A., Glynn R. J., Avorn J., Mogun H., and Brookhart M. A.. 2009. “High‐Dimensional Propensity Score Adjustment in Studies of Treatment Effects Using Health Care Claims Data.” Epidemiology 20 (4): 512–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Siering, U. 2008. “Germany” In Managing Chronic Conditions—Experience in Eight Countries, edited by Nolte E., Knai C., and McKee M., pp. 75–96. Copenhagen: World Health Organization on behalf of the European Observatory on Health Systems and Policies. [Google Scholar]
  39. Stock, S. , Drabik A., Buscher G., Graf C., Ullrich W., Gerber A., Lauterbach K. W., and Lungen M.. 2010. “German Diabetes Management Programs Improve Quality of Care and Curb Costs.” Health Affairs (Millwood) 29 (12): 2197–205. [DOI] [PubMed] [Google Scholar]
  40. Stuart, E. A. 2010. “Matching Methods for Causal Inference. A Review and Look Forward.” Statistical Science 25 (1): 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Windt, R. , and Glaeske G.. 2010. “Effects of a German Asthma Disease Management Program Using Sickness Fund Claims Data.” Journal of Asthma 47 (6): 674–9. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Appendix SA1: Author Matrix.

Click here for additional data file. (1.3MB, pdf)

Appendix SA2: List of Variables Included in Different Matching Methods.

Appendix SA3: Standardized Mean Differences of All Covariates Before and After Matching.

Appendix SA4: Table of Balance Measures Before and After the Application of Different Matching Techniques.

Appendix SA5: Patient Selection.

Click here for additional data file. (673.4KB, pdf)

Articles from Health Services Research are provided here courtesy of Health Research & Educational Trust

RESOURCES