Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Sep 23;6:33826. doi: 10.1038/srep33826

Ultrabroadband Design for Linear Polarization Conversion and Asymmetric Transmission Crossing X- and K- Band

Linbo Zhang 1, Peiheng Zhou 1,a, Haiyan Chen 1, Haipeng Lu 1, Haiyan Xie 1, Li Zhang 1, En Li 1,2, Jianliang Xie 1, Longjiang Deng 1
PMCID: PMC5034340  PMID: 27658929

Abstract

In this work, a high-efficiency and broadband reflective converter using ultrathin planar metamaterial (MM) composed of single-layered SRR is firstly realized. Numerical and experimental results demonstrate that the cross-polarization conversion reflectance above 0.84 is achieved from 8.6 to 18.6 GHz for linearly polarized (LP) incident waves under normal incidence. Subsequently, a multi-layered MM based on SRR enables a dramatic improvement of the recently demonstrated asymmetric transmission (AT) effect. Theoretical and measured results present that strong one-way transmission of two orthogonally polarized waves crossing C- and K- band has been observed. These two separated AT pass-bands have a function of selective polarization filter, which can be switched on/off by changing the polarization state of incident waves. The physical mechanisms are elucidated by taking advantage of electric fields and current distributions. Considering the broad bandwidth and the dual band, we believe that these two structures will be beneficial for designing polarization-controlled and selective transmission converter.

There is an increasing interest in using metal-dielectric structures to control the polarization and propagation states of electromagnetic (EM) waves1,2,3. In order to achieve such control it is necessary to create devices that have flexible manipulation of phase modulation and amplitude in reflection, transmission and absorption4,5,6,7. Metal-dielectric structures with strong birefringence and chirality have been demonstrated, with applications in quarter and half wave plates8,9,10, holograms11,12 and anomalous reflection13,14. Conventional polarization control devices based on optical gratings15 and dichroic crystals16 typically operate over narrow frequency bands, which may be broadened by stacking multiple structures or introducing a gradient in the helical pitch17,18. However, more bandwidth increases are usually achieved at the price of much bulkier devices, which are difficult to integrate within today’s miniaturized system.

Metamaterial (MM) – artificial EM structure with unconventional elements – has opened new routes towards the efficient manipulation of EM propagation due to its unusual properties19,20,21,22. Many basic MM structures, such as V-shaped antenna1, exhibit birefringence suitable for polarization conversion, which has been investigated in a number of theoretical and experimental works23,24,25,26,27. Broadband MM linear converters have been demonstrated in the short-wavelength infrared band by using high-refractive-index silicon cut-wire structure28. MMs-based polarimetric devices are particularly attractive in the microwave frequency range due to the lack of suitable natural materials for applications. Hao et al. demonstrated a reflective converter based on anisotropic MM, which could generate multiple resonance frequencies29. A MM converter -based electric-field-coupled resonator for such purpose was presented in refs 30 and 31. Meanwhile, linear converter in transmission mode is also interesting for many applications. Since the asymmetric transmission (AT) effect firstly observed by Fedotov et al.32, lots of sophisticated MM structures have been proposed33,34,35,36,37,38. Methods and designs have been proposed to enhance the magnitude of AT effect in the planar chiral MMs. In 2010, Menzel et al.39 reported a bi-layered chiral structure, achieving only magnitude of 0.25 for linearly polarized (LP) waves. Subsequently, Shi et al.40,41,42 proposed a kind of chiral MMs to achieve AT effect for LP waves. Despite its high polarization conversion efficiency, the above designs suffer from either very limited bandwidth or increased complexity. Recent years, some designs for broadband asymmetric transmission have been reported. In 2015, Cong et al.43 and Liu et al.44 presented L-shaped antenna in the teraherz range to manipulate EM waves. Cross-shaped MM was demonstrated by Wang et al.45,46, the AT bandwidth could be up to 33% of the central wavelength. Liu et al.47,48 proposed a multi-layered metallic structure, which can achieve a high magnitude of 0.94 and broadband AT effect for LP waves. In 2016, a cavity-based linear converter was showed by Wang et al.49, which exhibits very good performance with stable transmittance as 50%. Meanwhile, a three-layered sandwiched MM was proposed to achieve broadband AT effect in the near-infrared communication band50. The physical mechanisms of the polarization conversion and AT effect can be explicated by Lorentz-theory approach and Fabry-Perot like resonance model3,47,48,51,52. Thus, these intriguing features therefore make it possible to give us some new idea to design high magnitude and broadband converter.

In this work, we firstly present a high-efficiency and broadband reflective converter using ultrathin planar MM, which are capable of converting a LP wave into its orthogonal polarization. This device exhibits wideband property numerically as well as experimentally. The measured results show that the reflectance over 0.85 is achieved from 8.6 to 18.6 GHz for LP incident waves under normal incidence. In addition, a multi-layered MM based on SRR enables a dramatic improvement of the asymmetric transmission (AT) effect. Theoretical results show that the multi-layered MM can achieve cross-polarization with broad bandwidth and high efficiency for two orthogonal LP EM waves in two separated frequency regions, where LP waves can be mostly converted to its cross-polarization and then transmitted. The phenomenon can be functionalized as a dual-band polarization-selective filter by changing the polarization state of incident waves.

Results and Discussion

Unit cell design

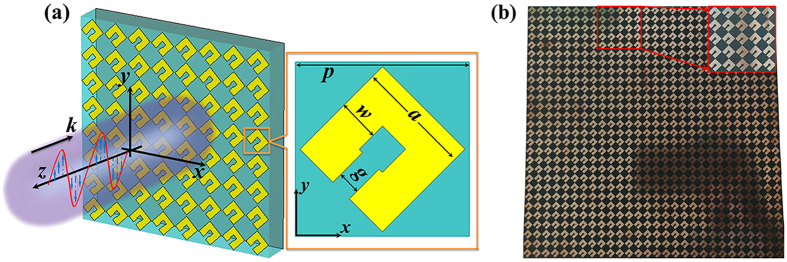
A schematic of the converter is illustrated in Fig. 1(a). It is composed of a copper-patterned layer of split-ring resonator (SRR) and a continuous metal ground plane, with a dielectric layer of Teflon in between. The optimized unit cell is chosen as periodic dimensions of p = 7.5 mm in x-y plane, and the thickness of dielectric layer is t = 2 mm in the propagation of EM wave, z direction. The parameters of SRR are as follows: a = 5 mm, w = 1.8 mm and g = 1 mm.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic of the reflective coverter. (b) Image of the sample with a unit cell period of p = 7.5, a = 5, w = 1.8, g = 1 and t = 2 (unit: mm).

The aforementioned geometrical parameters have been optimized by the commercial software CST Microwave Studio. In simulations, the conductivity of copper was σ = 5.8 × 107 S/m, and the Teflon was simulated with a dielectric function of ε = 2.65 × (1 + 0.002i). The frequency domain solver was carried out with unit cell boundary condition in the x-y directions and the floquet ports in the z-direction to extract S parameters.

Experimental results and characterization

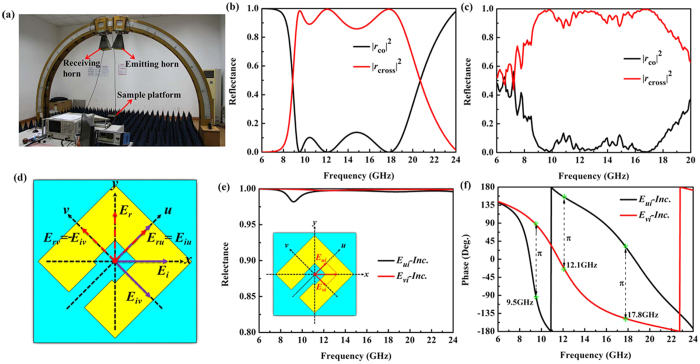
Device fabrication was using the conventional printed circuit board propocess with the structural parameters same as the simulated model. The sample image is shown in Fig. 1(b), which has an oversize of 300 mm × 300 mm, containing 40 × 40 unit cells. To experimentally characterize the performance of the converter, the reflectance dependent on frequency was measured by the United States Naval Research Laboratory (NRL) arch method53 as shown in Fig. 2(a). An Agilent 8720ET vector network analyzer and two broadband horn antennas were connected by a coaxial cable. Two antennas were used to emit and receive EM waves. The reflectances |rco|2 and |rcross|2 can be measured by rotating the horn antenna in the arch structure, as illustrated in Fig. 2(c). Due to the limitations of experimental conditions, the measurement is conducted only in the range of 6–20 GHz. The experimental results demonstrate that |rcross|2 remains above 0.85 from 8.6 to 18.6 GHz, little difference with the simulations (9.2 to 19.2 GHz) shown in Fig. 2(b). In addition, the simulated reflectances |rcross|2 are 0.98, 0.99 and 0.99 at resonant frequencies of 9.5 GHz, 12.1 GHz and 17.8 GHz, respectively; |rcross|2 are 0.99, 0.99 and 1.0 at resonant frequencies of 9.8 GHz, 12.4 GHz and 16.9 GHz for experiments. The reason of the minor shift of the measured reflectances may be the limited precision of fabrication geometry as well as the dielectric board material whose actual dielectric constant is slightly different from the value used in simulations.

Figure 2.

Figure 2

Open in a new tab

(a) Schematic of the polarization conversion measurement setup. (b) Simulated and (c) measured reflectance for co- and cross-polarized waves. (d) Schematic of the decomposition of linearly polarized incident and reflected waves. (e) Reflectance and (f) phase for a polarized wave along the u-and v-axes, respectively, demonstrating near-unity reflection and a π-phase shift under resonant frequencies.

To better understand the response of the converter, the incident wave, which is LP along x-direction, can be decomposed into two perpendicular components, u- and v-axis, respectively (Fig. 2(d)). The numerical simulated reflection amplitude and phase for the converter illustrated with polarization along u- and v-axis are illustrated in Fig. 2(e,f). It can be seen that the reflection amplitudes in the two curves are nearly the same and close to unity while the relative phase retardation is roughly π at the three resonant frequencies of 9.5 GHz, 12.1 GHz and 17.8 GHz. Taking the first resonant frequency of 9.5 GHz, e.g., we decompose the electric field vector of the incident and reflected waves as depicted in Fig. 2(d). Incident electric field Ei can be decomposed into two componenets Eiv and Eiu. Since the reflection phase difference along v and u direction is π, the reflective electric field Erv (Eru) is equal to the incident electric field −Eiv (Eiu). Then the total reflected field Er can be obtained and parallel to the y-axis, where the linear polarization conversion occurs, leading to a 90 degree polarization conversion. The same polarization conversion process applies for the other two resonant frequencies of 12.1 GHz and 17.8 GHz. We can understand the high conversion efficiency by modeling the field evolution upon multi-reflection process within the dielectric layer, where the consequence interference of polarization couplings results in constructive or destructive interference, respectively3,27,54,55. In addition, symmetric and antisymmetric modes supported by SRR are excited by the electric field configurations, which can be also explained the principle of our converter1,56.

Numerical simulations also show that the device maintains near-unity polarization conversion efficiency for variations of the dielectric spacer thickness and in the meantime, the high-frequency resonant peaks shift toward lower frequencies with increase of thickness t while the lowest resonant frequency hardly changes (Supporting Information Fig. S1). Similar situations are presented as variation of periodic unit p, for which the converter keeps conversion efficiency above 0.8 with bandwidth over 11.4 GHz for p ≤ 8.5 mm (Supporting Information Fig. S2). Meanwhile, variation of gap g and width w of SRRs could directively influence the positions of the highest and lowest resonant peaks, respectively (Supporting Information Figs S3 and S4).

In addition, the simulated and measured results show that this device is robust to variation of incident angle up to 30 degree for LP incident waves (Supporting Information Figs S5 and S6). However, the bandwidth of the converter is reduced when the incident angle is greater than 30 degree.

Demonstration of A Dual-Band Polarization Filter

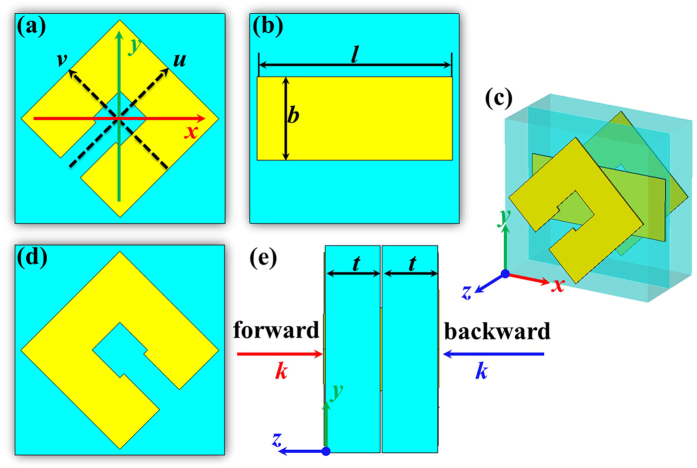
Many applications require linear polarization conversion in transmission mode, for which we replace the metal ground plane in our design. By properly introducing a metal cut-wire, a multi-layered MM is proposed as shown in Fig. 3, which is composed of a cut-wire sandwiched by two layers of SRR. The front and back metallic layers are consisted of the same SRR, but with the split directions perpendicular to each other, while the middle layer is parallel to x-axis. Numerical results demonstrate that the multi-layered MM is nearly transparent to incident LP waves in two separated AT passbands, where a LP wave can be mostly converted to its cross-polarization and then transmitted, while the same LP wave cannot pass through the MM in the opposite direction.

Figure 3. Schematic of the unit cell of the multi-layered linear converter.

Figure 3

Open in a new tab

Parameters of the SRR array and the spacer are the same as that in Fig. 1. (a) Front view of the structure, (b) geometry of cut-wire in the middle layer, (c) perspective view of the structure, (d) bottom metallic layer, and (e) right side of structure. Dimension (mm): p = 7.5, a = 5, w = 1.8, g = 1, l = 7, b = 3 and t = 2.

In order to better understand the selective AT effect based on the proposed multi-layered MM, terms of complex transmission coefficients Tijd in Jones matrix are presented, where tijd = |Tijd|. The subscripts i and j correspond to the polarization states of the transmitted and incident waves, which could be either v or u LP wave depicted in Fig. 3(a). The superscript d refers to the forward (f, along −z direction) or backward (b, along +z direction) wave propagations.

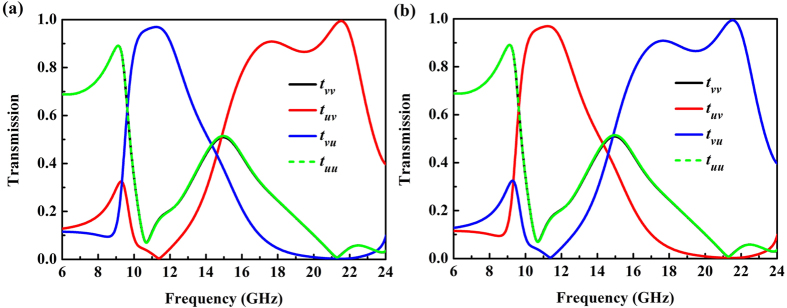
Figure 4 shows the simulated transmission coefficients in the multi-layered MM for the forward and backward propagating waves. The co-polarization transmission coefficient tvv of v-polarized wave coincides well with tuu of u-polarized wave under normal incidence. In contrast to co-polarization transmission, the cross-polarization transmission coefficient tuv is extremely different from tvu at the considered frequencies. These above two conditions ensure the presence of AT effect for LP waves33,34,35,36,37,38,39,40,41,42,43,44,47,48. Most interestedly, there are two separated passbands observed, demonstrating strong optical activity in the proposed MM, one for v-to-u polarization conversion and the other for u-to-v polarization conversion. In Fig. 4(a), the cross-polarization transmission coefficient tvu reaches a maximum of 0.98 at around 11.2 GHz. tvu above 0.8 can be achieved from 9.9 GHz to 12.5 GHz, and both the co-polarization transmission coefficients tvv and tuu are below 0.3. In this pass band, the v-polarized incident wave is mostly transmitted to u-polarized wave while the u-polarized incident wave is mostly blocked through the MM. Meanwhile, another obvious broad band for tuv above 0.8 can be observed from 16.1 GHz to 22.5 GHz. The cross-polarization transmission coefficient tuv reaches 0.91 and 0.99 at two resonant frequencies of 17.5 GHz and 21.5 GHz, respectively. Similarly, in this broad pass band, a v-polarized incident wave is mostly transmitted to u-polarized wave, while the u-polarized incident wave cannot pass through the MM. Otherwise, tuv and tvu interchange with each other when the propagation direction is reversed as depicted in Fig. 4(b).

Figure 4.

Figure 4

Open in a new tab

Transmission coefficients (absolute value) of linearly polarized waves in (a) forward (−z) direction and (b) backward (z) direction.

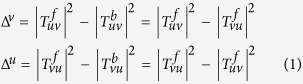graphic file with name srep33826-m1.jpg

As depicted in Fig. 4, tvv is exactly equal to tuu, which ensures zero AT effect of circular polarization waves but only for LP waves by this MM32,33,34,35,36. The AT parameter Δ can be calculated by Eq. (1), which is characterized as the difference between the transmissions of two opposite propagation directions34. Figure 5 presents the calculated AT parameter Δ for forward u- and v-polarized incident waves according to Eq. (1). It is observed that AT parameters are 0.94/−0.94, −0.82/0.82 and −0.99/0.99 for Δu/Δv at resonant frequencies of 11.2 GHz, 17.5 GHz and 21.5 GHz, respectively. Both Δu and Δv depict two opposite passbands over 0.75, respectively, from 10.0 to 12.2 GHz and from 16.8 to 22.3 GHz, which implys that a u/v-polarized wave in the forward direction is mostly allowed/forbidden in the former pass band, and forbiddened/allowed in the latter pass band. This interesting phenomenon demonstrates that the proposed MM can be used as a selective dual-band polarization filter. In addition, it is observed that the multi-layered MM maintains this broadband selective transmission property for incident angle up to 30 degree (Supporting Information Fig. S7).

Figure 5. Calculated asymmetric transmission parameter Δ.

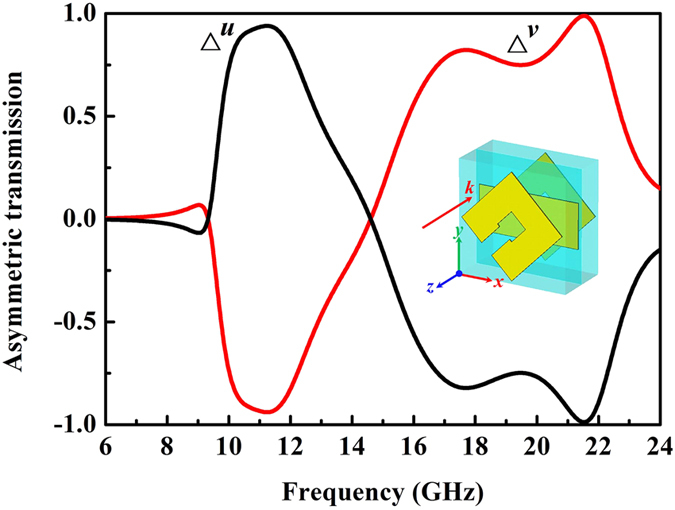
Figure 5

Open in a new tab

Black and red solid curves correspond, respenctively, to asymmetric transmissions of v and u linearly polarized waves in the forward (−z) propagation direction.

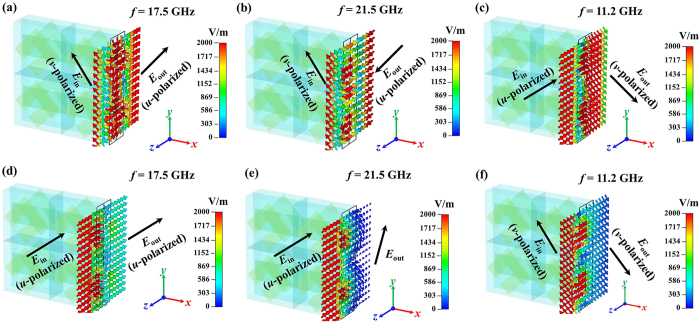
To understand the physical insight of the LP waves passed through the proposed MM, electric field configurations for incident waves along forward direction at resonant frequencies of 11.2 GHz, 17.5 GHz and 21.5 GHz are presented in Fig. 6. For the proposed MM, the electric fields depicted of v-polarized wave shown in Fig. 6(a,b) and u-polarized wave shown in 6(c) have been converted by 90°, which is clear that the v/u-polarized incident wave is transformed into an u/v-polarized output wave at the resonant frequencies. It is nearly transparent for a u/v-polarized wave shown in Fig. 6(d,f) but reflects most of the u/v-polarized wave as depicted in Fig. 6(e,f). By observation of the electric field magnitudes as shown in Fig. 6(d–f), we can see that reflectances tuu is about 0.3 and 0.05 at frequencies of 17.5 GHz and 21.5 GHz, respectively; tuv is around 0.2 at frequency of 11.2 GHz. These results coincide with the analysis results in Fig. 4.

Figure 6.

Figure 6

Open in a new tab

The electric field configurations in the multi-layered MM at resonant frequencies of 17.5 GHz, 21.5 GHz and 11.2 GHz for (a,b,f) a v-polarized wave, and (c–e) a u-polarized wave propagating along the forward (−z) direction.

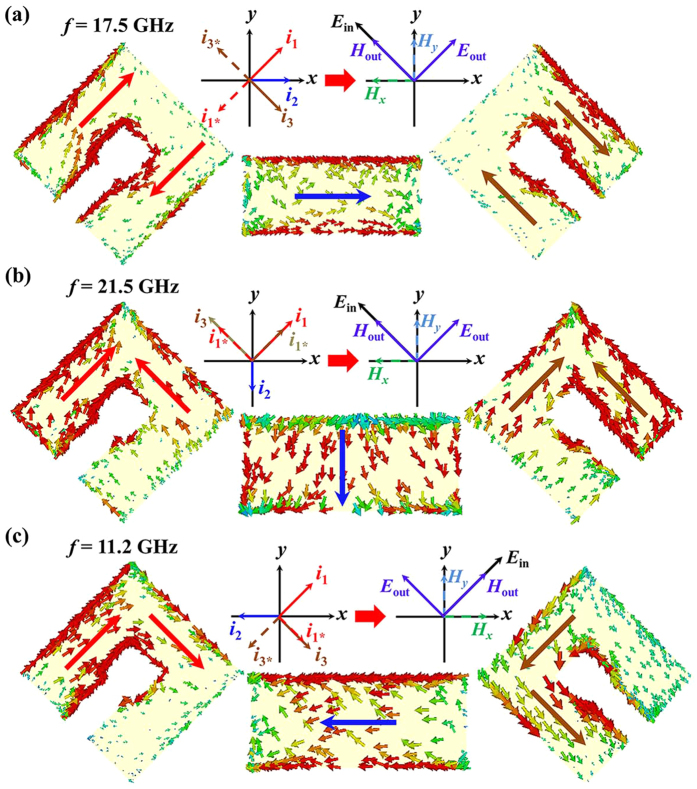
In order to understand the physical origin of the two passbands of AT effect, surface current distributions of the proposed MM are presented at the resonant frequencies of 17.5 GHz, 21.5 GHz and 11.2 GHz, respectively. In Fig. 7, the red, blue and brown solid arrows represent the current direction of top SRR layer, middle cut-wire layer and bottom SRR layer, respectively. As we know, the coupling effect between electric and magnetic fields plays an important role in a chiral or anisotropic MM57,58,59. It is observed from Fig. 7(a) that the induced x component Hx and y component Hy generated by the anti-symmetric and symmetric currents decomposed in x and y direction. Then the total magnetic field Hout parallel to incident electric filedEin can be obtained. The cross-coupling between Ein and Hout leads to a cross-polarization with a v-to-u polarization conversion. Thus, most energy of the v-polarized incident wave are transformed with a 90° rotation at resonant frequency of 17.5 GHz. Similarly, the transmitted features with polarization conversion occur at the other two resonant frequencies of 21.5 GHz and 11.2 GHz as shown in Fig. 7(b,c).

Figure 7.

Figure 7

Open in a new tab

Surface current distributions of the single-layered pattern for forward propagating (a,b) v- and (c) u-polarized waves at resonant frequencies of 17.5 GHz, 21.5 GHz and 11.2 GHz, respectively. The schematic current distribution is represented by colors on the metallic patterns (red for front SRR, blue for cut-wire, and brown for back SRR). The direction of current flow is indicated by arrows.

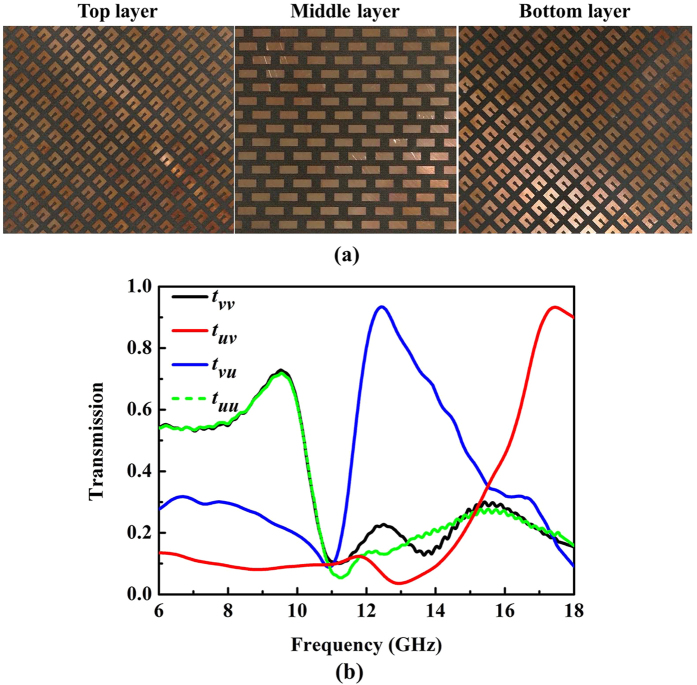
To validate the AT effect and dual-band polarization of the multi-layered structure, a 300 mm × 300 mm sample of the proposed structure is fabricated and measured, as shown in Fig. 8. Due to the limitations of experimental conditions, the measurement is conducted only in the range of 6–18 GHz. As depicted in Figure 8(b), we can see that the co-polarization transmission coefficient tvv of v-polarized wave nearly coincides well with tuu of u-polarized wave. Meanwhile, tuv is extremely different from the tvu at the considered frequencies. These phenomena verify the presence of AT effect for the proposed structure. The polarization conversion bandwidth of tuv over 0.75 can be achieved from 11.9 GHz to 13.4 GHz; transmission coefficient tuv is 0.93 at resonant frequency of 12.4 GHz. tvu above 0.75 can be achieved from 16.7 GHz to 18.0 GHz; and tvu reaches a maximum of 0.93 at resonant frequency of 17.4 GHz. However, we can see a discrepancy of the cross-polarization transmission coefficient tuv and tuv between the simulated and measured result. This is due to the small signal to noise ratio (SNR) for the test system in the process of calibration. Even though the discrepancy, AT effect and separated dual-band polarization conversion can still be realized.

Figure 8. Photographs of the top, middle and bottom of the experimental sample, respectively.

Figure 8

Open in a new tab

(b) Measured transmission coefficients tvv, tuv, tvu and tuu for forward propagating waves under normal incidence.

Conclusion

In summary, we have firstly demonstrated a reflective converter composed of a single-layered SRR both numerically and experimentally. The proposed converter can accomplish high efficiency and broad bandwidth for LP waves. Experimental results show that the cross-polarizaton conversion reflectance above 0.84 is achieved from 8.6 to 18.6 GHz for LP incident waves under normal incidence, and above 0.8 from 9.2 to 18.5 GHz for incident angle of 30 degree. Subsequently, a multi-layered MM based on SRR enables a dramatic improvement of the recently demonstrated asymmetric transmission (AT) effect, different from the properties in the previous papers34,35,36,37,38,39,40,41,42,47,48. It is found that the cross-polarization transmission coefficient over 0.8 of the proposed multi-layered MM can be achieved from 9.9 to 12.5 GHz for the u-polarized wave and from 16.1 to 22.5 GHz for the v-polarized wave in the two pass-bands, respectively. The broadband property can be maintained for incident angle up to 30 degree. These two separated AT pass-bands have a function of selective polarization filter, which can be switched on/off by changing the polarization state of incident waves. The physical mechanisms are elucidated by taking advantage of electric fields and current distribution. With the properties of broad bandwidth and high-efficiency, we believe that these two structures will be beneficial for designing polarization-controlled and selective transmission converter.

Methods

Finite element method modeling was performed using commercial software CST Microwave Studio. The frequency domain solver was carried out and a frequency sweep of 6–24 GHz used to produce the results shown in this paper.

To obtain the polarization conversion characteristic, both co-polarized and cross-polarized signals were measured. For the reflective converter, the sample was placed on the test platform in the experiment. The distance between antennas and sample was chosen far enough to avoid near field effect. Two standard linearly polarized horn antennas served as transmitter and receiver, respectively. An Agilent 8720ET vector network analyzer and the horn antennas were connected by a coaxial cable. Through rotating the receiving antenna by 90 degree, the horn antennas can be reconfigured between x and y polarization modes, so that we can obtain both the co- and cross-polarized reflectance. The separation angle between the two antennas is set to be less than 5 degree, which can be considered as the case of the normal incidence. For oblique incidence. the transmitting and receiving horn antennas were both moved along the arch trace structure to measure the reflectance.

Additional Information

How to cite this article: Zhang, L. et al. Ultrabroadband Design for Linear Polarization Conversion and Asymmetric Transmission Crossing X- and K- Band. Sci. Rep. 6, 33826; doi: 10.1038/srep33826 (2016).

Supplementary Material

Supplementary Information
srep33826-s1.pdf (782KB, pdf)

Acknowledgments

The authors are grateful to the supports from the National Natural Science Foundation of China under Grant Nos 51025208 and 61471097, the Program for Changjiang Scholars and Innovative Research Team in University, the Fundamental Research Funds under Grant No. ZYGX2013J029, and the Open Foundation of National Engineering Research Center of Electromagnetic Radiation Control Materials under Grant Nos. ZYGX2016K003-2.

Footnotes

Author Contributions L.Z., P.Z. and L.D. conceived the idea. L.Z., P.Z. and H.C. contributed equally to the numerical simulation and physical interpretations. H.L., Li Z., E.L. and J.X. fabricated the sample and carried out the experiment, L.Z., P.Z. and H.X. wrote the manuscript. All the authors have analyzed and discussed the results thoroughly and contributed to the manuscript.

References

  1. Yu N. F. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011). [DOI] [PubMed] [Google Scholar]
  2. Li G. et al. Continuous control of the nonlinearity phase for harmonic generations. Nat. Mater. 14, 607–612 (2015). [DOI] [PubMed] [Google Scholar]
  3. Grady N. K. et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 340, 1304–1307 (2013). [DOI] [PubMed] [Google Scholar]
  4. Aieta F. et al. Out-of-plane reflection and refraction of light by anisotropic optical antenna metasurfaces with phase discontinuities, Nano Lett. 12, 1702–1706 (2012). [DOI] [PubMed] [Google Scholar]
  5. Zhao Y., Belkin M. A. & Alù A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Comm. 3, 870 (2012). [DOI] [PubMed] [Google Scholar]
  6. Yang Y. et al. Valentine, Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Lett. 14, 1394–1399 (2014). [DOI] [PubMed] [Google Scholar]
  7. Cong L. et al. A perfect metamaterial polarization rotator. Appl. Phys. Lett. 103, 171107 (2013). [Google Scholar]
  8. Yu N. et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 12, 6328–6333 (2012). [DOI] [PubMed] [Google Scholar]
  9. Shalaev M. I. et al. High-efficiency all-dielectric metasurfaces for ultracompact beam manipulation in transmission mode. Nano Lett. 15, 6216–6266 (2015). [DOI] [PubMed] [Google Scholar]
  10. Kruk S. et al. Broadband highly-efficient dielectric metadevices for polarization control. APL Photonics 1, 030801 (2016). [Google Scholar]
  11. Larouche S. et al. Infrared metamaterial phase holograms. Nat. Mater. 11, 450–454 (2012). [DOI] [PubMed] [Google Scholar]
  12. Zheng G., Muhlenbernd H., Kenney M., Li G., Zentgraf T. & Zhang S. Metasurface holograms reaching 80% efficiency. Nat. Nanotech. 10, 308–312 (2015). [DOI] [PubMed] [Google Scholar]
  13. Ni X., Emani N. K., Kildishev A. V., Boltasseva A. & V Shalaev,. Broadband light bending with plasmonic nanoantennas. Science 335, 427–427 (2012). [DOI] [PubMed] [Google Scholar]
  14. Sun S. et al. High-efficiency broadband anomalous reflection by gradient metasurfaces. Nano Lett. 12, 6223–6229 (2012). [DOI] [PubMed] [Google Scholar]
  15. Born M. & Wolf E. Principles of Optics (Cambridge University Press, Cambridge, England, 1999). [Google Scholar]
  16. Hecht E. Optics (Addison Wesley, New York, 2002). [Google Scholar]
  17. Huang Y., Zhou Y. & Wu S. T. Broadband circular polarizer using stacked chiral polymer films. Opt. Express 15, 6414–6419 (2007). [DOI] [PubMed] [Google Scholar]
  18. Broer D. J., Lub J. & Mol G. N. Wide-band reflective polarizers from cholesteric polymer networks with a pitch gradient. Nature 378, 467–469 (1995). [Google Scholar]
  19. Zheludev N. I. & Kivshar Y. S. From metamaterials to metadevices. Nat. Mater. 11, 917–924 (2012). [DOI] [PubMed] [Google Scholar]
  20. Landy N. I., Sajuyigbe S., Mock J. J., Smith D. R. & Padilla W. J. Perfect metamaterial absorber. Phys. Rev. Lett. 100, 207402 (2008). [DOI] [PubMed] [Google Scholar]
  21. Kundtz N. & Smith D. R. Extreme-angle broadband metamaterial lens. Nat. Mater. 9, 129–132 (2010). [DOI] [PubMed] [Google Scholar]
  22. Schurig D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006). [DOI] [PubMed] [Google Scholar]
  23. Levesque Q. et al. Plasmonic planar antenna for wideband and efficient linear polarization conversion. Appl. Phys. Lett. 104, 111105 (2014). [Google Scholar]
  24. Black L. J., Wang Y., Groot C. H., Arbouet A. & Muskens O. L. Optimal Polarization Conversion in Coupled Dimer Plasmonic Nanoantennas for Metasurfaces. ACS Nano 8, 6390–6399 (2014). [DOI] [PubMed] [Google Scholar]
  25. Li Z. et al. High performance broadband asymmetric polarization conversion due to polarization-dependent reflection. Plasmonics 10, 1703–1711 (2015). [Google Scholar]
  26. Gao X. et al. Wideband and high-efficiency linear polarization converter based on double V-shaped metasurfaces. IEEE Trans. Antennas Propag. 63, 3522–3530 (2015). [Google Scholar]
  27. Zhang L. et al. Realization of broadband reflective polarization converter using asymmetric cross-shaped resonator. Opt. Mater. Express 6, 1393–1404 (2016). [Google Scholar]
  28. Yang Y. et al. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Lett. 14, 1394–1399 (2014). [DOI] [PubMed] [Google Scholar]
  29. Hao J. et al. Manipulating electromagnetic wave polarizations by anisotropic metamaterials. Phys. Rev. Lett. 99, 063908 (2007). [DOI] [PubMed] [Google Scholar]
  30. Chin J. Y., Liu M. & Cui T. J. Metamaterial polarizers by electric-field-coupled resonators. Appl. Phys. Lett. 93, 251903 (2008). [Google Scholar]
  31. Shi H., Zhang A., Zhang S., Li J. & Jiang Y. Dual-band polarization angle independent 90° polarization rotator using twisted electric-field-coupled resonators. Appl. Phys. Lett. 104, 034102 (2014). [Google Scholar]
  32. Fedotov V. A. et al. Asymmetric Propagation of Electromagnetic Waves through a Planar Chiral Structure. Phys. Pew. Lett. 97, 167401 (2006). [DOI] [PubMed] [Google Scholar]
  33. Fedotov V. A., Schwanecke A. S., Zheludev N. I., Khardikov V. V. & Prosvirnin S. L. Asymmetric transmission of light and enantiomerically sensitive plasmon resonance in planar chiral nanostructures. Nano Lett. 7, 1996–1999 (2007). [Google Scholar]
  34. Mutlu M., Akosman A. E., Serebryannikov A. E. & Ozbay E. Diodelike asymmetric transmission of linearly polarized waves using magnetoelectric coupling and electromagnetic wave tunneling. Phys. Rev. Lett. 108, 213905 (2012). [DOI] [PubMed] [Google Scholar]
  35. Singh R., Plum E., Menzel C., Rockstuhl C., Azad A. K., Cheville R. A., Lederer F., Zhang W. & Zheludev N. I. Terahertz metamaterial with asymmetric transmission. Phys. Rev. B 80, 153104 (2009). [Google Scholar]
  36. Menzel C. et al. Asymmetric transmission of linearly polarized light at optical metamaterials. Phys. Rev. Lett. 104, 253902 (2010). [DOI] [PubMed] [Google Scholar]
  37. Mutlu M., Akosman A. E., Serebryannikov A. E. & Ozbay E. Asymmetric transmission of linearly polarized waves and polarization angle dependent wave rotation using a chiral metamaterial. Opt. Express 19, 14290–14299 (2011). [DOI] [PubMed] [Google Scholar]
  38. Kenanakis G. et al. Three-Dimensional Infrared Metamaterial with Asymmetric Transmission. ACS Photonics 2, 287–294 (2015). [Google Scholar]
  39. Schwanecke A. S., Fedotov V. A., Khardikov V. V., Prosvirnin S. L., Chen Y. & Zheludev N. I. Nanostructured Metal Film with Asymmetric Optical Transmission. Nano Lett. 8, 2940–2943 (2008). [DOI] [PubMed] [Google Scholar]
  40. Shi. J. et al. Dual-band asymmetric transmission of linear polarization in bilayered chiral metamaterial. Appl. Phys. Lett. 102, 191905 (2013). [Google Scholar]
  41. Xu Y., Shi Q., Zhu Z. & Shi J. Mutual conversion and asymmetric transmission of linearly polarized light in bilayered chiral metamaterial. Opt. Express 22, 25679–25688 (2015). [DOI] [PubMed] [Google Scholar]
  42. Liu X. et al. Manipulating wave polarization by twisted plasmonic metamaterials. Opt. Express 4, 1003–1010 (2015). [Google Scholar]
  43. Cong L. et al. Polarization Control in Terahertz Metasurfaces with the Lowest Order Rotational Symmetry. Adv. Opt. Mater. 3, 1176–1183 (2015). [Google Scholar]
  44. Liu W. et al. Realization of broadband cross-polarization conversion in transmission mode in the terahertz region using a single-layer metasurface. Opt. Lett. 40, 3185–3188 (2015). [DOI] [PubMed] [Google Scholar]
  45. Wang Y. H. et al. Broadband asymmetric transmission by rotated bilayer cross-shaped metamaterials. J. Phys. D: Appl. Phys. 48, 485306 (2015). [Google Scholar]
  46. Wang Y. H. et al. Broadband high-efficiency transmission asymmetry by a chiral bilayer bar metastructure. J. Appl. Phys. 117, 173102 (2015). [Google Scholar]
  47. Liu D., Xiao Z., Ma X. & Wang Z. Asymmetric transmission of linearly and circularly polarized waves in metamaterial due to symmetry-breaking. Appl. Phys. Express 8, 052001 (2015). [Google Scholar]
  48. Xiao Z., Liu D., Ma X. & Wang Z. Multi-band transmissions of chiral metamaterials based on Fabry-Perot like resonators. Opt. Express 23, 7053–7061 (2015). [DOI] [PubMed] [Google Scholar]
  49. Wang J. et al. Cavity-based linear polarizer immune to the polarization direction of an incident plane wave. Opt. Lett. 41, 424–427 (2016). [DOI] [PubMed] [Google Scholar]
  50. Ji R. et al. Giant and broadband circular asymmetric transmission based on two cascading polarization conversion cavities. Nanoscale 8, 8189–8194 (2016). [DOI] [PubMed] [Google Scholar]
  51. Novitsky A. V., Galynsky V. M. & Zhukovsky S. V. Asymmetric transmission in planar chiral split-ring metamaterials: Microscopic Lorentz-theory approach. Phys. Rev. B 86, 075138 (2012). [Google Scholar]
  52. Muhlig S. et al. Multipole analysis of meta-atoms. Metamaterials 5, 64–73 (2011). [Google Scholar]
  53. Vinoy K. L. & Jha R. M. Radar Absorbing Materials: From Theory to Design and Characterization, Chap. 5 (Boston, MA: Kluwer Academic Publishers, 1966). [Google Scholar]
  54. Chen H. T. et al. Antireflection coating using metamaterials and identification of its mechanism. Phys. Rev. Lett. 105, 073901 (2010). [DOI] [PubMed] [Google Scholar]
  55. Chen H. T. Interference theory of metamaterial perfect absorbers. Opt. Express 20, 7165–7172 (2012). [DOI] [PubMed] [Google Scholar]
  56. Blanchard R. et al. Modeling nanoscale V-shaped antennas for the design of optical phased arrays. Phys. Rew. B 85, 155457 (2012). [Google Scholar]
  57. Chin J. Y., Lu M. & Cui T. J. Metamaterial polarizers by electric-field-coupled resonators. Appl. Phys. Lett. 93, 251903 (2008). [Google Scholar]
  58. Rogacheva A. V., Fedotov V. A., Schwanecke A. S. & Zheludev N. I. Giant gyrotropy due to electromagnetic-field coupling in a bilayered chiral structure. Phys. Rev. Lett. 97, 177401 (2006). [DOI] [PubMed] [Google Scholar]
  59. Strikwerda A. C. et al. Comparison of birefringent electric split-ring resonator and meanderline structures as quarter-wave plates at terahertz frequencies. Opt. Express 17, 136–149 (2009). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep33826-s1.pdf (782KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES