Methodological approach to determine minor, considerable, and major treatment effects in the early benefit assessment of new drugs

Abstract

At the beginning of 2011, the early benefit assessment of new drugs was introduced in Germany with the Act on the Reform of the Market for Medicinal Products (AMNOG). The Federal Joint Committee (G‐BA) generally commissions the Institute for Quality and Efficiency in Health Care (IQWiG) with this type of assessment, which examines whether a new drug shows an added benefit (a positive patient‐relevant treatment effect) over the current standard therapy. IQWiG is required to assess the extent of added benefit on the basis of a dossier submitted by the pharmaceutical company responsible. In this context, IQWiG was faced with the task of developing a transparent and plausible approach for operationalizing how to determine the extent of added benefit. In the case of an added benefit, the law specifies three main extent categories (minor, considerable, major). To restrict value judgements to a minimum in the first stage of the assessment process, an explicit and abstract operationalization was needed. The present paper is limited to the situation of binary data (analysis of 2 × 2 tables), using the relative risk as an effect measure. For the treatment effect to be classified as a minor, considerable, or major added benefit, the methodological approach stipulates that the (two‐sided) 95% confidence interval of the effect must exceed a specified distance to the zero effect. In summary, we assume that our approach provides a robust, transparent, and thus predictable foundation to determine minor, considerable, and major treatment effects on binary outcomes in the early benefit assessment of new drugs in Germany. After a decision on the added benefit of a new drug by G‐BA, the classification of added benefit is used to inform pricing negotiations between the umbrella organization of statutory health insurance and the pharmaceutical companies.

1. Introduction

Following experiences in other countries, at the beginning of 2011 a procedure for the early benefit assessment of new drugs was introduced in Germany with the Act on the Reform of the Market for Medicinal Products (Arzneimittelmarktneuordnungsgesetz, AMNOG) (BMG, 2010a). Social Code Book V (Sozialgesetzbuch, SGB V), which regulates statutory health care services, was amended in accordance with AMNOG (§35a SGB V). The two main organizations involved in the early benefit assessment are the Federal Joint Committee (Gemeinsamer Bundesaussschuss, G‐BA) and the Institute for Quality and Efficiency in Health Care (Institut für Qualität und Wirtschaftlichkeit im Gesundheitswesen, IQWiG). The G‐BA is the main decision‐making body in statutory health care and specifies which health care services are to be provided by the statutory health insurance (SHI) funds. IQWiG is an independent, nongovernment, and nonprofit health technology assessment (HTA) agency and is mainly commissioned by the G‐BA and occasionally by the Federal Ministry of Health. Its primary responsibility is the production of HTA reports on the patient‐relevant benefit of drugs and nondrug interventions. These reports are used to inform evidence‐based decision‐making by the G‐BA. On the basis of the new health care legislation, the G‐BA holds overall responsibility for the assessment of all new drugs entering the German market since 1 January 2011. The G‐BA generally commissions IQWiG with the actual assessment, which examines whether a new drug shows an added benefit over the current standard therapy (i.e., the “appropriate comparator therapy” specified by the G‐BA). The results of the assessment form the basis of negotiations on the new drug's reimbursement price, which should refer to the existence and extent of added benefit. These negotiations are held by the SHI umbrella organization and the pharmaceutical companies.

The main components of the assessment are defined in the Regulation for Early Benefit Assessment of New Pharmaceuticals (Arzneimittel‐Nutzenbewertungsverordnung, ANV) (BMG, 2010b), which supplements the provisions of §35a SGB V. For instance, the ANV specifies according to which criteria the appropriate comparator therapy should be chosen and defines that an added benefit of the new drug is present if the drug shows a higher quantitative or qualitative benefit than the appropriate comparator therapy. In this context, “benefit” is defined as a patient‐relevant treatment effect. The ANV also specifies the determination of the extent of added benefit according to certain key points. In this context, during its first early benefit assessment IQWiG (2011) was faced with the task of developing a transparent and plausible approach for operationalizing how the extent of added benefit was to be determined (IQWiG, 2013a, Section 3.3.3). This approach was also to consider IQWiG's specific role in the German health care system and in particular its relationship with the G‐BA. Whereas in other health care systems HTA agencies (e.g., the National Institute for Health and Care Excellence, NICE) are responsible for both assessments and appraisals of health care interventions, assessments in Germany are conducted by IQWiG and appraisals by the G‐BA. Stakeholders in the health care system, including patients (albeit without a voting right), are represented in the G‐BA. In addition to considering scientific evidence, it is their responsibility and right to contribute health policy and value dimensions to the discussions and decisions. In contrast, IQWiG does not possess such a mandate. Although it should be acknowledged that there is no sharp transition from the assessment to the appraisal phase, a guiding principle in the development of an approach to determine the extent of added benefit was preferably to avoid value judgements at this stage, and instead adopt a formal and abstract approach reflecting the scientific evidence and thus providing results that serve as a basis for further consultations.

Section 2 covers the methodological approach developed by IQWiG to determine the extent of added benefit of a new drug in the assessment of dossiers provided by pharmaceutical companies. Details of the legal requirements and their amendments, which form the basis for the approach, are presented in Sections 2.1 and 2.2. The determination of the extent of added benefit at outcome level and the key points to be considered here are described in Sections 2.3 and 2.4. The basic principle and methods for deriving the thresholds for the extent of added benefit and the resulting specific thresholds for all outcome categories and extent categories are described in Sections 2.5 and 2.6. The validity of the determined thresholds is examined by means of Monte Carlo simulations in Section 2.7. Section 3 contains a discussion of IQWiG's approach.

2. Methodological approach

2.1. 2.1 Legal requirements

For the early benefit assessment of a new drug, the pharmaceutical company submits a dossier to the G‐BA containing a systematic review of the available (published and unpublished) evidence on the new drug versus the appropriate comparator therapy. The assessment has to be carried out immediately after the new drug enters the market, that is generally shortly after regulatory approval. In the dossier the company has to explain the probability and extent of the added benefit of a new drug. The probability of added benefit is based on the validity of the evidence presented and describes how reliable the conclusion on added benefit is. For the extent of added benefit, the following categories are specified in the law:

• Major added benefit

• Considerable added benefit

• Minor (more than marginal) added benefit

• Nonquantifiable added benefit (potentially minor, considerable, or major)

• No added benefit

• Less benefit (than the appropriate comparator therapy)

For the first three categories, the ANV also provides a definition as well as examples of criteria for particular consideration (BMG, 2010bb, §5 (7)). These criteria describe qualitative characteristics (type of outcome) and also explicitly quantitative characteristics (e.g., “major” versus “moderate” increase in survival time). In addition, a hierarchical ranking of outcomes is obviously intended, as sometimes the same modifier (e.g., “relevant”) results in a different extent of added benefit for different outcomes.

The details of the primarily relevant categories of extent of added benefit (minor, considerable, major) are shown in Table 1 (text in normal font). On the basis of these legal requirements, it was IQWiG's responsibility to operationalize the extent of added benefit for the early benefit assessment. The criteria provided in the ANV for the extent of the added benefit designate (legal) terms. Some of these terms are clearly defined (e.g., “survival time”, “serious adverse events”) and some are not (e.g., “alleviation of serious symptoms”). In addition, the criteria listed are not allocated to all categories. For instance, examples of “survival time” are given only for the categories “considerable” and “major” added benefit.

Table 1.

Determination of extent of added benefit—Ranked criteria according to the ANV plus amendments, as well as effect sizes for generation of thresholds^{a )}

		Outcome category
		All‐cause mortality	Serious (or severe) symptoms (or late complications) and adverse events	Health‐related quality of life	Nonserious (or nonsevere) symptoms (or late complications) and adverse events
Extent category	Major: sustained and great improvement in the therapy‐relevant benefit, which has not previously been achieved versus the appropriate comparator therapy	Major increase in survival time RR1 = 0.50	Long‐term freedom or extensive avoidance RR1 = 0.17	Major improvement RR1 = 0.17	Not applicable
	Considerable: marked improvement in the therapy‐relevant benefit, which has not previously been achieved versus the appropriate comparator therapy	Moderate increase in survival time RR1 = 0.83	Alleviation or relevant avoidance RR1 = 0.67	Important improvement RR1 = 0.67	Important avoidance RR1 = 0.33
	Minor: moderate and not only marginal improvement in the therapy‐relevant benefit, which has not previously been achieved versus the appropriate comparator therapy	Any increase in survival time	Any reduction	Relevant improvement	Relevant avoidance RR1 = 0.67

^aAmendments to ANV in italics.

ANV, Arzneimittel‐Nutzenbewertungsverordnung (regulation for early benefit assessment of new pharmaceuticals).

The criteria allocated to the categories are not to be regarded as conclusive. For instance, even if an increase in survival time is classified as less than “moderate”, it cannot be assumed that the legislator would not at least acknowledge a “minor” added benefit. Furthermore, the outcome “(health‐related) quality of life”, which is explicitly defined as a criterion of benefit in §2 (3) ANV, is not mentioned at all in the list of criteria for the extent of added benefit (BMG, 2010b).

2.2. 2.2 Amendments to legal requirements

On the basis of the legal requirements it is reasonable and necessary to extend the list of criteria by means of criteria that are qualitatively and quantitatively comparable. These amendments to the ANV requirements were made by IQWiG and are shown in Table 1 (text in italics). On the basis of these amendments the outcome categories are structured to illustrate the ranking of outcomes intended in the ANV and to consider disease severity according to §5 (7) ANV (BMG, 2010bb). For this purpose, the outcomes are grouped as follows, according to their relevance:

1. All‐cause mortality.

2. Serious (or severe) symptoms (or late complications); serious (or severe) adverse events, health‐related quality of life.

3. Nonserious (or nonsevere) symptoms (or late complications), nonserious (or nonsevere) adverse events.

Health‐related quality of life is regarded to be of equal importance as serious (or severe symptoms), late complications, and adverse events. The potential categories of extent of added benefit for nonserious outcomes are restricted to “minor” and “considerable”.

2.3. Determining the extent of added benefit at outcome level

The above amendments to the legal requirements highlight two points: On the one hand, the extent of added benefit depends on the quality of outcomes; there is thus a hierarchy of outcomes. On the other, the verbal specifications of the different categories of extent of added benefit vary, depending on the outcome. This suggests (firstly) determining the extent of added benefit separately for each outcome.

In accordance with the ANV, the term “benefit” is defined as an “effect” (§2 (3)) and the term “added benefit” is defined as such an effect compared with the appropriate comparator therapy (BMG, 2010b, §2 (4)). It can be inferred from these definitions that the extent of added benefit must be determined by taking into account both the hierarchy of outcomes and effect sizes. For the development of a methodological approach to determine the extent of added benefit this means that, for each outcome separately, the effect size—independent of its direction—is classified into one of the three categories of extent (minor, considerable, major); hereinafter referred to as “extent categories.” The basic approach aims to derive thresholds for confidence intervals (CIs) for relative effect measures depending on the effects to be achieved, which in turn depend on the quality of the outcomes and the extent categories.

It will not always be possible to quantify the extent of effects at outcome level. For instance, if a statistically significant effect on a sufficiently valid surrogate is present, but no reliable estimate of this effect on a patient‐relevant outcome is possible, then the (patient‐relevant) effect cannot be quantified. In such and similar cases, only an effect of a “nonquantifiable” extent can be concluded.

2.4. Key points for determining the extent of added benefit at outcome level

The ANV provides no details on the questions as to which effect sizes for the individual outcomes result in which extent category, or which effect measures should be chosen for the assessment. In principle, these questions can only be partly answered from a methodological point of view. Nevertheless, IQWiG is required to assess the extent of added benefit presented in the dossiers (BMG, 2010b, §7 (2)). To restrict to a minimum at this stage the value judgements that will necessarily be made in the further deliberation process, the following measures are required:

1. Explicit operationalization to ensure a transparent approach.

2. Abstract operationalization to achieve the best possible consistency between early benefit assessments.

Against this background a suitable effect measure must first be chosen. The present paper is limited to the situation in which binary data are available (analysis of 2 × 2 tables). For binary data IQWiG chose to use relative effect measures for the following reasons:

Relative effect measures—for example, the relative risk (RR) and the odds ratio (OR)—show the following advantages over absolute measures such as the risk difference (RD):

1. The risk difference does not describe the effectiveness of therapy as such, as this difference strongly depends on the baseline risk in the control group. However, the baseline risk varies between regions, populations, and over the course of time, as well as particularly between control groups receiving different comparator therapies. A risk difference should thus be interpreted as a descriptive measure of a specific study, not as a fixed measure of a specific treatment procedure; this is also and primarily a problem in meta‐analyses (Smeeth et al., 1999). This great susceptibility to external conditions calls into question the transferability of absolute effect measures from clinical studies to the daily healthcare setting. It is therefore common practice preferably to express effects shown in clinical studies as relative risks, odds ratios, or hazard (or incidence) ratios (Deeks, 2002).

2. The degree of the risk difference is limited by the degree of the baseline risk (absolute risk in the control group). If this baseline risk is 0.01, then the risk difference can never exceed 0.01 (or if it is 0.1, the risk difference can never exceed 0.1 etc.). The risk difference could only reach the optimum value of 1 if the baseline risk was 1. For instance, if an absolute risk reduction of at least 0.2 was defined as a substantial therapeutic improvement, then, for this example of a requirement, in diseases with (long term) survival rates of > 0.8, generally a major added benefit (for the corresponding outcome) would no longer be presentable.

3. A further disadvantage of the use of the absolute risk reduction as an effect measure to operationalize the determination of the extent of added benefit is that an exact time point must be defined at which this absolute risk reduction is determined (e.g., after 1, 2, 5, or 10 years), if no generally accepted definitions are available (e.g., 30‐day mortality for myocardial infarction).

In summary, absolute risk reductions may have more of an impact in a situation of individual decision making, but relative effect measures are more suitable for general conclusions in terms of an assessment of the added benefit of a drug.

Relative measures have in common that the zero effect (no group difference) is 1. In the following text, we address effects below 1, from which effects above 1 can be calculated by using the reciprocal.

For the result to be classified as a minor, considerable, or major added benefit, the methodological approach for determining the extent of added benefit at outcome level stipulates that the (two‐sided) 95% CI of the effect undercuts the respective threshold in terms of a shift in the hypothesis boundary. In comparison with the examination of point estimates, such an inferential statistical approach has two main advantages: (i) the precision of the estimate is considered in the assessment; and accordingly, (ii) the probability of statistical errors can be limited to the usual small values (e.g. 5%).

2.5. Derivation of thresholds for the extent of added benefit

As usually required for the approval of a new drug, we assume that two pivotal studies are available. The basic principle is as follows: a specific true effect corresponds to a specific extent category (e.g., a relative risk of 0.5 corresponds to a “major” extent of added benefit). The sample size of the two studies is chosen so that for this true effect, there is a specific power (e.g. 80%) for the conventional hypotheses for the testing of a statistically significant difference. For all hypothesis boundaries shifted from the null effect (to show relevant superiority), this type of study has reduced power. In order to maintain the same power for the shifted hypothesis of interest as specified for the testing of the conventional (nonshifted) hypotheses, the sample size would have to be increased—either within the study or by combining several studies.

This principle is outlined in Fig. 1: the pooled result of the two studies has a higher precision. The hypothesis boundary for the shifted hypotheses (i.e., the threshold) is then precisely selected so that the power for the conventional hypotheses of the two individual studies corresponds to the power for the shifted hypotheses of the combined (pooled) analysis.

Figure 1.

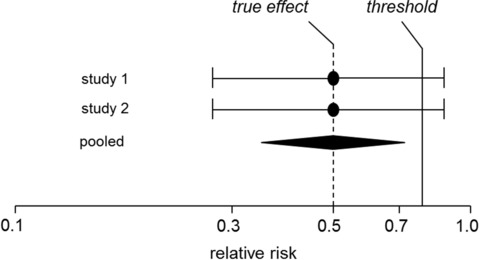
Outline of the basic principle for deriving thresholds.

The starting point for the derivation of thresholds is the question as to how large the true effects have to be in order to be classified, for instance, as “major”. For this purpose, a relative risk of 0.50—proposed by Djulbegovic et al. (2006) as a requirement for a “breakthrough”—was defined as an effect of a “major” extent for the outcome “all‐cause mortality”. For this true effect (0.5), the question arises as to how the threshold should be chosen to actually achieve the extent “major” with adequate power.

The starting point is the planning of a (fictional) study to test the conventional hypotheses

$$H_0:RR\ge R{R}_{0}vs.H_1:RR<R{R}_0$$

on the basis of the relative risk $\left(R{R}_0=1\right)$. The relative risk is assumed to be $RR=p_2/p_1$, whereby p ₂ and p ₁ represent the risk of the test and control group, respectively. The required sample size is calculated by specifying the significance level α, the power $1-\beta$, the risk in the control group p ₁, and the true effect $R{R}_1$ (and thereby $p_2=R{R}_1·{\mathrm{p}}_1$). If n ₁ = n ₂ applies for the sample sizes of both groups, the overall sample size N = n ₁ + n ₂ is calculated by

$$N=4\frac{{\left[z_{1-\alpha }{f}_1+z_{1-\beta }{f}_2\right]}^2}{{\left[p_2-R{R}_0{p}_1\right]}^2},$$ (1)

whereby $z_q$ is the q‐quantile of $N\left(0,1\right)$ and $f_1=f_1\left(p_1,p_2\right)$ as well as $f_2=f_2\left(p_1,p_2\right)$ are sole functions of p ₁and p ₂:

$$f_1\left(p_1,p_2\right)=\sqrt{\left(\frac{p_1}{2}+\frac{p_2}{2}\right)\left(1-\frac{p_1}{2}-\frac{p_2}{2}\right)}$$

$$f_2\left(p_1,p_2\right)=\sqrt{\frac{p_1\left(1-p_1\right)}{2}+\frac{p_2\left(1-p_2\right)}{2}}$$

(sample size formulas for Pearson's χ²‐test according to documentation of the “power” procedure of the SAS software (SAS Institute, 2009); see Section 2.7 for background information).

Solving formula (1) for $R{R}_0$ results in

$$R{R}_0=\frac{1}{p_1}\left[p_2+\frac{2}{\sqrt{N}}\left(z_{1-\alpha }{f}_1+z_{1-\beta }{f}_2\right)\right].$$ (2)

For a study with the power $1-{\beta }_1$ and the hypothesis boundary $R{R}_0=1$, formula (1) results in an overall sample size of

$$N_1=4\frac{{\left[z_{1-\alpha }{f}_1+z_{1-{\beta }_1}{f}_2\right]}^2}{{\left[p_2-p_1\right]}^2}.$$

It should be noted that this calculation for RR ₀ = 1 and n ₁ = n ₂ corresponds to the formula by Farrington and Manning (1990). The use of a sample size of $N=c{N}_1$ increased by the factor c and a power specification of $1-{\beta }_2$ for the shifted hypotheses in formula (2), results in the hypothesis boundary

$$R{R}_0=\frac{1}{p_1}\left[p_2+\frac{2\left(z_{1-\alpha }{f}_1+z_{1-{\beta }_2}{f}_2\right)}{\sqrt{c·4\frac{{\left[z_{1-\alpha }{f}_1+z_{1-{\beta }_1}{f}_2\right]}^2}{{\left[p_2-p_1\right]}^2}}}\right]=\frac{1}{p_1}\left[p_2-\frac{p_2-p_1}{\sqrt{c}}·\frac{\left(z_{1-\alpha }{f}_1+z_{1-{\beta }_2}{f}_2\right)}{\left(z_{1-\alpha }{f}_1+z_{1-{\beta }_1}{f}_2\right)}\right].$$

In the case of $\beta ={\beta }_1={\beta }_2$ the hypothesis boundary is independent of the choice of β:

$$R{R}_0=\frac{1}{p_1}\left[p_2-\frac{p_2-p_1}{\sqrt{c}}\right]=\left(1-\frac{1}{\sqrt{c}}\right)RR+\frac{1}{\sqrt{c}}.$$

This hypothesis boundary serves as the threshold CI_S for the upper limit of the two‐sided 95% CI for the relative risk. Assuming the normal case of two studies, it can be assumed that the sample size is twice as large, so that $c=2$ is chosen. The threshold CI_S only depends on the assumed true effect (RR ₁):

$$C{I}_S=R{R}_1\left(1-\frac{1}{\sqrt{2}}\right)+\frac{1}{\sqrt{2}}.$$

This hypothesis boundary serves as a threshold $C{I}_S$ for the upper limit of the two‐sided 95% CI for the relative risk.

This consequently results in a threshold of approximately 0.85 for the true effect of 0.5 specified above. For this threshold of 0.85, the simultaneous requirement for feasibility and stringency can be regarded as fulfilled.

In a next step, for the matrix of the extent of the effects, the other true effects are specified and the corresponding thresholds determined. In this context, it should be noted that, on the basis of the outcome category “mortality”, the requirements should increase for less serious outcomes, and on the basis of the extent category “major”, should decrease for lower extent categories (see below). In this context, a division into sixths for the true effects was shown to be a pragmatic solution. The specified true effects $R{R}_1$ are presented in Table 1 and can be used to calculate the thresholds according to the formula above. For practical application the thresholds are rounded to 0.05.

In the specific assessment of the added benefit the 95% CI of the effects of the individual outcomes are compared with these rounded thresholds. For the three extent categories (minor, considerable, major), Table 2 displays the thresholds to be undercut for each of the three categories of the quality of outcomes (mortality, serious symptoms etc., nonserious symptoms etc.).

Table 2.

Thresholds for determining the extent of an effect

Extent category	Outcome category
	All‐cause mortality	Serious (or severe) symptoms (or late complications) and adverse events, as well as quality of lifea )	Nonserious (or nonsevere) symptoms (or late complications) and adverse events
Major	0.85	0.75 and risk ≥ 5%b )	Not applicable
Considerable	0.95	0.90	0.80
Minor	1.00	1.00	0.90

^aPrecondition (as for all patient‐reported outcomes): use of a validated or established instrument, as well as a validated or established response criterion.

^bRisk must be at least 5% for at least one of the two groups compared.

According to this, the thresholds vary with regard to the two dimensions “outcome category” and “extent category”. The greater the relevance ascribed to the outcome, the closer the thresholds lie to 1. This takes into account the ANV's requirement to consider disease severity. In contrast, the greater the determined extent of the effect, the further the thresholds lie from 1.

The specific thresholds for all outcome categories and extent categories are described in the following section. It should be noted that, depending on the available data, the CIs are calculated from one, two or more studies. Even though the derivation of thresholds is based on the normal case of two studies, these thresholds can be applied independently of the number of available studies.

2.6. Thresholds at outcome level

2.6.1. All‐cause mortality

With the usual significance level of 5%, any statistically significant increase in survival time is at least classified as “minor added benefit”, since for all‐cause mortality the ANV's requirement that an effect should be “more than marginal” is regarded to be fulfilled by the outcome itself. The threshold referring to the 95% CI is thus 1 here. An increase in survival time is classified as a “considerable” effect if a threshold of 0.95 is undercut. An increase in survival time is classified as being “major” if the threshold of 0.85 is undercut by the upper limit of the 95% CI.

2.6.2. Serious (or severe) symptoms (or late complications), serious or (severe) adverse events, health‐related quality of life

For serious (or severe) symptoms (or late complications) and serious (or severe) adverse events, any statistically significant reduction also represents at least a “minor” effect, as the requirement of “more than marginal” is already fulfilled by the quality of the outcome itself.

In contrast to the desired effects on all‐cause mortality, for the above outcomes a “considerable” effect requires that a threshold of 0.90 must be undercut and a “major” effect requires that a threshold of 0.75 is undercut. To derive a major effect also requires that the risk of the examined event should be at least 5% in at least one of the groups compared. This additional criterion supports the relevance of the event at population level and allows for the special requirements for this category of added benefit.

The precondition for determining the extent of added benefit for outcomes on health‐related quality of life (as for all patient‐reported outcomes) is that both the instruments applied and the response criteria must be validated or at least generally recognized. If these results are dichotomous in terms of responders and nonresponders, the above criteria for serious symptoms apply (risk for the category “major” should be at least 5%).

2.6.3. Nonserious (or nonsevere) symptoms (or late complications), nonserious (or nonsevere) adverse events

The specification of thresholds for the nonserious (or nonsevere) symptoms (or late complications) and the nonserious (or nonsevere) adverse events takes into account the lower severity versus the first two outcome categories. As a matter of principle, the effect for nonserious outcomes should not be classified as “major”. To classify an effect as “considerable” or “minor” the thresholds of 0.80 or 0.90 respectively must be undercut. In the latter case, this is based on the requirement for minor added benefit specified in §5 (7) ANV that there must be a moderate, and not only marginal, improvement. It is thus implied that effects (also statistically significant ones) only assessed as “marginal” lead to classification into the category “no added benefit”.

2.7. Validity of thresholds

The formula used in Section 2.5 for the relationship between the true effect and the threshold is independent of the other requirements and is based on the algorithm used in the “power” procedure of the software SAS. This algorithm also includes shifted null hypotheses. The corresponding documentation (SAS Institute, 2009) refers to the work by Fleiss et al. (1980), which does not, however, actually address shifted null hypotheses. A query to the Technical Support Section of SAS showed that documentation of the validity of this algorithm for shifted null hypotheses has evidently not been published. The question arises as to which true effects are required in more precise calculations to reach the respective extent category with high probability.

The true effects were thus determined by means of Monte Carlo simulations as follows:

1. The significance level for the above hypothesis is 2.5% and the power is 90%. The parameter $R{R}_1$ runs through all values between 0.2 and 0.95 at step sizes of 0.01. The risk in the control group p ₁ runs through all values between 0.05 and 0.95 at step sizes of 0.05. For each of these tuples ($R{R}_1$, p ₁) the required sample size n is calculated using $R{R}_0=1$ according to the formula by Farrington and Manning (1990) and then doubled ($m·2n$).

2. For each triple ($R{R}_1$, p ₁, m) a threshold T runs through all values between 1 and 0 in a descending order with a step size of –0.005. For each T the power for the above hypothesis is approximated with $R{R}_0=T$. The significance level is 2.5%. For this purpose 50,000 2 × 2 tables are simulated with a random generator, the upper CI limit for the relative risk is calculated by means of the normal distribution approximation and the delta method for estimation of variance. Subsequently, the proportion of simulation cycles is determined for which the upper CI limit is smaller than T. The T cycle is stopped as soon as an approximated power is smaller than 90%. The corresponding triple ($R{R}_1$, p ₁, T) is documented in a list.

3. After the cycle of all parameters in Steps 1 and 2, all triples are chosen from the list for which the threshold $T$deviates less than 0.01 from one of the values 0.75, 0.80, 0.85, 0.90, or 0.95.

Figure 2 shows the resulting (more precise) true effects depending on the risk in the control group for all thresholds specified above (significance level 5%, power 90%, points approximated by smoothed curves). The curves are almost constant over a wide range of risks and decline slightly at risks close to 1. The further away the threshold is from the zero effect (1) the stronger the declining trend. This means that the true effects, depending on the risk in the control group, are constant over a wide range, but decrease with an increasing risk in the control group, in particular in the case of lower thresholds. The approximative formula (1) used to derive the thresholds is therefore sufficiently precise for thresholds close to 1; however, for thresholds lying further away from 1, the required true effects vary with the risk in the control group.

Figure 2.

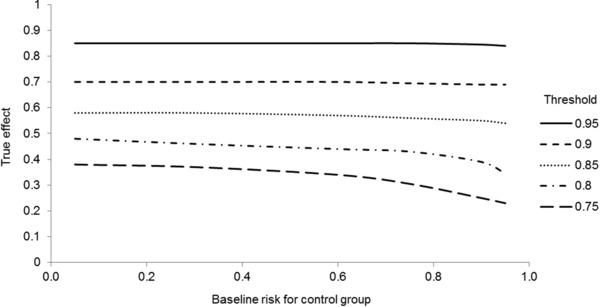
True effects determined by Monte Carlo simulations by means of the thresholds in Table 2, depending on baseline risk.

Table 3 contains the ranges (depending on the risk of the control group) of the required true effects per outcome category and extent category.

Table 3.

True effects determined by Monte Carlo simulations on the basis of the thresholds in Table 2

Extent category	Outcome category
	All‐cause mortality	Serious (or severe) symptoms (or late complications) and adverse events as well as quality of life	Nonserious (or nonsevere) symptoms (or late complications) and adverse events
Major	0.53–0.58	0.24–0.38	Not applicable
Considerable	0.84–0.85	0.69–0.71	0.34–0.48
Minor	Not applicable	Not applicable	0.69–0.71

In relation to all‐cause mortality, true relative risks of about 0.55—that is still corresponding to about a halving of the risk—are to be specified for the extent “major”. For the extent “considerable” the true effect must lie at about 0.85. For serious symptoms and comparable outcomes, to be classified as a “major” extent, a true reduction in risk to about a quarter to a third of the risk is required. Compared with the originally specified true effects (see Table 1) good consistency is provided for thresholds lying close to 1. For the thresholds lying further away from 1, the simulation results show slightly more moderate requirements for the strength of the true effects. The division of the thresholds as defined in Table 2 seems reasonable and practicable.

CIs for the relative risk are calculated here by means of the normal distribution approximation and the delta method for estimation of variance. This approach was chosen as it represents the usual calculation method in analyses of clinical studies. Farrington and Manning (1990) proposed a test for shifted hypotheses based on the restricted maximum likelihood method. We repeated the simulation described above and in Step 2 calculated the test‐based confidence limits using their approach; interestingly, the thresholds calculated in this way were largely constant for each baseline risk. These thresholds correspond to the left ends (low baseline risk) of the curves in Fig. 2. Both calculation methods thus agree well for low baseline risks or greater thresholds. In other cases one could potentially favour Farrington and Manning's approach; however, CIs based on this method have so far rarely been presented in analyses of clinical studies.

3. Discussion

3.1. Classification of the magnitude of effects

The wish to be able to assess the effects of interventions not only in a binary sense (“effects are/are not present”) is not new. This is mostly expressed by the question as to whether the effects are “clinically relevant”. In this context, differences observed between intervention groups should not be interpreted solely by demonstration of statistical significance as effects of any magnitude. Such effects should rather achieve a specified magnitude and thus be “clinically relevant”. The discussion of this question is complicated by the different levels in which clinical relevance can be expressed and in particular by the mixing of these levels (Thomas, 2009). Whereas there is an almost universally valid agreement regarding statistical significance, namely a (mostly two‐sided) significance level of 5%, such an agreement does not exist for the classification of effect sizes into relevant or nonrelevant. It is commonly argued that this would not be possible anyway, as the particular clinical context always needs to be considered. However, this is not very convincing, as the same argument of course applies to the use of a universal significance level. It is self‐evident that clinical aspects must be considered in the definition of clinical relevance. In this regard, different thresholds were defined for outcomes of different quality. Overall, for the distinctive outcomes per therapeutic indication, this enables a specific representation of the respective clinical problem.

Beyond a binary approach, the classification of clinically relevant effects into the categories “minor”, “considerable”, and “major” is stipulated by the ANV, and must be used by IQWiG. One may query whether the use of only three categories is sufficient. In some situations a more detailed classification might be more appropriate; however, this applies to any ordinal classification. In principle, a continuous measure to describe the magnitude of effects is also conceivable. Ultimately, the legislator deemed classification into three categories to be sufficient.

The classification of clinically relevant effects was not first introduced by AMNOG. For instance, several years ago, for pricing purposes the French HTA agency “Haute Autorité de Santé” (HAS) introduced four categories to classify effects shown in drug studies (low, moderate, significant, major). However, how this classification is to be exactly operationalized cannot readily be inferred from the publicly available (English‐language) sources. In a paper published in 2010, which summarizes the results of a discussion about issues concerning the reimbursement of cancer drugs in France (also involving HAS), it is even explicitly excluded that such an operationalization is possible in terms of an allocation of effect sizes to the individual categories (at least for cancer drugs) (de Sahb‐Berkovitch et al., 2010). Regulatory authorities also face similar difficulties; for example, in the operationalization of a “significant benefit” for orphan designation (EMA, 2010; EMA, 2012) or a “substantial improvement” for breakthrough therapy (FDA, 2014).

IQWiG therefore had no other option but to develop its own approach in order to meet the requirement specified in Section 2.4 of a preferably abstract, but also transparent operationalization. The approach involves the following steps:

1. Determination of the positive and negative effects for single patient‐relevant outcomes.

2. Classification of the identified effects into the extent categories “minor”, “considerable” and “major”.

3. Summary and assessment of the effects and, if applicable, weighing of positive and negative effects (also taking into account the absolute effects of the single outcomes).

In this context, it should be noted that the methodological approach presented in this paper refers solely to the second, albeit crucial, step. Unfortunately, in previous discussions with stakeholders concerning the methods described and applied in the first dossier assessment (IQWiG, 2011), Steps 2 and 3 were not always clearly separated. Step 3 is necessary as, according to the legal requirements, a single conclusion on the added benefit of a drug must be drawn. Besides the hierarchy of outcomes contained in the ANV, the weighing of effects considers the extent of effects at outcome level. As this weighing may contain value judgements, the overall conclusion on added benefit is explicitly described as a proposal in the IQWiG dossier assessments. The final decision on the extent of added benefit is the G‐BA's responsibility.

The European Medicines Agency (EMA, 2009) has initiated intensive research efforts and consultations for some years, especially with regard to Step 3. Even if HTA agencies and regulatory authorities have basically different responsibilities, they are connected by common challenges. It remains to be seen whether the final results of EMA's research efforts are compatible with the approach presented here. So far, 4 out of 5 work packages have been completed and published, and EMA is planning a public consultation period after the fifth package, a training phase for assessors, has been completed.

3.2. Use of confidence limits

As stated in Section 2.4, the use of confidence limits to classify the extent of added benefit has two main advantages. In contrast to the use of point estimates, the precision of the estimate is considered and the probability of statistical errors can be controlled. As early benefit assessments are conducted immediately after market entry, that is usually shortly after regulatory approval, in most cases only clinical studies submitted in the approval process are available; sometimes just one study may be available. To achieve a certain extent of added benefit, a certain distance of the CI from the zero effect is required. However, studies used for drug approval are powered to demonstrate “simple” significance. As a result, if the assumptions of the sample size calculation are correct, the CI will be close to the zero effect. The problem may increase if studies are discontinued prematurely following the results of preplanned interim analyses or if only certain subgroups are considered in the early benefit assessment because of restrictions to the approved patient population in the summary of product characteristics.

The operationalization approach outlined in Section 2.5 takes this problem into account. As at least two studies are usually needed for drug approval, the CI thresholds are chosen precisely so that the power required to demonstrate a certain extent of added benefit is not decreased. If only one study is available, the power requirement is obviously lower. Of course, the use of a resource (sample size) to prove a weaker statement (statistically significant difference) on predefined certainties (error probabilities) cannot at the same time, and with the same level of certainty, serve to prove a stronger statement (e.g., considerable extent of added benefit). The problem cannot be solved statistically. Either one increases the resource or decreases certainty.

The use of point estimates instead of CIs is also unfavorable for studies with preplanned interim analyses. Such studies are usually discontinued (and final analyses performed at the time of discontinuation) if the results are so “extreme” that the discontinuation rule applies. However, in these cases the point estimate is biased (Bassler et al., 2013; Schou and Marschner, 2013). This problem does not occur with type 1 errors and CIs (if adequately adjusted). Overall, the use of the proposed CI thresholds is a pragmatic solution, avoiding the disadvantages of point estimates.

3.3. Effect measures

Even if we assume that the approach presented in principle fulfils the requirements for an explicit and abstract operationalization, several questions remain open. For conceptional reasons, the relative risk was chosen as an effect measure for deriving thresholds. Data from 2 × 2 tables can be easily transformed into such relative risks, even if other effect measures (e.g., the absolute risk reduction or odds ratio) were used in the original analyses. However, compared with both of these effect measures the relative risk has the disadvantage of not being symmetrical to the center of the distribution of the baseline risk. It can thus generally be calculated in two ways, depending on whether the risk refers to the case of an event or counter‐event (e.g., survival versus death, response versus nonresponse). This is irrelevant for the statement on significance specified in Step 1 of the approach (conventional, nonshifted hypotheses), as in such a case the p‐value of a single study is invariant and plays a subordinate role in meta‐analysis. However, this does not apply to the distance of the CI limits to the zero effect.

One option for handling this problem is to decide in advance, for each binary outcome (by means of content criteria under consideration of the type of outcome and underlying disease), what type of risk is to be assessed, that of an event or counter‐event. It is doubtful whether relevant content criteria are always actually available for this purpose.

It is surprising that the (at least sometimes) unfavorable asymmetry characteristic of the relative risk is hardly discussed in the methodological literature (Cummings, 2009). In the discussion of this topic it has been argued that “in many situations it is natural to talk about one of the outcome states as being an event” (Higgins and Green, 2011). This may be the case for some outcomes but for highly relevant outcomes such as mortality it is not. In addition, it is rarely explicitly described that there is an upper limit for an increase in the relative risk, whereas this does not apply to a decrease in the relative risk toward zero. This almost necessarily results in friction when weighing decisions, in particular when the “natural perspective” and the extent of added benefit are combined. A symmetrization of the relative risk may be an option here. However, at first the statistical characteristics of such an effect measure would have to be examined.

The use of a symmetrical effect measure would be a further alternative. Recourse to the absolute risk reduction is not meaningful for the reasons presented in Section 2.4. The odds ratio does not possess the favorable characteristic used in Section 2.5, namely, that the thresholds can be derived solely from the underlying (true) desirable effect. Moreover, unfavorable statistical characteristics are also being discussed with regard to this effect measure, for instance, the problem of noncollapsibility (Pang et al., 2013).

The main patient‐relevant outcomes are often operationalized as “time to occurrence of an event” (e.g. survival time). If certain conditions are fulfilled, the hazard ratio is the suitable effect measure for the comparison of groups with regard to this type of outcome. The “anchor” for the threshold matrix is also determined from the estimates on the hazard ratio. It can be queried whether the thresholds derived from the relative risk can also be transferred to the hazard ratio. In Section 2.4, we pointed out that a main advantage of the relative risk versus the absolute risk reduction was that it does not need to be specified which baseline risks should be used or for which time points baseline risks need to be estimated. If one intended to specify other thresholds for the hazard ratio, the meaning of which is very similar to the (epidemiological) relative risk (from a 2 × 2 table), then one would have to use baseline risks. Because in principle, under certain circumstances, a relative risk can be converted into a hazard ratio and vice versa, but only if a baseline risk (in the control group) or a fixed time point for estimating the baseline risk is specified. This should be avoided and therefore in the current approach the same thresholds are used for the relative risk and hazard ratio.

Besides, in the same way it could generally be queried to what degree specification of the significance levels (which is usually two‐sided and at a level of 5%) can be transferred from one effect measure to the other. For good reason specifications related to certain effect measures have so far been dispensed with.

Finally, the problem remains as to how to handle outcomes that are recorded on a continuous, quasi‐continuous, ordinal, or nominal measurement level. The simplest solution is to convert such data into binary outcomes by means of suitable cut‐off values. Of course such a conversion can also cause problems; in particular efficiency may suffer and the choice of thresholds could potentially have been data driven. Alternatively, in individual cases it should be investigated whether relative risks can be approximated (da Costa et al., 2012) to use the corresponding thresholds for determining the extent of the effect. The final option, albeit an unsatisfactory one, is to classify the extent as “nonquantifiable”.

3.4. Limitations and points for further research

Our approach is based on the ideal situation where two approval studies with treatment groups of a balanced sample size are available and where the proposed universal thresholds can be applied. The following issues remain open:

• -Do situations exist where one should deviate from the universal thresholds?
• -Do unequal sample sizes of treatment groups affect the feasibility of the approach?
• -Do violations of the prespecifed assumptions of a study affect the feasibility of the approach?
• -How can an added benefit derived from effects on (valid) surrogate endpoints be quantified beyond the extent “nonquantifiable”?

However, most of these issues also apply to the conventional binary approach (statistically significant versus not statistically significant).

4. Summary

In summary, we assume that the methodological approach presented here provides a robust, transparent, and thus predictable foundation to determine minor, considerable, and major treatment effects on binary outcomes in the early benefit assessment of new drugs in Germany. This should enable reliable conclusions on the extent of added benefit of new drugs beyond the mere investigation of point estimates and the discussion of their relevance. However, we realize that our approach needs to be developed further. Unfortunately, specific and constructive proposals have so far been lacking (IQWiG, 2013b), but are still very welcome.

Conflicts of interest

All authors are employed by IQWiG.