Lightwave-driven quasiparticle collisions on a sub-cycle timescale

Abstract

Ever since Ernest Rutherford first scattered α-particles from gold foils¹, collision experiments have revealed unique insights into atoms, nuclei, and elementary particles². In solids, many-body correlations also lead to characteristic resonances³, called quasiparticles, such as excitons, dropletons⁴, polarons, or Cooper pairs. Their structure and dynamics define spectacular macroscopic phenomena, ranging from Mott insulating states via spontaneous spin and charge order to high-temperature superconductivity⁵. Fundamental research would immensely benefit from quasiparticle colliders, but the notoriously short lifetimes of quasiparticles⁶ have challenged practical solutions. Here we exploit lightwave-driven charge transport^7–24, the backbone of attosecond science^9–13, to explore ultrafast quasiparticle collisions directly in the time domain: A femtosecond optical pulse creates excitonic electron–hole pairs in the layered dichalcogenide tungsten diselenide while a strong terahertz field accelerates and collides the electrons with the holes. The underlying wave packet dynamics, including collision, pair annihilation, quantum interference and dephasing, are detected as light emission in high-order spectral sidebands^17–19 of the optical excitation. A full quantum theory explains our observations microscopically. This approach opens the door to collision experiments with a broad variety of complex quasiparticles and suggests a promising new way of sub-femtosecond pulse generation.

Following the principle of high-energy accelerators, their solid-state counterparts should prepare, accelerate, and collide quasiparticles while detecting the outcomes. This can be realized only if all steps are accomplished faster than the quasiparticle’s ultrashort lifetime⁶. Preparing the quantum states of quasiparticles by femtosecond lasers is already well established²⁵. Ultrafast acceleration, in turn, may harness latest breakthroughs of strong-field control: The carrier wave of an intense laser pulse has been applied to ionize atoms or molecules and recollide their fragments when the sign of the light-field changes¹⁰. The excess energy of the collision is released as high-order harmonics of the laser frequency, which may emerge in attosecond bursts⁹, carrying key structural and dynamical information of the participants^11,12. Recently this idea of sub-cycle control has been extended to solids where lightwaves have driven dynamical Bloch oscillations^20,21, interband quantum interference²⁴ and high-order harmonic generation^20–24 (HHG). The microscopic mechanisms, however, are complex since the lightwave drives an inseparable combination of interband excitation^21,24,26, i.e., quasiparticle preparation, and intraband acceleration^20–24,26. The recent observation of high-order sideband generation (HSG) in gallium arsenide quantum wells¹⁸ has suggested a way to disentangle these steps. Following optical preparation of coherent excitons²⁷, a strong terahertz (THz) field of frequency vTHz modulates the interband resonance such that spectral sidebands at even multiples of vTHz emerge^17–19. This observation has been modelled by THz-driven electron–hole collisions, similarly to the three-step model of HHG in atomic gases^7,8. Yet, the potential of HSG for real-time quasiparticle collisions has remained untapped.

Here, we introduce a sub-cycle quasiparticle collider. A femtosecond optical pulse prepares coherent excitons in tungsten diselenide (WSe₂), at a well-defined phase of a THz driving field (E_THz). This phase defines how E_THz accelerates and collides electrons and holes, thereby yielding photon emission by pair annihilation, which is detected as high-order sidebands. We reveal the sub-cycle quantum dynamics of quasiparticle collisions, model the microscopic process by a full quantum theory, and utilize the data to extract key information on the colliding species. Finally, we compare the process to HHG in the same material.

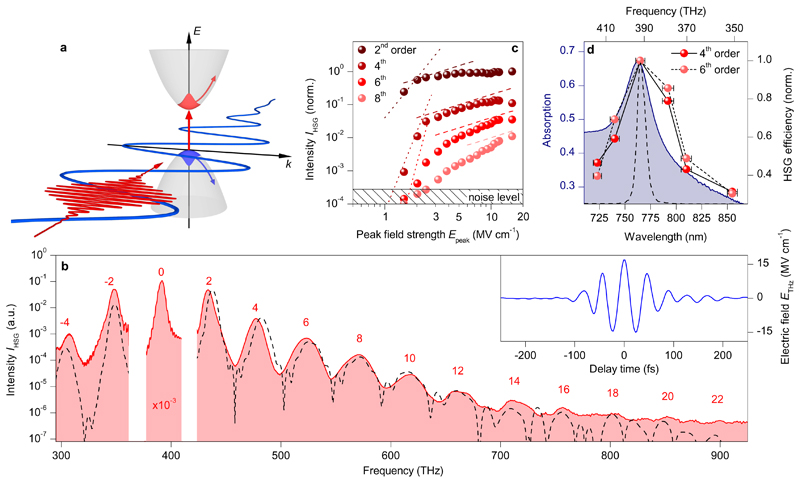
As a member of the class of transition metal dichalcogenides, WSe₂ features strongly bound Wannier excitons^27,28 and unique spin-valley coupling²⁹. Even in its bulk form, WSe₂ has been reported to exhibit an exciton binding energy of the order of 0.1 eV at its direct bandgap³⁰, stabilizing these quasiparticles still at room temperature. In a first experiment, a 100-fs excitation pulse (red waveform in Fig. 1a) centred at a photon energy of 1.621 eV (centre frequency, 392 THz) resonantly prepares coherent excitons at the direct band gap of WSe₂ (thickness, 60 nm) located at the K and K’ points in momentum space. A co-propagating intense THz pulse (blue waveform in Figs. 1a, b; centre photon energy, hv_THz = 95 meV, centre frequency, v_THz = T^-1 = 23 THz; peak electric field in air, E_peak = 17 MV cm^-1; see ‘Experimental setup’ in Methods) modulates the excitonic polarization and gives rise to HSG^18,19. The resulting intensity spectrum I_HSG includes sidebands of positive and negative orders n, spaced at 2vTHz (Fig. 1b). Spectral components up to n = 22 are clearly visible, while the intensities of negative orders drop much faster with decreasing frequencies. The new frequency components feature the same polarization as the interband excitation pulse (Extended Data Figure 1). In contrast to perturbative scaling $(I_{\text{HSG}}\sim E_{\text{peak}}^{2\text{n}}),$ the sideband intensity grows linearly with E_peak for intermediate peak fields depending on the sideband order and even saturates at the highest field strengths (Fig 1c, see also Extended Data Figure 2 for the influence of the interband excitation fluence). Finally, I_HSG peaks if the interband excitation is resonant with the excitonic absorption peak (Fig. 1d), underpinning its excitonic origin. Apart from the broadening of the sidebands due to the ultrashort duration of E_THz, these findings agree well with previous time-integrated studies¹⁸.

Figure 1. High-order sideband generation in tungsten diselenide.

a, Schematic of the experiment in reciprocal space: An interband excitation pulse (red waveform) creates an excitonic polarization in WSe₂ (red, vertical arrow), while a strong multi-THz field (blue waveform) simultaneously accelerates the wavepackets of electron and hole (curved arrows) within their respective bands (parabolas). b, Measured intensity spectrum (red) of high-order sidebands from WSe₂ (thickness, 60 nm; sample at room temperature) driven by a phase-locked THz transient featuring a centre frequency of 23 THz and external peak field strengths of 17 MV cm^-1 (see inset; Keldysh parameter γ = 0.08 < 1) under resonant optical excitation at a frequency of 392 THz (denoted by ‘0’, finite numerals denote the order of sidebands). The black dashed curve shows the calculated intensity spectrum I_HSG. c, Recorded high-order sideband intensity I_HSG of orders 2 to 8 as a function of driving peak field strength. Dotted lines follow a perturbative scaling law, I_HSG $\sim E_{\text{peak}}^{2\text{n}}),$ dashed lines mark a linear scaling. d, Measured generation efficiency of the 4^th- and 6^th-order sideband for different excitation wavelengths (red spheres). Error bars depict the bandwidth (FWHM) of the excitation spectra (excitation spectrum at 392 THz shown as a dashed curve). The shaded area shows the measured exciton resonance in the absorption spectrum of the sample.

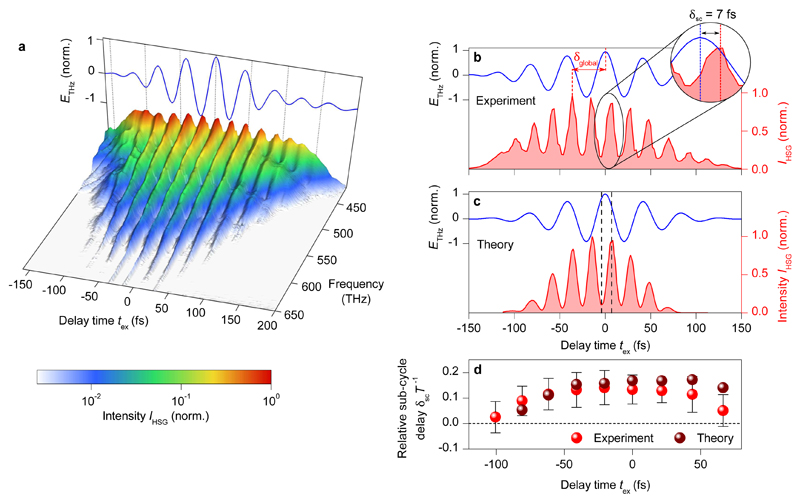
To directly resolve the underlying sub-cycle quantum dynamics, we now prepare the coherent excitons within 10 fs, i.e., significantly faster than a single oscillation period T of the THz wave. Figure 2a depicts the spectral shape of the observed sideband intensity I_HSG as a function of the delay between the excitation pulse and the peak of the THz driving field, t_ex. Electro-optic detection allows us to determine the complete waveform E_THz on the same absolute timescale (Fig. 2a, b, blue curve). The spectrogram in Fig. 2a follows a nearly Gaussian temporal envelope, resembling the THz envelope. Interestingly, I_HSG is strongly modulated along the time axis with a period of T/2, i.e., there is a sub-cycle criterion for ‘good’ and ‘bad’ preparation times t_ex.

Figure 2. Sub-cycle electron-hole recollisions.

a, Spectrally resolved high-order sideband intensity I_HSG as a function of delay time t_ex between the THz driving field (blue curve, compare also panel b) and a 10-fs interband excitation pulse (colour-coded, see key). b, c, Measured (b) and calculated (c) high-order sideband intensity I_HSG (red, spectrally integrated between 435 THz and 650 THz) on the same timescale as the driving waveform (blue), which peaks with a global delay δ_global after I_HSG. On a sub-cycle scale, the recorded sideband intensity (red) peaks at a distinct time delay δ_sc after the nearest extrema of the driving waveform (see zoom-in to panel b). d, Sub-cycle delay of I_HSG in units of the driving period T for subsequent driving half-cycles at their respective delay times as measured (bright red spheres, error bars: standard deviation of δ_sc for 25 consecutive measurements) and calculated (dark red spheres). The horizontal black dashed line marks δ_sc T^-1 = 0.

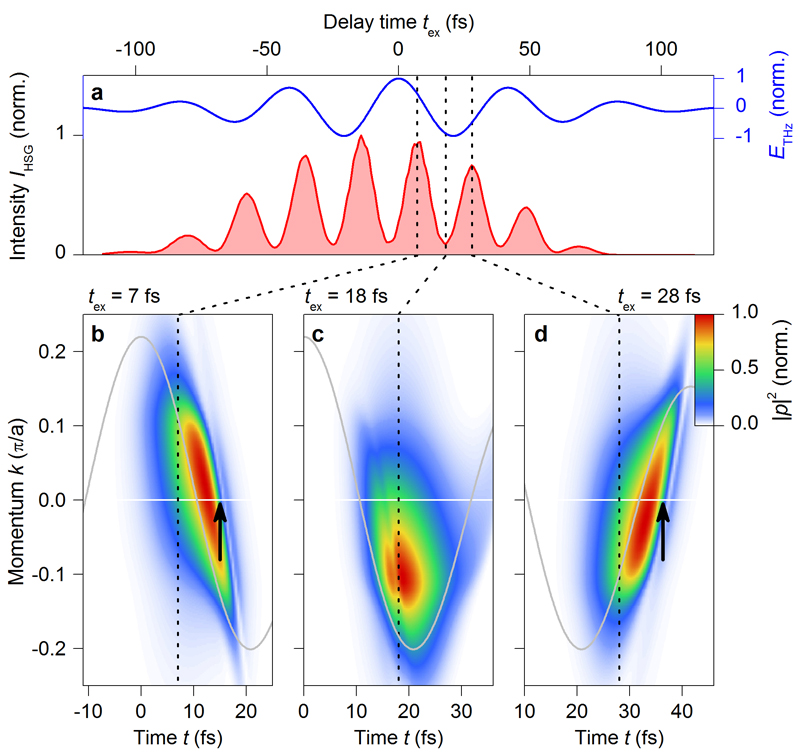
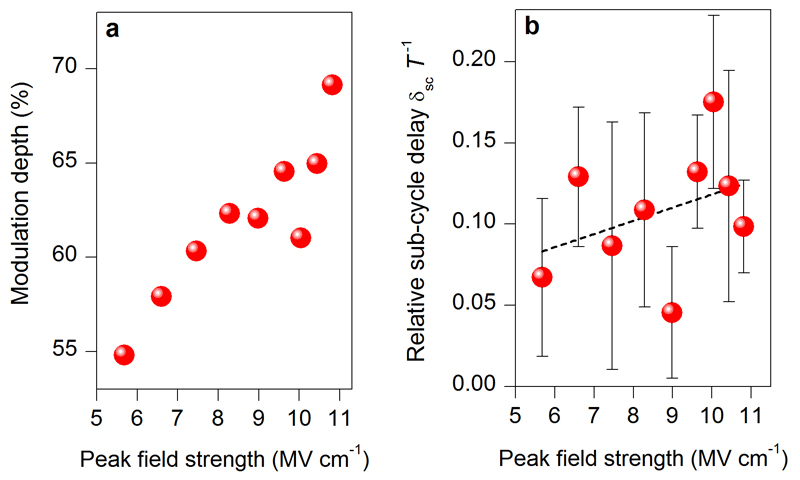
For a quantitative timing analysis, Fig. 2b compares E_THz (blue curve) with the spectrally integrated intensity I_HSG (red shaded curve). Remarkably, the strongest THz half-cycle occurs at a delay δ_global ≈ T with respect to the most intense sideband peak. This retardation rules out instantaneous optical nonlinearities as the microscopic origin of HSG. A detailed comparison of E_THz and I_HSG also reveals a sub-cycle delay δ_sc of the observed sideband bursts relative to the THz crests (see magnified inset in Fig. 2b). For subsequent half-cycles of the driving field, δ_sc initially increases, reaches a maximum value of ~ T/8 at the centre of the THz pulse and slightly decreases afterwards (Fig. 2d).

To link these signatures of I_HSG with the microscopic quasiparticle motion, we analyse the experiment with a full quantum mechanical model based on the semiconductor Bloch equations (SBEs) (see ‘Microscopic model of HSG’ in Methods). For a 100-fs preparation pulse, the experimentally observed HSG spectrum is well reproduced by our calculations (Fig 1b, black dashed curve), showing a similar modulation and intensity roll-off on the high- and low-frequency side. Using a 10-fs preparation pulse, the calculations quantitatively reproduce the temporal characteristics of I_HSG (Fig. 2c), including even delicate features such as δ_sc (Fig. 2d).

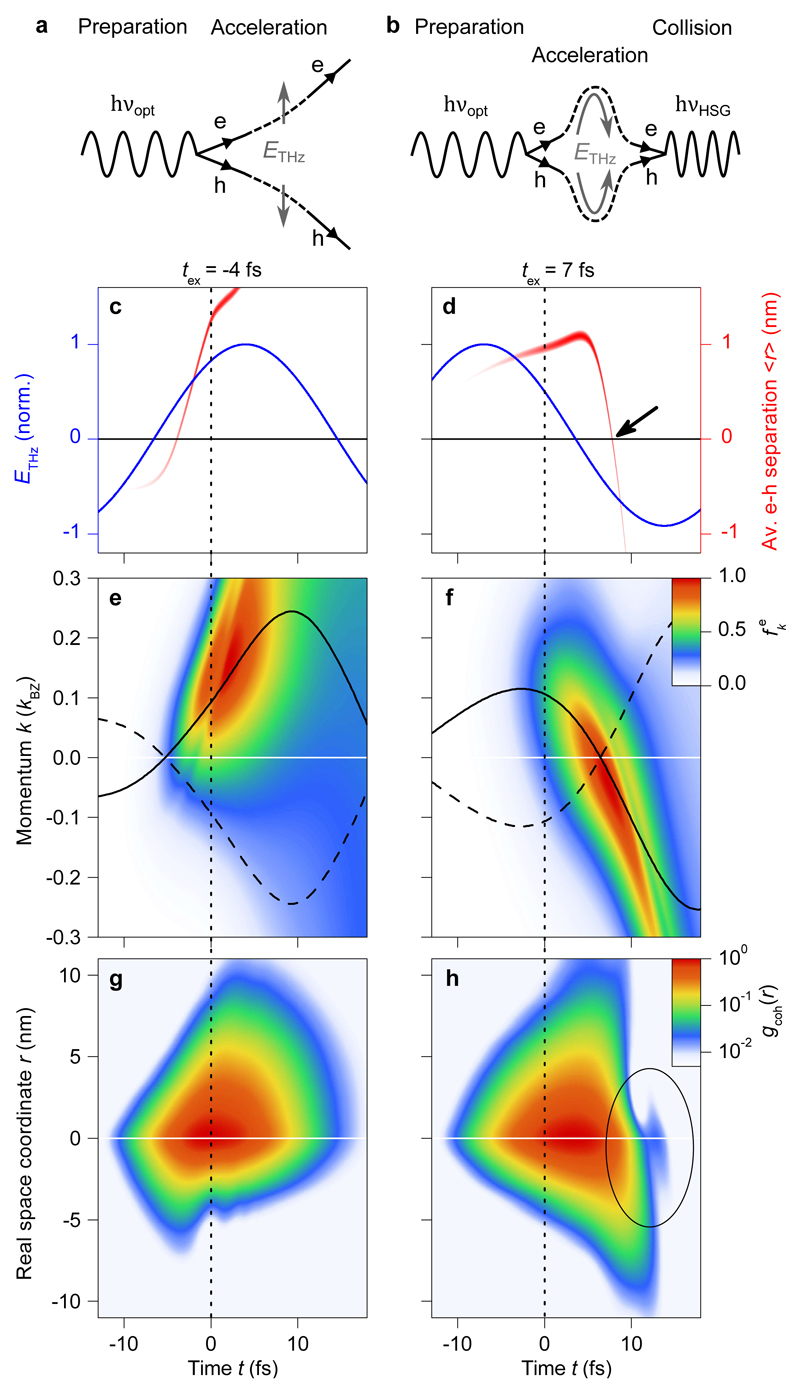
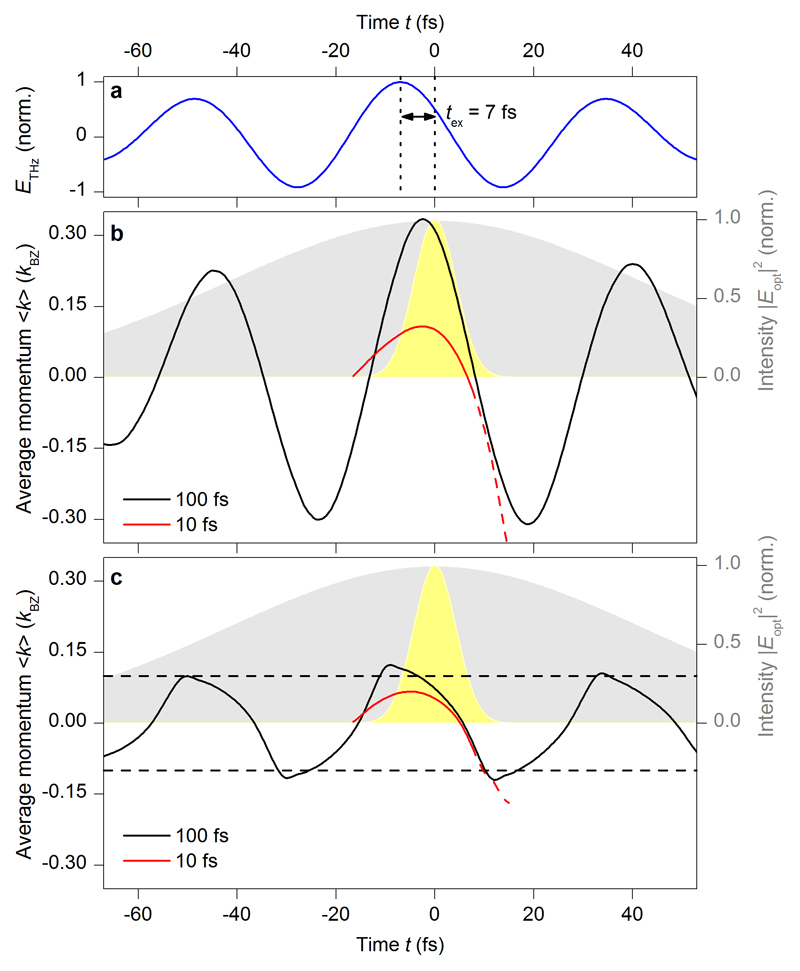
Figure 3 visualizes the underlying microscopic quasiparticle dynamics for two characteristic preparation times t_ex, corresponding to minimum (t_ex = -4 fs, Figs. 3c, e, g) and maximum HSG (t_ex = 7 fs, Figs. 3d, f, h), respectively. The two quasiparticle-collider sequences are schematically illustrated by Feynman diagrams in Figs. 3a and b. For t_ex = -4 fs, the coherent excitons are prepared shortly before a THz field crest (see vertical dashed lines in Figs. 2c and 3c). Immediately after optical preparation, the average momentum of the electron (Fig. 3e, solid curve) and the hole (dashed curve) are located in the vicinity of the K and K’ points of the Brillouin zone (defined as k = 0). The strong THz field accelerates the distribution function of the electron, $f_k^{\text{e}}$ (Fig. 3e, false-colour plot), and the hole, $f_k^{\text{h}}$ (not shown) away from k = 0, driving the electron and hole wavepackets apart. A qualitatively different situation occurs for t_ex = 7 fs (Figs. 3d, f, h) where the coherent excitons are prepared shortly before a zero crossing of the THz field (vertical dashed lines in Figs. 2c and 3d). Now the mean momenta change sign, i.e., the initially separating electron and hole are set on a recollision path (Fig. 3f).

Figure 3. Quantum simulation of sub-cycle electron-hole collisions underlying HSG.

a, b, Schematic Feynman diagrams depicting electron-hole (e-h) pair creation by a near-infrared photon (hv_opt) and acceleration by E_THz: Only for ‘good’ excitation times (b), the acceleration leads to a collision and annihilation of the electron-hole pair, thereby emitting a sideband photon hv_HSG. c, d, Trajectories (red, the intensity of the line represents the density of coherent excitons) tracing the real-time evolution (time t) of mean electron-hole separation (weighted average of g_coh(r)) for characteristic delays t_ex corresponding to minimum (c) and maximum HSG emission (d, compare Fig. 2c). Vertical black dotted lines highlight t = 0, which marks the peak of the excitation pulse. While electrons and holes are initially separated, they rapidly recollide (zero excursion marked by the black horizontal lines; time of recollision is highlighted by the black arrow in panel d) upon reversal of the driving field (blue curves), inducing a strong HSG signal (d). For ‘bad’ excitation times, the electron-hole separation increases monotonically, prohibiting recollisions (c). e, f, Occupation $f_k^{\text{e}}$ of the first conduction band as a function of time t and crystal momentum k for delays of t_ex = -4 fs and 7 fs, respectively (colour-coded, see key). Horizontal white lines mark k = 0. Black solid (dashed) curves trace the weighted average excursion of electrons (holes) in reciprocal space. g, h, Coherent electron-hole correlation function g_coh(r) in dependence on time t and real space coordinate r. Interference patterns occur after the abrupt collapse of coherence caused by e-h recollision (highlighted by the black ellipse in h) which are absent for t_ex = -4 fs (g). Horizontal white lines mark r = 0.

Particle preparation of typical accelerators is spatially precise and collisions are monitored in real space. Our concept follows the relative motion of quasiparticles, and the preparation is precise in terms of the quasiparticles’ relative coordinate because the optical pulse creates them in a single, spatially correlated excitonic state described by a pair correlation function²⁷ (see ‘Coherent electron-hole pair-correlation function’ in Methods). Figures 3g and h display its coherent part, g_coh(r) which defines how electrons are coherently coupled to holes as a function of their relative distance, r (reciprocal space representation in Extended Data Figure 3). In both panels, g_coh(r) is maximum close to the peak of the optical pulse before it decays by ultrafast dephasing (dephasing time T₂ < T/2). Figures 3c and d show the corresponding mean electron–hole separation 〈r〉. Suitable t_ex (Fig. 3d) allows the THz field (Figs. 3c and d, blue curve) to separate and collide the electron–hole pairs at high energy. Due to this ballistic motion, maximum HSG occurs for preparation times that are offset with respect to the field crests causing the distinct delay δ_sc observed in Fig. 2d. The precise temporal structure seen in the experiment can only be reproduced if excitation-induced dephasing²⁷ is taken into account (see ‘Effect of excitation induced dephasing on HSG’ in Methods and Extended Data Figures 4, 5, and 6). For ‘bad’ timing t_ex, in contrast, the electron and the hole are monotonically driven apart (Fig. 3c), suppressing collisions (see diagram in Fig. 3a). The situation is analogous to a cyclotron where electrons are effectively accelerated only if they are injected at the right phase of the alternating accelerator field.

Whereas the average intraband dynamics 〈r〉 resembles semiclassical trajectories (see Figs. 3c and d), the connection between quasiparticle collision and HSG requires a full quantum theory. Like electron-positron pairs in vacuum, colliding electron-hole pairs in a solid are subject to pair annihilation, where a high-energy photon may be emitted, leading to sideband signals. Indeed this microscopic annihilation dynamics manifests itself in g_coh(r) (Fig. 3h). After significant spreading of g_coh(r), electron–hole collision is prompted by an abrupt termination of the correlation function due to pair annihilation. Subsequently interference patterns occur among the residual fragments that survive the collision (see black ellipse in Fig. 3h). These distinct collision-induced annihilation features are absent in the case of ‘bad’ injection times where the coherence gradually abates due to dephasing (Fig. 3g). The details of g_coh(r) are a direct manifestation of the many-body interactions governing the internal structure of the exciton, and they leave their immediate hallmarks in the temporal and spectral response in HSG.

Detection of HSG, combined with precise preparation and acceleration, delivers an in-depth view on quasiparticles. Like in particle colliders, one can expose the scattering products by systematic variation of key parameters, such as the strength, frequency, and duration of the preparation and THz pulses, as well as their relative delay t_ex. In the Methods chapter ‘Data landscape of quasiparticle colliders’, we provide first examples of how to retrieve material-specific information such as the exciton binding energy, scattering times and Coulomb enhancement of the collisional cross section via dedicated analyses of the multi-dimensional data landscape of I_HSG. Especially, the collision events recorded in our experiments bear the hallmarks of an exciton binding energy around 60 meV.

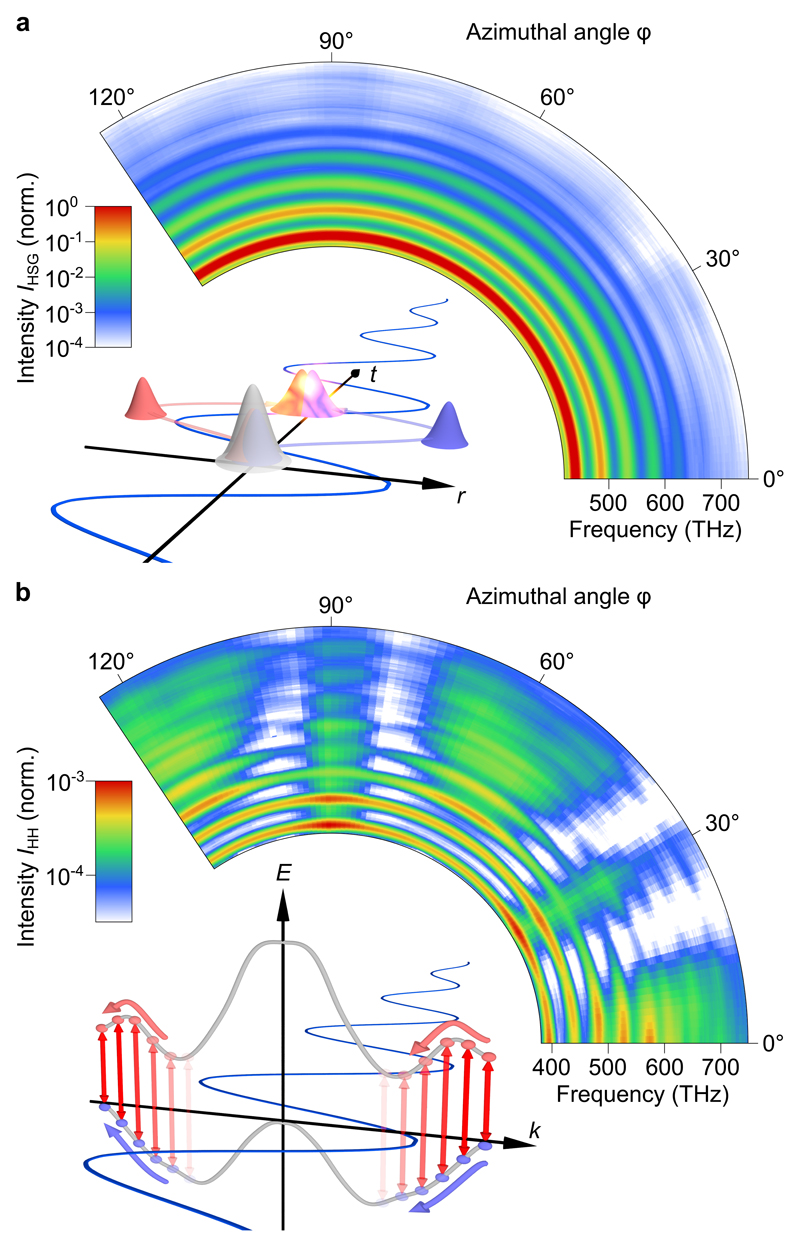
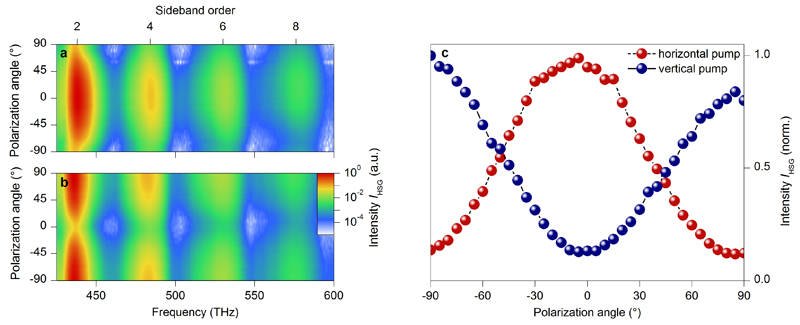
Well-defined initial momenta and relative spatial coordinates of the electrons and holes are a prerequisite for controlled collisions. The direction of acceleration in the WSe₂ crystal, in contrast, is less relevant, as seen in Fig. 4: The high-order sideband spectra show virtually no dependence on the azimuthal in-plane angle φ of the THz polarization. This behaviour is compatible with our theoretical expectation that coherent electron–hole wavepackets in HSG remain rather close to k = 0 (Fig. 3f). Both, Coulomb attraction between electrons and holes and fast dephasing keep the coherent electron– hole excursions within a region where the effective mass is approximately isotropic (see Fig. 1a). Additionally, HSG probes the interband polarization of colliding electrons and holes only at spatial overlap²⁷ (inset of Fig. 4a).

Figure 4. Experimental comparison of high-order sideband and high-order harmonic generation.

Spectrally resolved high-order sideband intensity I_HSG (a, narrow-band exciton preparation at a frequency of 392 THz) and high-order harmonic intensity I_HH (b) as a function of the azimuthal orientation (angle φ) of the WSe₂ sample (normal incidence; colour-coded, both intensity scales are normalized to the maximum HSG signal, see respective key). While high-order sidebands show virtually no dependence on φ, the high-harmonic spectra reflect the six-fold symmetry of WSe₂. Insets: a, Real-space visualization of THz-driven electron-hole recollisions: Upon excitation of a bound electron-hole pair (grey), the carriers (red and blue wavepackets) are accelerated and recollided by the strong light field (blue) to recombine at r = 0, giving rise to high-order sideband emission. b, Schematic of high-order harmonic generation: a polarization between valence and conduction band (grey) is induced by a strong multi-THz field (blue) and simultaneously accelerated within the bands (red and blue spheres, curved red and blue arrow). During this process, the coherent interband polarization is continuously modified (red vertical arrows).

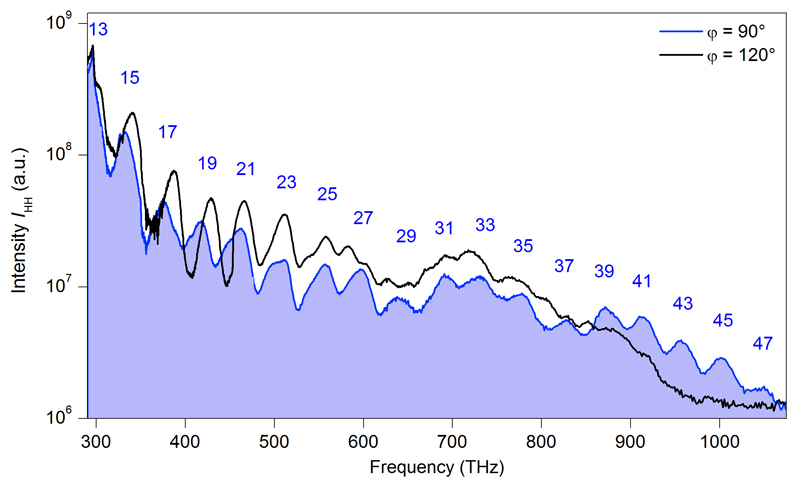
This unique characteristic of the quasiparticle collider becomes particularly clear when we compare the dynamics with HHG in the same sample, which is readily achieved by applying the strong THz field without optical preparation of excitons. A typical high-harmonic spectrum exhibiting odd orders up to n’ = 47 is depicted in Extended Data Fig. 7. The intensity of HHG is smaller by approximately one order of magnitude than HSG for frequencies below 650 THz. Due to the non-perturbative, non-resonant excitation of Bloch electrons with simultaneous acceleration by the strong-field bias^20,21,24,26, the initial carrier distribution is smeared out throughout the entire Brillouin zone. Furthermore, coherent interband polarization can emit photons at any point in momentum space (see inset of Fig 4b). This situation manifests itself by a critical dependence of the intensity and shape of high-order harmonics on φ (Fig. 4b), reflecting the six-fold symmetry of WSe₂ in the layer plane.

In conclusion, we demonstrate the realization of quasiparticle collisions in the time domain. We excite, accelerate, and collide coherent electron–hole pairs in WSe₂ resulting in ultrabroad sideband emission. On a sub-cycle scale, we directly trace the retarded, ballistic wavepacket dynamics and retrieve key information such as exciton binding energy, scattering time, and the Coulomb enhancement of the collisional cross section. As in conventional particle accelerators, our optical excitation pulse prepares electron and hole wavepackets with uncertainty-limited momenta and relative spatial coordinates. Yet their absolute position is only defined to within the relatively large focal spot size, which may be overcome in future near-field experiments by preparing excitons in a nanometre-sized interaction region. Both in the quasiparticle collider as well as in its large-scale counterpart, intrinsic characteristics of the collision become accessible by detecting the concomitantly emitted high-frequency radiation. The high density of quasiparticles in solids helps in generating relatively intense, all-coherent and ultrabroadband radiation which may pave the way to novel sub-femtosecond light sources; its sub-cycle modulation may furthermore facilitate information processing at optical clock rates. Most importantly, large-scale colliders have opened the door to the world of elementary particles. Likewise, we anticipate THz-driven real-time collisions – operating on much smaller, widely tuneable length and energy scales – to become a key to a wide zoo of quasiparticles in some of the most fascinating playgrounds of modern materials sciences. Examples range from excitons, trions, biexcitons or dropletons in quasi-two-dimensional atomic monolayer systems, via Dirac-like quasiparticles in graphene and topological insulators to polarons in materials featuring strong electron-phonon coupling. This scheme may also be extended to optically excited quasiparticles in unconventional superconductors and contribute to the revelation of some of the outstanding enigmas of condensed matter.

Methods

Experimental setup

Intense, phase-locked waveforms in the far- to mid-infrared spectral region (multi-terahertz range) are generated by difference frequency mixing of two spectrally detuned near-infrared pulse trains from a dual optical parametric amplifier pumped by a titanium-sapphire laser amplifier^21,24. The few-cycle transients feature peak fields of up to approximately 1 V/Å (Ref. 31). A super-continuum source based on filamentation in an yttrium aluminium garnet crystal delivers ultrabroadband white-light pulses covering the whole near-infrared and visible range. Both pulse trains are collinearly superimposed with an indium-tin-oxide-coated beam splitter and focused onto the tungsten diselenide sample under normal incidence using a gold-coated parabolic mirror. A mechanical delay stage in the excitation beam path allows us to temporally delay the pulses with respect to each other.

The sample under study is a 60-nm-thick sheet of WSe₂ which has been cleaved using a viscoelastic gel film and placed on a CVD-grown diamond substrate. For resonant, narrow-band excitation of the excitonic polarization in WSe₂, optical band pass filters featuring a transmittance bandwidth of 10 nm are employed (compare Figure 1d). For the time-resolved measurements, the bandwidth of the excitation pulse is adjusted in the Fourier plane of a prism compressor which enables the needed pulse duration of 10 fs. Spectral components of the excitation pulse above 400 THz are filtered out to avoid the resonant generation of a high density of unbound electron–hole pairs. All experiments have been performed at room temperature and in ambient air. No sample degradation was observed during the whole course of experiments.

The spot sizes of the excitation pulse and the THz pulse at the sample are 22 µm and 85 µm, respectively (intensity full-width at half-maximum). The generated high-order sideband intensity I_HSG as well as the high-order harmonic intensity I_HH is recorded with a spectrograph featuring a cooled silicon CCD camera. All spectra are corrected for the grating efficiency and the quantum efficiency of the detector.

The pulse energy of the narrowband excitation amounts to approximately 0.1 nJ in our current experiments. A comparison of the spectral components of the excitation and the sideband signals yields an energy conversion efficiency of approximately 0.1 % in the 60-nm-thick WSe₂ sample for the applied excitation fluence (~25 µJ cm^-2). Therefore, we estimate the energy in the high-order sideband pulse train as roughly 0.1 pJ.

Replacing the WSe₂ sample by a 6.5-µm-thick zinc telluride (ZnTe) detector crystal allows for electro-optic detection of the driving field. To this end, we carefully place the crystal into the THz focus at the same position and account for the complex detector response³². The delay time t_ex between the THz waveform and the near-infrared excitation pulse enables a direct temporal correlation of the driving waveform with the recorded trace of high-order sideband emission. To describe the microscopic dynamics following exciton creation, a second timescale t is introduced, which describes the real time evolving for a fixed value of t_ex as shown, for instance, in Fig. 3.

Microscopic model of HSG

A complete quantum description of optical^33,34 and THz excitations^21,24,35,36 of solids follows from the semiconductor-Bloch equations²⁷ (SBEs). Compared to earlier HSG models¹⁹, the SBEs fully include many-body effects beyond isolated electron–hole pairs, the interplay of HSG vs. HHG, nonparabolic dispersions and dephasing as well as relaxation processes. The SBE read

$$\mathbf{\text{i}}\hslash \frac{\partial }{\partial t}{p}_{\mathit{k}}={\tilde{\epsilon }}_{\mathit{k}}{p}_{\mathit{k}}-\hslash {\Omega }_{\mathit{k}}(t)\left(1-f_{\mathit{k}}^{\text{e}}-f_{-\mathit{k}}^{\text{h}}\right)+\mathbf{\text{i}}\left|e\right|{\mathit{E}}_{\text{THz}}(t){\nabla }_{\mathit{k}}{p}_{\mathit{k}}+{\Gamma }_{\mathit{k}},$$ (1)

$$\hslash \frac{\partial }{\partial t}{f}_{\mathit{k}}^{\text{e}}=-2\mathrm{Im}\left[\hslash {\Omega }_{\mathit{k}}(t)p_{\mathit{k}}^{*}\right]+\left|e\right|{\mathit{E}}_{\text{THz}}(t){\nabla }_{\mathit{k}}{f}_{\mathit{k}}^{\text{e}}+{\Gamma }_{\mathit{k}}^{\text{e}},$$ (2)

$$\hslash \frac{\partial }{\partial t}{f}_{\mathit{k}}^{\text{h}}=-2\mathrm{Im}\left[\hslash {\Omega }_{-\mathit{k}}(t)p_{-\mathit{k}}^{*}\right]+\left|e\right|{\mathit{E}}_{\text{THz}}(t){\nabla }_{-\mathit{k}}{f}_{-\mathit{k}}^{\text{h}}+{\Gamma }_{\mathit{k}}^{\text{h}},$$ (3)

where p_k is the microscopic interband polarization and $f_k^{\text{e}}$ $\left(f_k^{\text{h}}\right)$ defines the electron (hole) occupation in a conduction-band (valence-band) state with a crystal momentum ℏk. Physically, p_k defines the transition amplitude of exciting an electron from one band to another while ℏk is conserved. As an optical field E_opt(t) induces such a transition, it eventually generates occupations $f_k^{\text{e}}$ and $f_k^{\text{h}}$ The presented SBEs can straightforwardly be generalized for multiple bands^21,37,38.

As an inverse process, electrons recombine with holes via photon emission. The coherent part of this process yields radiative decay of the polarization²⁷ and the corresponding emission spectrum is³⁵ I = |ωP(ω) + iJ(ω)|². The Fourier transforms of the macroscopic polarization P(t) = ∑_kd_cv(k)p_k + c.c. and the macroscopic current $\mathit{\text{J}}(t)={\Sigma }_{\lambda ,\mathit{k}}{\mathit{\text{j}}}_{\mathit{k}}{f}_{\mathit{k}}^{\lambda }$ contain the dipole and current matrix elements ${\mathit{d}}_{\text{cv}}(\mathit{k})\text{and}\hspace{0.17em}{\mathit{j}}_{\mathit{k}}^{\lambda }=\frac{\left|e\right|}{\hslash }{\nabla }_{\mathit{k}}{\epsilon }_{\mathit{k}}^{\lambda }{\mathit{e}}_{\text{THz}},$ respectively, where e_THz is the polarization direction of E_THz. The currents in a given band λ are defined by its energy dispersion ${\epsilon }_{\mathit{k}}^{\lambda }.$

Since electrons and holes are charged particles, they experience a strong Coulomb force, which creates nontrivial many-body effects among p_k, $f_k^{\text{e}},\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}{f}_k^{\text{h}}$ during their finite lifetime. For example, the strength of the field excitation becomes renormalized,

$$\hslash {\Omega }_{\mathit{k}}(t)={\mathit{d}}_{\text{cv}}(\mathit{k})\mathit{E}(t)+{\displaystyle \sum _{\mathit{k}\mathbf{\text{'}}}{V}_{\mathit{k}-\mathit{k}\mathbf{\text{'}}}{p}_{\mathit{k}\mathbf{\text{'}}}},$$ (4)

by the Coulomb matrix element V_k, while its unnormalized part is a product of d_cv(k) and the total field E = E_opt + E_THz containing also the THz field E_THz. The Coulomb sum within Ω_k(t) results in excitonic resonances in the polarization²⁷. The single-particle transition energy ε_k becomes renormalized, too:

$${\tilde{\epsilon }}_{\mathit{k}}={\epsilon }_{\mathit{k}}-{\displaystyle \sum _{\mathit{k}\mathbf{\text{'}}}{V}_{\mathit{k}-\mathit{k}\mathbf{\text{'}}}\left[f_{\mathit{k}\mathbf{\text{'}}}^{\text{e}}+f_{\mathit{k}\mathbf{\text{'}}}^{\text{h}}\right].}$$ (5)

Additionally, phonon, photon and Coulomb interactions yield scattering contributions Γ_k, ${\Gamma }_{\mathit{k}}^{\text{e}},\text{and}{\Gamma }_{\mathit{k}}^{\text{h}}$ due to high-order correlations³³. We include microscopic scattering with the approximation ${\Gamma }_{\mathit{k}}=-\text{i}\frac{\hslash }{T_2(\mathit{k})}{p}_{\mathit{k}}$ which includes excitation-induced dephasing (EID) via the k-dependent scattering time T₂(k), as explained in ‘Effect of excitation induced dephasing on HSG’ in Methods. Microscopically, ${\Gamma }_{\mathit{k}}^{\text{e}},\text{and}{\Gamma }_{\mathit{k}}^{\text{h}}$ induce a relaxation of electron and hole distributions, which we implement using a phenomenological relaxation towards a symmetric carrier distribution via ${\Gamma }_{\mathit{k}}^{\lambda }=-\frac{1}{2\tau }\left[f_{\mathit{k}}^{\lambda }+f_{-\mathit{k}}^{\lambda }\right]$ (Ref. 24).

Our experiments show that high-order sideband generation (HSG) excites carriers only in the vicinity of the K-point where WSe₂ electrons and holes can be described with an effective mass approximation. To determine the general aspects of the interplay of HSG and high-harmonic generation (HHG), we use a one-dimensional (1D) two-band model³⁵, and adjust V_k to produce a binding energy E_B = 60 meV (corresponding to 14.5 THz) for the 1s-exciton state³⁰. We match electrons and holes to produce the same effective mass m_e = m_h = 0.52 m₀ (Ref. 39) close to the K-point. We solve the closed system of coupled differential equations (1)-(3) numerically using a Runge-Kutta algorithm.

We have confirmed that a two-dimensional (2D) computation produces essentially the same HSG results. Note that bulk WSe₂ features a layered structure where electron-hole motion is free only within each 2D layer. However, only a 1D computation is numerically feasible to fully include HHG, Bloch oscillations, and a nonparabolicity in the dispersion ε_k The 1D computations also confirm that HHG is an order of magnitude weaker than HSG, as in the experiment.

Coherent electron-hole pair-correlation function

The excitations underlying HSG can be investigated in real space by following the electron-hole pair correlation function

$$g_{\text{eh}}(\mathit{\text{r}})\equiv \langle {\widehat{\rho }}_{\text{e}}(r){\widehat{\rho }}_{\text{h}}(0)\rangle ,$$ (6)

containing operators for electron and hole densities ${\widehat{\rho }}_e\text{and}{\widehat{\rho }}_{\text{h}}$ respectively. As discussed in Ref. 33, the envelope of ${\widehat{\rho }}_e\left(\mathit{r}\right)\text{and}{\widehat{\rho }}_{\text{h}}\left(0\right)$ determines how electrons move with respect to holes on length scales larger than the unit cell. The resulting g_eh(r) defines the conditional probability of finding an electron at position r when a hole is at the origin.

To identify the coherent electron–hole acceleration, it is convenient to separate incoherent and coherent contributions from g_eh(r). Following the derivation in Ref. 33, we find

$$g_{\text{eh}}(\mathit{\text{r}})=g_{\text{inc}}(\mathit{\text{r}})+g_{\text{coh}}(\mathit{\text{r}}),$$ (7)

with the coherent part g_coh(r) = |p(r)|² and the incoherent part g_inc(r) = ρ_eρ_h + Δg_eh(r) which is proportional to the product of electron and hole densities, to the lowest order. The formation of pairwise, incoherent correlations generates an additional contribution Δg_eh(r). However, g_coh(r) is independent of correlation formation and is exclusively defined by the coherent polarization p(r) which is given by the Fourier transform of p_k and describes the relative motion of electron-hole coherences. In other words, g_coh(r) defines how coherently generated electrons are distributed with respect to the holes in real space. Since the SBEs fully include the many-body aspects of the polarization dynamics p_k, g_eh(r) generalizes the descriptions of following a single electron-hole pair during HSG^19,40.

Effect of excitation-induced dephasing on HSG

To quantify collision dynamics under different conditions, Extended Data Figure 6b compares the mean wave vector

$$\langle \mathit{\text{K}}\rangle =\frac{{{\displaystyle {\sum }_k\mathit{\text{K}}\left|p_k\right|}}^2}{{{\displaystyle {\sum }_k\left|p_k\right|}}^2}$$ (8)

of the electron-hole wave packet for a 10-fs-long (red curve) and a 100-fs-long (black curve) optical excitation pulse centred at t_ex = 7 fs, while the dephasing is kept constant (T₂ = 12 fs). The THz waveform (Extended Data Figure 6a) is identical for both optical excitations. The respective envelope of the excitation pulse is shown as the gray (yellow) shaded area for the 100 fs (10 fs) pulse.

We observe that the electron-hole wavepackets are accelerated to much higher momentum states in the case of the long (100 fs) excitation pulse compared to the short (10 fs) excitation pulse. As discussed in the main text, a zero crossing of 〈k〉 enables collisions and annihilation of optically generated coherent excitons. For the short excitation pulse, the magnitude of |p_k|² significantly drops after the recollision. Therefore, the motion of residual coherent electron-hole pairs is indicated by the red dashed curve while the dominant |p_k|² motion is plotted as red solid curve. For the long excitation pulse, the excitonic polarization |p_k|² is generated continuously, such that it is not diminished substantially by the collisions. The corresponding mean wave-vector 〈k〉 is plotted as a black curve in Extended Data Figure 6b and c.

Applying a constant dephasing time T₂ implies that all excitonic components of the polarization decay with an identical rate. However, the Coulomb interaction scatters polarization with the excited electron-hole distributions, yielding a strong exciton-state dependent excitation-induced dephasing³³ (EID). More specifically, the 1s-exciton state (which is tightly bound around the K-point) features lower scattering rates than other exciton states that spread out in k, which is included by introducing a k-dependent dephasing time T₂(k) as shown in the inset of Extended Data Figure 4a: For low k, T₂(k) is 12 fs while it decreases to 2 fs at elevated k. Comparably fast dephasing times have also been observed in previous studies^24,41,42. Additionally, the large temporal modulations in the HSB intensity as shown in Fig. 2a in the main text imply dephasing times T₂ which are significantly shorter than one half cycle of the THz driving field (T₂ << T/2 = 22 fs).

To determine the effect of EID on electron-hole collisions, Extended Data Figure 6c shows 〈k〉 for the momentum-dependent dephasing T₂(k). By comparing the black curves (100-fs-long excitation) in Extended Data Figures 6b and 6c, we conclude that EID reduces the maximum excursion by roughly a factor of 3 compared to the constant dephasing result. The mean momentum trajectory 〈k〉 for the short (10 fs) excitation pulse is less affected by EID owing to the reduced maximum displacement.

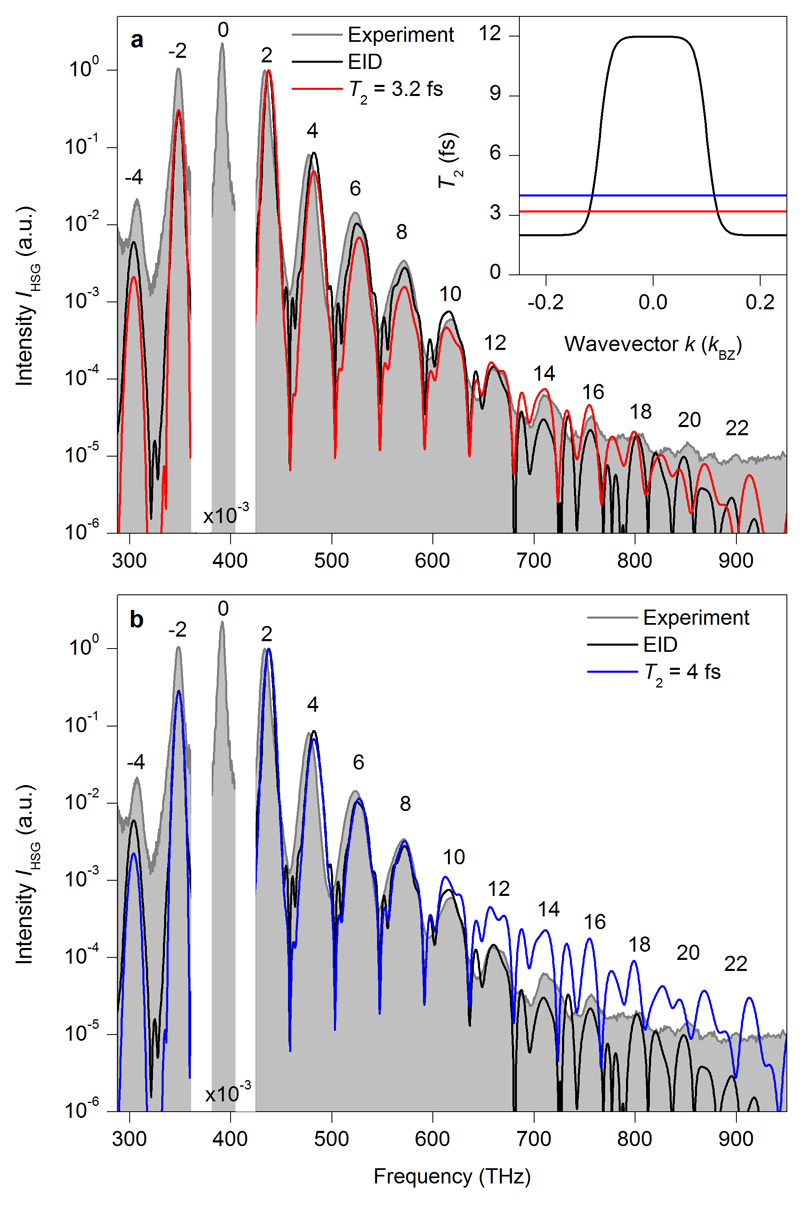
Extended Data Figure 4 compares the measured, time-integrated HSG spectra (shaded area) with computations including EID (black curves), a constant dephasing T₂ = 3.2 fs (a, red curve), and T₂ = 4 fs (b, blue curve), respectively. We observe that only calculations taking EID into account explain the height of all observed sidebands. More specifically, the simulations using a constant dephasing achieve good agreement only for either low order sidebands (n < 8, T₂ = 4 fs) or sidebands above 600 THz (T₂ = 3.2 fs). In numbers, T₂ = 4 fs (T₂ = 3.2 fs) overestimates (underestimates), e.g., the 10th (4th) sideband order by a factor of 1.9 (1.7). This result implies that EID induces nontrivial spectral imprints on the HSG spectrum. These modulations obviously result from anharmonic electron-hole acceleration identified in Extended Data Figure 6c.

In general, the SBE approach systematically describes the creation of coherent excitons, quasiparticle acceleration, collision-related annihilation, as well as the interplay of HSG and HHG contributions and the influence of many body effects such as EID or phonon scattering processes as suggested by Ref. 43. Only some aspects of these intriguing effects can be quantitatively analysed using either a semiclassical approach or a quantum description of a single electron-hole pair. Since many-body effects can induce drastic changes to HSG and HHG, it is clear that the SBE analysis is needed to properly parametrize any simplified model.

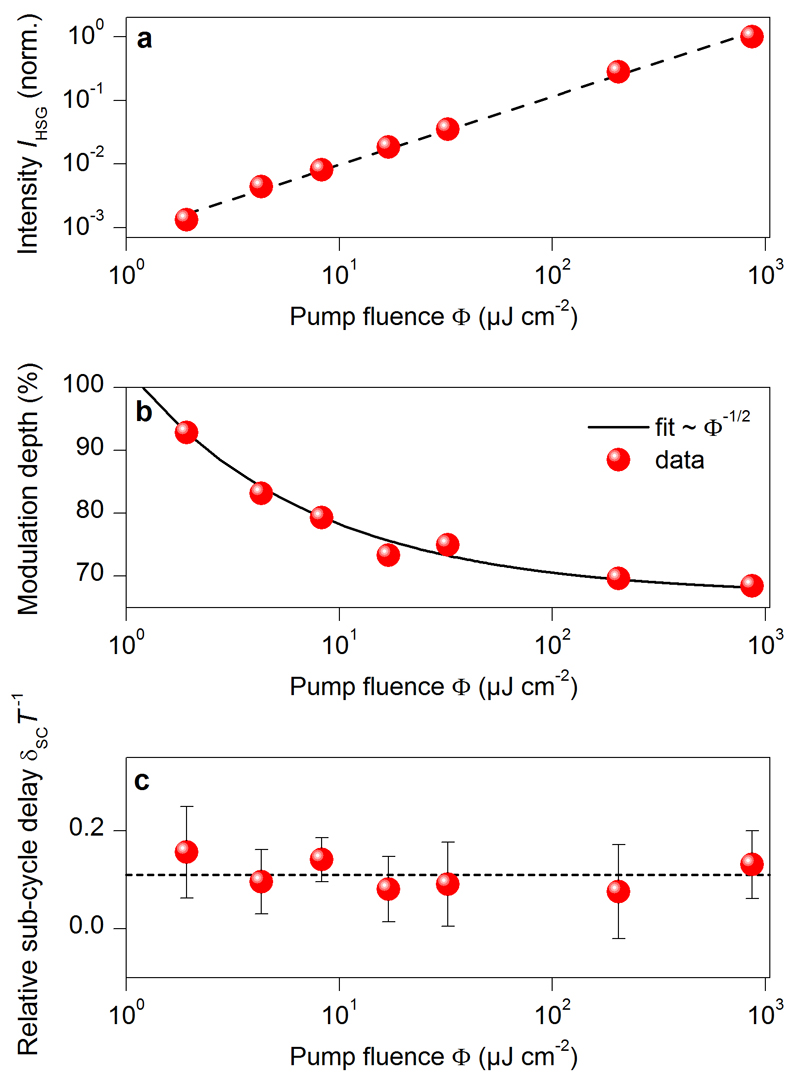
Influence of excitation fluence

With increasing optical fluence Φ, the measured sideband intensity increases linearly (Extended Data Figure 2a). However, the modulation depth of time-resolved traces of I_HSG is found to decrease (Extended Data Figure 2b). This feature may be most intuitively explained considering that a growing density of excitons may instantly lead to phase-space filling and broadening causing less well-defined initial conditions for electron–hole recollisions. A potential increase of dephasing rates, in contrast, does not seem to be a dominant factor since faster dephasing should result in an increase of the modulation depth, i.e. the opposite effect of what we observe. Additionally, the sub-cycle delay δ_sc, which is sensitively dependent on the dephasing time T₂, does not change substantially with varying excitation fluence implying that major density-driven effects on T₂ have not built up yet (Extended Data Figure 2c). However, such excitation-induced effects are important for the case of narrowband excitation analysed in Fig. 1 and Extended Data Fig. 4.

Data landscape of quasiparticle colliders

In regular optical spectroscopy, system resonances of interest are often imbedded within the spectral range of the applied pump field. Our quasiparticle collider spectrally separates the relevant features from the pump as distinct sidebands. Additionally, each sideband order can contain different aspects of the collisions. As in conventional colliders, the scattering-generated radiation produces a wealth of information about the (quasi)particles. Here, we study the HSG intensity I_HSG as a function of the HSG frequency v_HSG, the field strength E_λ, the duration τ_λ, and the central frequency v_λ of the optical preparation pulse (λ = opt) and the THz waveform (λ = THz), as well as their mutual delay t_ex, generating at least, eight-dimensional data sets

$$I_{\text{HSG}}(v_{\text{HSG}},E_{\text{THz}},{\tau }_{\text{THz}},v_{\text{THz}},E_{\text{opt}},{\tau }_{\text{opt}},v_{\text{opt}},t_{\text{ex}}).$$

As typical for colliders, such a wealth of data reveals details of colliding quasiparticles only through a dedicated identification process. For example, Fig. 3 demonstrates how changing t_ex yields a direct detection of the electron–hole recollision. We will next illustrate a few additional possibilities to extract exciton-related details from the HSG scattering data.

As shown in Extended Data Fig. 4, broadening of sideband resonances is directly related to exciton decay rates which depend on the excitation parameters. This effect is often referred to as excitation-induced dephasing^44,45, which can be controlled, e.g., by changing E_opt (Ref. 34). We have also confirmed that the exciton binding energy E_B strongly influences the overall strength of the HSG signal. For example, a ten-fold increase of E_B amplifies I_HSG roughly by the same amount as a result of Coulomb enhancement of the collisional cross section. Hence, a variety of material- and excitation-dependent exciton features may be deduced by quantitatively analyzing the strength and width of I_HSG resonances.

By changing the optical pump frequency v_opt, one can deduce differential changes in HSG spectra that sensitively monitor material details. We propose measuring a two-dimensional I_HSG(v_HSG, v_opt) set to follow spectral changes at the second-order sideband and to define a normalized spectrum

$$I(v,v_{\text{opt}})\equiv \frac{I_{\text{HSG}}(v_{\text{HSG}}-v_{\text{opt}},v_{\text{opt}})}{I_{2\text{SB}}},$$

where v = (v_HSG − v_opt) is the frequency scale centered around v_opt and I_2SB = I_HSG(v_opt + 2v_THz, v_opt) is the peak intensity of the second-order sideband. This normalization produces spectra that do not depend on the absolute intensity scale – a quantity that is difficult to determine experimentally for a wide range of frequencies v_opt. From the difference of two spectra measured with pump frequencies $v_{\text{opt}}-\frac{\Delta v_{\text{opt}}}{2}\text{and}{v}_{\text{opt}}+\frac{\Delta v_{\text{opt}}}{2},$ respectively, we deduce a finite differential

$$\Delta I(v,v_{\text{opt}})=\frac{1}{\Delta v_{\text{opt}}}\left[I\left(v,v_{\text{opt}}-\frac{\Delta v_{\text{opt}}}{2}\right)-I\left(v,v_{\text{opt}}+\frac{\Delta v_{\text{opt}}}{2}\right)\right],$$

which approaches the derivative 𝜕I/𝜕v_opt in the limit Δv_opt → 0.

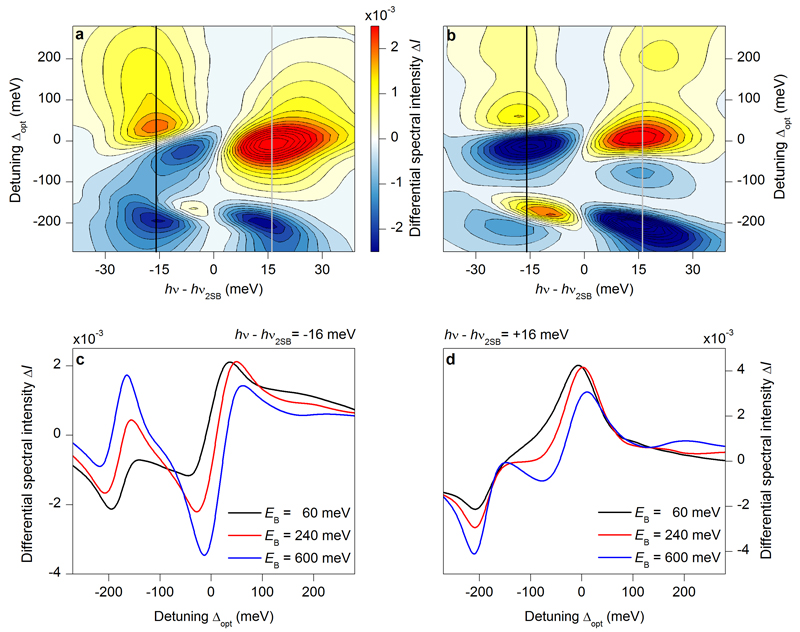
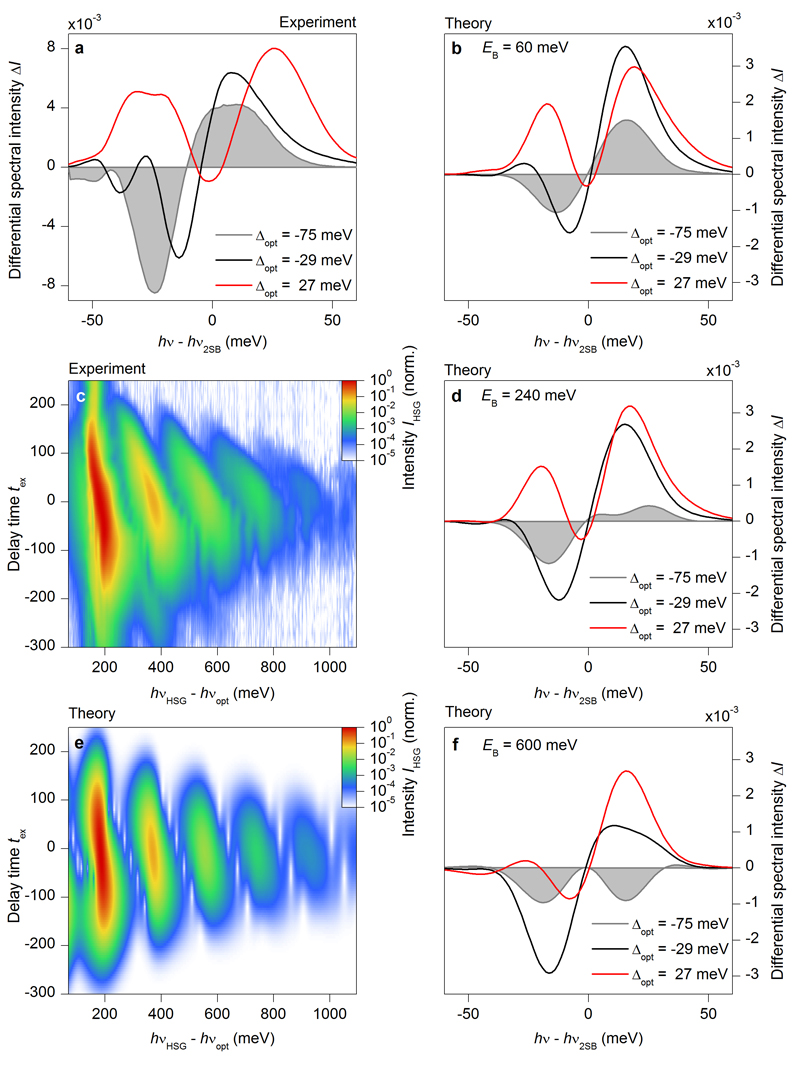
Extended Data Figures 8a and b show computed ΔI(v, v_opt) for two 1s-exciton binding energies, E_B = 60 meV (a) and E_B = 600 meV (b) when hv_opt is expressed in terms of the detuning Δ_opt with respect to the 1s-exciton energy hv_1s as hv_opt = hv_1s + Δ_opt. These contours produce rich spectral information which differs strongly for the two exciton binding energies, demonstrating that ΔI(v, v_opt) exposes material-dependent properties. For E_B = 60 meV, ΔI(v, v_opt) exhibits dominantly negative changes for Δ_opt< 0, implying decreasing I_HSG for negative detuning. Since Δ_opt > 0 yields mainly positive ΔI(v, v_opt), a clear dispersive shape is observed around the resonant excitation (Δ_opt = 0). For E_B = 600 meV, a positive island appears within the Δ_opt< 0 region, which implies that I_HSG can be enhanced also for negative Δ_opt, in contrast to the E_B = 60 meV case. Additionally, also Δ_opt>0 produces a new feature because the positive islands split into a double-peaked structure for E_B = 600 meV.

In order to analyze the quantitative dependence of ΔI(v, v_opt) on E_B, Extended Data Figures 8c and d show slices of ΔI(v, v_opt) at fixed values of h(v − v_2SB) = +16 meV (c) and -16 meV (d) for three different binding energies E_B = 60 meV (black curve), 240 meV (red curve), and 600 meV (blue curve). The slice at -16 meV shows only one positive peak for Δ_opt > 0 and remains negative at Δ_opt < 0 for E_B = 60 meV (black curve). Increasing the exciton binding energy gradually creates a new maximum within the region of negative detuning. This transition from a single to a double-peaked structure can be exploited to assign the exciton binding energy as shown below. Monitoring the slices at h(v − v_2SB) = +16meV reveals a smooth, narrow, and single-peaked structure close to Δ_opt = 0 for E_B = 60 meV (black curve). In contrast, higher binding energies produce a more structured shape.

To construct differential spectra ΔI(v, v_opt) experimentally, we measure HSG spectra for narrowband pump pulses at different frequencies v_opt (see Fig. 1b and d) while varying t_ex. Extended Data Figure 9c shows the resulting intensity map I_HSG(v, v_opt, t_ex) for resonant excitation hv_opt = hv_1s, while the corresponding computation is shown in Extended Data Figure 9e. Both experiment and theory show the same spectral structure, including t_ex-dependent changes in the intensity and shape. A similar level of agreement is realized also for non-resonant excitations (not shown), paving the way to thorough theory-experiment comparison of the differential spectra.

Based on Extended Data Figure 8, we expect the strongest dependence of ΔI(v, v_opt) on E_B for a finite detuning Δ_opt from the 1s-exciton resonance. We therefore compare experimental traces ΔI(v, v_opt) at t_ex = -20 fs for three different detunings Δ_opt = -75 meV (shaded area), -29 meV (black curve), and 27 meV (red curve) in Extended Data Figure 9a. A negative Δ_opt produces a dispersive lineshape to ΔI(v, v_opt), i.e., a dip followed by a zero-crossing and a peak, which implies a shift of the underlying HSG intensity with a change in v_opt. For positive Δ_opt, a double-peaked structure indicates a broadening of the HSG peaks. For a binding energy of E_B = 60 meV, these line shapes are well reproduced by the theoretical computations using the same detuning Δ_opt and excitation conditions as in the experiment, as shown in Extended Data Figure 9b.

Extended Data Figures 9d and f show the corresponding calculated differentials ΔI(v, v_opt) when the exciton binding energy is increased to E_B = 240 meV (d) and E_B = 600 meV (f). While Δ_opt = - 29 meV (black curve) and Δ_opt = 27 meV (red curve) produce a similar shape as for E_B = 60 meV, the peak amplitude of the differential curve for Δ_opt = -75 meV (shaded area) greatly decreases for an intermediate binding energy of E_B = 240 meV and turns into a negative dip for the largest binding energy. This structural change in ΔI(v, v_opt) can be utilized to deduce the exciton binding energy. We find that the experimental data is consistent with E_B = 60 ± 20 meV, which agrees well with values reported in literature^30,46,47.

Extended Data

Extended data Figure 1. Polarization of high-order sidebands.

a, b, False colour plot of the spectral intensity of high-order sidebands (generated under resonant, spectrally narrow optical excitation) of orders 2 to 8 as a function of their polarization for horizontal (a) and vertical (b) polarization of the interband excitation pulse. The polarization angle is defined such that 0° corresponds to a horizontally polarized excitation. c, Spectrally integrated sideband intensity in dependence on the polarization angle.

Extended data Figure 2. Pump fluence dependence of time-resolved high-order sideband generation.

a, The measured high-order sideband intensity I_HSG (spectrally and temporally integrated, red spheres) scales linearly with the pump fluence Φ, as indicated by a guide to the eye (black dashed line). b, The modulation depth of the spectrally integrated temporal trace of I_HSG (red spheres, comp. Figure 2b) decreases with increasing pump fluence, closely following a fit (black curve) proportional to the inverse square-root of the pump fluence. c, In contrast, the relative sub-cycle delay δ_scT^-1 does not substantially change with increasing pump fluence. Red spheres represent the average of δ_scT^-1 over the nine dominant consecutive high-order sideband peaks (compare Fig. 2d) for different pump fluences while the error bars indicate their standard deviation. The black dashed line marks the mean value of the displayed data points.

Extended data Figure 3. Coherent excitonic polarization dynamics in k-space.

a, Computed high-order sideband intensity I_HSG (red shaded area) and driving waveform (blue). Vertical black dotted lines highlight characteristic delay times t_ex at extrema of I_HSG. b-d, Coherent interband polarization |p|² as a function of time t and reciprocal space coordinate k for distinct delay times t_ex according to maximum (b, t_ex = 7 fs; d, t_ex = 28 fs) and minimum (c, t_ex = 18 fs) HSG emission (colour-coded, see key). Horizontal white lines mark k = 0. The driving field is depicted as grey curves and the recollision times (compare Fig. 3d) are highlighted by black arrows.

Extended data Figure 4. Influence of dephasing on high-order sideband generation.

The measured sideband spectrum (shaded area) is compared with computations using constant dephasing times of T₂ = 3.2 fs (a, red curve), T₂ = 4 fs (b, blue curve) and a momentum-dependent dephasing model as presented in Fig. 1 (a, b, black curves). The sideband orders n are indicated above the relevant peaks. All spectra are normalized to the sideband peak corresponding to n = 2. The inset in panel a depicts the corresponding dephasing times T₂(k) as a function of the wave-vector k, while the red (blue) horizontal line indicates a constant decay level T₂ = 3.2 fs (T₂ = 4 fs).

Extended data Figure 5. Field scaling of time-resolved high-order sideband generation.

a, Scaling of the modulation depth (comp. discussion in ‘Influence of excitation fluence’ in Methods) of temporal traces of high-order sideband intensity with the driving peak field strength. An increase in the modulation depth hints towards a faster dephasing T₂. b, Sub-cycle delay δ_sc in units of the driving period T averaged over the eight most dominant sideband peaks as a function of the peak field. The error bars represent the standard deviation of the eight peaks and the dashed line depicts a linear fit to the data points.

Extended data Figure 6. Influence of excitation-induced dephasing.

a, Terahertz waveform used in the computations. b, c, Mean electron excursion 〈k〉 calculated with a constant dephasing T₂ = 12 fs (b) and EID (c) for a delay of t_ex = 7 fs (see vertical dotted lines in a). The shaded areas indicate the intensity envelopes of the excitation pulse with a full width at half maxima of 10 fs (yellow) and 100 fs (gray), respectively. The corresponding mean momenta 〈k〉 are shown as red and black curves, respectively. The red-dashed curves show 〈k〉 after the electron-hole collision. The dashed horizontal lines mark the positions in k-space, where the scattering time T₂(k) switches from slow to fast dephasing.

Extended data Figure 7. High-order harmonic generation in tungsten diselenide.

An intensity spectrum (blue shaded area) of terahertz-driven high-order harmonic generation in 60-nm-thick WSe₂ shows distinct peaks at odd orders n’ = 13 to n’ = 47 (indicated by numerals) of the fundamental frequency v_THz = 22.3 THz (peak electric field in air, 21 MV cm^-1; ϕ = 90°). An intensity spectrum for φ = 120° is also shown as a black curve. The spectral intensity has been corrected for the grating efficiency as well as the quantum efficiency of the employed spectrograph.

Extended data Figure 8. Differential sideband spectroscopy.

a, b, Contours of differential spectra ΔI(v, v_opt) (see key) as a function of h(v – v_2SB) and detuning Δ_opt computed for an excitonic binding energy of E_B = 60 meV (a) and E_B = 600 meV (b). The black and grey vertical lines mark the positions of the slices shown in (c) and (d), respectively. c, d, Snapshots of ΔI(v, v_opt) at fixed values of |h(v – v_2SB)| = 16 meV below (c) and above (d) the second-order sideband peak for three different binding energies E_B = 60 meV (black curve), E_B = 240meV (red curve), and E_B = 600 meV (blue curve).

Extended data Figure 9. Quantitative analysis of the binding energy.

a, Measured differential spectra ΔI(v, v_opt) for three different detunings Δ_opt = -75 meV (shaded area), Δ_opt = -29 meV (black curve), and Δ_opt = 27 meV (red curve) as a function of v, centered at the position of the second sideband v_2SB. b, d, f Computed differential spectra ΔI(v, v_opt) for binding energies of E_B = 60 meV (b), E_B = 240 meV (d), and E_B = 600 meV (f) and detunings Δ_opt as in the experiment shown in panel a. c, e, Colour-coded representation of measured (c) and calculated (e) HSG spectra for Δ_opt = 0 (intensity scale, see key) as a function of v_HSG and delay t_ex.