Insight solutions are correct more often than analytic solutions

Abstract

How accurate are insights compared to analytical solutions? In four experiments, we investigated how participants’ solving strategies influenced their solution accuracies across different types of problems, including one that was linguistic, one that was visual and two that were mixed visual-linguistic. In each experiment, participants’ self-judged insight solutions were, on average, more accurate than their analytic ones. We hypothesised that insight solutions have superior accuracy because they emerge into consciousness in an all-or-nothing fashion when the unconscious solving process is complete, whereas analytic solutions can be guesses based on conscious, prematurely terminated, processing. This hypothesis is supported by the finding that participants’ analytic solutions included relatively more incorrect responses (i.e., errors of commission) than timeouts (i.e., errors of omission) compared to their insight responses.

Introduction

Albert Einstein once described how he achieved his insights by making “a great speculative leap” to a conclusion and then tracing back the connections to verify the idea (Holton, 2006). Research has generalised this concept by showing that many people’s insights involve the sudden emergence of a solution into awareness as a whole – a “great speculative leap” – in which the processes leading to solution are unconscious and can be consciously reconstructed only after the fact (Metcalfe & Wiebe, 1987; Smith & Kounios, 1996). The alternative solving strategy is analysis: the conscious, deliberate search of a problem space to find a solution (Ericsson & Simon, 1993; Metcalfe & Wiebe, 1987; Newell & Simon, 1972). In contrast to the all-or-none availability of insight solutions, analytic solutions yield intermediate results because analytic processing is largely available to consciousness (Kounios, Osman, & Meyer, 1987; Meyer, Irwin, Osman, & Kounios, 1988; Sergent & Dehaene, 2004; Smith & Kounios, 1996).

Once achieved, insight solutions typically seem obvious and certain, a feeling which Topolinski and Reber (2010) hypothesised to be a consequence of the highly fluent processing that suddenly propels an unconscious idea into awareness. Einstein wrote, “At times I feel certain I am right while not knowing the reason” (Schilpp, 1979). Indeed, the history of great discoveries is full of successful insight episodes, fostering a common belief that when people have an insight they are likely to be correct. However, this belief has never been empirically tested and may be a fallacy based on the tendency to report only positive cases and neglect insights that did not work. This study tests the hypothesis that the confidence people often have about their insights is justified.

There are reasons to doubt the hypothesis that insight solutions are typically more accurate. For example, one might reasonably assume that analytic processing should leads to more accurate solutions because it is available to consciousness and proceeds in a deliberate step-by-step fashion, making it possible to monitor one’s progress and, when necessary, make adjustments to ensure that the eventual solution is correct. In contrast, because insight solutions are produced below the threshold of consciousness, it is not possible to monitor and adjust processing before the solution enters awareness.

Another reason to question the supposedly superior accuracy of insights is the possibility that the confidence that people place in them could cause the illusion that an idea was derived by insight rather than the experience of an insight instilling confidence. According to this idea, it is not that insights are more accurate. Rather, more accurate solutions may be labelled as insights after the fact.

Although this idea has the appeal of simplicity, it does not account for key findings. For example, Metcalfe (1986) tracked ratings of how close participants felt reaching a solution (“warmth”) and found that warmth ratings did not increase until the last 10 s before the solution to insight problems, whereas warmth ratings during the solving of analytic problems showed a more incremental increase. Furthermore, when Metcalfe examined responses participants gave when they showed incremental versus sudden increase in warmth ratings, she found that responses associated with sudden jumps in warmth (i.e., insights) were correct more often than responses associated with incremental increases warmth (i.e., analytic solving). Thus, differences between insight and analytic processing precede solution.

Other findings provide additional support for the notion that insight processing is qualitatively different from analytic processing and that these differences precede solution. Bowden and Jung-Beeman (2003a) presented compound remote associates (CRA) problems to participants followed by a single word that they were instructed to verbalise as quickly as possible. For unsolved problems, following verbalisation participants indicated whether the word was the solution to the preceding problem and then indicated whether this realisation had come to them incrementally (i.e., analytically) or suddenly (insightfully). Participants verbalised the word more quickly when it was the solution to the preceding problem. Moreover, this priming effect was strongest when the solution word was accompanied by an Aha! experience and when the word was laterally displayed to the right hemisphere. This demonstrated differential insight and analytic solving prior to the recognition of the solution.

Importantly, neuroimaging studies demonstrate that there are different patterns of brain activity during and prior to solving by insight versus analysis (Jung-Beeman et al., 2004; Kounios et al., 2006; Subramaniam, Kounios, Parrish, & Jung-Beeman, 2009). Indeed, even before a person sees a problem, his or her pattern of brain activity predicts whether that problem will be solved analytically or by insight (Kounios et al., 2008; Subramaniam et al., 2009). Most recently, Salvi, Bricolo, Franconeri, Kounios, & Beeman, (2015) showed that people blink and move their eyes differently prior to solving by insight versus solving analytically.

Perhaps most important, a study by Kounios et al. (2008) revealed a pattern of errors during solving that suggests different cognitive strategies for problem solving via insight and analysis. They found that participants who solve predominantly by insight tend to make errors of omission (i.e., time outs) rather than errors of commission (i.e., incorrect responses), whereas participants who tend to solve analytically make errors of commission rather than errors of omission. They proposed that when confronted with a deadline, an insight solver will time out when the insight does not arrive in time; in contrast, an analytic solver will be able to guess, often incorrectly, before the deadline because the participant can offer as a potential solution the hypothesis that she or he was evaluating just before the deadline. (In the discussion, we explain how this model can account for differences in accuracy between insight and analytic responses.)

Thus, insight and analytic solutions are produced by different cognitive strategies and are not a product of arbitrary retrospective labelling. Any difference in accuracy between insight and analysis, therefore, cannot be reduced to a difference in confidence.

We assessed the relative accuracies of insight and analytic solutions in four experiments that used linguistic (i.e., CRA problems), visual (degraded object recognition, or “visual aha,” problems) or mixed linguistic-verbal problems (anagrams and rebus puzzles). The basic experimental procedure was constant across all of the experiments. Participants had 15 s (16 s in Experiment 2) to press a button immediately on solving each problem¹. They then provided their solution (without receiving accuracy feedback) and indicated how they had achieved their proposed solution, whether by insight or analysis (Bowden, Jung-Beeman, Fleck, & Kounios, 2005). Experiments 1 and 2 were performed in the United States using English; Experiments 3 and 4 were performed in Italy using Italian. There were three possible outcomes: (1) participants could be more accurate when solving analytically than when solving insightfully, (2) participants could be more accurate when solving with insight, as anecdotal reports suggest and (3) there could be no consistent relationship between problem-solving style and accuracy.

Experiment 1 – CRAs

Method

Participants

Thirty-eight undergraduate students (age M = 20.12; standard deviation (SD) = 3.04; 22 females) from Northwestern University (Evanston, IL) participated for partial course credit. All participants were right-handed native speakers of American English.

Stimuli and apparatus

For each of 120 CRA word problems (Bowden & Jung-Beeman, 2003b; Mednick, 1962, 1968), three stimulus words (e.g., crab, pine and sauce) were presented simultaneously. To reach the solution, solvers had to think of a single additional word (apple) that could form a common compound word or familiar two-word phrase with each of the three problem words (crab apple, pineapple, applesauce – Figure 1(A)). CRA problems can be solved by insight or analysis. Self-reports differentiating between insight and analytic solving have demonstrated reliability in numerous behavioural and neuroimaging studies (e.g., Bowden & Jung-Beeman, 2007; Jung-Beeman et al., 2004; Kounios & Beeman, 2014; Subramaniam et al., 2009). Eyelink Experiment Builder software (SR Research) was used to program the experiment for both stimulus presentation and response recording. Eye-blink and eye-movement data indicating further differences between insight and analytic processing are reported elsewhere (Salvi, Bricolo, et al., 2015). The 120 CRAs were randomly presented across four blocks.

Figure 1.

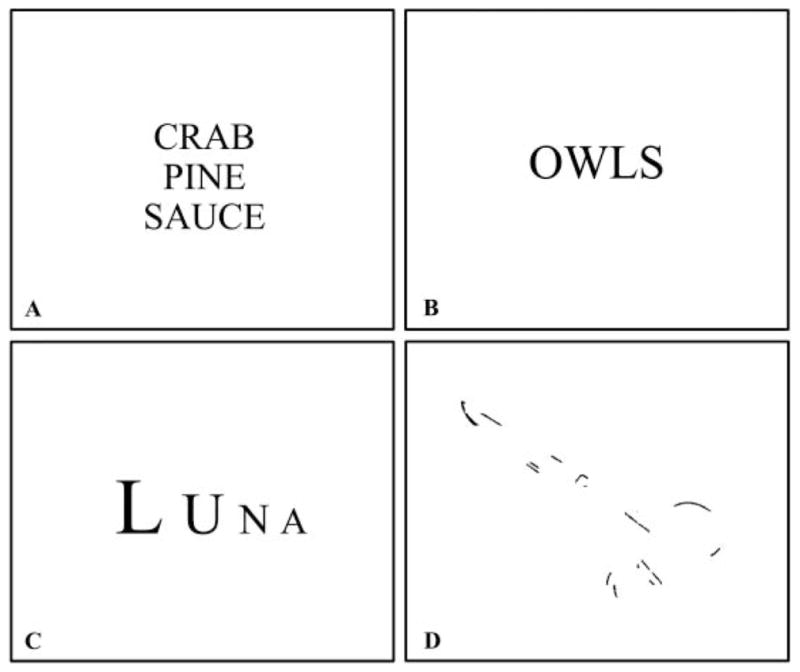
Each panel represents an example of the items used in the experiments. Specifically: 1(A) represents an example of CRAs, the solution is “apple”; 1(B) represents an example of anagrams, the solution is “SLOW”; 1(C) represents an example of rebus puzzle, the solution is luna calante “decreasing/waning moon” and 1(D) represents an example of visual aha problems, the solution is “scissors”.

Procedure

Prior to the experiment, participants were given three practice CRA problems and instructions² regarding how to distinguish insight from analytic problem solving (Jung-Beeman et al., 2004; Kounios et al., 2006). Solving a CRA problem via insight was described as the answer suddenly coming to mind, being somewhat surprising, and with the participant having difficulty stating how the solution was obtained (“feeling like a small Aha! moment”). Solving the CRA problem analytically was described as the answer coming to mind gradually, using a strategy such as generating a compound for one word and testing it with the other words, and being able to state how the solution was obtained. Furthermore, they were told that the problems ranged in level of difficulty and that they would, therefore, be unable to solve all of them. Participants were informed that there were no right or wrong answers in reporting solutions as insight or analytic and that neither of these solving styles is better nor worse than the other. The problems were displayed centred in a column in black lower case letters against a white background and were presented in a random order. Each trial began with a 0.5 s fixation plus sign followed by the three problem words. Participants were instructed to read the three words and to press a button immediately if they could solve the problem within the 15 s time limit, 0.5 s after which a screen message prompted them to verbally report their solution. No feedback was given to the participants regarding the accuracy of their solution. After each response (correct or incorrect), participants had to press a button to indicate whether the solution was achieved insightfully or analytically.

Results

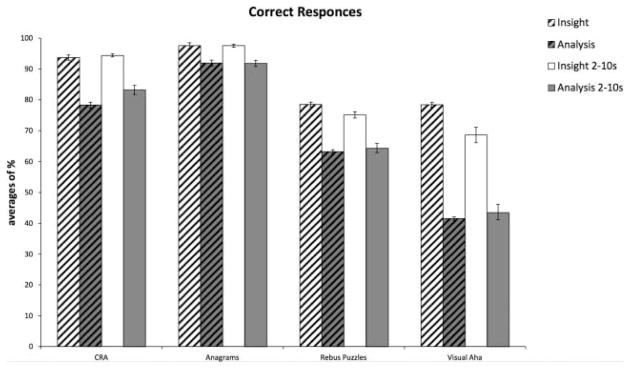
Participants responded (correctly or incorrectly) to 47.7% of problems (mean n of responses, M = 60.2; SD = 16.2); the remaining problems (when participants ran out of time) were discarded and considered as errors of omission. Of all responses labelled as insight, an average of 93.7% were correct (mean n of responses, M = 29.3, SD = 11.4); of all responses labelled as analytic, an average of 78.3% were correct (mean n of responses, M = 19.1, SD = 11.2). Significantly more problems solved with insight were correct compared to those solved via analysis (t(37) = 5.66; d = .99; 95% confidence interval (CI) [.09; .21]; p < .001); significantly more errors were labelled as analytic than insightful (t(37) = −5.71; d = −1.02; 95% CI [−.22; −.10]; p < .001).

A secondary analysis with a narrower response window was performed to examine a time period in which insight and analytic responses occurred approximately equally often. The analyses were similar to those just described except that only those responses with latencies within the 2 to 10 s time-window were included. Responses made during the first 2 s were excluded because participants might impulsively report those as insights (Cranford & Moss, 2012). The secondary analyses also excluded responses produced during the last 5 s of the time-window when participants might be more likely to guess to avoid timing out without making a response. Indeed, participants’ response accuracies were reliably lower during the final 5 s (34.1% errors; mean n of errors, M = 5.1, SD = 5.2) than during the preceding 10 s across the solution types (10.5% errors; mean n of errors, M = 5.1; SD = 4.6; t(37) = −4.41, d = −.70; 95% CI [−.20; −.07], p < .001). For answers given in the last 5 s, significantly more errors were labelled as analytic (29.4% errors; mean n of errors, M = 4.4, SD = 4.6) than insight (4.7% errors; mean n of errors, M = 0.7, SD 0.9; t(27) = −3.51; d = −.70; 95% CI [−.32; −.08]; p < .005). By confining this secondary comparison to a narrower time-window, we ensured that comparisons of analytic and insight accuracies were not contaminated with very quick or very slow guesses. Specifically, 77.8% (mean n of responses, M = 45.2, SD = 11.6) of the answers were given between 2 and 10 s. For insight responses within this time-window (61.8% of all responses; mean n of responses, M = 27.3, SD = 11.9), an average of 94.4% (mean n of responses, M = 25.4, SD = 10.3) were correct. Of analytic responses (38.2%; mean n of responses, M = 16.9, SD = 10.6), an average of 83.2% (mean n of responses, M = 14.5, SD = 10.1) were correct. Significantly more problems solved with insight were correct compared to those solved via analysis (t(37) = 3.55; d = .74; 95% CI [.04; .17]; p < .005), and significantly more errors were labelled as analytic than insight (t(33) = −3.61; d = −.81; 95% CI [−.19; −.05]; p < .001) (see Figure 2).

Figure 2.

The per cent of problems correctly solved compared by type of problems (CRA, anagrams, rebus puzzle and visual aha), solution style (insight or analysis) and across two time windows (the whole problem or excluding the first 2 and the last 5 s). For each type of problem, significantly more correct problems were produced via insight compared to analysis. Errors bars indicate 95% confidence intervals. Note as mentioned in the text, 16 s were given to participants to solve the anagrams task; therefore, the second time-window considered goes from 2 to 11 s.

Experiment 1 discussion

In both the full and the narrower time windows, participants provided more accurate responses when they solved by insight than analysis. The generality of this finding was tested in the following three experiments by varying the types of problems. Additionally, in Experiment 1, participants could label their solutions only as “insight” or “analytic”. In Experiment 2, we expanded their labelling options to include “unsure”.

Experiment 2 – anagrams

Method

Participants

Fifty-one undergraduate students (M = 20.5 years; SD = 2.7; 25 females) were paid $15 each to participate in the experiment. Participants’ electroencephalograms (EEGs) were recorded during this experiment (the EEG data will be reported elsewhere). All participants were right-handed, native speakers of American English.

Stimuli and apparatus

The stimuli were 180 anagrams (109 four-letter and 71 five-letter anagrams – see Figure 1(B)) generated by a computer program (Vincent, Goldberg, & Titone, 2006). Each anagram had only a single solution. Fifty per cent of the anagrams were presented as real words that could be rearranged to spell one other word (e.g., OWLS – solution SLOW) and 50% were presented as non-words that could be rearranged to spell one other word (e.g., LAGO – GOAL). The mean bigram sum of the solutions was 5954.91 (SD = 2555.31). The mean word frequency (Francis & Kucera, 1982) for the solutions was 54.75 per million (SD = 93.79). Self-reports differentiating between insight and analytic solving have demonstrated reliability in EEG studies (Kounios et al., 2008). The stimuli were written in black lower case letters on a white background and were presented at the centre of the screen in a randomised order.

Procedure

A practice block of 14 anagrams preceded the experiment. The instructions were similar to those given in Experiment 1. Each trial began with a 0.5-s fixation plus-sign followed by an anagram displayed at the centre of the screen. Participants were given 16 s to respond by pressing a mouse button as quickly as possible upon solving each problem; 0.5 s after each response, a screen message prompted them to verbally report their solution. They were given no accuracy feedback. After verbalising each solution, participants had to press a button to indicate whether the solution had been achieved insight-fully or analytically or whether they were not sure how they had solved it. The experimental session took approximately 1 hour.

Results

Participants responded to 73% of the problems (mean n of responses, M = 130, SD = 23.2); trials on which a participant timed out without responding were considered errors of omission and were not included in these analyses. No significant difference was found between word and nonword stimuli. Of all responses labelled as insights, an average of 97.6% were correct (mean n of responses, M = 72.4; SD = 30.2); of all responses labelled as analytic, an average of 91.9% were correct (mean n of responses, M = 51.9; SD = 30.1). Significantly more insight responses were correct compared to analytic responses (t (50) = 2.78; d = 1.50; 95% CI [.01; .09]; p < .01); significantly more errors of commission were labelled as analytic than insight (t(50) = −2.79; d = .60; 95% CI [−.1; −.06]; p < .01). Participants were unsure about how they solved the problems (whether by insight or analysis) for 2.2% of their responses (mean n of responses, M = 2.8; SD = 6.2); 77.3% of these unsure responses were correct. As in Experiment 1, an additional analysis with a narrower response window was used that included only responses made after the first 2 s and before the final 5 s (i.e., a time-window from 2 to 11 s). Specifically, 68.7% of the responses were made between 2 s and 11 s (mean n of responses, M = 89.2, SD = 16.3). Of all responses in this time-window that were labelled as insights (55.3% of all responses; M = 49.3, SD = 21.8), an average of 97.6% (mean n of responses, M = 48, SD = 5) were correct and of all those labelled as analytic (44.7%; mean n of responses, M = 39.6, SD = 24.3) an average of 91.8% (mean n of responses, M = 37.4, SD = 15.1) were correct. Significantly more problems solved with insight were correct compared to those solved via analysis (t(50) = 2.64; d = .51; 95% CI [.01; .10]; p < .05) and significantly more errors were labelled as analytic than insight (t(46) = −2.66; d = .53; 95% CI [−.01; − 2.66]; p < .05). In 1.9% of the cases (mean n of responses, M = 1.7; SD = 3.7) participants were unsure about how they solved a problem (neither via insight nor analysis); 1.6% of the times they were correct. As in Experiment 1, participants’ response accuracies were reliably lower in the final 5 s (11.1% errors; mean n of errors, M = 2.5, SD = 1.6) than in the preceding 11 s (4.3% errors; mean n of errors, M = 3.8; SD = 4.1; t(45) = −4.3 d = −.76; 95% CI [−.12; −.04]; p < .001). For responses made during the last 5 s, significantly more errors were labelled as analytic (8.3% errors; mean n of errors, M = 1.9, SD = 1.6) than insights (2.9% errors; mean n of errors, M = 0.6; SD = 1.1; t(27) = −3.37; d = −1.08; 95% CI [−.44; −.12]; p < .001) (see Figure 2).

Experiment 2 discussion

Experiment 2 replicated the results obtained in Experiment 1. In both the full and narrower time-windows, participants provided more accurate responses when they solved by insight than by analysis. This finding was robust to the change in the type of problem and the inclusion of an “unsure” option as an alternative to the “insight” and “analytic” strategy judgments. Experiment 3 used a different type of mixed linguistic-visual problem and was conducted in a different language and country.

Experiment 3 – rebus puzzles

Method

Participants

One hundred and ten undergraduate students (age M = 21.2; SD = 4.8; 81 females) from the University of Milano-Bicocca participated in the experiment for partial course credit. All participants were right-handed, native Italian speakers.

Stimuli and apparatus

Eighty-eight Italian rebus puzzles (Salvi, Costantini, Bricolo, Perugini, & Beeman, 2015; see Figure 1(C)) were administered to participants. Each participant received a block of 32 balanced trials. To solve each rebus puzzle, participants had to combine verbal and visual clues to make a common phrase, such as: LUNA – solution: luna calante, “decreasing/waning moon”; Ciclo, Ciclo, Ciclo (i.e., Cycle, Cycle, Cycle) – solution: triciclo, “tricycle”; T+U+T+T+O – solution: tutto sommato, “all summate”, a common Italian phrase which could be translated as “all things considered”. Rebus puzzles have been demonstrated to be a valid source of insight problems (MacGregor & Cunningham, 2008) which, like CRAs (Experiment 1) and anagrams (Experiment 2), can be solved either with insight or analytically (Salvi, Costantini, et al., 2015). The Inquisit (2012) software package was used for stimulus presentation, randomisation and response recording.

Procedure

Prior to the experiment, participants were given four practice rebus puzzles and instructions regarding how to distinguish insight from analytic problem solving similar to those given in Experiment 1. Each trial began with a prompt screen. When ready, participants pressed the keyboard spacebar to initiate the display of a rebus puzzle. Participants had 15 s to solve each puzzle. They were instructed to press the keyboard spacebar again immediately upon solving the puzzle. Next, they were prompted to type the solution and judge how they had solved the problem, via insight or analysis. No feedback was given to the participants regarding the accuracy of their solution. The experiment took approximately 30 minutes.

Results

Participants responded to 64.6% of problems given (mean n of responses, M = 20.7, SD = 4.3); the rest were time-out errors of omission that were not analysed further. Of all answers labelled as insight, an average of 78.5% were correct (mean n of responses, M = 10.4, SD = 5); of all answers labelled as analytic, an average of 63.2% were correct (mean n of responses, M = 5.3; SD = 4.7). Significantly more problems solved with insight were correct compared to those solved via analysis (t(109) = 6.08; d = .66; 95% CI [.13; .27]; p < .001); significantly more errors were labelled as analytic than as insights (t(109) = −3.71; d = −.72; 95% CI [−.05; −3.7]; p < .001). As in Experiments 1 and 2, we ran a secondary analysis with a narrower time-window that included only the responses with latencies between 2 and 10 s (61.2% of the responses). In this time-window, of answers labelled as insights, an average of 75.1% were correct (mean n of responses, M = 5.7, SD = 3.2); of responses labelled as analytic, an average of 64.4% (mean n of responses, M = 3.4, SD = 2.9) were correct. Significantly more problems solved with insight were correct compared to those solved via analysis (t(109) = 4.19; d = .39; 95% CI [.25; 4.1]; p < .01); significantly more errors were labelled as analytic than as insights (t(103) = −2.10; d = −.39; 95% CI [−.16; −.004]; p < .05).

As in Experiments 1 and 2, participants’ response accuracies were reliably lower in the final 5 s (58.6% errors; mean n of errors, M = 1.5, SD = .8) than in the preceding 10 s (28.1% errors; mean n of errors, M = 3.6; SD = 18.3; t(108) = −4.82; d = −.61; 95% CI [−.26; −.11]; p < .001). Of responses during the last 5 s, significantly more errors were labelled as analytic (39.2% errors; mean n of errors, M = 1.0, SD = .8) compared to insights (19.4% errors; mean n of errors, M = 0.5, SD = .73, t(109) = −4.82; d = −1.63; 95% CI [−.5; −.18]; p < .001) (see Figure 2).

Experiment 3 discussion

Experiment 3 replicated Experiments 1 and 2. In both the full and narrower time-windows, participants’ insight responses to rebus problems were more accurate than their analytic responses. These results were robust to a change in type of problem and language. In Experiment 4, we used an additional, more purely visual, type of problem.

Experiment 4 – visual aha

Method

Participants

Twenty-seven native Italian-speaking students (21 females) of the University of Milano-Bicocca participated in the experiment for partial course credit (M = 22.3 years of age, SD = 1.9). All participants were right handed.

Stimuli and apparatus

Stimuli consisted of 50 fragmented line drawings of animate and inanimate objects taken from Snodgrass and Vanderwart, (1980) (see Figure 1(D) for an example). Participants were asked to identify these objects at level 2 of segmentation (very low information). The level of picture segmentation refers to stimuli in which segments containing black pixels were randomly and cumulatively deleted to produce seven incrementally fragmented versions of each picture (Snodgrass & Corwin, 1988; Figure 1(D) shows an example of level 2). Insight has been noted in perception (Porter, 1954; Rubin, Nakayama, & Shapley, 1997, 2002), and picture recognition has been demonstrated to be valid task for studying insight problem solving (e.g., Ludmer, Dudai, & Rubin, 2011). Eyelink Experiment Builder software (SR Research) was used to randomise and present stimuli and record responses.

Procedure

Prior to the experiment, participants were given three practice trials and instructions regarding how to distinguish insight from analytic problem solving. These instructions were similar to those given in Experiment 1. Each trial began with a 0.5 s fixation cross followed by the stimulus figure. Participants had 15 s to recognise each figure. When a participant pressed a mouse button to indicate that he or she had solved the problem, a screen message prompted him or her to verbally report the solution. There was no accuracy feedback. Following the response, participants were prompted to press a button to indicate whether they had solved the problem via insight or analysis. The experiment took approximately 30 minutes.

Results

Participants responded to 71.8% of the problems (mean n of responses, M = 35.9, SD = 6.5), the remaining problems (when participants run out of time) were discarded and considered as errors of omission. Of all answers labelled as insights, an average of 78.4% were correct (mean n of responses, M = 16.6, SD = 6.7); of all answers labelled as analytic, an average of 41.5% were correct (mean n of responses, M = 6.7, SD = 4.7). Significantly more problems solved with insight were correct compared to those solved via analysis (t(26) = 7. 47; d = 1.85; 95% CI [.26; .46]; p < .001); significantly more errors were labelled as analytic than as insights (t(26) = −7.47; d = −1.85; 95% CI [−.46; −.26]; p < .001). As in Experiments 1, 2 and 3, we ran additional analyses with a 2 to 10s time-window. Specifically, 61.2% of the answers had latencies between 2 and 10 s (mean n of responses, M = 22, SD = 4.7). Of all answers labelled as insights, an average of 68.6% (mean n of responses, M = 7.2, SD = 4.4) were correct and 31.4% (M = 3.2, SD = 2.7) were errors; of all answers labelled as analytic, an average of 43.6% (mean n of responses, M = 5.3, SD = 4.2) were correct and an average of 56.4% (mean n of responses, M = 6.3, SD = 3.56) were errors. Significantly more problems solved with insight were correct compared to those solved via analysis (t(25) = 4.36; d = 1.24; 95% CI [.13; .36]; p < .01), and significantly more errors were labelled as analytic than insight (t (26) = −4.36; d = −1.08; 95% CI [−.36; −.13]; p < .001).

Participants’ errors during the final 5 s were higher (72.1% errors; mean n of errors, M = 2.1, SD = 1.6) than during the preceding 10 s (43.2% errors; mean n of errors, M = 9.5, SD = 4.4; t(26) = −3.52; d = −.94; 95% CI [−.39; −.10]; p < .005). For responses made during the last 5 s, significantly more errors were labelled as analytic (85.3% errors; mean n of errors, M = 1.9, SD = 1.5,) compared to insights (14.7% errors; M = .2, SD = .4; t(26) = −1.08; d = 1.27; 95% CI [−.80; −.51]; p < .001) (see Figure 2).

Experiment 4 discussion

Using visual problems, Experiment 4 replicated the results obtained in Experiments 1, 2 and 3. In both the full time-window and the narrower time-window, participants’ insight solutions were more accurate than their analytic solutions. This finding was robust to the change in problem type and language.

Discussion

Insight solutions were more accurate than analytic solutions in all four experiments. Thus, the feeling of confidence people often express about their sudden insights appears to be justified, at least for the types of problems typically used in laboratory studies of insight.

Why should insightful solving lead to greater accuracy than analytic solving? Prior research offers an explanation based on analyses of participants’ errors. Kounios et al. (2008) found that participants who solved anagrams predominantly by insight tended to either report the correct solution or time out, rarely offering incorrect responses. In contrast, participants who tended to solve anagrams analytically produced more incorrect responses but fewer timeouts relative to insightful solvers (see also Metcalfe, 1986).

This finding is consistent with results showing that insight solving is an all-or-none process while analytic solving is incremental (Smith & Kounios, 1996). Incremental analytic solving affords partial information on which a participant can base a guess just before the response deadline, hence the relative lack of timeouts. Conversely, insightful all-or-none solving does not yield intermediate results – in the absence of a meaningful potential guess, participants who tend to rely on insight will more often time out when faced by an imminent deadline. This notion explains the fact that in the current experiments there was a preponderance of incorrect responses identified as analytic during the last 5 s before the response deadline.

If analytic processing enables participants to respond based on active, but potentially incorrect, solution hypotheses, then why do not insight solutions afford a similar capability? Some problems are difficult to solve because the relevant concepts are remotely associated and are thus only weakly activated by the presentation of the problem. For example, the words of the CRA problem pine/crab/sauce are not strongly related to each other. Thus, in a spreading activation model (e.g., Collins & Loftus, 1975), there is little or no direct mutual priming of these concepts. Furthermore, the solution word, apple, is not the strongest associate of any of the problem words. However, weak spreading activation from each of the problem words will converge and summate on the solution word. This summated activation can accrue continuously (Collins & Loftus, 1975) and can be sufficient to achieve consciousness, though the individual subthreshold activations are not strong enough to achieve consciousness and provide accessible partial information. However, the threshold for consciousness is apparently an all-or-none boundary, hence the sudden awareness of an insight when the summated activation accrues to a sufficient level.

The same model can be applied to the other types of problems. For anagrams, the weak, unconscious associations are between letters or groups of letters that form the solution word. For rebus and visual aha problems, the unconscious associations are among weakly activated visual elements and the meaning of the solution.

In sum, this model explains that insight processing yields no partial solution information on a trial-by-trial basis because of subthreshold processing prior to the suddenly available solution. In contrast, analytic processing can yield better-than-chance guessing because it can produce guesses based on processing of suprathreshold activation candidates, some of which are correct.

We also note that performance on the problem-types differed in their overall accuracies. We attribute these accuracy differences (much lower in the rebus and the visual aha tasks than in the CRA and anagram tasks) to the different levels of difficulty inherent in these tasks. Multiple factors affect solutions accuracy, including the difficulty of deriving a candidate solution (determined by complexity of the rules) and the difficulty of recognising that a candidate solution fulfils the requirements of the problem. These factors are at least somewhat independent.

The problems used in these experiments differ considerably on these two factors. For example, CRAs have very few rules – add a fourth word so that the three compound words or common phrases are formed. The word can be added before or after each of the three words and, within the same problem, some can form compounds and some can form phrases. This paucity of rules can make it difficult to produce a solution. However, once a solution is produced, it is relatively easy to verify that it is acceptable as long as the solver knows the phrases or compound words. Anagrams are the most constrained of the 4 problem types. There is one simple, clear rule – rearrange the letters until they spell a word. Assuming the person knows the solution word, recognition of a successful solution is trivial. Knowledge of common English words and their orthography restricts the possible combinations of letters. Furthermore, the low number of letters in the anagrams used (4 or 5), and the fact that there is only one solution make the likelihood of recognising a correct solution high.

In contrast, rebus problems have multiple features that are not always consistently meaningful. For example, the size of the letters or their placement may be vital to the solution in one rebus puzzle but irrelevant in another. There are also multiple ways to interpret features, for example in the LUNA problem the decreasing size of the letters could be thought of as declining, decreasing, getting smaller, waning, etc., and only one fits the saying that is the solution. Additionally, even if they are very popular, some of the sayings may be unknown to some of the participants, so verifying the solution can be difficult.

Visual aha problems present a straightforward task–identify the object. However, there is no restriction on what the object can be (natural or man-made — an apple, a helicopter, a frog, etc.) and pixels have been removed randomly, so finding a solution is difficult. Moreover, once a possible solution is produced, it can be difficult to verify because, for example, a degraded line drawing of an apple can look very similar to a degraded line drawing of a peach, pear or baseball.

Between-task performance differences might also be accounted for by task-related variability in the difficulty of solving particular types of problems by analysis. Participants may be more ready to quit analytical solving too soon for problems that require more working-memory capacity. In contrast, unconscious insight solving uses little or no working-memory capacity and it is not subject to premature termination. Therefore, problems whose analytic solving requires more processing capacity will yield larger insight-analytic solving-accuracy differences.

Despite these differences among the problems, the finding that insight solutions are correct more often than analytic solutions was found for all four types of problems.

By including widely used sets of problems such as the CRAs and anagrams in this study, we were able to make comparisons to tasks like rebus puzzles and the visual aha problems that have been used to study insight problem solving only recently (Ludmer, Dudai, & Rubin, 2011; MacGregor & Cunningham, 2008; Salvi, Costantini, et al., 2015). Though further research should continue to compare performance for different types of problems, we believe that the consistency of the present results (obtained with a single experimental protocol) suggests that a core set of solving strategies (insight and analytic) and strategy-judgment processes operate across the types of problems.

One limitation of this study is that it is not yet known whether these results and this model generalise from laboratory puzzles to real-world problems that may be more complex and do not have a response deadline. At this point, there is no evidence against the notion that such laboratory puzzles provide a satisfactory model for real-world problem solving. However, future research should aim to test this idea in more ecologically valid ways.