Graph Theory and Cognition: An Alternative Avenue for Examining Neuropsychological Status in Epilepsy

Abstract

The recent revision of the classification of the epilepsies released by the ILAE Commission on Classification and Terminology (2005–2009) has been a major development in the field. Papers in this section of the special issue were charged with examining the relevance of other techniques and approaches to examining, categorizing and classifying cognitive and behavioral comorbidities. In that light, we investigate the applicability of graph theory to understand the impact of epilepsy on cognition compared to controls, and then the patterns of cognitive development in normally developing children which would set the stage for prospective comparisons of children with epilepsy and controls. The overall goal is to examine the potential utility of other analytic tools and approaches to conceptualize the cognitive comorbidities in epilepsy. Given that the major cognitive domains representing cognitive function are interdependent, the associations between the neuropsychological abilities underlying these domains can be referred to as a cognitive network. Therefore, the architecture of this cognitive network can be quantified and assessed using graph theory methods, rendering a novel approach to the characterization of cognitive status. In this article we provide fundamental information about graph theory procedures, followed by application of these techniques to cross-sectional analysis of neuropsychological data in children with epilepsy compared to controls, finalizing with prospective analysis of neuropsychological development in younger and older healthy controls.

1. Introduction

As noted in the Introduction by the editors of this special issue of Epilepsy & Behavior, there has been spirited debate concerning the benefits and drawbacks of the new approach to classifying the epilepsies released by the ILAE Commission on Classification and Terminology (2005–2009). While concerned with the classification of the epilepsies themselves, this system, and the classification systems before it, have had significant implications for the way cognitive and behavioral comorbidities in epilepsy are conceptualized. This is because of the longstanding tradition of examining comorbidities in line with contemporary classification of epilepsy syndromes. While a reasonable approach, there is growing appreciation that forces other than epilepsy syndrome may be important factors underlying the expression of cognitive and behavioral comorbidities. In that light, papers in this section of the special issue were charged with examining the relevance of other techniques and approaches to examining, categorizing and classifying cognitive and behavioral comorbidities.

In this contribution we investigate a novel approach to characterizing the impact of childhood epilepsy on the global landscape of cognition, defined by the interaction of multiple cognitive domains. Given that different cognitive domains are inter-dependent with each other [1], the associations between the neuropsychological abilities underlying these domains could be referred as a cognitive network. Thus, the architecture of the cognitive network can be quantified and assessed using formal methods to determine network conformation, i.e., graph theory.

Graph theory is a versatile tool that can be used to probe the topology of any system that can be identified as a network. This methodology has been applied to investigations of electrophysiological and imaging networks, as well as examination of brain structures, that have revealed global disruption in brain architecture and function in patients with epilepsy [2-7]. Large scale structural morphometrical brain changes have been correlated with specific cognitive deficits in epilepsy [8-9]; however, to date, there have been few examinations of neuropsychological measures considered as a cognitive network themselves using graph theory [10-11].

Graph theory, in essence, can provide a measure of the architectural organization of cognitive function, as defined by the network formed by the interrelationships between multiple cognitive abilities and domains. As such, graph theory is an expansion on conventional statistical approaches such as factor or clustering analyses because it permits the evaluation not only of grouping of cognitive modules, but also the participation of cognitive functions/domains within the entire cognitive architecture. For this reason, cognitive networks may provide novel insights into the cross-sectional status and longitudinal changes in cognitive structure, especially in regard to the abnormal conformation that may be driven by pathological that may be driven by pathological processes. Even though cognitive networks are not individualized measures (i.e., they arise from group wise correlations) they can be used to infer how individual test metrics may be related to the overall cognitive network under investigation. We wish to emphasize that the cognitive network we will be investigating is based on the specific tests that comprise a conventional neuropsychological battery; therefore, it should not be confused with well-known anatomical/functional cognitive-related brain regions.

Here we will first provide some fundamental information about graph theory procedures, followed by application of these techniques to neuropsychological data in children with epilepsy compared to healthy controls, followed by examination of natural occurring prospective changes in the cognitive networks of normally developing control participants.

2. Graph Theory

Graphs are mathematical representations of complex networks in the form of nodes (e.g., brain regions, cognitive tests) and edges or links (connections or correlations between nodes). Therefore, graph theory is the study of such graphs. There are different kinds of graphs that can be constructed, however, the most common ones in the field of neuroscience are binary and weighted graphs, either undirected (symmetric) or directed (non-symmetric). Directed graphs are those that convey causality or directionality of effect. For example, directed graphs could be constructed to investigate temporal causality in functional connectivity studies in order to understand the origin and propagation of a temporal signal [12]; therefore, graphs are non-symmetric (the value of the link or edge from node A to B is not the same as the one from B to A). Undirected graphs are those that reflect the relationship between different nodes or regions without any regard to direction (e.g. covariance analyses of brain structure or function); therefore, these graphs are said to be symmetric (the value of the link from node A to B is the same as the one from B to A). When the type of graph is chosen, it can then be investigated using the natural weights of the connections (i.e. correlation coefficient in a fMRI analysis) or by binarizing the matrix (1 if there is a connection, 0 if there is no connection between a pair of nodes) at a given threshold or range of thresholds (see below). The type of graph to use is based on the data and hypotheses of the study under consideration.

The nodes in a graph in the neurosciences could be anatomical regions based on various brain atlases (e.g. AAL, Freesurfer’s Desikan Killiany or Destrieux atlases), or functionally defined areas [13]. The connections between nodes in functional MRI, DTI, or high-resolution structural MRI could convey a network of functional associations, white matter connectivity, or regional covariance (i.e. volumetric analyses), respectively. The nodes and edges form a NxN matrix or network, in which N is the number of defined nodes. Once nodes are defined and a graph is obtained, thresholding should be performed in order to remove spurious connections. The main types of thresholding are statistical or topological. Statistical thresholding is based on the significance of the connections between nodes, while topological thresholding is based on the strength of the connections between nodes. There are two main ways of performing topological thresholding: either by performing absolute thresholding versus proportional thresholding. In the former, every connection is included in the graph if it is greater than the specified correlation value, while in the later only the strongest links (higher weight) within the chosen percentage value would be included in the graph. For example, in an undirected network (symmetric matrix) of N number of nodes, the total possible number of edges or connections would be N(N-1)/2. This means that for a network of 100 nodes, a proportional threshold of 10% would show 495 edges out of the 4,950 possible connections in the fully connected network. Since proportional thresholding provides the same number of links given the same number of nodes under study, group analyses can be possible. For the remainder of this discussion we will be referring to topological thresholding by performing proportional thresholding, unless stated otherwise. Graph theory measures can be acquired at a certain threshold or over a range of threshold values also known as the sparsity value, density, or cost.

2.1 Graph theory measures

Once a graph is calculated, different measures can be obtained in order to investigate its properties, which include metrics of segregation, integration, and centrality. A graph that shows segregation is one that allows for subgraphs to exist, which might represent specialized processes taking place within the network. An integrated graph is one that is capable of interchanging information between regions in an efficient manner. Centrality measures explain those nodes that play an important role in the configuration of the graph [14]. Some of the most common graph measures that investigate such properties are described below:

Characteristic path length

The characteristic path length is a measure that reflects the average separation between two nodes in the network [15]; therefore, a measure that provides information about the level of integration in the graph. However, this measure diverges when nodes in the network are disconnected (have no neighbors), which usually happens at low graph densities. Given that global measures (i.e., global measures of integration) should be acquired over a range of graph densities in order to be certain that the results are not driven by the chosen threshold, results from this metric could be introducing confounding information (if nodes are disconnected). Therefore, for this work we are using the harmonic mean instead (see below).

Harmonic mean and global efficiency

Harmonic mean, H_m is a measure of global integration in the graph. It is defined as the inverse of the global efficiency, E, which is the average of the inverse of each of the shortest paths (direct connections between nodes) in the network [16]. The lower the values of H_m the higher the integration of the network, therefore the higher the graph efficiency. Given that H_m is calculated as the inverse of the global efficiency, which only considers connected nodes, this measure does not suffer from divergence as the characteristic path length.

Local clustering coefficient and local efficiency

The local clustering coefficient is a measure of local segregation in the network. It is defined as the ratio of the number of connections between each node’s neighbors to the total number of connections that would exist between them [15], therefore it lies between 0 and 1, with 0 representing no connections between a node’s neighbors and 1 having all possible connections. However, local efficiency is a measure based on the shortest paths between each node’s neighbors, which reflects how efficient is the communication between the immediate neighbors of a node [16].

Average clustering coefficient and transitivity

The average clustering coefficient is defined as the sum of the local clustering coefficient of each node divided by the total number of nodes in the network. Nodes with a lower number of connections with other nodes (lower degree) would have a higher probability for its neighbors to be connected to each other, which would lead to an average clustering coefficient driven heavily by contributions of lower degree nodes. To avoid this, transitivity can be used instead of average clustering coefficient to obtain a more accurate measure of global segregation. Transitivity is a measure that reflects how clustered a network is. It is calculated as the ratio of “triangles” (closed connections between three nodes) to “triplets” (connections between three nodes) in the network [17-18], therefore it lies between 0 and 1, with 1 indicating a fully clustered network.

Modularity index and community structure

The modularity or community structure of a network is the configuration of such network into segregated communities that contribute to the same processes. Unlike the other measures, modular/community structure is statistically estimated instead of computed exactly [19]. The modularity index is a measure of the goodness of the subdivision of the graph into communities; the higher its value, the stronger the modular structure of the graph [20]. Modular structure in a functional network is of great importance because it not only allows for specialized processes to happen but also provides functional containment of community perturbations that would be easily spread to the rest of the network otherwise. Therefore, it is a measure of network robustness [21].

Centrality measures

The degree of a node is the classic measure of centrality, and it reflects the number of connections the node has while ignoring its weight [22]. A node with high degree is said to have many neighbors or adjacent nodes; therefore, having high local influences. Another measure of centrality is the eigenvector centrality, which is a measure indicating the quality of connections in a node. A node with high eigenvector centrality is one that connects mainly to nodes with high degree or high eigenvector centrality themselves [22]. This measure is different from degree centrality in which two nodes could have the same degree but not necessarily the same EC given that this measure depends on how connected the neighbors of a node may be. This is an important measure to evaluate those nodes that connect to other highly connected nodes. Other relevant measure of centrality would be the subgraph centrality, which evaluates the number of closed walks (loops) in which a node participates while assigning higher weighting to subgraphs formed by fewer nodes [22]. Nodes with high subgraph centrality tend to “give” and “receive” information in an efficient manner. Finally, the betweenness centrality (BC) is a measure of the importance of a node in the communication of a network [20] since it is based on the number of shortest paths in which a node participates. Measures of centrality provide information about the importance of a node in the network of interest; therefore, a node with high centrality can be considered a hub of the network (see below).

Network hubs

The hubs of a network are the most important nodes for the configuration of a network [20], and can be calculated using different centrality measures or combinations of different measures (i.e. degree and participation coefficient [23]). For this discussion, however, hubs would be identified as nodes with high BC values.

3. Network Analysis and Graph Theory Applications

Graph theory analyses of brain-related networks have led to possible investigations of whole-brain functional connectivity (fMRI), white-matter connectivity (DTI), and gray matter covariance analyses (GM) in both healthy and populations with a CNS disease or disorder [9, 24-25]. Therefore, this method has the capacity to investigate the brain at its different levels as a whole. Recently, this methodology has been extended to investigate the interrelationship of different cognitive tests between healthy and epilepsy pediatric participants [11], which proved the versatility of this methodology solely based on cognitive measures themselves.

3.1 Graph theory and cognition

It is well known that neuropsychological status can be adversely affected in the childhood epilepsies, even among the so-called benign idiopathic epilepsies. In such cases intelligence is typically average but with abnormalities in specific areas of cognitive ability including language, memory, executive function or processing speed [26]. Prospective investigations tracking children from the time of onset and diagnosis indicate that cognitive differences can be present at or near the time of diagnosis with these differences typically maintained over time, without evidence of progressive decline or significant improvement out to five years later [27-28].

These cognitive patterns have been developed and characterized by analysis of individual test scores, combinations of test scores, or factor scores at baseline and prospectively in some studies. While cognitive differences between participants with epilepsy and normally developing children can be identified and tracked over time with sophisticated test batteries, unclear, however, is how these diverse cognitive abilities and domains interact with one another in the epilepsy and control participants, if the interrelationships are different, and if so, in what ways. Also unclear is how these cognitive interrelationships and networks may change over time with maturation. Increasing chronological age is of course associated with the development and specialization of discrete cognitive skills (e.g., executive functions in adolescence) in the context of maturational brain changes; cognitive abilities increase from infancy to adulthood, however, depending on people’s skills they either decline or stay the same.

One approach to examine the network of cognitive abilities and their integration is by using graph theory techniques. As noted previously, these analytic approaches have been utilized in neuroscience research in epilepsy, but rarely has cognition been the sole focus of examination.

In a recent publication from our group, we investigated the cognitive networks of children with idiopathic epilepsy compared to a normally developing group of children without epilepsy [11]. Table 1 presents the neuropsychological measures that were administered to the cohort representing measures of intelligence, academic achievement, language, memory, executive function and processing speed.

Table 1.

Neuropsychological Test Battery

	Abbreviation	Test name	Cognitive ability
1	IQVOCS	WASI Vocabulary	Verbal intelligence
2	IQBDS	WASI Block Design	Nonverbal Intelligence
3	IQSIMS	WASI Similarities	Verbal intelligence
4	IQMRS	WASI Matrix Reasoning	Nonverbal intelligence
5	PPVTSTN	Peabody Picture Vocabulary Test	Language (word recognition)
6	EVTSTN	Expressive Vocabulary Test	Language (word naming)
7	READSTN	WRAT-IV Reading	Word recognition
8	SPELSTN	WRAT-IV Spelling	Spelling
9	ARITSTN	WRAT-IV Arithmetic	Arithmetic calculation
10	IQDSYMS	WISC-IV Digit symbol	Speed
11	WLLSS	Children’s Memory Scale-III	Verbal memory
12	WLDSS	Children’s Memory Scale-III	Verbal memory
13	CPOMT	Continuous Performance Test-II	Executive function (attention)
14	CPCOMMT	Continuous Performance Test-II	Executive function (attention)
15	CPRTBLKT	Continuous Performance Test-II	Executive function (attention)
16	LETFLUS	D-KEFS Letter Fluency	Language (lexical fluency)
17	CATFLUS	D-KEFS Category Fluency	Language (semantic fluency)
18	CATSWS	D-KEFS	Executive function (category switching)
19	COLSS	D-KEFS Color-Word	Speed
20	WORDSS	D-KEFS Color-Word	Speed
21	INHSS	D-KEFS Inhibition	Executive function (response inhibition)
22	CORSORS	D-KEFS Card Sorting Test	Executive function (problem solving)
23	BNTTOT	Boston Naming Test	Language (naming)

To begin, Figure 1 presents the adjacency matrices for the control participants (Figure 1, left) and children with idiopathic epilepsy (Figure 2, right) [11]. It can be appreciated that groups present specific differences in cognitive correlations. For example, control subjects presented high correlations between tests of coding (speed) and inhibition (tests 10 and 21, respectively, from Table 1) while children with epilepsy presented stronger cross-correlations between tests of intelligence, language, and academic achievement (the first nine tests from Table 1). In order to acknowledge topological group differences, the community structure of cognitive graphs was calculated (Figure 2). As can be seen, the control group showed higher modular organization than the children with epilepsy. This can be observed in the separation that exists between nodes in healthy controls while children with epilepsy had nodes that were closer together and therefore presenting reduced modular organization (Figure 2, right).

Figure 1. Adjacency matrices.

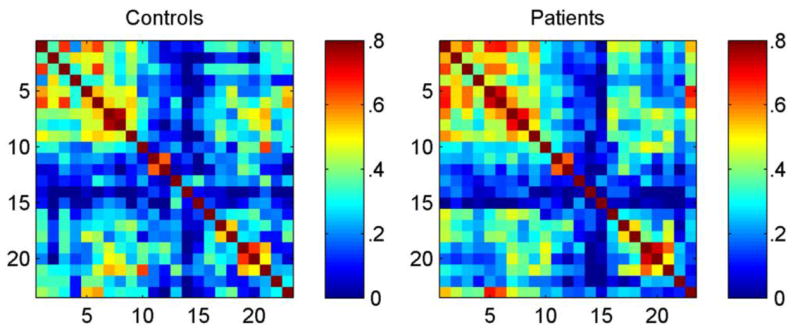
Adjacency matrices demonstrating the cross-correlations between scores in neuropsychological tests for controls (left) and patients (right). Neuropsychological tests are numbered in accordance with Table 1. Reproduced with permission.

Figure 2. Community structure of cognitive landmarks.

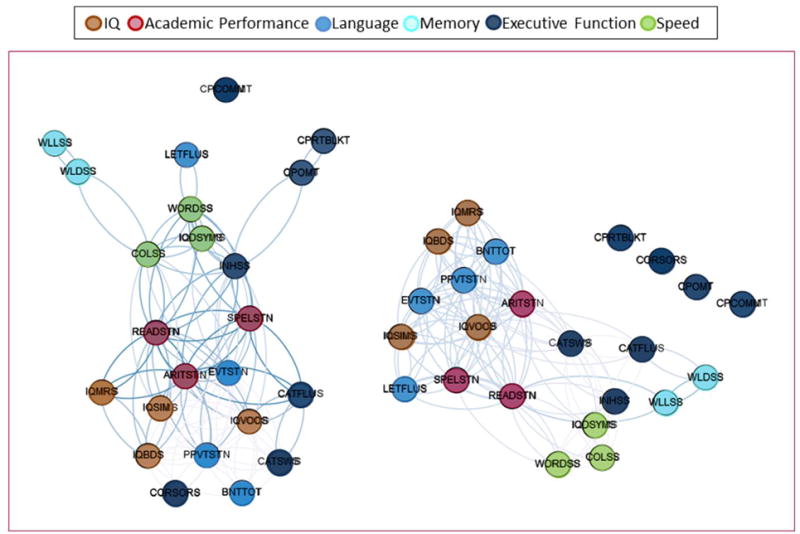
Two-dimensional graph representation illustrating the spatial relationship between cognitive tests in controls (left) and children with epilepsy (right). The spatial distribution of nodes was calculated using the force-atlas graph algorithm, where nodes that demonstrated stronger connections are located closer in space, whilst nodes with fewer connections tend to drift away. Nodes with a similar color belong to the same domain. Reproduced with permission.

In the above analysis [11] the age of participants ranged from 8 to 18 years; however it is possible that these cognitive interrelationships might be affected by the chronological age and developmental stage of the participants at the time of assessment. Given that different chronological ages and stages are accompanied by varying cognitive sophistication, and that cognitive organization could be influenced by it, it would be reasonable to expect age-related differences in cognitive network topology. Therefore, we expanded the work of Kellermann et al [11] using our control participants and dividing the group at its median age (11.8 years) in order to examine cognitive networks at a younger (below median age) and older (above median age) age of development. Furthermore, we investigated cognitive networks at two time points — two years apart — in order to examine prospective changes in the development of cognitive networks over time as a function of initial age. Complete details of the methodology can be found in the supplemental file 1.

To investigate network integration and segregation in these healthy children, calculations of the harmonic mean and transitivity, respectively, were undertaken. Statistical testing was performed using Student’s t-test and correcting for multiple comparison using Bonferroni correction. From baseline to follow-up, the younger healthy participants demonstrated increases in H_m being significant at each density level (Figure 3A). Thus, a less efficient global network configuration with increased connection path length appeared over the 2 years. In contrast, the older healthy participants showed a significant reduction in H_m from baseline to follow-up at each density level (Figures 3B), which denoted that path length shortened over time with a more efficient network structure. Thus, a more integrated and efficient cognitive network developed over 2 years in the older but not younger healthy children.

Figure 3. Harmonic mean at baseline and follow-up evaluations.

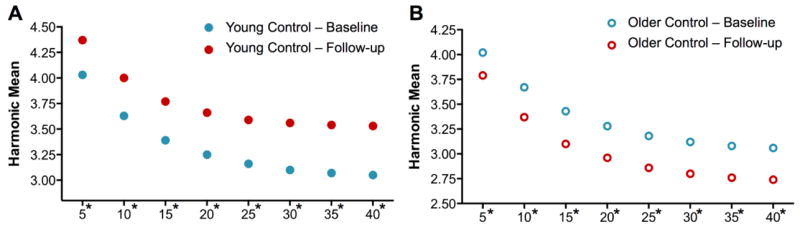
Harmonic mean for (A) young and (B) older healthy participants at baseline (blue) and follow-up (red).

*Significant difference between time points (corrected for multiple comparisons).

In terms of transitivity, the younger healthy participants demonstrated a reduction from baseline to 2-year follow-up that was significant at each density level (Figure 4A), while the older participants had higher clustering values at follow-up that were significant over the density range below 20% (Figure 4B).

Figure 4. Transitivity at baseline and follow-up evaluations.

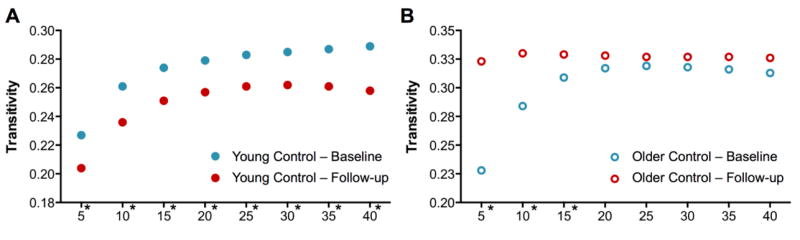
Transitivity in (A) younger, and (C) older healthy participants at baseline (blue) and follow-up (red).

*Significant difference between time points (corrected for multiple comparisons).

The community structure of both young and older healthy participants at each time point was calculated (Figure 5) in order to qualitatively visualize developmental group differences. Differences could be easily discerned between groups whereby the older healthy participants seemed to present the most efficient developmental change, which could be appreciated in the modular arrangement of nodes. However, cognitive networks of younger healthy participants did not seem as organized as might be anticipated. The modularity index reflects such qualitative results in which older controls presented a significant increase while younger controls presented similar values of modularity index at each time point (figure 1S in the supplementary file 2).

Figure 5. Community structure at baseline and follow-up evaluations.

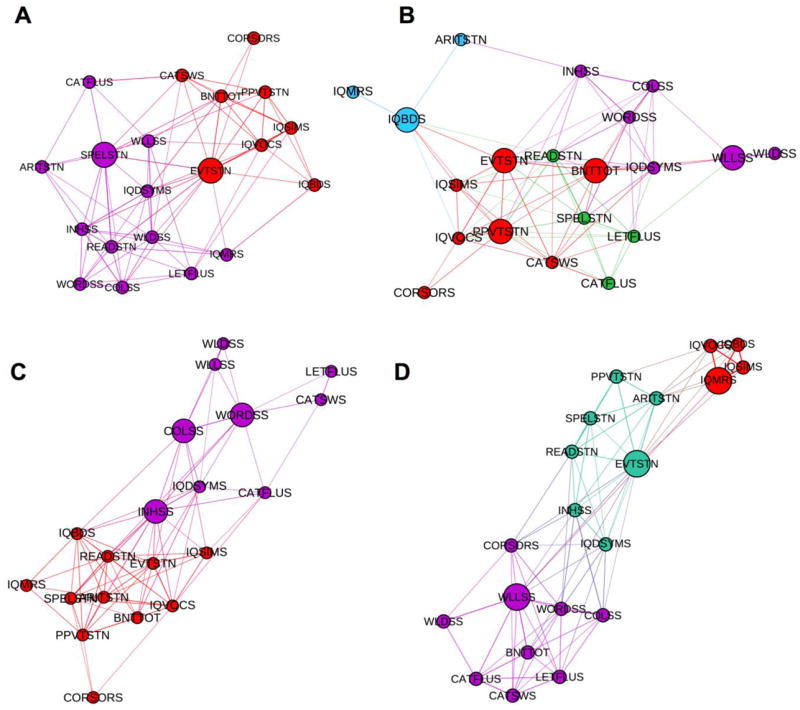
Community structure for young and older participants at baseline (A, and C, respectively) and at follow-up (B, and D, respectively). Again, the spatial distribution of nodes was calculated using the force-atlas graph algorithm, where nodes that demonstrated stronger connections are located closer in space, whilst nodes with fewer connections tend to drift away. Nodes with a similar color belong to the same module, whereas each modules is composed of nodes with the highest connectivity strength between in-module nodes, and the lowest association with the nodes outside a module. Bigger circles represent the hubs of the network.

In Figure 5, the bigger spheres represent the hubs of the network based on BC, which are those tests that facilitate the interactions between other nodes. The change in the number of hubs between baseline and follow-up in the group of young healthy participants was more dynamic than in the group of older healthy participants, again as might be expected. The younger group started with two hubs in language based abilities (spelling and naming) (SPELSTN and EVTSTN) at baseline and increased to five at follow-up, consisting of expressive and receptive language (BNTTOT, EVTSTN, PPVTSTN), memory (WLLSS), and nonverbal intelligence (IQBDS) (Figure 5A-B). The older group of healthy participants had three hubs at each time point but the membership of the hubs changed over time with baseline hubs consisting of executive function and speed (INHSS, COLSS, WORDSS) and follow-up hubs comprised of language, nonverbal intelligence, and memory (EVTSTN, IQMRS, WLLSS) (Figure 5C-D).

In summary, younger healthy participants presented a different number of hubs accompanied by a change in their number at the different evaluations, while older participants presented the same number of hubs at both time-points although the membership of hubs differed to some degree across evaluations as well. The combination of no change in the number of hubs with a change in their membership observed in older participants represents a less dynamic development in the local aspects of cognitive topology compared to younger participants, as expected.

4.0 Limitations and Future Directions

While the application of graph theory to neuropsychological data in epilepsy is novel and potentially informative, several conceptual and practical issues should be kept in mind. Comparing the work of Kellerman et al [11] with this analysis it is evident that investigation of cognition at different developmental stages might render a different/clearer depiction of cognitive development. For example, younger control participants present less defined modular structure at baseline than older controls, therefore our previous analysis [11] on controls may be driven by the older subjects. As is most often the case, here we are presenting and discussing group profiles, within which there is much individual variability. Further examination of this individual variability, as well as determining whether there are groups of individuals (or phenotypes) with similar cognitive networks would be both theoretically interesting and clinically interesting and meaningful.

In addition, an important conceptual point is that, unlike most uses of graph theory, the nodes in this case are scores on cognitive tests, which themselves are comprised of perceptual, cognitive, and output (speech, motor) components associated with complex brain implementation. Traditionally, most graph theory applications start with measures that have, to varying degrees of granularity, temporal and spatial grounding in the brain (e.g., EEG electrodes, clusters of BOLD activity, gray matter volume, white matter tracts). These nodes are generally not considered to be further composed of spatially distributed brain networks (although one could argue that they could be). In these methods there is an implicit assumption of parallelism. That is, the spatial representation and connections depicted by the graph theory measures have parallel representations in the brain at either a structural or functional level. A reverse inference process is then undertaken to define the cognitive activity involved. In the case of neuropsychological test performance as nodes, the nodes themselves are implemented by spatially distributed networks in the brain. Accordingly, the normal assumption of parallelism between graph theory measures and brain network organization appears to be lost. In the case of neuropsychological test scores, where a node has a known cognitive purpose/function, graph theory provides a forward inference process to define what must solely be considered the network organization properties of test measurements.

Another consideration is that neuropsychological data are unlike other outcome measures, such as structural imaging processed through a standard package (e.g., FreeSurfer) where a fixed set of output measures is available internationally for analysis — a common language so to speak. Neuropsychological assessment is quite different from that state of affairs. While there is general appreciation of the important common domains of cognition (e.g., intelligence, language, perception, memory, executive function, sensorimotor abilities), within those domains there is a wide range of available measures with no “gold standard”, further confounded by language and cultural differences internationally. This lack of a common core set of “output measures” for cognition will likely serve to limit progress and contribute to heterogeneity in findings until a common set of measures are widely used (e.g., NIH Toolbox).

The results presented here provide the broadest overview of cognitive networks and their changes overtime in children with epilepsy compared to controls. The neuropsychology of epilepsy literature traditionally has been extremely interested in how variations in the disorder (e.g., seizure frequency and severity; age of onset and duration; medication type, number and dose) affect mentation generally or specific cognitive domains in particular (e.g., memory). These factors were not examined here and represent opportunities for further research going forward as is the opportunity to examine how controlling for overall intelligence may impact the networks represented.

4. Conclusions

Traditional analyses of neuropsychological data when comparing groups of interest (e.g., healthy control versus neurological disorder group) consist of direct comparisons of each metric between groups in a pairwise corrected fashion, comparison of impairment indices (number or percent of impaired scores in an administered test battery), reduction of test batteries to factor scores and group comparison of those metrics, and other approaches. It has been known for decades that there is a “positive manifold” across these measures (positive correlations), but there has been little examination, especially within epilepsy research, of the presence and nature of the interrelationships between these test measures and how such interrelationships differ between groups, both cross-sectionally and longitudinally.

This application of graph theory techniques to cross-sectional neuropsychological data in children with epilepsy and prospective analysis of neuropsychological data in healthy participants provide a new avenue to characterize and understand the impact of epilepsy and its treatment on cognitive networks and “circuitry development”, something heretofore not undertaken given the inherent limitations associated with traditional psychometric analyses of human cognitive data. Thus, it is fair to suggest that presentation and comparison of standard test metrics does not convey the dynamic and changing complexity in the interrelationships among discrete cognitive skills, the maturation of the cognitive network over time, and the differences between groups in these metrics. From a neuropsychological perspective, the children with epilepsy are “maintaining” their overall cognitive skills but in a very different fashion compared to controls. These changing dynamics in cognitive networks over time surely has a neurobiological contribution and a future challenge is to relate developments in the cognitive network to alterations in brain networks and lack thereof. And most pertinent to the topic of this special issue, how will these conceptualizations of cognition and cognitive change “map” onto the classification systems of epilepsy.

Highlights.

• Human cognition is composed of several interdependent cognitive domains.

• Associations of underlying neuropsychological abilities can be considered a cognitive network.

• Cognitive status based on domain interactions can be assessed using graph theory.

• Controls demonstrate higher cognitive modularity than children with epilepsy.

• Orderly age-dependent development of cognitive networks in controls can be shown.