Pulsed and oscillating gradient MRI for assessment of cell size and Extracellular space (POMACE) in mouse gliomas

Abstract

Solid tumor microstructure is related to aggressiveness of tumor, interstitial pressure and drug delivery pathways that are closely associated with treatment response, metastatic spread and prognosis. In this study, we introduce a novel diffusion MRI data analysis framework, Pulsed and Oscillating gradient MRI for Assessment of Cell size and Extracellular space (POMACE), and demonstrate its feasibility in a mouse tumor model.

In vivo and ex vivo POMACE experiments were performed on mice bearing the GL261 murine glioma model (n=8). Since the complete diffusion time-dependence is in general non-analytical, the tumor microstructure was modeled in an appropriate time/frequency regime by impermeable spheres (radius R_cell, intracellular diffusivity D_ics) surrounded by extracellular space (approximated by constant apparent diffusivity D_ecs in volume fraction ECS). POMACE parametric maps (ECS, R_cell, D_ics, D_ecs) were compared with conventional diffusion weighted imaging metrics, electron microscopy (EM), alternative ECS determination based on effective medium theory (EMT), and optical microscopy performed on the same samples.

It was shown that D_ecs can be approximated by its long-time tortuosity limit in the range [1/(88 Hz) - 31 ms]. ECS estimations (44±7% in vivo and 54±11% ex vivo) were in agreement with EMT-based ECS and literature on brain gliomas. Ex vivo, ECS maps correlated well with optical microscopy. Cell sizes (R_cell=4.8±1.3 in vivo and 4.3±1.4 μm ex vivo) were consistent with EM measurements (4.7±1.8 μm).

In conclusion, R_cell and ECS can be quantified and mapped in vivo and ex vivo in brain tumors using the proposed POMACE method. Our experimental results support that POMACE provides a way to interpret the frequency- or time-dependence of the diffusion coefficient in tumors in terms of objective biophysical parameters of neuronal tissue, which can be used for non-invasive monitoring of preclinical cancer studies and treatment efficacy.

INTRODUCTION

Solid tumor microstructure is related to aggressiveness of tumor, interstitial pressure and drug delivery pathways that are closely associated with treatment response, metastatic spread and prognosis (1–4). In particular, the extracellular space volume fraction (ECS) has been recognized as a strong biomarker for tumor response and treatment efficacy (1). Similarly, differences in cell size can reflect various cancer types (5) or apoptosis following treatment (6). However, very few methods provide an accurate estimation of the ECS (7) or dimensions of the relevant cellular structures at the microscopic scale. In addition, many of these approaches involve radioactive extracellular tracers, optical imaging or iontophoresis (7–9), which are invasive and cannot be translated to clinical cases.

Diffusion MRI has been recognized as a potentially powerful non-invasive tool to probe tumor microenvironment (10–12), but the apparent diffusion coefficient (ADC) remains only a qualitative marker for cellularity (11,13). Since a diffusion measurement at a fixed diffusion time is affected by multiple factors, such as cell size, cell density, composition of the extracellular matrix, and compartmental diffusivities, recent work have focused on temporal diffusion spectroscopy (i.e. time-dependent diffusion) combined with tissue modeling (14,15) to gain insight on the ECS and cell size. This approach was successful in identifying cortical areas of various cellularity ex vivo (16), and recognizing apoptotic from healthy cells in vitro (17). However, to date, there has not been any report on characterizing the tumor cell size and ECS volume fraction in vivo and ex vivo using temporal diffusion spectroscopy.

The time-dependence of the diffusion coefficient indicates the presence of barriers that restrict the otherwise free diffusion. The relationship between diffusion time dependence and the size of the restricting compartment has been studied for the brain (14,18–20) and muscle tissues (21–24). The characteristic time for restrictive effects is τ_R ~ L²/D, where L is a typical distance water molecules travel to encounter the barriers and D is the diffusivity of the bulk fluid. For cancer cells, with radius ~ 4 μm and D ~ 1.5 μm²/ms, the effects of restriction is expected to be observed when diffusion time is about τ_R ~ 10 ms. This means that diffusion times ranging from a substantially shorter than 10 ms to a substantially longer than 10 ms are required to study restricted diffusion in cancer cells. It is not trivial to achieve this particular range of diffusion times using either pulsed gradient spin echo (PGSE) or oscillating gradient spin echo (OGSE) diffusion experiment alone on conventional preclinical hardware. Hence, we consider a combination of both sequences in this study.

PGSE and OGSE-based diffusion inside simple structures, such as impermeable cylinders and spheres, have been investigated earlier (14,25). Recent studies have used these geometrical models to assess the degree of vasculature of various tumors (26), or identify cancer cells of different sizes in vitro (27) or in vivo following chemotherapeutic treatment (25). However, the functional dependence of the extracellular diffusivity at low frequency is non-analytic due to the disordered arrangement of restrictions, and is thereby fundamentally distinct from that in regular geometries (24). Simple Gaussian diffusion models are in general inadequate for quantifying tissue properties whenever the measurements are mostly sensitive to low frequencies or long times (19,20). In addition, even in the simplest models, the large number of parameters required to model the tumor microenvironment affects the fits robustness, making these studies very sensitive to a priori assumptions or knowledge on the underlying microstructure, which can be very disordered and/or spatially heterogeneous in the case of aggressive tumors (28–30).

In this study, we introduced a novel data acquisition and analysis framework referred to as Pulsed and Oscillating gradient MRI for Assessment of Cell size and Extracellular space (POMACE) and investigated the feasibility of using POMACE to estimate the extracellular space volume fraction and cell size of brain tumors in vivo and ex vivo. ECS measurements from in vivo and ex vivo POMACE experiments were compared with an alternate ECS estimation method based on effective medium theory (EMT). In addition, optical microscopy was performed on the same samples, and Electron Microscopy (EM) was performed for the assessment of cell radius on the same cell line. The scope of our study was limited to solid tumor tissue and it did not include normal brain tissue that requires different geometrical considerations and experimental conditions.

THEORY - POMACE

1. Diffusion model of tumor microstructure

In the POMACE framework, we assume the simplest case of a tumor microstructural model in which the diffusion MR signal S can be expressed, in absence of exchange, as the sum of signals from intra- and extra-cellular spaces, S_ics and S_ecs, respectively;

$$S=(1-\mathit{ECS})\ast S_{\mathit{ics}}+\mathit{ECS}\ast S_{\mathit{ecs}}$$ [1]

In general, tissue complexity manifests itself in the non-Gaussian diffusion (31,32), characterized by the presence of the higher-order terms in the cumulant expansion of MR signal S (33),

$$ln(S)=-bD+(K/6)·{(bD)}^2+\cdots$$ [2]

where D and K represent the diffusion and kurtosis coefficients (34), and by the time-dependence of all the cumulants: D(τ), K(τ), … (35). The requirement to use short diffusion times in this study limits the range of practically achievable b-values to under 1 ms/μm², even with OGSE sequences and on preclinical scanners with strong gradient inserts compared to clinical scanners. For such low b-values, second and higher order terms of the cumulant expansion are negligible (33). As a result, for each diffusion time τ (or equivalently, oscillation frequency ω ~ 1/τ), the total diffusion MR signal can be adequately described by a single diffusion coefficient equal to the weighted average of both diffusion coefficients:

$$D(\tau )=-\underset{b\to 0}{lim}\frac{\partial }{\partial b}lnS(\tau )=(1-\mathit{ECS})·D_{\mathit{ics}}(\tau )+\mathit{ECS}·D_{\mathit{ecs}}(\tau ).$$ [3]

The lowest order approximation of this cumulant expansion (also known as DTI regime) (14,25,36) was previously shown valid in this range of b-values and for this tumor model (37).

Furthermore, the cell membrane is considered impermeable in the range of diffusion times used in this study (τ <31 ms). It allows one to assume no exchange of the water molecules between the intracellular and extracellular spaces, cf. Eq. [1]. This hypothesis is supported by previous studies of intracellular water residence time that reported 400 ms for human breast tumors (38), 317±17 ms for fixed human myelogenous leukemia K562 cells (39), 344±1.3 ms in viable human brain tumor (40) and 146–714 ms for tumor cells undergoing apoptosis (41). The range of relatively short diffusion times probed in this experiment is selected intentionally in order to neglect the influence of membrane permeability on time-dependent diffusion.

2. Intracellular compartment

Here we represent cancer cells by identical spheres of radius R_cell, and free intracellular diffusivity D_ics. In the DTI regime, the signal attenuation inside impermeable spheres due to diffusion-encoding gradients S_ics = exp(−b · D_app(R_cell, D_ics)) was derived for cosinusoidal OGSE (14) and PGSE (25), and successfully applied to cellular and nuclear (42) as well as axonal size estimation (43). For an integer number of oscillations:

$$D_{\mathit{OGSE}}(\omega )=2D_{\mathit{ics}}{(\omega {\tau }_R)}^2\sum _n\frac{1}{({\mathrm{\mu }}_n^2-2)}\left\{\frac{1}{{\mathrm{\mu }}_n^4+{(\omega {\tau }_R)}^2}+\frac{2{\mathrm{\mu }}_n^2\frac{{\tau }_R}{\delta }}{{({\mathrm{\mu }}_n^4+{(\omega {\tau }_R)}^2)}^2}\left[exp\left(-{\mathrm{\mu }}_n^2\frac{\delta }{{\tau }_R}\right)-1+exp\left(-{\mathrm{\mu }}_n^2\frac{\mathrm{\Delta }}{{\tau }_R}\right)\left[1-cosh\left({\mathrm{\mu }}_n^2\frac{\delta }{{\tau }_R}\right)\right]\right]\right\}$$ [4]

where δ is the gradient duration, Δ the inter-gradient duration and ${\tau }_R=R_{\mathit{cell}}^2/D_{\mathit{ics}}$ represents the characteristic diffusion time for a cell. For a spherical geometry, μ_n is the nth root of the function ∂j₁(μ)/∂μ, where j₁(μ) = (sin(μ) − μ · cos(μ))/μ² is the spherical Bessel function of the first kind, which is equivalent to the formulation in (14). For OGSE, the diffusion time can be approximated by π/2ω.

Using the same formalism, the formula for spherical attenuation with PGSE is given by:

$$D_{\mathit{PGSE}}(\tau =\mathrm{\Delta })=4\frac{R^2}{(\mathrm{\Delta }-\delta /3)}{\left(\frac{{\tau }_R}{\delta }\right)}^2\sum _n\frac{1}{{\mathrm{\mu }}_n^6({\mathrm{\mu }}_n^2-2)}\left\{{\mathrm{\mu }}_n^2\frac{\delta }{{\tau }_R}-1+exp\left(-{\mathrm{\mu }}_n^2\frac{\delta }{{\tau }_R}\right)+exp\left(-{\mathrm{\mu }}_n^2\frac{\mathrm{\Delta }}{{\tau }_R}\right)\left[1-cosh\left({\mathrm{\mu }}_n^2\frac{\delta }{{\tau }_R}\right)\right]\right\}$$ [5]

originally derived by Murday and Cotts (25). For PGSE, the inter-gradient duration Δ is identified as the diffusion time τ.

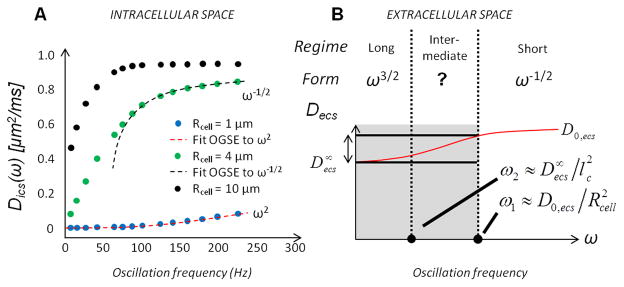
Eq. [4] scales as D_OGSE(ω) ~ ω² in the very long time limit (ω → 0). In the short time limit (ω → ∞), it behaves as ω⁻¹/² in agreement with (44,45). Such trend of time-dependent intracellular diffusivity is illustrated in Fig. 1A. It can be noted that the frequency range of the long and short time regimes depends on the particular cell size and intracellular diffusivity. For instance, Fig. 1A demonstrates that OGSE diffusion data with R_cell = 1 μm are in the long time regime for f_OGSE = [100–200] Hz, whereas those with R_cell = 4 μm and beyond are in the short time regime.

Figure 1.

Frequency-dependent diffusion inside (A) the intracellular space for various cell radii (numerical calcul, R_cell = 1/4/10 μm, blue/green/black circles) and (B) extracellular space in the long / intermediate / short time regime. A. Oscillation frequencies f_OGSE in the range [0–225] Hz are best suited to detect time-dependent changes from the intracellular compartment in cancer cells (R_cell = 4 μm). B. The analytical expression for diffusion in the ECS in the intermediate time domain is in general unknown (second column). Outside the short-time regime (i.e. within the grey area), small time-dependent variations are expected from the extracellular compartment (double arrow), compared to intracellular diffusivity changes inside cancer cells (Fig. 1A, green).

3. Extracellular compartment (general case)

The time-dependence of diffusion in the ECS depends on the multiple pathways available to water molecules, which in turn depends on the specific geometrical arrangement and packing disorder of cells (24). How each of these parameters impact the ECS diffusion is unknown. Depending on the range of diffusion times/frequencies probed in the study, different assumptions can be made to properly model the tumor microenvironment. In addition, ECS short/intermediate/long time regimes do not necessarily match those defined for the intracellular compartment.

3.1. Short time regime (τ ~ ω⁻¹ ≪ τ_R)

The Mitra (or short time) limit (44,46) characterizes the time/frequency regime where the mean displacement of water molecules labeled using magnetic field gradients is negligible compared to the distance between restrictions imposed by the micro-environment (i.e. cell membranes). The universal form of the OGSE diffusion coefficient in this regime, valid for both intra- and extracellular spaces, is characterized by a linear relationship with ω^−1/2 (45). For a cosinusoidal waveform, the analytical expression of the OGSE-measured diffusion coefficient D(ω) is fully described by the medium free diffusivity D₀ and the surface-to-volume ratio of the restrictions S/V (44,45), such that:

$$D(\omega )=D_0(1-c(N)·c_d·S/V·\sqrt{D_0/\omega }),c_d=1/3\sqrt{2}$$ [6]

for isotropic diffusion in d=3 dimensions relevant for glioma in the gray matter. Here ω is the oscillation frequency (ω = 2πf_OGSE), and c(N) is a correction factor monotonically decreasing with the number of oscillations N (47), $c(N)=\{4\pi N\ast C(2\sqrt{N})+3\ast S(2\sqrt{N})\}/(2\pi N)$ (where C(x) and S(x) are the Fresnel functions) such that c(∞) = 1.

3.2. Long time regime (τ ~ ω⁻¹ ≫ τ_R)

Based on the micro-structural organization, it is possible to grasp a functional form of the ECS diffusion in the very long time limit (Fig. 1B, left column). For OGSE, since short-range disorder is more likely to characterize relatively dilute structures such as cancer cells lacking any particular long-range order, the diffusion coefficient can be expressed as $D_{\mathit{ecs}}(\omega )=D_{\mathit{ecs}}^{\infty }+\text{const}·{\omega }^{d/2}$ in d dimensions (see Fig. 2A in (24)). For PGSE, it was previously shown (24,48) that, in 3 dimensions, the extracellular D(τ) increases in the long time limit (τ → ∞) with the inverse of time, as in:

$$D(\tau )=D^{\infty }+A/\tau +O({\tau }^{-3/2}),$$ [7]

where A is a structure-dependent positive parameter independent of diffusion time τ. Based on Eq. [5], the functional form of Eq. [7] is also valid at long times for the intracellular compartment, with D^∞ = 0.

3.3. Intermediate time regime

While the molecular restrictions inside impermeable spherical boundaries can be quantified for any oscillation frequency (14), there is to date no analytical solution for the diffusion in the ECS at intermediate times/frequencies (Fig. 1B, second column). As a result, modeling the diffusion coefficient outside the very short/long time regime is not trivial. Depending on the oscillation frequency range and cellular size, the time-dependence of the overall diffusion coefficient can be dominated by each of the two compartments (intra- or extracellular). Boundaries between short and intermediate (ω₁), and between intermediate and long time regimes (ω₂₎ are related to the free/restricted diffusivities $D_{\mathit{0},\mathit{ecs}}/D_{\mathit{ecs}}^{\infty }$ and characteristic packing correlation length l_c and cell size R_cell (l_c ≳ R_cell), as in ω₁ = D_0,ecs/R_cell and ${\omega }_2=D_{\mathit{ecs}}^{\infty }/l_c$, such that ω₁ ≳ ω₂, Fig. 1B. The extent of this regime depends therefore on the particular packing arrangement of the medium (l_c vs. R_cell).

4. Extracellular compartment (approximation)

The PGSE/OGSE time/frequency range sensitizes MR acquisitions to specific diffusion lengths (i.e. cellular sizes). While diffusion in small structures is highly restricted (Fig. 1A, R_cell≥1 μm) in the range [50–225] Hz accessible with our scanner, this domain is well adapted to capture major time-dependent changes inside larger cancer cells (Fig. 1A, R_cell = 4 μm). Outside the ECS short time regime (i.e., f_OGSE < 88 Hz (37)), D_ecs cannot be described analytically. However, relatively small change in D_ecs, compared to that in D_ics, is expected for diffusion times longer than the characteristic time scale τ_R, as depicted by the double arrow in Fig. 1B. A similar situation was highlighted by a recent simulation study in one dimension (Fig. 1C in (24)). In 3 dimensions, due to the many pathways accessible to water molecules around “compact” restrictions such as spherical cells, and due to relatively low cellular packing in brain gliomas (ECS ~ 40–50 %, see (1)), we expect an overall small difference between $D_{\mathit{ecs}}^{\infty }$ and its free value D_0,ecs. (The EMT estimate, discussed around Eq [9] below, yields $D_{\mathit{ecs}}^{\infty }\approx \sqrt{0.5}{D}_{0,\mathit{ecs}}$ for ECS occupying 50% of the volume, suggesting the overall drop from D_0,ecs to $D_{\mathit{ecs}}^{\infty }$ of about 30%.) These observations suggest that the overall diffusion coefficient time-dependence, in the range [1/(88 Hz) - 31 ms], mainly originates from the intracellular compartment. Hence, we hypothesized that the diffusion in the ECS, D_ecs, can be practically viewed as time-/frequency-independent outside the short time regime (i.e., f_OGSE < 88 Hz) and thereby can be approximated by its tortuosity limit $D_{\mathit{ecs}}\cong D_{\mathit{ecs}}^{\infty }$. The diffusion-weighted extracellular MR signal is then given by S_ecs = exp(−bD_ecs). As explained earlier, this assumption is not trivial and its validity will be investigated further with our experimental data in this study. While $D_{\mathit{ecs}}^{\infty }$ provides an inferior bound for D_ecs, a superior bound can be derived from the Mitra regime, as Eq. [6] still holds for f_OGSE = 88 Hz (26).

5. POMACE parameter estimation

The proposed POMACE model has four parameters (ECS, R_cell, D_ics, and D_ecs) to characterize tumor microstructure. Note that this model is based on the geometrical considerations relevant to tumor cells, not normal brain tissue, as described above. Among the four parameters, we can utilize an additional relationship between ECS and D_ics in the short time regime. For OGSE, it was previously shown that the Mitra regime is reached in the GL261 mouse glioma model for oscillation frequencies f_OGSE above 88 Hz, as illustrated in supplementary Figure S1: above that threshold, the S/V estimation based on Eq. [6] is independent of temperature as it reflects purely geometric restrictions (37). Since D(ω) varies linearly with ω^−1/2 in each compartment (intra-/extracellular) in this short time regime, the functional form given by Eq. [6] remains valid for the weighted average D defined in Eq. [3] and, in particular, for its asymptotic limit D₀ at infinite frequencies. Then, our system of equations simplifies to:

$$D_0=(1-\mathit{ECS})·D_{\mathit{ics}}+\mathit{ECS}·D_{0,\mathit{ecs}},$$ [8a]

$$D(\tau )=(1-\mathit{ECS})·D_{\mathit{PGSE}}(\tau ,R_{\mathit{cell}},D_{\mathit{ics}})+\mathit{ECS}·D_{\mathit{ecs}},\text{and}$$ [8b]

$$D(\omega )=(1-\mathit{ECS})·D_{\mathit{OGSE}}(\omega ,R_{\mathit{cell}},D_{\mathit{ics}})+\mathit{ECS}·D_{\mathit{ecs}}.$$ [8c]

The estimation of the POMACE model parameters is performed in two steps: (1) estimate D₀ and S/V from the OGSE data in the short diffusion time via Eq. [6]; (2) estimate the four model parameters (ECS, R_cell, D_ics, and D_ecs) by fitting Eq. [8b/c] to the PGSE and low-frequency OGSE data with Eq. [8a] as a constraint for ECS and D_ics, using a fixed D_0,ecs (as described in Methods section).

6. Alternative ECS estimation via the Effective Medium Theory

Using the Effective Medium Theory (EMT), the long time limit of the diffusion coefficient D^∞ was derived for packed erythrocytes surrounded by extracellular space (49). In the approximation of impermeable membranes, the link between D^∞ and ECS (equation [2] from ref. (49)) becomes independent of the sphere radius R_cell and simplifies to:

$$D^{\infty }=\mathit{ECS}·D_{\mathit{ecs}}^{\infty }=\mathit{ECS}·(EC{S}^{1/2}·D_{0,\mathit{ecs}})=EC{S}^{3/2}·D_{0,\mathit{ecs}},$$ [9]

where D_0,ecs is the free diffusivity in the ECS in the absence of restrictions. The EMT value $D_{\mathit{ecs}}^{\infty }$ and the EMT-based ECS estimates (via Eqs. [7] and [9]) will be compared to the D_ecs and ECS fit estimates based on the system of equations [8], under the same hypotheses of impermeable membranes and free extracellular diffusivity values (2.7/1.94 μm²/ms in vivo/ex vivo). Compared to POMACE, the EMT framework is expected to provide a more robust ECS estimation, due to the small number of parameters to fit, at the expense of cell size information.

METHODS

Noise propagation study

A noise propagation study was performed to assess the uncertainty in POMACE model parameter estimation. DWI data were generated based on Eqs. [3–6], and Gaussian noise was added to the diffusion coefficient estimation (SNR=25/50/100, two data-points per time/frequency, n=600). The influence of initial guess was minimized by starting from the true parameter set used to generate the data. Estimation of the model parameters from the low frequency OGSE and PGSE noisy data was performed with and without the additional constraint in Eq. [8a].

Animal model

Female C57BL/6 mice (n=8, 6–8 weeks) were used to generate murine orthotopic glioma models. GL261 cells (n=10⁶), suspended in 5 μL phosphate buffered saline (PBS), were injected into the subcortex (2.5 mm depth) using a Hamilton syringe (1 μL/min) (36). All mice were treated in strict accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals, and the experimental procedures were performed in accordance with the Institutional Animal Care and Use Committee at the New York University School of Medicine.

In vivo imaging protocol

MRI experiments were conducted using a 7T Biospec micro-MRI system (Bruker Biospin MRI, Ettlingen, Germany) equipped with a Bruker BGA-9S gradient coil (750 mT/m gradient strength). All mice were scanned once between 2 and 4 weeks after tumor implantation. Animals were imaged using an in-house built quadrature Litz coil. Mice were anesthetized and positioned inside a custom-built mouse mold (50). A bite bar and head strap were used to ensure minimal motion during the scan. Respiration and temperature were closely monitored and kept stable (60±10 bpm and T=35±1°C) throughout the entire MR session. General anesthesia was maintained using 1.5% isoflurane in air. In vivo DWI consisted of OGSE and PGSE measurements, probing four diffusion times Δ = 6/9/16/31 ms for PGSE (δ=2/3 ms), and ten oscillation frequencies in the range [65–225] Hz for the fast-ramp cosinusoidal OGSE (51) (total number of oscillations 2≤N≤10). Previous studies (37) revealed mono-exponential signal behavior, i.e., negligible Intra-Voxel Incoherent Motion effect, and isotropic diffusion in the tumor for b<0.4 ms/μm² (=400 s/mm²). Hence, diffusion-weighting gradients were applied in only one direction (1, 1, 1), using b=[0, 0.2, 0.4] ms/μm². Scans were performed with a single slice positioned at the tumor center. The Spin-Echo EPI scan parameters were: TR/TE = 3000/70 ms, Bandwidth 300 kHz, 1 readout segment, number of averages NA=20, number of repetitions NR=2, pixel resolution 0.25x0.25x1.5 mm, matrix 80x80, acquisition time 6 min per frequency/diffusion time, and total scan time 84 min. Diffusion times and oscillation frequencies were randomly sampled during the session. The whole series was repeated twice to monitor any changes due to temperature/motion. Representative images for OGSE EPI and corresponding diffusion coefficient maps (in vivo and ex vivo) can be found online (supplementary materials Fig. S2).

Ex vivo sample preparation

Mice were sacrificed following the in vivo imaging. Following transcardiac perfusion (PBS + 4% PFA), the brains were extracted, preserved in multiple sucrose solutions and kept in optimal-compound temperature media using the protocol described in (36). After embedding, 5 μm and 100 μm thickness sections were cut for immunohistochemical (IHC) staining of GLUT1/hematoxylin and ex vivo MR imaging, respectively.

Prior to ex vivo imaging, brain sections were rehydrated in PBS for two hours and sealed between two coverslips (48). Provided proper sealing, previous ex vivo experiments using this particular setup and diffusion imaging protocol showed minimal tissue dehydration and MR distortion, very good stability of the samples during overnight scans and a good image reproducibility, both at room temperature and at 37°C (37).

Ex vivo MR coil and DWI protocol

A dual-coverslip histology coil was used for ex vivo scans (52). Each sample placed in the histology coil (n=8) was carefully positioned in the horizontal plane and kept at room temperature. The diffusion-weighting direction was set in the horizontal plane to minimize any coverslip-induced restriction effect. The ex vivo MR protocol was adjusted as follows: NA=40, NR=6, and total acquisition time 11 hours. Other than that, the scan protocol for ex vivo DWI scan was same as the in vivo scan as our pilot study found that the diffusivity changes between in vivo and ex vivo scans were well within the expected 30% change due to temperature decreased from 37 °C to 20 °C.

Local temperature was monitored using (i) a thermocouple placed next to the histocoil and (ii) repetitions of the diffusion protocol through the entire session, such that any drift in temperature would be detected via temporal changes of the measured diffusion coefficient. No drift was observed during ex vivo imaging, neither at scan nor session level. The imaging slice thickness (1.5 mm) was chosen larger than the sample thickness (0.1 mm) so that small drifts perpendicular to the imaging plane would not impact MR measurements through the imaging session. In addition, EPI trajectories were re-acquired for each scan and the water frequency adjusted every hour to compensate for potential slow drifts of the water frequency. No tissue deformation was detected during the imaging session. B-values could not be adjusted (i.e. increased) for the decreased diffusivities expected during ex vivo scans at room temperature due to hardware limitations, resulting in a two-fold SNR decrease compared to in vivo scans.

Optical Microscopy

The same ex vivo samples used for MRI were immersed in PBS, mounted between two coverslips (n=8) and imaged with optical microscopy (Zeiss LSM510 confocal microscope), at x10 magnification, without staining. Depending on sample size, 18 to 90 images were acquired sequentially within a rectangular grid. High resolution images were stitched together using the “Stitching” Fiji plugin for ImageJ (53).

Electron Microscopy

One additional animal was sacrificed at Day 14 after tumor implantation. Its brain was perfused with PBS (30s) followed by a fixative solution (2% PFA, 2.5% Glutaraldehyde, 0.1M sucrose) (one hour). After dissection of the brain, the tumor was extracted for further fixation (two hours, same fixative) and kept at 4 °C overnight. The sample was then rinsed in a series of PB (Na2HPO4+NaH2PO4) solutions (0.1 then 0.2M), fixed in osmium tetroxide, rinsed in double distilled water, dehydrated in a series of alcohol solutions (30 to 95%), and rinsed in ethanol then propylene oxide (PO). It was then left in a PO:EMbed812 solution (proportions: 1:1 for one hour followed by 1:2 overnight at 4°C). The next day, the sample was rinsed twice in a mixture of EMbed812 and anhydrides (two times two hours in fresh solution), then embedded at 65°C. After 4 days at 65°C, the sample was trimmed for EM gridding.

EM was performed on thin sections (70 nm) at x2560 magnification (0.013 μm in plane resolution). Sixty eight images were acquired within a grid covering 100x160 μm². After stitching of high resolution images (53), 300 cells were identified, and 60 were randomly chosen for cell size estimation, leading to 95% confidence interval on the average cell radius below 0.5 μm. Due to their elliptical shape, the mean radius was estimated as half of the average of their large and small sides, as measured with ImageJ.

Data Analysis

Preliminary post-processing steps included co-registration of DWI scans using an in-house routine (Matlab, the Natick) in order to compensate for potential motion of the animal/sample. Regions of Interests (ROIs) were manually drawn in all 8 mice to delineate the tumor inside the mouse brain on ADC maps derived at oscillation frequency f_OGSE = 225 Hz that provided maximal contrast between tumor and normal brain. At voxel level, in vivo and ex vivo high frequency OGSE data (f_OGSE > 88 Hz) were first spatially smoothed (3x3 square kernel) and the diffusion coefficient D(ω) fitted to Eq. [6] in order to determine the free diffusivity D₀ in the short time regime. The diffusion coefficient obtained with low-frequency OGSE (f_OGSE < 88 Hz) and PGSE (6 < τ < 31 ms) was then fitted at once to Eqs. [8b] and [8c] in order to determine the structural parameters ECS and R_cell and the apparent extracellular diffusivities D_ecs inside the tumor. The intracellular free diffusivity D_ics was fully determined by ECS, D₀ and D_0,ecs according to Eq. [8a]. The free extracellular diffusivity in the short time limit D_0,ecs was fixed at 2.7 μm²/ms (90% of water free diffusivity at 37°C). Two tailed unpaired Student’s t-tests were performed to assess the difference in the mean estimates between in vivo and ex vivo data, due to potential differences in slice location and thickness (1.5 vs 0.1 mm for in vivo and ex vivo, respectively).

Spearman correlation coefficients were calculated between ECS, R_cell, D_ics, D_ecs, and the diffusion values calculated at different diffusion times τ = Δ_PGSE = 6/9/16/31 ms and oscillation frequencies f_OGSE = 65/75/88/100/125/140/160/180/200/225 Hz. The data analysis was performed using in-house Matlab codes (Mathworks, Natick, MA).

Validation of the constant D_ecs approximation in the long time limit

Estimations inside spheres of various radii (based on Eq. [5]) suggest that the intracellular diffusion calculated for long times with PGSE ( $\tau \gg R_{\mathit{cell}}^2/D_{\mathit{ics}}$) has already reached its long-time limit. In this regime, the mean square displacement 〈 x² 〉 = 6 * D(τ) * τ is constant and the intracellular difusion can be approximated by Eq. [7] with $D_{\mathit{ics}}^{\infty }=0$ (R_cell = 4 μm, R²=0.98). Would that limit be achieved for our PGSE measurements, Eq. [3] simplifies at infinite times with $D_{\mathit{ics}}^{\infty }=0$, and $D_{\mathit{ecs}}^{\infty }$ provides a lower bound for the constant diffusivity D_ecs attributed to the ECS during the POMACE non-linear fitting to the PGSE and low-frequency OGSE data.

As both the in vivo and ex vivo PGSE data adhere very well to the 1/t asymptotic dependence, these data were fitted to Eq. [7] at tumor level (n=8). Based on high coefficients of determination R², D^∞ was extracted and converted to $D_{\mathit{ecs}}^{\infty }$ using the mean ECS estimation (based on Eq. [9]) inside the tumor.

In addition, D_ecs (f = 88 Hz) was calculated at tumor level (n=8) using Eq. [6] with D_0,ecs =2.70 / 1.94 μm²/ms (in vivo / ex vivo) and S/V estimates in the short-time regime to provide a superior bound for D_ecs in the range f_OGSE < 88 Hz. The independently obtained D_ecs (f = 88 Hz) and $D_{\mathit{ecs}}^{\infty }$ distributions were compared using non parametric tests (Mann-Whitney U test, n=8) in order to justify the use of a constant diffusion in the ECS in the range f_OGSE < 88 Hz.

ECS estimation via the Effective Medium Theory

Monte Carlo simulations performed for various geometrical shapes in two dimensions (54) have shown that the two-dimensional analog of Eq. [9] holds well for low cell packing (ECS > 40 %); furthermore, the mean-field theory approach used to deriving this result is generally expected to hold better for higher spatial dimensions. Therefore, we believe its application to tumors prone to necrosis is at least minimally justified; ultimately, its results still need to be independently validated (as we do here by comparing it with the approach based on Eqs. [8]).

PGSE-based D^∞ extrapolations (from Eq. [7]) were performed at voxel level, converted to ECS maps using Eq. [9] with D_0,ecs= 2.70 or 1.94 μm²/ms for in vivo or ex vivo (based on PBS measurements), respectively, and compared to the ECS estimates derived with POMACE using the combination of PGSE and low frequency OGSE data.

RESULTS

Uncertainty in parameter estimation

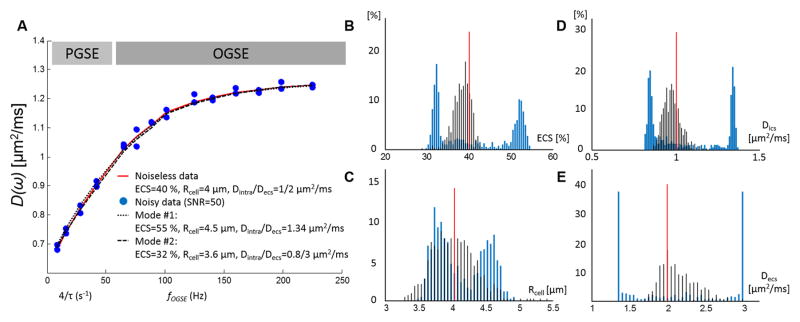
Noise propagation was used to assess the uncertainty in estimation of the POMACE model parameters. The four parameters (ECS, R_cell, D_ics, and D_ecs) estimated by fitting the above model to the simulation data had bimodal distributions with their modes away from their nominal values (see blue distributions Fig. 2B–E). For D_ics and D_ecs, the two modes correspond to the case where intra- and extracellular diffusivities are equal or when they are constrained by boundary conditions (D_ecs< 3 μm²/ms).

Figure 2.

Time-dependent diffusion over-fitting with four independent variables. A. Combination of PGSE and OGSE data (light and dark gray) in the range [31 ms ; 225 Hz] based on Eq. [3–6] and realistic estimates (ECS = 40%, R_cell = 4 μm, D_ics/D_ecs=1/2 μm²/ms, D_0,ecs = 2.7 μm²/ms). When fitting four independent variables, small variations due to noise (blue circles, SNR=50, 2 time-points per time / frequency) lead to bimodal distributions (blue lines) of the estimated ECS fraction (B), cell radius (C), intra-(D) and extracellular diffusivities (E). The red lines correspond to the parameter nominal values. Alternatively, when D_ics is fully constrained based on Eq. [8a] and OGSE data in the short time regime (f_OGSE > 88 Hz), the distributions of the parameter estimates (black lines) are centered around the nominal values.

The approach of constraining ECS and D_ics by fixing D_0,ecs using Eq. [8a] during the estimation resulted in unimodal distributions of all four parameters with their modes close to the nominal values, (Fig. 2B–E, black distributions and red line). For SNR=50 (Fig. 2A, typical SNR for ex vivo experiments ~60), the median values of the four parameters (ECS, R_cell, D_ics and D_ecs) were 4.5 %, 0.1 %, 1.8 %, and 7.2 % off from the nominal values and the coefficients of variation (CV = standard deviation/mean, or interquartile range/median) are 5, 8, 5, and 13 %, respectively. A two-fold increase/decrease in SNR (SNR=100/25, data not shown) resulted in an equivalent twofold decrease/increase on the CV compared to SNR=50, suggesting an increased precision on the estimation of in vivo parameters (typical in vivo SNR ~ 120) and validating this approach in vivo and ex vivo.

Characterization of tumor micro-environment (ECS, R_cell, D_ics, D_ecs)

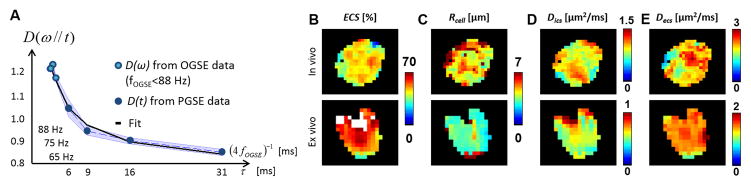
The time-dependence of the diffusion coefficient obtained in vivo with low-frequency OGSE data (f_OGSE < 88 Hz) and PGSE data (Fig. 3A) was fitted to Eq. [8b] and [8c], respectively, in order to extract parametric maps of ECS, R_cell, D_ics and D_ecs in the tumor (Fig. 3B–E, first line). For visualization purposes, the OGSE dataset was attributed to an equivalent diffusion time τ_eq = 1/4 f_OGSE, as in (51). This process was repeated for the ex vivo experiment on thin brain sections inserted in the MR histocoil. Representative examples of ex vivo parametric maps are illustrated in Fig. 3B–E (bottom line). Regions of elevated ECS (>70%) are highlighted white in ECS maps (Fig. 3B).

Figure 3. PGSE and low frequency OGSE time dependence.

A. In the tumor, PGSE (open circles) and OGSE data (closed circles) are fitted to Eq. [8b] and [8c]. The standard deviation over the ROI is indicated by the blue area. Parametric maps of ECS (B), R_cell (C), D_ics (D) and D_ecs (E) inside the tumor in vivo / ex vivo (top / bottom line). White areas in ECS maps indicate regions of very low cellular density (ECS>70 %).

The tumor area used for MRI analysis (number of voxels × in-plane spatial resolution) was respectively 7.0 ± 5.0 mm² and 10.2 ± 7.5 mm² for in vivo and ex vivo (n=8). The mean distributions of ECS, R_cell, D_ics and D_ecs in the tumor are presented in Table 1. In vivo and ex vivo mean R_cell measurements were consistent with each other (4.8 and 4.4 μm). Individual voxel values ranged from 2.5 to 44 μm. A two-fold factor was found between D_ecs and D_ics, in vivo and ex vivo. In addition, D_ics and D_ecs were similarly affected by the lower temperature in ex vivo MRI (−16/−21 %). Differences between in vivo and ex vivo diffusivities were smaller than the differences expected due to temperature difference (−30% in PBS), suggesting changes at cytoplasmic level. Interestingly, the ex vivo data provided higher ECS estimates (ΔECS=10 %, P<0.01) than the in vivo data acquired at 37 °C.

Table 1.

In vivo (n=1056) and ex vivo (n=1073) fit estimates for the tumor environment. Only voxels with physically realistic values (D_ecs in [0–3] μm²/ms, R_cell in [0–10] μm, ECS in [0–100] %) were included in this analysis.

	ECS [%]	Rcell [μm]	Dics [μm2/ms]	Decs [μm2/ms]
In vivo	44 ± 7	4.8 ± 1.3	0.96 ± 0.21	2.06 ± 0.35
Ex vivo	54 ± 11	4.3 ± 1.4	0.76 ± 0.25	1.72 ± 0.25

At tumor level (n=8), a small correlation was found between tumor size and mean cell radius (Spearman correlation coefficient ρ = 0.4), and between tumor size and cell radius standard deviation within the tumor (ρ = 0.65). The mean cell radius for small / large tumors (analysis area below / above 100 voxels, i.e. 6.25 mm²) was 3.8 ± 0.7 and 5.2 ± 1.8 μm, respectively.

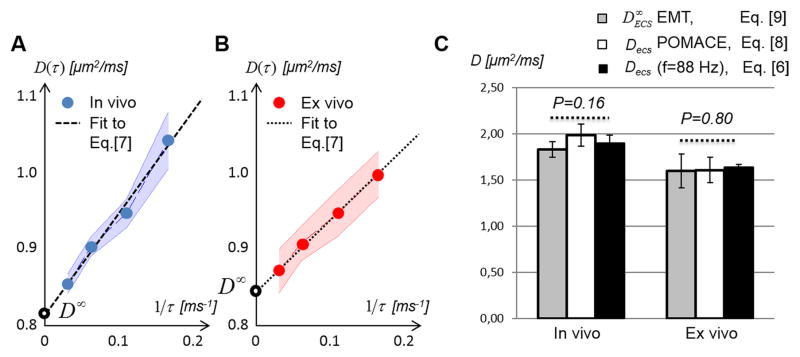
Extracellular diffusivity in the long time regime

The long time limit is well characterized by a linear relationship between D(τ) and 1/τ (24). As illustrated in Fig. 4A–B, a very good agreement was found between the functional form - Eq. [7] - characterizing this regime and both the in vivo (Fig. 4A, R²=0.89±0.11) and ex vivo (Fig. 4B, R²=0.98±0.02) PGSE data. Based on this result, the extrapolation of the PGSE data to infinite diffusion times (D^∞) provides an estimation $D_{\mathit{ecs}}^{\infty }=D^{\infty }/\mathit{ECS}$ for the extracellular diffusivity at infinitely long times.

Figure 4. Long time-dependence of the diffusion coefficient in the tumor.

Both A. in vivo and B. ex vivo PGSE-based D(τ) decrease linearly with 1/τ. Standard deviations within the tumor ROI are represented by the blue / red areas. C. Comparison of the ECS diffusivities derived from the POMACE model (D_ecs, white) with values extrapolated from the PGSE data in the long time regime ( $D_{\mathit{ecs}}^{\infty }$, grey), and from the short-time regime at f_OGSE = 88 Hz (black) for in vivo (left column) and ex vivo (right column) PGSE measurements.

From the short-time regime, following Eq. [6], with surface to volume ratio S/V = 0.57 ± 0.05 // 0.34 ± 0.04 μm⁻¹ (n=8) and D_0,ecs = 2.70 // 1.94 μm²/ms (in vivo // ex vivo), we find D_ecs (f = 88 Hz) = 1.90 ± 0.09 and 1.64 ± 0.03 μm²/ms, in vivo and ex vivo respectively.

The comparison of the D_ecs, D_ecs (f = 88 Hz) and $D_{\mathit{ecs}}^{\infty }$ distributions is presented in Fig. 4C. Based on the model-free extrapolation of the PGSE data, $D_{\mathit{ecs}}^{\infty }$ was not found significantly different (Mann-Whitney U test, P=0.16) from D_ecs (f = 88 Hz) (Fig. 4C, 1.83 ± 0.09 vs. 1.90±0.09 μm²/ms) in vivo. Similarly, no significant difference (Mann-Whitney U test, P=0.80) was found between the ex vivo D_ecs (f = 88 Hz) and $D_{\mathit{ecs}}^{\infty }$ (Fig. 4C, right columns, 1.64±0.04 vs. 1.60±0.18 μm²/ms). These results suggest that the true extracellular diffusivity is not varying much in our time- or frequency range (maximum 3% difference between the average D_ecs (f = 88 Hz) and $D_{\mathit{ecs}}^{\infty }$) and can be considered constant when modeling the tumor micro-environment in the diffusion time / oscillation frequency range used in this study: f < 88 Hz and τ< 31 ms.

Correlation with Diffusion Metrics

Table 2 shows the correlation coefficients ρ between one of the POMACE parameters (ECS, R_cell, D_ics, D_ecs) and conventional DWI metrics - D(ω) or D(t) at four different frequencies/times as representative examples. The complete tables (14 frequencies / times, in vivo / ex vivo) can be accessed online in the supporting materials (Table S1–2). ECS was found mainly correlated with diffusion coefficients obtained with PGSE (Table 2, bold in first two columns), supporting the link between long time diffusion and cellularity. On the other hand, the correlation between D_ics and D(τ) increased mildly as the diffusion time decreased / frequency increased (ρ =0.74/0.62 for f_OGSE=225 Hz). R_cell and D_ecs were not found strongly correlated to any of the diffusion metrics.

Table 2.

Pearson’s correlation coefficients between ECS, R_cell, D_ics, D_ecs and diffusion coefficients obtained at two diffusion times (31/9 ms) and oscillation frequencies (65/225 Hz) derived in vivo (white) and ex vivo (gray).

Corr.	DPGSE (31ms)		DPGSE (9ms)		DOGSE (65Hz)		DOGSE (225Hz)
ECS	0.45	0.73	0.46	0.69	0.22	0.41	0.29	0.51
Rcell	0.19	0.19	0.37	0.23	0.23	0.22	0.14	0.18
Dics	0.21	0.25	0.40	0.36	0.65	0.61	0.74	0.62
Decs	0.19	0.13	0.08	0.15	0.30	0.31	0.13	0.21

EMT-based ECS mapping

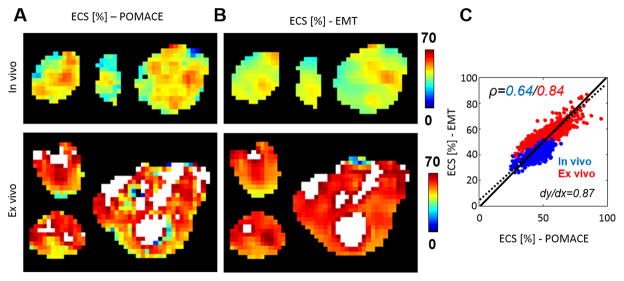
The comparison of voxel-based ECS distributions is presented in Table 3. As illustrated in Fig. 5A & B, mean in vivo values of both models were 44 %. Coefficients of variation were lower for EMT (CV = 11 vs. 16%), as reflected by more homogeneous ECS maps (Fig. 5B). Similar results were found with the ex vivo data (mean ex vivo ECS = 54 % vs. 56 %, CV = 13 vs. 20 %). Both ECS metrics were found strongly correlated at voxel level (Fig. 5C, ρ =0.64 / 0.84, in vivo / ex vivo, blue / red) with a slope close to unity (Fig. 5C, dy/dx=0.87 vs. 1.0, dotted vs. plain line).

Table 3.

Comparison of ECS distributions for the two models. Only voxels with physically realistic values (D_ecs in [0–3] μm²/ms, R_cell in [0–10] μm, ECS in [0–100] %) were included in this analysis.

ECS [%]	2CM - Eq. [8]	EMT, Eq. [9]
In vivo	44 ± 7	44 ± 5
Ex vivo	54 ± 11	56 ± 7

Figure 5. Comparison of ECS parametric maps.

derived from A. the POMACE (Eqs. [8]) and B. EMT applied to the PGSE data (Eq. [9]) in three representative tumors. Areas of high ECS (>70%) are highlighted in white. C. At voxel level, ECS measurements appear strongly correlated in vivo (ρ =0.64) and ex vivo (ρ =0.84). The complete dataset (in vivo + ex vivo) is best fitted via the dotted line (slope=0.87). The unity line is plotted for visualization purposes.

Histology

Due to high heterogeneity within the tumor and mechanical distortions during tissue preparation, different features were observed in the brain sections used for ex vivo MRI compared to the adjacent sections used for immunohistochemistry (IHC) (5 μm thickness), making it non-trivial to directly correlate ECS maps with IHC. In some cases, areas of various cell density could be detected in the tumor, which appear to match with the pattern of ECS estimated using MRI. Due to the mismatch between IHC and MRI sections, optical microscopy was preferred to IHC for the validation of ex vivo ECS maps.

Optical Microscopy

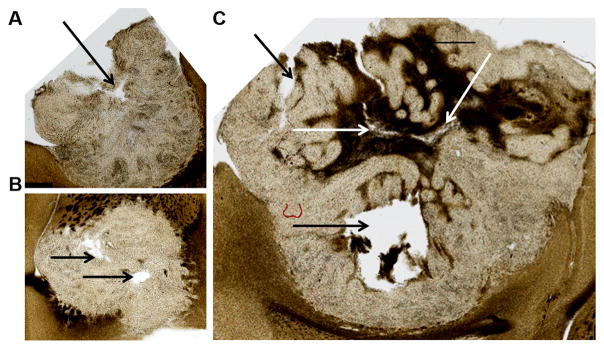
Microscopy (Fig. 6A–C) was performed without additional staining on the same brain sections used for ex vivo MRI (Fig. 5A–B, ex vivo panel) in order to prevent mismatch due to tissue fixation, distortion, and slice thickness. As a result, microscopic images appeared blurry at cellular level, as several cellular layers (R_cell<10 μm) were superimposed within the 100 μm brain section. At tumor level, a good correlation was found between the necrotic areas observed with microscopy (indicated by the black and white arrows in Fig. 6) and the locations of high ECS based on ex vivo MRI (white areas in Fig. 5A–B, ECS > 70%). Similarly, regions of low ECS appear to match areas of tumor infiltration in gray and white matter located near the rim of the tumors. These results, made possible via the use of an MR histocoil, could suggest that the ECS values obtained using the time-dependence of the diffusion coefficient accurately depict the structural organization of the tumor at cellular level.

Figure 6. Optical microscopy.

performed on brain sections (100 μm thickness) used for ex vivo MRI (corresponding to Fig. 5A–B, ex vivo panel). Necrotic areas (black/white arrows) match the regions of high ECS (>70 %) estimated using MRI (Fig. 5). Similarly, regions of low ECS appear to match areas of tumor infiltration in Gray and White Matter.

Electron Microscopy

The tumor cell radius was measured using EM images (see Fig. S3A–B in supplementary materials). A representative raw EM image with corresponding cell delineation can be found online (supplementary materials, Fig. S3). From the 60 cells randomly chosen in the tumor, the estimated radius was 4.7 ± 1.7 μm (with 0.4 μm 95% confidence interval on the mean cell radius), which is in good agreement with the R_cell estimated using in vivo and ex vivo MRI (4.8 ± 1.3 // 4.3 ± 1.4 μm). Interestingly, both methods provided very similar results for the cell dimensions despite potential structural changes due to the different tissue fixation methods required prior to EM imaging or ex vivo MRI.

DISCUSSION

Our results demonstrate that the proposed POMACE framework can be used to gain insight into the tumor microenvironment. Using a simple model of impermeable spheres for cancer cells, the extracellular space and cell radius can be quantified and used to characterize the tumor microstructure. Our ECS measurements, in agreement with ECS literature in brain tumors (see Table 1 in (1)), reflected the dramatic changes in ECS observed with optical microscopy on the same samples. In particular, micro-necrotic regions were easily detected using MRI. In vivo and ex vivo estimates of the cell radius were consistent, and in agreement with that measured in EM images of the same cell line, suggesting this method can be applied to estimate cell size in vivo non-invasively.

The approximation used to identify the ADC as the diffusion coefficient in Eq. [3] was checked retrospectively. Since D_ics and D_ecs estimates are on the order of 1.0 and 2.7 μm²/ms, a slight non-Gaussianity arises from the linear combination of MRI signals when b≠0. This can be calculated, numerically from the comparison of D=ECS*D_ecs+(1−ECS)*D_ics with ADC=−log(S_total)/b, or equivalently from assessing the second-order term (b²) in the Taylor expansion of the overall MRI signal: ΔD = (b/2)*ECS*(1−ECS)*(D_ecs−D_ics)^2, resulting in both cases in an overall 8% relative difference at b=0.4 ms/μm². These errors were found below the accuracy of our diffusion measurements, which were on average and at voxel level 10 ± 9 %.

Realistic modeling of tumor tissue is complex. The functional form of the time-dependence of a diffusion coefficient depends on the particular packing and structural disorder of the medium (24,55,56), which is unknown. It is tempting to tackle this fundamental problem by probing the extremely short and/or long time limit, where the functional form of the time-dependence is known. In those regimes, several physical parameters can in addition be neglected and/or simplified.

In the very short time regime, the cellular micro-architecture (including cell size, shape and packing) can be simply characterized by the surface-to-volume ratio S/V of the cell walls, and the diffusion time-dependence is fully expressed by two independent parameters: D₀ and S/V (44,46). D₀ represents the medium free diffusivity (in absence of restrictions) and S/V the purely geometrical restrictions. Although promising via its link to cellularity, the utility of this approach to characterize cancer remains to be investigated. The extension of this work to larger tumor cells, as described in (26), should be straightforward, as most of the time-dependence occurs at lower frequencies that are easily probed on preclinical scanners. In contrast, in healthy brain structures, such as gray or white matter, very high oscillation frequencies (f_OGSE > 1kHz) are required to probe the Mitra regime due to smaller cellular sizes (19); feasible diffusion times using an MRI system similar to what used in our study correspond to the long time asymptotic approach of the tortuosity limit as both axons and dendrites are very narrow.

In the long time regime, the diffusion coefficient D(τ) in three-dimensional random media reaches towards its asymptotical limit D^∞ as 1/τ; in our case, this behavior should describe the extra-cellular diffusivity. Since the intracellular diffusion becomes fully constrained by cellular membranes, the corresponding intracellular diffusivity approaches zero also as 1/τ. This justifies the usage of Eq. [7] to determine the overall tortuosity asymptote. Practically, in the absence of strong variations of the extracellular medium, numerous studies have used a PGSE-based ADC as a successful inverse surrogate for cell density (11,13,57).

Here it is important to note that it is the three-dimensional random packing geometry that allows us to use the simple extrapolation formula [7] and to not model the time dependence in the extra-cellular space explicitly. Generally, one should be careful to investigate the role of time dependence in the extra-cellular space. For example, in the two-dimensional random packing geometry of diffusion transverse to axonal tracts, the corresponding extra-cellular diffusivity approaches its tortuosity limit much slower, as (ln τ)/τ (19), than the 1/τ approach (24) in the three-dimensional random geometry. As a result, diffusion time dependence in the extra-axonal space has been recently shown to provide the dominant contribution to the overall time dependence, and to strongly confound axonal diameter estimates (19,20). Recent study shows that including the extracellular diffusivity time dependence leads to axonal diameter estimates about 3–5 smaller than when the time dependence is not included, which in turn makes the estimated diameter values below the practical detection limit (58).

Approaching the long-time regime with PGSE was used here as a tool to (1) extrapolate towards the tortuosity limit D^∞ which is, formally speaking, experimentally unreachable; and (2) validate the assumption of a constant diffusivity in the ECS in our range of times and frequencies. Note that the latter required only limited prior knowledge on cell size (R_cell < 8 μm) in addition to the POMACE assumptions (impermeable membranes and free extracellular diffusivity = 2.7/1.94 μm²/ms in vivo / ex vivo). Results were highly encouraging, as a maximum 10% relative difference was found between D_ecs (f_OGSE = 88 Hz) and this long time limit $D_{\mathit{ecs}}^{\infty }$. These small D_ecs changes outside the short-time regime were found consistent with EMT-based $D_{\mathit{ecs}}^{\infty }$ estimates, following Eq. [9] and ECS literature in brain glioma (see Table 1 in (1)). Large ECS volume fractions (~50 %) lead indeed to elevated ratios $D_{\mathit{ecs}}^{\infty }/D_{0,\mathit{ecs}}=\sqrt{\mathit{ECS}}~0.70$, comparable with D_ecs/D_0,ecs estimations from the short-time regime (Eq. [6]) using realistic ECS parameters (D_0,ecs=2.7 μm²/ms, S/V=0.4 μm⁻¹) and oscillation frequency (D_ecs/D_0,ecs = 0.76 at f_OGSE = 88 Hz). Based on this, all of the time dependence of the diffusion coefficient in the range [1/(88 Hz) – 31 ms] was entirely attributed to intracellular restrictions, and ECS and R_cell unambiguously extracted from Eq. [8b–c]. For this purpose, estimations based on Eq. [8b] suggested that the diffusion times used in this study (6 < τ < 31 ms) were sufficient to consider that the long time regime was reached inside the cells (D linear with 1/τ).

In principle, if our time-independent approximation for ECS diffusivity does not hold, the time-dependence of the diffusion in the ECS would need to be accounted for when fitting D(ω)/D(τ). This can be problematic, as fits become extremely unstable when allowing for D_ecs to vary with frequency or time. For PGSE this is due to the very similar functional forms of intra- and extracellular diffusivities approaching the long time regime (see Eq. [7]). As a result, these compartments cannot be resolved in the absence of strong constraints. Another way to effectively constrain fitting is acquiring higher-order diffusion metrics such as kurtosis terms; however, this requires stronger diffusion weighting and extra scan time. Five-parameter models (combining OGSE at 40 and 80 Hz and a single PGSE with τ=52 ms) were shown successful in identifying cell pellets of various size (R_cell=10/20 μm) (27). However, only relative ECS changes could be demonstrated in solutions of various but unknown cellular densities. Since their model assumes constant diffusivity in the ECS for PGSE, the ECS quantification accuracy would benefit from additional PGSE measurements in this intermediate range. In general, the ECS diffusion time-dependence can only be neglected under certain circumstances (specific time range vs. cellular dimensions, low cellular packing, dimensionality of the problem – in particular, 3 dimensions is much more favorable in this respect than 2 dimensions), that must be thoroughly investigated and validated. In addition, for longer diffusion times, recent studies (39) suggest that the influence of cellular permeability on the measured diffusion coefficient cannot be neglected and should be accounted for in Eq. [4–5]. This constitutes a minor limitation to our study, as only the longest diffusion time (31 ms) was near the boundary of the range safe to assume cells can be considered impermeable (around one-tenth of the water residency time) (38–41). With the multiple shorter diffusion times using PGSE, Δ=6, 9, and 16 ms, which are less likely affected by the exchange effect, we expect that the error induced by a potential small bias in the fit due to the measurement at Δ=31ms is not considerably large.

In general, particular caution was taken to ensure the validity of the many assumptions used throughout this study. In addition to pilot studies investigating IVIM effects and diffusion isotropy in the tumor, MR parameters were fixed when possible. Only the diffusion time / period and number of oscillations were allowed to vary during the experiment. Small and constant b-values ([0–0.4] ms/ μm²) ensured that the mono-exponential “DTI” regime was maintained and additional orders of the MR signal cumulant expansion (33) could be neglected for all diffusion times / frequencies. Similarly, TE and TR values were kept constant (70/3000 ms) to minimize the influence of potential different relaxation times in the two compartments.

Ex vivo diffusivities were found significantly smaller than in vivo, although the experimental difference (D_PGSE, D₀, D_ics and D_ecs decreased by 15, 25, 20 and 16 %, respectively) did not reach the expected decrease due to temperature between 37 and 20 degrees (−30 %, as measured in PBS). Since cellular size were found similar in vivo and ex vivo, these changes must be explained by changes at microstructural level triggered during the fixation process and impacting cellular permeability and/or ECS content, such as the removal of small extracellular structures during the fixation process. It was beyond the scope of this study to determine the exact underlying changes caused by the tissue preparation for ex vivo experiment. However, because there can be substantial differences between in vivo MRI and histopathological assessment for the same reason, the ex vivo MRI experiment was included for cross-validation of the model with other ex vivo methods in this study.

The two approaches to quantify the ECS in vivo and ex vivo (low-frequency OGSE+PGSE vs. EMT) provided very similar results in the tumor. In addition, both methods matched well with the structural information extracted from the ex vivo microscopy data, suggesting both methods are suitable to extract the true extracellular fraction. EMT-based ECS maps were found in general more homogeneous, likely to be a result of the lesser number of fit parameters. However, combining diffusion at different scales (OGSE+PGSE) provided an additional estimate of the cellular radius R_cell, while D^∞ extrapolation in the long time limit is - for impermeable structures - independent of cell size (49). In addition, the EMT assumes that the extracellular diffusivity D_0,ecs is homogenous and unconstrained, while the “apparent” constant diffusivity D_ecs is allowed to vary in the other model. The latter could constitute an advantage in situations prone to changes in the extracellular medium, such as post-injury states or ischemia (59). Here should be noted that, since both techniques make similar assumptions – the validity of which is discussed earlier -, they do not provide fully independent ECS estimation.

Both MRI-based ECS quantification approaches highlighted an increase of the ECS (average ΔECS=+10%) ex vivo. This result is counterintuitive, as brain structures (including the extracellular matrix) are known to shrink under the influence of tissue fixatives used for sample preparation (60). This cellular shrinkage process remains however small after PFA fixation (61) and tumor expansion could be facilitated by the skull removal and rehydration process, partially releasing tumor interstitial pressure. In addition, we cannot exclude partial removal of low packed cells during the fixation and sectioning process, explaining why our data did not support evidence of ECS shrinkage due to tissue fixation. Additional ex vivo measurements prior to tissue sectioning would help answer this question.

The validation of the ECS estimates was made possible by using a histocoil (52) allowing for the imaging of very thin brain slices (100 μm) that could be imaged using a different modality (optical microscopy in this case). In addition, sufficient SNR was maintained all around the sample (in vivo / ex vivo SNR = 120/60) to derive parametric maps despite a fifteen-fold decrease in slice thickness. Another utility of the histocoil lies in the possibility to perform ex vivo MRI at various temperatures. This can be used as an additional tool to probe different diffusion time regimes (37).

Despite providing the right order of magnitude for cell size, EM cell size measurements were only performed in one animal and limited number of cells (n=60), which might not be representative of the full cohort. In addition, the estimation method used in this study would lead to cell size underestimation for highly aspherical cells intersecting the EM imaging plane. To date, direct correlation of MRI and EM is not possible due to differences in slice thicknesses and tissue preparation, justifying this approach to estimate cell size. Since MRI estimates only pointed out a small difference in mean cell radius between small and large tumors (3.8 vs. 5.2 μm), any bias when comparing EM performed at 14 days and MRI estimates obtained between 14–28 days would remain small.

Kucheryavykh et al (62) reported that the radius distribution becomes larger at the later stage of tumor growth to (15–60 um in diameter). Similarly, Resende et al (63) reported that GL261 size was around 10–20 um in diameter at the early stage and increases to 14–52 um in the later stage of about 3 weeks post tumor implantation. These two studies were conducted with brain slices, whereas our study was based on the measurement of tumor in the intact brain. In this study, we found a weak correlation between tumor size and mean cell radius (ρ = 0.4) and a stronger correlation between tumor size and cell radius standard deviation within the tumor (ρ = 0.65), suggesting cancer cells could indeed become larger at later stage, but the mean cell radius remained on the same order of magnitude (R_cell = 3.8 ± 0.7 vs. 5.2 ± 1.8 μm for the small and large tumors). Despite this difference in experimental conditions, the estimated cell radius from our study is quite close to the ex vivo measurements that can be appreciated in supplementary Figure S3.

The quantitative comparison of MRI- and IHC-based ECS estimates failed due to differences in structure between two consecutive brain sections of different thicknesses (100 vs. 5 μm). Although qualitative comparisons on several neighboring slices support the validity of MRI-ECS measurement, a rigorous multimodal correlation can only be achieved via consecutive MRI and IHC of thin brain sections (5–10 μm). This would however degrade MR performances and generate additional diffusion restrictions in the sample. This problem can be solved using 3D ex vivo MRI followed by histology, provided the tissue integrity is well preserved during preparation and sectioning.

Although the ECS can also be estimated from DCE-MRI, the accuracy of ECS measurement in DCE-MRI can be affected by multiple factors, such as arterial input function, tissue Gd relaxivity, pre-contrast T1, RF coil sensitivity, and water exchange between vascular, intra- and extracellular compartments (64). It is beyond the scope of our study to include another MRI modality with its own uncertainty in measuring ECS. Future studies are needed to compare the POMACE-measured ECS with that of DCE-MRI.

Other diffusion models relevant for cancer studies have used the vascular compartment directionality (26), exchange rate (65) or micro FA approach (66) in order to characterize tumor microstructure, often at the expense of accurate extracellular space quantification. On the other hand, the present technique focuses on estimation of the cell size and extracellular space fraction, which has been recognized as a strong biomarker for treatment efficacy (1).

The proposed method in this study can be translated to clinical scanners with additional restrictions on the OGSE frequency range depending on the gradient hardware limitations. The geometrical model would also remain valid for various brain tumors as the size of human cancer cells are in the same order of magnitude as those of the murine glioma cells used in this study. The OGSE frequency and diffusion time ranges can be adjusted in order to optimize the measurement condition for the specific size of any particular cancer type. However, it should be stressed that the proposed method cannot be applied to the normal brain tissues even in the mouse brain, as some of the fundamental assumptions (directionality, cell size, geometry, packing density) used for our method may not be valid. Smaller neuronal structures require a substantially higher range of oscillating gradient frequencies to achieve sufficiently short time range to estimate S/V. A higher packing density in normal brain compared to glioma is another critical factor that affects the approximation of negligible diffusion time-dependence in the ECS. In addition, many of murine brain regions, including the cortical ribbon, have structural alignment that gives a rise to diffusion anisotropy. Hence, assessment of time-dependence of diffusion in normal brain tissue requires a considerably different approach than the method proposed in this study. In fact, one of the motivations for this study was to develop a specific measurement method appropriate for cancer cells given their differences from normal brain tissue.

The model analysis in the proposed method is based on the ADC values at individual diffusion times and oscillating gradient frequencies, such that it is not directly affected by many of the acquisition parameters. The most critical parameter for the model is the diffusion time and frequency range as it is supposed to include both short-time AND long-time regimes for cancer cells. As long as the data acquisition includes multiple measurements in these two regimes for our target tissue, we do not expect that the choice of individual diffusion times and frequencies would influence the outcome of the analysis. In this study, the diffusion times and frequencies were chosen to cover the whole available spectrum, thus ensuring maximal sensitivity to the diffusion time-dependence. Future study is warranted to further investigate and optimize the selection of the diffusion times for characterization of cancer cells.

In summary, it is possible to characterize the tumor microenvironment inside a loosely packed mouse glioma cells both in vivo and ex vivo, using the time-dependence of the diffusion coefficient and a simple model of impermeable spheres when appropriate diffusion times are used. The combination of PGSE and OGSE data and the proposed POMACE framework of analysis provide a quantitative means to estimate both the cell radius and extracellular space fraction, that can be used as non-invasive MRI markers to assess micro-necrotic areas, modification of the extracellular matrix, tumor progression or treatment response.

Supplementary Material

Supp Table S1-S2

Supporting Table S1. Pearson’s correlation coefficients between ECS, R_cell, D_ics, D_ecs and diffusion coefficients obtained in vivo at multiple times / frequencies. Only voxels with physically realistic values (D_ecs in [0–3] μm²/ms, R_cell in [0–10] μm, ECS in [0–100] %) were included in this analysis.

Supporting Table S2. Pearson’s correlation coefficients between ECS, R_cell, D_ics, D_ecs and diffusion coefficients obtained ex vivo at multiple times / frequencies. Only voxels with physically realistic values (D_ecs in [0–3] μm²/ms, R_cell in [0–10] μm, ECS in [0–100] %) were included in this analysis.

Abbreviations

ADC

Apparent Diffusion Coefficient

CV

Coefficient of Variation

DCE

Dynamic Contrast Enhanced MRI

DTI

Diffusion Tensor Imaging

ECS

extracellular space

EM

Electron Microscopy

EMT

Effective Medium Theory

GL261

mouse Glioma 261

GLUT1

Glucose Transporter 1

IHC

Immuno-histochemistry

PB(S)

Phosphate Buffered (Saline) solution

PFA

Paraformaldehyde

POMACE

Pulsed and Oscillating gradient MRI for Assessment of Cell Size and Extracellular space

PGSE/OGSE

Pulsed/Oscillating Gradient Spin Echo

ROI

Region of Interest

S/V

Surface-to-Volume ratio