Sheathless electrokinetic particle separation in a bifurcating microchannel

Abstract

Particle separation has found practical applications in many areas from industry to academia. Current electrokinetic particle separation techniques primarily rely on dielectrophoresis, where the electric field gradients are generated by either active microelectrodes or inert micro-insulators. We develop herein a new type of electrokinetic method to continuously separate particles in a bifurcating microchannel. This sheath-free separation makes use of the inherent wall-induced electrical lift to focus particles towards the centerline of the main-branch and then deflect them to size-dependent flow paths in each side-branch. A theoretical model is also developed to understand such a size-based separation, which simulates the experimental observations with a good agreement. This electric field-driven sheathless separation can potentially be operated in a parallel or cascade mode to increase the particle throughput or resolution.

I. INTRODUCTION

Separating particles (both biological and synthetic) from a mixture is a critical step to many applications in both industrial and academic areas. Microfluidic devices, as a viable alternative to bench-top analytical devices, have been increasingly used for particle separation due to advantages in efficiency, resolution, portability, and cost.^1,2 Compared with the batch-wise separation methods such as electrophoresis³ and field flow fractionation,⁴ continuous-flow microfluidic separation techniques are more favored for their ease of integration with up/downstream components and their potential to achieve high throughput.^5,6 A variety of force fields, which can be either externally applied or internally induced, have been demonstrated to continuously separate particles in microfluidic devices^7–9 ranging from hydrodynamic^10–13 to electrical,^14,15 acoustic,¹⁶ optical,¹⁷ and magnetic¹⁸ forces. Among them, the most widely used is dielectrophoresis (DEP), a force exerted on a particle by a non-uniform electric field.¹⁹ The magnitude of this force is a function of the particle's morphology (e.g., size and shape) as well as the particle and suspending medium's electrical properties (i.e., conductivity and permittivity).²⁰ Hence, the DEP has become a powerful tool in the microfluidic devices for manipulating the micro/nano-sized particles due to its sensitivity.^{14,15,19–21}

Traditionally, AC voltages are employed to create electric field gradients on and between the activated microelectrodes for DEP, where the magnitude and the frequency of AC voltages can each be tuned to optimize the particle separation.^22,23 However, there exist distinct disadvantages for such electrode-based DEP (eDEP) devices including the fabrication complexity and surface degradation of metal electrodes.²⁴ Recently, DC voltages have been used to generate DEP for particle separation via the electric field gradients formed around inert micro-insulators (e.g., hurdles, posts, and turns).^25–30 This so-called insulator-based DEP (iDEP) technique³¹ eliminates the electrode issues with eDEP. Moreover, the induced DC electrokinetic flow can drive the particle solution, which makes the additional pumping force unnecessary.³² However, the iDEP devices are more prone to Joule heating effects due to the locally amplified electric field around insulators.^33,34 More recently, the DC-biased AC voltages have also been utilized in the iDEP devices to both enhance particle separation and mitigate Joule heating effects via an independent control of DC electrokinetics and AC DEP.^35,36

We develop in this work a new type of DC electric field-driven particle separation method in a bifurcating microchannel. This continuous sheath-free electrokinetic separation exploits the inherent wall-induced electrical lift to focus particles towards the centerline of the main-branch and deflect them to size-dependent flow paths in each side-branch. Such an electrically originated lift force arises from the asymmetric electric field induced around a near-wall particle due to the unmatched electrical properties between the particle and the suspending medium.^37–40 This force has been recently demonstrated by our group to separate the particles by size in a T-shaped microchannel.⁴¹ However, a sheath flow is required to pre-focus the particle mixture, which complicates the flow control, reduces the particle throughput, and dilutes the separated particles. The electrical lift has also been utilized by our group to counter-balance the curvature-induced DEP to achieve a size-based particle separation in a single-spiral microchannel.⁴² However, the location of the inlet reservoir at the center of the spiral significantly complicates both the particle injection and the integration with the upstream component. Moreover, the nonlinear architecture makes spirals difficult to be parallelized for the enhanced particle throughput.

Compared to existing electric field-driven separation techniques,^{21–23,31,32} our proposed electrical lift-based particle separation in a bifurcating microchannel avoids the issues of electrode fabrication/degradation in eDEP^15,24 and minimizes the issues of potentially strong Joule heating effects in iDEP.^34,35 Moreover, it keeps the advantages of iDEP where the applied DC electric field not only pumps the particle solution but also focuses and separates the suspended particles continuously. Therefore, the additional pumping of particle suspension that is necessary for external force-based (e.g., magnetic, acoustic, and optic field-induced) active separation techniques^5–9 is eliminated. Also, the sheath flow(s) that is required to pre-focus particles in the streamline-based passive separation techniques including deterministic lateral displacement⁴³ and pinched flow fractionation¹⁰ is eliminated. There are a few sheath-free passive particle separation methods such as hydrodynamic filtration⁴⁴ and hydrophoresis,⁴⁵ where, however, either a complex network of microchannels⁴⁴ or a complicated fabrication of in-channel grooves⁴⁵ is involved. The inertia-based particle separation in Newtonian⁴⁶ or in non-Newtonian⁴⁷ fluids is another sheathless passive separation method, where the former takes place only in high Reynolds number flows and the latter necessitates the addition of polymers into the particle suspension. Our proposed electrokinetic particle separation in a bifurcating microchannel is anticipated to find niche applications that deal with a small amount of samples.²⁴ It is also noted that a similar design of bifurcating microchannels has been recently demonstrated to separate particles by size using the viscoelasticity induced lateral migration in polymer solutions.^48,49

II. EXPERIMENTAL SECTION

A. Microchannel fabrication

The bifurcating microchannel was fabricated with polydimethylsiloxane (PDMS) using the standard soft lithography technique. Its CAD (computer-aided design) drawing was printed onto a flexible transparency at a resolution of 10 000 dpi (CAD/Art Service), which was used as a photomask in the photolithography. SU-8 25 photoresist (MicroChem Corp., Westborough, MA) was spin-coated on a clean glass slide (WS-400B-6npp/lite, Laurell Technologies, North Wales, PA) with a uniform thickness as per the protocol. This slide was then subjected to a two-step soft bake (65 °C for 4 min and 95 °C for 8 min) on a hot plate (HP30A, Torrey Pines Scientific, Carlsbad, CA). Following that, the photoresist film was covered by the photomask and exposed to 365 nm UV light (ABM Inc., San Jose, CA) for 30 s. After a two-step hard bake (65 °C for 2 min and 95 °C for 4 min), the UV-exposed photoresist was developed in the SU-8 developer solution (MicroChem Corp., Westborough, MA) for 10 min followed by another two-step hard bake (65 °C for 1 min and 95 °C for 5 min). The positive replica of the photoresist on the glass slide served as the mold of the bifurcating microchannel.

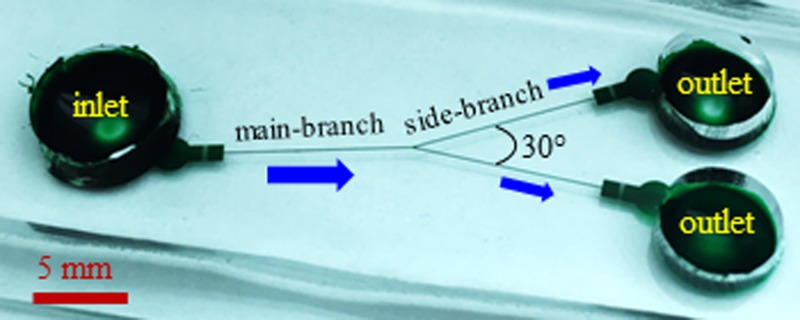
Next, the microchannel mold was placed in a petri dish and covered with liquid PDMS (Sylgard 184, Dow Corning Corp., Midland, MI) that was prepared at a precursor to curing agent ratio of 10:1 by weight. The petri dish was then degassed in a vacuum oven (13–262-280A, Fisher Scientific, Pittsburg, PA) for 15 min before being placed in a gravity convection oven (13-246-506GA, Fisher Scientific, Pittsburg, PA) at 70 °C for 3 or 4 h. Prior to experiment, the cross-linked PDMS was cut out using a scalpel and punched with three reservoir holes. Immediately after a plasma treating (PDC-32G, Harrick Scientific, Ithaca, NY) for 1 min, the channel side of the PDMS slab was bonded to a clean glass slide. Finally, a drop of the pure working solution (i.e., with no particles suspended) was dispensed into one of the reservoirs, which wetted the entire microchannel by capillary force and helped maintain the channel walls hydrophilic. Fig. 1 shows a picture of the fabricated bifurcating microchannel. The main-branch and the two side-branches are each 10 mm long with a uniform rectangular cross-section of 65 μm (width) × 40 μm (depth). The angle between the two side-branches is 30°. There is a 2 mm-long, 900 μm-wide expansion with embedded posts in front of each reservoir for the purpose of blocking out debris or enhancing particle separation.

FIG. 1.

Picture of a fabricated bifurcating microchannel (filled with green dye for clarity) used in experiments. The main-branch and the two side-branches are each 10 mm long and have a uniform rectangular cross-section of 65 μm width (measured) and 40 μm depth (measured). The block arrows indicate the fluid and particle flow directions during the separation experiment.

B. Particle manipulation

The particle solution was made by mixing the original suspensions of 5 μm- and 15 μm-diameter spherical polystyrene particles (Sigma-Aldrich, St. Louis, MO) followed by a dilution in 1 mM phosphate buffer. The final particle concentration in the solution was estimated to be 10⁶–10⁷ particles per milliliter with an approximate population ratio of 5:1 between 5 μm and 15 μm particles. To avoid particles adhering to channel walls, Tween 20 (Fisher Scientific, Pittsburg, PA) was added into the solution at a volume ratio of 0.5%. The electrokinetic motion of particles was driven by a DC electric field which was generated by a high-voltage power supply (Glassman High Voltage Inc., High Bridge). The pressure-driven particle drifting was minimized by carefully balancing the liquid heights in the three reservoirs before each experiment. Particle motion was visualized by an inverted microscope (Nikon Eclipse TE2000U, Nikon Instruments, Lewisville, TX) equipped with a CCD camera (Nikon DS-Qi1MC). Digital videos were recorded at a rate of 20 frames per second with an exposure time of 1 ms. Superimposed images were obtained by stacking the frames in a 30 s video at an interval of 5 frames using the Nikon imaging software (NIS-Elements AR 3.22). Images were also processed in ImageJ software (National Institute of Health) using the function “Analyze Particles.” The obtained particle center positions were used to plot the probability distribution function (PDF) in Excel (Microsoft).

III. THEORETICAL SECTION

A. Mechanism of particle separation

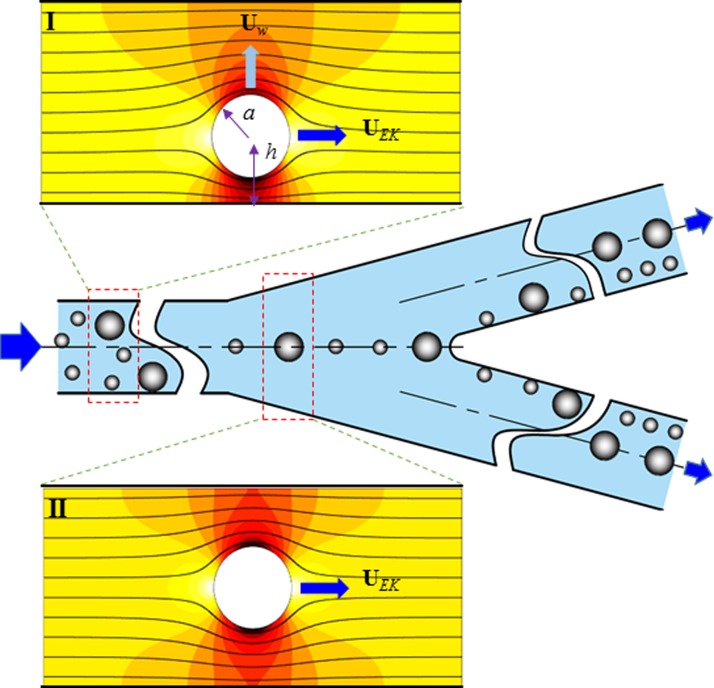
As demonstrated in previous studies,^37–40 the presence of a finite-sized particle distorts the otherwise uniform electric field in a rectangular microchannel (see inset I of Fig. 2). This happens as long as the particle has a dissimilar electric property (e.g., conductivity under DC electric fields and permittivity under AC electric fields) from that of the suspending fluid,⁵⁰ which is often true for both biological and synthetic particles in real applications.^19,20,51,52 The resulting electric field gradients exert an electrical “lift” force on the particle pushing it away from the channel wall.^41,42 Such a wall-induced lateral migration, U_w, has been theoretically proved by Yariv⁵³ to bear the following analytical form for a remote spherical particle of radius a:

$${\mathbf{U}}_w=\frac{\epsilon a{\mathbf{E}}^2}{32\eta }{\left(\frac{a}{h}\right)}^4\mathbf{n},$$ (1)

where ε is the fluid permittivity, E is the applied axial DC electric field, η is the fluid dynamic viscosity, h is the perpendicular distance of the particle center from the wall (see inset I of Fig. 2), and n is the unit vector normal to the wall. Note that Eq. (1) is only valid for a single isolated particle near a dielectric plane,⁵³ and hence unable to correctly predict U_w of the concentrated particles due to the influence of particle-particle interactions.^19,20,50 This transverse particle motion competes with the axial electrokinetic motion, U_EK (a combination of fluid electroosmosis and particle electrophoresis),

$${\mathbf{U}}_{\mathit{E}\mathit{K}}=\frac{\epsilon \left({\zeta }_p-{\zeta }_w\right)}{\eta }\mathbf{E}={\mu }_{\mathit{E}\mathit{K}}\mathbf{E},$$ (2)

where ζ_p is the particle zeta potential, ζ_w is the wall zeta potential, and μ_EK is the electrokinetic particle mobility. Note that the wall confinement effect on particle electrophoresis is neglected in Eq. (2). This effect in a rectangular microchannel has been found in an earlier experiment⁵⁴ to be within those in a slit channel and in a cylindrical channel. It was estimated using the formulae derived by Keh and Anderson⁵⁵ to be less than 5% for the electrokinetic motion of a 15 μm-diameter particle in a 40 μm-deep slit channel or a 40 μm-diameter cylindrical channel.

FIG. 2.

Schematic illustrating the mechanism of continuous-flow sheath-free electrokinetic particle separation in a bifurcating microchannel. Particles undergo a lateral migration, U_w, due to the wall-induced electrical lift force (see inset I), which competes with the axial electrokinetic motion, U_EK, resulting in a three-dimensional particle focusing along the centerline of the main-branch (see inset II). At the bifurcation, the focused two types of particles enter into either side-branch from near the inner wall, and are then continuously separated based on the difference in the particle velocity ratio, i.e., U_w/U_EK in Eq. (3). The background color and lines in the two insets represent the electric field contour (the darker the larger magnitude) and electric field lines (similar to fluid streamlines⁵⁷), respectively.

The combined result of the transverse and axial particle motions in Eqs. (1) and (2), respectively, is a three-dimensional continuous focusing of particles towards the channel centerline,⁵⁶ where the electrical lift force vanishes due to the transversely symmetric electric field gradients (see inset II of Fig. 2). At the bifurcation, each of the focused particles can enter into either side-branch due to the channel symmetry. However, as all particles are deflected away from near the inner channel wall in each side-branch (see Fig. 1), they will be continuously separated based on the difference in the transverse to axial particle velocity ratio, i.e.,

$$\frac{U_w}{U_{\mathit{E}\mathit{K}}}=\frac{\frac{\epsilon a{E}^2}{32\eta }{\left(\frac{a}{h}\right)}^4}{{\mu }_{\mathit{E}\mathit{K}}E}=\frac{a}{32}{\left(\frac{a}{h}\right)}^4\frac{E}{{\zeta }_p-{\zeta }_w}.$$ (3)

Note that particles also experience a dielectrophoretic force at the bifurcation due to the local channel curvature,²⁹ which works with the electrical lift to further push the particles away from the channel walls at a size-dependent rate and hence enhances the size-based separation. Such a sheathless electrokinetic separation applies in principle to the particles of dissimilar surface charges (i.e., ζ_p leading to a difference in electrokinetic particle mobility, μ_EK).²⁹ Particles that differ in both size and charge can also be separated using this method as long as their velocity ratios in Eq. (3) are not equal. This separation can be improved by the use of a higher electric field and/or a longer channel. The effect of the channel width will be discussed later in Sec. IV (see Eqs. (8) and (9) as well as the derivations of these two equations in the supplementary material).

B. Simulation of particle trajectories

To understand and predict the electrokinetic particle separation in a bifurcating microchannel, we developed a Lagrangian tracking method-based model in MATLAB (MathWorks) to simulate particle trajectories. This model considers only the one-way actions of the electric field and fluid flow field on the particle motion while the influences of the particle on the electric and flow fields are both neglected. It has been validated in our recent work of sheath-flow particle separation in a T-shaped microchannel via the wall-induced electrical lift.⁴¹ The following assumptions were made to simplify the model: (1) the interactions among particles are negligible because of the use of a dilute particle suspension; (2) the electrokinetic particle mobility, μ_EK in Eq. (2), remains unvaried in the entire microchannel, which has been validated for particles not touching a channel wall;⁵⁵ (3) the rotation of a particle is small or has little effect on its translation; (4) the variation of fluid properties is negligible because the estimated temperature rise due to Joule heating, ΔT = σE²D_h²/k (electric conductivity, σ = 210 μS/cm, hydraulic diameter of the microchannel, D_h = 49.5 μm, and thermal conductivity, k = 0.6 W/m K)^58,59 is less than 0.5 °C even for the highest electric field used in our experiments; (5) the particle inertia is insignificant due to the small low Reynolds number (Re = ρU_EKD_h/η < 0.1 at the highest electric field, where ρ is the fluid density and equal to that of water).

The instantaneous position of the particle center, r_p, was calculated by integrating the particle velocity, U_p, with respect to time, t,

$${\mathbf{r}}_p={\mathbf{r}}_0+{\int }_0^t{\mathbf{U}}_p(\tau )d\tau ,$$ (4)

$${\mathbf{U}}_p={\mathbf{U}}_{\mathit{E}\mathit{K}}+{\mathbf{U}}_{\mathit{D}\mathit{E}\mathit{P}}+{\mathbf{U}}_w,$$ (5)

where r₀ is the initial particle position and U_DEP is the velocity of particle DEP. For spherical polystyrene particles used in this work, U_DEP in DC electric fields is given by^41,42

$${\mathbf{U}}_{\mathit{D}\mathit{E}\mathit{P}}=-\frac{\epsilon a^2}{3\eta }\left(\mathbf{E}•\nabla \right)\mathbf{E},$$ (6)

which is negative (i.e., negative DEP) due to the much smaller particle conductivity than the fluid conductivity (i.e., the Clausius-Mossotti factor is −0.5).^19,20,50 It is important to note that DEP exists only in the regions with inherent electric field gradients in the absence of particles, including the reservoir-expansion and expansion-branch (both main- and side-branches) interfaces as well as the bifurcation. The electric field distribution was solved from Laplace's equation using a 2D model in COMSOL (COMSOL Inc.) that covers exactly one half of the bifurcating microchannel (with reservoirs) due to symmetry. The electrokinetic mobility, μ_EK in Eq. (2), was measured by tracking single particles in the main-branch of the microchannel, and found to be approximately identical for 5 μm and 15 μm particles used in our experiment at μ_EK = 2.4 × 10⁻⁸ m²/(V s). Any discrepancy in μ_EK (i.e., either particle has a greater mobility value) between the two types of particles will affect the relative value of the particle velocity ratios, i.e., U_w/U_EK in Eq. (3), which can either enhance or reduce the separation.

We did not use U_w in Eq. (1) to calculate the particle velocity U_p in our model because the former has been demonstrated in our previous studies^38,41,56 to underestimate the wall-induced transverse particle motion. Instead, we developed a 3D numerical model in COMSOL to directly calculate the electrical lift force via the integral of Maxwell stress tensor over the particle surface^20,50 (see the supplementary material for the detailed procedure). The computed force was then fitted to an exponential curve, which, by balancing with Stokes' drag, results in the following formula for U_w used in Eq. (5):

$${\mathbf{U}}_w=C_0\frac{\epsilon a{\mathbf{E}}^2}{6\pi \eta }\text{exp}\left(C_1\gamma +C_2{\gamma }^2+C_3{\gamma }^3\right)\mathbf{n},$$ (7)

where the fitting constants C₀ to C₃ are dependent on the particle size and given in Table I, and γ = (h − a)/a is the non-dimensional gap between the particle and wall (see inset I of Fig. 2). The viscosity and permittivity of the suspending fluid were assumed to be the same as those of water at 20 °C, i.e., η = 1.0 × 10⁻³ kg/(m s) and ε = 7.1 × 10⁻¹⁰ C/(V m).

TABLE I.

The fitting constants, C₀ to C₃, in the formula of wall-induced transverse particle motion, U_w, in Eq. (7).

Particle diameter	C0	C1	C2	C3
5 μm	1.1587	−4.0584	1.2664	−0.1618
15 μm	1.2282	−4.3029	1.6373	−0.2999

IV. RESULTS AND DISCUSSION

A. Demonstration of particle separation

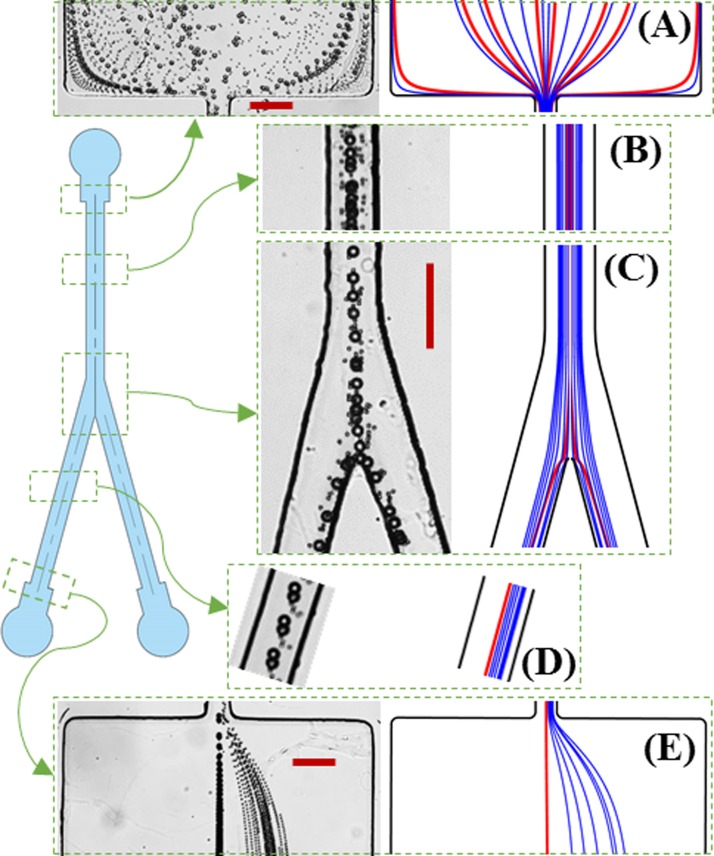
Fig. 3 demonstrates the continuous-flow electrokinetic separation of 5 μm- and 15 μm-diameter spherical particles in a bifurcating microchannel. The left and right halves of each panel show the superimposed particle images and theoretically predicted particle trajectories, respectively. The applied DC voltage at the channel inlet is 800 V while the two outlets are both grounded (see Fig. 1). The resulting average electric field is 520 V/cm in the main-branch and 260 V/cm in each side-branch. At the entrance of the main-branch (Fig. 3(a)), the two types of particles are uniformly mixed and dispersed. The expansion ahead of the main-branch, where six posts are embedded for filtering out any PDMS debris or particle cluster (see Fig. 1), appears to have a negligible influence on the particle behavior at the entrance of the main-branch via DEP.³⁶ Moreover, as the particle velocity is about U_p = 1.3 mm/s in the main-branch, the calculated particle Reynolds number is Re_p = 2ρU_pa/η = 0.02 for 15 μm particles, indicating a negligible contribution from the fluid and particle inertia in our experiment.⁶⁰ Both types of particles get deflected towards the center of the main-branch by the wall-induced electrical lift (Fig. 3(b)). However, the larger particles already travel in a single file along the centerline before reaching the bifurcation while the smaller ones still form a narrow band around the centerline (Fig. 3(c)).

FIG. 3.

Demonstration of a continuous-flow sheathless electrokinetic separation of 5 μm and 15 μm-diameter spherical particles in a bifurcating microchannel: superimposed images (left in each panel) and predicted trajectories (right in each panel, blue and red lines are for 5 μm and 15 μm particles, respectively) at the entrance (a) and middle (b) of the main-branch, the bifurcation (c), the middle (d), and exit (e) of one side-branch. The inlet reservoir is at 800 V DC and the two outlet reservoirs are both grounded. The scale bars represent 100 μm.

At the bifurcation, both types of particles enter into either side-branch from near the inner wall (Fig. 3(c)) and are then deflected towards its centerline at a size-dependent rate as it happens in the main-branch (Fig. 3(b)). Therefore, the larger particles migrate towards their equilibrium position along the centerline faster leaving the smaller ones behind (Fig. 3(d)). The result is two continuously displaced particle sub-streams at the exit of either side-branch, whose separation distance is further amplified in the subsequent expansion region due to the hydrodynamic spreading in a laminar flow (Fig. 3(e)).¹⁰ It is important to note that neither type of particles can come into contact with the channel walls at the bifurcation because of the repulsions from both the electrical lift force and the dielectrophoretic force. The experimentally observed particle size-dependent electrokinetic deflection, focusing, and separation process in the bifurcating microchannel is predicted with a good agreement in our model (see the right half in each panel of Fig. 3, blue and red lines are for 5 μm and 15 μm particles, respectively). Our model also predicts that the angle between the two side-branches has an insignificant impact on particle separation. This is because the angle does not affect the electrical lift force in each branch, and the particle DEP induced (and hence restricted) at the bifurcation has only a limited influence on the particle motion. Therefore, if needed, the angle between the side-branches can be decreased to reduce the footprint of the bifurcating microchannel.

The throughput of the demonstrated sheathless electrokinetic particle separation in Fig. 3 is about 12 μl/h, which is an order of magnitude higher than that in a T-shaped microchannel with a sheath-flow focusing.⁴¹ It can be enhanced by increasing the depth of the bifurcating microchannel or operating multiple microchannels in parallel that are arranged in, for example, the radial direction of a circle.⁶¹ The particle throughput can also be enhanced by increasing the concentration of particles in the suspension. This is, however, limited by the increasing particle-particle interactions which can lead to the formation of particle pearl chains and lower the separation efficiency and purity.^10,19,20 Moreover, there is a clear gap between the 5 μm and 15 μm particle streams in Fig. 3, so the efficiency (defined as the percentage of a type of particles collected at its preferred outlet) and purity (defined as the ratio of the targeted to the total collected particles at an outlet) of this separation are both nearly 100% (not exactly perfect due to the attachment of some 5 μm particles to 15 μm ones). We have also implemented the separation of 5 μm and 10 μm particles in the bifurcating microchannel (see an image in the supplementary material). The result implies that it is possible to separate a ternary mixture of 5 μm, 10 μm, and 15 μm particles. The particle size resolution can be further improved if the particles to be separated are all fully focused in the main-branch.

B. Effect of electric field magnitude

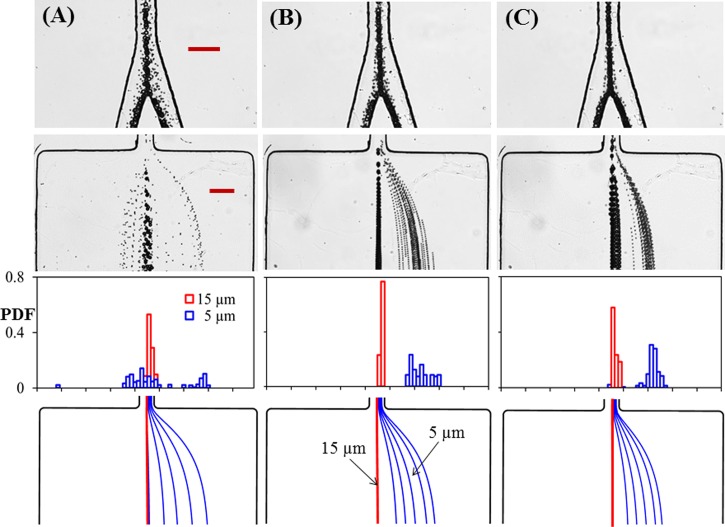
Fig. 4 presents the electric field effect on the the electrokinetic separation of 5 μm and 15 μm particles in the bifurcating microchannel. The DC voltage applied to the inlet reservoir is varied from 600 V to 800 V and 1000 V, correspnding to an average electric field of 390 V/cm, 520 V/cm, and 650 V/cm, respectively, in the main-branch. Fig. 4(a) shows that at 600 V the wall-induced electrical lift is insufficient to focus 5 μm particles within one-half of the channel width in the main-branch, which leads to their spreading across the centerline of either side-branch (see the superimposed image in the top row of Fig. 4(a)). Consequently, the 5 μm particle and 15 μm particle streams still overlap with each other at the exit of the side-branch as viewed from both the superimpose image (second row) and the particle PDF plot (third row) in Fig. 4(a). This unsuccessful particle separation is qualitatively predicted by our model in Fig. 4(a) (bottom row), where the larger deviation for the smaller particles may be due to their size and electrokinetic mobility variations that further deteriorate focusing on the experiment but are not considered in the simulation.

FIG. 4.

Effect of electric field magnitude on the electrokinetic separation of 5 μm and 15 μm particles in the bifurcating microchannel: the DC voltage applied to the inlet reservoir is 600 V (a), 800 V (b), and 1000 V (c), respectively, for the three columns from left to right. The correspnding electric fields in the main-branch are approximately 390 V/cm, 520 V/cm, and 650 V/cm. The four panels from top to bottom in each column show the supperimposed images at the bifurcation and at the exit of one side-branch, the experimentally determined PDF of the separated particles, and the predicted particle trajectories (blue and red lines are for 5 μm and 15 μm particles, respectively) at the exit of the side-branch. The scale bars represent 100 μm.

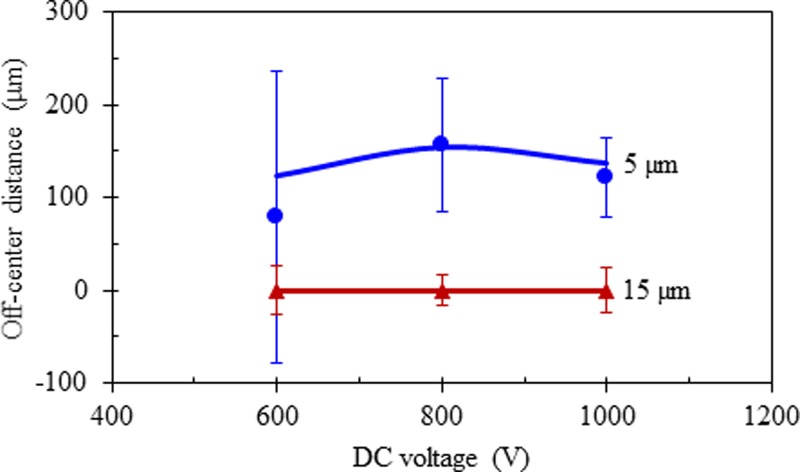
The insufficient particle focusing issue in Fig. 4(a) can be resolved simply by increasing the DC electric field (or alternatively increasing the length of the main-branch at a fixed electric field), which is demonstrated in Fig. 4(b) for 800 V and in Fig. 4(c) for 1000 V. However, the PDF plots in Fig. 4 (third row) for these two voltages indicate that particle separation is not necessarily better at the higher electric field even though the 5 μm particle stream therein does become narrower in both the main-branch and the side-branch (see the imposed images in the top and second rows of Fig. 4). This is because the stream of 5 μm particles also moves closer to that of 15 μm particles (whose position remains unvaried along the channel centerline for all three tested voltages) in the side-branch at an increased electric field, which can be viewed from the predicted particle trajectories in Fig. 4 (bottom row). A quantitative comparison between the experimentally and theoretically obtained off-center positions of 5 μm and 15 μm particle streams at the exit of the bifurcating microchannel is shown in Fig. 5. The experimental data (symbols with error bars) were measured directly from the images in Fig. 4, where the symbols correspond to the center positions of the separated particle streams and the error bars cover the span of the particle stream widths. The observed variation of particle separation distance, which first rises and then drops with the increasing electric field, is reasonably predicted by the theoretical model.

FIG. 5.

Quantitative comparison of the experimentally measured (symbols with error bars, obtained from the images in Fig. 4) and theoretically predicted (lines) off-center positions of the separated 5 μm and 15 μm particle streams at the exit of one side-branch of the bifurcating microchannel.

C. Guideline for particle separation

The above analysis sets up the applicable range of electric field for electrokinetic particle separation in a bifurcating microchannel. For consistency, we use the electric field in the main-branch in the following description. The lower limit in electric field should be no less than the value at which the smaller particles (more precisely, those with a smaller velocity ratio, i.e., U_w/U_EK in Eq. (3)) are focused to a stream of one half of the channel width along the centerline of the main-branch. This electric field in the main-branch, E_lower, may be estimated using the following equation (see the derivation in the supplementary material):

$$E_{\mathit{l}\mathit{o}\mathit{w}\mathit{e}\mathit{r}}=\frac{{\zeta }_p-{\zeta }_w}{512L_{m-b}}{\left(\frac{w}{a}\right)}^5,$$ (8)

where L_m–b is the length of the main-branch and w is its width. Note that this electric field value is dependent on both the particle size (i.e., radius a) and the particle charge (i.e., zeta potential ζ_p), and hence is not necessarily calculated from the properties of the smaller particles.

The upper limit in electric field should be no more than the value at which the smaller particles (or those with a smaller velocity ratio, U_w/U_EK) can be focused (or more accurately speaking, deflected) to the centerline of the side-branch. The corresponding electric field in the main-branch, E_upper, may be estimated using the equation below (see the derivation in the supplementary material)

$$E_{\mathit{u}\mathit{p}\mathit{p}\mathit{e}\mathit{r}}=\frac{{\zeta }_p-{\zeta }_w}{8L_{s-b}}{\left(\frac{w}{a}\right)}^5,$$ (9)

where L_s–b is the length of the side-branch. Therefore, the operating electric field for the proposed electrokinetic particle separation in a bifurcating microchannel can vary in a fairly large range (specifically, from 1 to 64 times of the value estimated from Eq. (8) for L_m–b = L_s–b in our current channel design), which significantly eases the device control. Using the parameters in the model, we find that the predicted lower limit in electric field from Eq. (8) is around 500 V/cm, which is comparable to the experimental value in Fig. 4. However, we did not test the accuracy of the predicted higher limit in electric field from Eq. (9) because Joule heating takes effects at high electric fields.^58,59 It is important to note that the specific values of the two electric fields in Eqs. (8) and (9) are both dependent on the channel length. The longer the main-/side-branch, the smaller electric field is required to deflect/focus the particles via the wall-induced electrical lift.

V. CONCLUSIONS

We have developed in this work a new type of electrokinetic particle separation technique in a bifurcating microchannel. This technique is capable of separating particles based on the difference in intrinsic properties, e.g., size, charge (see Eq. (3)), and potentially shape (due to the dependence of the electrical lift on particle shape, see the analysis in the supplementary material), in a continuous sheath-free manner. It exploits the wall-induced non-inertial electrical lift force to achieve the automatic three-dimensional particle focusing in the main-branch and the continuous transverse particle separation in each side-branch. We have demonstrated this technique through a label-free separation of 5 μm and 15 μm spherical polystyrene particles in an overall 2 cm-long bifurcating microchannel. The effect of the DC voltage imposed to the inlet reservoir is studied, from which the applicable range of electric field for this separation technique is discussed. We have also developed a theoretical model to understand and simulate the particle behavior in the bifurcating microchannel. The predicted particle trajectories are found to agree reasonably well with the experimental observations. Due to the intrinsic low speed in electrokinetic flows, our proposed particle separation offers a limited throughput, which may be enhanced by operating multiple linear bifurcating channels in parallel and/or increasing the particle concentration. However, the resulting Joule heating effects⁵⁹ and/or particle-particle interactions⁵⁰ may affect the separation efficiency. Moreover, the involvement of high DC electric field in the separation may cause damages to biological entities,²⁴ which can be mitigated by the use of DC-biased AC electric fields.^33–36,62 In addition, this separation can potentially be run in a cascade tree-type microchannel for a heterogeneous particle mixture (i.e., of three or more particle types) at an improved resolution.

SUPPLEMENTARY MATERIAL

See the supplementary material for details on the determination of Eq. (7) in the theoretical model, the derivation of Eqs. (8) and (9) for the operating conditions in particle separation, the image for the electrokinetic separation of 5 μm and 10 μm particles in a bifurcating microchannel, and the analysis of the effect of particle shape on electrical lift force.