Abstract
The ability to drive microcentrifugation for efficient micromixing and particle concentration and separation on a microfluidic platform is critical for a wide range of lab-on-a-chip applications. In this work, we investigate the use of amplitude modulation to enhance the efficiency of the microcentrifugal recirculation flows in surface acoustic wave microfluidic systems, thus concomitantly reducing the power consumption in these devices for a given performance requirement—a crucial step in the development of miniaturized, integrated circuits for true portable functionality. In particular, we show that it is possible to obtain an increase of up to 60% in the acoustic streaming velocity in a microdroplet with kHz order modulation frequencies due to the intensification in Eckart streaming; the streaming velocity is increasing as the modulation index is increased. Additionally, we show that it is possible to exploit this streaming enhancement to effect improvements in the speed of particle concentration by up to 70% and the efficiency of micromixing by 50%, together with a modest decrease in the droplet temperature.
I. INTRODUCTION
The ability to drive intense micromixing and rapid particle concentration at the microscale is notoriously difficult due to the laminarity of flow that is typical of conventional microfluidic devices, as reflected by the Reynolds numbers associated with flows in these devices, which are commonly order 1 and below (Stone et al., 2004). Many attempts have been made to address poor mixing in these devices, which include the fabrication of structures and channel geometries to passively disrupt the flow laminarity, or the introduction of external fields, e.g., electric, magnetic, and acoustic fields, among others, to actively drive chaotic advection (Nguyen and Wu, 2005). Passive mixing strategies, while simple, however, often require fabrication of complex geometries, whereas the active mixers often require large and cumbersome benchtop ancillary equipment such as signal generators, amplifiers, and capillary pumps, which prohibit miniaturization and integration of the microfluidic device when true portability is required in some applications (Yeo et al., 2011). Concomitantly, it is even more difficult to drive centrifugal recirculation in microfluidic devices to exploit hydrodynamic concentration of particles for sample preconcentration, which is extremely useful, for example, for purification (e.g., separation of red blood cells from plasma) or as a means to increase detection speed, sensitivity, and selectivity in biosensors (Yeo et al., 2011). Most attempts to achieve particle concentration in microfluidic devices have been to employ trapping forces, generated optically (Dholakia et al., 2008), electrically (Cheng et al., 2007; Cho et al., 2007; Hwang and Park, 2009; Lewpiriyawong et al., 2012; and Harrison et al., 2015), acoustically (Laurell et al., 2007 and Lin et al., 2012), or magnetically (Pamme et al., 2006 and Zeng et al., 2013), to drive local aggregation. A disadvantage of these schemes in addition to similar constraints in the necessity for large ancillary equipment for the provision of external fields, however, is that such trapping is only useful under stationary or weakly flowing conditions as the hydrodynamic drag forces arising from the flow in drops and channels are usually sufficient to cause dispersion of the aggregated particle clusters.
Surface acoustic waves (SAWs) offer an attractive alternative to these technologies to induce micromixing and particle concentration, together with the possibility for driving a wide suite of microfluidic operations (Yeo and Friend, 2014; Ding et al., 2013; and Destgeer and Sung, 2015) such as droplet and microchannel transport (Schmid et al., 2012; Baudoin et al., 2012; Dentry et al., 2014; Collingnon et al., 2015; and Jung et al., 2016), particle trapping (Shi et al., 2008, 2009; Chen et al., 2014; Destgeer et al., 2013, 2014, and 2015), cooling and heating (Kondoh et al., 2009; Shilton et al., 2015; and Ang et al., 2015), and jetting and atomization (Qi et al., 2008; Tan et al., 2009; and Winkler et al., 2015). The underlying mechanism that enables these operations is the acoustic streaming (Yeo and Friend, 2014) that arises from the fluid–structural interactions associated with the undulating boundary as the SAW traverses the surface of the piezoelectric substrate beneath the fluid (Manor et al., 2012 and 2015). Not only is SAW acoustic streaming an efficient means for driving chaotic micromixing (Frommelt et al., 2008b; Shilton et al., 2011; and Jo and Guldiken, 2013) but it also has the advantage of battery-powered operation via a portable driver circuit, therefore permitting miniaturization and integration of the entire actuation platform together with the chip-based operation (Martins et al., 2014). More recently, Shilton et al. (2014) demonstrated downward scalability to nanolitre volumes while still maintaining the ability to rapidly mix the fluids in a droplet, made possible by increasing the SAW frequency to GHz order (Dentry et al., 2014). On the other hand, the same SAW platform has been shown to be a powerful tool for driving chip-scale microcentrifugation, in which the azimuthal flow recirculation (in a droplet) that arises is sufficiently intense to rapidly concentrate particles suspended in the flow (Shilton et al., 2008; Glass et al., 2012; Li et al., 2007; and Destgeer et al., 2016), which can then be exploited for sample preconcentration to enhance biomolecular detection sensitivity and selectivity (Bourquin et al., 2011).
Parenthetically, we note a similar technique that relies on azimuthal recirculation to induce micromixing and particle concentration has been earlier demonstrated through the use of interfacial shear driven by the ionic wind generated at the tip of singular electrodes raised to sufficiently large voltages that result in atmospheric discharge (Yeo et al., 2006a,b; Arifin et al., 2007; and Hou et al., 2007). Besides the requirement for extremely high voltages and non-planar electrodes, such schemes are also considerably more inefficient given the need for interfacial shear to drive liquid recirculation in the bulk, unlike in the present case wherein the acoustic energy from the SAW is directly transmitted as bulk sound waves in the liquid, which, in turn, drives the streaming. This is reflected in the concentration time scales, which are on the order 1–10 s compared to 102–103 s with discharge-driven flows. Moreover, it is also possible to obtain much longer range convection with the SAW given that this is governed by the attenuation length of the sound wave in the fluid, which can hence be tuned with the applied SAW frequency; for particle concentration, the requirement is simply that the attenuation length is below that of the drop dimension (Destgeer et al., 2016).
In this study, we investigate the possibility of enhancing the acoustic streaming velocity through the use of an amplitude modulation scheme and subsequently demonstrate that this can be exploited to significantly improve the efficiency of concentrating microparticles and also micromixing atop the SAW device. A similar strategy was previously employed by Rajapaksa et al. (2014) to enhance the rate of atomization for nebulizer applications, in which it was shown that a twofold increase in the rate with the same input power is attainable. Unlike SAW atomization, however, which requires high intensity acoustic fields (commensurate with acoustic Reynolds numbers (Rozenberg, 1971) , where U1 the acoustic particle velocity, λf the acoustic wavelength in the liquid and , in which μ and are the shear and bulk viscosities of the liquid, respectively) to destabilize the air–liquid interface, our focus in this work is confined to weaker acoustic fields () wherein the deformation of capillary waves at the air–interface is negligible and hence the acoustic energy supplied to the fluid by the SAW is largely converted to driving the acoustic streaming recirculation within the drop. In this respect, the amplitude modulation is expected to assume a completely distinct role compared to that for SAW atomization where the role of the kHz order modulation was predominantly applied to excite bulk vibration modes of the drop associated with capillary–inertia resonance (Blamey et al., 2013) in order to destabilize its interface.
II. EXPERIMENT
The SAW device used in the study comprised a 128° rotated Y-cut X-propagating, single-crystal lithium niobate (LiNbO3) piezoelectric substrate fabricated with a focusing elliptical single-phase unidirectional transducer (FE-SPUDT) (Shilton et al., 2008) with 30 finger pairs (see Fig. 1) using standard UV photolithography. In particular, the FE-SPUDT was constructed from 750 nm thick aluminium atop a 4 nm thick chromium layer, both sputter deposited on the LiNbO3 substrate. To generate the SAWs, a sinusoidal electric signal generated from a primary wavefunction generator (WF1966, NF Corporation, Japan) was amplified using a high frequency amplifier (25A250A, Amplifier Research, USA), and subsequently applied to the FE-SPUDT. The frequency of the electrical signal was set at 30.5 MHz in order to match the resonant frequency of the FE-SPUDT, determined by the spacing of its fingers. For amplitude modulation, a secondary wavefunction generator (DG 1022, Rigol, China) was connected to the primary function generator; modulation frequencies of fm = 1, 5, 10, 15, and 20 kHz were employed.
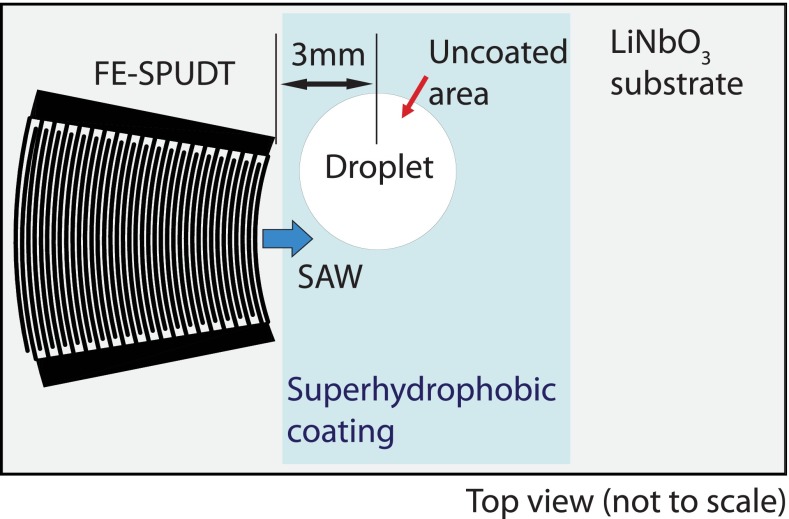
FIG. 1.
Schematic illustration of the SAW device on which a focusing elliptical single-phase unidirectional transducer (FE-SPUDT) is patterned. The approximate location where the droplet is placed on the device to break the symmetry of the acoustic radiation into the liquid and hence to generate azimuthal recirculation within it is shown.
In order to quantify the total input electric power of the modulated signal to the SAW device, the modulation index (Frenzel, 2007) was first calculated, in which is the modulating signal voltage, the carrier signal voltage, and and the maximum and minimum RMS voltages, respectively. The voltages were measured using a voltage probe (TPP 0201, Tektronix, USA) connected to an oscilloscope (TDS 2012C, Tektronix, USA). The total input electric power of the modulated signal can then be calculated (Frenzel, 2007) from , in which is the RMS power of the carrier signal and the carrier signal current, wherein and are the maximum and minimum RMS currents, respectively, measured using an AC current probe (P6022, Tektronix, USA). We note that the SAW device was not designed to match the impedance of the source, i.e., a fraction of the input power is reflected back to the source due to the mismatch in the source and device impedances.
In each experiment, a controlled volume of deionized (DI) water was carefully pipetted onto the substrate. In order to generate the azimuthal recirculation necessary to drive particle concentration and micromixing in the droplet, the droplet is placed asymmetrically such that only a part of it lies in the SAW propagation path following the symmetry breaking procedure suggested in preceding studies (Shilton et al., 2008 and Li et al., 2007). In this case, the droplet was placed such that the center of the droplet is approximately 3 mm from the leading edge of the transducer, as illustrated in Fig. 1. In order to maintain its shape, the droplet is confined in a circular area by patterning a thin layer of superhydrophobic coating (NeverWet, Rustoleum, USA) on the substrate with a 5 mm diameter circular exclusion (bare surface) where the droplet is to be placed in order to prevent its spreading under the SAW excitation. The superhydrophobic modification was carried out by directly spraying two coating layers—a base coat and a top coat—on the SAW device, allowing 30 min of drying time at room temperature in between the application of each layer. Prior to spraying, the 5 mm diameter circular exclusion area was masked using tape. The experiments in Sections II A, II B and II C were then conducted to first measure the acoustic streaming velocity within the droplet and hence to subsequently quantify the effectiveness of the amplitude modulation in enhancing acoustic streaming and thus particle concentration and micromixing.
A. Enhancement in acoustic streaming
To investigate the relationship between the amplitude modulation frequency fm and the acoustic streaming velocity diameter fluorescently-tagged polystyrene spherical microparticles (Polysciences, USA) were suspended in deionized water droplets with volume at a concentration of approximately 5%. We note here that the streaming velocities are insensitive to the particle size in the 1–10 μm range where the tracer particles are sufficiently large that Brownian diffusion effects can be neglected but sufficiently small such that their presence does not disrupt or influence the flow field. These tracer particles were then illuminated using a 480 nm fluorescence light source (AM4113t-GFBW, Dino-Lite, Taiwan) and their motion tracked using a high speed camera (M310, Phantom, USA) operating at 300 frames/s connected to an optical microscope (BX41M, Olympus, Japan) at 20× magnification. The particles were tracked using the supplied camera software (PCC 2.2, Phantom, USA) from which their average velocities can be determined, which is a good approximation of the acoustic streaming velocity . These velocity measurements were carried out for three different input powers We: 22 mW, 92 mW, and 156 mW. For each input power, different amplitude modulation frequencies fm—1, 5, 10, 15, and 20 kHz—were examined. Additionally, the temperatures of the substrate and the droplet were measured using a thermal imager (TIM160, Micro-epsilon, Germany) at a record rate of 100 Hz.
B. Particle concentration efficiency
To demonstrate the efficiency of using amplitude modulation to improve the particle concentration process, we employ the same high speed imaging system to visualize the particle dynamics. More specifically, we determine the time required to concentrate the particles suspended in the droplet through a pixel intensity analysis (Mathematica 9.0, Wolfram, USA) of successive grayscale image frames acquired from the high speed video. The normalized standard deviation in the pixel intensity can be calculated by dividing the standard deviation of the pixel intensities for a given frame with respect to that for the first frame. The concentration time tc can then be defined as the time required for the normalized standard deviation to reach a constant value (Shilton et al., 2008 and Li et al., 2007). The effects of three different sizes of fluorescent polystyrene microparticles, 6 μm, 10 μm, and 25 μm, used without further surface modification, in 5 μl deionized water droplets with the concentration held approximately at 5% were examined. For each particle size, the experiments were repeated using the different input powers and amplitude modulation frequencies specified above.
C. Micromixing efficiency
Finally, we demonstrate the use of amplitude modulation to improve the mixing process in the droplet. To observe the mixing process, a small amount of 1.5 μl dark blue food dye was pipetted onto a 6 μl glycerin droplet; the total volume of the droplet after addition of the dye is 7.5 μl. To minimize initial mixing due to convective currents that could arise during pipetting, high viscosity glycerin was used in this experiment instead of deionized (DI) water and the introduction of the dye to the droplet was carried out slowly and with care (Shilton et al., 2008). The mixing process was then recorded using the same high speed camera system but with a high intensity bright-field illuminator (OSL, Thorlabs, USA). The normalized standard deviation in the pixel intensity was used to quantify the mixing performance by calculating a mixing efficiency; a value of 0 represents perfect mixing, whereas a value of 1 represents the no mixing case. In addition, an effective diffusivity can be approximated from a linear regression of the plot of the normalized standard deviation in the pixel intensity against time (Shilton et al., 2008); the gradient of the slopes in the plots of the normalized standard deviation in the pixel intensity as a function of time is proportional to −D/L2, in which D is the diffusivity and L the characteristic length scale of the droplet. The experiments were conducted for several different modulation frequencies (1, 5, and 15 kHz) and input powers (107, 165, and 264 mW).
III. NUMERICAL ANALYSIS
To gain qualitative insight on how the amplitude modulation leads to an intensification of the flow, we turn to a simplified two-dimensional numerical model for acoustic streaming, which consists of boundary layer streaming () and Eckart streaming (), the latter arising due to dissipation of the sound energy as the SAW leaks into the droplet at the Rayleigh angle (Friend and Yeo, 2011 and Yeo and Friend, 2014); is the characteristic length scale of the streaming. The governing equations are the continuity equation (Morse and Ingard, 1986 and Nyborg, 1988)
| (1) |
the Navier-Stokes equation
| (2) |
and a thermodynamic relationship describing the adiabatic process (Beyer, 1988 and Rozenberg, 1971)
| (3) |
where p is the pressure, u = (u, w) the fluid velocity, t the time, and in which c is the sound speed. The subscript “0” denotes the fluid properties at equilibrium and c0 is the isentropic sound speed for small-signal amplitudes. Under the assumption of infinitesimally small amplitude waves, the method of successive approximations can be employed to linearize the equations above wherein a perturbation expansion in the small parameter ϵ = U/c0 ≪ 1, where U is the characteristic acoustic particle velocity, is imposed on the pressure and density fields (Morse and Ingard, 1986 and Nyborg, 1988)
| (4) |
| (5) |
| (6) |
By substituting Eqs. (4)–(6) into Eqs. (1)–(3), the first-order (acoustic field) approximations to these equations can then be written as (Morse and Ingard, 1986 and Nyborg, 1988)
| (7) |
| (8) |
and
| (9) |
Given the assumption of small amplitude deformations, we note that these linear equations are strictly applicable only when the acoustic field is weak, i.e., .
At the next order, the fluid motion consists of a superposition of the steady-state and time-oscillating harmonic flows. Time averaging all terms, the second-order (acoustic streaming) approximation to Eqs. (4)–(6) become
| (10) |
| (11) |
and
| (12) |
wherein refers to time averaging of the terms within and the subscript “dc” refers to the steady-state terms. Combining Eqs. (10) and (11) and separating the first-order quantities from the remaining terms, we obtain an expression for the steady-state acoustic streaming force density (Morse and Ingard, 1986 and Nyborg, 1988)
| (13) |
and
| (14) |
Equations (7)–(9) can then be solved to model the acoustic wave propagation in the fluid, whereas Eqs. (12)–(14) can be solved to model the acoustic streaming (Tan et al., 2010). A finite difference time domain numerical scheme (Schröder and Scott, 2000) was used to obtain solutions to these equations on a two-dimensional rectilinear (x−y) computational domain (Fig. 2) of dimension 4 mm × 2 mm; the longer axis constituting the y-direction. Given a grid size Δx = Δy = 2 μm, approximately 24 computational nodes are assigned to a wavelength λf. On the surface of the acoustic radiator (0 ≤ x ≤ 4 mm and y = 0), a sinusoidal boundary condition for the first-order instantaneous acoustic velocity is imposed to simulate the SAW propagation on the LiNbO3 substrate (Frenzel, 2007)
| (15) |
| (16) |
as shown in Figure 3(a). , and being the velocity of the SAW on the LiNbO3 substrate. represents the peak amplitude of the SAW and um = wm the peak amplitude of the modulation wave; the modulation index is thus approximated from . To allow for the attenuation of the SAW along the substrate surface beneath the droplet due to leakage of its energy into the liquid, we have imposed a characteristic attenuation length (Shilton et al., 2014 and Frommelt et al., 2008a), which can be approximated as . The other three boundaries are approximated by perfectly matched layer conditions (Tan et al., 2010, 2009; and Schröder and Scott, 2000). We note that at the low excitation powers used to drive micromixing and particle concentration, the deformation of the droplet interface is typically negligible and hence the motion of the air–liquid interface is not considered in the analysis. To ensure computational stability, the Courant criterion was adopted (Anderson, 1995).
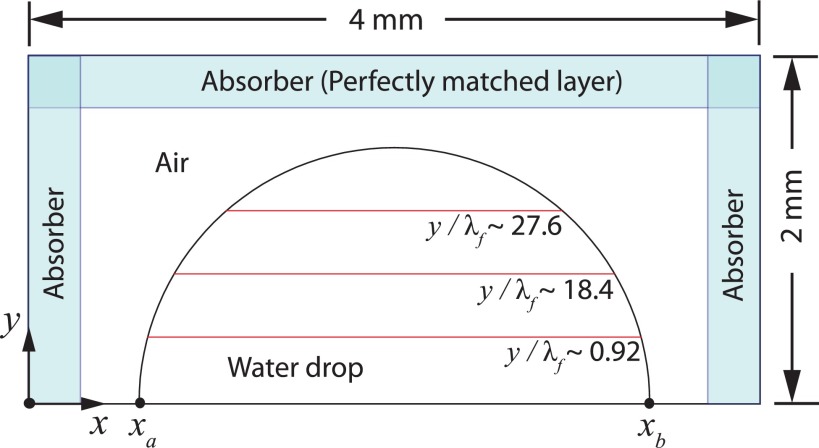
FIG. 2.
A two-dimensional schematic of the computational domain used to model the propagation of the acoustic waves. The drop is assumed to be a hemisphere of diameter Dd = 3.6 mm. The boundary condition that simulates the SAW propagation is applied from xa to xb. The average acoustic streaming velocity is computed at three different heights: , and .
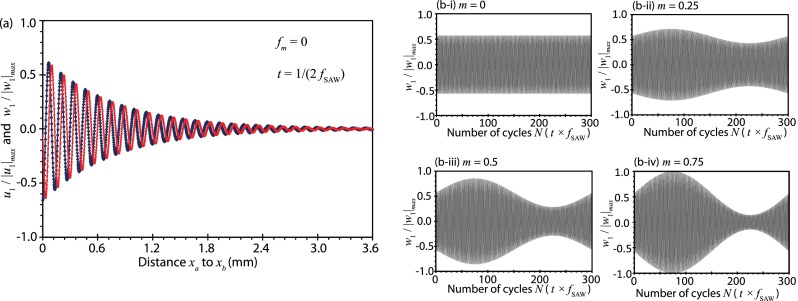
FIG. 3.
(a) Instantaneous velocity boundary condition (Eqs. (15) and (16)) in the x-direction u1 (◇) and the y-direction w1 (×) imposed on the substrate surface (y = 0) from xa to xb (see Fig. 2) in the absence of amplitude modulation (fm = 0). The attenuation of the SAW along the substrate surface is approximated as , where is the characteristic SAW attenuation length. (b) Variation in the acoustic velocity in the y-direction w1 at x = xa as a function of the number of cycles for different modulation indices: (i) m = 0 (no modulation), (ii) m = 0.25, (iii) m = 0.5, and (iv) m = 0.75; the frequency of the SAW is fSAW = 30 MHz and the modulation frequency is fm = 100 kHz.
Two distinct hydrodynamic forces—the streaming force within the viscous boundary layer of thickness (Morse and Ingard, 1986) and that outside the boundary layer—are dominant in the flow within the droplet (Manor et al., 2015 and Rezk et al., 2014). Given that the characteristic length scale of the droplet , it is possible to assume that the streaming force within the viscous boundary layer is insignificant as compared to that outside the boundary layer, and, as such, adopt larger grid spacings than the boundary layer thickness, i.e., , to reduce computational cost. We note that the acoustic streaming outside the boundary layer is associated with thermoviscous attenuation, which, for the case of a plane sound wave propagating in an unbounded medium and for , where is the relaxation time (Kinsler et al., 2000), is characterised by an attenuation coefficient (Hamilton et al., 1998) defined by , where , in which μ and are the shear and bulk viscosities of the liquid.
IV. RESULTS AND DISCUSSION
A. Enhancement in acoustic streaming
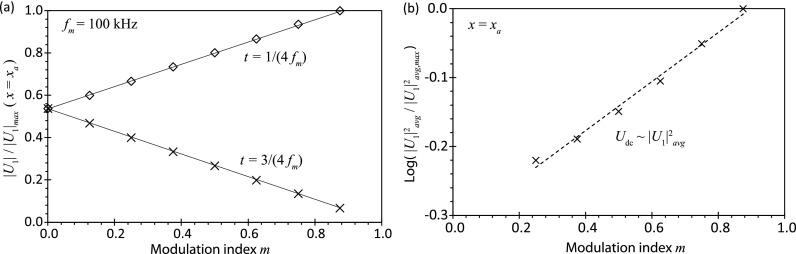
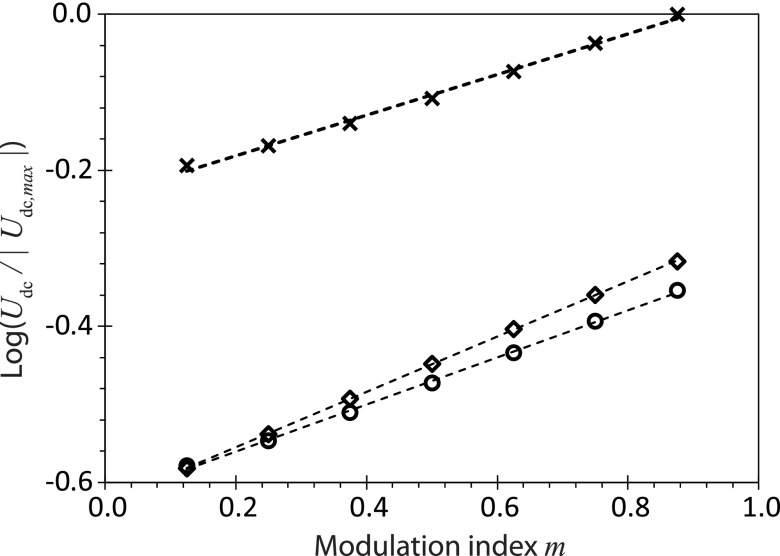
It can be seen from Fig. 3(b-ii–iv), which examines the acoustic velocity along the y-direction at a fixed arbitrary location x = xa, that the maximum acoustic velocity amplitude increases, whereas the minimum acoustic velocity amplitude decreases in the presence of amplitude modulation (m > 0), and that this change in the velocity amplitude is sensitive to the modulation index m: increasing m leads to larger maximum acoustic velocity amplitudes and smaller minimum acoustic velocity amplitudes. At the same location (x = xa), it is then possible to evaluate the change in the amplitudes of the maximum and minimum acoustic velocities for different modulation indices, from which we observe a linear dependence of their magnitudes on the modulation index (Fig. 4(a)); note that for fm = 100 kHz, the maximum acoustic velocity amplitude occurs at (or n = 75), whereas the minimum acoustic velocity amplitude occurs at (or n = 225), being the number of cycles. Given that the steady-state acoustic streaming velocity scales as the square of the instantaneous acoustic velocity, i.e., , which we estimate as the average of the squared acoustic velocity amplitude at the maximum and minimum points, i.e., , it can be seen from Fig. 4(b) that the acoustic streaming velocity increases with increasing modulation index as .
FIG. 4.
(a) Change in the magnitude of the acoustic velocity at x = xa for different modulation indices m over two different time cycles: t = 1/(4 fm) representing the maximum amplitude (◇) and t = 3/(4 fm) representing the minimum amplitude (×). Note that m = 0 represents the case where amplitude modulation is absent. The trendlines were added to aid visualization. (b) Average squared values of the acoustic velocity amplitude at x = xa at the two different time cycles for different modulation indices. The dotted line represents a least square fit (R2 = 0.991) and suggests that .
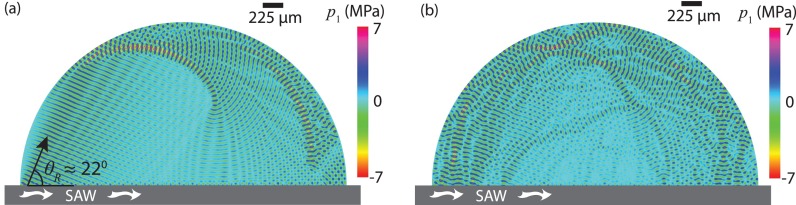
Figure 5 shows the instantaneous acoustic pressure p1 within a Dd = 3.7 mm droplet, which is slightly smaller than that used in the experiment Dd ≈ 5 mm due to limitations in the domain size we are able to simulate, at (n = 200) and (n = 300), arising as a consequence of leakage of the SAW energy from the substrate into the droplet, when no amplitude modulation is present (m = 0). It can be seen that strong standing waves inside the droplet arise after 300 cycles (Fig. 5(b)), consistent with the results shown by Brunet et al. (2010). Despite the simplicity of the approximate model, the computed magnitude of the steady-state streaming velocity Udc, on the order 10−3 m/s, is consistent with that in the experiments in Fig. 7. More importantly, the intensification of the acoustic streaming in the droplet with amplitude modulation, i.e., increasing m, can be qualitatively captured by averaging the magnitude of the acoustic streaming velocity at three different heights y/λf = 9.2, 18.4, and 27.6 as shown in Fig. 6 for a modulation frequency fm = 100 kHz, which we shall observe are consistent with that observed in the experiments in Fig. 7(a) (fm = 100 kHz and fSAW = 30.5 MHz); the relationship obtained from the experimental results, i.e., , is consistent with the numerical results (Fig. 6). Additionally, we also observe in Fig. 6 that the enhancement in the streaming velocity becomes increasingly prominent the further the distance from the substrate surface, i.e., larger y/λf, suggesting that the increase in streaming velocity with amplitude modulation is more significant for larger droplets.
FIG. 5.
Acoustic pressure field p1 in a droplet of diameter Dd = 3.6 mm (≫λf ≈ 49 μm) at time (a) and (b) arising from sound wave transmission into the liquid as a consequence of the SAW propagation along the substrate beneath it; fSAW = 30 MHz and m = 0 (no amplitude modulation). It can be seen in (a) that the sound wave leaks into the droplet at the Rayleigh angle (for water c0 ≈ 1480 m/s and for LiNbO3 substrate cSAW ≈ 3990 m/s) and that strong standing waves are formed in the droplet at .
FIG. 7.
(a) Experimental results depicting the relationship between the acoustic streaming velocity Udc and the modulation index m at three different modulation frequencies fm = 5 kHz (◇), fm = 50 kHz (△), and fm = 100 kHz (×) in a 5 μl droplet suspended with 6 μm particles. The power is fixed at We = 20 mW. The dotted lines represent least square fit—R2 = 0.999 (◇), R2 = 1.000 (△), and R2 = 0.999 (×)—and suggests that , consistent with that shown in Fig. 6. (b) Experimental results showing the relationship between the acoustic streaming velocity and the modulation frequency fm at two different powers We = 92 mW (×) and We = 156 mW (○) in a 5 μl droplet suspended with 6 μm particles. The case fm = 0 represents the condition in the absence of amplitude modulation. The piezoelectric substrate is excited by 30.5 kHz SAWs. Error bars indicate a ±2 standard deviation (95% confidence level) from the mean. Trendlines in (b) were added to aid visualization.
FIG. 6.
Results from the numerical simulation showing the relationship between the average acoustic streaming velocity and the modulation index m at three different heights in the droplet: y ≈ 9.2λf (◇), 18.4λf (○), and 27.6λf (×) (see Fig. 2). The modulation frequency is fixed at fm = 100 kHz and m = 0 represents the case where amplitude modulation is absent. The dotted lines represent least square fit—R2 = 1.000 (◇), R2 = 0.999 (○), and R2 = 0.996 (×)—and suggests that Udc ∼ 10 m.
Figure 7(b) shows that the acoustic streaming velocity increases by approximately 30% in experiments with low frequency amplitude modulation (fm = 1 kHz) compared to the case in which the signal was not modulated (fm = 0). Further monotonic increases in the acoustic streaming velocity can then be obtained by increasing the amplitude modulation frequency until about 10 kHz, after which any further changes in the streaming velocity become insignificant. The reduction in the streaming velocity when fm < 10 kHz can be attributed to the increase in the modulation wavelength λm/4 beyond the thermoviscous attenuation length α−1, i.e., λm/4 > α−1, which results in a decrease in the acoustic streaming velocity until it approaches the value for the streaming velocity in the absence of amplitude modulation (fm = 0). This can be seen more clearly when one notes that the modulation wavelength λm/4 at fm = 10 kHz, which is approximately 37 mm, becomes comparable to the attenuation length α−1 ≈ 40 mm for fSAW = 30.5 MHz. Overall, we find a maximum increase in Udc of up to 60% with amplitude modulation frequencies up to 20 kHz.
To ensure that the higher peak of modulated acoustic waves (see Fig. 3) does not drastically increase the temperature (as a consequence of viscous dissipation of the sound wave in the liquid), we measured the droplet temperature as well as the substrate surface temperature, both initially and after 5 min of excitation, under different conditions. As can be seen in the temperature measurements tabulated in Table I, the surface temperature of the substrate appears to be almost identical regardless of whether amplitude modulation is employed or not, suggesting that it poses no significant effect on heat generation within the substrate, which is to be expected since viscous dissipation only occurs in the liquid when sound waves, generated as a consequence of leakage of energy from the SAW into the liquid, propagate through it. In contrast, we note that amplitude modulation causes the droplet to be heated by 7° to 8 °C—1° to 2 °C lower than that in the absence of amplitude modulation where temperature increases of 9 °C for the same input power and droplet volume are measured. This reduction in droplet temperature with amplitude modulation can be attributed to the increase in convective heat transport as a result of the higher streaming velocities. In any case, such a reduction in temperature, while modest, is an advantage, especially where biological assays are employed in the SAW microfluidic platforms since heating can have adverse implications on the retention of the structural and functional viabilities of these biomolecules (Yeo and Friend, 2014).
TABLE I.
Measured substrate surface (in the absence of the droplet) and droplet temperatures, initially (T0) and after 5 min (T5), both in the absence (fm = 0 kHz) and in the presence (fm = 15 kHz) of amplitude modulation. The input power is held constant at 156 mW. Where a droplet is present, its volume is held constant at 5 μl.
| Substrate surface | Droplet | |||
|---|---|---|---|---|
| fm (kHz) | 0 | 15 | 0 | 15 |
| T0 (°C) | 22.9 ± 0.1 | 22.9 ± 0.2 | 21.0 ± 0.1 | 21.0 ± 0.2 |
| T5 (°C) | 29.4 ± 0.5 | 29.5 ± 0.3 | 30.1 ± 0.3 | 28.2 ± 0.1 |
B. Particle concentration efficiency
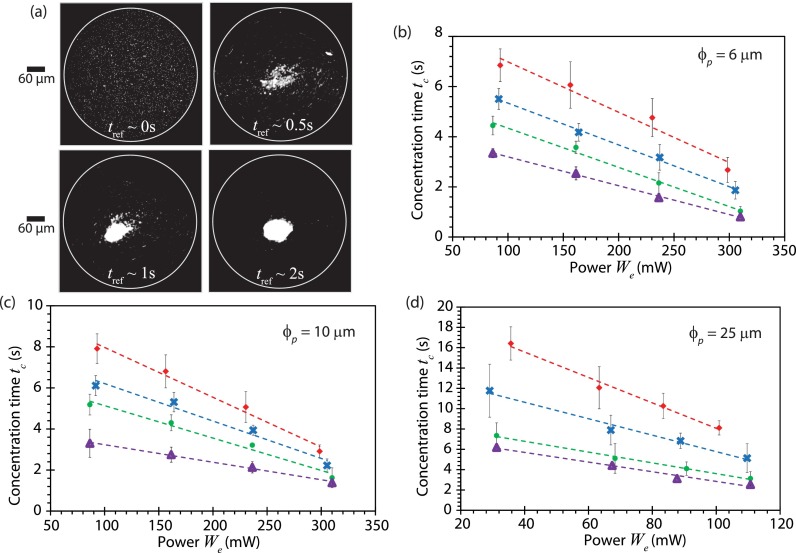
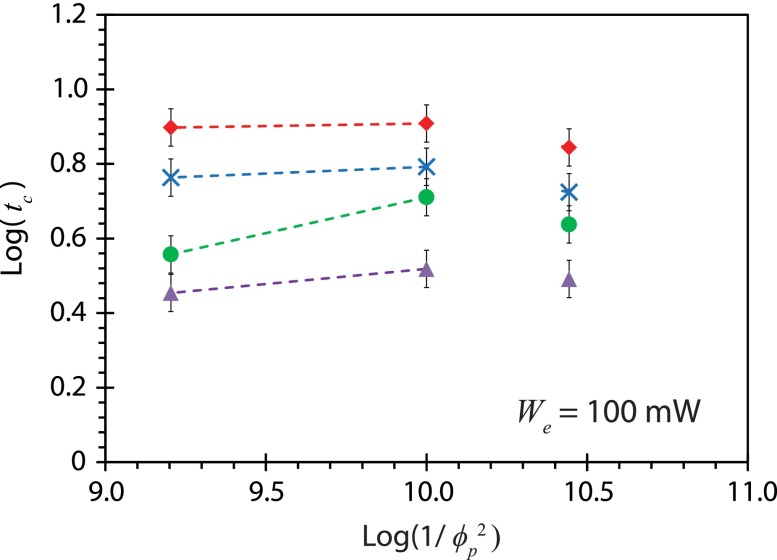
The particle concentration process in a 5 μl droplet driven by the SAW microcentrifugation flow is illustrated in Fig. 8(a) wherein the time tc it takes for microparticles of various dimensions to concentrate at the center of the droplet as a function of the input power We and at different modulation frequencies is reported in Figs. 8(b)–8(d). It can be seen in all cases that the concentration time decreases significantly as the amplitude modulation frequency is increased, as expected given the increase in the acoustic streaming velocity and, as a consequence, the drag and the shear rate. The former is an important consideration if the particle concentration occurs in the bulk due to secondary meridional convection (Raghavan et al., 2010), whereas the latter is important in the shear-induced migration dominant mechanism responsible for particle concentration on the free surface of the droplet (Shilton et al., 2008 and Li et al., 2007), which is the prevalent mechanism in the present case. This can be seen by the linear relationship between the concentration time and the particle size scaling (see Fig. 9), consistent with that for shear-induced migration into a vortex (Li et al., 2007) , in which is the shear rate, and ψ the local particle volume fraction in the vortex. The concentration time tc for particles does not fit the trend; as reported by Li et al. (2007), this is due to the aggregation of small particles (), resulting in larger effective particle sizes and hence a decrease in the concentration time.
FIG. 8.
(a) Successive time-sequence images showing the concentration of diameter particles suspended in a 5 μl water droplet excited at We ≈ 300 mW when subjected to amplitude modulation at a frequency of fm = 1 kHz. Measured concentration times for (b) , (c) , and (d) diameter particles suspended in a 5 μl water droplet excited at different powers We and under different amplitude modulation conditions: fm = 0 (without modulation) (◇), fm = 1 kHz (×), fm = 5 kHz (●), and fm = 15 kHz (△). Error bars indicate a ±2 standard deviation (95% confidence level) from the mean. Trendlines were added to aid visualization.
FIG. 9.
Relationship between the concentration time tc interpolated from the data in Fig. 8 as a function of the particle dimension scaling for a fixed input power (100 mW), under different amplitude modulations condition: fm = 0 (without modulation) (◇), fm = 1 kHz (×), fm = 5 kHz (●), and fm = 15 kHz (△). Error bars indicate a ±2 standard deviation (95% confidence level) from the mean.
With increasing amplitude modulation frequencies, it can be seen in all cases from Fig. 8 that the improvement in particle concentration speed, however, diminishes. This is because the increase in acoustic streaming velocities begins to taper beyond approximately 10 kHz in Fig. 7(b). For a fixed input power of 100 mW, we observe the reduction in the particle concentration time between the case of no amplitude modulation (fm = 0 kHz) and modulation at 15 kHz to be 50%, 58%, and 69% for , and 25 μm microparticles, respectively.
Interestingly, we note that particles with sufficiently large dimensions, which would not have concentrated without amplitude modulation since the shear-induced drag is insufficient to overcome the acoustic radiation force which expels the particles to the droplet periphery (Rogers et al., 2010), are able to concentrate when amplitude modulation is imposed. A simple explanation is that the drag force for a given particle size increases linearly with the acoustic streaming velocity, which is enhanced by a factor of two or three under amplitude modulation of the signal, as observed in Fig. 7(b). On the other hand, the increase in the acoustic radiation pressure which opposes the drag force is increased marginally when the kHz order modulation is imposed over the MHz order SAW due to the fourth power scaling of the radiation force with frequency (King, 1934). As such, the crossover particle size (Rogers et al., 2010) above which particles no longer concentrate in the centre of the droplet significantly shifts to much larger particle sizes when amplitude modulation is imposed, thus facilitating the concentration of particles with much larger dimensions. It then follows that amplitude modulation therefore forms a useful strategy to circumvent the particle size limitation when concentration is desired, without necessitating a change in the SAW frequency. Dynamic concentration and expulsion of the particles can also be obtained by switching on and off the amplitude modulation, thus constituting a very simple but yet powerful tool for selective particle manipulation.
C. Micromixing efficiency
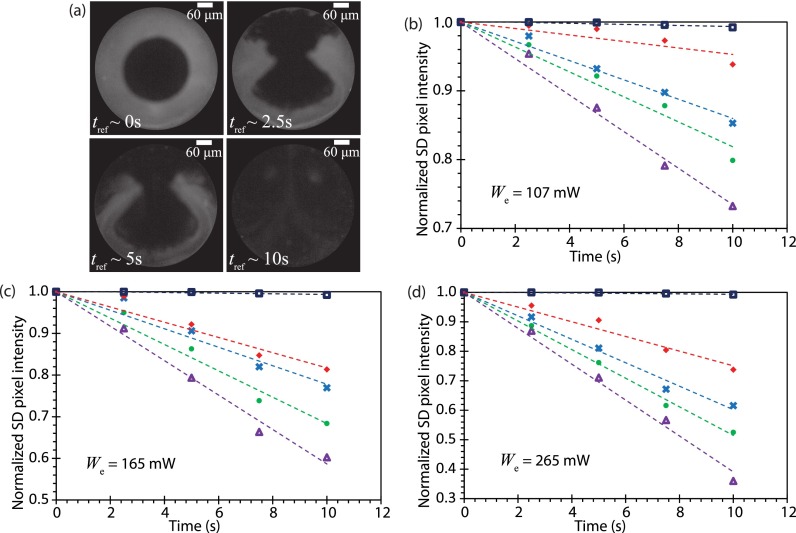
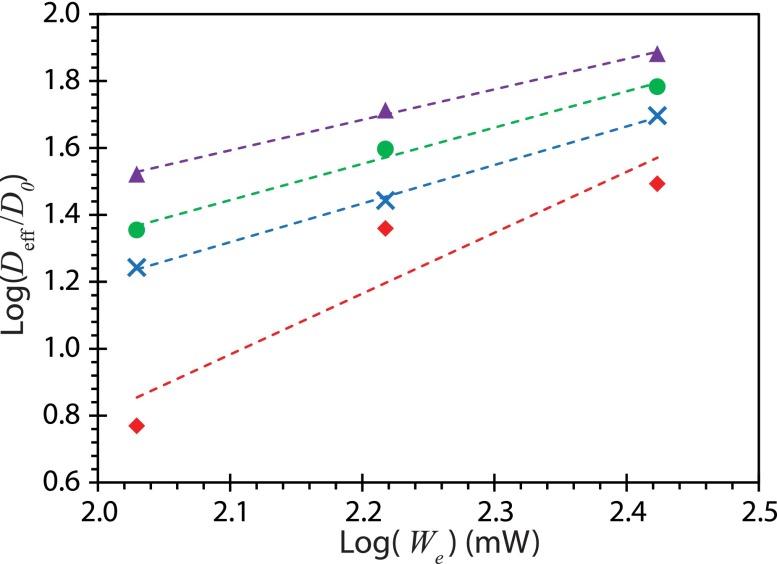
Figure 10(a) shows sequential images illustrating the mixing process under SAW excitation while Figs. 10(b)–10(d) reports the normalized standard deviation in the pixel intensity from which the efficiency of mixing of a 1.5 μl dye into the 6 μl glycerine droplet can be determined. After 10 s, the improvement in mixing efficiency between the fm = 0 (no modulation) and fm = 15 kHz cases is approximately 22%, 26%, and 51% when the input power is We = 107, 165, and 265 mW, respectively, demonstrating that significant improvement in the micromixing (lower normalized standard deviation) can be achieved with amplitude modulation, due to the larger acoustic streaming velocities and hence stronger convection within the droplet. Given that the slopes of the curves are proportional to , the mixing enhancement due to the acoustic streaming induced convection can be approximated by the ratio between an effective diffusivity due to the SAW-driven convective-mixing Deff to the diffusivity in its absence D0 (Shilton et al., 2008). Figure 11 shows a comparison of the mixing enhancement as a function of the input power for the different modulation frequencies. It is then possible to compare the effectiveness of mixing afforded by each modulation frequency through a single power law : n = 1.82 for fm = 0 (without modulation), n = 1.15 for fm = 1 kHz, n = 1.08 for fm = 5 kHz, and n = 0.91 for fm = 15 kHz.
FIG. 10.
(a) Successive time-sequence images showing the mixing progress of 1.5 μl of dye into a 6 μl glycerine droplet excited at We = 265 mW when subjected to amplitude modulation at a frequency of fm = 15 kHz (the droplet circumference is delineated by the circles in the images). Normalized standard deviation in the pixel intensity to quantify the efficiency of mixing 1.5 μl of dye into a 5 μl glycerine droplet for three different input powers: (b) We = 107 mW, (c) We = 165 mW, and (d) We = 265 mW, and various modulation frequencies: fm = 0 (without modulation) (◇), fm = 1 kHz (×), fm = 5 kHz (●), and fm = 15 kHz (△). Trendlines were added to aid visualization.
FIG. 11.
Effect of the input power We on the mixing enhancement, approximated as the ratio of the effective diffusivity Deff to the diffusivity due to pure diffusional mixing D0 in the absence of SAW-driven convection. Four different conditions were examined: fm = 0 (without modulation) (◇), fm = 1 kHz (×), fm = 5 kHz (●), and fm = 15 kHz (△).
V. CONCLUSIONS
In this work, we have demonstrated a simple technique to increase the acoustic streaming velocity in SAW droplet microfluidic platforms via amplitude modulation, thus reducing the power requirement which is crucial in the development of a portable integrated microfluidic platform. Unlike previous attempts in which an amplitude modulation scheme was employed under strong acoustic field intensities () to induce capillary wave destabilization and breakup for liquid atomization (Rajapaksa et al., 2014), the work here focuses on systems with low acoustic field intensities () where interfacial deformation is negligible. In particular, the acoustic streaming velocity is observed to intensify by increasing the modulation index, which results in larger peak acoustic-velocity amplitudes of the modulated SAWs; from our numerical simulations, we expect this increase in streaming velocity to become more significant with larger droplets. Increasing the modulation frequency is also observed to produce a similar enhancement effect: a 30% enhancement in the streaming velocity is observed with an amplitude modulation frequency of 1 kHz, increasing to approximately 60% at 10 kHz for fSAW = 30 MHz. The enhancement, however, is observed to diminish when the quarter-wavelength associated with the modulation frequency becomes comparable and subsequently shorter than the thermoviscous attenuation length, i.e., , at increasing modulation frequencies; beyond approximately fm ≈ 10 kHz, no further increases in the streaming velocity were observed. We further note that any enhancement in the acoustic streaming with amplitude modulation is accompanied by a modest reduction in the droplet temperature, which is a further advantage particularly for biomicrofluidic applications. Such intensification in acoustic streaming with amplitude modulation is also seen to translate into faster and more efficient microcentrifugation-driven particle concentration, reducing the time taken to concentrate particles in the centre of the droplet between 50% and 70% depending on the particle size. Similarly, the mixing efficiency in the droplet is observed to improve by approximately 50% with the amplitude modulation scheme.
ACKNOWLEDGMENTS
M.K.T. gratefully acknowledges funding for this work from the Fundamental Research Grant Scheme, Ministry of Higher Education Malaysia, through Project Grant No. FRGS/1/2015/SG02/MUSM/03/1. L.Y.Y. is supported by a Future Fellowship from the Australian Research Council under Grant No. FT130100672.
References
- 1. Anderson, J. D. , Computational Fluid Dynamics: The Basics with Application ( McGraw-Hill, 1995), p. 261. [Google Scholar]
- 2. Ang, K. M. , Yeo, L. Y. , Friend, J. R. , Hung, Y. M. , and Tan, M. K. , J. Aerosol Sci. , 48 (2015). 10.1016/j.jaerosci.2014.10.004 [DOI] [Google Scholar]
- 3. Arifin, D. R. , Friend, J. R. , and Yeo, L. Y. , Biomicrofluidics , 014103 (2007). 10.1063/1.2409629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Baudoin, M. , Brunet, P. , Matar, O. B. , and Herth, E. , Appl. Phys. Lett. , 154102 (2012). 10.1063/1.3701725 [DOI] [Google Scholar]
- 5. Beyer, R. T. , Nonlinear Acoustics: The Parameter B/A, edited by Hamilton M. F. and Blackstock D. T. ( Academic Press, 1988), pp. 25–40. [Google Scholar]
- 6. Blamey, J. , Yeo, L. Y. , and Friend, J. R. , Langmuir , 3835 (2013). 10.1021/la304608a [DOI] [PubMed] [Google Scholar]
- 7. Bourquin, Y. , Reboud, J. , Wilson, R. , Zhang, Y. , and Cooper, J. M. , Lab Chip , 2725 (2011). 10.1039/c1lc20320g [DOI] [PubMed] [Google Scholar]
- 8. Brunet, P. , Baudoin, M. , Matar, O. B. , and Zoueshtiagh, F. , Phys. Rev. E , 036315 (2010). 10.1103/PhysRevE.81.036315 [DOI] [PubMed] [Google Scholar]
- 9. Chen, Y. , Li, S. , Gu, Y. , Li, P. , Ding, X. , Wang, L. , McCoy, J. P. , Levine, S. J. , and Huang, T. J. , Lab Chip , 924 (2014). 10.1039/c3lc51001h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Cheng, I.-F. , Chang, H.-C. , Hou, D. , and Chang, H.-C. , Biomicrofluidics , 021503 (2007). 10.1063/1.2723669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Cho, S. K. , Zhao, Y. , and Kim, C.-J. , Lab Chip , 490 (2007). 10.1039/b615665g [DOI] [PubMed] [Google Scholar]
- 12. Collingnon, S. , Friend, J. , and Yeo, L. , Lab Chip , 1942 (2015). 10.1039/C4LC01453G [DOI] [PubMed] [Google Scholar]
- 13. Dentry, M. B. , Yeo, L. Y. , and Friend, J. R. , Phys. Rev. E , 013203 (2014). 10.1103/PhysRevE.89.013203 [DOI] [PubMed] [Google Scholar]
- 14. Destgeer, G. , Cho, H. , Ha, B. H. , Jung, J. H. , Park, J. , and Sung, H. J. , Lab Chip , 660 (2016). 10.1039/C5LC01104C [DOI] [PubMed] [Google Scholar]
- 15. Destgeer, G. , Ha, B. H. , Jung, J. H. , Park, J. , and Sung, H. J. , Lab Chip , 4665 (2014). 10.1039/C4LC00868E [DOI] [PubMed] [Google Scholar]
- 16. Destgeer, G. , Ha, B. H. , Park, J. , Jung, J. H. , Alazzam, A. , and Sung, H. J. , Anal. Chem. , 4627 (2015). 10.1021/acs.analchem.5b00525 [DOI] [PubMed] [Google Scholar]
- 17. Destgeer, G. , Lee, K. H. , Jung, J. H. , Alazzam, A. , Park, J. , and Sung, H. J. , Lab Chip , 4210 (2013). 10.1039/c3lc50451d [DOI] [PubMed] [Google Scholar]
- 18. Destgeer, G. and Sung, H. J. , Lab Chip , 2722 (2015). 10.1039/C5LC00265F [DOI] [PubMed] [Google Scholar]
- 19. Dholakia, K. , Reece, P. , and Gu, M. , Chem. Soc. Rev. , 42 (2008). 10.1039/B512471A [DOI] [PubMed] [Google Scholar]
- 20. Ding, X. , Li, P. , Lin, S.-C. S. , Stratton, Z. S. , Nama, N. , Guo, F. , Slotcavage, D. , Mao, X. , Shi, J. , Costanzo, F. , and Huang, T. J. , Lab Chip , 3626 (2013). 10.1039/c3lc50361e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Frenzel, L. , Principles of Electronic Communication Systems ( McGraw-Hill, 2007). [Google Scholar]
- 22. Friend, J. R. and Yeo, L. Y. , Rev. Mod. Phys. , 647 (2011). 10.1103/RevModPhys.83.647 [DOI] [Google Scholar]
- 23. Frommelt, T. , Gogel, D. , Kostur, M. , Talkner, P. , Hänggi, P. , and Wixforth, A. , IEEE Trans. Ultrason., Ferroelectr., Freq. Control , 2298 (2008a). 10.1109/TUFFC.928 [DOI] [PubMed] [Google Scholar]
- 24. Frommelt, T. , Kostur, M. , Wenzel-Schafer, M. , Talkner, P. , Hanggi, P. , and Wixforth, A. , Phys. Rev. Lett. , 034502 (2008b). 10.1103/PhysRevLett.100.034502 [DOI] [PubMed] [Google Scholar]
- 25. Glass, N. R. , Shilton, R. J. , Chan, P. P. Y. , Friend, J. R. , and Yeo, L. Y. , Small , 1881 (2012). 10.1002/smll.201102282 [DOI] [PubMed] [Google Scholar]
- 26. Hamilton, M. F. , Il'inskii, Y. A. , and Zabolotskaya, E. A. , Dispersion, edited by Hamilton M. F. and Blackstock D. T. ( Academic Press, 1998) pp. 151–175. [Google Scholar]
- 27. Harrison, H. , Lu, X. , Patel, S. , Thomas, C. , Todd, A. , Johnson, M. , Raval, Y. , Tzeng, T.-R. , Song, Y. , Wang, J. , Li, D. , and Xuan, X. , Analyst , 2869 (2015). 10.1039/C5AN00105F [DOI] [PubMed] [Google Scholar]
- 28. Hou, D. , Maheshwari, S. , and Chang, H.-C. , Biomicrofluidics , 014106 (2007). 10.1063/1.2710191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Hwang, H. and Park, J.-K. , Lab Chip , 199 (2009). 10.1039/B811740C [DOI] [PubMed] [Google Scholar]
- 30. Jo, M. C. and Guldiken, R. , Sens. Actuators A , 1 (2013). 10.1016/j.sna.2013.03.028 [DOI] [Google Scholar]
- 31. Jung, J. H. , Destgeer, G. , Ha, B. H. , Park, J. , and Sung, H. J. , Lab Chip , 3235 (2016). 10.1039/C6LC00648E [DOI] [PubMed] [Google Scholar]
- 32. King, L. V. , Proc. R. Soc. London A , 212 (1934). 10.1098/rspa.1934.0215 [DOI] [Google Scholar]
- 33. Kinsler, L. E. , Frey, A. R. , Coppens, A. B. , and Sanders, J. V. , Fundamentals of Acoustics ( John Wiley & Sons, 2000). [Google Scholar]
- 34. Kondoh, J. , Shimizu, N. , Matsui, Y. , Sugimoto, M. , and Shiokawa, S. , Sens. Actuators A , 292 (2009). 10.1016/j.sna.2008.11.007 [DOI] [Google Scholar]
- 35. Laurell, T. , Petersson, F. , and Nilsson, A. , Chem. Soc. Rev. , 492 (2007). 10.1039/B601326K [DOI] [PubMed] [Google Scholar]
- 36. Lewpiriyawong, N. , Yang, C. , and Lam, Y. C. , Microfluid Nanofluid , 723 (2012). 10.1007/s10404-011-0919-x [DOI] [Google Scholar]
- 37. Li, H. , Friend, J. R. , and Yeo, L. Y. , Biomed. Microdevices , 647 (2007). 10.1007/s10544-007-9058-2 [DOI] [PubMed] [Google Scholar]
- 38. Lin, S.-C. S. , Mao, X. , and Huang, T. J. , Lab Chip , 2766 (2012). 10.1039/c2lc90076a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Manor, O. , Rezk, A. R. , Friend, J. R. , and Yeo, L. Y. , Phys. Rev. E , 053015 (2015). 10.1103/PhysRevE.91.053015 [DOI] [PubMed] [Google Scholar]
- 40. Manor, O. , Yeo, L. Y. , and Friend, J. R. , J. Fluid Mech. , 482 (2012). 10.1017/jfm.2012.293 [DOI] [Google Scholar]
- 41. Martins, A. M. G. , Glass, N. R. , Harrison, S. , Rezk, A. R. , Porter, N. A. , Carpenter, P. D. , Plessis, J. D. , Friend, J. R. , and Yeo, L. Y. , Anal. Chem. , 10812 (2014). 10.1021/ac502878p [DOI] [PubMed] [Google Scholar]
- 42. Morse, P. M. and Ingard, K. U. , Theoretical Acoustics ( McGraw-Hill, 1986). [Google Scholar]
- 43. Nguyen, N.-T. and Wu, Z. , J. Micromech. Microeng. , R1 (2005). 10.1088/0960-1317/15/2/R01 [DOI] [Google Scholar]
- 44. Nyborg, W. L. , Acoustic Streaming, edited by Hamilton M. F. and Blackstock D. T. ( Academic Press, 1988), pp. 207–231. [Google Scholar]
- 45. Pamme, N. , Eijkel, J. C. , and Manz, A. , J. Magn. Magn. Mater. , 237 (2006). 10.1016/j.jmmm.2006.04.008 [DOI] [Google Scholar]
- 46. Qi, A. , Yeo, L. Y. , and Friend, J. R. , Phys. Fluids , 074103 (2008). 10.1063/1.2953537 [DOI] [Google Scholar]
- 47. Raghavan, R. V. , Friend, J. R. , and Yeo, L. Y. , Microfluid. Nanofluid. , 73 (2010). 10.1007/s10404-009-0452-3 [DOI] [Google Scholar]
- 48. Rajapaksa, A. , Qi, A. , Yeo, L. Y. , Coppel, R. , and Friend, J. R. , Lab Chip , 1858 (2014). 10.1039/C4LC00232F [DOI] [PubMed] [Google Scholar]
- 49. Rezk, A. R. , Manor, O. , Yeo, L. Y. , and Friend, J. R. , Proc. R. Soc. A , 20130765 (2014). 10.1098/rspa.2013.0765 [DOI] [Google Scholar]
- 50. Rogers, P. R. , Friend, J. R. , and Yeo, L. Y. , Lab Chip , 2979 (2010). 10.1039/c004822d [DOI] [PubMed] [Google Scholar]
- 51. Rozenberg, L. D. , High-Intensity Ultrasonic Fields ( Plenum Press, 1971). [Google Scholar]
- 52. Schmid, L. , Wixforth, A. , Weitz, D. A. , and Franke, T. , Microfluid. Nanofluid. , 229 (2012). 10.1007/s10404-011-0867-5 [DOI] [Google Scholar]
- 53. Schröder, C. T. and Scott, W. R. , IEEE Trans. Geosci. Remote Sens. , 1505 (2000). 10.1109/36.851950 [DOI] [Google Scholar]
- 54. Shi, J. , Mao, X. , Ahmed, D. , Colletti, A. , and Huang, T. J. , Lab Chip , 221 (2008). 10.1039/B716321E [DOI] [PubMed] [Google Scholar]
- 55. Shi, J. , Mao, X. , Ahmed, D. , Colletti, A. , and Huang, T. J. , Lab Chip , 3354 (2009). 10.1039/b915113c [DOI] [PubMed] [Google Scholar]
- 56. Shilton, R. , Tan, M. K. , Yeo, L. Y. , and Friend, J. R. , J. Appl. Phys. , 014910 (2008). 10.1063/1.2951467 [DOI] [Google Scholar]
- 57. Shilton, R. J. , Mattoli, V. , Travagliati, M. , Agostini, M. , Desii, A. , Beltram, F. , and Cecchini, M. , Adv. Funct. Mater. , 5895 (2015). 10.1002/adfm.201501130 [DOI] [Google Scholar]
- 58. Shilton, R. J. , Travagliati, M. , Beltram, F. , and Cecchini, M. , Adv. Mater. , 4941 (2014). 10.1002/adma.201400091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Shilton, R. J. , Yeo, L. Y. , and Friend, J. R. , Sens. Actuators B , 1565 (2011). 10.1016/j.snb.2011.09.007 [DOI] [Google Scholar]
- 60. Stone, H. A. , Stroock, A. D. , and Ajdari, A. , Annu. Rev. Fluid Mech. , 381 (2004). 10.1146/annurev.fluid.36.050802.122124 [DOI] [Google Scholar]
- 61. Tan, M. K. , Friend, J. R. , Matar, O. K. , and Yeo, L. Y. , Phys. Fluids , 112112 (2010). 10.1063/1.3505044 [DOI] [Google Scholar]
- 62. Tan, M. K. , Friend, J. R. , and Yeo, L. Y. , Phys. Rev. Lett. , 024501 (2009). 10.1103/PhysRevLett.103.024501 [DOI] [PubMed] [Google Scholar]
- 63. Tan, M. K. , Yeo, L. Y. , and Friend, J. R. , EPL , 47003 (2009). 10.1209/0295-5075/87/47003 [DOI] [Google Scholar]
- 64. Winkler, A. , Harazim, S. M. , Menzel, S. B. , and Schmidt, H. , Lab Chip , 3793 (2015). 10.1039/C5LC00756A [DOI] [PubMed] [Google Scholar]
- 65. Yeo, L. Y. , Chang, H.-C. , Chan, P. P. Y. , and Friend, J. R. , Small , 12 (2011). 10.1002/smll.201000946 [DOI] [PubMed] [Google Scholar]
- 66. Yeo, L. Y. and Friend, J. R. , Annu. Rev. Fluid Mech. , 379 (2014). 10.1146/annurev-fluid-010313-141418 [DOI] [Google Scholar]
- 67. Yeo, L. Y. , Friend, J. R. , and Arifin, D. R. , Appl. Phys. Lett. , 103516 (2006a). 10.1063/1.2345590 [DOI] [Google Scholar]
- 68. Yeo, L. Y. , Hou, D. , Maheshswari, S. , and Chang, H.-C. , Appl. Phys. Lett. , 233512 (2006b). 10.1063/1.2212275 [DOI] [Google Scholar]
- 69. Zeng, J. , Chen, C. , Vedantam, P. , and Xuan, T.-R. T. X. , Microfluid. Nanofluid. , 49 (2013). 10.1007/s10404-012-1126-0 [DOI] [Google Scholar]