Physical characterization of nanoparticle size and surface modification using particle scattering diffusometry

Abstract

As the field of colloidal science continues to expand, tools for rapid and accurate physiochemical characterization of colloidal particles will become increasingly important. Here, we present Particle Scattering Diffusometry (PSD), a method that utilizes dark field microscopy and the principles of particle image velocimetry to measure the diffusivity of particles undergoing Brownian motion. PSD measures the diffusion coefficient of particles as small as 30 nm in diameter and is used to characterize changes in particle size and distribution as a function of small, label-free, surface modifications of particles. We demonstrate the rapid sizing of particles using three orders-of-magnitude less sample volume than current standard techniques and use PSD to quantify particle uniformity. Furthermore, PSD is sensitive enough to detect biomolecular surface modifications of nanometer thickness. With these capabilities, PSD can reliably aid in a wide variety of applications, including colloid sizing, particle corona characterization, protein footprinting, and quantifying biomolecule activity.

I. INTRODUCTION

In bio-nanotechnology, nanoparticles are used as vehicles for nanomedicine,^1,2 visual aids in point-of-care diagnostics,^3–6 markers in immunohistochemistry,^7,8 and detectors in biosensor design.^9,10 In these applications, the biomolecules that are conjugated onto nanoparticles can vary dramatically in size, with Stokes radii as small as 7 Å and as large as 1 μm,¹¹ and corresponding molecular weights ranging from <10 000 Da to >300 000 Da. Without a fluorescent label, it can be difficult to determine the tethering of these biomolecules to the particle surface,^12,13 and gold nanoparticles often quench fluorescence.¹⁴ Nonetheless, it is important to characterize the addition of biomolecules to nanoparticles, especially in applications where biological activity, proper structural folding, and catalysis are key characteristics of the biomolecule.

Current methods of characterizing nano- and microparticle synthesis and surface modifications include surface enhanced Raman spectroscopy (SERS),¹⁵ Fourier transform infrared spectroscopy (FTIR),^16,17 electron microscopy,^18,19 ultraviolet-visible spectroscopy (UV-Vis),²⁰ dynamic light scattering (DLS),^15,21 and nanoparticle tracking analysis (NTA). Of these techniques, DLS is the most commonly used,²² measuring particles from the micrometer range down to sub-nanometer sizes.²³ For accurate measurements, this well-established method²⁴ requires information from the user such as refractive index (RI) and absorption coefficient of the particles along with temperature and viscosity of the fluid medium.²⁵ This information is not always known a priori and surface modifications may, in fact, change some of these properties. Other techniques such as FTIR, electron microscopy, and SERS require specialized equipment and substantial expertise to carry out accurate measurements. Additionally, NTA calculates particle size based on their trajectories in space²⁶—which is based on the technique Particle Tracking Velocimetry (PTV).²⁷ The multiple calculated trajectories are used to calculate the averaged mean squared displacement (MSD) curve which is used to determine the diffusion coefficient.²⁶ This is known as a Lagrangian approach.²⁸ While NTA is a great tool for characterizing nanoparticle size, the technique is time-consuming and is less reproducible as compared to DLS.²⁷ In order to facilitate the translation of colloidal science to a broader scientific community, there is a need to develop robust and practical particle characterization techniques. These tools should be easy to integrate into current laboratory workflows and be able to perform on-chip characterization in a microfluidic environment.¹⁹

In this work, we demonstrate for the first time that Particle Scattering Diffusometry (PSD) can characterize a large range of particles, from micro- to nanoscale, based on their size, polydispersity, and surface modifications. PSD can perform these measurements with high accuracy in high-throughput and low-volume applications. PSD technique measures the Brownian motion over a cross-section within the solution, known as an Eulerian approach.^29–32 In PSD, unlike methods such as NTA, particles are analyzed in a continuum, meaning that individual trajectories are not calculated, but rather correlation is used to determine the difference in the displacement of many particles between image frames. Because groups of particles are analyzed using correlation, PSD is statistically robust.^30,31 Using PSD, we can determine particle surface functionalization on-chip using a conventional optical microscope.

II. EXPERIMENTAL

A. Gold nanoparticle preparation

N-Hydroxysuccinimide Ester (NHS)-activated 100 nm gold nanoparticles (Cytodiagnostics, ON, Canada) were conjugated via primary amine chemistry to the surface lysines of bovine serum albumin (BSA) (Sigma Aldrich, St. Louis, MO), lysozyme (Sigma Aldrich, St. Louis, MO), or calmodulin (Enzo Life Sciences, Farmingdale, NY) following standard Cytodiagnostics protocols. Briefly, each conjugation reaction was initiated with addition of the proteins to lyophilized gold nanoparticles at a final concentration of 0.133 mg/ml. It was followed by gentle agitation at room temperature for 2 h. 10 μl of 1.0 M Tris was added to 90 μl of the particle solution to block any non-reacted NHS groups remaining on the beads' surfaces. Samples were incubated at a final concentration of 100 mM Tris with agitation for another hour. Following this, samples were diluted in 20 mM Hepes pH 7.4 containing 100 mM NaCl, and then centrifuged for 30 min at 400 × g to remove buffer and free protein. Conjugated samples were resuspended in NaCl-free 20 mM Hepes buffer to minimize charge effect at a particle concentration of 5.75 × 10⁹ particles/ml.

B. Polystyrene microparticle preparation

300 nm, 520 nm, 1 μm, and 2 μm red fluorescent polystyrene microparticles (Fluoro-Max, Thermo Scientific, MA) were centrifuged according to the manufacturer's protocols. Particles were resuspended in 20 mM Hepes pH 7.4 in order to maintain buffer conditions similar to the prepared gold nanoparticles. Fluorescent particles were ultrasonicated for 15 s post-centrifugation to ensure full dispersion and resuspension.

C. Dynamic light scattering (DLS) measurements

The DLS measurements were taken to confirm the accuracy of PSD as a particle characterization tool. Both Malvern Zetasizer's Nano ZS and Nano ZS90 models were used. Measurements were taken to ensure that both instruments provided the same readings. All samples were analyzed to determine their hydrodynamic radius as well as the Polydispersity Index (PdI) of the sample prior to analysis with Transmission Electron Microscopy (TEM) or PSD. Particles were dispersed in 20 mM Hepes pH 7.4. Standard 1 ml disposable polystyrene cuvettes were used (DTS0012, Malvern Instruments, Westborough, MA). The Zeta potentials of these modifications were recorded with DTS1060 cuvettes (Malvern Instruments, Westborough, MA).

D. TEM measurements

400 mesh Formvar carbon coated copper grids (FCF400-Cu-50, Electron Microscopy Sciences, Hatfield, PA) were used for imaging. First, the grids were treated with glow discharge in order to facilitate wetting of the surface. 5 μl of the gold particle sample was placed onto the mesh for 2 min followed by negative staining with 0.2% uranyl acetate (UA) in order to discern the protein layer on the particle surface. All samples, including the bare gold, were negatively stained for uniformity in measurement across all particle samples. Samples were imaged with a Tecnai T20 TEM (FEI, Hillsboro, OR). All gold nanoparticle and protein corona image processing and size measurements from the TEM images were completed in the Gatan Digital Micrograph software.

E. PSD measurements

Glass coverslips (No. 1 Thickness, Erie Scientific, Portsmouth, NH) were rinsed and ultrasonicated with water, acetone, isopropanol, and ethanol sequentially and dried with compressed air. Glass surfaces were treated using corona discharge for wettability of the sample. 2 mm thick adhesive silicon wells (HT-6135, McMaster-Carr, Elmhurst, IL) were adhered onto the glass coverslips. 7 μl of nanoparticle samples were pipetted into the fluid chambers and covered with a second glass coverslip to reduce evaporative effects in the solution. The liquid touched both the top and bottom glass coverslips in order to avoid free surfaces which otherwise induced both vibrations. The 100 nm gold nanoparticle samples contained in the glass coverslip apparatus were observed using dark field microscopy due to the Rayleigh scattering. Dark field microscopy was performed using a 0.9 numerical aperture (NA) dark field air condenser (Nikon Instruments, Inc., Melville, NY) which was integrated in an inverted Nikon TE2000U microscope. 300 nm, 520 nm, 1 μm, and 2 μm polystyrene particles were imaged with a 40× extra long working distance (ELWD) objective lens (0.6 NA) under fluorescence microscopy via a fluorescent illumination lamp (Xcite series 120PC, EXFO Life Sciences & Industrial Division, Toronto, Canada) attached to the inverted microscope. The particles were imaged using a CCD camera (1200 × 1600 pixels²) with a 2 × 2 binning at 13.3 fps (16-bit grayscale PCO.1600, PCO AG, Germany). Individual pixel size was 7.4 × 7.4 μm². Image acquisition was controlled using the PCO software (CamWare V3.07, PCO AG, Germany). PSD measurements of all prepared particle samples were taken within hours of each other to maintain the same temperature and viscosity conditions, required for assuming ratiometric diffusion coefficients. Using this camera setup, 3000–4000 particles were captured in each image. 100 frames were recorded per PSD measurement to discern the change of Brownian motion between the different particle solutions while maintaining short time durations for potential comparison between this technique and other laboratory sizing methods. For the PdI measurements with PSD, experiments were performed in triplicate in order to compare with DLS, which also performs its measurements in groups of three.

F. PSD data post-processing

Dark field images were analyzed in EDPIV (http://www.edpiv.com), a PIV analysis software. The interrogation area was determined as the average display in which 8–10 particles were maintained within the area. Data were either ensemble averaged (for ratiometric diffusion coefficient) or individually measured per interrogation area (for PdI and protein layer distribution estimates). Correlation data were post-processed and fit to a 5-point Gaussian distribution. The correlation peak widths were calculated for both cross-correlation (s_c) and autocorrelation (s_a) data to determine the diffusion coefficient using an in-house MATLAB code.

III. RESULTS AND DISCUSSION

A. Particle scattering diffusometry fundamentals

The principles underlying Particle Scattering Diffusometry (PSD) involve measuring the diffusivity of nanoparticles undergoing Brownian motion in a two-dimensional imaging plane. The PSD experimental setup is shown schematically in Fig. 1, wherein particles undergoing Brownian motion are imaged under dark field microscopy. Depending on the sensitivity of the camera, dark field microscopy allows imaging of particles as small as 30 nm in diameter—or even smaller. This size is well below the diffraction limit. Much of the size range of nanoparticles typically used in bionanotechnology applications (anywhere between 1 and 100 nm) fall within the range of dark field microscopy. Thus, with a relatively straightforward microscopy setup, surface modification of nanoparticles, such as formation of a biomolecule corona, can be quantitatively characterized. Furthermore, the smaller the ratio of nanoparticle size to corona thickness, the larger the relative change in nanoparticle diffusivity and the larger the PSD signal.

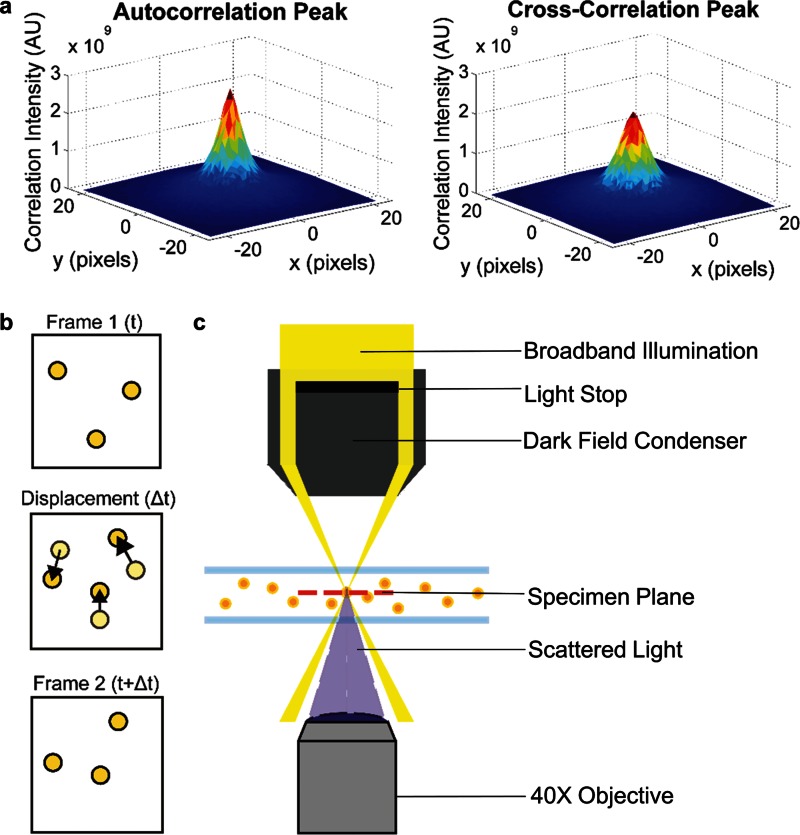
FIG. 1.

Particle scattering diffusometry. (a) The autocorrelation and cross-correlation peaks calculated using PSD. Autocorrelation peaks are taller and narrower than that of the cross-correlation peaks. The difference between the peak areas (along with magnification and time between image frames) provides the diffusion coefficient value (Eq. (1)). (b) A schematic of sequential images where frame 1 is at time t and frame 2 is at time t + Δt. The nanoparticle displacement, Δt, due to Brownian motion is shown where light yellow particles represent nanoparticle position at time t (Frame 1) and dark yellow particles represent nanoparticle position at time t + Δt (Frame 2). (c) A schematic of the PSD experimental setup. A dark field condenser is integrated in an inverted microscope. The condenser blocks most of the white light source, allowing the light to focus to a small point within the specimen plane but outside the collection angle of the objective lens. Only the light scattered by the particles is collected by the 40× objective lens.

During data analysis, each frame of the recorded video is partitioned into smaller interrogation areas such that, on average, it contains 8–10 particles.³³ The diffusion coefficient is calculated from two different correlations which are determined using Fast Fourier Transforms (FFTs). The first is the autocorrelation, which is determined by correlating an interrogation area with itself. The second is the cross-correlation, calculated by correlating an interrogation area from an image acquired at time t₁ with the same interrogation area from an image acquired at time t₁ + Δt, where Δt is the time between consecutive video frames³² (Fig. 1(b)). Because PSD measures Brownian motion in two-dimensions, using interrogation areas that contain multiple particles is statistically robust as particles move in and out of the z-plane. The diffusion coefficient can be calculated from the auto and cross-correlation peak widths using a rearranged expression derived from the work of Olsen and Adrian³⁴

$$D=\frac{s_c^2-s_a^2}{16M^2\Delta t},$$ (1)

where the diffusion coefficient D is determined from s_c and s_a, which are the cross- and autocorrelation peak widths measured at 1/e of the correlation peak height (Fig. 1(a)).³⁵ M represents the magnification under which the particle images were recorded. This fundamental equation was originally established in the context of Particle Image Velocimetry (PIV) applications to relate the uncertainty in velocity measurements to temperature. However, it is used in PSD to determine the diffusion coefficient of a species of particles. Because Brownian motion is essentially thermal noise, a large population of repeated measurements is needed in order to accurately measure it. The diffusion coefficients calculated from each interrogation area in an image can be averaged together to produce a more precise measure of the diffusion coefficient over the entire image. Averaging over more image frames increases the precision. The diffusion coefficient calculated from the particles' motion can be related to fluid and particle parameters via the Stokes-Einstein equation³⁶

$$D=\frac{\mathit{k}\mathit{T}}{6\pi \mu a},$$ (2)

where T is the absolute temperature, μ is the dynamic viscosity of the fluid medium, k is the Boltzmann's constant, and a is the hydrodynamic radius. Combining these relationships, we can see that the particle hydrodynamic radius a is inversely proportional to diffusion coefficient and hence to the area difference between the cross-correlation and autocorrelation peaks (multiply the numerator of Eq. (1) by π to see this). Thus, PSD can be used to characterize properties that affect nanoparticle size.

In addition to calculating the diffusion coefficient of a nanoparticle population, we have also established that PSD can measure the Polydispersity Index (PdI) of the sample. PdI is defined as the standard deviation (σ) of the particle diameter distribution divided by the mean particle diameter

$$PdI={\left(\frac{\sigma }{2a}\right)}^2.$$ (3)

PdI is used to estimate the average uniformity of a particle solution, and larger PdI values correspond to a larger size distribution in the particle sample. PdI can also indicate nanoparticle aggregation along with the consistency and efficiency of particle surface modifications throughout the particle sample. A sample is considered monodisperse when the PdI value is less than 0.1.³⁷

To calculate the PdI of a nanoparticle sample using PSD, the diffusion coefficient values from each interrogation area are plotted in a histogram and a normal distribution is fit to the data. From this fit, the PdI is calculated by using Eq. (3). Thus, if there is a large distribution in the diffusion coefficients calculated from each interrogation area, the particle PdI is correspondingly large. Conversely, small distributions in calculated diffusion coefficients lead to small PdI values and indicate monodisperse samples.

B. PSD experimental setup

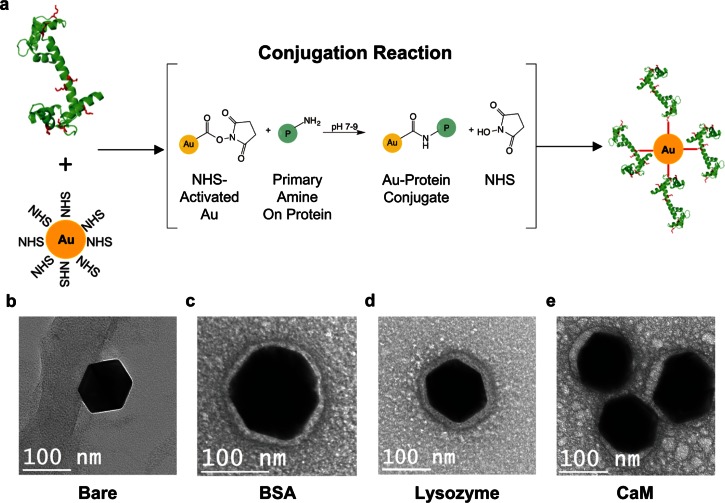
In order to characterize biomolecule conjugation onto nanoparticles, several biologically relevant proteins (bovine serum albumin, lysozyme, and calmodulin) were covalently attached to gold nanoparticles (AuNPs). PSD was used to measure the difference in Brownian motion between these samples compared to bare AuNPs. These proteins were chosen due to their widespread use in various important biological applications and difference in size and charge from each other (Table I). Bovine serum albumin (BSA) is a well-characterized blood serum protein that is commonly used as a blocking agent to minimize nonspecific protein interactions and nonspecific protein adsorption onto surfaces. Lysozyme is a hydrolase enzyme found in eukaryotes as part of the innate immune system.³⁸ It is often used in vitro to break down bacterial cell walls³⁹ and used widely in protein crystallography.⁴⁰ Calmodulin (CaM) is a calcium ion (Ca²⁺) binding protein found in all eukaryotic cells. It modulates cellular responses to Ca²⁺ flux by binding and activating over 100 downstream target proteins.^41–43 Calmodulin, along with green fluorescent protein, have been engineered to be intracellular Ca²⁺ biosensors.⁴⁴ BSA, lysozyme, and CaM were separately covalently attached to N-Hydroxysuccinimide (NHS) functionalized AuNPs via primary amine chemistry (Fig. 2(a)).

TABLE I.

Essential properties of the proteins, BSA, CaM, and lysozyme, used in this study. The molecular weight (MW) and Stokes Radii show the range of protein sizes. The isoelectric point (pI) relates to protein charge. The number of surface lysines indicates the number of locations, where the protein may bind to the AuNP by virtue of the primary amine on lysine.

Protein	MW (kDa)	Stokes radius (nm)	pI	Number of surface lysines
BSA	66.50	3.4845	4.7	30–3546
Lysozyme	14.31	1.947	11.35	348
CaM	16.79	2.4949	5.4	7–850

FIG. 2.

Nanoparticle bioconjugation. (a) Proteins, in this schematic CaM, are introduced to 100 nm NHS-activated AuNPs where the NHS on the particle and primary amine on surface lysines of the protein (in red) react to form covalent protein-conjugated nanoparticles. (b)–(e) Transmission Electron Microscopy (TEM) images of bare, BSA, lysozyme, and CaM conjugated AuNPs, respectively. The AuNP itself appears as the larger dark object in the image. The protein corona can be seen as a halo-like feature around the particle circumference.

To determine the difference in the diffusion coefficient between the AuNP samples using PSD, we directly calculate the ratio of the average value of the diffusion coefficient of protein conjugated-AuNP samples to the average value of the diffusion coefficient of the bare AuNPs. This ratio also provides information as to whether or not protein conjugation has successfully taken place. The ratio of the diffusion coefficients of two particle species in solutions of identical temperature and viscosity is inversely proportional to the ratio of their diameters

$$\frac{D_{\mathit{A}\mathit{u}\mathit{N}\mathit{P}}}{D_{protein\_AuNP}}=\frac{a_{protein\_AuNP}}{a_{\mathit{A}\mathit{u}\mathit{N}\mathit{P}}},$$ (4)

where D_{protein_AuNP} and a_{protein_AuNP} are the diffusion coefficient and hydrodynamic radius of the protein conjugated particle while D_AuNP and a_AuNP are those of the bare AuNPs. From this equation, it can be seen that as particle size increases due to biomolecular conjugation the diffusion coefficient of the conjugated particles decreases.

Representing the diffusion coefficient of the biomolecular conjugated nanoparticles as a ratio allows us to measure the change in diffusion coefficient with fewer images and hence more quickly. When PSD is used to find the magnitude of the time-averaged diffusion coefficient, a large number of images must be recorded. Although this large image set reduces experimental error, absolute diffusion measurements can take as long as 20 min. Other nanoparticle sizing methods, such as DLS, are carried out at similar timescales. However, in PSD, when using the diffusion coefficient ratio to describe the change in nanoparticle diffusivity, far fewer image frames are needed to produce experimental accuracy similar to the absolute diffusion coefficient. For example, a t-test comparing the ratiometric diffusion coefficient approach using 100 image frames (∼8 s of data) and the ratiometric diffusion coefficient using 10 000 frames was found to be statistically insignificant (p > 0.05). In contrast, a t-test comparing the absolute diffusion coefficient using 10 000 frames was statistically different than the absolute diffusion coefficient using 100 image frames (p < 0.05). Therefore, we take advantage of the similarity in the scaled error to reduce the number of image frames and the overall measurement time.

There are a few guidelines to consider when designing a PSD experiment. In our current setup, the nanoparticles are contained within a fluid chamber designed to enclose several microliters of the sample. However, the volume of the particle sample is limited by the desired design of the fluid chamber. In order to avoid near-wall hindered diffusion, particles of any size must be imaged at least 10 particle diameters away from any wall or edge of the chamber. In practical terms, this means that the fluid chamber should be designed with sufficient height and depth to allow imaging of particles at least 10 particle diameters from the wall of the chamber. This is hardly a limiting factor when considering nanoparticle size. Another important consideration is that smaller particles (∼200 nm in diameter or less) must sufficiently scatter light to be visible. Metallic particles such as gold or silver are recommended. As metallic particles are conductive, heating from the microscope light source may increase particle Brownian motion. However, we expect heating to occur similarly among all particles, and as we investigate the ratiometric diffusion coefficient rather than the absolute magnitude, changes in temperature will not significantly change the PSD calculation. The concentration of these particles should be optimized such that particle-particle interactions, which also hinder diffusion, are avoided but the particles are still close enough together to capture many particles in each image, reducing measurement noise. This optimal particle concentration is determined so that, on average, particles are located at least 10 particle diameters away from one another. However, the effect of these particle interactions can be further quantified using equations derived by Batchelor, where we calculate that our experimental particle density affects the diffusion coefficient by less than 0.0001%.^51–53 The imaging chamber should also be designed as a closed system in order to minimize sample evaporation and unintentional flow through the chamber. Evaporation will cause a net fluid flow toward the interface that will make the PSD measurements more challenging to interpret. With adherence to these guidelines, PSD can be integrated with almost any micro- or nanofluidic device where the particles can be imaged.

C. Analysis of bioconjugated nanoparticles

Protein conjugation to AuNPs was analyzed using Zeta potential analysis, Transmission Electron Microscopy (TEM), Dynamic Light Scattering (DLS), and PSD. Measurements of nanoparticle Zeta potential and ratiometric diffusivity as determined by TEM, DLS, and PSD, respectively, for bare, BSA, lysozyme, and CaM conjugated gold nanoparticles are summarized in Table S1 (supplementary material). Bare, BSA, Lysozyme, and CaM conjugated particles had different Zeta potentials, which indicate protein attachment. This change in Zeta potential between the bare AuNP and the other three samples indicates protein attachment. TEM imaging showed that bare AuNPs have a hard and distinct edge (Fig. 2(b)), whereas protein treated particles had blurred boundaries that indicate the presence of a protein corona (Figs. 2(c)–2(e)). This indicates that the proteins have successfully attached to the gold particle surface, as the blurring specifies a less electron dense material (i.e., the protein), as compared to gold.^54,55 The diameter of the bare AuNPs measured with TEM was 125.82 ± 2.36 nm (n = 9). The protein layer thickness of each conjugated AuNP was 18.05 ± 3.19 nm for BSA, 32.69 ± 3.54 nm for lysozyme, and 15.16 ± 4.21 nm for CaM. Both the AuNPs and the protein layers of each particle sample were measured at eight equidistant locations. The thickness of the protein layers for the BSA, lysozyme, and CaM-conjugated AuNPs indicate that there was non-specific binding of protein onto the AuNP after the first protein layer was formed from the primary amine chemistry.

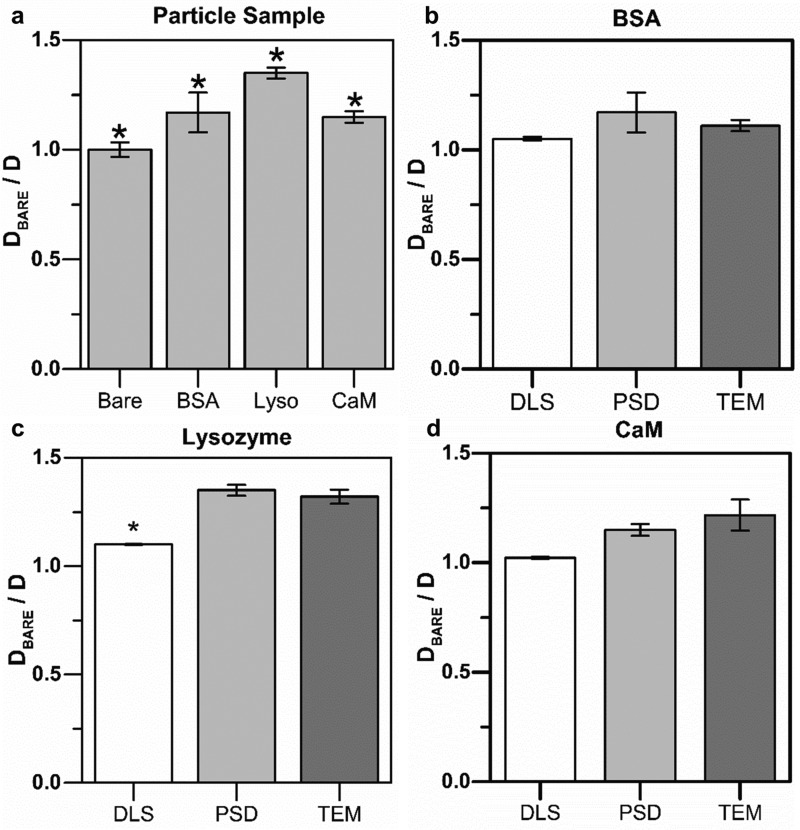
The ratiometric diffusion coefficient of the conjugated BSA, lysozyme, CaM, and bare AuNPs was calculated with PSD (Table S1, supplementary material and Fig. 3). We find a statistically significant difference (p < 0.05) in the ratiometric diffusion coefficient between the bare, CaM, BSA, and lysozyme coated AuNPs (Fig. 3(a)). For example, lysozyme AuNPs gave the biggest change in the diffusion coefficient, which correlates well with the change in particle size measured via TEM. On the other hand, CaM conjugated AuNPs have the smallest change in the PSD measured diffusion coefficient. These results demonstrate that PSD is sensitive enough to detect a significant difference between nanoparticles with different surface treatments.

FIG. 3.

Comparison of nanoparticle characterization techniques. (a) PSD was used to measure the normalized diffusion ratio for all four AuNP samples. Results show a statistically significant (p < 0.05) detectable difference in the ratiometric diffusion coefficient (D_bare/D) between each sample of the four sample groups (n = 24). The lysozyme conjugated gold nanoparticle sample is indicated by “Lyso.” (b)–(d) Comparing (D_bare/D) calculated from DLS, PSD, and TEM data for each protein conjugated AuNPs.

In order to validate the accuracy of the PSD method, we compared the normalized diffusion ratio determined by PSD to TEM and DLS data for each protein-conjugated sample (Figs. 3(b)–3(d)). In all cases (CaM, lysozyme, and BSA), there was no statistically significant difference between the TEM and PSD measurement techniques (p > 0.05) (Figs. 3(b)–3(d)). In contrast, the DLS measurements often exhibited lower normalized diffusion ratio values as compared to TEM and PSD, with statistically significant values between DLS and TEM and PSD measurements for the lysozyme conjugated particles (Fig. 3(c)). PSD measurements were also found to be consistently closer to TEM data in comparison to the DLS measurements. The difference between DLS and TEM for lysozyme, BSA, and CaM was 16.67%, 5.41%, and 16.02%, respectively, whereas the difference between the TEM and PSD data was 2.27% (lysozyme), 5.41% (BSA), and 5.57% (CaM).

D. Polydispersity index measurements

Polydispersity characterization is essential in nanoparticle applications, as it is difficult to control sample-wide uniformity with surface conjugation chemistry, and often aggregation of particles can occur. Currently, DLS is the most common PdI measurement method. Here, we demonstrate that PSD can also predict the uniformity of a nanoparticle solution using Polydispersity Index (PdI) as an indicator.

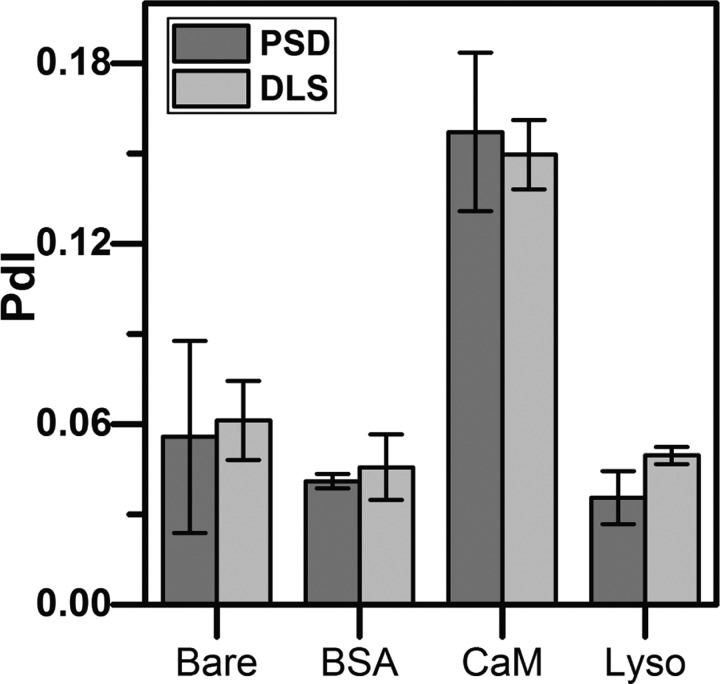
To calculate sample PdI using PSD, 100 image frames per data set are partitioned into interrogation areas. Diffusion coefficient values are calculated from the nanoparticles within each interrogation area, and the array of values are fit to a normal distribution. A normal distribution was chosen to directly compare our PdI measurements with DLS, which also uses a normal distribution in their model. The PdI of the normal distribution of the diffusion coefficient is calculated similarly to Eq. (3). However, we modify Eq. (3) in terms of the diffusion coefficient rather than in terms of particle size where we know that $D\propto \hspace{0.17em}\frac{1}{a}$. This leads to the algebraic manipulation of Eq. (3), where $PdI={(\frac{{\sigma }_{D^{-1}}}{D^{-1}})}^2$. In this case, ${\sigma }_{D^{-1}}$ is the standard deviation of the inverse diffusion coefficient and $D^{-1}$ is the mean value of the inverse diffusion coefficient. PdI measurements for both PSD and DLS are provided in Table S2 (supplementary material) and shown graphically in Fig. 4. We find that there is no statistically significant difference between the PdI values measured using PSD and DLS (p > 0.05). Both techniques determined that CaM conjugated nanoparticles showed the least uniformity between the samples with PdI values of 0.15–0.16, indicating that this sample is polydisperse (Fig. 4 and Table S2, supplementary material). Conversely, lysozyme coupled AuNPs displayed the highest degree of uniformity with PdI values of 0.035–0.05, indicating this sample is quite monodisperse (Fig. 4 and Table S2, supplementary material).

FIG. 4.

Polydispersity Index. Comparing the polydispersity index values between PSD and DLS for bare, BSA, CaM, and lysozyme conjugated AuNP samples. The difference in the polydispersity index between the two techniques is statistically insignificant (p > 0.05), indicating that PSD can be used as a tool to determine sample uniformity.

E. Comparing PSD with theoretical predictions

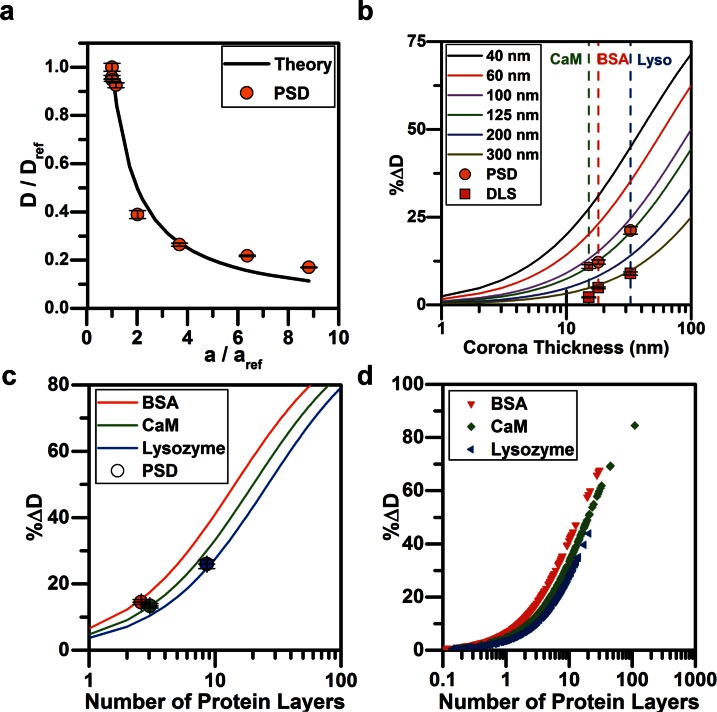
We wished to compare experimental measurements of nanoparticle diffusion by PSD to theoretical predictions of the diffusion coefficient by the Stokes-Einstein equation (Eq. (2)). To determine this, we experimentally measured the diffusion coefficients of non-conjugated particles with diameters of 100 nm, 300 nm, 520 nm, 1 μm, and 2 μm using PSD, as well as 100 nm particles conjugated to CaM, lysozyme, and BSA and compared them to diffusion coefficient of reference 100 nm gold nanoparticles ($D_{\mathit{r}\mathit{e}\mathit{f}}$). The radius of conjugated particles was known from TEM data. The theoretical ratiometric diffusion curve was calculated by $\frac{D}{D_{\mathit{r}\mathit{e}\mathit{f}}}=\frac{a_{\mathit{r}\mathit{e}\mathit{f}}}{a}$. As expected, the experimental ratiometric values closely follow the theoretical curve (Fig. 5(a)). The values of the ratiometric diffusion coefficients for these particles are presented in Tables S1 and S3 (supplementary material). The Root Mean Squared Error (RMSE) between PSD data and Stokes-Einstein predictions was found to be 6.04%. This small RMSE indicates that PSD can be used to determine the diffusion coefficient for a large range of particle sizes, extending beyond the nano-regime.

FIG. 5.

Theory vs. experiments. (a) The ratiometric diffusion coefficients for particles of 100 nm, 300 nm, 520 nm, 1 μm, and 2 μm in diameter, and 100 nm biomolecule conjugated particles were measured by PSD and compared with the diffusion coefficient of the 100 nm bare gold nanoparticles (Eq. (2)). The RMSE between theory and experiments was 6.04%. In (b)–(d), the %ΔD indicates the percent change in the diffusion coefficient. (b) The %ΔD was theoretically determined for particles ranging from 40 nm to 300 nm in diameter as a function of the biomolecule size conjugated to the AuNP. The experimental data points (for the BSA (red), CaM (green), and lysozyme (blue) conjugated AuNPs) were calculated from PSD and DLS results and compared with theory. The dotted lines correspond to the thickness of the layer of each biomolecule as measured by TEM. (c) The percent change in diffusion coefficient as a function of the number of protein layers added to the 100 nm AuNP. Each protein's Stokes radius changes the diffusion coefficient of the particle. Measurement of the %ΔD and knowledge of the protein stokes radius facilitates prediction of the average number of layers of protein present on the particle using PSD. (d) The number of predicted protein layers on BSA, CaM, and lysozyme conjugated nanoparticles is calculated from separate interrogation areas and each point is plotted to visualize the distribution within each treatment.

In order to identify how the diffusion coefficient of nanoparticles would be expected to change upon biomolecule corona deposition or covalent conjugation of biomolecules onto the nanoparticle surface, we predicted the percent change in diffusion coefficient of various nanoparticles ranging in diameter from 40 to 300 nm as greater amounts of biomolecules increased the hydrodynamic radius of the particles (a function of the corona deposition onto the surface) (Fig. 5(b)). We define a relationship between corona thickness and the nanoparticle hydrodynamic radius to be

$$thicknes{s}_{(corona)}=a_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}-a_{\mathit{b}\mathit{a}\mathit{r}\mathit{e}}.$$ (5)

Further, the percent change in diffusion coefficient is calculated using

$$\%\Delta D=\frac{D_{\mathit{A}\mathit{u}\mathit{N}\mathit{P}}-D_{protein\_AuNP}}{D_{\mathit{A}\mathit{u}\mathit{N}\mathit{P}}}\cdot 100.$$ (6)

Using Eqs. (2) and (6), the percent change in the diffusion coefficient can be theoretically calculated as

$$\%\Delta D=\left(1-\frac{a_{\mathit{A}\mathit{u}\mathit{N}\mathit{P}}}{a_{protein\_AuNP}}\right)\times 100.$$ (7)

The solid lines in Fig. 5(b), calculated using Eq. (7), predict how the diffusion coefficient of particles, ranging from 40 nm to 300 nm in diameter, would change as a function of thickness of the corona on the particle surface (1 nm–100 nm).

DLS and PSD were used to measure the percent change of the diffusion coefficient of bioconjugated nanoparticles (dots, Fig. 5(b)) to (i) compare these methods to predictions from Eq. (7) (solid lines Fig. 5(b)) and (ii) see how these methods compare with one another (dots Fig. 5(b), values in Table S4, supplementary material). Using PSD and DLS measurements, the diffusion coefficients of bare and biomolecule conjugated 100 nm AuNPs were measured directly and Eq. (6) was used to calculate the percent change in the diffusion coefficient. Across each characterization method, lysozyme conjugated AuNPs consistently had the largest percent change in diffusion coefficient, followed by CaM, and then BSA with the smallest percent change in diffusion coefficient (vertical dashed lines Fig. 5(b)). Furthermore, comparing DLS and PSD to predictions, it is seen that the change in the diffusion coefficient measured for the different biomolecules by PSD fall along the 125 nm curve and DLS measurements fall along the 300 nm curve. In contrast to TEM which is a direct measurement of physical particle size (and shows AuNPs to have an average diameter of 100 nm), PSD and DLS estimate particle hydrodynamic radius. Thus, it is not surprising that the PSD measurement falls along the 125 nm curve as the nanoparticle's effective hydrodynamic diameter is slightly increased due to an electric dipole layer that forms about the particle's surface.⁸ In contrast, the DLS data lie closest to the 300 nm curve. This indicates a larger inaccuracy in measuring the change in diffusion coefficient as a function of different size biomolecule additions. These discrepancies can be attributed to two factors: (1) the assumption in DLS that the particles in dispersion are spherical, and (2) as more biomolecule is added to the nanoparticle, the refractive index properties of the dispersing medium change.²² Given that DLS is an intensity-based measurement system, this can cause errors in the particle size measurement.^22–24

Characterizing the number of protein layers present on a nanoparticle is important for researchers performing layer-by-layer assemblies such as designing tunable vehicles for drug delivery devices.^6,56 Because NHS chemistry was used to covalently bind protein to the bare gold nanoparticle surface, it is expected that only one protein layer should be present on the particle surface. However, additional layers were present on the particles due to non-specific adhesion which was visually confirmed using TEM. We used these additional protein layers to our advantage by using PSD to characterize the number of protein layers were present on the AuNPs throughout the sample. By coupling the Stokes-Einstein equation (Eq. (2)) and the biomolecule Stokes radius (Table I) with PSD measurements (Table S1, supplementary material), we can estimate the average number of protein layers that constitute the nanoparticle corona. The diffusion coefficient measured with PSD is substituted into the Stokes-Einstein equation, calculating the overall thickness of the protein layer as follows:

$$\%\Delta D=\left(\frac{n(2*a_{\mathit{p}\mathit{r}\mathit{o}\mathit{t}\mathit{e}\mathit{i}\mathit{n}})}{a_{\mathit{A}\mathit{u}\mathit{N}\mathit{P}}+n(2*a_{\mathit{p}\mathit{r}\mathit{o}\mathit{t}\mathit{e}\mathit{i}\mathit{n}})}\right)\cdot 100,$$ (8)

where n is the number of protein layers attached to the particle. In Fig. 5(c), lines represent predictions from Eq. (8) where n is varied and the Stokes radius ($a_{\mathit{p}\mathit{r}\mathit{o}\mathit{t}\mathit{e}\mathit{i}\mathit{n}}$) is held constant for BSA, CaM, and lysozyme, respectively. These lines represent how the diffusion coefficient of nanoparticles would be expected to change as protein layers increase the protein corona. Experimental PSD measurements of the $\%\Delta D$ were used to estimate the average number of protein layers, n, that were conjugated to the AuNP surface (Fig. 5(c), dots). The lysozyme conjugated particles have the largest number of layers on the AuNP surface, whereas the BSA had the least amount. This agrees with TEM measurements and can be seen in Figs. 2(b)–2(e).

In addition to estimating the average number of protein layers on the nanoparticles, it is important to characterize the variation in the number of protein layers throughout the nanoparticle sample. For example, with antibody coated nanoparticles used for drug therapy, it is important to know how much of the therapeutic load is attached to the particle surface.^6,56 Particles with varying corona layers throughout the sample and particularly particles with a large number of layers may see effects in affinity,⁶ functionality,^6,57 and steric hindrance.^58,59 Therefore, we establish a method to use PSD measurements to estimate the variation in the protein layering within the sample. In a set of images, each interrogation area exhibits a different diffusion coefficient value. The range of these diffusion coefficient values is used to calculate the variation in the number of biomolecule layers of a particle sample. We first calculate the percent change of the diffusion coefficient (Eq. (6)) for each interrogation area (keeping $D_{\mathit{A}\mathit{u}\mathit{N}\mathit{P}}$ constant at 3.56 × 10⁻¹² m²/s) and using Eq. (8) to calculate the number of protein layers per interrogation area. The results for the variation of biomolecule layers for each sample (lysozyme, CaM, and BSA) are plotted in Fig. 5(d) where every point represents a measurement in a single interrogation area. If a bioconjugated sample is more uniform, then there will be a smaller distribution of points along the x-axis. With data presented in this way, one can visualize the distribution of the number of protein layers within a sample to complement the PdI measurement. For example, as shown in Fig. 5(d), lysozyme coated nanoparticles have the smallest distribution along the x-axis, indicating that the surface coating was more uniform throughout the sample. This agrees with the PdI measurement of the lysozyme particles (PdI = 0.036). In contrast, the CaM modified AuNPs have the largest distribution of number of protein layers, which is in agreement with the large PdI value (0.157). In our samples, we see that clusters of CaM-conjugated nanoparticle samples that have predicted layers of 100 and 200 layers, indicating nanoparticle aggregation. Visualizing the distribution of the number of protein layers in this way may be a useful technique for discerning nanoparticle aggregation. These differences might not be seen by visual inspection of a sample but can be readily discerned by estimating the distribution of the number of protein layers.

IV. CONCLUSIONS

We have developed Particle Scattering Diffusometry (PSD), which is the first time diffusometry has been used at the nanoscale to detect small changes in the Brownian motion. We demonstrate that PSD can be used to determine the size, uniformity, and protein corona thickness on nanoparticles while using less time than current techniques. Measuring protein-functionalization of AuNPs with PSD reveals that the technique can discern between small surface modifications with results similar to TEM measurements. PSD also measures the sample heterogeneity (PdI). The PdI is routinely used to characterize and optimize nanoparticle design and surface modifications. We also use PSD to characterize both the number of biomolecule layers within the protein corona on nanoparticles and its variation within a nanoparticle sample.

The methods established here represent significant improvement compared to current nanoparticle characterization methods. The sensitivity of PSD enables characterizing engineered nanoparticles with a standard optical microscope setup. No specialized laboratory measurement systems or imaging methods are required. PSD can be easily integrated into many microfluidic chips. This also allows measurement of nanoparticle samples in micro- to nanoliter sample volumes, which is several orders-of-magnitude less than that used in current laboratory characterization techniques. PSD measurements can be accurately assessed using just 100 image frames. This allows users to rapidly determine the change in particle diffusion after biomolecule conjugation.

In ongoing work, we are taking advantage of the rapidity of PSD measurements to detect changes in nanoparticle diffusivity at high time resolution. We expect that PSD measurements can be used to distinguish between particles of different sizes or surface chemistries simultaneously such that multiplexed measurements will be possible. In addition, PSD is not limited to protein-nanoparticle applications. We expect that PSD can also be used for analysis of small DNA, RNA, and peptide fragments, protein-cell receptor studies, or pathogen detection. Further developments in PSD would advance the bio-nanotechnology field into new application areas and provide improved quantitative measurements.

V. SUPPLEMENTARY MATERIAL

See supplementary material for experimental measurements of the nanoparticle ratiometric diffusion coefficients and Zeta potentials (Table S1), polydispersity index measurements (Table S2), particle size diffusion coefficient predictions (Table S3), and the percent change in diffusion coefficient measurements (Table S4).