Particle rotational trapping on a floating electrode by rotating induced-charge electroosmosis

Abstract

We describe a novel rotating trait of induced-charge electroosmotic slip above a planar metal surface, a phenomenon termed “Rotating induced-charge electro-osmosis” (ROT-ICEO), in the context of a new microfluidic technology for tunable particle rotation or rotational trap. ROT-ICEO has a dynamic flow stagnation line (FSL) that rotates synchronously with a background circularly polarized electric field. We reveal that the rotating FSL of ROT-ICEO gives rise to a net hydrodynamic torque that is responsible for rotating fluids or particles in the direction of the applied rotating electric field either synchronously or asynchronously, the magnitude of which is adjusted by a balance between rotation of FSL and amplitude of angular-direction flow component oscillating at twice the field frequency. Supported by experimental observation, our physical demonstration with ROT-ICEO proves invaluable for the design of flexible electrokinetic framework in modern microfluidic system.

I. INTRODUCTION

Electrically driven fluid flow (electro-osmosis) and particle motion (electrophoresis) are classical subjects of electrokinetics, experiencing a renaissance in microfluidics,¹ electrochemical,² and biochemical devices.³ For pumping in microfluidic channels, Ramos and co-workers at the end of the last century initially investigated AC electro-osmosis,⁴ which is a variant of induced-charge electro-osmosis (ICEO). Several years later, Bazant and Squires indicated that the underlying physical mechanism of an applied electric field acting on its own induced bipolar ionic charge within the diffuse screening cloud near a polarizable solid/electrolyte interface is more universal, hence coined the term ICEO to describe the phenomenon of nonlinear electroosmosis.⁵ The free charge for actuating electroosmosis originates from a balance between electrostatic attraction and surface ion diffusion,⁶ not necessarily requiring a dielectric gradient as in Maxwell-Wagner interfacial polarization (liquid or particle dielectrophoresis,^7,8 and perhaps there is circulating electrohydrodynamic (EHD) vortex due to tangential electrical stress at an electrical liquid-liquid interface⁹) or smeared structural polarizations (electrothermal induced flow^10–12). Since all of the AC electrohydrodynamic body forces on the fluid occur strictly within the double layer of molecular distances of the electrode surface, the ability to engender fluid flow by ICEO was also termed nanoshearing, as suggested by the research group of Trau.^13–16 ICEO derives directly from macroscopic RC coupling for sufficiently small induced zeta potential $\zeta$ in a homogeneous electrolyte of bulk conductivity $\sigma$, derivable from the microscopic ion transport process on a blocking electrode^17,18

$$C_{\mathrm{D}}\frac{\partial \zeta }{\partial t}=\sigma \mathit{n}\cdot \mathit{E},$$ (1)

where C_D is the diffuse layer capacitance and n is a unit outward normal pointing from the interface into the bulk. Traditionally, the background electric field generating ICEO is provided by a DC or AC standing-wave signal.^19–22 Under this circumstance, the ICEO slip velocity above the surface of a planar metal strip of half width R immersed in an electrolyte is obtained from the Helmholtz formula $\mathit{u}=\frac{–\epsilon \zeta \mathit{E}}{\eta }=\frac{–\epsilon E^{2}x\left(1+\text{cos}\left(2\omega t\right)\right)}{2\eta \left(1+\delta \right)\left(1+{\left(\omega {\tau }_{\mathit{R}\mathit{C}}\right)}^2\right)}{\mathit{e}}_{\mathit{x}}$ in terms of liquid permittivity $\epsilon$, liquid dynamic viscosity $\eta$, surface capacitance ratio $\delta$ of the induced double layer (IDL), and RC time scale ${\tau }_{\mathit{R}\mathit{C}}=R{C}_0/\sigma$ for double-layer capacitance C₀ coupling to the bulk resistance $R/\sigma$.¹⁸

The ICEO slip pattern converges on a metal surface along the direction of electric field, implying the flow direction remains the same in every half cycle of the AC field, during which ionic charge polarity alternates periodically. This results in a constantly fixed flow stagnation line (FSL) at x = 0 for conventional ICEO.^18,19

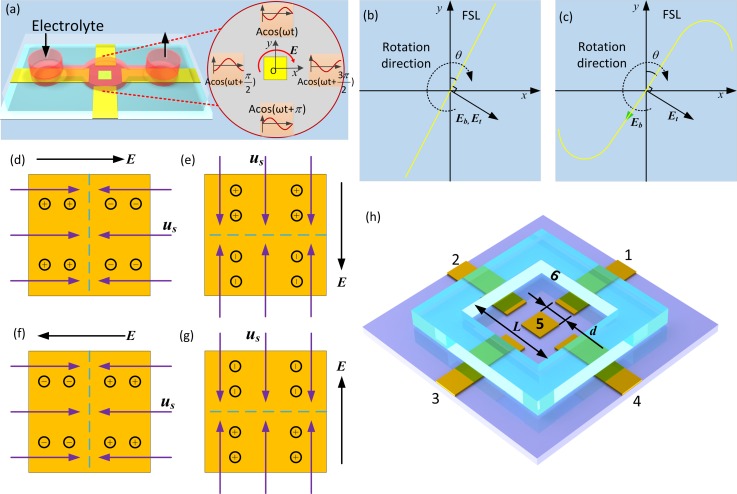
If applying a background rotating electric field (REF) rather than a standing-wave signal far from a planar metal surface, what will happen? Starting from this viewpoint, we introduce herein a new kind of ICEO slip above a planar metal surface (e.g., of a square shape) induced by a REF, termed as rotating induced-charge electroosmosis (ROT-ICEO), with the schematic of experimental setup shown in Fig. 1(a). As the field vector rotates, the REF exerts a “torque” on the bipolar ionic charge within the IDL that constantly rotates and redistributes (Figs. 1(b) and 1(c)), without obvious time delay at low frequency (Fig. 1(b)). In the meantime, a dynamic FSL begins to rotate synchronously with the diffuse screening cloud. This interesting rotational behaviour in the nonlinear electro-osmotic flow can conceivably produce rotating particle or fluid samples.

FIG. 1.

Three dimensional schematic of the experimental setup. (a) Four strip ITO driving electrodes with a quadrature configuration are patterned on a glass substrate. The nearest interelectrode distance along the x- or y-direction is L = 2 mm. A metal square of edge length d = 300 μm and negligible thickness is placed at the centre of four driving electrodes. A PDMS channel of 500 μm height with two electrolyte ports is reversibly bonded to the glass substrate with patterned electrodes to form a closed microfluidic chamber. A KCl electrolyte solution containing particle tracers or target particle samples is injected into the channel and finally fills the microchamber. A background rotating electric field $\mathit{E}(t)=\mathrm{Re}(((2A/L){\mathit{e}}_{\mathit{x}}+j(2A/L){\mathit{e}}_{\mathit{y}})e^{j\omega t})$ in the clockwise direction is nearly unaffected by the presence of the square floating electrode in the DC limit. (b) and (c) Transient behaviour of ROT-ICEO. (b) Phase diagram of the background field E_b, inducing surface tangential field E_t and FSL in the DC limit. (c) Phase diagram at slightly above the RC charging frequency. (d)–(g) The two dimensional phase diagram for the rotating FSL (dashed line) of ROT-ICEO occurring above a planar metal surface in a background rotating electric field. Transient ionic charge polarity and slip flow direction at different time instants: (d) t = 0; (e) t = T/4; (f) t = T/2; (g) t = 3 T/4. (h) The 3D geometrical model applied in numerical simulation (not to scale).

II. MATERIALS AND METHODS

A. Theoretical

We begin with the general physical description of ROT-ICEO for the asymptotic limit of thin electrical double layer and approximation of small induced zeta potential, in which a successive 90° phase-shifted applied field induces a charged cloud around a polarized surface and then drives the dipolar counter-ionic atmosphere into electrokinetic motion. A background REF $\mathit{E}(t)=\mathrm{Re}(E_0({\mathit{e}}_{\mathit{x}}+j{\mathit{e}}_{\mathit{y}}){\mathit{e}}^{j\omega t})$ of amplitude $E_0\approx 2A/L$ (Fig. 1(a)) (A is the voltage amplitude) rotating with angular frequency $\omega$ is imposed far from the metal square.^23,24 The transient ionic charge polarity and slip flow directions are shown in a sequence of images of Figs. 1(d)–1(g) as the field vector rotates clockwise, under the assumption of field frequency being low enough. The straight FSL clearly rotates clockwise with the inducing rotating field in a synchronous manner, and they are always mutually perpendicular. The ICEO vortices produced therefore rotate at a constant angular speed $\omega =2\pi f$, and therefore, may exert a kind of hydrodynamic torque on any particle sample trapped on the electrode surface.

In the DC limit, with complete double-layer charging, the induced zeta potential across the diffuse layer at metal/electrolyte interface is $\zeta =\frac{E_0}{1+\delta }\left(x\hspace{0.17em}\text{cos}\left(\omega t\right)–y\hspace{0.17em}\text{sin}\left(\omega t\right)\right)$ as the metal square floats in potential, and the ROT-ICEO slip velocity is given by $\mathit{u}=\frac{–\epsilon {E_0}^2}{\eta \left(1+\delta \right)}\left(x\hspace{0.17em}\text{cos}\left(\omega t\right)–y\hspace{0.17em}\text{sin}\left(\omega t\right)\right)\left(\text{cos}\left(\omega t\right){\mathit{e}}_{\mathit{x}}–\hspace{0.17em}\text{sin}\left(\omega t\right){\mathit{e}}_{\mathit{y}}\right)$ with a rotating FSL $y=\cot (\omega t)x$. The rotation phase diagram of ROT-ICEO flow and the background REF at such low frequencies (Fig. 1(b)) shows both components rotating with the same angular velocity in the co-field direction but with a π/2 phase shift. More normal Ohmic current arrives at the outer edge of Debye layer with increasing field frequency. A direct consequence of this is a deviation in the direction of tangential field component from that of the background REF. By increasing the frequency above the reciprocal RC charging time scale $f_{\mathit{R}\mathit{C}}=\sigma /2\pi R{C}_0$, saturation occurs (Fig. 1(c)). The maximum included angle between the surface tangential field (E_t) and background field (E_b) is −π/2, implying the induced field component and applied REF are completely out-of-phase. A curved FSL is formed via the complex electrochemical ion relaxation in a high-frequency REF (Fig.1(c)), as revealed by direct numerical simulation (DNS).

Using polar coordinates $(\rho ,\theta )$, we decompose the analytical ROT-ICEO slip velocity u in the DC limit into radial (${\mathit{u}}_{\mathit{\rho }}$) and angular (${\mathit{u}}_{\mathit{\theta }}$) components

(2).

$${\mathit{u}}_{\mathit{\rho }}=\frac{–\epsilon }{\eta }\frac{1}{1+\delta }{E_0}^2\frac{1}{2}\rho \left(1+\text{cos}\left(2\omega t+2\theta \right)\right){\mathit{e}}_{\mathit{\rho }},$$ (2a)

$${\mathit{u}}_{\mathit{\theta }}=\frac{–\epsilon }{\eta }\frac{1}{1+\delta }{E_0}^2\frac{–\rho }{2}\text{sin}\left(2\omega t+2\theta \right){\mathit{e}}_{\mathit{\theta }}.$$ (2b)

At higher field frequencies, we apply DNS to calculate the distribution of electrostatic potential and ROT-ICEO slip flow field (refer to the supplementary material for the detailed physical model), with the help of a commercial FEM software package COMSOL Multiphysics. The electrical field is governed by Eq. (S1) in the supplementary material, with corresponding boundary conditions shown in Table I and Fig. 1(h). Once the potential distribution is known, transient or time-averaged ROT-ICEO slip velocity on the square surface is calculated from Eq. (S5) or (S6) (supplementary material) by inserting the solution of electric field, respectively, without having to solve the full Stokes equation.

TABLE I.

Boundary conditions applied in numerical simulation.

Index	Boundary	B.C. for electrical problem ${\nabla }^2\tilde{\varphi }=0$
1	Electrode of 0° voltage	$\tilde{\varphi }=A$
2	Electrode of 90° voltage	$\tilde{\varphi }=jA$
3	Electrode of 180° voltage	$\tilde{\varphi }=-A$
4	Electrode of 270° voltage	$\tilde{\varphi }=-jA$
5	Squared floating electrode	$\sigma \mathit{n}\cdot \nabla \tilde{\varphi }=j\omega C_0(\tilde{\varphi }-\widetilde{{\varphi }_0})$, $\widetilde{{\varphi }_0}=0$
6	Insulating wall/electrolyte interface	$\mathit{n}\cdot \nabla \tilde{\varphi }=0$

B. Experimental

Electrodes were fabricated from indium-tin-oxide (ITO, Kaivo, China) glass by soft-lithography (Figure 2), starting with spinning-coating the AZ4620 positive photoresist (Resemi, China) onto ITO glass to yield a uniform protecting layer. It was then soft-baked at 60 °C for 7 min. Next, the ITO glass slide was exposed to UV light for 207 s. After that, the photoresist was developed for 7 min to produce the electrode pattern, and later post-exposure-baked at 110 °C for 15 min. The ITO glass was immersed in a hydrochloric acid solution for wet etching for 27 min to wipe off the remaining ITO layer. Finally, the remaining photoresist layer was sonicated in acetone for 10 min to be stripped off.

FIG. 2.

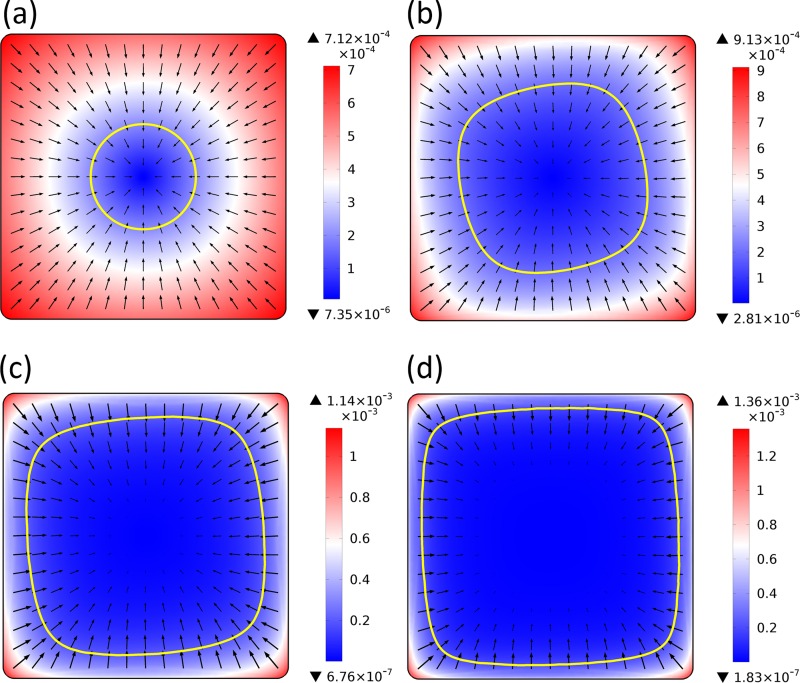
The time-averaged slip flow pattern of ROT-ICEO at different field frequencies: (a) 5 Hz; (b) 120 Hz; (c) 300 Hz; (d) 500 Hz.

Microchannels have a cuboid chamber for manipulation, generated from a polymethylmethacrylate (PMMA) mold. The polydimethylsiloxane (PDMS, Sil-More Industrial Ltd., USA, Sylgard 184A and Sylgard 184B) mixture is poured onto the mold followed by curing at 80 °C for 2 h. Next, the PDMS replicas with embedded microchannel are peeled off from mold. Finally, after an oxygen plasma treatment of 32 s (ZEPTO, Diener, Germany), the two components, including ITO electrode and PDMS slab, are aligned and bonded together to form a complete microfluidic device.

The working fluid is potassium chloride (KCl) aqueous solution, electrical conductivity of which was set at 1 mS/m, sufficiently low to meet the limit of dilute solution theory. Micro-rods are fabricated from SU-8 by photolithography. The rods are nominally 11 μm in diameter and of an average length of 47 μm. The AC sinusoidal signal was generated by a function generator (TGA12104, TTi, UK), magnified by a voltage amplifier (Model2350, TEGAM, USA). The movement and distribution of particles were visualized by an optical microscope (CKX41, Olympus, Japan) and recorded by a CCD camera (DP27, Olympus, Japan).

III. RESULTS AND DISCUSSION

A. Frequency-dependence of ROT-ICEO slip flow on the floating electrode

Since deriving the analytical solution beyond the DC limit in the presence of electrochemical ion relaxation is an insurmountable task for such a particular geometry, we subsequently present the results related to nonlinear electro-osmotic slip within a wide frequency range obtained from DNS. Taking the experimental parameter values listed in Table II, we calculated the time-averaged as well as the transient ICEO flow field at different time instants within an AC period.

TABLE II.

Physical and geometrical parameters used in current work.

Parameter	Implication	Value
f	AC field frequency	1–10 000 Hz
A	Voltage amplitude	4–5 V
D	Ionic diffusivity	2−9 m2/s
$\epsilon$	Liquid permittivity	7.083−10 F/m
$\sigma$	Liquid conductivity	0.001 S/m
$\lambda$	Debye length	$\sqrt{\mathrm{D\epsilon }/\sigma }=\mathrm{37}\mathrm{.6}\hspace{0.17em}\mathrm{nm}$
L	Interelectrode gap size	2 mm
$\eta$	Liquid dynamic viscosity	$\mathrm{0}\mathrm{.001}\hspace{0.17em}\mathrm{Pa}\hspace{0.17em}\mathrm{s}$
Cd	Diffuse-layer capacitance	$\epsilon /\lambda =\mathrm{0}\mathrm{.019}\hspace{0.17em}\mathrm{F/}{\mathrm{m}}^{\mathrm{2}}$
Cs	Stern-layer capacitance	0.2 F/m2
$\delta$	Surface capacitance ratio	Cd/Cs = 0.094
D	Edge length of the square floating electrode	300 μm
R	Characteristic charging length scale	d/9.25 = 32.4 μm
C0	Double-layer capacity	$C_d/(\mathrm{1+}\delta )=\mathrm{0}\mathrm{.017}\hspace{0.17em}\mathrm{F/}{\mathrm{m}}^{\mathrm{2}}$
tRC	RC charging time	$R{C}_0/\sigma =\mathrm{5}\mathrm{.58}\times \mathrm{1}{\mathrm{0}}^{\mathrm{-4}}\hspace{0.17em}\mathrm{s}$
fRC	RC charging frequency	$\sigma /\mathrm{2\pi R}{C}_0=\mathrm{285}\mathrm{.3}\hspace{0.17em}\mathrm{Hz}$

1. Time-averaged behavior of ROT-ICEO slip flow

In the DC limit, the analytical time-averaged ROT-ICEO slip flow $⟨{\mathit{u}}_{\mathit{\rho }}⟩=\frac{–\epsilon }{\eta }\frac{1}{1+\delta }{E_0}^2\frac{1}{2}\rho {\mathit{e}}_{\mathit{\rho }}$ exhibits a converging pattern, with a flow stagnation point (FSP) located at the centre of the electrode surface. The FSP draws in tracer particles from the surrounding liquid medium towards the centre (Fig. 2(a)). By increasing field frequency of up to 120 Hz, the slip flow pattern becomes asymmetric (Fig. 2(b)). With a further increase in frequency to 300 Hz and even above f_RC at 500 Hz, the symmetry of the surface slip flow gradually recovers (Figs. 2(c) and 2(d)), whereas the averaged flow velocity decreases through relaxation.

2. Transient nature of ROT-ICEO slip flow

The transient behaviour found in ROT-ICEO is even more subtle than its time-averaged effect. In the DC limit, the floating electrode behaves as an insulator through complete IDL screening. The synchronous rotation of the ICEO flow and applied REF is evident in Fig. 1(b). At 10 Hz, slightly above the DC limit (results not shown), the phenomenon is more complex. The tangential field at the electrode surface E_t (indicated by a red arrow) deviates by a small angle with respect to the background rotating field E_b (green arrow) from the complex double-layer charging. Note that the slightly inclined FSL is always perpendicular to E_t but not to E_b. At 300 Hz–500 Hz, slightly higher than f_RC, the floating electrode through double-layer charge relaxation gradually reverts to its original role as ideal conductor, and a large normal field component is injected into IDL.²⁵ Thus not only E_t decreases with frequency, but also its direction becomes difficult to ascertain in the high-frequency REF, in that E_t has a −π/2 phase shift relative to E_b at every time instant (Fig. 1(c)). The mechanism behind this may be related to the complex out-of-phase double-layer charging dynamics above the DC limit in a REF. Consequently, a curved FSL, the orientation of which coincides with E_b, rotates both clockwise and synchronously with the same field, and possesses an angle $\omega t–\pi /2$ relative to the y axis.

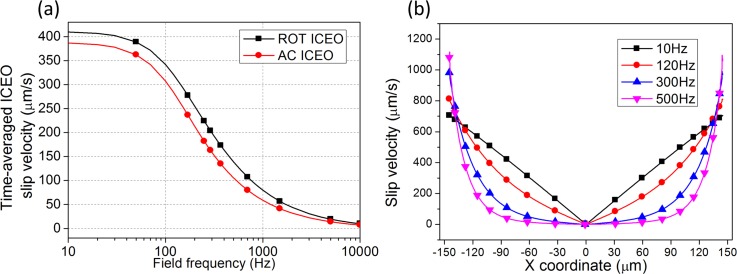
According to the range of field frequency applied, transient behaviour of ROT-ICEO can be depicted by two distinct schematic diagrams (Figs. 1(b) and 1(c)). At frequencies below the inverse RC charging time, E_t and E_b are nearly in phase, and in the DC limit, they are identical (Figs. 3(a)–3(c)). A straight FSL orthogonal to both E_b and E_t rotates synchronously with the same field. Because the ICEO flow velocity is maximized in the DC limit and the FSL has a very fast rotating line speed $v=2\pi f\rho$, the transient behaviour of ROT-ICEO at low field frequencies shows promise in microfluidic mixing applications. At higher field frequencies, because the slip flow is approximately along the direction of E_t, E_b is tangential to the curved FSL (Figs. 3(d)–3(f)), which is an entirely different situation from the parallel orientation at low frequencies. Moreover, the ICEO slip profile transforms gradually from being linear in the DC limit to being nonlinear above the RC relaxation frequency (Fig. 4(b)). At higher frequencies, the fluid motion is amplified near the electrode edge but is strongly suppressed around the FSP, implying less upward ICEO fluidic drag acting on the particle sample. In addition, though the relaxation characteristics of ROT-ICEO and ordinary AC-ICEO are similar, i.e., $u\left(f\right)=u\left(0\right)\frac{1}{1+{\left(\omega {\tau }_{\mathit{R}\mathit{C}}\right)}^2}$, ROT-ICEO is quicker than AC-ICEO over the entire frequency range, with a relaxation frequency (f_RC = 285 Hz) higher than for AC-ICEO (f_RC = 220 Hz). This implies a wider effective frequency range for ROT-ICEO compared with ordinary AC-ICEO (Fig. 4(a)). We would take advantage of this nonlinear feature around f_RC to produce a rapid but stable concentration of particle samples at the FSP drawn in from all directions by the ROT-ICEO bulk flow.

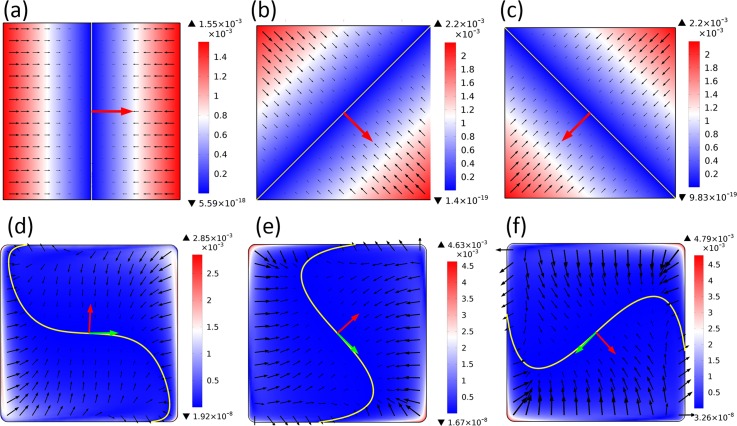
FIG. 3.

Transient behaviour of ROT-ICEO slip flow on the surface of a floating electrode at different time instant within an AC period for different characteristic field frequencies, with the green arrow, red arrow, and yellow line denoting the background field E_b, inducing surface tangential field E_t, and FSL, respectively. (a)–(c) in the DC limit, at (a) t = 0, (b) t = T/8, (c) t = 3 T/8. (d)–(f) for slightly above the RC charging frequency, at (d) t = 0, (e) t = T/8, (f) t = 3 T/8.

FIG. 4.

Theoretical estimates for the characteristics of ROT-ICEO slip flow: (a) Comparison of frequency-dependency of time-averaged ICEO slip velocity between ROT-ICEO and AC-ICEO. (b) Time-averaged slip velocity distribution of ROT-ICEO flow along the diagonal line of the floating electrode surface.

B. Particle behavior driven by ROT-ICEO slip

Above analysis of ROT-ICEO electrokinetic slip suggests to control particle motion via the relevant fluidic drag force. We consider the motion of a point particle in the flow field of ${\mathit{u}}_{\mathit{\rho }}$ and ${\mathit{u}}_{\mathit{\theta }}$ Eq. (2) for the DC limit, respectively.

Both the time-averaged radial slip $⟨{\mathit{u}}_{\mathit{\rho }}⟩=\frac{–\epsilon }{\eta }\frac{1}{1+\delta }{E_0}^2\frac{1}{2}\rho {\mathit{e}}_{\mathit{\rho }}$ and the corresponding transient one ${\mathit{u}}_{\mathit{\rho }}$ with an oscillating component have a FSP at the centre of metal square and cause a particle trapping process (supporting movie 1). Mathematically, since $\theta ={\theta }_0$ is obtainable from particle motion equation $d(\rho \hspace{0.17em}\text{cos}\hspace{0.17em}\theta ,\rho \hspace{0.17em}\text{sin}\hspace{0.17em}\theta )/\mathit{d}\mathit{t}={\mathit{u}}_{\mathit{\rho }}$, particle transient trajectory due to the action of ${\mathit{u}}_{\mathit{\rho }}$ is theoretically a straight line pointing towards the electrode center.

Driven by ${\mathit{u}}_{\mathit{\theta }}$ oscillating at twice of the field frequency, particle follows analytically the circular trajectory $\rho =r_0$, where $(r_0,{\theta }_0)$ is the initial particle location, namely, ${\mathit{u}}_{\mathit{\theta }}$ causes a kind of hydrodynamic torque that results in a net particle rotational velocity ${\Omega }_p$ in the co-field angular direction. The centre of rotation coincides with the central FSP, but the particle motional orbit is determined by r₀.

At first, we obtain the analytical solution of the particle motion equation $d(\rho \hspace{0.17em}\text{cos}\hspace{0.17em}\theta ,\rho \hspace{0.17em}\text{sin}\hspace{0.17em}\theta )/\mathit{d}\mathit{t}={\mathit{u}}_{\mathit{\theta }}$, which is equal to

(3).

$$\frac{d\theta }{\mathit{d}\mathit{t}}=-\frac{\epsilon }{2\eta }\frac{1}{1+\delta }{E}_0^2\hspace{0.17em}\text{sin}\left(2\omega t+2\theta \right),$$ (3a)

$$d\rho =0,$$ (3b)

where the effect of diffuse screening cloud at the surface of a charged colloid is excluded for the first demonstration of ROT-ICEO. Eq. (3a) equation can be well compared with Eq. (11) in Ref. 26, where traveling wave electrophoretic pumping of charged particles in a flow of air was theoretically studied, albeit without a double-layer screening effect.

1. Low-frequency synchronous motion

At low field frequencies, particles can rotate at a constant angular velocity in synchronism with the traveling wave. That is, with ${\theta }_0$ the initial position, a solution to Eq. (3) is

$$\theta ={\theta }_0-\omega t,$$ (4a)

$$\Omega =\frac{d\theta }{\mathit{d}\mathit{t}}=-\omega ,$$ (4b)

where substitution results in

$$\begin{array}{cc}{\theta }_0=\frac{1}{2}\arcsin \left(\frac{2\omega \eta \left(1+\delta \right)}{\epsilon E_0^2}\right);& \omega \le \frac{\epsilon {E_0}^2}{2\eta \left(1+\delta \right)}\end{array}.$$ (4c)

Thus, by adjusting its phase relative to the rotating field, the particle rotates counterclockwise at the wave frequency −$\omega$ in the direction of field. As the field frequency surpasses the peak electrokinetic flow velocity $\frac{\epsilon {E_0}^2}{2\eta \left(1+\delta \right)}$, it follows from Eq. (4b) that there is no ${\theta }_0$ consistent with a synchronous condition.

2. High-frequency asynchronous motion (time-averaged solution)

For $\omega \ge \frac{\epsilon {E_0}^2}{2\eta \left(1+\delta \right)}$, Eq. (3) can be written as

(5).

$$\frac{1}{2}{\int }_{{\xi }_0}^{\xi }\frac{d\xi }{\omega -\frac{\epsilon }{2\eta \left(1+\delta \right)}{E}_0^2\hspace{0.17em}\text{sin}(\xi )}={\int }_{t_0}^t\mathit{d}\mathit{t},$$ (5a)

$$\xi =2\omega t+2\theta .$$ (5b)

With ${\theta }_0$ the particle location when $t=t_0$, ${\xi }_0=2\omega t_0+2{\theta }_0$. Therefore, the high-frequency asynchronous motions are represented implicitly by the integral of Eq. (5)

$$\begin{array}{c}t-t_0=\frac{1}{\omega }\frac{1}{\sqrt{1-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)\omega }\right)}^2}}\\ \times \left(\arctan \frac{\frac{1+\text{cos}\hspace{0.17em}\xi }{\hspace{0.17em}\text{sin}\hspace{0.17em}\xi }-\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)\omega }}{\sqrt{1-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)\omega }\right)}^2}}-\arctan \frac{\frac{1+\text{cos}\hspace{0.17em}{\xi }_0}{\hspace{0.17em}\text{sin}\hspace{0.17em}{\xi }_0}-\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)\omega }}{\sqrt{1-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)\omega }\right)}^2}}\right).\end{array}$$ (6)

The time-averaged angular velocity, $⟨\frac{d\theta }{\mathit{d}\mathit{t}}⟩$, with $⟨\mathrm{A}⟩$ denoting the time-averaged value of A, follows from this expression by using it to determine the time $\Delta t$ needed for the particle to respond to one cycle of the driving function $\text{sin}\hspace{0.17em}\xi$. This is the time needed to advance from $\xi$ to $\xi +2\pi$

$$\begin{array}{cc}\Delta t=\frac{\pi }{\sqrt{{\omega }^2-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)}\right)}^2}}& \text{from}\hspace{0.17em}\xi \hspace{0.17em}\text{to}\hspace{0.17em}\xi +2\pi \end{array}.$$ (7)

Thus, the time-averaged time derivative of $\xi$ is given by

$$⟨\frac{d\xi }{\mathit{d}\mathit{t}}⟩=\frac{2\pi }{\Delta t}=2\sqrt{{\omega }^2-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)}\right)}^2}.$$ (8)

According to Eq. (5b), we obtain the time-averaged particle rotation rate in the direction of wave propagation

$$⟨\Omega ⟩=⟨\frac{d\theta }{\mathit{d}\mathit{t}}⟩=\frac{1}{2}⟨\frac{d\zeta }{\mathit{d}\mathit{t}}⟩-\omega =-\left(\omega -\sqrt{{\omega }^2-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)}\right)}^2}\right).$$ (9)

It is noteworthy that for $\omega$ ≫ $\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)}$

$$⟨\Omega ⟩\to -\frac{1}{2\omega }{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)}\right)}^2=-\frac{{\epsilon }^2{E}_0^4}{8\omega {\eta }^2{\left(1+\delta \right)}^2}=-\frac{{\epsilon }^2{E}_0^4}{16\pi f{\eta }^2{\left(1+\delta \right)}^2}.$$ (10)

3. Numerical simulation and physical description of transient behavior

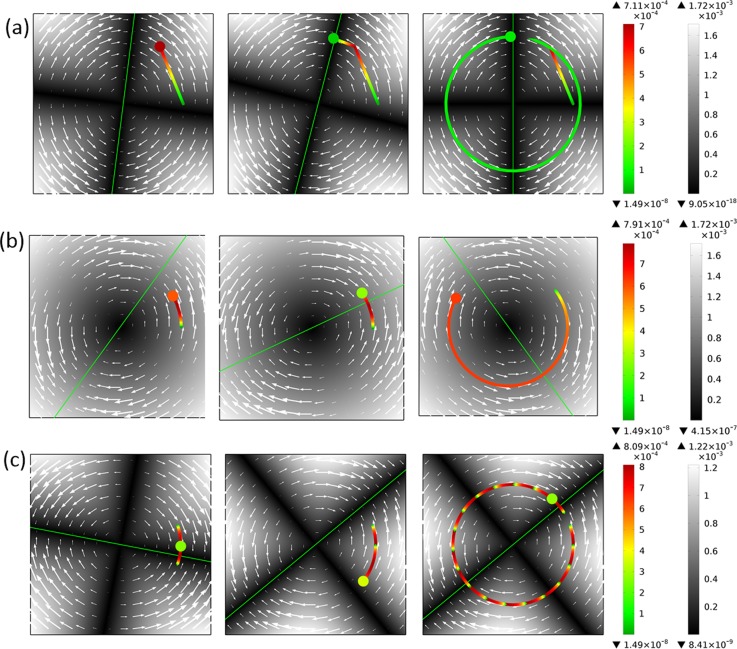
When rotation speed of FSL is slower than ICEO flow velocity, i.e., $2\pi f\rho <\left|u_{\theta }\right|\Rightarrow f\le f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}=\frac{\epsilon {E_0}^2}{4\pi \eta \left(1+\delta \right)}$, particle rotation rate ${\mathrm{\Omega }}_p\mathrm{=-2\pi f}$ (Eq. (4b)) is decided completely by the transient behaviour of dynamic FSL, and independent of initial particle location. After application of the AC voltage, particle at first moves against the field to find the rotating FSL, with the position ${\theta }_0=\frac{1}{2}\arcsin \left(\frac{2\omega \eta \left(1+\delta \right)}{\epsilon E_0^2}\right)$ given in Eq. (4c), and then try to follow the pace of dynamic FSL either in phase (far below f_peak, Fig. 5(a)) or with a certain spatial phase lag (around f_peak, Fig. 5(b)) in the stable stage of particle motion.

FIG. 5.

Demonstration of the importance of ROT-ICEO in producing rotating particle samples in the direction of applied rotating field on the surface of a metal square by solving $d(\rho \hspace{0.17em}\text{cos}\hspace{0.17em}\theta ,\rho \hspace{0.17em}\text{sin}\hspace{0.17em}\theta )/\mathit{d}\mathit{t}={\mathit{u}}_{\mathit{\theta }}$ numerically with arrows, line, the left and right bar indicating ${\mathit{u}}_{\mathit{\theta }}$, transient FSL, particle velocity, and $\left|{\mathit{u}}_{\mathit{\theta }}\right|$, respectively, for fixed E₀ = 10 V/mm (supporting movie 2): (a) for $f<f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$, particle moves to the position ${\theta }_0=\frac{1}{2}\arcsin \left(\frac{2\omega \eta \left(1+\delta \right)}{\epsilon E_0^2}\right)$ to first meet and then follow the rotating FSL, with a synchronous rotating rate ${\mathrm{\Omega }}_p\mathrm{=-2\pi f}$; (b) at $f=f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}=\frac{\epsilon {E_0}^2}{4\pi \eta \left(1+\delta \right)}$, particle always stays where the transient hydrodynamic torque is largest, thus the synchronous rotating mode becomes maximized with ${\Omega }_{\max }=-\frac{\epsilon {E_0}^2}{2\eta \left(1+\delta \right)}$; (c) at $f>f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$, particle locus oscillates constantly, but still performs a net co-field rotating motion, with the time-averaged rotating rate $⟨\Omega ⟩=-\left(\omega -\sqrt{{\omega }^2-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)}\right)}^2}\right)$.

At f = f_peak (Fig. 5(b)), there reaches an equilibrium between this angular-direction flow component and rotation of dynamic FSL, i.e., $2\pi f\rho =\left|{\mathit{u}}_{\mathit{\theta }}\right|$, the phase lag between the rotating motion of both particle and FSL becomes most important, and particle always stays where the transient hydrodynamic torque is largest, trying to maximize the particle rotation speed of ${\Omega }_{\max }=\frac{\epsilon {E_0}^2}{2\eta \left(1+\delta \right)}$.

Once f > f_peak, particle rotation supported by $\left|{\mathit{u}}_{\mathit{\theta }}\right|$ can no longer keep up with the dynamic FSL and become asynchronous with the REF (Fig. 5(c)). Under this circumstance, every time the rotating FSL passes it, the particle moves back and forward once, so that its locus oscillates with frequency twice that of the applied REF (Figs. 5(c) and 6(f)). Though there is no fixed phase relation between the dynamic FSL and particle rotation, particle still performs a net co-field rotating motion due to the action of a hydrodynamic torque from ${\mathit{u}}_{\mathit{\theta }}$. Within the high frequency range, the time-averaged rotating rate $⟨\Omega ⟩=-\left(\omega -\sqrt{{\omega }^2-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)}\right)}^2}\right)$ is given in Eq. (9). Even at higher frequencies, the rotation rate asymptotically approaches $-\frac{{\epsilon }^2{E}_0^4}{16\pi f{\eta }^2{\left(1+\delta \right)}^2}$ and is inversely proportional to the field frequency, as found from DNS as well. Interestingly, ${\mathrm{\Omega }}_p$ is determined by a combined effect of amplitude of angular velocity of ICEO flow field ${\Omega }_{\mathit{I}\mathit{C}\mathit{E}\mathit{O}}=\frac{\epsilon {E_0}^2}{2\eta \left(1+\delta \right)}$ and wave frequency $\omega =2\pi f$ of FSL, both of which are independent of particle locations, therefore, aids the synchronous rotation of a large number of particle samples. In this supportive role, we call ${\mathit{u}}_{\vartheta }$ the rotating flow component.

FIG. 6.

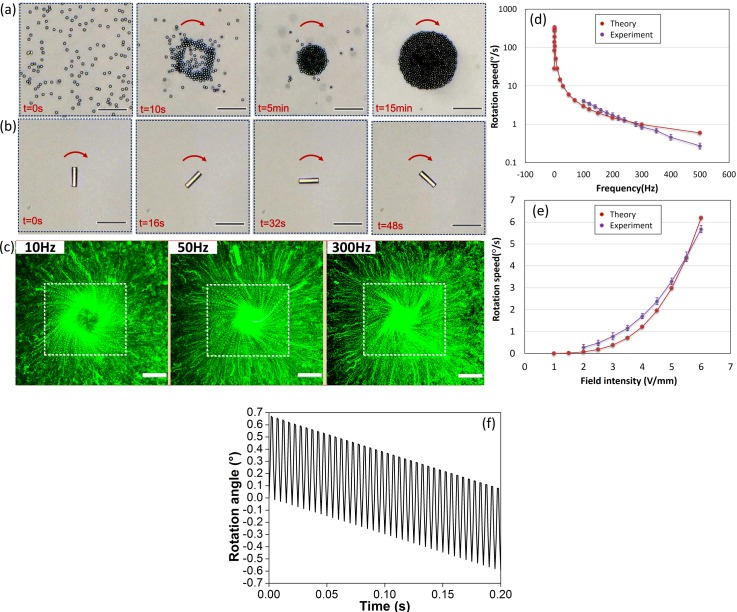
Experimental observation on rotational trapping of (a) a disk of silica particles of 4 μm in diameter(supporting movie 1); (b) an individual SU-8 rod of 11 μm in diameter and 47 μm in length on the surface of a metal square of d = 300 μm by ROT-ICEO with a rotating field of E0 = 5 V/mm and f = 200 Hz (100 Hz for the rod) (supporting movie 3). (c) Tracing of ROT-ICEO flow field with 500 nm fluorescent particles at different field frequencies (supporting movie 4). (d) and (e) Quantitative comparison of co-field particle rotation rate caused by ROT-ICEO between theory and experiment, (d) frequency-dependency of $⟨{\mathrm{\Omega }}_p⟩$ at fixed voltage amplitude 5 V; (e) Field intensity-dependency at f = 100 Hz. (f) Oscillating particle rotating motion in the co-field angular direction within the initial 0.2 s at f = 100 Hz as an example predicted by numerical simulation. The scale bar is 75 μm in (a)–(c).

To summarize, disregarding double-layer relaxation, the analytical solution for rotation rate of an ideal point particle from ROT-ICEO is

$$\left|⟨{\Omega }_p⟩\right|=2\pi f\hspace{1em}\text{for}\hspace{0.5em}f\le f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}=\frac{\epsilon {E_0}^2}{4\pi \eta \left(1+\delta \right)},$$ (11a)

$$\left|⟨{\Omega }_p⟩\right|=\left(2\pi f-\sqrt{{\left(2\pi f\right)}^2-{\left(\frac{\epsilon E_0^2}{2\eta \left(1+\delta \right)}\right)}^2}\right)\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}f\ge f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}},$$ (11b)

$$\left|⟨{\Omega }_p⟩\right|=\frac{{\epsilon }^2{E_0}^4}{16\pi f{\eta }^2{\left(1+\delta \right)}^2}\hspace{0.17em}\hspace{1em}\text{for}\hspace{0.5em}f\gg f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}.$$ (11c)

The time-averaged rotating phenomenon $\left|⟨{\Omega }_p⟩\right|$ can be approximated as a uniform circular motion of particles with the time-averaged trajectory $\{\begin{array}{l}\rho =r_0\\ \theta ={\theta }_0–\left|⟨{\Omega }_p⟩\right|\times t\end{array}$ (ignoring transient oscillating behaviour at twice the field frequency for $f>f_{\mathrm{peak}}$) in the direction of REF, with a maximum ${\left|⟨{\Omega }_p⟩\right|}_{\max }=\frac{\epsilon {E_0}^2}{2\eta \left(1+\delta \right)}$ at a critical field frequency $f=f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$ (Fig. 6(d)). The voltage amplitude A = 1–10 V is usually small in practical experiment to suppress other undesired non-equilibrium electro-surface phenomenon (NESP), resulting in a quite small value of the peak rotation frequency f_peak < 10 Hz. Since the effect of DC electrokinetics adversely affects the experimental results for $f\le f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$, we validate the analytical particle rotation rate Eq. (3) for the frequency range $f>f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$. Qualitative deflection of trajectories of 500 nm fluorescent particles in the direction of the field while they are drawn in towards the center of a metal square during the flow visualization experiment preliminarily demonstrates the correctness of our theory (Fig. 6(c)). Rotational trapping of a disk of silica spheres (Fig. 6(a)) and an individual SU-8 rod (Fig. 6(b)) successfully proves the existence of the two flow components ${\mathit{u}}_{\mathit{\rho }}$ (for particle trap) and ${\mathit{u}}_{\mathit{\theta }}$ (for particle rotation) in the above analysis, and we further quantify the value of $\left|⟨{\Omega }_p⟩\right|$ in the experiment to make a detailed comparison with our theory.

The frequency-dependence of ${\Omega }_p\propto 1/f$ from theory for f ≫ $f_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$ matches well with the experimental data below $f_{\mathit{R}\mathit{C}}=\sigma /2\pi R{C}_0\approx 300\hspace{0.17em}\mathrm{Hz}$(Fig. 6(d)). However, beyond $f_{\mathit{R}\mathit{C}}$ this downward trend ${\Omega }_p\propto 1/f$ given by theory overestimates that from experimental measurement, since electrochemical ion relaxation beyond the DC limit disregarded by current theory further decreases the flow velocity of ROT-ICEO. The voltage-dependent fourth-power growth trend of ${\Omega }_p\propto A^4$ from theory is derived in the absence of a wall friction force that may become important when ROT-ICEO is weak, as demonstrated by a good matching between theory and measurement data at moderate voltages, while some discrepancies are witnessed for small rotating rate (Fig. 6(e)).

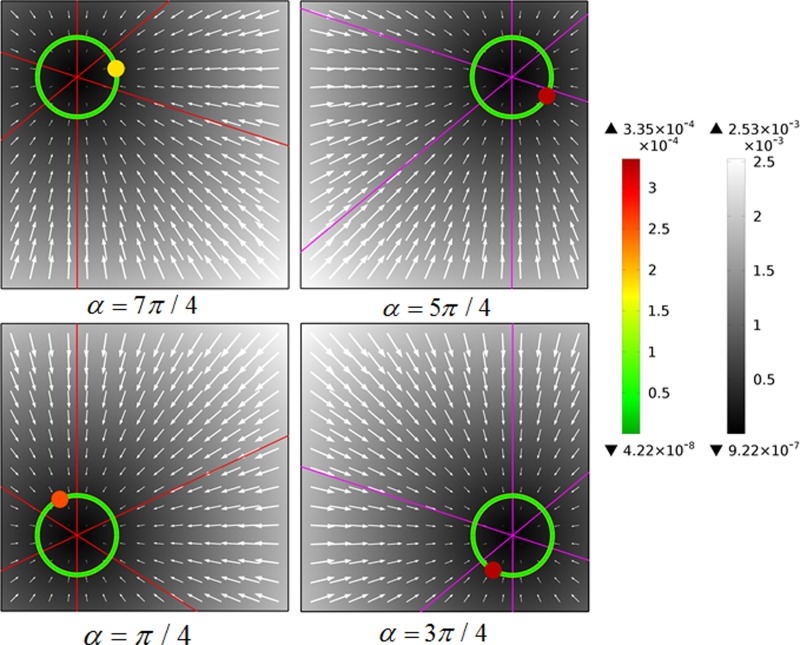
C. Tunable ROT-ICEO

We then demonstrate that the rotating axis of ROT-ICEO can be arbitrarily adjusted by imposing a gate voltage to the metal square, introducing the concept of “tunable ROT-ICEO.” We briefly analyse the contribution of first Fourier mode of the gate voltage $f_0=B\hspace{0.17em}\text{cos}\hspace{0.17em}(\omega t+\alpha )$. The biased induced zeta potential ${\zeta }^{\prime }=\zeta +\frac{1}{1+\delta }B\hspace{0.17em}\text{cos}\left(\omega t+\alpha \right)$ leads to an asymmetric slip

$$\mathit{u}=\frac{–\epsilon {E_0}^2}{\eta \left(1+\delta \right)}\left(\text{cos}\left(\omega t\right){\mathit{e}}_{\mathit{x}}\hspace{0.17em}–\hspace{0.17em}\text{sin}\left(\omega t\right){\mathit{e}}_{\mathit{y}}\right)\left(\left(x+\frac{B}{E_0}\text{cos}\hspace{0.17em}\alpha \right)\text{cos}\left(\omega t\right)–\left(y+\frac{B}{E_0}\text{sin}\hspace{0.17em}\alpha \right)\text{sin}\left(\omega t\right)\right),$$ (12)

with a transient FSL $y=\cot \omega t\left(x+\frac{B}{E_0}\text{cos}\hspace{0.17em}\alpha \right)–\frac{B}{E_0}\text{sin}\hspace{0.17em}\alpha$ on the electrode surface. FSL still rotates synchronously with the REF, but its rotating axis deviates from the electrode center O to $O\prime \left(x_1,y_1\right)=\left(–\frac{B}{E_0}\text{cos}\hspace{0.17em}\alpha ,–\frac{B}{E_0}\text{sin}\hspace{0.17em}\alpha \right)$ due to imposition of a second AC voltage to the gate electrode. We now use O′ as the origin of polar coordinate for analytical convenience, with $\theta \prime ={\text{tan}}^{–1}\frac{y–y_1}{x–x_1}$. Angular component of the slip velocity with respect to the new origin O′ becomes ${\mathit{u}}_{\mathit{\theta }\prime }=\frac{–\epsilon }{\eta \left(1+\delta \right)}{E_0}^2\frac{–\rho \prime }{2}\text{sin}\left(2\omega t+2\theta \prime \right){\mathit{e}}_{\mathit{\theta }\prime }$. The particle trajectory is mathematically still a circle $\rho \prime =r_0\prime$. The solution of the corresponding particle motion equation $d(\rho \prime \hspace{0.17em}\text{cos}\hspace{0.17em}\theta \prime ,\rho \prime \hspace{0.17em}\text{sin}\hspace{0.17em}\theta \prime )/\mathit{d}\mathit{t}={\mathit{u}}_{\mathit{\theta }\prime }$ is the same as the previous floating case, merely with the origin of polar coordinate shifted to O′. As a result, both the non-tunable and tunable ROT-ICEO induce intrinsically identical rotating trait $⟨{\Omega }_p⟩$ of particle samples. That is, imposing a second AC voltage to the gate electrode helps to adjust the rotational trapping center of particle samples, while does not play a role in affecting the rotating rate.

The time-averaged flow $⟨\mathit{u}⟩=–\frac{\epsilon }{\eta \left(1+\delta \right)}{E}_0\left(\frac{1}{2}B\left(\text{cos}\hspace{0.17em}\alpha {\mathit{e}}_{\mathit{x}}+\text{sin}\hspace{0.17em}\alpha {\mathit{e}}_{\mathit{y}}\right)+\frac{E_0}{2}\left(x{\mathit{e}}_{\mathit{x}}+y{\mathit{e}}_{\mathit{y}}\right)\right)$ is composed of a net pumping flow in an arbitrarily axial direction determined by the gate voltage and the original symmetric part (Fig. 7). We concern here for the case of $B\ll A$, so that the pumping effect may be trivial. The new FSP where particle samples are trapped has also shifted to O′. By taking B = A/10, $\alpha =\pi /4,3\pi /4,5\pi /4,7\pi /4$, we solve the particle motion equation in the transient flow field of tunable ROT-ICEO.

FIG. 7.

Demonstration of the concept of tunable ROT-ICEO by solving $d(\rho \prime \hspace{0.17em}\text{cos}\hspace{0.17em}\theta \prime ,\rho \prime \hspace{0.17em}\text{sin}\hspace{0.17em}\theta \prime )/\mathit{d}\mathit{t}={\mathit{u}}_{\mathit{\theta }\prime }$ numerically with the arrows, line, the left and right bar indicating $⟨{\mathit{u}}_{\mathit{\rho }\prime }⟩$, FSL, the particle transient velocity and $\left|{\mathit{u}}_{\mathit{\rho }\prime }\right|$, respectively.(The verification experiments refer to supporting movie 5.)

While particles are transported to the new FSP, the dynamic FSL rotating around O′ controlled by the gate voltage exerts a similar hydrodynamic torque on the particle sample as the previous case (Fig. 5), but the rotating axis O′ has now shifted to a desired position on the electrode surface (Fig. 7).

D. Exploring large-scale ROT-ICEO rotational trapping

Last but not least, trapping experiments with an array of multiple floating electrodes are performed (Fig. 8). By switching on the background REF, particle samples are quickly trapped via the action of $⟨{\mathit{u}}_{\mathit{\rho }}⟩$ on all of the electrode surfaces. As the electrodes along both x and y directions are widely spaced, the induced double-layer polarization of each floating electrode in the 4 × 4 array is independent. Consequently, ROT-ICEO for each electrode is independent of those of the other electrodes. Particles form circular disks on the four centralized electrodes, whereas asymmetric elliptical patterns are produced on the twelve periphery electrodes. This is because they are placed in closer proximity to the four driving electrodes where AC electro-osmotic flow has an adverse influence. Despite this small difference, both trapping and rotating mechanisms are in essence identical with the previous experiments with a single floating electrode. Consequently, performance of the particle rotational trap by a ROT-ICEO flow can be greatly enhanced by having a number of floating electrodes, there being no obvious increase in energy dissipation.

FIG. 8.

Trapping experiment with a 4 × 4 array of multiple floating electrodes: (a) initial uniform distribution of colloidal suspension on the electrode array; (b) rotational trapping results after switching on the background REF for 10 s, and (c) for 10 min. The scale bar is 150 μm.

IV. CONCLUSIONS

In summary, we demonstrate that ROT-ICEO with a rotating FSL causes stable rotation or rotational trap of micro-nano object using weak rotating electric fields. To our knowledge, the first report of this exciting experimental phenomenon effectively adds to a new category of current ICEO theory. The remarkable diversity and flexibility of ROT-ICEO in manipulating particles are witnessed by simultaneously translating and (or merely) rotating either a large crowd of particle samples or an individual micro-rod with desired motion trajectories. Furthermore, large-scale rotational trapping of colloidal particles due to ROT-ICEO is successfully achieved by using an array of multiple floating electrodes embedded within the background circularly polarized field. In the near future, ROT-ICEO would serve as a novel manipulation tool in the interdisciplinary realms of electrokinetics, electrochemistry, and microfluidics.

SUPPLEMENTARY MATERIAL

See supplementary material for the numerical simulation model of the PICEO slip flow field, as well as a series of experimental videos on microfluidic particle rotational trapping caused by ROT-ICEO.