Abstract
Purpose:
Accurate segmentation of pelvic organs in CT images is of great importance in external beam radiotherapy for prostate cancer. The aim of this studying is to develop a novel method for automatic, multiorgan segmentation of the male pelvis.
Methods:
The authors’ segmentation method consists of several stages. First, a pretreatment includes parameterization, principal component analysis (PCA), and an established process of region-specific hierarchical appearance cluster (RSHAC) model which was executed on the training dataset. After the preprocessing, online automatic segmentation of new CT images is achieved by combining the RSHAC model with the PCA-based point distribution model. Fifty pelvic CT from eight prostate cancer patients were used as the training dataset. From another 20 prostate cancer patients, 210 CT images were used for independent validation of the segmentation method.
Results:
In the training dataset, 15 PCA modes were needed to represent 95% of shape variations of pelvic organs. When tested on the validation dataset, the authors’ segmentation method had an average Dice similarity coefficient and mean absolute distance of 0.751 and 0.371 cm, 0.783 and 0.303 cm, 0.573 and 0.604 cm for prostate, bladder, and rectum, respectively. The automated segmentation process took on average 5 min on a personal computer equipped with Core 2 Duo CPU of 2.8 GHz and 8 GB RAM.
Conclusions:
The authors have developed an efficient and reliable method for automatic segmentation of multiple organs in the male pelvis. This method should be useful for treatment planning and adaptive replanning for prostate cancer radiotherapy. With this method, the physicist can improve the work efficiency and stability.
Keywords: automatic multiorgan segmentation, radiotherapy treatment planning, image segmentation, cancer treatment
1. INTRODUCTION
Prostate and bladder cancers are two common cancers in the male pelvis. In particular, prostate cancer is the most common cancer and the second leading cause of cancer death among men in the US.1,2 Radiotherapy is a major treatment modality for prostate cancer.3 The accuracy of the segmentation for pelvic organs plays a critical role in maximizing the efficacy of radiotherapy.
In current practice, the gross tumor volume and surrounding critical organs are manually delineated on planning CT images. However, such a manual segmentation process is both time-consuming and subjective, leading to large intraobserver and interobserver variations.4 Moreover, in adaptive radiotherapy, manual segmentation is very time consuming and instability on daily cone beam computed tomography (CBCT). For example, in online adaptive schemes, Ahunbay et al. proposed an online adaptive replanning method for prostate radiotherapy.5 In light of these, an automatic or semiautomatic segmentation method of pelvic organs on CT image is needed to improve the efficiency and accuracy of the delineation process.
There are two major challenges for the automatic segmentation of pelvic organs. First, CT images have a low soft tissue contrast in the pelvis due to the small intensity differences between organs (see Fig. 1). Therefore, segmentation solely based on the intensity of the image is difficult to obtain a reliable result. In the past, several methods have been proposed to address this challenge for segmentation in the lung,6–12 heart,13–17 and liver.18–22
FIG. 1.
Examples of the pelvic organs show low soft-tissue contrast on CT image.
The second challenge relates to the changing morphology of pelvic organs during the treatment course, due to normal physiological activities such as bowel filling and bowel gas, both on an interfractional basis and intrafractional basis. Several segmentation methods for the pelvic organs have been proposed to address the variability of the shape and appearance of the pelvic organs.23–26 The most popular category of these methods is the segmentation algorithm based on the deformation model.27–34 For example, Broadhurst et al. proposed a deformable model based on the histogram-statistics appearance model for prostate segmentation.32 Pizer et al. proposed a medial shape model to segment bladder, prostate, and rectum from CT images.27 Methods using deformable models based on the statistical information extracted from both organ shape and image appearance have been studied in recent years and these methods showed good performance for pelvic organs. However, segmentation results using these methods depend on a good initial model. Another class of methods is based on the deformable registration.35–37 Liao and Shen et al. presented a method to guide the deformable registration of prostate CT with an evaluation function.37 However, as mentioned earlier, the accuracy of registration-based methods can be unreliable because of the complex physiological activities in the pelvis.
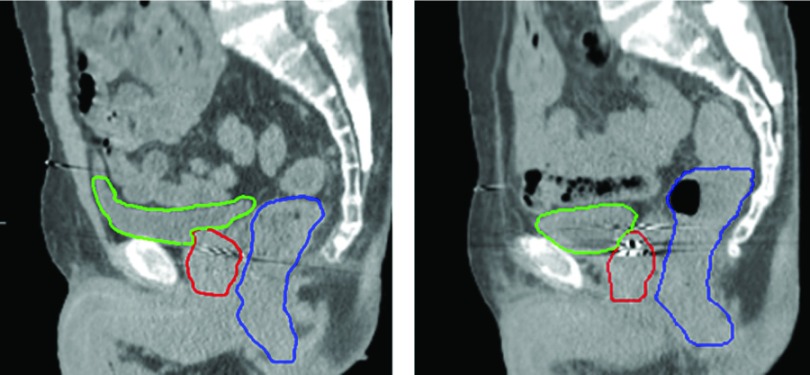
In recent years, the shape model based on prior knowledge and machine learning has been widely used in automatic segmentation of CT images. This type of methods uses a training dataset as the prior knowledge. The training dataset is divided into two kinds: population-based and patient-specific. The method based on the patient-specific model often has higher segmentation accuracy because the patient-specific dataset consists of several CT images from the same patients, and there is a large shape variation between different patients (see Fig. 2). For example, Stough et al. proposed a segmentation method based on regional appearance within a deformable model.38 Feng et al. proposed a segmentation method based on population and patient-specific statistics for radiotherapy.30 However, the patient-specific training dataset requires at least four CT scans from the same patient, prohibiting its use for the first few daily CT scans. On the other hand, population-based method can be used for every CT image during treatment. Nevertheless, these methods have limited segmentation accuracy.
FIG. 2.
Sagittal slices from two patients manually contoured by the same radiation oncologist. Prostate, bladder, and rectum were, respectively, contoured by red, green, and blue thick solid curves. The images show that the organ shapes and appearances are very different among patients. (See color online version.)
In this paper, we develop a novel automatic, multiorgan segmentation method based on CT images of prostate cancer patients using region-specific shape information. A statistical point distribution model using principal component analysis (PCA) is first built based on the training dataset to grossly capture the major variation of pelvic organs. A novel region-specific agglomerative hierarchical cluster model is established to further improve the segmentation accuracy. The aim of this study is to present a novel segmentation method and to evaluate its accuracy on a large number of CT images.
2. METHODS AND MATERIALS
The method is divided into two main parts. The first part is the training process which needed to be performed before the automatic segmentation. And this training process is just needed once to calculate the point distribution model and the region-specific hierarchical appearance cluster (RSHAC) model. The second part is the automatic segmentation part which mainly includes a coarse and refined segmentation process. The two models obtained in the training process will be used to guide the segmentation in this part. The whole flow chart of this method was shown in Fig. 3.
FIG. 3.
The flow chart of the whole method.
2.A. Patient data for training and testing
The training dataset included a total of 50 planning CT scans with a slice size of 512 × 512 and 200–400 slices (average 256) at a voxel resolution of 1.0 × 1.0 × 1.5 mm. The contours of the pelvic organs in the training dataset were manually delineated by an experienced medical physicist and reviewed by a radiation oncologist.
The CT images used for validation of the proposed segmentation method were from another twenty male patients with prostate cancer: twelve of them were in the early diagnosis of prostate cancer and the other eight patients were in the middle stage of the prostate cancer. The planning CT of these twenty prostate patients was used as the test data. The manual contour of these planning CTs will serve as references to test the segmentation accuracy.
2.B. Training process
In the training process, the shape model and appearance model of the multiple pelvic organs were calculated, respectively.
2.B.1. Preprocessing of the training data
First, the prostate, bladder, and rectum were manually delineated slice by slice for the 50 training datasets. And then one CT image of the 50 training datasets was randomly selected as the reference image. The rest 49 CT images from the training dataset were registered to the reference image using the rigid registration based on the pelvic bone (Fig. 4). And then the 2D slice-by-slice mesh was then connected to 3D triangular mesh based on “Marching cubes.”39 After the 3D triangular mesh was obtained, the jagged contours were smoothed using a simple Laplacian smoothing operation by moving each vertex to the average position with neighboring vertices.40 The smoothing method was performed with five iterations. Second, the number of triangles was reduced by a down-sampling process. The triangle meshes of the pelvic organs were reduced to 10% of the original mesh size. After the down-sampling, the vertices’ number of the contour of each organ was about 3000. Therefore, each contour with about 3000 points was adjusted to 3000 points by an up-sample or down-sample. This up- or down-sample was averaged distributed in the whole contour according to the number of vertices which were needed to be increased or decreased. Third, the contour was smoothed again by the same method of the first step. Finally, due to the volume shrinkage caused by smoothing, the contour meshes were magnified to the same volume as the original ones. After all contours of the data sets were confirmed, each contour was mapped to binary image after the second rigid registration based on the pelvic bone between each CT image. The binary images will be well registered by the free-form deformation registration based on B-spine.41 The vertex-to-vertex between each two contours mesh will be found by applying the calculated deformable field to the contour vertex using tri-liner interpolation (Fig. 5). And the whole preprocessing was shown in Fig. 6.
FIG. 4.
(a) The training dataset containing 50 CT images of pelvic organs. (b) All the pelvic organs were aligned by pelvic bone, and the outline of each color represents one kind of organs (prostate, bladder, and rectum were contoured by red, green, and blue solid curves, respectively). (See color online version.)
FIG. 5.
(a) The bladder contours from two patients were mapped to two binary images. The cyan and red represent each image and the white represents the overlap of these two images. (b) Applying the B-spline free-form deformable registration, the two binary images were well registered. This deformation field will be applied to contour vertex using tri-liner interpolation. (See color online version.)
FIG. 6.
The preprocessing of modeling with (a) the original 2D slice-by-slice mesh, (b) initial 3D triangular mesh, (c) contour with only one smooth process, and (d) the final contour with down-sampling and second smoothing.
The shapes of the pelvic organs were parameterized by the set of positions of L (L = 3000) contour vertex of each organ. If we denote as the position of the jth point in the ith CT in the training dataset, then the surface shape vector can be represented as
| (1) |
2.B.2. Establishment of a point distribution model of pelvic organs
In this process, it was assumed that the set of surface shape vector could be seen as samples from a random process. For anatomical reasons, displacements of L vertices due to the deformation of pelvic organs were highly correlated, which implied that the dimensionality of the multivariate statistical problem was actually much smaller than 3 × L. For a 3 × L dimensional problem with N (N = 50) samples, we used a method from multivariate statistics, PCA,42,43 to model the anatomical shape variation of pelvic organs. The eigenmodes which represent the shape variation of the pelvic organs will be used to guide the segmentation of the validation images.
After the parameterization of the pelvic organs in the training dataset, the geometry of the pelvic organs in image i (i = 1, …, N) was represented by the shape vector pi. According to the shape vector, the mean vector p0 of the N vector was first computed by
| (2) |
Next, a covariance matrix C with dimensions 3L × 3L which represents the shape variation of the pelvic organs was calculated,
| (3) |
After the matrix C was obtained, we decomposed the shapes of the deformed organ by the following formula:
| (4) |
where qn represent the eigenvectors of the covariance matrix of the input data p, corresponding to the N eigenvalues λn. The coefficients ψn were normally distributed random variables with zero means and the corresponding eigenvalues λn as variances.
In order to reduce the number of point distribution models, we need to choose M (M < N) eigenmodes to represent the deformation pattern of the pelvic organs. The mean residual error R[M] was calculated as follows:
| (5) |
| (6) |
| (7) |
where is the 3D vector of local representation error of the jth vertex and ith contour.
Finally, the number of eigenmodes M = 15 was chosen such that 95% of the pelvic organs’ shape variation was described and the mean residual R[M] close to 0. The eigenmodes and the corresponding weight matrix will be used for the segmentation process on validation CT images.
2.B.3. Establishment of an appearance model of pelvic organs
In order to improve the segmentation accuracy and efficiency, a reliable, region-specific appearance model of pelvic organs was established, which is the core part of the proposed method. In this process, each contour of pelvic organ was divided into five patch surfaces according to the suggestion of the chosen experienced radiation oncologist. At first, three radiation oncologists divided each pelvic organ of two chosen CT volume data into five patches independently. In this chosen process, the mutual information between two patch areas was calculated. And then, the mutual information between each pair of corresponding patch from the two CT data was calculated and averaged. At last, the radiation oncologist with the largest average mutual information was chosen to decide the patch pattern. After the patch pattern was obtained, the patch pattern was transformed to the 50 CT images of the training dataset based on the surface mapping vectors obtained in the preprocessing stage (the patch pattern on one of the CT images was shown in Fig. 7). For each surface patch, 50 CT images of the dataset which have been divided were grouped together for hierarchical clustering calculation using similarity based on the cross-correlation between the different patches as the figure of merit. In the hierarchical clustering process, N (N = 50) surfaces were first traded as N clusters. The distance between each two clusters was calculated using cross-correlation. The two clusters with the smallest distance were combined to a new cluster. After then, the number of the clusters was decreased to N − 1. The average surface of this new cluster will be calculated as the representative of this cluster. And then the two clusters with the smallest distance were combined to a new cluster in the same way. This clustering calculation will be performed until all the N original clusters were combined (the number of cluster decreased to 1). After the clustering calculation was finished, each cluster was transformed to its corresponding profile by sampling voxel values along the normal direction of the contour surface. Finally, an agglomerative hierarchical cluster tree was established (see Fig. 8). The automatic segmentation will be performed from the first layer to the last layer of the agglomerative hierarchical cluster tree. After the segmentation in first layer, the next layer was chosen based on the similarity respective between the next two profiles. And the final surface of this patch will be obtained after the segmentation on the last layer of the agglomerative hierarchical cluster tree. In this process, the number of the profiles in the tree was a key influence of this algorithm. The segmentation results of each patch will be highly improved when the number of the profiles was huge enough to include every form of this patch.
FIG. 7.
(a) Pelvic organs were divided into five surface patches on the chosen shape. (b) The patch instance in one slice. In (a) and (b), the five surface patches were marked by green, yellow, red, purple, and pink, respectively. The overlap areas between each patch were marked by the average color of the corresponding patch. (See color online version.)
FIG. 8.
For each surface patch, an agglomerative hierarchical cluster tree for the 50 profiles is calculated using similarity between the profiles as the figure of merit. (a) The patch pattern reflected by one slice in one of the 50 profiles. (b) The 50 patch surface of one patch region. (c) The agglomerative hierarchical cluster tree with 50 nodes in the last layer corresponding to the 50 profiles.
2.C. Automatic segmentation on new images
This segmentation method uses principal component analysis to model organ shapes and hierarchical clustering to model the appearance of each organ surface patch. Coarse and refined segmentations are done iteratively for each surface patch to find the best reference patch profile via a hierarchical cluster decision tree. Final segmentation is obtained using the generated global reference profile.
The segmentation process on the validation CT images was divided into three stages. First, a rigid registration was performed between the validation CT and the chosen CT image of the training dataset. Second, each patch in the validation CT was segmented with a coarse segmentation and a refined segmentation based on the RSHAC and PCA eigenmodes. Last, the segmentation results of the five patches were combined to form a new segmented CT image as the initial segmentation of the whole validation CT [see Fig. 9(a)], and the final segmentation image was obtained with a coarse segmentation followed by a refined segmentation process on the new validation CT just acquired.
FIG. 9.
Flow chart of the automatic segmentation process on the validation CT images. (a) The flow chart of the segmentation process of each patch and five patches made up the initial segmentation of the pelvic organs. (b) The process of finding the best patch in the agglomerative hierarchical cluster tree. The x-axis was the sequence number of 50 profiles. The red line is the example of a search path to the most similar patch of the 50 profiles. (See color online version.)
The pelvic organ contour of each patch on the validation CT was initialized after the rigid registration based on the pelvic bone with one of the CT images in the training dataset. The initial surface patch of the validation CT will be the surface patch of the chosen training CT. After the registration, the contour of the pelvic organs on the validation CT was initialized to five patch . For each patch of the validation CT, the most similar patch in the RSHAC model will be found through several segmentation processes with two steps of each level of the tree model [Fig. 9(b)].
During the segmentation process on the RSHAC model, PCA modes were used as the guidance information in each segmentation calculation. Besides the deformation pattern stipulated by the eigenmodes, a cost function Ec based on the directional gradient field was also needed to measure how well the deformed contour matched the underlying edge of the pelvic organs on the validation CT image. For this purpose, the extra interior and exterior contours of each patch ci,int and ci,ext were created by shrinking and expanding the vertices of the initial contour ci=1,2,3,4,5 by 5 mm along the normal direction to each vertex.
The segmentation of patch No. 1 was chosen as an example of the segmentation process on the RSHAC model. (The segmentation of all the five patches was performed in the same time.) The segmentation contour was deformed starting from the initial contour c1 by changing which was the weight matrix of the eigenmodes based on the PCA modes,
| (8) |
At the same time, interior contour candidate and exterior contour candidate were also deformed in the same way.
The cost function Ec was used to measure how well the deformed contour matched the underlying edge of the pelvic organs on the validation CT image. The cost function was evaluated on the interior, central, and exterior contours to capture information of the neighborhood of the edge of the pelvic organs,
| (9) |
where Num is the number vertex in this patch. and denote the intensity of the reference image and validation image sampled by the vertex of contour c. and are the directional gradient values on the jth vertex of the interior and exterior reference contours. and are the directional gradients on the jth vertex of the interior and exterior segmentation contours.
The optimum shape vector P* was selected when the cost function Ec achieves the smallest value,
| (10) |
where σi is the square root of the eigen value λi. The search for the optimum shape parameter vector was carried out by a simplex optimizer within the interval to minimize the cost function of Ec.
After the optimum shape vector was obtained, the coarse segmentation process on this layer of the RSHAC model was finished. The most similar patch in this layer was found based on the similarity measure between the segmented validation patch and each patch of this layer.
However, the RSHAC model was established based on the training dataset. The similarity patch needs an adjustment to match the real situation of the validation CT. So a new cost function of the refined segmentation process was defined and used to adjust the chosen patch to match the underlying edge of this patch on the validation CT,
| (11) |
where ESimilarity denotes the level of similarity between the validation image and reference image,
| (12) |
where and denote the marginal entropies of the surface area between the interior and exterior contours of the validation image and the reference image; denotes their joint entropy, which is calculated from the joint histogram of the two surface areas.
In order to constrain the segmentation to be smooth, the penalty term ECurvature was introduced to regularize the refined segmentation. The general form of such a penalty term has been described by Wahba.44 In 3D, the penalty term takes the following form:
| (13) |
where Volume denotes the volume of the image domain. This quantity is the 3D counterpart of the 2D bending energy of a thin-plate of metal and defines a cost function which is associated with the smoothness of the segmentation.
In order to prevent the possibility of overlapping between the pelvic organs, a penalty term EOverlap is defined. For two pelvic organs PO1 and PO2, the EOverlap was defined as the ratio of the volume of intersection to the volume of union between PO1 and PO2,
| (14) |
where EOverlap represent the degree of overlapping between each two pelvic organs.
After the refined segmentation of patch 1, the segmentation of one layer in the RSHAC model was finished. This segmentation process will continue in the next layer until the most similar patch in the last layer (one of the 50 profiles in this tree) was found and adjusted. The segmentation of the five patches was finished at the same time. In the last, preliminary contour of the whole three pelvic organs was obtained by making the union of the five segmented surface of corresponding patch. And the overlap areas and holes between each two patches were averaged and interpolated. The pelvic organs of the validation CT were accurately localized and contoured after an adjustment based on using ECurvature and EOverlap.
2.D. Validation of segmentation results
In order to evaluate the performance of this automatic segmentation, the 210 validation CT images were manually delineated by an experienced medical physicist. The Dice similarity coefficient (DSC) between the automated and manually segmented validation CT images was first chosen as the evaluation criterion.45 Specifically, DSC is defined as
| (15) |
where Va∩m denotes the number of voxels in the overlapping area between the validation image segmented by the automatic (a) and the manual (m) methods. Similarly, Va and Vm denote the number of voxels in the validation image, respectively, segmented by the automatic (a) and the manual (m) methods.
In order to further access the performance of this method, the mean absolute distance (MAD) was also calculated. The MAD is the average of absolute differences between each value in a dataset and the average value of this dataset. In the validation process, the dataset used for the calculation of MAD consists of the surface distance (SD) between the automated and manual segmentation results. The SD is calculated by the distance between the surfaces of each pelvic organ of the manual and automated segmentation images along 1000 rays directed to the spherical surface from the centroid of the manually contoured validation CT. The results of the evaluation will be introduced in Sec. 3.
3. EXPERIMENT RESULTS
We first determined the number of eigenmodes required in the PCA point distribution model. In order for the PCA model to accurately represent the deformation pattern of the pelvic organs, the average residual errors need to be controlled within 1 mm. At the same time, the number of eigenmodes needs to be as small as possible to minimize overfitting and reduce computational complexity. In Fig. 10, we can see 15 eigenmodes represented more than 95% (95.2%) of the pelvic organs’ shape variation. So we chose 15 eigenmodes for the segmentation process to balance the accuracy and efficiency.
FIG. 10.
The integral of the eigenvalues for the training dataset as a function of the number of PCA modes. The sum of all eigenvalues was normalized to 100%. The square column which represents the 15th eigenmodes was marked by a green circle.
The whole process of the automatic segmentation process took on average 5 min on a personal computer equipped with Core 2 Duo CPU of 2.8 GHz and 8 GB RAM. An example was shown in Fig. 11, the comparison between automatically and manually segmented contours.
FIG. 11.
The automatically segmented pelvic organ contour (red, green, and blue thick solid curves) and manually delineated contours of the pelvic organs (yellow thick solid curves) were overlaid on a sagittal section of a validation CT image. (See color online version.)
In order to quantify the accuracy of the automatic segmentation method on the validation dataset, we showed the average DSC value of each patient. The average test values of these patients were shown by histogram in Fig. 12 (after ordering). And the average MAD of each patient was shown in Fig. 13.
FIG. 12.
The DSC of prostate (blue), bladder (orange), and rectum (gray) for twenty patients. (See color online version.)
FIG. 13.
The average MAD of prostate (blue), bladder (orange), and rectum (gray) for twenty patients. (See color online version.)
The automatic segmentation results of the prostate and bladder agreed well with those based on manual segmentation. The average DSC of the prostate is 0.751 (range: 0.697 and 0.834). Our segmentation results of the prostate were consistent across patients with the maximum difference of 0.137 in terms of DSC, suggesting its robustness against differences of the prostate anatomy. The performance in the case bladder was slightly better, with an average DSC of 0.783, and sixty percent of the DSC value of the bladder was over 0.80. However, the segmentation of the rectum was not as good, with the average DSC being only 0.573, and the highest DSC value being less than 0.70. The spatial discrepancy based on MAD showed a similar trend. As mentioned earlier, many methods have been proposed about the automatic segmentation of the pelvic organs in the CT of prostate cancer. In order to intuitively contrast these methods, the parameters of these methods were shown in Table I.
TABLE I.
The comparison of different methods.
| Method | Gao et al. (Ref. 24) | Gao et al. (Ref. 28) | Shao et al. (Ref. 29) | Feng et al. (Ref. 30) | Ourmethod | |
|---|---|---|---|---|---|---|
| Prostate | Mean DSC | 0.87 ± 0.04 | 0.86 ± 0.05 | 0.88 ± 0.02 | 0.89 ± 0.05 | 0.75 ± 0.07 |
| Mean MAD (cm) | NA | NA | NA | NA | 0.37 | |
| Bladder | Mean DSC | 0.92 ± 0.05 | 0.91 ± 0.10 | 0.86 ± 0.08 | NA | 0.78 ± 0.08 |
| Mean MAD (cm) | NA | NA | NA | NA | 0.303 | |
| Rectum | Mean DSC | 0.88 ± 0.05 | 0.79 ± 0.20 | 0.84 ± 0.05 | NA | 0.57 ± 0.08 |
| Mean MAD (cm) | NA | NA | NA | NA | 0.604 |
In Table I, the results of our method were not the best because our method is very dependent on the size of the training dataset. But the increase of the size of the training dataset also results to the biggest improvement on our method. And our method is very suitable for the medical big data which is very popular in recent years. Our method can get huge promotion based on this research. Furthermore, to achieve better contrast effect, 52 CT images from five patients were manually delineated by another physicist. The average MAD of each patient between the pelvic contours from two physicists was calculated and shown in Fig. 14.
FIG. 14.
The average MAD of five patients between the pelvic contours from two physicists.
Through Fig. 14, we can see that the average MAD of prostate and bladder was little better than us. But due to the large physiological changes of the rectum, the MAD values of rectum were also unsatisfactory. The overall average MAD of the 52 CT was 0.601 cm which was almost the same with us.
4. DISCUSSION
In this paper, we presented a novel automatic, multiorgan segmentation method based on CT images of prostate cancer patients. We validated the accuracy and robustness of the method using a large number of CT images from a new group of patients independent of the training dataset. The key contributing factor to the success of our method is the region-specific agglomerative hierarchical cluster model for refining the result on top of the PCA-based gross segmentation. The segmentation accuracy without this fine-tuning process decreased sharply with the average DSC being only 0.567.
The relatively lower segmentation accuracy for rectum compared with prostate and bladder is likely due to the large variations between each situation of the rectum (mainly bowl filling and bowl gas). The relatively small size of our training dataset (50 CT images of eight patients) may not be sufficient to capture all the possible changes of the rectum. Also, the manual contour of rectum is highly variable between different observers given a decreased soft-tissue contrast near the colon and rectum interface, which may contribute to the lower accuracy.
In previous work, Davis et al. proposed a method based on patient-specific registration,35 with a mean DSC slightly better than ours. However, this method was based on the patient-specific database, so it cannot segment the first few CT scans during treatment. Further, like most previous methods, their method was used for segmentation of prostate only. On the contrary, our method does not have the imposed restriction of training dataset and we can segment the prostate, bladder, and rectum at the same time.
This method was based on a hypothesis that the surface contours of each patch area in the validation CT image could be found in the RSHAC model when the training data set was large enough. So the segmentation accuracy in this study was limited by two main points. The first point is the rationality of the patch pattern based on the experience of doctors. The patch pattern in this study was limited by the opinions from doctors and the performance of the work station. So the patch pattern in this study was just the optimal pattern in these limitations. And that was why the EOverlap was used in the cost function while the patch in this patch pattern had overlap areas because the optimal segmentation results should have little overlap areas between each patch contour. The second point is the size of the training data set. The training data with 50 CT images in this study were far not large enough to include all the shapes of each patch area. Even so, the DSC values in this study were still around 80%. The segmentation result could already use as reference samples to help the physicists to speed up their work.
So there are mainly three ways to improve the accuracy of the segmentation results. The first way is increasing the diversity of the alternative patch pattern and improving the performance of the workstation to unfreeze the limitation of the patch number. The second way is expanding the training dataset. The diversity of the pelvic organ variations can be better represented by the RSHAC model with the expanded training dataset. For a single patient, the third way is changing the region-specific model from population based to specific patient based. Along with the increased number of daily CT images which from the same patient become available in fractionated radiotherapy, a new RSHAC model can be established, which will be only used for the segmentation of the specific patient.
For future work, we plan to develop a web-based platform to streamline image visualization, segmentation, and validation on a large database. Finally, we note that even with suboptimal results in certain patients, the automatic segmentation of the prostate, bladder, and rectum can be a good starting point for the subsequent manual delineation.
5. CONCLUSION
We have presented a novel method for automatic, multiorgan segmentation based on CT images of the male pelvis. We combined the PCA-based point distribution model with RSHAC model to achieve accurate, robust, and efficient automatic segmentation of multiple pelvic organs on CT images. This method should be useful in future radiation treatment planning and adaptive radiotherapy for prostate cancer.
ACKNOWLEDGMENTS
Dengwang Li and Pengxiao Zang contributed to this work equally. The author would like to express great thanks to the staff in the Shandong Cancer Hospital and Institute for their valuable suggestions to this work. This work is supported by NIH/NIBIB (Grant Nos. 1R01-EB016777 and 1R00CA166186), NSFC (Grant Nos. 61471226 and 61201441), and research funding from Shandong Province (Grant No. JQ201516). Thanks to the support of Taishan scholar project of Shandong Province.
CONFLICT OF INTEREST DISCLOSURE
The authors have no COI to report.
REFERENCES
- 1.Jemal A., Siegel R., Ward E., Murray T., Xu J., Smigal C., and Thun M. J., “Cancer statistics 2006,” CA-Cancer J. Clin. , 106–130 (2006). 10.3322/canjclin.56.2.106 [DOI] [PubMed] [Google Scholar]
- 2.Tarver T., “Cancer facts and figures 2012. American Cancer Society (ACS),” J. Consum. Health Internet , 366–367 (2012). 10.1080/15398285.2012.701177 [DOI] [Google Scholar]
- 3.Shen D., Lao Z., Zeng J., Zhang W., Sesterhenn I. A., Sun L., Moul J. W., Herskovits E. H., Fichtinger G., and Davatzikos C., “Optimized prostate biopsy via a statistical atlas of cancer spatial distribution,” Med. Image Anal. , 139–150 (2004). 10.1016/j.media.2003.11.002 [DOI] [PubMed] [Google Scholar]
- 4.Collier D. C., Burnett S. S., Amin M., Bilton S., Brooks C., Ryan A., Roniger D., Tran D., and Starkschall G., “Assessment of consistency in contouring of normal-tissue anatomic structures,” J. Appl. Clin. Med. Phys. , 17–24 (2003). 10.1120/1.1521271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ahunbay E. E., Peng C., Holmes S., Godley A., Lawton C., and Li X. A., “Online adaptive replanning method for prostate radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. , 1561–1572 (2010). 10.1016/j.ijrobp.2009.10.013 [DOI] [PubMed] [Google Scholar]
- 6.Hu S., Hoffman E. A., and Reinhardt J. M., “Automatic lung segmentation for accurate quantitation of volumetric x-ray CT images,” IEEE Trans. Med. Imaging , 490–498 (2001). 10.1109/42.929615 [DOI] [PubMed] [Google Scholar]
- 7.Tschirren J., Hoffman E. A., McLennan G., and Sonka M., “Intrathoracic airway trees: Segmentation and airway morphology analysis from low-dose CT scans,” IEEE Trans. Med. Imaging , 1529–1539 (2005). 10.1109/TMI.2005.857654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gu Y., Kumar V., Hall L. O., Goldgof D. B., Li C. Y., Korn R., Bendtsen C., Velazquez E. R., Dekker A., Aerts H., and Lambin P., “Automated delineation of lung tumors from CT images using a single click ensemble segmentation approach,” Pattern Recognit. , 692–702 (2013). 10.1016/j.patcog.2012.10.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Aykac D., Hoffman E. A., McLennan G., and Reinhardt J. M., “Segmentation and analysis of the human airway tree from three-dimensional x-ray CT images,” IEEE Trans. Med. Imaging , 940–950 (2003). 10.1109/TMI.2003.815905 [DOI] [PubMed] [Google Scholar]
- 10.Armato S. G. and Sensakovic W. F., “Automated lung segmentation for thoracic CT: Impact on computer-aided diagnosis,” Acad. Radiol. , 1011–1021 (2004). 10.1016/j.acra.2004.06.005 [DOI] [PubMed] [Google Scholar]
- 11.Kuhnigk J. M., Dicken V., Bornemann L., Bakai A., Wormanns D., Krass S., and Peitgen H. O., “Morphological segmentation and partial volume analysis for volumetry of solid pulmonary lesions in thoracic CT scans,” IEEE Trans. Med. Imaging , 417–434 (2006). 10.1109/TMI.2006.871547 [DOI] [PubMed] [Google Scholar]
- 12.Korfiatis P., Skiadopoulos S., Sakellaropoulos P., Kalogeropoulou C., and Costaridou L., “Combining 2D wavelet edge highlighting and 3D thresholding for lung segmentation in thin-slice CT,” Br. J. Radiol. , 996–1005 (2014). 10.1259/bjr/20861881 [DOI] [PubMed] [Google Scholar]
- 13.Zheng Y., Barbu A., Georgescu B., Scheuering M., and Comaniciu D., “Four-chamber heart modeling and automatic segmentation for 3-D cardiac CT volumes using marginal space learning and steerable features,” IEEE Trans. Med. Imaging , 1668–1681 (2008). 10.1109/TMI.2008.2004421 [DOI] [PubMed] [Google Scholar]
- 14.Ecabert O., Peters J., Schramm H., Lorenz C., Von Berg J., Walker M. J., Vembar M., Olszewski M. E., Subramanyan K., Lavi G., and Weese J., “Automatic model-based segmentation of the heart in CT images,” IEEE Trans. Med. Imaging , 1189–1201 (2008). 10.1109/TMI.2008.918330 [DOI] [PubMed] [Google Scholar]
- 15.Isgum I., Staring M., Rutten A., Prokop M., Viergever M. A., and Van Ginneken B., “Multi-Atlas-based segmentation with local decision fusion—Application to cardiac and aortic segmentation in CT scans,” IEEE Trans. Med. Imaging , 1000–1010 (2009). 10.1109/TMI.2008.2011480 [DOI] [PubMed] [Google Scholar]
- 16.Zheng Y., Barbu A., Georgescu B., Scheuering M., and Comaniciu D., “Fast automatic heart chamber segmentation from 3D CT data using marginal space learning and steerable features,” in IEEE Conference on Computer Vision (IEEE, Rio de Janeiro, 2007), pp. 1–8. [Google Scholar]
- 17.Kirisli H. A., Schaap M., Metz C. T., Dharampal A. S., Meijboom W. B., Papadopoulou S. L., Dedic A., Nieman K., De Graaf M. A., Meijs M. F. L., and Cramer M. J., “Standardized evaluation framework for evaluating coronary artery stenosis detection, stenosis quantification and lumen segmentation algorithms in computed tomography angiography,” Med. Image Anal. , 859–876 (2013). 10.1016/j.media.2013.05.007 [DOI] [PubMed] [Google Scholar]
- 18.Bae K. T., Giger M. L., Chen C. T., and C. E. Kahn, Jr., “Automatic-segmentation of liver structure in CT images,” Med. Phys. , 71–78 (1993). 10.1118/1.597064 [DOI] [PubMed] [Google Scholar]
- 19.Soler L., Delingette H., Malandain G., Montagnat J., Ayache N., Koehl C., Dourthe O., Malassagne B., Smith M., Mutter D., and Marescaux J., “Fully automatic anatomical, pathological, and functional segmentation from CT scans for hepatic surgery,” Comput. Aided Surgery , 131–142 (2001). 10.3109/10929080109145999 [DOI] [PubMed] [Google Scholar]
- 20.Zhang S., Zhan Y., Dewan M., Huang J., Metaxas D. N., and Zhou X. S., “Towards robust and effective shape modeling: Sparse shape composition,” Med. Image Anal. , 265–277 (2012). 10.1016/j.media.2011.08.004 [DOI] [PubMed] [Google Scholar]
- 21.Chu C., Oda M., Kitasaka T., Misawa K., Fujiwara M., Hayashi Y., Nimura Y., Rueckert D., and Mori K., “Multi-organ segmentation based on spatially-divided probabilistic atlas from 3D abdominal CT images,” in Medical Image Computing and Computer-Assisted Intervention (MICCAI) (Springer, Berlin, Heidelberg, 2013), Vol. 8150, pp. 165–172. [DOI] [PubMed] [Google Scholar]
- 22.Li D., Liu L., Kapp D. S., and Xing L., “Automatic liver contouring for radiotherapy treatment planning,” Phys. Med. Biol. , 7461–7483 (2015). 10.1088/0031-9155/60/19/7461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Freedman D. and Zhang T., “Interactive graph cut based segmentation with shape priors,” IEEE Computer Society Conference on Computer Vision and Pattern Recognition (IEEE, Los Alamitos, CA, 2005), Vol. 1, pp. 755–762. [Google Scholar]
- 24.Gao Y., Shao Y., Lian J., Wang A. Z., Chen R. C., and Shen D., “Accurate segmentation of CT male pelvic organs via regression-based deformable models and multi-task random forests,” IEEE Trans. Med. Imaging , 1532–1543 (2016). 10.1109/TMI.2016.2519264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Li W., Liao S., Feng Q., Chen W., and Shen D., “Learning image context for segmentation of the prostate in CT-guided radiotherapy,” Phys. Med. Biol. , 1283–1308 (2012). 10.1088/0031-9155/57/5/1283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gao Y., Liao S., and Shen D., “Prostate segmentation by sparse representation based classification,” Med. Phys. , 6372–6387 (2012). 10.1118/1.4754304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pizer S. M., Fletcher P. T., Joshi S., Gash A. G., Stough J., Thall A., Tracton G., and Chaney E. L., “A method and software for segmentation of anatomic object ensembles by deformable m-reps,” Med. Phys. , 1335–1345 (2005). 10.1118/1.1869872 [DOI] [PubMed] [Google Scholar]
- 28.Gao Y., Lian J., and Shen D., “Joint learning of image regressor and classifier for deformable segmentation of CT pelvic organs,” Medical Image Computing and Computer-Assisted Intervention-MICCAI (Springer, New York, NY, 2015), Vol. 9351, pp. 114–122. [Google Scholar]
- 29.Shao Y., Gao Y., Wang Q., Yang X., and Shen D., “Locally-constrained boundary regression for segmentation of prostate and rectum in the planning CT images,” Med. Image Anal. , 345–356 (2015). 10.1016/j.media.2015.06.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Feng Q., Foskey M., Chen W., and Shen D., “Segmenting CT prostate images using population and patient-specific statistics for radiotherapy,” Med. Phys. , 4121–4132 (2010). 10.1118/1.3464799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen S., Lovelock D. M., and Radke R. J., “Segmenting the prostate and rectum in CT imagery using anatomical constraints,” Med. Image Anal. , 1–11 (2011). 10.1016/j.media.2010.06.004 [DOI] [PubMed] [Google Scholar]
- 32.Broadhurst R. E., Stough J., Pizer S. M., and Chaney E. L., “Histogram statistics of local model-relative image regions,” in Deep Structure, Singularities, and Computer Vision (Springer, Berlin, Heidelberg, 2005), Vol. 3753, pp. 72–83. [Google Scholar]
- 33.Lay N., Birkbeck N., Zhang J., and Zhou S., “Rapid multi-organ segmentation using context integration and discriminative models,” in Information Processing in Medical Imaging (Springer, Berlin, Heidelberg, 2013), Vol. 7917, pp. 450–462. [DOI] [PubMed] [Google Scholar]
- 34.Lu C., Zheng Y., Birkbeck N., Zhang J., Kohlberger T., Tietjen C., Boettger T., Duncan J., and Zhou S., “Precise segmentation of multiple organs in CT volumes using learning-based approach and information theory,” in Medical Image Computing and Computer-Assisted Intervention (MICCAI) (Springer, Berlin, Heidelberg, 2012), Vol. 7511, pp. 462–469. [DOI] [PubMed] [Google Scholar]
- 35.Davis B. C., Foskey M., Rosenman J., Goyal L., Chang S., and Joshi S., “Automatic segmentation of intra-treatment CT images for adaptive radiation therapy of the prostate,” in Medical Image Computing and Computer-Assisted Intervention (MICCAI) (Springer, Berlin, Heidelberg, 2005), Vol. 3749, pp. 442–450. [DOI] [PubMed] [Google Scholar]
- 36.Malsch U., Thieke C., Huber P. E., and Bendl R., “An enhanced block matching algorithm for fast elastic registration in adaptive radiotherapy,” Phys. Med. Biol. , 4789–4806 (2006). 10.1088/0031-9155/51/19/005 [DOI] [PubMed] [Google Scholar]
- 37.Liao S. and Shen D., “A learning based hierarchical framework for automatic prostate localization in CT images,” in Prostate Cancer Imaging. Image Analysis and Image-Guided Interventions (Springer, Berlin, Heidelberg, 2005), Vol. 6963, pp. 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stough J. V., Broadhurst R. E., Pizer S. M., and Chaney E. L., “Regional appearance in deformable model segmentation,” in Information Processing in Medical Imaging (Springer, Berlin, Heidelberg, 2007), Vol. 4584, pp. 532–547. [DOI] [PubMed] [Google Scholar]
- 39.Lorensen W. E. and Cline H. E., “Marching cubes: A high-resolution 3D surface construction algorithm,” Comput. Graphics , 163–196 (1987). 10.1145/37402.37422 [DOI] [Google Scholar]
- 40.Nealen A., Igarashi T., Sorkine O., and Alexa M., “Laplacian mesh optimization,” in Proceedings of the 4th International Conference on Computer Graphics and Interactive Techniques, Australasia and Southeast Asia (ACM GRAPHITE, New York, NY, 2006), pp. 381–389. [Google Scholar]
- 41.Rueckert D., Sonoda L. I., Hayes C., Hill D. L., Leach M. O., and Hawkes D. J., “Nonrigid registration using free-form deformations: Application to breast MR images,” IEEE Trans. Med. Imaging , 712–721 (1999). 10.1109/42.796284 [DOI] [PubMed] [Google Scholar]
- 42.Söhn M., Birkner M., Yan D., and Alber M., “Modelling individual geometric variation based on dominant eigenmodes of organ deformation: Implementation and evaluation,” Phys. Med. Biol. , 5893–5908 (2005). 10.1088/0031-9155/50/24/009 [DOI] [PubMed] [Google Scholar]
- 43.Jolliffe I., Principal Component Analysis (John Wiley & Sons, Ltd., New York, NY, 2002). [Google Scholar]
- 44.Wahba G., Spline Models for Observational Data (Siam, Philadelphia, PA, 1990). [Google Scholar]
- 45.Dice L. R., “Measures of the amount of ecologic association between species,” Ecology , 297–302 (1945). 10.2307/1932409 [DOI] [Google Scholar]