The neural representation of objects formed through the spatiotemporal integration of visual transients

Abstract

Oftentimes, objects are only partially and transiently visible as parts of them become occluded during observer or object motion. The visual system can integrate such object fragments across space and time into perceptual wholes or spatiotemporal objects. This integrative and dynamic process may involve both ventral and dorsal visual processing pathways, along which shape and spatial representations are thought to arise. We measured fMRI BOLD response to spatiotemporal objects and used multi-voxel pattern analysis (MVPA) to decode shape information across 20 topographic regions of visual cortex. Object identity could be decoded throughout visual cortex, including intermediate (V3A, V3B, hV4, LO1-2,) and dorsal (TO1-2, and IPS0-1) visual areas. Shape-specific information, therefore, may not be limited to early and ventral visual areas, particularly when it is dynamic and must be integrated. Contrary to the classic view that the representation of objects is the purview of the ventral stream, intermediate and dorsal areas may play a distinct and critical role in the construction of object representations across space and time.

1. Introduction

A fundamental function of the visual system is to parse the environment into surfaces and objects. As difficult as this problem is for the seemingly simple case of static, unoccluded objects, self-motion and object motion complicate the task by creating complex, dynamic patterns of visual stimulation that must be segmented and grouped over space and time. The relative motion of objects and observers can make previously visible object parts occluded as nearer objects pass in front of farther ones, while other, once invisible parts become gradually revealed over time. Under certain circumstances, the visual system is able to overcome the problem of such dynamic occlusion and represent what we will refer to as spatiotemporal objects. Spatiotemporal objects arise though the spatial and temporal integration of piecemeal information from object surfaces and the interpolation of missing, never-visible regions (Palmer et al., 2006). Here, we applied functional magnetic resonance imaging (fMRI) to identify neural correlates of the processes that underlie the representation of spatiotemporal objects.

A number of studies have examined the behavioral aspects of spatiotemporal object perception. In general, humans are quite good at identifying moving objects that are seen through a narrow slit (anorthoscopic viewing) or many small apertures (Plateau 1836; Zöllner, 1862; von Helmholtz 1867/1962; Parks 1965; Hochberg 1968; Mateeff, Popov, and Hohnsbein 1993; Palmer et al. 2006). How does the visual system know whether two object fragments are aligned and can be integrated if both are in motion and only one is visible at a time? Palmer et al. (2006) proposed that the position, orientation, and velocity of object fragments are encoded and stored when visible and then updated during occlusion to maintain correspondences with visible fragments. Intermediate, never-visible regions are interpolated between visible and occluded regions. These integration, updating, and interpolation processes operate together to unify object parts separated across space and time in order to construct representations of spatiotemporal objects. Although there is an extensive literature examining the neural representation of occluded objects that are static (Edelman et al. 1998; Grill-Spector et al. 1998b; Kourtzi and Kanwisher 2000, 2001), little work has been done to identify the neural correlates of spatiotemporal object perception (Yin et al. 2002; Ban et al. 2013).

Static object representations have traditionally been localized to the “what” visual processing stream which includes regions along the posterior and ventral temporal lobes (Tanaka 1996; Ishai et al. 1999; Haxby et al. 2001; Pietrini et al. 2004; for reviews, see DiCarlo, Zoccolan, and Rust 2012; Kravitz et al. 2013; Grill-Spector and Weiner 2014). The ventral pathway is thought to be hierarchically organized: information from striate cortex (V1) is sequentially processed by subsequent areas leading to more complex and abstract representations (Van Essen and Maunsell 1983; Riesenhuber and Poggio 1999; Serre et al. 2007). Evidence for such a representational hierarchy comes from increasing receptive field sizes, increased response latencies, and increasing complexity of the preferred stimuli as one advances through the cortical areas that make up the hierarchy, eventually arriving at representations that can be used for object identification and categorization (Rousselet et al. 2004; Hegdé and Van Essen 2007; Kravitz et al. 2013).

Information from striate cortex is also thought to be passed, in parallel, along a dorsal, “where” pathway that extends from the occipitoparietal cortex to the intraparietal sulcus (IPS) and the parietal cortex (Mishkin et al. 1983; Goodale and Milner 1992; Goodale et al. 1994; but see de Haan and Cowey 2011). This pathway has been associated with eye movements (Sereno, Pitzalis, and Martinez 2001), the allocation of attention to objects (Ikkai and Curtis 2011), spatial attention (Silver et al. 2005), and object manipulation and planning (Goodale et al. 1994). Recently, it has been suggested that the dorsal pathway trifurcates, with each branch responsible for distinct functions: from posterior parietal cortex (PPC), one pathway leads to prefrontal areas including the dorsolateral prefrontal cortex (DLPFC) and is involved in spatial working memory; the second pathway leads to premotor areas and is involved in motor planning and spatial action; the third pathway leads to the medial temporal lobe and is involved in spatial navigation (Kravitz et al. 2013).

Moving, dynamically occluded objects are not easily captured by the functions of either the dorsal or ventral pathways. Interaction with objects and navigation through the environment require accurate representations of relative spatial relationships for coordinated movement and grasping. These relationships include the precise representation of an object's 3D shape, orientation, position and motion relative to the observer. Object recognition and categorization, in contrast, ignore such spatially and temporally specific information, and instead require stable, position-, size, and rotation-invariant representations that allow for recognition across a variety of spatial configurations and viewpoints. This invariant representational scheme poses a problem for how the visual system might recover and represent the structure of objects that only become visible gradually over time. Consider two different parts of an object that are seen successively, one at a time. In order to understand how they relate to each other spatially, that they form a single perceptual unit, and what the global form of that object is, non-invariant information about position and velocity is needed in order to accurately group these object fragments over time. On the other hand, such information is abstracted away by successive shape processing areas as it is passed along the ventral stream. It is our central hypothesis that the neural correlates of spatiotemporal objects – objects whose shape gradually emerges over space and time – may therefore span both pathways and representational schemes.

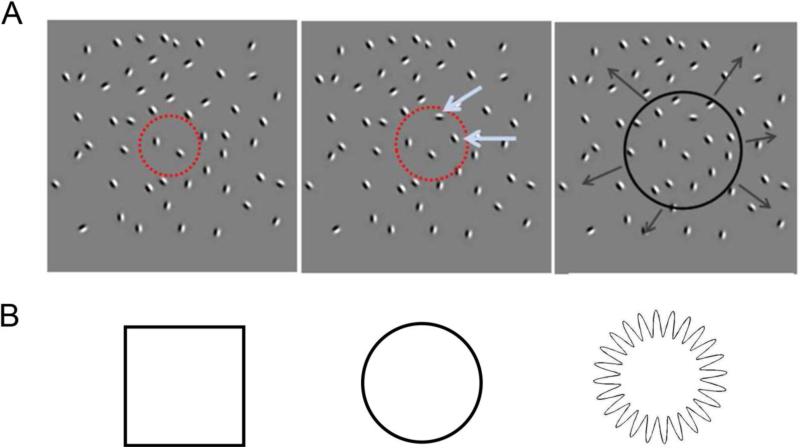
Here, we examine spatiotemporal objects that are produced by spatiotemporal boundary formation (SBF). SBF is the perception of illusory boundaries, global form, and global motion from spatiotemporally sparse element transformations (Shipley and Kellman 1993, 1994, 1997). Most commonly, this results from the gradual accretion and deletion of texture elements as when one surface passes in front of another, similarly textured surface (Gibson et al. 1969). Texture accretion and deletion are, however, just one of a wide variety of element transformations that can give rise to the percept of illusory boundaries and global form. In a typical SBF display, an invisible or virtual object moves in a field of undifferentiated elements. Whenever an element enters or exits the boundary of the object, the element changes in some property such as color, shape, orientation, or position. The sequence of element transformations results in the perception of an illusory contour corresponding to the virtual object's boundary despite the fact that no information about the object is present in any single frame. Illusory figures can be seen even in sparse displays when only a single element transforms per frame (Shipley and Kellman 1994). SBF is therefore a spatiotemporal process in that information about the object's shape arrives gradually over time and is incomplete, with many regions of the boundary missing and requiring interpolation. SBF is also a robust phenomenon – shapes can be seen even though their properties may change in between element transformations such as changes in orientation, velocity, size, and even curvature (i.e., non-rigid deformations; see Erlikhman, Xing, and Kellman 2014). An example of an SBF stimulus and the shapes used in the study can be seen in Figure 1 and Movie 1. In the experiment reported here, SBF shapes were generated by either the rotation or displacement of Gabor elements in an array of randomly placed and oriented Gabors.

Figure 1. Stimulus displays exemplifying spatiotemporal boundary formation (SBF) as used in the current experiments.

A. An invisible object (red dotted circle, Frame 1) expanded and contracted. Elements entering the boundary of the object (blue arrows, Frame 2) rotated or were displaced by a small amount. The resulting percept (Frame 3) was of expanding and contracting illusory contours. B. The three shapes used in the experiment. The boundaries of the third shape could not be recovered because of the rapid modulation of the contour relative to the density of the background elements. The resulting percept was of flickering elements in a ring-like configuration, but without a clearly-defined form as for squares and circles. This served as the control, no-shape condition.

Spatiotemporal boundary formation provides a uniquely suitable test-bed for examining spatiotemporal object perception. First, in static views of these displays, no form information is present; all perceived forms are the result of dynamic integration and interpolation processes that define spatiotemporal objects. Second, a wide variety of element transformations can be used to produce the same global figures, making it possible to extract spatiotemporal object representations that are independent of local stimulus properties. Finally, it is simple to create displays that contain element transformations, but which do not form a global percept, producing a natural control comparison.

Using SBF stimuli, we were able to disentangle the contributions of global motion, which was present in all displays, from spatiotemporal form perception, which only occurred for a subset of stimuli, all while controlling for local image features. We presented these stimuli to observers while simultaneously recording Blood Oxygen Level Dependent (BOLD) activity using fMRI. We examined how the construction of spatiotemporal objects and their shape modulated BOLD activity across a comprehensive set of functionally defined, topographically organized regions of visual cortex. These regions of interest (ROIs) span the earliest stages of cortical processing and encompass large portions of both the ventral and dorsal processing streams. In addition to exploring the nature of spatiotemporal object perception in general, to our knowledge this is the first study examining the neural correlates of SBF in particular.

2. Materials and Methods

2.1. Participants

Eleven observers (one female, 10 male) participated in the experiment. All observers were right-handed, reported normal or corrected-to-normal vision, and reported no history of neurological disorders. Observers provided written consent. Observers participated in three scanning sessions: one for a high-resolution anatomical image, one for retinotopic mapping, and one for the experiment. Data were collected for two subjects but were never used because retinotopic mapping was not performed for those subjects. One subject had a permanent retainer and so good alignment could not be attained across sessions. The other subjects dropped out of the study after the functional scan, but before the retinotopy data could be collected.

2.2. Apparatus and Display

The stimulus computer was a 2.53 GHz MacBook Pro with an NVIDIA GeForce 330M graphics processor (512MB of DDR3 VRAM). Stimuli were generated and presented using the Psychophysics Toolbox (Brainard 1997; Pelli 1997) for MATLAB (Mathworks Inc., Natick, MA). Stimuli were presented on a Cambridge Research System (Kent, UK) LCD BOLDscreen display (60 Hz refresh rate) outside of the scanner bore and viewed with a tangent mirror attached to the head coil, which permitted a maximum of visual area of 19.3° × 12.1°. In all experiments, stimulus presentation was time locked to functional MRI (fMRI) acquisition via a trigger from the scanner at the start of image acquisition.

2.3. MRI Apparatus/Scanning Procedures

All data were acquired at the University of California Davis Imaging Research Center on a 3T Skyra MRI System (Siemens Healthcare, Erlangen, Germany) using a 64 channel phased-array head coil. Functional images were obtained using T2* fast field echo, echo planar functional images (EPIs) sensitive to BOLD contrast (SBF experiment: TR = 2 s, TE = 25 ms, 32 axial slices, 3.0 mm², matrix size = 80 × 80, 3.5 mm thickness, interleaved slice acquisition, 0.5 mm gap, FOV = 240 × 240, flip angle = 71°; retinotopic mapping: same, except 32 axial slices, TR = 2.5 s). High-resolution structural scans were collected to support reconstruction of the cortical hemisphere surfaces using FreeSurfer from T1 (MPRAGE, TR=2230 ms, TE=4.02 ms, FA=7°, 640x640 matrix, res =0.375×0.375×0.8 mm) and T2 (TR=3s, TE=304 ms, FA=7°, 640×640 matrix, res =0.375×0.375×0.8 mm) images.

2.4. Retinotopic Mapping

A color and luminance varying flickering checkerboard stimulus was used to perform standard retinotopic mapping (Swisher et al. 2007; Arcaro et al. 2009; Killebrew, Mruczek and Berryhill 2015). Participants performed 8 runs of polar angle mapping and 2 runs of eccentricity mapping. For both polar angle and eccentricity mapping, participants were instructed to maintain fixation on a central spot while covertly attending to a rotating wedge (45° width, 0.5° to 13.5° or 8° to 13.5° eccentricity, 40 s cycle, alternating clockwise and counterclockwise rotation across runs) or expanding/contracting ring (1.7° width, traversing 0° to 13.5° eccentricity, 40 s cycle plus 10 s blank between cycles, alternating expanding and contracting direction across runs) stimulus and to report via a button press the onset of a uniform gray patch in the stimulus that served as that target. Targets appeared, on average, every 4.5 s.

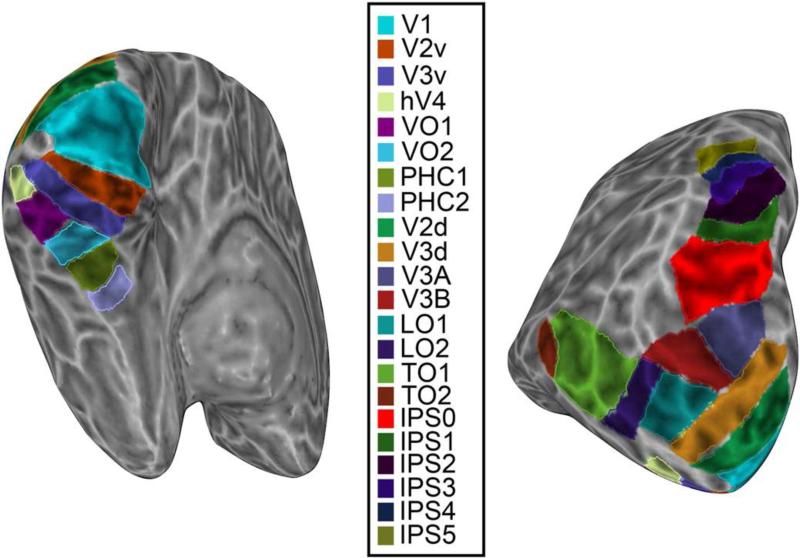
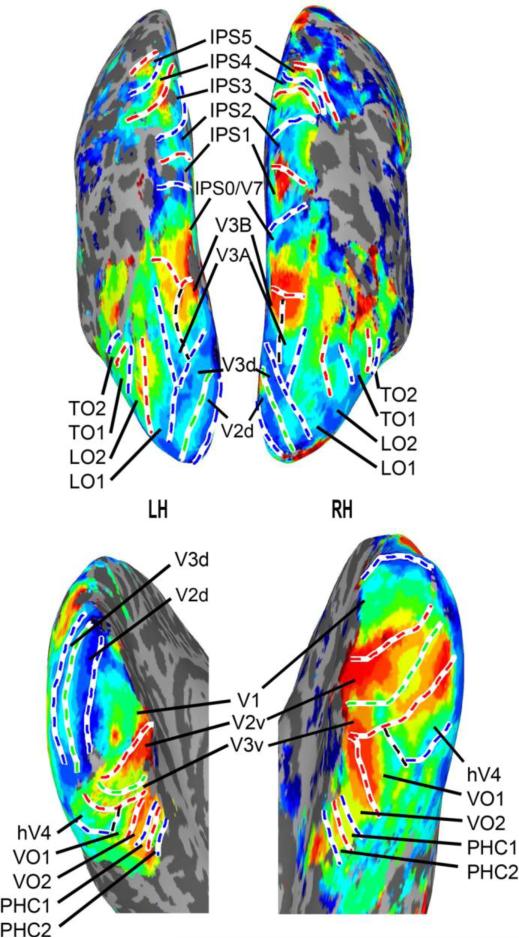
Polar angle and eccentricity representations were extracted from separate runs using standard phase encoding techniques (Bandettini et al. 1993; Sereno et al. 1995; Engel, Glover and Wandell 1997). For each participant, we defined a series of topographic ROIs on each cortical hemisphere surface using AFNI/SUMA (Figure 2). Borders between adjacent topographic areas were defined by reversals in polar angle representations at the vertical or horizontal meridians using standard definitions (Sereno et al. 1995; DeYoe et al. 1996; Engel et al. 1997; Press et al. 2001; Wade et al. 2002; Brewer et al. 2005; Larsson and Heeger 2006; Kastner et al. 2007; Konen and Kastner 2008a; Amano et al. 2009; Arcaro et al. 2009; for review, see Silver and Kastner 2009; Wandell and Winawer 2011). In total, we defined 22 topographic regions in each cortical hemisphere: V1, V2v, V2d, V3v, V3d, hV4, VO1, VO2, PHC1, PHC2, V3A, V3B, LO1, LO2, TO1, TO2, IPS0, IPS1, IPS2, IPS3, IPS4, and IPS5. For the present study, dorsal and ventral V2 and V3 were combined, resulting in a final set of 20 ROIs. A detailed description of the criteria for delineating ROI borders can be found in Wang et al. (2015). Retinotopy for a single sample subject is shown in Figure 3. All ROIs were identified in all 9 subjects.

Figure 2. Regions of interest for a single subject's left hemisphere shown on an inflated cortical surface.

Early and ventral visual areas can be seen in the image on the left; intermediate and dorsal areas in the image on the right.

Figure 3. Retinotopy for a single sample subject on an inflated cortical surfaces.

The top row depicts intermediate and dorsal regions. The bottom row depicts ventral regions. The left column corresponds to the left hemisphere (LH) and the right column to the right (RH). Note that thresholds vary across the four images to best illustrate the boundaries between ROIs.

2.5. Stimulus

In stimulus blocks, the display area was filled with a 36 × 36 array of Gabor elements (spatial frequency: 1.5 cpd; diameter: 0.67°) on a gray background. The elements were odd-symmetric and were constructed by multiplying a sine wave luminance grating with a circular Gaussian. The elements were arranged in a pseudorandom fashion by dividing the display area into equally sized regions and placing an equal number of patches in a random position within each region. This ensured that there were no clusters of patches or large empty areas and minimized overlap between elements. A red fixation dot (diameter: 0.3°) was drawn in the center of the screen.

A virtual object was defined to be centered on the middle of the display. The object was “virtual” in the sense that its boundaries were not luminance defined edges and were used only to determine which elements transformed (see below). The virtual object expanded and contracted over the course of a presentation block. As the object boundary passed the center of a Gabor element, that element changed position by moving in a random direction by 18 arc min or changed orientation to a new, random orientation. Both orientation and position changes of this magnitude have been previously shown to produce SBF (Shipley and Kellman 1993; Erlikhman, Xing, and Kellman 2014). At the beginning of a stimulus block, the virtual object was set to have a random diameter between 2° and 12° and expanded or contract at a rate of 1.5% of its size per frame up to a maximum diameter of 12° and a minimum diameter of 2°. Upon reaching a minimum or maximum diameter, the virtual object reversed scaling direction. Virtual objects were squares, circles, or “no shape”. The no shape condition used high frequency radial frequency patterns (Wilkinson, Wilson, and Habak 1998) defined by the following equation:

$$r\left(\theta \right)=r_0(1+A\sin (\omega \theta +\phi ))$$

where r is the radius of the pattern at polar angle θ, r₀ is the mean radius, A is the modulation amplitude, ω is the spatial frequency, and φ is the angular phase. A was set to 0.3, ω was set to 24, and φ was set to 0. r₀ was set to 1°, although the final scale of the shape was randomized at the start of each stimulus block under the constraints described above. The high frequency of the pattern combined with the amplitude setting defined a circular shape with a highly modulated contour (Figure 1B, right). Shapes with complex contours with high curvature are difficult to recover in SBF (Shipley and Kellman 1993). The resulting percept was of a changing region of elements, but without a clearly defined boundary or shape. We therefore refer to this condition as “no shape” because independent, random element transformations were seen without a clear global shape percept. The design of the control stimulus ensured that changes occurred in similar regions of the display as for square and circle conditions and that the overall number of element transformations was comparable.

Each stimulus block lasted for 16 s. A run consisted of interleaved stimulus and blank blocks (12 s). All six types of stimulus blocks (3 shape conditions (square, circle, no shape) and 2 transformation conditions (rotation, displacement)) appeared once per run. A balanced Latin square design was used to determine stimulus block order across 12 total runs. Because of this counterbalancing, the stimulus sequence was not reversed within each run. Blank blocks were included at the start and end of each run and between each stimulus block so that each stimulus block was preceded and followed by a blank block. During a blank block, only the fixation point was shown on a gray background. In total, a run consisted of 7 blank blocks and 6 stimulus blocks.

2.6. Fixation task

Subjects performed a change-detection fixation task to ensure that they maintained focus during the experiment. On each frame, there was a 5% chance that a red fixation dot changed color from red to green for 300 ms. Subjects had 0.5 s to press a button on the button box to indicate that they detected the color change. There was an enforced minimum delay of 5 s between each color change. At the end of each run, subjects were shown their change detection performance for that run.

2.7. Data Preprocessing

Functional MRI data were analyzed using AFNI (http://afni.nimh.nih.gov/afni/; Cox 1996), SUMA (http://afni.nimh.nih.gov/afni/suma, Saad et al. 2004), FreeSurfer (http://surfer.nmr.mgh.harvard.edu; Dale, Fischl, and Sereno 1999; Fischl, Sereno, and Dale 1999), MATLAB, and SPSS Statistics 22 (IBM, Armonk, NY). Functional scans were slice-time corrected to the first slice of every volume and motion corrected within and between runs. The anatomical volume used for surface reconstruction was aligned with the motion-corrected functional volumes and the resulting transformation matrix was used to provide alignment of surface-based topographic ROIs with the SBF dataset.

2.8. General Linear Model

For each voxel, functional images were normalized to percent signal change by dividing the voxelwise time series by its mean intensity in each run. The response during each of the 6 conditions (circles-rotating, circles-shifting, squares-rotating, squares-shifting, no shape-rotating, no shape-shifting) was quantified in the framework of the general linear model (Friston, Frith, Turner, & Frackowiak, 1995). Square-wave regressors for each unique condition and cue were generated and convolved with a model hemodynamic response function (BLOCK model in AFNI's 3dDeconvolve function) accounting for the shape and temporal delay of the hemodynamic response. Nuisance regressors were included to account for variance due to baseline drifts across runs, linear and quadratic drifts within each run, and the six-parameter rigid-body head motion estimates. The resultant Beta weights derived for each of the six conditions of interest represent the observed percent signal change in response to the corresponding stimulus.

2.9. Univariate analysis

For the univariate analysis, all 12 experimental runs were input into the general linear model described above. Voxel selection was based on the ROI masks and an unsigned F-contrast threshold that corresponded to an uncorrected p-value of 0.007. Results were qualitatively similar when no F-contrast thresholding was used for voxel selection. The contrast was applied across conditions and tested for effects in any direction, and therefore did not bias the detection of effects between conditions (Sterzer, Haynes, & Rees, 2008).

For each subject, the Beta weights were averaged across these voxels separately for each condition, resulting in average Beta weight value per ROI, per condition, per subject. The weights within each ROI were then normalized (z-scored) across conditions by subtracting the mean activation across all conditions and dividing by the standard deviation (Caplovitz & Tse, 2007). Normalized weights represent relative, condition-specific activity within an ROI.

Group-level effects were identified using repeated-measures ANOVAs and a priori contrasts. Mauchly's test for sphericity was performed for each ANOVA to test for heterogeneity of variance. Whenever a significant result for Mauchly's test was found, the Greenhouse-Geisser correction was applied. In order to control for multiple comparisons, for all sets of statistical tests, including the multivariate tests in the next section, the false discovery rate (FDR) was computed using Storey's procedure (Storey 2002; Storey and Tibshirani 2003). A default value of λ = 0.5 was used to estimate π₀ (Krzywinski and Altman 2014). Whenever π₀ was 0 (e.g. because all tests were significant), a more conservative setting of π₀ = 1 was used, which corresponds to the original Benjamini-Hochberg procedure (Benjamini and Hochberg 1995).

2.10. Multivariate pattern analysis

For the multivariate pattern analysis (MVPA), the general linear model described above was applied on a run-wise basis. Voxel selection was based on the same ROI masks and threshold used in the univariate analysis. Thus, the same voxels were used in both analyses. Three separate analyses were performed for each ROI. First, a support vector machine (SVM; Cortes and Vapnik 1995) was trained to discriminate between the different elemental transformation types by comparing the patterns evoked by stimuli containing element rotation versus those containing element displacements, irrespective of shape. A second SVM was used to discriminate between the different shape conditions by comparing the patterns evoked by either shape (circles or squares) versus no shape. A third SVM was trained to classify patterns across shape types by comparing squares versus circles (the no shape conditions were excluded from this analysis). Standard leave-one-out cross-validation was used to evaluate classification performance for each of the three classifiers (Pereira, Mitchell, and Botvinick 2009). Classifiers were trained on patterns from 11 of the 12 runs and tested on the remaining run. This procedure was repeated iteratively until all 12 runs served as the testing run. The final classification performance measure was computed by averaging classification performance across all validation folds. This produced an SVM classification performance measure for one subject in one ROI. The procedure was then repeated across all ROIs and all subjects and averaged across subjects. t-tests were performed at the group level (i.e., cross-validated classification performance averaged across subjects) to compare against chance performance (50%).

3. Results

3.1. Behavioral Results

All subjects were able to detect the fixation point change with a high degree of accuracy across all experimental runs. Average detection performance across all subjects and runs was 95% for responses that occurred within the allowed time. Across all subjects, lowest performance was 90.67% and highest performance was 98.93%. These accuracies were based on responses that occur within 0.5 s of the fixation point color change. If a correct responses were counted as those that occurred within 1.5 s of fixation point color change, average performance was 97.26%, minimum performance was 94.49%, and maximum performance was 99.47%. All subjects were therefore likely maintaining attention on the central fixation point for the duration of the experiment. There were no significant differences in task performance across the six stimulus conditions (F_2.1,17.1 = 0.830, uncorrected p > 0.46, η²_p = 0.094) suggesting that differences in activation across conditions cannot be attributed to differences of attention.

3.2. Univariate Analyses

An initial 2 × 6 × 20, three-way, repeated-measures ANOVA (hemisphere x stimulus type x ROI) was applied to identify any potential hemispheric asymmetries in stimulus responses. There was no main effect of hemisphere (F_1,7 < 0.001, p > 0.99, η²_p < 0.001), no interactions between hemisphere and the two other variables (hemisphere x stimulus type: F_5,35 = 0.016, p > 0.83, η²_p = 0.057 ; hemisphere x ROI: F_19,133 < 0.001, p > 0.99, η²_p < 0.001), and no three-way interaction (F_95,665 = 0.696, p > 0.98, η²_p = 0.090). Raw Beta weights were therefore averaged across hemispheres and re-normalized to increase the power of the subsequent analyses. The hemisphere-averaged data were then submitted to a 6 × 20, two-way, repeated-measures ANOVA (stimulus type x ROI). There were no significant main effects of either stimulus type (F_5,35 = 2.26, p > 0.07, η²_p = 0.244) or ROI (F_19,133 = 0.765, p > 0.75, η²_p = 0.099). However, there was a significant interaction between stimulus type and ROI (F_95,665 = 2.11, p < 0.001, η²_p = 0.232).

To further investigate this interaction, a 2 × 3, two-way, repeated-measures ANOVA with the factors of transformation type (shift, rotate) and stimulus type (no shape, circle, square) was performed within each ROI. The main effects and interactions for all ROIs are shown in Table 1. For ease of reading, ROIs were grouped based on typical division of the visual system into early and intermediate areas, and ventral and dorsal pathways. There was a main effect of shape in areas, VO1, VO2, PHC1, LO2, V3A, V3B, and IPS0. A significant effect of transform was found only in IPS5. An interaction between shape and transformation type was found in VO1, TO2, and IPS2.

Table 1.

	Transformation Type			Shape			Interaction
ROI	F(1,8)	p	η 2 p	F(2,16)	p	η 2 p	F(2,16)	p	η 2 p
Early Visual Areas
V1	0.029	>0.86	0.004	0.44	>0.65	0.052	0.682 (1.09,8.77)	>0.44	0.079
V2	0.137	>0.72	0.017	2.68	>0.09	0.251	0.312 (1.12,8.96)	>0.61	0.038
V3	O.OO1	>0.97	0.001	1.84	>0.19	0.187	0.629	>0.54	0.073
Intermediate Visual Areas
V3A	1.34	>0.28	0.144	22.5	<0.002	0.738	0.733 (1.20, 9.58)	>0.49	0.084
V3B	0.194	>0.67	0.024	5.99	<0.01	0.428	1.40	>0.27	0.149
hV4	0.395	>0.54	0.047	0.153	>0.85	0.019	1.91	>0.18	0.193
LO1	0.064	>0.80	0.008	0.178	>0.83	0.022	0.736	>0.49	0.084
LO2	1.86	>0.20	0.189	4.39	<0.03	0.354	0.983 (1.09,8.73)	>0.35	0.109
Dorsal Visual Areas
TO1	2.601	>0.14	0.245	3.02	>0.07	0.274	2.89	>0.08	0.265
TO2	0.943	>0.36	0.105	2.25	>0.13	0.219	4.90	<0.03	0.380
IPSO	1.21	>0.30	0.132	8.21	<0.005	0.506	2.96 (1.11, 8.67)	>0.11	0.270
IPS1	0.565	>0.47	0.066	3.28	>0.06	0.291	3.83 (1.26, 10.1)	>0.07	0.324
IPS2	0.010	>0.92	0.001	2.04	>0.16	0.203	4.65	<0.03	0.368
IPS3	0.425	>0.53	0.050	2.31	>0.13	0.224	3.60	>0.05	0.311
IPS4	0.850	>0.38	0.108	2.75	>0.09	0.282	1.10	>0.36	0.136
IPS5	6.42	<0.04	0.478	1.54	>0.24	0.181	1.77	>0.20	0.202
Ventral Visual Areas
VO1	2.06	>0.18	0.205	9.31	<0.003	0.538	4.137	<0.04	0.341
VO2	0.024	>0.88	0.003	12.3	<0.002	0.606	2.54 (1.25,10.0)	>0.13	0.241
PHC1	0.317	>0.58	0.038	8.62	<0.004	0.519	1.45	>0.26	0.154
PHC2	0.206	>0.66	0.025	1.74	>0.20	0.179	2.07	>0.15	0.205

Note. Significant effects are bolded. Degrees of freedom for the F-statistic are given in the column headings, except when sphericity was violated and a Greenhouse-Geisser correction was applied, in which case the degrees of freedom are given in parentheses within the cells containing the F-statistic.

Three planned contrasts were also performed: (1) a comparison of average Beta weights between element rotation and element displacement conditions (irrespective of stimulus type); (2) between the two shape conditions (circles and squares) and the no shape condition, irrespective of element transformation type and (3), between circles and squares, irrespective of element transformation type, excluding the no shape condition. These analyses were carried out separately for each ROI. FDR was computed separately for each contrast. The results are shown in Table 2 for each of the three contrasts respectively.

Table 2.

Rotation vs. Displacement				Shape vs. No Shape			Circle vs. Square			Circle vs. No Shape			Square vs. No Shape
ROI	F(1,8)	p	η 2 p	F(1,8)	p	η 2 p	F(1,8)	p	η 2 p	F(1,8)	p	η 2 p	F(1,8)	p	η 2 p
Early Visual Areas
V1	0.029	>0.86	0.004	0.576	>0.47	0.067	0.039	>0.84	0.005	0.379	>0.55	0.045	0.713	>0.42	0.082
V2	0.137	>0.72	0.017	2.32	>0.16	0.225	3.47	>0.10	0.302	0.478	>0.50	0.056	5.05	>0.05	0.387
V3	0.001	>0.97	0.000	2.36	>0.16	0.227	1.06	>0.33	0.117	0.888	>0.37	0.100	3.43	>0.10	0.300
Intermediate Visual Areas
V3A	1.34	>0.28	0.144	22.9	<0.002	0.741	21.4	<0.003	0.728	8.88	<0.019	0.526	40.7	<0.001	0.836
V3B	0.194	>0.67	0.024	6.69	<0.033	0.455	3.80	>0.08	0.322	2.54	>0.15	0.241	14.5	<0.006	0.645
hV4	0.395	>0.54	0.047	0.075	>0.79	0.009	0.463	>0.51	0.055	0.183	>0.68	0.022	0.006	>0.93	0.001
LO1	0.064	>0.80	0.008	0.151	>0.70	0.018	0.273	>0.61	0.033	0.282	>0.61	0.034	0.046	>0.83	0.006
LO2	1.86	>0.20	0.189	5.57	<0.047	0.410	2.56	>0.14	0.242	4.15	>0.07	0.342	5.34	<0.50	0.400
Dorsal Visual Areas
TO1	2.60	>0.14	0.245	4.00	>0.08	0.333	1.15	>0.31	0.126	2.01	>0.19	0.201	5.19	>0.052	0.394
TO2	0.943	>0.36	0.105	3.45	>0.10	0.301	0.168	>0.69	0.021	1.97	>0.19	0.198	4.32	>0.071	0.351
IPS0	1.21	>0.30	0.132	6.44	<0.036	0.446	13.7	<0.007	0.632	1.21	>0.30	0.131	18.5	<0.004	0.698
IPS1	0.565	>0.47	0.066	1.73	>0.22	0.178	5.01	>0.05	0.385	0.005	>0.94	0.001	6.59	<0.034	0.452
IPS2	0.010	>0.92	0.001	0.855	>0.38	0.097	4.69	>0.06	0.369	0.005	>0.94	0.001	3.91	>0.08	0.329
IPS3	0.425	>0.53	0.050	0.341	>0.57	0.041	7.05	<0.030	0.468	0.117	>0.74	0.014	2.79	>0.13	0.259
IPS4	0.850	>0.38	0.108	0.210	>0.66	0.029	7.27	<0.032	0.509	2.39	>0.17	0.255	0.397	>0.54	0.054
IPS5	6.42	<0.04	0.478	0.790	>0.40	0.101	2.81	>0.13	0.286	0.013	>0.91	0.002	3.07	>0.12	0.305
Ventral Visual Areas
VO1	2.06	>0.18	0.205	10.3	<0.014	0.562	6.56	<0.035	0.451	4.61	>0.06	0.365	15.8	<0.005	0.633
VO2	0.024	>0.88	0.003	24.9	<0.001	0.757	3.64	>0.09	0.313	5.71	<0.045	0.416	64.7	<0.001	0.890
PHC1	0.317	>0.58	0.038	15.3	<0.005	0.657	1.34	>0.28	0.143	5.00	>0.05	0.385	44.0	<0.001	0.846
PHC2	0.206	>0.66	0.025	3.95	>0.08	0.331	0.275	>0.61	0.033	1.73	>0.22	0.178	3.730	>0.09	0.318

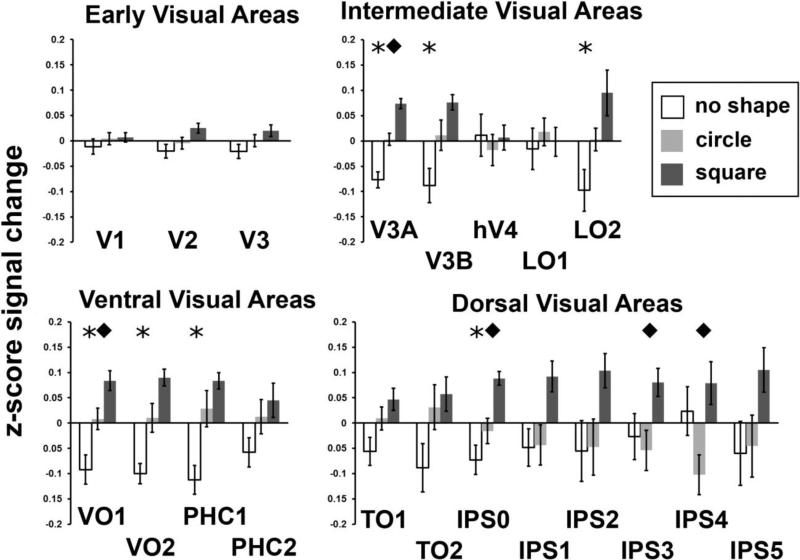
There was no significant difference between element transformation types in any ROIs except for IPS5. FDR for this analysis was 1, indicating that the finding for IPS5 was likely a false positive. Note that this contrast is the same as the transformation factor in the ANOVA. For the shape vs. no shape contrast, there was a significant effect of shape in intermediate areas V3A, V3B, LO2, and dorsal area IPS0. Additionally, a significant effect of shape was found in three ventral areas, VO1, VO2, and PHC1. The FDR for this analysis was 0.057. Post-hoc contrasts were conducted to determine whether these univariate effects were primarily driven by activation to the square or the circle stimuli. Circles produced larger activation than the no shape condition in V3A and VO2 (FDR = 0.4), while squares showed larger activation than the no shape condition in V3A, V3B, LO2, IPS0, IPS1, VO2, and PHC1 (FDR = 0.0375). The results for all ROIs are shown in Table 2.

Differences in activation for squares and circles irrespective of transformation type and excluding the no-shape condition were found mostly in intermediate and dorsal areas: V3A, IPS0, IPS3, and IPS4. Several other areas were marginally significant: V3B, IPS1, and IPS2. No effect was found in any early visual areas. The only ventral area in which there was a significant difference was VO1. The FDR for this analysis was 0.10.

These results are also represented graphically in Figure 4 in which the z-scored % signal change is shown for each stimulus type and ROI, split in the same way as in the tables, and averaged across transformation type. Visual examination of Figure 4 reveals that the difference between squares and circles in all ROIs except for V1, hV4, and LO1 was driven by greater activation to squares. While Figure 4 shows normalized data, un-normalized, positive beta weights were observed for all conditions and all ROIs except for PHC2. In PHC2, circles when the transformation was element rotation and non-shapes for both types of element transformation had small negative beta weights between −0.007 and −0.08.

Figure 4. Activation across conditions and ROIs.

Data are shown for the no-shape (white), circle (light gray), and square (dark gray) conditions for early, intermediate, ventral, and dorsal visual areas. Error bars are standard errors. Normalized (z-scored) % signal change across all voxels in the specified ROI, averaged across hemispheres, element transformations (rotation and displacement), and across all subjects. Stars indicate significant difference in a contrast between shapes (circle and square) and no shape. Diamonds indicate a significant difference in a contrast between circles and squares.

3.3. Multivariate pattern analysis

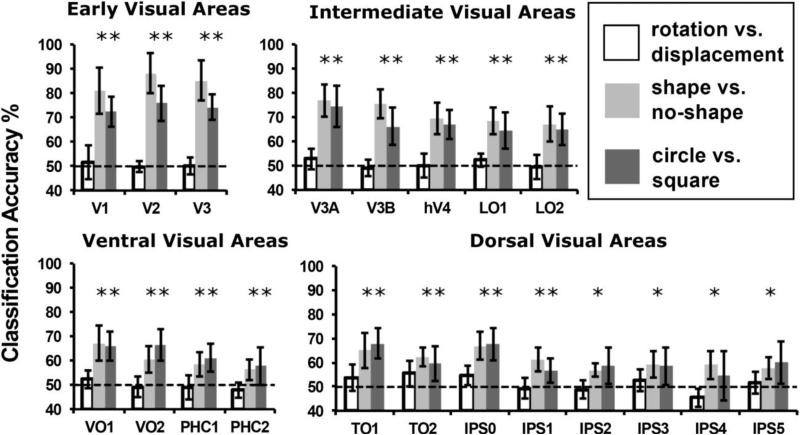
SVM classifiers were used to test whether Beta weight patterns could predict (1) element transformation type (rotation or displacement), (2) shape condition (shape or no shape), and (3) shape type (circle or square) (Cortes and Vapnik 1995; Kamitani and Tong 2005). Because there were three shape types, but only two element transformation types, there were more stimulus blocks for training the transformation type classifier than either of the shape classifiers. The results are shown in Figure 5. Data are divided by ROI groups in a similar manner as the tables.

Figure 5.

Cross-validated classification accuracy averaged across subjects. Data split by ROI for early, intermediate, ventral, and dorsal visual areas. Data shown for decoding of element rotation vs. displacement (white), shape (circle or square) vs. no shape (light gray), and circle vs. square (dark gray). Chance performance for all classifiers was 50%. Error bars indicate 95% confidence intervals.

Classification performance was never above chance for shifting vs. rotating stimuli in any ROI (white bars, p > 0.05). Shapes were discriminable from the non-shape condition in all ROIs (light gray bars, p < 0.05). FDR for these tests was 0.05. Highest classifier performance was in early visual areas, V1 (80.86%, t(8) = 6.37, p < 0.001), V2 (88.27%, t(8) = 9.059, p < 0.001) and V3 (85.19%, t(8) = 8.418, p < 0.001), and in V3A (80.86%, t(8) = 7.85, p < 0.001). Circles were discriminable from squares in all ROIs (p < 0.05) except PHC2, IPS2, IPS3, IPS4, and IPS5 (dark gray bars, ps > 0.05). FDR for this analysis was 0.067. Highest classification performance was in areas V1 (72.45%, t(8) = 7.108, p < 0.001), V2 (75.93%, t(8) = 6.959, p < 0.001), V3 (74.31%, t(8) = 8.750, p < 0.001), and V3A (74.54%, t(8) = 5.644, p < 0.001).

Because in the univariate analysis squares gave overall greater activity than circles, separate, pair-wise classifications were performed between each of the shapes and the non-shape to examine whether the classification of shapes in general vs. non-shapes was primarily driven by the square stimulus. The results were qualitatively similar when limiting comparison to circles vs. no shape or squares vs. no shape. Squares were discriminable from non-shapes above chance in all ROIs and circles were discriminable from non-shapes in all ROIs except for IPS4, IPS5, VO1, and PHC2. FDR for these classifications was 0.063 and 0.05 respectively. Overall, this indicates that the shape vs. non-shape classification was not driven entirely by the square stimulus.

In addition, we examined whether the classification results were driven primarily by differences in patterns of activity or by univariate effects within each ROI. The univariate effect for each condition was removed by subtracting the average of the Beta weights for each condition within each ROI for each subject (Coutanche 2013). The MVPA analysis was then repeated for all pairwise classifications (circle vs. square, circle vs. no shape, and square vs. no shape). Across all three comparisons, classification accuracy did not differ by more than 5% for any ROI compared to the original analyses. All classification accuracies that were significant in the original analysis remained so except for circles vs. squares in IPS2, IPS4, and IPS5 and for squares vs. no shape in IPS2. FDR for the three classifications was 0.063, 0.063, and 0.053 respectively. This suggests that across most ROIs, shape classification was based on the multivariate pattern of activity and was not driven primarily by a univariate difference across conditions.

4. Discussion

Despite similar local features/information across all stimuli, we observed larger responses in our univariate analysis to circles and squares than to the control stimulus in areas V3A, V3B, LO2, IPS0, VO1, VO2, and PHC1. In these areas, an increase in the amplitude of the BOLD response corresponded to the successful representation of an SBF object. All subjects reported that no clear form or illusory contours were visible in the control, “no-shape” condition in which the stimulus was a radial frequency pattern with a high frequency (Figure 1B). In all other respects, the no-shape control stimulus was similar to the square and circle stimuli: all displays contained the same number of Gabor elements, rotations or displacements of those elements, and expanding and contracting radial motion induced by the element transformations. The difference in activation between the shape and no shape stimuli suggests that these regions were responding to more than just global motion (Koyama et al. 2005; Harvey et al. 2010), which was present in all conditions. Within these ROIs, the square stimulus produced the largest response, perhaps reflecting the prioritized representation of corners (Troncoso et al. 2007). Importantly, however, even for the square condition, corners were not explicitly represented in the image and had to be constructed over time along with the rest of the figure. Moreover, in any static view of all displays, no global shape was visible. Thus, the increase in BOLD activity observed in these areas likely arises from the integration of sparse element changes over space and time and the interpolation of missing contour regions.

The MVPA analysis revealed that the effects of spatiotemporal integration were not restricted to the overall BOLD amplitude within the ROIs described above. The pattern classifiers were able to dissociate the distributed patterns activity in response to the shape (circle or square) and no-shape condition across all ROIs. While such a finding may be expected for example, in area hV4, which has been associated with the processing of form information (Wilkinson et al. 2000; Mannion, McDonald, and Clifford 2010), we observe this to also be the case in areas TO1 and TO2, regions that would overlap with hMT+ if a motion-localizer were performed (Amano et al. 2009). Indeed, neural correlates of spatiotemporal objects were also observed throughout the posterior parietal cortex (IPS0-5). Moreover, in all ROIs except the highest-level regions PHC2 and IPS2-5, the patterns of activity in response to circles and squares were also dissociable and each shape's activity was dissociable from activity in the no-shape condition. Shape-identity (circles or squares) specific patterns of activity were found in several areas associated with dorsal stream processing including V3A-B, TO1-2, and IPS0-1. These findings suggest a role for the dorsal stream in the accumulation of dynamic shape information over time and the ultimate binding of that information into completed perceptual units. Such an interpretation agrees with previous findings that there may exist joint representations of shape and positional information (Newell et al. 2005; Harvey et al. 2010) and that localize form-motion interactions to those areas (Caplovitz and Tse 2007).

Interestingly, element transformation type (rotation vs. displacement) could not be decoded anywhere, including early visual areas which one may have expected to be sensitive to local changes in the image. The fact that transformation type could not be decoded in any ROI further suggests that the observed shape-specific patterns of activation correspond to global shape information. However, the interaction between shape and transformation type (and a very helpful reviewer) suggests that there may be a difference between transformation types for only the shape stimuli. We therefore performed a follow-up analysis examining differences in activation between transformation types for only the square and circle stimuli. There was a significant effect of transformation type in IPS1, IPS2, IPS3, and IPS5. This may reflect the fact that one of the transformation types was better for forming SBF shapes than the other. Although it has been suggested that as long as transfromations are detectable by the visual system, they would produce SBF (Shipley and Kellman 1993), it is not the case that all transformation types produce illusory contours with the same strength (Shipley and Kellman 1994). For example, equiluminant color transformation produce no illusory figures whatsoever (Cicerone et al. 1995). Such completion effects may only be observed in IPS instead of other object areas like LOC because IPS may serve a constructive role while LOC has been shown to be relatively contrast-invariant (Avidan et al. 2002). That is, the representations in ventral object areas may be more abstract than those in dorsal ones.

A constructive role for the dorsal pathway is further supported by activation patterns in the IPS, areas of which were also found to be sensitive to SBF stimuli. Unlike LOC and other ventral regions, areas along the IPS appear to be orientation-, rotation-, and viewpoint-selective (James et al. 2002; Sakata, Tutsui, and Taira 2005; but see Konen and Kastner 2008b). They are also implicated in visual grouping (Xu and Chun 2007) and the integration of disparity information in the construction of 3D shape representations (Chandrasekaran et al. 2007; Georgieva et al. 2008, 2009; Durand et al. 2009). Spatiotemporal integration requires a consistent reference frame within which positional information from the object's contours and surfaces can be combined as they move and are gradually revealed. When a contour fragment becomes invisible (i.e., through occlusion or in between transforming elements as in SBF displays), the visual system must maintain a persisting representation that takes into account changes in position and orientation while the fragment is not visible (Newell et al. 2005; Palmer et al. 2006). When another, adjacent contour fragment becomes visible, the visual system must determine whether it is aligned with the previously visible fragment (Shipley and Kellman 1997; Palmer et al. 2006; Erlikhman and Kellman 2015). A rotation-invariant representation would not be able to differentiate between aligned and unaligned fragments. The fact that individual frames of the SBF stimulus contain no local or global form cues suggests a functional role for dorsal areas in the construction of shape representations over space and time. A cluster of regions along the dorsal pathway, including hMT+, the kinetic occipital area (KO, overlapping with LO1, LO2, and V3B), and the superior lateral occipital region (SLO, overlapping with V3B) may support such a form-motion integration process. These regions have been found to respond to both shape and motion information, and are involved in motion-defined surface segmentation, structure-from-motion, and 3D form perception (Dupont et al. 1997; van Oostende et al. 1997; Kourtzi et al. 2001; James et al. 2002; Kriegeskorte et al. 2003; Murray, Olshausen, and Woods 2003; Peuskens et al. 2004; Larsson and Heeger 2006; Sarkheil et al. 2008; Schultz, Chuang, and Vuong 2008; Farivar 2009). The present results agree with this interpretation.

Areas along the dorsal pathway have been previously implicated in the representation of spatiotemporal objects (Braddick et al. 2000; Farivar 2009; Hesselmann and Malach 2011; Caclin et al. 2012; Zaretskaya et al. 2013; Wokke et al. 2014). In particular, the parietal lobe, intermediate areas V3A and V3B/KO, and IPS are thought to be involved in perceptual organization of dynamic forms and structure-from-motion (Orban et al. 1999; Braddick et al. 2000; Paradis et al. 2000; Vanduffel et al. 2002; Kellman et al. 2005; Orban 2011). Recently, Lestou et al. (2014) reported a patient with dorsal lesions to the IPS who was impaired in discriminating Glass patterns (Glass 1969; Glass and Perez 1973). Because Glass patterns are static images that do not contain any motion, it has been proposed that the dorsal processing stream and the IPS in particular may be critical in processing global form in general. Indeed, several studies have found that dorsal and parietal regions are involved in the perception of global form (Otswald et al. 2008), static, 2D shape (James et al. 2002; Fang and He 2005; Konen and Kastner 2008b), and 3D shape (Durand et al. 2009).

However, both structure-from-motion displays and Glass patterns make it difficult to disentangle motion, form, and spatiotemporal processes. Structure-from-motion displays contain global motion of the 3D shape, local motion of individual dot elements used to create the shape, and the global form signal itself. Areas that respond to structure-from-motion have also been found to respond to global motion patterns with no form information (Paradis et al. 2000; Braddick et al. 2001; Koyama et al. 2005; Otswald et al. 2008), static 2D shape (Denys et al. 2004; Konen and Kastner 2008b), occluded objects (Olson et al. 2003), static 3D shape (Chandrasekaran et al. 2007; Georgieva et al. 2008, 2009; Durand et al. 2009), and 2D contour segments in macaques (Romero et al. 2012, 2013, 2014). Likewise, Glass patterns, while having a global organization, do not have a form per se, at least not in the sense of continuous or bounding contours. Furthermore, even though Glass patterns are static, they may be thought of as containing implied motion between dots. Static images that contain implied motion can also activate motion-sensitive regions (Kourtzi and Kanwisher 2000; Senior et al. 2000; Krekelberg et al. 2005; Osaka et al. 2010).

A recent study has presented a way of separating these aspects of spatiotemporal object perception. Zaretskaya et al. (2013) showed four pairs of dots with each pair in a separate quadrant. The two dots of each pair rotated about the center of their quadrant. This created a bistable percept: observers saw either local rotation of each pair, or a grouping of four dots, one from each quadrant, into a square. Activity fluctuations in the superior parietal lobe and anterior IPS (aIPS) correlated with the global grouping percept and not that of local element motions. TMS applied to the area over the aIPS reduced the duration that subjects reported seeing the global percept. Because both percepts arose from the same display, differences in activation cannot be attributed to differences in display properties or local motion signals, and instead are attributed to a global, Gestalt grouping process. However, while the elements could be grouped to define the corners of a square, there was no actual shape information nor were illusory contours seen. The activation could therefore reflect differences in global motion patterns engendered by the different ways in which the elements could be grouped. This leaves open the question of whether shape information is represented in parietal and dorsal areas.

Here, we show that in addition to shape / no-shape sensitivity, dorsal and parietal areas exhibit patterns of activation from which shape identity can be decoded. These regions may therefore be involved in more than just the accumulation of spatiotemporal object information that is then sent on to other (i.e. ventral) areas. Rather, some form of shape representation may be encoded in areas V3A-B, LO1-2, TO1-2, and IPS0-1. Pairwise classifications in these areas even when the univariate effect was removed, suggests that the identity information is represented in multi-voxel patterns of activity, as does not simply reflect a univariate “shape” effect. One possibility is that at least some of these regions are encoding the shape's contour curvature, which has been previously shown to correlate with activity in V3A (Caplovitz and Tse 2007). In particular, curvature discontinuities, such as the corners of the square stimulus, have been shown to modulate activity in these areas (Troncoso et al. 2007). Corners may serve an important function as trackable features and may account for the greater observed activation for square as opposed to circle stimuli. This may also account for why square stimuli produced a larger univariate effect overall than circles and why squares were better discriminable than circles from the no shape, control stimulus.

From a theoretical perspective, spatiotemporal object perception involves both motion and form processing at both local and global levels. The relative spatial positions and local motions of object fragments must be integrated into coherent perceptual units with a single global form and global motion. However, the distinction between functional regions associated with these processes is not clear-cut. Neurons in area hMT+, a region associated with motion processing, respond not only to global motion in random dot displays which have no global forms (Tanaka and Saito 1989; Duffy and Wurz 1991; Zeki et al. 1991; Tootell et al. 1995; Wall et al. 2008; Harvey et al. 2010), but also to shape (Kourtzi et al. 2001; Caclin et al. 2012), disparity-defined, 3D shape (Chandrasekaran et al. 2007), and may also be involved in motion-defined surface segmentation (Wokke et al. 2014). Additionally, putative object areas such as the lateral occipital complex (LOC) and area hV4 (also referred to as V4v), responds to both second order motion stimuli and form (Malach et al. 1995; Grill-Spector et al. 1998a, 2000; Mendola et al. 1999; Kastner, De Weerd, and Ungerleider 2000; although see Seiffert et al. 2003). Intriguingly, there is also evidence that viewpoint- and scale-invariant shape representations may exist in both ventral (LOC) and dorsal (IPS1-2) areas (Konen and Kastner 2008b). One intriguing possibility is that dorsal areas are critically involved in the construction of spatiotemporal representations, which are then sent on to ventral areas for recognition. A recent study has provided some evidence for just such a connection by identifying a white matter pathway (the vertical occipital fasciculus) that connects ventral regions hV4 and VO1 with intermediate regions V3A-B (Takemura et al. 2015).

Finally, it was interesting to observe that shape / no-shape classification was high in early visual areas (V1-3). Because both shape and no shape displays contained the same background elements, we hypothesize that differential activation in these areas is likely due to feedback during object and illusory contour perception from later visual areas in either the dorsal or ventral streams. Feedback projections from motion areas (MT/MST) to V1 have been implicated in figure-ground discrimination of moving objects (Hupé et al. 1998; Pascual-Leone and Walsh 2001; Juan and Walsh 2003). Cells in V1 have also been found to respond to structure-from-motion, which also involves the coherent motion of texture elements along a surface (Grunewald, Bradley, and Andersen 2002; Peterhans, Heider, and Baumann 2005). Structure-from-motion displays also produce illusory contours at the surface boundary, as in SBF. Cells in V1 and V2 have been shown to also respond to both 2D, 3D, and moving illusory contours (von der Heydt, Peterhans, and Baumgartner 1984; Peterhans and von der Heydt 1989; Bakin, Nakayama, and Gilbert 2000; Seghier et al. 2000; Lee and Nguyen 2001; Ramsden, Hung, and Roe 2001). Feedback also arises from LOC to early visual areas during the perception of illusory contours (Murray, M. et al. 2002, 2004; Murray, Schrater, and Kersten 2004). From the present experiment, it cannot be determined whether activity in these early visual areas reflects feedback from dorsal or ventral areas, or whether it corresponds exclusively to illusory contour formation in SBF. It may be that feedback from both dorsal and ventral areas interact in V1 during the perception of SBF.

It may be surprising that shape could be decoded in early visual areas given that activity in V1 has been reported to be reduced during shape perception (Murray, S. et al. 2002; Dumoulin and Hess 2006; Shmuel et al. 2006; de-Wit et al. 2012). This reduction in activity might support predictive coding models of cortex (Rao and Ballard 1999; Friston 2009), according to which activity in early areas is reduced when more of the visual scene can be “explained away”, as perhaps, by a larger grouping or perceptual organization. Reduced activity has also been explained by efficient coding models, in which feedback inhibits noise that might disrupt the global percept, therefore serving to sharpen the representation (Murray et al. 2004; Kok et al. 2012; de-Wit et al. 2012). We did not find any such reduction; in fact, there was a general trend of increased activity for squares and circles in V1-3, similar to what was observed in other visual areas (Figure 4). Previous studies that did find reduction of activity, only found a reduction for completed shapes, but not during the perception of structure-from-motion, which is more similar to SBF displays (Murray, S. et al. 2002). For SBF, inhibition of early inputs would disrupt the constructive process necessary to maintain the global shape. This may account for the lack of reduction in the present study. Alternatively, because SBF shapes produce illusory contours, it may be that these contours increased activity in V1 and V2 (von der Heydt, Peterhans, and Baumgartner 1984; Peterhans and von der Heydt 1989; Grosof, Shapely, and Hawken 1993; Seghier et al. 2000; Ramsden, Hung, and Roe 2001).

In summary, we found that spatiotemporal object identity can be decoded throughout visual cortex, including intermediate, parietal, and dorsal areas. These areas may play a distinct role in the integration of visual fragments over space and time. This suggests that object representation and spatial representations may not be neatly divided between two processing streams; rather, global form may be constructed via connections and feedback between many visual areas.

Highlights.

• Spatiotemporal illusory contours activate intermediate and dorsal visual areas.

• Illusory shape identity could be decoded in V3A/B, LO, TO and IPS.

• These areas are involved in construction of object representations over time.

• Shape information is not restricted to ventral visual areas.