MRSI via Fully-Refocused Spatiotemporal Encoding with Polychromatic Spectral Pulses

Abstract

A novel method for the rapid acquisition of quality multi-slice 2D images targeting a small number of spectroscopic resonances, is introduced and illustrated. The method exploits the robustness derived from recently proposed spatiotemporal encoding (SPEN) methods, when operating in the so-called “fully refocused” mode. Fully-refocused SPEN provides high-fidelity single-shot images thanks to its refocusing of all offset-derived effects throughout the course of the acquisition. This, however, prevents exploiting such robustness also for spectroscopic imaging. This work proposes a solution to this limitation, based on the use of polychromatic refocusing pulses. It is shown that if used to address a series of a priori known resonance positions, these pulses can lead to quality spectroscopic images in a small number of scans – generally equal or slightly larger than the number of targeted peaks. This strategy is explored in combination with both fully-refocused SPEN and echo-planar-imaging (EPI) acquisitions. The expected SPEN advantages were observed in both phantom-based models, and in in vivo results of fat and water separation in mice at 7T.

1. Introduction

Magnetic resonance spectroscopic imaging (MRSI) plays numerous roles in contemporary research (1–3). The faithful maps of individual metabolites that it provides may help elucidate relationships between the brain’s structure, function, and metabolism, as well as to diagnose the status of healthy and malignant tissues (4). ¹H MRSI has also become an increasingly important tool in mapping the fine structure of water/fat resonances (5); further interest has been triggered by the advent of hyperpolarized forms of ¹³C-based MRSI (6–8). A potential liability of this kind of experiments –particularly in the latter two cases– can be their long sampling-defined experimental times. Traditional chemical shift imaging (CSI) experiments devote two phase-incremented plus one slice-incremented dimension to monitor the spatial distributions, as well as a time-domain for acquiring a spectroscopic free induction decay (FID). To reduce the acquisition time demands of the ensuing four-dimensional-like experiment, a variety of fast spectroscopic imaging strategies have been introduced over the years. Foremost among these in terms of sampling efficiency is Mansfield’s Echo-Planar Spectroscopic Imaging (EPSI) proposition (9), where one of CSI’s phase-encoded spatial dimensions is probed by an oscillating gradient acting throughout the course of the acquisition, thereby lifting the need for one of the nested indirect domains. While of widespread use in a number of scenarios (10,11), EPSI requires gradient strengths that may not always be available in order to deliver undistorted spectral images with a sufficiently wide spectral bandwidth. Moreover, like its purely spatial echo-planar-imaging (EPI) predecessor, EPSI requires a precise compensation of eddy current and of timing inaccuracies in order to avoid ghosting effects, and/or the need to collect ancillary and time-taxing “navigator” scans for compensating for inexactitudes at a post-acquisition processing level.

During recent years, alternatives to both EPI and EPSI have been demonstrated, based on so-called spatiotemporal encoding (SPEN) principles (12–14). In these experiments the imaging information is not monitored in reciprocal space, but rather in direct space with the aid of a frequency-swept radiofrequency (RF) pulses. Figure 1a presents a prototypical SPEN experiment (14) that we use as starting point for this study. In it spins are assumed excited by a slice-selective pulse, followed by an adiabatic sweep acting over a time T_enc and over a bandwidth defined by the targeted field of view FOV_y while under the action of an encoding gradient G_enc, that without loss of generality we shall assume is applied along the y-direction. This imparts on the spins a spatially-dependent quadratic phase

$${\varphi }_{enc}(y)=\frac{\gamma G_{enc}{T}_{enc}}{FO{V}_y}{y}^2+const.$$ (1)

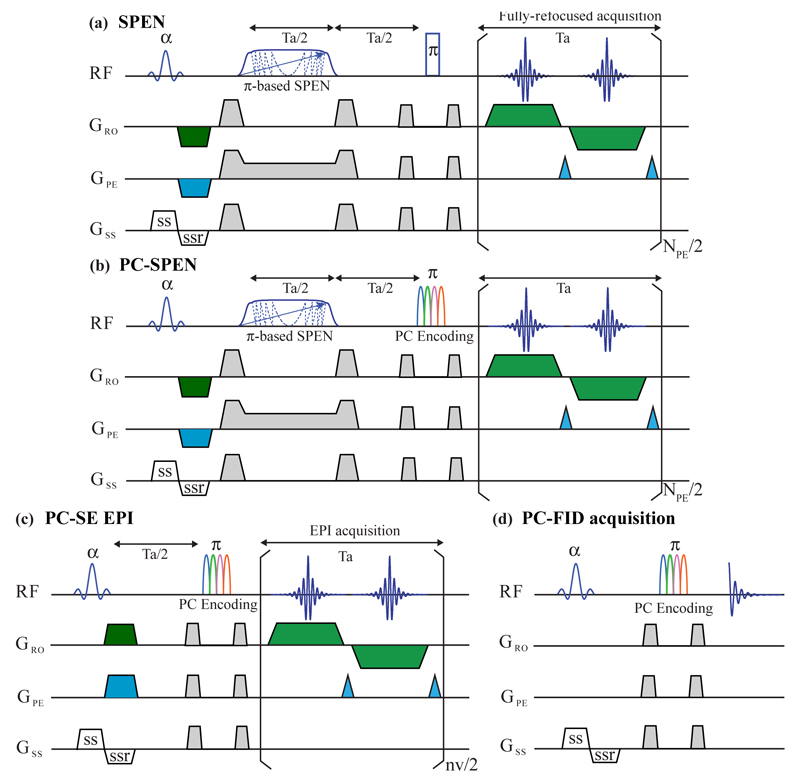
This represents a parabolic profile from which signal will only arise from the so-called stationary point y₀ fulfilling (∂φ_enc/∂y)_y=y0 = 0. Subsequent application of a gradient pulse with area |k_prg| = γG_encT_enc will shift this parabola to one edge of the FOV_y; acquisition in the presence of a gradient G_acq acting over a time t will displace this stationary point throughout the FOV, leading to a FID delivering the spatial profile ρ(y) without the need for a Fourier transformation (FT) of the data. This in turn allows one to acquire images using gradient strengths exceeding the values normally demanded by EPI’s Nyquist considerations, resulting in images that are more immune to the shift or field inhomogeneity offsets along this low-bandwidth axis. A complication associated to the use of 180° swept pulses for the encoding, is that they will not only help spatiotemporally encode the targeted slice, but will also invert the remaining spins in the sample. To deal with this the sequence in Figure 1a incorporates a second inversion pulse, reinstating all the spins that were not addressed by the initial slice selection back to their thermal equilibrium positions. In principle this procedure can be implemented by positioning this second inversion prior to the initial excitation, or after the data acquisition. In the specific example shown in Fig. 1a the pulse is placed immediately before the single-slice 2D MRI acquisition. The SPEN sequence being considered is also timed so as to fulfill the demands imposed by full-refocusing (14), a special kind of echo aiming to remove all field and shift heterogeneities, which demands that the time elapsed since a particular y-dependent spin-packet is excited until the time it is inverted by the swept 180° echoing pulse, be equal to the subsequent delay elapsed until its stationary-phase condition is fulfilled. Such timing refocuses field inhomogeneity and other offset effects throughout T_acq, leading to images that are largely freed from T₂* distortions. Fully-refocused sequences performing their encoding via an inversion pulse also need to time the duration of their sweeps according to T_enc = T_acq/2, and separate the sweep with another T_acq/2 delay from the second inversion pulse (14). Notice as well that as in previous 2D SPEN proposals, the scheme in Figure 1a operates in a so-called “Hybrid” mode (13); in it the 1D advantages just described are used to impart robustness along the more vulnerable low-bandwidth dimension of the scan, whereas a traditional oscillatory gradient is used to image the readout axis.

Figure 1.

(a) Fully-refocused SPEN imaging sequence, incorporating a slice-selective excitation, an adiabatic passage 180° pulse (indicated by a phase-modulated shape), and a hard 180° pulse refocusing spins excited by the slice-selective pulse while returning all remaining spins back to thermal equilibrium. Also indicated are the various slice-selection, pre-winding and purging gradients needed for a multislice single-shot 2D operation. (b) PC-SPEN sequence, replacing the second 180° pulse in (a) with a phase-modulated polychromatic (PC) pulse, in order to enable the separation of the spectral peaks. (c) Analogous PC-SE-EPI sequence, replacing SE-EPI’s refocusing 180° pulse with a PC counterpart. (d) Purely spectroscopic PC-FID analog of the spectroscopic imaging sequences in (b,c), with a PC pulse following a slice selection, leading to a spin-echo where the various sites’ contributions to a 1D time-domain acquisition appear phase modulated.

While capable of delivering some of the highest quality images so far recorded in a single scan, this full refocusing approach will –by the nature of its design– be free from chemical shift information. Thus, while it has been shown that processing the phase of SPEN 2D image acquisitions can convey the chemical shifts of the emitting sites –thus delivering single-shot 2D spatial / 1D spectral correlations in tens of milliseconds (14–16)– such processing is not feasible under full-refocusing conditions. Indeed a simple analysis reveals that under such situation, the scaling factor multiplying all chemical shifts is identically zero. With this as background, the question arises whether it is possible to endow such high-fidelity imaging experiments, with an additional spectral dimension. While we have so far failed to devise ways of acquiring fully-refocused SPEN images with spectroscopic information in a single scan, the present study explores what could be an efficient way of achieving this in a small number of shots. The key assumption of this compressed MRSI acquisition scheme is that, in a majority of cases, the number of resonances targeted in such studies is relatively small, and their positions are either a priori known or can be determined relatively fast by 1D MRS. With this assumption as background, possibilities emerge to acquire MRSI data in a small number of scans –equal essentially to the number of resonances being addressed. Indeed, with chemical shifts known, the images of various peaks can be resolved in an efficient manner by collecting EPI- or SPEN-based imaging data sets, where individual peak contributions have been differentially encoded as either phase or amplitude modulations. Hadamard encoding, for instance, has been extensively used for acquiring multidimensional spectra in such fashion (17–19). We have recently demonstrated similar alternatives based on phase-modulated polychromatic (PC) pulses (20,21). The present study describes the principles, the implementation and the potential of MRSI forms based on resolving the images of different sites based on such PC pulses. In vitro and in vivo versions of PC-EPI and fully-refocused PC-SPEN were devised and compared; both methods could deliver spectroscopic images in a small number of shots, even if a superior performance of the latter technique when dealing with field heterogeneities was found.

2. Methods

The starting point of this study incorporates into the sequence shown in Fig. 1a, a PC pulse discriminating sites as described in Ref. (21). An efficient way of doing so is by replacing the hard, broadband 180°-pulse already included in the fully-refocused SPEN sequence, by a polychromatic counterpart that will also act as inversion pulse for all N resonances to be addressed by the MRSI experiment (Figure 1b).^a The sought PC pulse will thus be synthesized as a sum of N selective components, each centered at the n-th off-resonance frequency {Ω_n}_n=1…N being targeted, and endowed with an envelope $P_{180}^n(t)$ that imparts an inversion at each of the sites. This means that for those regions that were not targeted by the initial slice-selective excitation, the PC pulse will restore all spins that were inverted by the swept SPEN encoding pulse back to equilibrium, thereby facilitating multi-slice operation. To enable these pulses to distinguish among the sites that were already excited and encoded, the phases of these envelopes will be modulated by imparting onto the n-th component of the PC pulse an artificial e^{i2π(m-1)(n-1)/M} phase factor, and increment this multiplier over the course of 1≤m≤M scans. This manipulation distinguishes the response of each resonance –thereby enabling the separation of their associated images– via their multiplication by the encoding matrix E = {e^{i2π(m-1)(n-1)/M}}_{m=1…M, n=1…N}. This matrix is equivalent to that arising from a discrete Fourier encoding, meaning that if M ≥ N, each site’s response can be extracted in a noiseless, artifact-free manner via an inverse FT. In combination with efficient imaging approaches like fully-refocused SPEN or spin-echo (SE) EPI, this enables the rapid spectroscopic separation of multi-slice 2D images. Figure 1c illustrates the form that this would adopt in the case of SE-EPI; for completion Figure 1d illustrates a purely spectroscopic case, where PC pulses would be tested to evaluate their potential for separating chemical sites in a conventional 1D SE experiment.

While this PC-based approach should in principle separate the images originating from different targeted sites, and even though the full refocusing condition eliminates chemical shift evolution over the course of the SPEN acquisition, the positions stemming from a given chemical site will still be subject in this kind of experiments, to chemical shift miss-registration effects. For the k-dimensions involved along SPEN’s readout axis or SE EPI’s phase-encoded and readout axes, these shifts will be as usual and given by Ω_n/γG_eff, where G_eff is the time-averaged gradient acting over the course of these k-samplings. Along the SPEN-encoded axis miss-registration will derive as well from the fact that the swept pulse will address different spatial positions, depending on the offset imparted by the chemical shift. Indeed the quadratic encoding phase in the presence of an off-resonance Ω_n will differ from that given by Eq (1), and will be given at the beginning of the signal acquisition by

$${\phi }_{acq}(t=0)=\frac{\gamma G_{enc}{T}_{enc}}{FO{V}_y}{y}^2+\left(\frac{{\Omega }_n{T}_{enc}}{FOV}-k_{prg}\right)y+const.$$ (2)

Notice that in addition to the quadratic and the purging gradient term, there will be a linear displacement proportional to Ω_n. Given that all the parameters involved in this displacement (including the offset, which is an input parameter of the PC pulse) are known, all these displacements can be corrected upon post-processing the data, and each spectral contribution thus be cleaned from its shift-derived miss-registration along all spatial axes.

3. Experimental

The performance and robustness of the PC-based approaches just described were assayed in vitro on a phantom composed of three tubes containing separate choline chloride (Cho, 50 mM), N-Acetyl-L-Aspartic acid (NAA, 250 mM) and sodium lactate (Lac, 125 mM) solutions, all immersed in a water tube. In vivo water/fat separation tests were also implemented, on a mouse’s abdomen. All acquisitions were carried out on a 7T/120mm horizontal magnet using a quadrature birdcage coil probe (Agilent Technologies, Santa Clara, CA), and operated by a DirectDrive2^® console. As an aid in setting up the sequences in Fig. 1 spin-echo multi-shot (SEMS) and gradient-echo multi-shot (GEMS) images were also recorded, using sequences taken from the scanner’s software libraries. PC-SE-EPI experiments were collected using modifications of the scanner-supplied sequences that included 180° PC pulses; as in the original scanner-based sequences, these acquisitions demanded the acquisition of ancillary navigator scans for co-processing even and odd readout echo sets (no such need arises in the super-resolved processing of the SPEN data (22–24)). The SPEN and PC-SPEN sequences were custom written and installed as stand-alone packages in the scanner’s VNMRJ^® software. This allowed us to execute the image acquisition and subsequent data processing directly with the console’s environment, and thus enjoy from the latter’s native Fourier processing facilities, image display capabilities, etc. Such acquisition and processing macros are available upon request. Animal protocols and maintenance were done in accordance with guidelines of the Institutional Committee on Animals of the Weizmann Institute of Science (IACUC protocol 10790514).

In order to calculate the 180° PC pulses all the written sequences read basic RF calibration parameters, as well as the {Ω_n}_1≤n≤N frequencies of interest. With this, M ≥ N excitation waveforms were calculated as

$$P{C}_m={\displaystyle {\sum }_{n=1}^N{P}_{180}^n({\Omega }_n)}{e}^{i\pi (m-1)(n-1)/M},$$ (3)

with 1≤m≤M the scan index and $P_{180}^n({\Omega }_n)$ a selective 180° Gaussian waveform centered at a frequency Ω_n. These waveforms were 20 and 5 ms long for the in vitro and in vivo tests, respectively, and were always clocked out at 4 µs dwell times. With this encoding, the image of the n-th site component could be disentangled as a discrete inverse FT $I_n={\displaystyle {\sum }_{n=1}^N{I}_m^{SPEN/EPI}{e}^{-i2\pi (m-1)(n-1)/M}}$ , where $I_m^{SPEN/EPI}$ denotes the SPEN or EPI data afforded by the m-th scan. The combined acquisition/processing package also included this Fourier-based disentanglement of all the individual spectral images, their correct re-positioning based on the chemical shift offsets targeted and on the pulse sequence parameters used, and the processing of all SPEN-encoded axes using super-resolution algorithms (24).

4. Results

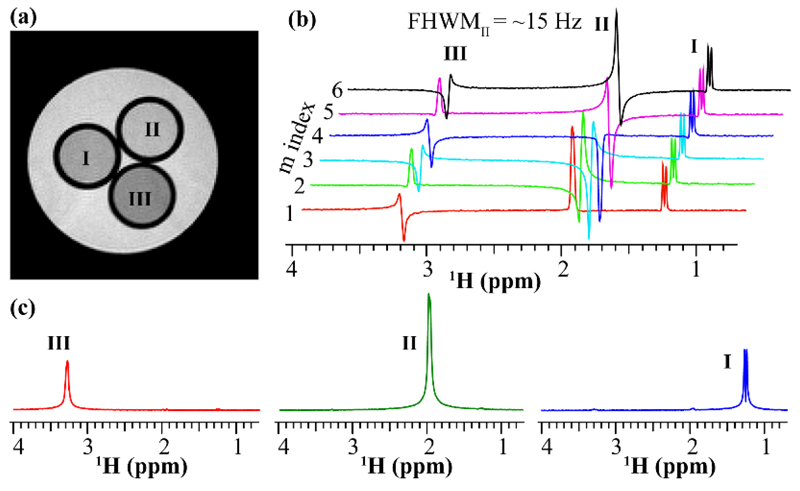
The performance and robustness of the PC-based approaches just described were assayed on the phantom shown in Figure 2a, made up of three methyl-containing metabolites (NAA, Lac, Cho) dissolved in H₂O/D₂O (90%/10%) and surrounded by a per-protio water tube. Figure 2b illustrates the phase variations that the methyl peaks exhibit, upon incrementing the phases of the PC pulse components as indicated by the recipe in Eq. (3). While the absolute phases of the peaks are not relevant, and even though field inhomogeneities and J-coupling effects prevented a straightforward phasing of the peaks even for the m = 0 case, these distortions will be constant throughout the scans. FT of this PC-FID set then evidence spectra with peak-specific phase modulations that correctly reflect the phases imparted by the pulses. Thanks to these modulations, a discrete FT successfully disentangles each resonance on its own (Fig. 2c). Notice that while in principle four PC-modulated scans should suffice to deliver these resonances (three to account for the methyl peaks and one for the water), an M = 6 overdetermination improved the resulting spectral separation.

Figure 2.

Phantom test for the PC-FID encoding sequence (Fig. 1d) performed on three tubes containing separate choline (III: Cho, 50 mM), N-Acetyl-L-Aspartic acid (II: NAA, 250 mM) and sodium lactate (I: Lac, 125 mM) solutions, immersed in a fourth, 15 mm diameter water tube. (a) Reference SEMS image collected for full-width at half maximum (FWHM) values of ~15 Hz. (b) Six spectra acquired using the sequence in Fig. 1d with an M = 6 PC phase modulation. (c) Well-separated spectra corresponding to the resonances I, II and III.

Figure 3 exemplifies how similar concepts can be extended to single-slice 2D imaging acquisitions, using the PC-SPEN approach introduced in Fig. 1b. Once again the modulations derived from the PC pulses are evidenced in the phases of the various images (Fig. 3a); also evidenced upon comparing these results with the reference SEMS image presented in Fig. 2a, are the effects of a chemical shift miss-registration that effectively makes the tubes “collide”. This does not prevent us from untangling the contributions arising from the individual sites based on the discrete FT procedure (Fig. 3b). As the chemical shift offsets of each contribution that has been resolved in this manner are known, the relations given above can be used to shift each image along a priori known x- and y-axes displacements, and position them into their correct locations within a common frame (Fig. 3c). Notice as well the relatively low levels of cross-talk among the various site’s contributions.

Figure 3.

Implementing PC-SPEN spectroscopic imaging in the phantom introduced in Figure 2. (a) Array of six SPEN images modulated by PC pulses imparting the desired Fourier encoding on three targeted spectral components. (b) Results arising from an inverse FT processing of the six PC-SPEN images shown in (a): panels b-1 to b-3 show the first three decoded images, while b-4 is a sum image of b-1 to b-3. (c) Idem as (b), but after the PC-separated chemical shift component images were corrected by shift-derived miss-placements. Marked by squares in (c-4) are regions of interests selected for calculating the residual cross-talk level. These are indicated in panels (c-1)-(c-3), and were calculated by dividing the residuals arising at the positions of the non-selected components, by the targeted signals corresponding to each component within the marked green/magenta/blue squares. Scan parameters: FOV = 20×20 mm²; matrix size = 64×64 slice thickness = 4 mm; Ta = 24.6 ms; bandwidth of the 180° adiabatic encoding pulse = 4.88 kHz; PC pulse duration = 20 ms; PC phase increments M = 6; repetition time TR = 2 sec. Total scan time was 25 min, including the averaging of 128 PC-encoded experiments for SNR improvement.

As mentioned, the same procedure could be implemented equally well on PC-encoded versions of the SE EPI experiment. Figure 4 compares results arising from such PC-encoded SE-EPI and SPEN experiments, collected on the phantom introduced in Fig. 2a for two different levels of field inhomogeneities. The relative signal-to-noise ratios (SNRs) as well as the residual cross-talk levels among the different locations of various chemical sites, are also indicated. These tests reveal that whereas both sequences perform nearly equal under homogeneous field conditions, the SNR is better and the distortions are less prominent when relying on fully refocused SPEN for collecting the imaging information in inhomogeneous field conditions. The latter can be appreciated by noting the deviations from an ideal circular shape evidenced by the SE-EPI images in row (d) of the Figure.

Figure 4.

Comparing the performance, SNR and cross-talk levels, of PC-encoded fully refocused SPEN and SE-EPI MRSI experiments. (a, b) Spectrally-resolved images (including corrections due to shift-derived miss-registrations) collected by PC-SE-EPI and by PC-SPEN in a homogeneous field (FWHM ~ 10 Hz). (c, d) Idem but acquired in an inhomogeneous field (FWHM ~100 Hz). Scan parameters were as in Figure 3. Rectangles on the right-hand panels indicate the regions chosen to calculate the average SNR and cross-talk levels, which also proceeded as in Figure 3. Cyan circles indicating the diameter of each sample have been included to aid in appreciating the robustness of the various methods.

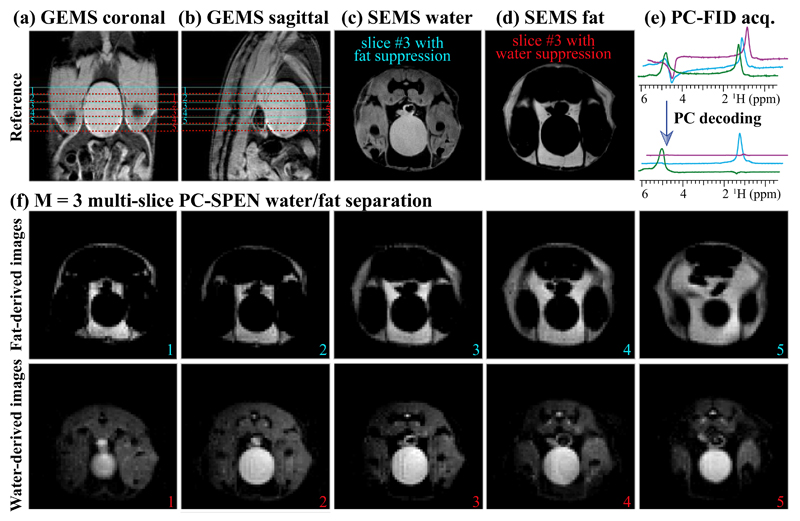
Figure 5 shows an application of the PC-SPEN sequence to the separation of water and fat components, in in vivo multi-slice MRSI experiments targeting the inferior abdomen region of a mouse. The scout images for the targeted organs are shown in Figs. 5a and 5b; notice that due to the chemical shift difference between the targeted water and fat peaks, ~970 Hz, the water-derived and the fat-derived slices appear at slightly different locations (the slice selective pulse bandwidth being ~ 2 kHz). The PC-SPEN cycle employed M = 3 scans, and both water- and fat-derived images could be well and easily separated in all five slices –with no interference from motions in these experiments acquired without respiratory triggering.

Figure 5.

Illustrating the fat/water separation capabilities of PC-SPEN, when applied to an abdominal mouse scan at 7T. (a, b) Scout images corresponding to the five-slices illustration of the lower panels; centers of the miss-registered water and fat slices are marked in red and cyan lines, respectively. (c, d) Illustrative slices acquired with SE multi-shot sequences involving fat and water suppression, respectively. (e) Spectra arising from the PC-FID sequence in Fig. 1d with a three-scan modulation, before and after the spectral Fourier processing. (f) Water/fat separation achieved using the PC-SPEN sequence applied on five representative slices, for this M = 3 PC encoding. Common parameters of these images: FOV =40 × 40 mm²; slice thickness = 2 mm; adiabatic sweep SPEN bandwidth =10.9 kHz; PC pulse duration = 5 ms. The total scan duration for SEMS was 11 min, while that for the multi-slice PC-SPEN was 15 sec using a M = 3 PC phase modulation and a TR = 5 sec (for all slices). The slight signal decay at the edges of the SPEN images reflects the WURST-like (25) edges of the adiabatic encoding pulses.

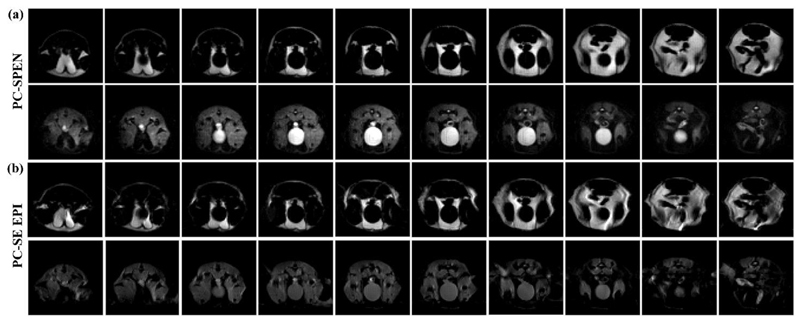
Figure 6 expands on these results by comparing fully-refocused SPEN and SE-EPI spectroscopic images, arising when applying similar PC-based strategies to the acquisition of a larger number of slices. Like their Figure 5 counterparts these images were collected without respiratory synchronization, thus becoming susceptible to motion-derived distortions. The robustness of the SPEN approach to these distortions as well as to susceptibility-derived effects, becomes even more evident in these longer acquisitions. Indeed, repeated comparisons of EPI and SPEN versions of this experiment reveal that the former’s sensitivity to motions derives in part from inaccuracies in the “navigator” scans that EPI’s processing algorithm requires for providing ghost-free images; these navigator-derived corrections become progressively less useful with respiratory motions, demanding in turn either a constant refreshing of the corrective scans or a need to tolerate larger spatial distortions along the low-bandwidth dimensions. By contrast, as SPEN’s super-resolution reconstruction proceeds in a reference-less manner (24), motion-derived distortions become less of an issue. Also evidenced by these data is the good performance of the SPEN approach to dense multi-slicing, despite these sequences’ inclusion of two spatially-broadband inversion pulses. This feature, which is also evidenced by the SE EPI images, also benefited from the fact that the multi-slicing loop was included within the PC’s m-cycling one: this maximizes the time needed before every slice is re-excited, and allowed us to operate using 90° excitation pulses.

Figure 6.

In vivo fat/water separation comparisons of the PC-SPEN and PC-SE EPI multi-slicing methodologies, as applied to abdominal mouse investigations at 7T. (a) Water/fat separation from 10 slices arising from a PC-SPEN sequence with M = 3. (b) Idem but from a PC-SE-EPI sequence. Common parameters of these images were as in Fig. 5; the total scan duration for the PC-SPEN scan was 30 sec, while the PC-SE-EPI scan required 60 sec (the additional time stemming from EPI’s reliance on reference scans for joint co-processing of even/odd phase-encoded lines).

5. Discussion and Conclusions

The present study discussed a new spectral encoding mode, that in combination with either SPEN- or SE EPI-based imaging approaches provides a fast way of retrieving multi-slice 2D spatial / 1D spectral MRSI data. The method leverages a priori information about the resonance frequencies of the peaks to be targeted, and disentangles the multiple contributions of such peaks to any given image by imparting on them a series of Fourier-encoded phase modulations. A simple, stable numerical procedure then makes the acquisition of site-resolved images straightforward. While the phase incrementation involved in this spectral disentanglement procedure necessitates a number of scans equal or greater than the resonances to be discriminated, the ensuing approach can be merged with ultrafast imaging techniques and thereby lead to efficient MRSI acquisitions. The ensuing method was assayed using two different kinds of acquisition modules: spin echo EPI, and fully-refocused SPEN acquisitions. Both of these methods delivered comparable images in “well behaved” cases; i.e., when scans were free from strong field inhomogeneities and/or motion effects. Cross-talk effects among the different components are then always small, and sensitivity penalties associated to the spectral separation minimal. As non-idealities become stronger, however, the advantages of operating within SPEN’s full-refocusing, self-referenced environment that had been documented in water-based imaging cases, also became evident for these MRSI scenarios. Multi-slice implementations were also found remarkably simple in this SPEN case due to the use of a pair of 180° pulses –one for performing the spatial and the other for performing the spectral encoding; this helped reverse all the sites and positions that had not been addressed by the initial excitation back to thermal equilibrium, as demanded by multi-slice operation. An initial slice-selective pulse of arbitrary flip angle, including optimized Ernst or hyperpolarized excitation angles if so desired (26, 27), could then be chosen to maximize spectral sensitivity per unit acquisition time. A final aspect worth remarking of all these PC variants was the good level of water suppression evidenced by all the metabolite-based experiments; although implemented in aqueous solutions, the built-in water suppression arising from the spectrally-selective PC-pulses flanked by strong crusher gradients, coupled to the spectral separation afforded by the PC phase-cycling, lead to clean spectral separations and flat baselines.

Notwithstanding these benefits, a number of factors may challenge the effectiveness of the PC-based spectral decoding. One of these was noted over the course of the study, and relates to chemical shift miss-registration effects. While these are less sever in SPEN-based than in EPI-based experiments due to the stronger gradients that the former sequence uses, they are still clearly evidenced in the images. The spectral separation procedure allowed one to compensate for these miss-registrations, via well-defined displacements that can be applied along the high- and low-bandwidth dimensions. Another issue that may complicate the implementation of the PC separation is the presence of a homonuclear J evolution, on the peaks being resolved. Such J-coupling evolution is partly compensated by the narrow band-ness of the PC pulses, which under suitable conditions may act as a source of “heteronuclear” 180° decoupling pulses for the resonances being decoded. Thanks to this selectivity signals in the spectra shown in Fig. 2a –as well as in the spectra that underlie the image separations in Figures 3 and 4– show nicely behaved, in-phase multiplets for every methyl peak, despite the J-couplings affecting some of them. Another limitation that will affect the execution of these experiments, relates to the spectral separation of the peaks to be addressed. Excessive crowding of the peaks would lead to a need for long PC pulses, with strong T₂ and homonuclear J-coupling losses ensuing. Also important might be field inhomogeneity effects, which although the fully-refocused SPEN sequences know how to handle well, may lead to an overlap among the spectral components being disentangled by the individual PC components. Yet another limitation to these spectroscopic imaging experiments, might be limited sensitivity. Still, even if demanding several scans for the sake of improving SNR, the use of short MRSI acquisition cycles like those involved in the PC-based encoding should lead to more robust data in in vivo experiments subject to natural instabilities, than EPSI-like counterparts. This hypothesis is being tested with additional preclinical and clinical studies.

Abbreviations

CPMG

Carr-Purcell Meiboom-Gill

CSI

Chemical Shift Imaging

EPI

Echo-Planar Imaging

EPSI

Echo-Planar Spectroscopic Imaging

FID

Free Induction Decay

FOV

Field of View

FT

Fourier Transform

FWHM

Full Width at Half Maximum

GEMS

Gradient-Echo Multi-Shot

MRI

Magnetic Resonance Imaging

MRS

Magnetic Resonance Spectroscopy

MRSI

Magnetic Resonance Spectroscopic Imaging

PE

Phase-Encode

PC

Polychromatic

RF

Radio frequency

RO

Read-Out

SE

Spin-Echo

SEMS

Spin-Echo Multi-Shot

SNR

Signal-to-Noise Ratio

TE

Echo Time

TR

Repetition Time