HyperSPASM NMR: A New Approach to Single-Shot 2D Correlations on DNP-Enhanced Samples

Abstract

Dissolution DNP experiments are limited to a single or at most a few scan, before the non-Boltzmann magnetization has been. This makes it impractical to record 2D NMR data by conventional, t₁-incremented schemes. Here a new approach termed HyperSPASM to establish 2D heteronuclear correlations in a single scan is reported, aimed at dealing with this kind of challenge. The HyperSPASM experiment relies on imposing an amplitude-modulation of the data by a single Δt₁ indirect-domain evolution time, and subsequently monitoring the imparted encoding on separate echo and the anti-echo pathway signals within a single continuous acquisition. This is implemented via the use of alternating, switching, coherence selection gradients. As a result of these manipulations the phase imparted by a heteronucleus over its indirect domain evolution can be accurately extracted, and 2D data unambiguously reconstructed with a single-shot excitation. The nature of this sequence makes the resulting experiment particularly well suited for the collecting indirectly-detected HSQC data on hyperpolarized samples. The potential of the ensuing “HyperSPASM” method is exemplified with natural-abundance hyperpolarized correlations on model systems.

1. Introduction

By establishing unambiguous connectivity, two-dimensional (2D) NMR conveys unique information about a molecule’s structure and dynamics at an atomic resolution. 2D NMR correlations typically require a full sampling of two time-domains according to Nyquist criteria [1–2]; as one of these domains involves a t₁ delay within a pulse sequence, this necessitates multiple repetitions and extended experimental timescales. Numerous proposals have emerged to reduce these acquisition times, including sparse sampling techniques [3–8] and other non-Fourier methods [9–10]. Although facilitating higher-throughput and faster high-D NMR spectroscopy, these approaches still do not eliminate the necessity for collecting multiple scans. Such requirement for multiple acquisitions complicates the prospects of combining 2D NMR with dissolution Dynamic Nuclear Polarization (DNP) [11–13]. Dissolution DNP is a promising emerging technique [14], whereby a hyperpolarized spin state is created in a cryogenic solid and then suddenly melted so as to exploit it for a dramatic sensitivity enhancement in solution NMR or MRI. This hyperpolarization, however, decays with the longitudinal relaxation time T₁, and it cannot be preserved at the level of constancy normally demanded by conventional 2D NMR acquisitions. By contrast, ultrafast 2D techniques that rely on spatio-temporal encodings to monitor the indirect-domain evolution [15–16], have been shown capable of making full use of this hyperpolarization [17–19]. While spatio-temporal methods can deliver 2D NMR spectra in a single scan without a priori knowledge, they face a number of technical limitations. Most prominent among these is the signal-to-noise penalty associated with having to acquire data along two spectral dimensions simultaneously. Given that the per-scan noise in these methods increases as the root of the number of elements along F₁, this may be particularly onerous when this axis involves nuclei that, like ¹³C, are associated with sharp resonances spanning a wide frequency range. This Communication presents an alternative for acquiring single-shot 2D hyperpolarized data, Single-Point Amplitude-Separated Multi-dimensional (SPASM) NMR, that is specifically designed to bypass these limitations and to maximize the sensitivity enhancement provided by dissolution DNP.

The SPASM approach draws from two previous developments in the area of accelerated multidimensional acquisitions. One of these is single-point evaluation of the evolution dimension (SPEED) spectroscopy [20], where correlations among resolved chemical sites are sought from the phase shift imparted on F₂ peaks when 2D data are acquired for a known Δt₁ t₁-value. This information can be exploited owing to the defined distortions that this F₁ evolution will introduce on the I(F₂) shape of peaks along the direct domain, as given by

$$S\mathit{\left(}{t}_{\mathit{1}},F_{\mathit{2}}\mathit{\right)}\approx \mathit{\text{exp}}{\mathit{\left(}\mathit{2}\pi i{F}_{\mathit{1}}\Delta t_1\mathit{\right)}}^{.}I{\mathit{\left(}{F}_{\mathit{2}}\mathit{\right)}}^{.}\mathit{\text{exp}}\mathit{\left[}\mathit{2}\pi i\mathit{\left(}{\varphi }_{\mathit{0}}+F_{\mathit{2}}{\varphi }_{\mathit{1}}\mathit{\right)}\mathit{\right]}$$ (1)

Although well-defined, notice that an ambiguity remains in this determination owing to the last term in eq. 1, involving the constant and linear phase distortions ϕ₀, ϕ₁ of common occurrence in 1D NMR. In order to remove these unknowns while preserving the experiment’s single-shot character, we propose to incorporate onto it a second development from the 2D NMR literature: the switched acquisition time (SWAT) experiment [21]. Originally proposed for the simultaneous collection of N- and P-type 2D COSY data, this method operates by imposing an initial coherence-selection encoding gradient during t₁, and subsequently interleaving coherence selection decoding gradients between sampled points in t₂. Moreover, following the decoding of the first t₂-point, each of these coherence decoding gradients is applied with a strength corresponding to twice the action of the initial coherence encoding; this allows one to “jump” from echo- to anti-echo acquisition FIDs between consecutively sampled data point.

Combining the principles underlying these two techniques, SPEED and SWAT, along the guidelines shown in Fig. 1, allows one to resolve the indirect-dimension ambiguity remaining in eq. 1 within a single-scan sequence. Indeed, even if constrained to a single t₁ value Δt₁, the phase distortions in the resulting acquisition can be summarized as

$$\begin{array}{l}{S}_N\mathit{\left(}\Delta t_{\mathit{1}},F_{\mathit{2}}\mathit{\right)}\approx \mathit{\text{exp}}{\mathit{\left(}-\mathit{2}\pi i{F}_{\mathit{1}}\Delta t_{\mathit{1}}\mathit{\right)}}^{.}I{\mathit{\left(}{F}_{\mathit{2}}\mathit{\right)}}^{.}\mathit{\text{exp}}\mathit{\left[}\mathit{2}\pi i\mathit{\left(}{\varphi }_{\mathit{0}}+F_{\mathit{2}}{\varphi }_{\mathit{1}}\mathit{\right)}\mathit{\right]}\\ S_P\mathit{\left(}\Delta t_{\mathit{1}},F_{\mathit{2}}\mathit{\right)}\approx \mathit{\text{exp}}{\mathit{\left(}+\mathit{2}\pi i{F}_{\mathit{1}}\Delta t_{\mathit{1}}\mathit{\right)}}^{.}I{\mathit{\left(}{F}_{\mathit{2}}\mathit{\right)}}^{.}\mathit{\text{exp}}\mathit{\left[}\mathit{2}\pi i\mathit{\left(}{\varphi }_{\mathit{0}}+F_{\mathit{2}}{\varphi }_{\mathit{1}}\Delta t_{SWAT}\mathit{\right)}\mathit{)}\mathit{\right]}\end{array}$$ (2)

where Δt_SWAT is the delay between N and P’s initial acquisition time. Given that this delay is known, the difference required by each F₂-peak of N- and P-spectra for achieving its correct phasing:

$$\Delta \varphi \mathit{\left(}{F}_{\mathit{2}}\mathit{\right)}={\mathit{\text{tan}}}^{-\mathit{1}}\mathit{\left[}im\mathit{\left(}{S}_P\mathit{\right)}/re\mathit{\left(}{S}_P\mathit{\right)}\mathit{\right]}-{\mathit{\text{tan}}}^{-\mathit{1}}\mathit{\left[}im\mathit{\left(}{S}_N\mathit{\right)}/re\mathit{\left(}{S}_N\mathit{\right)}\mathit{\right]}=\mathit{4}\pi F_{\mathit{1}}\Delta t_{\mathit{1}}+F_{\mathit{2}}\Delta t_{SWAT}$$ (3)

can ascertain the F₁ offset to be correlated with this peak –all while remaining in a single-shot acquisition mode and without incurring in the sensitivity penalties of space-encoded ultrafast NMR.

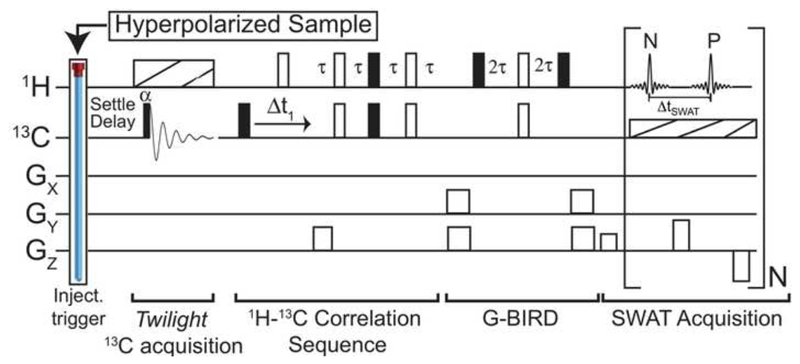
Figure 1.

HyperSPASM pulse sequence for establishing single-shot 2D heteronuclear correlations on DNP-enhanced samples. A single-t₁ (Δt₁) 2D heteronuclear sequence –with full and open rectangles representing π/2 and π pulses, dashed rectangles denoting broadband decoupling, and τ = 1/(4J_CH) set by one-bond heteronuclear couplings– establishes the ¹³C-¹H correlations. The absolute phase evolution imparted by Δt₁ is unravelled by the independent, single-shot monitoring of echo and anti-echo (N, P) modulations as aided by pulsed G_Z gradients. The sequence includes a G_X,G_Y-BIRD element [22] to suppress background signals from ¹²C bonded protons, and thereby enable the acquisition of ¹³C-decoupled direct domain line shapes that can be independently and reliably phased to pure absorption. An initial twilight {¹H}¹³C spectrum is also acquired using a low flip-angle pulse before the acquisition, as an aid to remove potential folding artifacts in F₁.

2. Experimental Methods

The usefulness of HyperSPASM was explored within the context of ex situ DNP. Such dissolution DNP experiments are well suited for heteronuclear correlations whereby the slowly-relaxing ¹³C nuclei are hyperpolarized, and then monitored indirectly in correlation with J-coupled protons having a higher detection sensitivity. The HyperSPASM experiment thus assayed (Fig. 1) resembles a reversal of the traditional HETCOR sequence [23]. Notice as well that a small-tip-angle ¹³C “twilight” 1D acquisition is collected as complement to SPASM, and is meant to provide an unambiguous accounting of all the ¹³C positions expected along the F₁ domain.

Samples were hyperpolarized in an Oxford Hypersense polarizer (Tubney Woods, UK) for 5 hours (pyridine) and 3.25 hours (indazole). Pyridine was hyperpolarized by BDPA radicals at ≈40 mM with an equal volume of d₆-DMSO. Indazole was hyperpolarized in a 1:1 solution of d₆-DMSO/sulfolane with 40 mM BDPA [24]. Approximately 4 mL of methanol-d₄ were used to dissolve both samples. The encoding gradient following the indirect evolution delay (Δt₁) was set to 20 G/cm, which then determined the decode gradient immediately before SWAT acquisition by the ratio (ɣ _C/ɣ _H) to be approximately 5 G/cm and the SWAT acquisition gradients to be approximately 10 G/cm. All of the aforementioned coherence selection gradients were applied for a length of 200 µs. The y and z gradients used in the GBIRD element had amplitude 30 G/cm and a length of 400 µs. The HyperSPASM experiment shown in Figure 1 was repeated for 2 transients (where the ¹³C twilight acquisition was collected only on the first transient) to achieve complete suppression of the ¹²C-bonded protons, where the phase of the 90-degree carbon pulse preceding Δt₁ was inverted and the resulting signals were subtracted by alternating the receiver phase. As an additional step to achieve background signal suppression, the correlation sequence was preceded by a 90-degree pulse on the ¹H channel followed by an approximately 13.3 G/cm gradient on the PFG X-axis channel for a duration of 1 ms, to saturate any initial ¹H magnetization such that it would not contribute to the detected signal.

3. Results

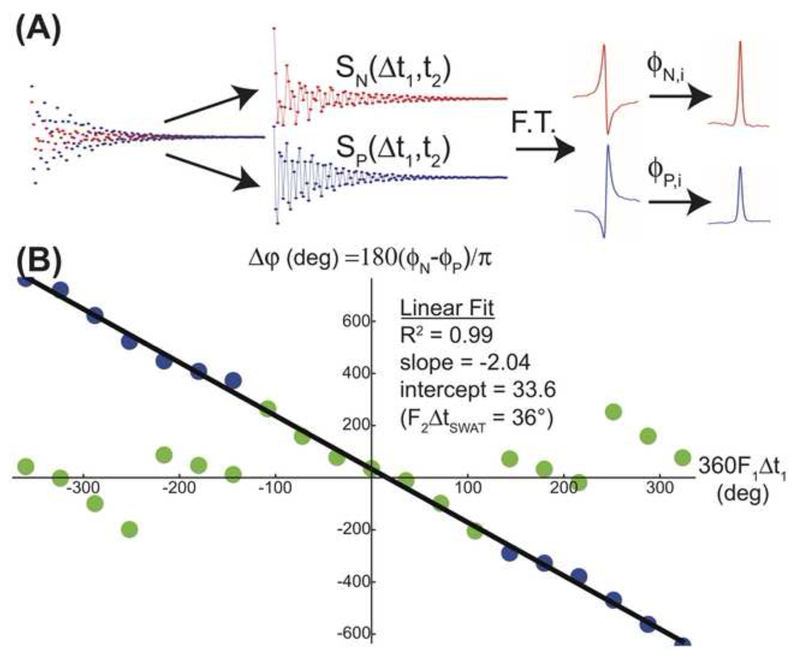
To better visualize the workings of the resulting scheme, Figure 2 illustrates SPASM’s operation for a heteronuclear correlation in a model compound. Notice the phase-wrapping that naturally occurs as the F₁ offset exceeds ±0.5/Δt₁; it follows from plots of this type that Δt₁ not only imposes this frequency range but also ΔF₁’s resolution limit. According to repetitive SPASM measurements and their ensuing P/N-phasing, we estimate this random uncertainty at ca. 0.015/Δt₁.

Figure 2.

Experimental demonstration of SPASM’s ability to measure indirect-domain evolution frequencies, illustrated for a model Chloroform case whose ¹³C offset was systematically shifted over 2 kHz in 100 Hz steps for a fixed indirect evolution delay Δt₁ = 1 ms. (A) Post-acquisition processing involves separating the experimental data into alternating points corresponding to N (echo) and P (anti-echo) FIDs. Once individually Fourier transformed and phased to yield purely-absorptive 1D spectra, each peak leads to the phase parameters ϕ_N,i and ϕ_P,i from which the indirect frequency can be determined (eq. 2). (B) Phase difference exhibited by CHCl₃’s sole ¹H resonance when acted upon by the SP-SWAT sequence as a function of an artificially-varying indirect frequency offset F₁. Green data points illustrate the periodic phase wrapping arising from the limits on a measurable phase difference Δϕ = ϕ_N-ϕ_p; phase-unwrapping yields the blue points, in excellent fit with the prediction of eq. 3.

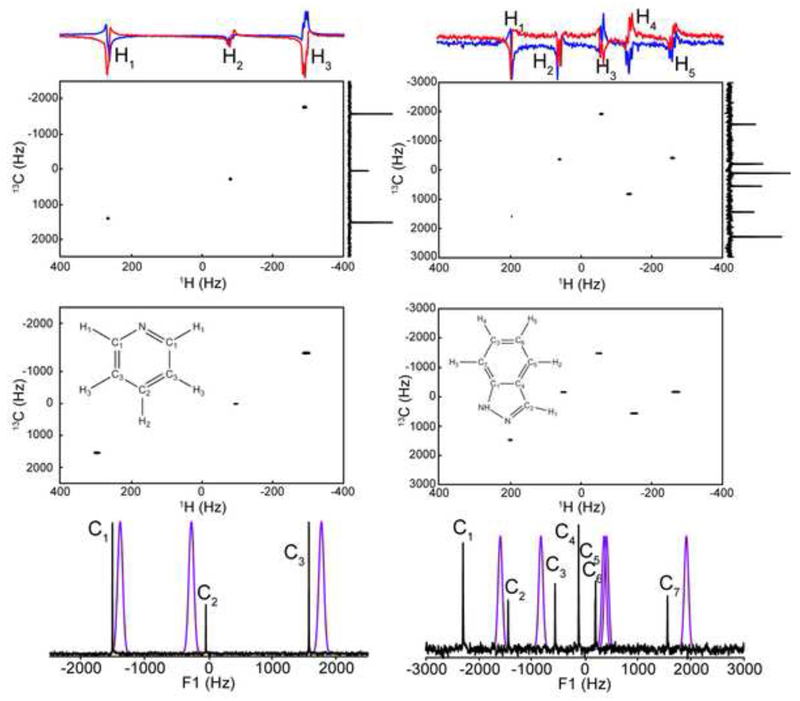
Figure 3 illustrates the ensuing results for pyridine and for indazole. Notice that with a suitable placing of the RF channel’s offsets in the center of the corresponding spectra, the experiment had no difficulties in correlating each ¹H/¹³C coupled pair while monitoring free evolution data –this, despite the latter shifts spanning nearly 3 kHz in F₁. The single-shot correlation shows excellent agreement with HSQC [25] data acquired and processed [26] in a conventional manner. The ¹³C “twilight” 1D acquisition further validates the genuine frequencies of all indirect-domain peaks from SPASM data. Still, it is interesting to note certain systematic deviations between the positions of the ¹³C peaks observed by this pre-acquisition scan and the SPASM predictions for all peaks that were analyzed. We ascribe these deviations to minor timing errors in the implementation of the gradient’s and pulse’s waveforms, whose exact value was unknown and therefore ignored in the F₁-domain estimations.

Figure 3.

HyperSPASM correlations established for natural-abundance pyridine (left) and indazole (right). The 2D correlations generated by the pulse sequence (upper panels) arise from phasing the illustrated 1D traces – N/echo spectrum in red, P/anti-echo spectrum in blue. Each of these was collected using the sequence in Fig. 1, N= 256 acquisition loops, Δt₁= 150 µs, and two phase-cycled transients for an optimal suppression of the ¹²C-bonded protons (important to retrieve reliable phased data). Shown in the lower 2D panels are conventional HSQC spectra acquired with 256 t₁ increments. HyperSPASM data were acquired at sample concentrations of ≈3 mM for pyridine and 20 mM for indazole, the HSQCs stem from concentrated (approximately 25% pyridine, 1 M indazole) samples. The 1D spectra (bottom) compare the predicted F₁ peak locations calculated from eq. 3 (violet) against the experimental DNP-enhanced twilight ¹³C data (black); widths in the calculated peaks reflect the phasing uncertainty, translated into Hz.

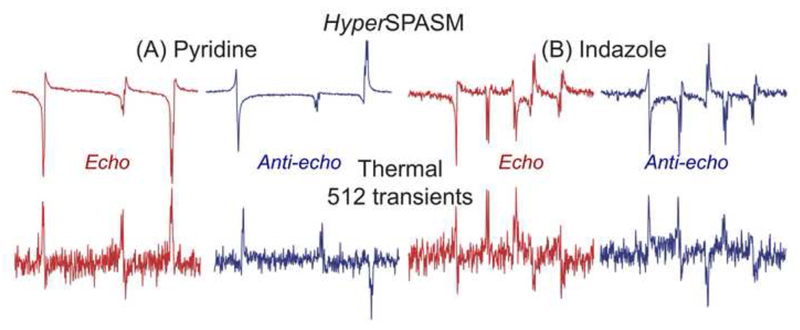
To further assess the experimental sensitivity benefit incurred from the dissolution DNP process, the results obtained with HyperSPASM were compared with results obtained on the same sample after spins have returned to thermal equilibrium. Both experiments used the pulse sequence in Figure 1 (without the twilight ¹³C acquisition), and the latter was repeated for 512 transients. Figure 4 presents this control, and reveals ca. 670x and 120x average enhancements for P/N acquisitions on pyridine and indazole dissolutions, respectively. When factoring in the additional γ_H/γ_C sensitivity afforded by these ¹H-detected experiments it follows that nearly very modest sensitivity penalties over the conventionally detected 1D DNP-enhanced ¹³C experiment results –despite the more complex nature of the used pulse sequence and the 2D correlated information arising thereof. Also interesting to note is the 180° phase shift differences characterizing all peaks in the hyperpolarized vs the thermal spectra illustrated in Figure 4; given the identical pulse sequences that were utilized to collect these two data sets, we ascribe this difference to the opposing states of ¹³C polarization that characterized the initial states in these experiments.

Figure 4.

Comparing SPASM’s sequence performance on DNP-enhanced samples (one post-twilight scan - top) vs the same sequence executed after spins have returned to their thermal equilibrium (bottom), for both pyridine (A) and indazole (B). We ascribe the ≈180˚ phase difference between hyperpolarized and thermal spectra to the differing initial conditions of the starting ¹³C polarization.

4. Discussion and Conclusions

This study introduced a new approach to establish 2D NMR correlations, whereby single-delay phase distortions can be translated into F₁ shifts. This can be attained in a single scan by the simultaneous acquisition of the echo and anti-echo sets arising from amplitude-modul0ated data involving a single Δt₁ time. The experiment is unequivocal and accurate, providing a convenient platform for extracting DNP-enhanced 2D correlations. Being free from the need to fully sample two domains in a single scan, the acquired spectra also promise remarkable signal-to-noise improvements vis-à-vis ultrafast 2D NMR. This technique could thereby be advantageously extended beyond its integration of DNP and into other kinds of time-pressed experiments, like the monitoring of real time chemical processes at seconds or sub-second timescales [27]. Despite all these promises, this technology still faces a number of basic limitations related to the extraction of frequencies from a single time point. One of these relates to folding/phase-wrapping ambiguities, which can usually be alleviated by adding the aforementioned 1D “twilight” measurement. Another limitation stems from the inter-relation between the spectral width that can be characterized in F₁, and the accuracy of these characterizations –both of which end up defined by the same parameter Δt₁. Arguably, however, the most constraining limitation stems from the requirement that all peaks of interest be resolved along the direct dimension. In effect, should one F₂ peak be correlated to multiple F₁ sites, phasing such resonance into a reliable purely-absorptive line shape from which a definite F₁ offset value could be read from the ϕ_N and ϕ_P parameters, does not appear feasible. For large complex molecules like proteins, or for multi-site homonuclear correlation experiments such as TOCSY, the sequence in Figure 1 would seem of little use. The use of additional manipulations, however, could help alleviate this problem. One could envision, for instance, incorporating additional coherence-selecting gradients encoding supplementary Δt₁ values, from which the ensuing ambiguities could be resolved. Research to solving this matter and exploring its applications, are currently in progress.

Highlights.

• A new approach to establish 2D hetero-correlations in a single scan is reported

• The method imposes amplitude modulations during an indirect-domain evolution delay, and subsequently monitors the effects of these encodings on separate echo and the anti-echo signals.

• The potential of the ensuing “HyperSPASM” method is exemplified with HSQC-type correlations on model hyperpolarized samples