Ultrafast anisotropic protein quake propagation after CO photodissociation in myoglobin

Significance

Scattering in solution conducted at X-ray free-electron lasers in principle provides a probe for the ultrafast dynamics of proteins. However, extracting useful structural information from the experimental signals remains a major challenge. Here, we used molecular-dynamics simulations to model the ultrafast “quake-like” dissipation of energy in myoglobin. The simulations provide a detailed atomistic movie of the protein quake, and they help to translate solution scattering signals into functional protein dynamics. Remarkably, we further find that accounting for solvent dynamics is crucial to avoid misinterpretation of time-resolved solution scattering data.

Abstract

“Protein quake” denotes the dissipation of excess energy across a protein, in response to a local perturbation such as the breaking of a chemical bond or the absorption of a photon. Femtosecond time-resolved small- and wide-angle X-ray scattering (TR-SWAXS) is capable of tracking such ultrafast protein dynamics. However, because the structural interpretation of the experiments is complicated, a molecular picture of protein quakes has remained elusive. In addition, new questions arose from recent TR-SWAXS data that were interpreted as underdamped oscillations of an entire protein, thus challenging the long-standing concept of overdamped global protein dynamics. Based on molecular-dynamics simulations, we present a detailed molecular movie of the protein quake after carbon monoxide (CO) photodissociation in myoglobin. The simulations suggest that the protein quake is characterized by a single pressure peak that propagates anisotropically within 500 fs across the protein and further into the solvent. By computing TR-SWAXS patterns from the simulations, we could interpret features in the reciprocal-space SWAXS signals as specific real-space dynamics, such as CO displacement and pressure wave propagation. Remarkably, we found that the small-angle data primarily detect modulations of the solvent density but not oscillations of the bare protein, thereby reconciling recent TR-SWAXS experiments with the notion of overdamped global protein dynamics.

Functional protein dynamics occur on various timescales, ranging from tens of femtoseconds for bond breaking, up to milliseconds and seconds for large-scale conformational transitions or protein folding. Observing and explaining such transitions, if possible in a time-resolved manner, has remained a central goal of molecular biophysics. A popular model system used to study proteins dynamics has been the 18-kDa protein myoglobin (Mb), the protein of first known tertiary structure (1). Mb contains an iron-porphyrin heme group that reversibly binds small gas molecules such as molecular oxygen (O₂) or carbon monoxide (CO). Mb is abundant in the muscle tissue of vertebrates, where it plays an important role in the transport and storage of O₂ and in the biochemistry of nitric oxide (2, 3).

Because the CO–iron bonds in a Mb ensemble can be coherently photolysed with a laser flash within only 50 fs (4), a range of time-resolved techniques has been applied to probe various aspects of the structural dynamics after CO photodissociation, such as energy dissipation, CO dynamics, or heme doming (5–15). Three-dimensional movies of Mb conformational transitions were derived by means of time-resolved crystallography, which recently reached subpicosecond time resolution (16–19). These experimental studies were complemented by several pioneering molecular-dynamics (MD) simulations that revealed the Mb dynamics with atomic detail, with some focus on heat dissipation, vibrational dynamics, as well as ligand migration (20–28).

Time-resolved small- and wide-angle X-ray scattering (TR-SAXS, TR-WAXS, TR-SWAXS) is an emerging technique used to track conformational transitions in solution. The method has been applied to follow chemical reactions of small molecules (29–31) as well as structural dynamics of photoactive proteins (32–41). Thanks to the advent of X-ray free-electron lasers, TR-SWAXS experiments have reached subpicosecond time resolution, thus detecting the ultrafast dynamics of proteins. Hence, TR-SWAXS is able to track the ultrafast dissipation of energy in proteins triggered by a local perturbation, due to, for instance, the breaking of a chemical bond or the deposition of energy upon photon absorption (42, 43). Such dynamics of energy dissipation have been referred to as “protein quakes” (44). These new experiments provide valuable insight into the ultrafast dynamics of proteins in solution, but they also raised new questions. Oscillations in the small-angle data detected by recent TR-SWAXS experiments were interpreted as underdamped oscillations of the entire protein (43), thus challenging the long-standing notion of overdamped large-scale protein dynamics (45, 46). However, the structural interpretation of SWAXS patterns has remained problematic mainly for two reasons. First, SWAXS patterns contain only few independent data points (for Mb, $\sim 14$ data points at a maximum momentum transfer of 1 Å⁻¹) (47), whereas proteins contain orders of magnitude more degrees of freedom. Second, scattering contributions from the hydration layer complicate the interpretation of the patterns; as shown here, solvent effects may even dominate the signals. These complications preclude a straightforward fitting of structural models against TR-SWAXS data without significant risk of overfitting.

MD simulations have been used to interpret experimental data of low information content via back-calculating experimental signals from the simulation frames. To apply this strategy to TR-WAXS data, we recently developed an algorithm for the calculation of isotropic and anisotropic TR-SWAXS patterns from explicit-solvent MD simulations, which we here used to study the ultrafast dynamics after CO photodissociation in Mb. The calculations are fully based on explicit-solvent MD, thus accounting for scattering contributions from density modulations in the hydration layer (48, 49).

Results

Time-Resolved WAXS Patterns.

The CO dissociation was modeled classically, as done previously (ref. 28 and references therein), by instantaneously switching the force field from the CO bound to the dissociated state. Assuming an excitation laser of 532-nm wavelength and a reaction enthalpy of 96.5 kJ⋅mol⁻¹, we added the appropriate amount of kinetic energy to the nitrogen atoms of the porphyrin ring to ensure that the total amount of dissipated energy agrees with experimental conditions (SI Materials and Methods). The dissociation kinetics was similar to previous studies, characterized by cooling of the CO within 300 fs due to collisions with protein atoms, and a cooling of the heme within 1–2 ps, followed by slower relaxations (Fig. S1) (5, 10).

Fig. S1.

Cooling of the CO (Left) and cooling of the heme plane, taken as the porphryin atoms plus the iron (Right). The kinetic energy $E_{\text{kin}}$ was translated to a temperature T via $E_{\text{kin}}=f{k}_{\mathrm{B}}T/2$, where $k_{\mathrm{B}}$ denotes the Boltzmann constant and f denotes the number of degrees of freedom, taking constraints into account ($f=5$ for CO and $f=36.5$ for the heme plane). CO cooled within $\sim$ 300 fs due to collisions with protein atoms. The heme plane cooled rapidly within 1–2 ps, starting from $\sim$ 400 K, followed by slower relaxations beyond the 5-ps timescale shown here. These findings are compatible with previous reports (5, 10). The CO temperature curve implies that, in our simulations, $\sim$ 40% ($\sim$ 55 kJ⋅mol⁻¹) of the excess energy accumulated in kinetic energy of the CO, before the CO collided with protein atoms. This value appears reasonable in the light of recent quantum-chemical calculations, reporting the potential energy surface of the dissociating quintet state of the heme–CO complex (19), but the value appears somewhat too large in the light of early spectroscopic experiments (10). The temperatures in this figure were averaged over 8,500 dissociation simulations conducted with a TIP4P-Ew water model (see SI Materials and Methods for details).

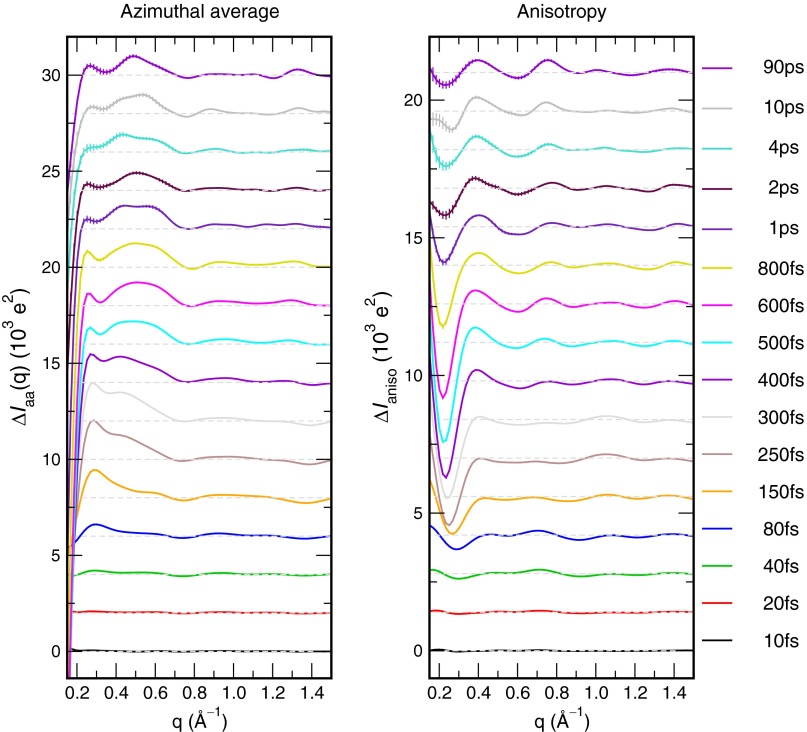
TR-WAXS experiments report the difference in scattering intensity of the system before and after CO photodissociation, as a function of the time delay $\mathrm{\Delta }t$ after excitation. We computed 2D difference patterns from $\sim$10,000 100-ps simulations of CO photodissociation, combined with $\sim$ 10,000 simulations of Mb in the ground state (Fig. 1). Fig. 2A and Fig. S2 present typical TR-WAXS patterns, and the azimuthal average over the detector $I_{\text{aa}}\left(q,\mathrm{\Delta }t\right)$ is shown in Fig. 2B. Here, the momentum transfer is defined as $q=4\pi {\lambda }^{-1}\sin \left(\theta \right)$, where $2\theta$ is the scattering angle and λ is the wavelength of the X-ray beam. Because heme is a circular absorber, Mb in which the heme plane is oriented parallel to the excitation laser polarization is excited with higher probability, leading to anisotropic ensembles of excited and ground-state Mb (50). Hence, additional structural details are given by the anisotropy $\mathrm{\Delta }{I}_{\text{aniso}}\left(q\right)$ of the TR-WAXS patterns (48, 51, 52), here computed as the difference between the horizontal and vertical cuts on the detector (Fig. 2C and Fig. S3). These reciprocal-space signals are rationalized in real space in Fig. 2F and Movie S1, visualizing the CO movements and the protein quake propagation in terms of electron density differences after photodissociation, averaged over $\sim$ 10,000 simulations. In addition, Fig. 2G quantifies the protein quake in terms of time-resolved center-of-mass displacement of a number of residues and α-helices.

Fig. 1.

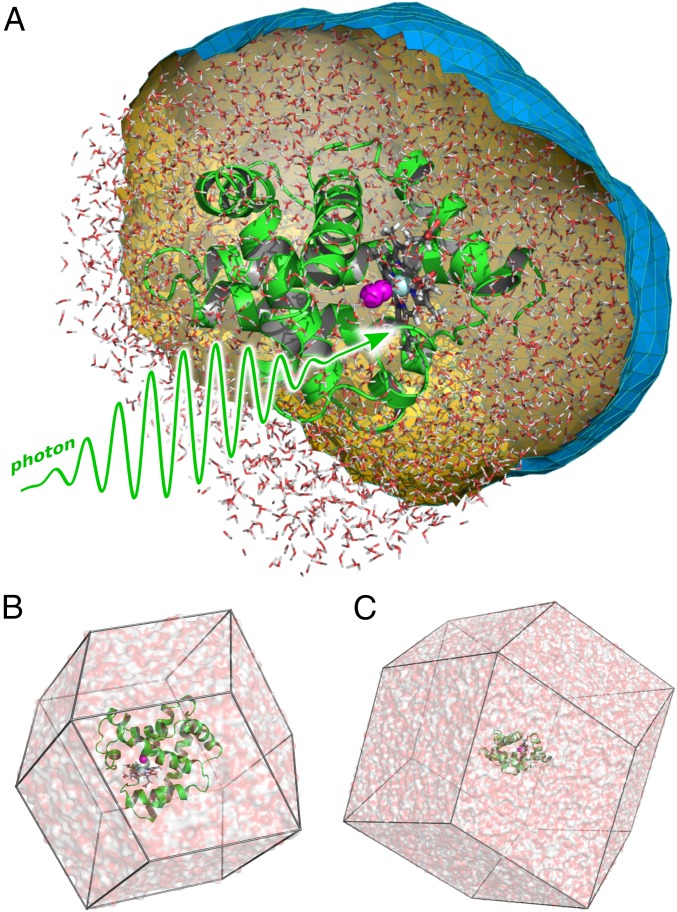
(A) Molecular representation of myoglobin (Mb). The backbone trace is shown as green cartoon, the heme as gray sticks, CO as magenta spheres, and iron as light blue sphere. A spatial envelope, here at a distance of 6 Å from all protein atoms, is shown as blue/orange surface. Water atoms (white/red sticks) inside the envelope contribute to the SWAXS calculations. (B) Typical small and (C) large simulation system of Mb, used to compute WAXS and SAXS patterns, respectively.

Fig. 2.

(A) Time-resolved anisotropic WAXS patterns of Mb in units of $e^2$. (B) Azimuthal average over the detector for time delays between 10 fs and 90 ps, and (C) anisotropy of the WAXS patterns, taken as the difference between the horizontal and vertical cuts in A. Curves at $\mathrm{\Delta }t>10$ fs were offset for clarity. (D and E) Azimuthally averaged intensities at 0.28 and 0.75 Å⁻¹ versus time delay (B, orange and green bars), computed from the whole system (blue), or by omitting the CO atoms (red). (F) Isosurfaces of the electron density difference maps at 20 fs, 150 fs, 400 fs, and 1.0 ps after photodissociation. Green and red surfaces indicate increased and reduced density, respectively. Opaque green and red surfaces: $\pm 400$ e⋅nm⁻³; transparent green and red surfaces: $\pm 100$ e⋅nm⁻³. Additional time delays are visualized in Movie S1. (G) Time-resolved center-of-mass displacement of a number of residues (top three panels) and α-helices (bottom panel), with respect to their position at $\mathrm{\Delta }t=0$, as indicated in the legends. The density differences in F and curves in G illustrate the propagation of the protein quake.

Fig. S2.

Time-resolved anisotropic WAXS intensity patterns (in units of $e^2$) computed from an average over $\sim$ 10,000 simulations. The time delay $\mathrm{\Delta }t$ is indicated in the subplots. y axis: direction of the excitation laser; x axis: direction of the excitation laser polarization.

Fig. S3.

Vertical cut (Left) and horizontal cut (Right) over anisotropic TR-WAXS patterns shown in Fig. 2A and Fig. S2. Curves at $\mathrm{\Delta }t>10$ fs were offset for clarity.

Within 100 fs after photodissociation, the CO was fully displaced along the heme normal, which manifests in $I_{\text{aa}}\left(q,\mathrm{\Delta }t\right)$ as a permanent minimum at $q=0.75$ Å⁻¹ (Fig. 2B, green bar). Indeed, the signals lack this minimum when the CO atoms are omitted from the WAXS calculations (Fig. 2E and Fig. S4). Hence, the ultrafast appearance of the $q=0.75$ Å⁻¹ minimum, which is compatible with recent TR-WAXS experiments (43), primarily reflects the CO displacement, complementing previous studies that interpreted features in the WAXS patterns mainly as fingerprints for tertiary conformational transitions (34, 43, 53). Simultaneously, a transient signal at 0.28 Å⁻¹ built up within 250 fs (Fig. 2 B, orange bar, and D), which is much less dependent on the CO atoms. Because the time courses of the 0.28 Å⁻¹ signal and of the protein quake visible in Movie S1 are similar, we suggest that the 0.28 Å⁻¹ signal is the main fingerprint of the protein quake in reciprocal space. Because this signal had diminished at 500 fs, it might have been invisible to recent TR-WAXS experiments by Levantino et al. (43) with a time resolution of $\sim$500 fs. In line with reports by Ihee and coworkers (51), our simulations predict highly anisotropic patterns, reflecting that the CO displacement as well as the follow-up protein dynamics occur in an oriented manner with respect to the heme plane (Fig. 2 C and F).

Fig. S4.

Azimuthal average (Left) and anisotropy (Right) of the TR-WAXS patterns, computed from the coordinates of the protein (including heme) and solvent, but omitting the CO. In contrast to the TR-WAXS computed from the whole system (including CO), no minimum at $q=0.75$ Å⁻¹ appears, suggesting that this minimum primarily reflects the displacement of the CO after photodissociation.

On longer timescales, picosecond dynamics manifest as a separate well at $q=0.35$ Å⁻¹ appearing after $\mathrm{\Delta }t>1$ ps, as also observed in experimental data (34, 41, 43, 53). This peak was found to be less prominent in simulation compared with experiments, possibly because the applied MD force field did not reproduce the doming of the heme structure (Fig. 2D; see also SI Discussion for simulations with an alternative force field). However, the overall reasonable agreement to experimental TR-WAXS data suggests that the dynamics in the simulations resemble the experimental conditions.

As visualized in Fig. 2F and Movie S1, the pressure wave (or protein quake) propagated anisotropically, whereas the most rapid propagation occurred perpendicular to the heme plane: within 100 fs, Leu-29 and the proximal His-93 were perturbed by the dissociated CO and by the displaced iron, respectively, thus shifted away from the heme plane (Fig. 2G). Until a time delay of 150 fs, these perturbations further propagated across the backbones of helices B and F into Ile-30 and Ala-94, triggering damped oscillations with a period between 300 and 450 fs, compatible with recent findings from serial femtosecond crystallography (19). At 500 fs, nearly the complete helices B and F were perturbed. In contrast, in the direction parallel to the heme plane, the propagation occurred with a significant delay. Within 100 fs, the side chain of Phe-43 shifted, as also observed by crystallography (19), but it took $\sim$ 300 fs until this perturbation had propagated into the backbone of helix C. In helix E, Val-68 and His-64 were likewise perturbed by the dissociating CO within 100 fs, but this perturbation hardly propagated into the backbone of helix E, even until 1 ps. In addition, the CO moved between 150 and 500 fs from the pocket between Leu-29, Leu-32, Phe-43, His-64 further toward Ile-107 and into the distal pocket, rationalizing why Ile-107 was perturbed with delay of $\sim$ 500 fs (Fig. 2G, magenta) (19). The relaxation after the initial pressure wave occurred also in an asynchronous manner. For instance, the displacements of Leu-29 had relaxed at 450 fs, of Phe-43 side chain at 650 fs, and of the backbone of helix C at 1 ps. Taken together, the excess energy propagated as a pressure wave within $\sim$500 fs across the protein in a highly anisotropic and asynchronous manner, and the wave is echoed in the TR-WAXS pattern as a transient anisotropic peak at $q=0.28$ Å⁻¹.

Time-Resolved SAXS Patterns.

It is well established that the density of the hydration layer of proteins may differ from the density of bulk water, thus contributing to the overall density contrast detected by SAXS experiments (54). Accordingly, we observed that the pressure wave triggered by CO dissociation propagated across the hydration layer and further into bulk water, with significant fingerprints in the SAXS patterns. To account for such effects, we conducted 10,000 additional simulations of Mb in a larger simulation box (Fig. 1C). The time-resolved change of the solvent density averaged from these simulations showed that the pressure wave had reached the protein surface after 300 fs, and subsequently propagated into the solvent with the speed of sound (Fig. 3B).

Fig. 3.

Analysis of the small-angle scattering data. (A) Mb (green cartoon) and explicit water (sticks) enclosed by envelopes with distance of 1, 7, 17, and 27 Å (blue surfaces). (B) Time-resolved change of the solvent density after CO photodissociation versus distance from the protein, demonstrating the propagation of a pressure wave across the hydration layer within $\sim$ 2 ps after CO photodissociation. Blue circles: Peak propagation expected from the speed of sound (1.48 nm/ps). (C) Time evolution of the radius of gyration after CO photodissociation $\mathrm{\Delta }{R}_g^{\text{Guin}}\left(t\right)$ extracted from the Guinier analysis, thus taking hydration layer contributions into account. Color coding indicates calculations from different distance d of the envelope from the protein (see legend). (D) Volume of the protein taken from the forward intensity $I\left(q=0\right)$. (E) Increase of radius of gyration of the bare protein $\mathrm{\Delta }{R}_g^{\text{Prot}}$, ignoring any solvent effects.

Guided by these solvent density curves, we first computed the SAXS patterns including explicit solvent contributions up to a distance of 17 Å from the protein, as solvent contributions from larger distances added systematic errors due to tiny drifts in the solvent density. The apparent change in the radius of gyration $\mathrm{\Delta }{R}_g^{\text{Guin}}\left(\mathrm{\Delta }t\right)$ and total protein volume $\mathrm{\Delta }{V}^{\text{Guin}}\left(\mathrm{\Delta }t\right)$ were computed by fitting the Guinier approximation to the buffer-subtracted SAXS curves, $\text{ln}\left[I\left(q\right)/I\left(0\right)\right]=-{\left(q{R}_g^{\text{Guin}}\right)}^2/3$, thus accounting for scattering contributions from the hydration layer (SI Materials and Methods). The results are presented in Fig. 3 C and D as black curves, which resemble the curves fitted by Levantino et al. (43) against experimental TR-SAXS data. In particular, $\mathrm{\Delta }{R}_g^{\text{Guin}}$ exhibited an oscillatory shape with a maximum after $\sim$ 1 ps, whereas the increase in $\mathrm{\Delta }{V}^{\text{Guin}}$ is delayed. However, the magnitude of the modulations were smaller in the simulations, and a second shallow oscillatory peak observed in experiments was not reproduced by our calculations.

Strikingly, the radius of gyration of the bare protein $\mathrm{\Delta }{R}_g^{\text{Prot}}$, computed purely from the protein atomic coordinates, exhibited a highly different temporal course compared with $\mathrm{\Delta }{R}_g^{\text{Guin}}$ (Fig. 3E and Fig. S5). Namely, $\mathrm{\Delta }{R}_g^{\text{Prot}}$ is characterized by an ultrafast increase within $\sim$650 fs up to only one-half the value observed in $\mathrm{\Delta }{R}_g^{\text{Guin}}$, followed by an overdamped decay to the new equilibrium value. Similar dynamics were found from the center-of-mass displacements of the α-helices (Fig. 2G and Fig. S6). This apparent discrepancy between $\mathrm{\Delta }{R}_g^{\text{Guin}}$ and $\mathrm{\Delta }{R}_g^{\text{Prot}}$ can be rationalized by computing $\mathrm{\Delta }{R}_g^{\text{Guin}}$ taking an increasing thickness of solvent into account (Fig. 3C, black and colored curves; illustrated in Fig. 3A and Fig. S7), yielding $\mathrm{\Delta }{R}_g^{\text{Guin}}$ curves that differ purely due to modulations of the solvent density. As expected, taking nearly no solvent into account (Fig. 3C, red) leads to an $\mathrm{\Delta }{R}_g^{\text{Guin}}$ progression that is identical to the $\mathrm{\Delta }{R}_g^{\text{Prot}}$ computed from the solute atoms, with a maximum at $\sim$ 650 fs. When increasing the thickness of the included hydration layer, the maximum in $\mathrm{\Delta }{R}_g^{\text{Guin}}$ increases and shifts to longer $\mathrm{\Delta }t$, reflecting a delayed escape of the pressure wave from the envelope. Likewise, the time course of $\mathrm{\Delta }{V}^{\text{Guin}}$ strongly depends on the thickness of solvent taken into account, demonstrating that $\mathrm{\Delta }{V}^{\text{Guin}}$ is also dominated by solvent contributions (Fig. 3D, black and colored curves). This analysis shows that TR-SAXS experiments with subpicosecond time resolution can detect the propagation of the pressure wave into the solvent. The dynamics of the bare protein, however, contribute only partly to the SAXS signal and may therefore be hidden by signals from the solvent density modulations.

Fig. S5.

Increase of the radius of gyration of the bare protein $\mathrm{\Delta }{R}_g^{\text{Prot}}$, computed from the atomic coordinates of the protein atoms (including heme) after photodissociation. Black curve: averaged over $\sim$ 8,500 simulations of the small simulation system with TIP4P-Ew water; red curve: averaged over $\sim$ 10,000 simulations of the small system with TIP3P water, as used for all other explicit-solvent simulations. The figure demonstrates that $\mathrm{\Delta }{R}_g^{\text{Prot}}\left(\mathrm{\Delta }t\right)$ hardly depends on the applied water model. $\mathrm{\Delta }{R}_g^{\text{Prot}}$ was scaled by ${\rho }_p/\left({\rho }_p-{\rho }_{\text{bulk}}\right)$ (${\rho }_{\text{bulk}}=334$ e⋅nm⁻³, ${\rho }_p=440$ e⋅nm⁻³) to allow direct comparison with the radius of gyration computed from a Guinier analysis. See Materials and Methods for details.

Fig. S6.

COM displacements of a number of residues (Top) and α-helices (Bottom), with respect to their position at $\mathrm{\Delta }t=0$, as indicated by the legends. Overdamped oscillations of Leu-29, Ile-30, His-93, and Ala-94 were observed with periods between 300 and 450 fs triggered by the dissociating CO and displaced iron. No indications for more global oscillations on a picosecond timescale are visible.

Fig. S7.

Mb with an increasingly thick hydration layer, as defined by the envelope (blue surface), at distances d of 1, 7, 17, and 27 Å from the protein atoms (see labels). Water molecules (red/white sticks) enclosed by the envelope were included in the calculations of SAXS/WAXS patterns.

SI Materials and Methods

Molecular Dynamics Simulations.

Simulation system and parameters.

The initial structure of horse heart myoglobin (Mb) was taken from the Protein Data Bank [PDB ID code 1DWR (61)]. The structure was placed into a simulation box of a dodecahedron, solvated with TIP3P water molecules (64), and the box was neutralized with two sodium ions. One set of control simulations was conducted with the TIP4P-Ew water model (Fig. S5) (65). A small simulation system containing 9,205 water molecules was used to compute the WAXS patterns, whereas a large system containing 70,188 water molecules was used for the SAXS calculations (Fig. 1 B and C). Interactions of the protein were described by the CHARMM22^∗ force field (62). CO was described by the three-site model developed by Straub and Karplus (25). The simulations were conducted with the Gromacs simulation software, version 4.6 (63). Electrostatic interactions were calculated with the particle mesh Ewald method (66), and dispersive interactions were described by a Lennard–Jones potential with a cutoff at 1.2 nm. The SETTLE algorithm was used to constrain water molecules, and LINCS was used to constrain all other bond lengths (67, 68). Hydrogen atoms were described as virtual sites, allowing a time step of 4 fs during equilibrium simulations.

MD simulations for WAXS calculations.

The initial frames used to simulate photodissociation were taken from equilibrium simulations. Initial frames of the small simulation system were taken from a 240-ns replica exchange MD simulation. Accordingly, 56 replicas at temperatures between $298.15$ and $400.02$ K were simulated. We observed rapid exchanges between the replicas, indicative of good sampling in the ground state replica. The temperature was controlled using velocity rescaling ($\tau =1$ ps) (69), and the pressure was kept at 1 bar using the Parrinello–Rahman barostat ($\tau =5$ ps) (70). The first 5 ns were removed for equilibration. From the remaining simulation time, 9,792 frames were taken. To generate continuous trajectories at the time point of photodissociation, the atomic coordinates and velocities at full floating-point precision were taken and used as initial coordinates and velocities for the follow-up simulations. From each frame, the simulation was branched into two 100-ps simulations: one simulation was continued in the MbCO ground state; the other simulation simulated the CO dissociation. For the WAXS calculations, frames from both branches at identical simulation times were compared. That procedure ensures the same level of conformational sampling in the generated ensembles of the ground state and excited state. To the contrary, taking the ground-state ensemble simply from a single long ground-state trajectory would lead to artifacts. The conformational sampling in a single long trajectory differs from the sampling in 10,000 100-ps simulations, which would manifest in a difference WAXS pattern purely due to differences in conformational sampling.

MD simulations for SAXS and solvent density calculations.

The initial structure of the large simulation system was taken from an equilibrated frame of the small system. The small system was placed into a large simulation box of a dodecahedron, filled by additional water, and equilibrated for another 50 ps. For photodissociation simulation, 9,890 initial frames were taken from a follow-up 100-ns equilibrium simulation, picking a frame every $\sim$ 10 ps. Again, to generate continuous trajectories, the atomic coordinates and velocities were taken from the equilibrium simulation at full floating-point precision, and used as starting coordinates and velocities for the dissociation simulations (see below). Each simulation was run for 5 ps, and simulation frames were stored every 10 fs.

To reduce the statistical errors, SAXS curves and solvent density at time delay $\mathrm{\Delta }t$ were computed from the simulation frames within a time interval between $\mathrm{\Delta }t-50\hspace{0.17em}\text{fs}$ and $\mathrm{\Delta }t+50\hspace{0.17em}\text{fs}$. At small $\mathrm{\Delta }t$, for which SAXS curves were computed for tightly spaced time delays, the interval range of 50 fs was reduced such that each simulation frame was used for only one $\mathrm{\Delta }t$.

CO photodissociation.

The total energy that is added to the system upon excitation was estimated as the difference between (i) the enthalpy of the reaction $\mathrm{\Delta }H$, which was reported between 88.7 and 107.5 kJ⋅mol⁻¹ (ref. 71; we used 96.5 kJ⋅mol⁻¹), and (ii) the energy added by one photon of the excitation laser $E_{\text{ph}}=224.9$ kJ⋅mol⁻¹ (532-nm wavelength). Hence, we assumed that a classical energy of $\mathrm{\Delta }{E}_b=E_{\text{ph}}-\mathrm{\Delta }H=128.2$ kJ⋅mol⁻¹ was added to the system upon CO photodissociation.

We modeled the CO dissociation based on the classical force fields described above, using the following steps: (i) the covalent bond and energy exclusions between CO and heme were removed, thus instantaneously switching from the force field of a six-coordinated to a five-coordinated iron, similar to previous studies (ref. 28 and reference therein). This step removes the bonded energy terms between CO and heme, but it adds the nonbonded energy terms that were excluded in the presence of the bond. The respective change in the force field potential energy is dominated by the new Lennard–Jones (LJ) potential between CO and heme, leading to an increase in potential energy. (ii) The increase $\mathrm{\Delta }{V}_{\text{ff}}$ of the sum of the LJ and short-range coulomb potentials of the system upon C–Fe bond removal was computed, as given by the force field in the presence and absence of the bond. Notably, a small change in the dihedral potential due to the removal of the bond (typically a few kilojoules per mole) was not added to $\mathrm{\Delta }{V}_{\text{ff}}$. On average, $\mathrm{\Delta }{V}_{\text{ff}}$ was $\sim$87 kJ⋅mol⁻¹. (iii) To simulate the absorption of a single photon, the required excess energy was calculated as $E_{\text{ex}}=\mathrm{\Delta }{E}_b-\mathrm{\Delta }{V}_{\text{ff}}$. On average, $E_{\text{ex}}$ was $\sim$41 kJ⋅mol⁻¹. (iv) This excess energy was added to the system by increasing the kinetic energy of the four nitrogen atoms of the porphyrin ring by $E_{\text{ex}}/4$ each. Accordingly, the velocity ${\mathbf{v}}_j$ of nitrogen atom j was scaled to $f_j{\mathbf{v}}_j$, where $f_j=1+E_{\text{ex}}/\left(2m_N{v}_j^2\right)$ and $m_N$ is the mass of a nitrogen atom. To simulate the absorption of two or three photons, the same procedure was applied but using $E_{\text{ph}}=449.8$ kJ⋅mol⁻¹ or $E_{\text{ph}}=674.7$ kJ⋅mol⁻¹, respectively (Figs. S8 and S9, red and black curves).

Fig. S8.

Increase of the radius of gyration of the bare protein $\mathrm{\Delta }{R}_g^{\text{Prot}}$ upon CO photodissociation for Mb in vacuum. In vacuum, Mb exhibits underdamped oscillations because the pressure wave (or protein quake) cannot dissipate into the solvent but is instead reflected at the water/vacuum interface. The increase in $\mathrm{\Delta }{R}_g^{\text{Prot}}$ is smaller in vacuum, presumably because the vacuum conditions favor overcompacted Mb conformations compared with solution conditions. Each $\mathrm{\Delta }{R}_g^{\text{Prot}}$ curve shown here represents an average over 8,500 simulations. $\mathrm{\Delta }{R}_g^{\text{Prot}}$ was scaled by ${\rho }_p/\left({\rho }_p-{\rho }_{\text{bulk}}\right)$ (${\rho }_{\text{bulk}}=334$ e⋅nm⁻³, ${\rho }_p=440$ e⋅nm⁻³) to allow direct comparison with the radius of gyration computed from a Guinier analysis. See Materials and Methods for details.

Fig. S9.

Increase of the radius of gyration of the bare protein $\mathrm{\Delta }{R}_g^{\text{Prot}}$, computed from the atomic coordinates of the protein atoms (including heme) after photodissociation, and averaged over $\sim$ 10,000 simulations of the small simulation system. Absorption of additional photons was simulated as described in Materials and Methods. $\mathrm{\Delta }{R}_g^{\text{Prot}}$ was scaled by ${\rho }_p/\left({\rho }_p-{\rho }_{\text{bulk}}\right)$ (${\rho }_{\text{bulk}}=334$ e⋅nm⁻³, ${\rho }_p=440$ e⋅nm⁻³) to allow direct comparison with the radius of gyration computed from a Guinier analysis. See Materials and Methods for details. Including the CO atoms yields $\mathrm{\Delta }{R}_g^{\text{Prot}}$ curves that are nearly identical to the curves shown here, suggesting that CO hardly contributes to $\mathrm{\Delta }{R}_g^{\text{Prot}}$. The zero photon curve (blue) fluctuates within the statistical uncertainty up to 5 ps. For times larger than 5 ps, small systematic patterns appear, presumably due the onset of temperature and pressure coupling at 5 ps (SI Materials and Methods).

Because the LJ potential between CO and heme might differ from the energy surface of the dissociative quintuplet state (19), the dynamics of CO dissociation predicted from the classical force fields might differ from results from quantum chemical calculations in the first $\sim$ 100 fs. However, the protocol ensures the correct amount of energy is added to the heme/CO complex, which eventually manifests in the protein quake.

The first $5\hspace{0.17em}\text{ps}$ after dissociation were simulated in the NVE ensemble with a time step of 0.5 fs. Indeed, we found that pressure coupling at the pronounced nonequilibrium conditions at small $\mathrm{\Delta }t$ would lead to artifacts. After 5 ps of the simulations used to compute WAXS patterns, the temperature was kept at 300 K using velocity rescaling (69), and the pressure was controlled at 1 bar using the weak coupling scheme ($\tau =5$ ps) (72). Because hydrogen atoms were described as virtual sites (see above), a time step of 4 fs was applied after 5 ps. After $40\hspace{0.17em}\text{ps}$, the pressure control was switched to the Parrinello–Rahman barostat ($\tau =5$ ps) (70).

Vacuum simulations of Mb.

The initial coordinates of Mb were taken from an equilibrated simulation frame of the small explicit-solvent simulation system. The systems were simulated without periodic boundary conditions, using a cutoff at 1.2 nm for the LJ interactions and no cutoff for the coulomb interactions. In equilibrium simulations, the temperature was controlled at 298.15 K with a stochastic dynamics integration scheme ($\tau =0.07$ ps). All other parameters were identical to the explicit-solvent simulations.

To generate starting configurations for CO dissociation simulations, we carried out five 40-ns simulations in vacuum. Frames were taken every 2 ps from the first 17 ns of one trajectory that exhibited a reasonably low root mean-square deviation (RMSD) of the C_α atoms of $\sim$1.7 Å, computed with respect to the initial coordinates. (The RMSD in explicit solvent was typically $\sim$ 1.3 Å.) This procedure ensured that the ensemble used to trigger CO dissociation in vacuum resembles the ensemble in explicit solvent. The protocol for CO dissociation simulations was identical to the protocol described above, except that the systems were simulated using a stochastic dynamics integration scheme with a very large coupling constant ($\tau =100$ ps), corresponding to nearly constant-energy conditions on the 10-ps timescale.

As a side note, we also tested equilibrium and CO dissociation simulations of Mb using implicit-solvent models. However, in those simulations, Mb exhibited an increased RMSDs of backbone atoms and increased radii of gyration, suggesting some loss of the atomic packing, presumably as a consequence of the approximations underlying the implicit-solvent models. Because the loss of atomic packing may influence the quake propagation, implicit-solvent simulations were not further considered.

Calculation of TR-SWAXS Patterns.

We recently introduced an algorithm to compute isotropic and anisotropic TR-WAXS patterns from explicit-solvent MD simulations (48). Following this algorithm, a difference term was computed, corresponding to a ground-state–subtracted structure factor:

$$\begin{array}{c}{\tilde{D}}_0^{\prime }\left(\mathbf{q}\prime ,\mathrm{\Delta }t\right)=\langle {\left|{\tilde{E}}_0\left(\mathbf{q}\prime ,\mathrm{\Delta }t\right)\right|}^2\rangle -\langle {\left|{\tilde{G}}_0(\mathbf{q}\prime )\right|}^2\rangle \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-2\hspace{0.17em}\text{Re}\left[\langle {\tilde{E}}_0\left(\mathbf{q}\prime ,\mathrm{\Delta }t\right)-{\tilde{G}}_0(\mathbf{q}\prime )\rangle {\rho }_s{\tilde{\mathrm{\Theta }}}_0^{\ast }\left(\mathbf{q}\right)\right].\end{array}$$ [S1]

Here, $\mathbf{q}\prime$ denotes the momentum transfer in the reference frame of the protein. The symbols ${\tilde{G}}_0\left(\mathbf{q}\right)$ and ${\tilde{E}}_0\left(\mathbf{q},\mathrm{\Delta }t\right)$ denote the Fourier transform of the electron density of the protein and nearby water molecules for the ground state and excited state, respectively. The explicit water molecules contributing to ${\tilde{G}}_0$ and ${\tilde{E}}_0$ were defined by a spatial envelope that encloses the protein at a preselected distance d (Fig. 1A, Fig. S7, and SI Materials and Methods). ${\tilde{\mathrm{\Theta }}}_0$ is the Fourier transform of the envelope, ${\rho }_s$ is the density of pure water, $\text{Re}$ is the real part, and the asterisk denotes complex conjugate. ${\tilde{G}}_0$ and ${\tilde{E}}_0$ were computed after superimposing the protein onto a reference structure, as indicated by the subscript 0. For each absolute value of q, ${\tilde{D}}_0^{\prime }\left(\mathbf{q}\prime ,\mathrm{\Delta }t\right)$ was calculated on a sphere of 1,500 $\mathbf{q}\prime$ vectors, which were distributed by the spiral method (49).

At low intensities of the excitation laser, the 2D SWAXS pattern can be computed from two independent components (48). (i) The isotropic component is given by a uniform average over spheres in $\mathbf{q}\prime$ space, corresponding to the intensity computed by common SWAXS prediction software:

$$\mathrm{\Delta }{I}_{\text{iso}}\left(q,\mathrm{\Delta }t\right)=\frac{1}{4\pi }{\displaystyle {\int }_{|\mathbf{q}\prime |=q}d\mathbf{q}\prime \hspace{0.17em}{\tilde{D}}_0^{\prime }\left(\mathbf{q}\prime ,\mathrm{\Delta }\right)}.$$ [S2]

(ii) An anisotropic component is given by a spherical integral weighted by a second spherical harmonic:

$$\mathrm{\Delta }{I}_{\mathbf{m}}\left(q,\mathrm{\Delta }t\right)=\frac{1}{4\pi }{\displaystyle {\int }_{|\mathbf{q}\prime |=q}d\mathbf{q}\prime \left[3{\left(\mathbf{m}\cdot \mathbf{q}\prime /q\right)}^2-1\right]{\tilde{D}}_0^{\prime }(\mathbf{q}\prime )},$$ [S3]

where $\mathrm{\Delta }{I}_{\mathbf{m}}\left(q,\mathrm{\Delta }t\right)$ depends on the orientation of the excitation dipole moment. Because heme is a circular absorber, $\mathbf{m}$ refers to the normal of the heme’s plane. For a circular absorber, the radial (or azimuthal) average of the 2D scattering pattern is given by the following:

$$\mathrm{\Delta }{I}_{\text{aa}}\left(q,\mathrm{\Delta }t\right)=-e^{-6D_r\mathrm{\Delta }t}\left(\frac{1}{8}-\frac{3q^2}{32k^2}\right)\mathrm{\Delta }{I}_{\mathbf{m}}+\mathrm{\Delta }{I}_{\text{iso}},$$ [S4]

which is presented in Fig. 2B. Here, k is the momentum of the X-ray beam. Hence, $\mathrm{\Delta }{I}_{\text{aa}}$ decays toward $\mathrm{\Delta }{I}_{\text{iso}}$ with a time constant of $1/\left(6D_r\right)$, where $D_r$ denotes the rotational diffusion constant. Because we focused in this work on time delays that are much shorter than the timescale of rotational diffusion of Mb, effects from rotational diffusion were neglected. In addition, we ignored contributions from excited but not dissociated MbCO, justified by the high quantum yield and only rare cases of rapid CO rebinding (73).

We assumed the following experimental setup for the anisotropic TR-WAXS experiment: the X-ray beam is pointing in horizontal x direction and the detector is located behind the sample in the $yz$ plane, where y denotes the second horizontal and z denotes the vertical axis. The excitation laser is pointing in z direction, and the laser polarization vector in y direction. For this setup, the difference intensity between horizontal and vertical cuts is given by the following:

$$I_{\text{aniso}}\left(q,\mathrm{\Delta }t\right)=-e^{-6D_r\mathrm{\Delta }t}\left(\frac{3}{4}-\frac{3q^2}{16k^2}\right)\mathrm{\Delta }{I}_{\mathbf{m}},$$ [S5]

which is presented in Fig. 2C.

Radius of Gyration of the Bare Protein.

The radius of gyration of the bare protein, thus not taking solvent contributions into account, was computed as follows. First, the radius of gyration of the protein in vacuum was computed using the following:

$${\left[{\tilde{R}}_g^{\text{Prot}}\left(\mathrm{\Delta }t\right)\right]}^2={\left({\displaystyle \sum _{i=0}^{N_p}{n}_{e,i}}\right)}^{-1}{\displaystyle \sum _{i=0}^{N_p}{n}_{e,i}{\left[{\mathbf{r}}_i\left(\mathrm{\Delta }t\right)-{\mathbf{R}}_s\left(\mathrm{\Delta }t\right)\right]}^2},$$ [S6]

where $N_p$ is the number of protein atoms (protein, heme, and iron), $n_{e,i}$ and ${\mathbf{r}}_i$ are the number of electrons and the position of atom i, respectively; ${\mathbf{R}}_s$ is the electron-weighted center of mass (COM); and $\mathrm{\Delta }t$ denotes the time delay after photodissociation. Subsequently, the radius of gyration at time delay zero was subtracted, $\mathrm{\Delta }{\tilde{R}}_g^{\text{Prot}}\left(\mathrm{\Delta }t\right)={\tilde{R}}_g^{\text{Prot}}\left(\mathrm{\Delta }t\right)-{\tilde{R}}_g^{\text{Prot}}\left(t=0\right)$. Notably, the radius of gyration given by Eq. S6 is computed by common software tools such as the Gromacs tool g_gyrate, although such tools typically adopt a mass-weighted (and not electron-weighted) definition.

Importantly, ${\tilde{R}}_g^{\text{Prot}}$ corresponds to the radius of gyration of the protein in vacuum, whereas the radius of gyration extracted from the Guinier analysis $R_g^{\text{Guin}}$ is the radius of gyration of the electron density contrast between protein and water. Hence, modulation of the protein’s electron density upon propagation of the pressure wave manifest in a smaller change in ${\tilde{R}}_g^{\text{Prot}}$ compared with the change in $R_g^{\text{Guin}}$, merely due to the different contrast definition (see next paragraph). To compare the modulation in the radius of gyration of the bare protein with $R_g^{\text{Guin}}$, we thus corrected via the following:

$$\mathrm{\Delta }{R}_g^{\text{Prot}}\left(\mathrm{\Delta }t\right)=\frac{{\rho }_p}{{\rho }_p-{\rho }_{\text{bulk}}}\mathrm{\Delta }{\tilde{R}}_g^{\text{Prot}}\left(\mathrm{\Delta }t\right),$$ [S7]

where the protein density was taken as ${\rho }_p=440$ e⋅nm⁻³ and the water density as ${\rho }_{\text{bulk}}=334$ e⋅nm⁻³.

Eq. S7 can be rationalized as follows. The radius of gyration $R_g$ of a density $\rho \left(\mathbf{r}\right)$ is given by the following:

$$R_g^2=\frac{{\displaystyle \int \rho \left(\mathbf{r}\right){\left(\mathbf{r}-{\mathbf{R}}_s\right)}^2\text{d}\mathbf{r}}}{{\displaystyle \int \rho \left(\mathbf{r}\right)\text{d}\mathbf{r}}}.$$ [S8]

Here, the density $\rho \left(\mathbf{r}\right)$ may either denote the density contrast with respect to vacuum or with respect to bulk water. Let us consider a small conformational transition that changes the density from $\rho \left(\mathbf{r}\right)$ to $\rho \prime \left(\mathbf{r}\right)=\rho \left(\mathbf{r}\right)+\delta \hspace{0.17em}\rho \left(\mathbf{r}\right)$, leading to a small change in the radius of gyration from $R_g$ to $R_g^{\prime }=R_g+\mathrm{\Delta }{R}_g$. Assuming that (i) the total number of electrons and (ii) the COM do not change upon the conformational transition, we have the following:

$${\displaystyle \int \delta \hspace{0.17em}\rho \left(\mathbf{r}\right)\text{d}\mathbf{r}}=0,$$ [S9]

$${\displaystyle \int \mathbf{r}\hspace{0.17em}\delta \hspace{0.17em}\rho \left(\mathbf{r}\right)\text{d}\mathbf{r}}=0.$$ [S10]

Using Eqs. S9 and S10, we obtain for the new radius of gyration after the transition:

$$R_g^{\prime 2}=\frac{{\displaystyle \int \rho \prime \left(\mathbf{r}\right){\left(\mathbf{r}-{\mathbf{R}}_s\right)}^2\text{d}\mathbf{r}}}{{\displaystyle \int \rho \prime \left(\mathbf{r}\right)\text{d}\mathbf{r}}},$$ [S11]

$$=R_g^2+\frac{{\displaystyle \int \delta \hspace{0.17em}\rho \left(\mathbf{r}\right){\left(\mathbf{r}-{\mathbf{R}}_s\right)}^2\text{d}\mathbf{r}}}{{\displaystyle \int \rho \left(\mathbf{r}\right)\text{d}\mathbf{r}}}.$$ [S12]

Keeping contributions up to order $\mathrm{\Delta }{R}_g$, we have the following:

$$R_g^{\prime 2}-R_g^2\approx 2R_g\mathrm{\Delta }{R}_g$$ [S13]

and

$$\mathrm{\Delta }{R}_g=\frac{1}{2R_g}\frac{{\displaystyle \int \delta \rho \left(\mathbf{r}\right){\left(\mathbf{r}-{\mathbf{R}}_s\right)}^2\text{d}\mathbf{r}}}{{\displaystyle \int \rho \left(\mathbf{r}\right)\text{d}\mathbf{r}}}.$$ [S14]

The numerator of the right-hand side of Eq. S14 does not depend on the contrast definition (vacuum or bulk water). The denominator, however, depends on the contrast definition. If $\rho \left(\mathbf{r}\right)$ denotes the density of the protein in vacuum, we have ${\displaystyle \int \rho \left(\mathbf{r}\right)\text{d}\mathbf{r}}\approx {\rho }_p{V}_p$, where $V_p$ is the protein volume. In contrast, if $\rho \left(\mathbf{r}\right)$ denotes the density contrast with respect to bulk water, we obtain ${\displaystyle \int \rho \left(\mathbf{r}\right)\text{d}\mathbf{r}}\approx \left({\rho }_p-{\rho }_{\text{bulk}}\right)V_p$. Consequently, Eq. S14 suggests that the same conformational transition $\rho \left(\mathbf{r}\right)\to \rho \left(\mathbf{r}\right)+\delta \hspace{0.17em}\rho \left(\mathbf{r}\right)$ leads to a change of the radius of gyration in vacuum that is reduced by a factor of $\left({\rho }_p-{\rho }_{\text{bulk}}\right)/{\rho }_p$ compared with the change of the radius of gyration taken from the Guinier fit.

Calculation of the Apparent Radius of Gyration $R_g^{\text{Guin}}$ and Protein Volume $V^{\text{Guin}}$ from the SAXS Patterns.

In contrast to the WAXS calculations (see below), we did not compute the SAXS difference patterns with respect to the ground state, but we computed instead buffer-subtracted SAXS patterns. The buffer scattering was computed from an equilibrium simulation of 165,716 TIP3P water molecules in a cubic simulation box, as described previously (49). In contrast to our previous work (49), we did not correct the density of the solvent to some experimental value, because that procedure leads to artifacts after the pressure wave leaves the spatial envelope. $R_g^{\text{Guin}}$ and the forward intensity $I\left(q=0\right)$ were computed by fitting the buffer-subtracted SAXS curves to the Guinier approximation $\text{ln}\left[I\left(q\right)/I\left(0\right)\right]=-{\left(q{R}_g^{\text{Guin}}\right)}^2/3$ in the range $q<0.08$ Å⁻¹. Here, $I\left(q\right)$ denotes the isotropic SAXS pattern, computed by taking the average over all protein orientations (Eq. S2). Notably, $I\left(q\right)$ [or $I_{\text{iso}}\left(q\right)$] is not identical to the azimuthal average over the detector $I_{\text{aa}}\left(q\right)$ (Fig. 2B) (48). For large envelopes enclosing a large amount of water (Fig. S7, $d=27$ Å), the calculation of the absolute $R_g^{\text{Guin}}$ becomes increasingly inaccurate because (i) the SAXS pattern is computed as a difference between two increasingly large numbers; and (ii) because of a small solvent density mismatch between the protein and the pure-water simulation system (49), which we cannot correct during the nonequilibrium simulations described here (see above). Hence, we focused on the changes in $R_g^{\text{Guin}}$ and $I\left(q=0\right)$ with respect to $t=0$, $\mathrm{\Delta }{R}_g^{\text{Guin}}$, and $\mathrm{\Delta }I\left(q=0\right)$, which are much less affected by such uncertainties.

The forward intensity $I\left(0\right)$ is the square of the overall contrast in number of electrons: $I\left(0\right)={\left(N_{e,p}-V^{\text{Guin}}{\rho }_{\text{bulk}}\right)}^2$, where $N_{e,p}$ and $V^{\text{Guin}}$ are the number of electrons and the apparent volume of the protein, respectively. Hence, the change in the protein volume was computed as $\mathrm{\Delta }{V}^{\text{Guin}}\left(\mathrm{\Delta }t\right)=-{\rho }_{\text{bulk}}^{-1}\left[\sqrt{I\left(0,t=\mathrm{\Delta }t\right)}-\sqrt{I\left(0,t=0\right)}\right]$.

Spatial Envelope Used to Define Water Contributing to the Scattering Calculations.

The construction of the envelope was described in detail previously (49). In short, the envelope was constructed based on an icosphere, which is constructed from a regular icosahedron by recursively subdividing its triangular faces into four smaller triangles. Subsequently, each vertex of the icosphere was moved in radial direction until the vertex had a distance of d from all protein atoms in an equilibrium simulation.

For the WAXS calculations, the envelope was constructed at a distance of 7 Å from the protein. For the SAXS calculations, to analyze the propagation of the pressure wave into the bulk water, envelopes were constructed at distances of 1, 7, 17, and 27 Å from all of the protein atoms (Fig. S7 and Fig. 3A). With an increasingly larger envelope, water molecules at an increasingly larger distance from the protein are taken into account while computing the SAXS patterns. In turn, effects from the pressure wave on the SAXS pattern are detected only while the pressure wave is inside of the envelope.

Solvent Density Calculation.

The solvent density as a function of distance from the protein was computed by constructing a series of envelopes around the protein atoms at distances d from 1 Å up to 37 Å with a spacing of $\delta d=2$ Å. Subsequently, the average number of electrons $N_e\left(d\right)$ in each of these envelopes was taken from all simulation frames used for the respective time delay (see above). The density was taken as ${\rho }_{\text{solvent}}\left(d+\delta d/2\right)=\left(N_e\left(d+\delta d\right)-N_e\left(d\right)\right)/\left(V_e\left(d+\delta d\right)-V_e\left(d\right)\right)$, where $V_e\left(d\right)$ denotes the volume of the envelope at distance d from the protein. The change in the solvent density (Fig. 3B) is reported as the difference compared with the average density within the first 100 fs after photodissociation, in which the pressure wave has not yet reached the hydration layer.

COM Displacements.

The COM displacements $\mathrm{\Delta }{R}_{\text{COM}}\left(t\right)$ of a set of residues and α-helices were computed as follows (Fig. 2G and Fig. S6). First, each structure was superimposed onto a reference structure using a RMSD fit with the backbone atoms. Subsequently, the COMs of the residues and helices were averaged within 10 blocks of $\mathrm{\sim }$1,000 simulations. The residue COMs were computed from the coordinates of all atoms of the respective residue, and the COMs of the helices were computed from the backbone atoms of the respective helix. For each block, the COM distance to the COM at $\mathrm{\Delta }t=0$ was computed. Subsequently, the distance was averaged over the 10 blocks.

Error Calculation.

All errors were computed by grouping the $\sim$10,000 (or $\mathrm{\sim }$8,500) simulations into 10 blocks of 1,000 (or 850) simulations. All quantities were first computed for each block. Subsequently, the average and the SE were computed from the 10 blocks. Errors are reported as 1 SD.

Impedance Estimates of Water and Protein.

The mechanical impedance of a material is defined as $Z={\rho }_{m}c$, where ${\rho }_m$ and c denote the mass density and the velocity of sound, respectively. To estimate the reflection index of the pressure wave (or sound wave) at the protein/water interface, the impedances were taken as follows. For water, we used ${\rho }_m=\mathrm{1,000}$ kg/m³ and $c=\mathrm{1,480}$ m/s, which yields $Z_w=1.48\times {10}^6$ kg/(m²⋅s). The speed of sound in the protein was previously computed as $\sim$2,300 m/s from normal mode analysis (59). Assuming that the mass density of the protein is 1,450 kg/m³ (74), we obtain for the impedance of the protein $Z_p=3.34\times {10}^6$ kg/(m²⋅s).

SI Discussion

The heme model of the applied Charmm22^∗ force field does not reproduce the domed structure of the heme in the five-coordinated state after photodissociation (13). This discrepancy to experimental findings most likely explains remaining residuals between simulated and experimental TR-WAXS patterns, as apparent in a less pronounced $I_{\text{aa}}\left(q\right)$ minimum at $q=0.35$ Å⁻¹ in the calculated patterns after 1 ps. Hence, we also tested alternative parameters for the five-coordinated heme suggested by Meuwly et al. (60), which induce a permanent displacement of the iron atom with respect to the heme plane toward the proximal histidine. In addition, we applied in-house modifications on the iron–nitrogen bond lengths for the same purpose. Although these force field modifications reproduced the displacement of the iron atom with respect to the heme plane, the relative depth of the minima at $q=0.35$ Å⁻¹ and $q=0.75$ Å⁻¹ exhibited a larger discrepancy to experimental data (34, 43). Hence, either more expensive quantum-chemical calculations (19) or a classical protocol mimicking the heme relaxation in more detail might be required to achieve a correctly domed heme structure and truly quantitative agreement with the experimental TR-WAXS patterns.

Discussion

MD simulations provide atomistic insight into the time evolution of protein quakes, that is, the ultrafast dissipation of excess energy in response to a local perturbations, such as the breaking of a chemical bond. By comparing the simulations to TR-SAXS, TR-WAXS, and time-resolved crystallographic data, we validated that the dynamics in simulation resemble the experimental conditions. We showed that the protein quake and the CO displacement leave characteristic fingerprints in the anisotropic scattering patterns, thus allowing us to interpret features in the reciprocal-space signals in terms of specific real-space conformational dynamics.

Our simulations suggest that the protein quake triggered by CO photodissociation is characterized by a single pressure wave that propagates in a highly anisotropic and asynchronous manner across the protein matrix. The pressure wave propagated perpendicular to the heme plane, in the direction of the initial momenta of the CO and iron just after bond breaking. Notably, the computed difference electron density maps reported here for the femtosecond-to-picosecond time range (Fig. 2F) resemble the anisotropic distribution of experimental features in a difference electron density map for a crystallized dimeric hemoglobin at 100-ps time delay (55). This may be taken as an indication that ultrafast dynamics may underlie transitions into long-living states. The perturbation parallel to the heme plane occurred with delay, and parts of the protein were not perturbed even picoseconds after the trigger. The quake did not propagate along the backbone trace, as envisioned in the pioneering work by Ansari et al. (44). Instead, the momentum of the primary perturbation as well as modulations in local packing and compressibility emerge as the main determinants for protein quake propagation. After $\sim$ 300 fs, the pressure peak started to propagate across the hydration layer. The pressure pattern in the hydration shell did not exhibit any indication for underdamped oscillations but instead resembles the patterns observed for explosive blast waves (56), that is, a pressure peak was followed by a pressure minimum at $\sim$1 ps, which relaxed back to the equilibrium value at $\sim$ 2 ps. Taken together, protein quakes are a striking example for the coupling between solvent and protein dynamics (57).

The theory of sound suggests that only a small fraction of the energy propagating with the protein quake is reflected at the protein/water interface. The ratio of the reflected energy may be estimated by the reflection coefficient $R={\left[\left(Z_w-Z_p\right)/\left(Z_w+Z_p\right)\right]}^2$, where $Z_w$ and $Z_p$ denote the mechanical impedances of water and protein, respectively (58). The impedance is defined as $Z={\rho }_{m}c$, where ${\rho }_m$ is the mass density and c is the speed of sound. Assuming that the speed of sound in the protein is 2.3 nm/ps (59), one obtains a reflection coefficient of only $\sim$15%, which seems to be too low to allow underdamped oscillations of the protein (SI Materials and Methods). To further test the influence of the solvent on Mb dynamics, we carried out additional CO dissociation simulations with the protein in vacuum at constant energy conditions, thus imposing a reflection coefficient of $R=100$%. In contrast to Mb in water, Mb in vacuum showed clear underdamped oscillations with a period $\sim$ 1.8 ps (Fig. S8). Hence, the internal friction of Mb is small and would per se allow underdamped oscillations. For Mb in solvent, however, because the impedances of protein and water are similar, the protein quake energy dissipates into the solvent, leading to overdamped protein dynamics.

TR-SAXS and TR-WAXS experiments have recently become available with unprecedented time resolution, opening new opportunities to follow ultrafast protein dynamics such as protein quakes (42, 43). Because the interpretation of the reciprocal-space signals is notoriously difficult, these new experiments raised new questions. Levantino et al. (43) observed underdamped oscillations in the $\mathrm{\Delta }{R}_g^{\text{Guin}}$ and $\mathrm{\Delta }{V}^{\text{Guin}}$ after CO photodissociation in Mb, which were interpreted as underdamped oscillations of the protein. This interpretation was surprising because large-scale collective motions of proteins in water were assumed to be overdamped and subject to low Reynolds numbers (46). Our simulations offer an alternative interpretation of the TR-SAXS data. We found that $\mathrm{\Delta }{R}_g^{\text{Guin}}$ and $\mathrm{\Delta }{V}^{\text{Guin}}$ are dominated by modulations of the solvent density. Hence, the small-angle data of Mb report on protein dynamics only up to $\sim$500 fs, after which the signals are dominated by the propagation of the pressure wave into the solvent. These findings highlight the importance of accurately modeling the solvent effects when interpreting solution scattering data. The dynamics of the radius of gyration of the bare protein ($R_g^{\text{Prot}}$) was characterized by a ballistic expansion up to $\sim$650 fs followed by an overdamped relaxation up to 1.7 ps, thus compatible with the long-standing concept of overdamped global protein dynamics. To further validate these conclusions, we modeled the absorption of multiple photons, thereby (i) increasing the total amount of dissipated energy and (ii) modulating the energy fractions dissipated via the CO and via the heme (Fig. S9). The additional energy led to a larger increase of $R_g^{\text{Prot}}$ followed by additional picosecond relaxation, but the protein dynamics did not change qualitatively.

Remaining slight discrepancies in the WAXS patterns around 0.4 Å⁻¹ suggest that the energy dissipated via the CO compared with the iron were not fully reproduced by the classical force fields. We also tested the effect of switching to the force field suggested by Karplus and coworkers (60) upon photodissociation, which explicitly models the displacement of the iron with respect to the heme plane in the five-coordinated state. As expected, this force field reproduced the doming of the heme, but the discrepancy in the WAXS patterns increased, suggesting that more expensive quantum chemical methods might be required to model the dynamics of iron displacement and heme doming accurately (12, 13, 19). Additional discrepancies might originate from the fact that, in contrast to experimental conditions, our TR-WAXS calculations are assuming a low excitation laser intensity (48). Regarding the analysis of $\mathrm{\Delta }{R}_g^{\text{Guin}}$ and $\mathrm{\Delta }{V}^{\text{Guin}}$, we note that the calculations are accurate up to $\sim$2 ps after photodissociation, after which the pressure wave leaves the envelope. At longer delay times, when the pressure wave has propagated further into bulk water, the explicit-solvent calculations would require a very large envelope, thereby suffering from systematic errors due to tiny drifts in the overall solvent density (Fig. 3 C and D, green curves). Hence, SAXS calculations for long time delays might benefit from continuum models in future studies.

To conclude, our simulations suggest that the protein quake in Mb is characterized by a single pressure peak that propagates anisotropically and asynchronously through the protein matrix, followed by an overdamped relaxation. The pressure wave manifests (i) as a transient anisotropic peak in the WAXS patterns in the subpicosecond range, and (ii) as picosecond modulations of $\mathrm{\Delta }{R}_g^{\text{Guin}}$ and $\mathrm{\Delta }{V}^{\text{Guin}}$ as the wave propagates across the hydration layer into bulk solvent. The simulations thus provide atomic insight into ultrafast dynamics of proteins, and they aid the interpretation of scattering experiments conducted at free-electron lasers.

Materials and Methods

The initial structure of horse heart Mb was taken from the Protein Data Bank [PDB ID code 1DWR (61)]. All simulations were conducted in explicit solvent, if not stated otherwise. Simulations used to compute the WAXS patterns and the modulations in electron density (Fig. 2) contained 9,205 explicit-solvent water molecules (Fig. 1B). Simulations used to compute SAXS patterns contained 70,188 explicit-solvent water molecules (Fig. 1C). SAXS/WAXS patterns were computed following the explicit-solvent calculations we introduced recently (48, 49). The protein was described by the CHARMM22^∗ force field (62). The simulations were conducted with the Gromacs software (63). More details are provided in SI Materials and Methods (64–74).