Covalent bonds against magnetism in transition metal compounds

Significance

A mechanism by which orbital degrees of freedom can strongly affect magnetic properties of systems with correlated electrons is proposed. Using analytical treatment and numerical simulations, both in general and for some particular substances, we show that the formation of covalent bonds on part of the orbitals may strongly reduce magnetic moments and explain magnetic properties of different 4d and 5d transition metal oxides. In particular, orbital-selective effects may result in suppression of double exchange—one of the main mechanisms of ferromagnetism in transition metals and compounds, such as colossal magnetoresistance manganites or CrO₂—the materials used in many devices.

Abstract

Magnetism in transition metal compounds is usually considered starting from a description of isolated ions, as exact as possible, and treating their (exchange) interaction at a later stage. We show that this standard approach may break down in many cases, especially in 4d and 5d compounds. We argue that there is an important intersite effect—an orbital-selective formation of covalent metal–metal bonds that leads to an “exclusion” of corresponding electrons from the magnetic subsystem, and thus strongly affects magnetic properties of the system. This effect is especially prominent for noninteger electron number, when it results in suppression of the famous double exchange, the main mechanism of ferromagnetism in transition metal compounds. We study this mechanism analytically and numerically and show that it explains magnetic properties of not only several 4d–5d materials, including Nb₂O₂F₃ and Ba₅AlIr₂O₁₁, but can also be operative in 3d transition metal oxides, e.g., in CrO₂ under pressure. We also discuss the role of spin–orbit coupling on the competition between covalency and magnetism. Our results demonstrate that strong intersite coupling may invalidate the standard single-site starting point for considering magnetism, and can lead to a qualitatively new behavior.

Transition metal (TM) compounds present one of the main playgrounds in a large field of magnetism (1–3). Usually, when considering magnetic properties of these systems, one starts from the, as exact as possible, treatment of isolated TM ions or such ions in the surrounding of ligands, e.g., TMO₆ octahedra. A typical situation for a moderately strong crystal field is the one in which d electrons obey the Hund’s rule, forming a state with the maximal spin. For a stronger crystal field low-spin states are also possible, but also in this case electrons in degenerate subshells, e.g., $t_{2g}$ electrons, first form a state with maximal possible spin. Then, these large total spins interact by exchange coupling with the neighboring TM ions. This interaction, a superexchange for integer electron occupation (4), or a double exchange for partially filled d levels (5), is then treated using this starting point with this total spin of isolated ions, taking into account the hopping between sites (leading in effect to magnetic interaction) as a weak perturbation, which does not break the magnetic state of an ion.

For heavier elements, such as $4d$ or $5d$ TM, one should also take into account the relativistic spin–orbit (SO) coupling, which couples the total spin S as dictated by the Hund’s rule, with the (effective) orbital moment L. In any case, it is usually assumed that the “building blocks” for further consideration of the magnetic interactions are such isolated TM ions with the corresponding quantum numbers.

However, especially when we go to heavier TM ions, such as $4d$ and $5d$, also the spatial extent of the corresponding d orbitals increases strongly, and with it the effective d–d hopping, t (2). One can anticipate a possibility for this hopping to become comparable with or even exceed the intra-atomic interactions, such as the Hund’s coupling, $J_H$, and spin–orbit coupling λ. In such a case the standard approach described above may break down and one has to include intersite effects from the very beginning. We claim that this indeed happens in many $4d$ and $5d$ systems with appropriate geometries. The resulting effect is that, for example, in a TM dimer with several d electrons per ion, some electrons, namely those occupying the orbitals with the strongest overlap, form intersite covalent bonds, i.e., the singlet molecular orbitals (MO). In this case such electrons become essentially nonmagnetic and “drop out of the game,” so that only d electrons in orbitals without such a strong overlap may be treated as localized, contributing to localized moments and to eventual magnetic ordering. The result would be that the effective magnetic moment of a TM ion in such situation would become much smaller than the nominal moment corresponding to the formal valence of an ion. Below we demonstrate that this effect is indeed realized in many TM compounds, especially those of $4d$ and $5d$ elements. Besides reducing the magnetic moment of an ion, this mechanism can suppress the well-known double exchange (DE) mechanism of (ferro)magnetic ordering—the main mechanism of ferromagnetism in systems with a fractional occupation of the d levels.

Before presenting the main results, let us emphasize that the interplay between the formation of covalent bonds, spin–orbit coupling, and intra-atomic exchange interaction discussed in the present paper is very important for intensively studied nowadays $4d$ and $5d$ transition metal oxides such as $\alpha -$RuCl₃ (6, 7), Li₂RuO₃ (8, 9), LiZn₂Mo₃O₈ (10, 11), and Na₂IrO₃ (12–14). Competition of these interactions results in highly unusual physical properties in these systems: Kitaev spin liquid, valence–bond condensation, and different topological effects.

Qualitative Considerations

We start by simple qualitative arguments, considering a two-site problem with, for example, three electrons per dimer, occupying two types of orbitals: orbital c (the corresponding creation and annihilation electron operators at the site i with the spin σ are $c_{i\sigma }^{†}$, $c_{i\sigma }$), with intersite hopping $t_c$, and another orbital, d, with a very weak hopping $t_d$ (which we for simplicity at the beginning put to zero). In reality the c orbitals could be, for example, the strongly overlapping $xy$ orbitals in the situation when the neighboring TMO₆ octahedra share edges, i.e., have two common oxygens, see Fig. 1A, or the $a_{1g}$ orbitals in the common face geometry, Fig. 1B; the orthogonal orbitals ($zx$, $yz$ in the first case or $e_g^{\pi }$ orbitals in the second) would then play a role of localized d orbitals (for a more detailed treatment of these situations see, e.g., refs. 15–17).

Fig. 1.

Orbitals having large overlap (c orbitals in our notations) and corresponding level splitting with the formation of bonding and antibonding orbitals for transition metal dimers in different geometries: (A) common edge geometry and xy orbitals, and (B) common face geometry and $a_{1g}-$ orbitals.

In this case we can consider two different limiting states. In the state depicted in Fig. 2A we put two electrons into the localized d orbitals, and the remaining electron occupies the “itinerant” c orbital, hopping back and forth from site 1 to site 2, or occupying the bonding state $\left(c_{1\uparrow }^{†}+c_{2\uparrow }^{†}\right)/\sqrt{2}$. To optimize the Hund’s intra-atomic exchange, this “hopping” electron would have its spin parallel to the spins of the localized electrons, and its delocalization stabilizes the state with maximum spin, here $S_{tot}=3/2$. This is, in essence, the double exchange mechanism of ferromagnetism, first proposed by Zener for just such a dimer (5). It is easy to see that the energy of this DE state is

$$E_{DE}\hspace{0.17em}=\hspace{0.17em}-t_c-J_H.$$ [1]

For simplicity we ignore here the contribution of the onsite Coulomb (Hubbard) interaction, see a more complete treatment below. We also treat the Hund’s interaction

$$H_{Hund}\hspace{0.17em}=\hspace{0.17em}-J_H\left(1/2\hspace{0.17em}+\hspace{0.17em}2{\overrightarrow{S}}_1{\overrightarrow{S}}_2\right),$$ [2]

in the mean-field approximation, where ${\overrightarrow{S}}_1$ and ${\overrightarrow{S}}_2$ are the total spins on sites 1 and 2.

Fig. 2.

Two competing electronic configurations with different total spin $S_{tot}$: (A) DE and (B) MO states for a dimer with two orbitals (c and d) per site and three electrons.

This DE state is definitely the most favorable state for a strong Hund’s interaction. Indeed, in all papers on double exchange (5, 18, 19) one makes such an approximation, most often by simply setting $J_H$ to infinity. This is a reasonable assumption for most $3d$ compounds at ambient conditions, for which $J_H\sim$ 0.7–0.9 eV, usually (much) larger than the effective d–d hopping (direct, or via ligands), which is typically 0.1–0.3 eV. However, when we go to $4d$, and especially $5d$ systems, the situation may change drastically: $J_H$ is reduced (20) (to $\sim$ 0.5–0.6 eV for $4d$ and $\sim$ 0.5 eV for $5d$ elements; ref. 21); whereas, the spatial extension of d-wave function, and the corresponding overlap and d–d hopping strongly increase, so that $t_c$ can easily be of order of 1.0–1.5 eV, as e.g., in Li₂RuO₃ (8) or Y₅Mo₂O₁₂ (22). In this case we can form a different state (illustrated in Fig. 2B), redistributing electrons between d orbitals: we now put two electrons on the itinerant c orbitals, so that they form a singlet state in the bonding orbital of Fig. 2B (actually a molecular orbital state):

$$|MO\rangle \hspace{0.17em}=\hspace{0.17em}\left(c_{1\uparrow }^{†}+c_{2\uparrow }^{†}\right)\left(c_{1\downarrow }^{†}+c_{2\downarrow }^{†}\right)/2,$$ [3]

leaving one electron on localized d orbitals. In effect, the total spin of this state (we call it for short the MO state) is not 3/2, as for the DE state of Fig. 2A, but only $S_{tot}=1/2$. The energy of this state in our simple approximation is

$$E_{MO}\hspace{0.17em}=\hspace{0.17em}-2t_c\hspace{0.17em}-\hspace{0.17em}{J}_H/2.$$ [4]

Comparing the energies [1] and [4], we see that the MO state with suppressed double exchange and strongly reduced total spin is more favorable if

$$2t_c\hspace{0.17em}>\hspace{0.17em}{J}_H.$$ [5]

Thus, we observe that in this simplified model the covalent bonding, defined by the hopping $t_c$ (which can include also the hopping via ligands), can suppress the DE.

One can use a more general wave function of MO type, with two electrons in the c orbitals with the total $S=0$, and one localized electron with $S=1/2$ in d orbitals. For example, if we put d electron with spin $\uparrow$ at a site 1, we can take generalized MO state in the form

$$|\widetilde{MO}\rangle =\left(\alpha c_{1\uparrow }^{†}+\beta c_{2\uparrow }^{†}\right)\left(\beta c_{1\downarrow }^{†}+\alpha c_{2\downarrow }^{†}\right)/2,$$ [6]

with the variational parameters α, β such that $\alpha >\beta$, so as to win the Hund’s exchange energy with the $d_{1\uparrow }$ electron (at the expense of some loss of the bonding energy). This would stabilize the MO (or rather $\widetilde{MO}$) state ever more, shifting the critical value $J_H^c$ needed for stabilizing DE state to larger values (i.e., $J_H^c\sim 6t_c$, and not $J_H^c\sim 2t_c$ as follows from Eq. 3). That is, the electron hopping can be even more efficient in suppressing DE than it follows from the simple estimate in Eq. 5.

Model Consideration

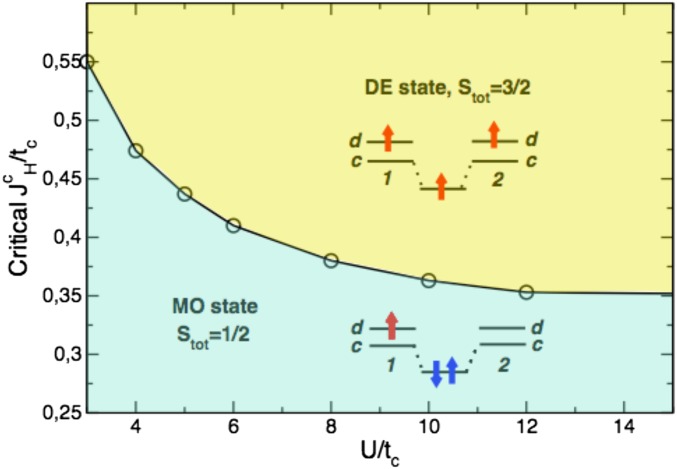
In fact such a model with two orbitals per site and three electrons per dimer can be solved exactly (see the details in Supporting Information; here and below we used the Hubbard model within the Kanamori parameterization rather than a simplified expression for the interaction term given in Eq. 2), including also the onsite Coulomb (Hubbard) repulsion U, besides the Hund’s rule exchange $J_H$ and the hopping of d and c orbitals ($t_c$ and $t_d$). The corresponding phase diagram for $T=0$ K is shown in Fig. 3. One may see that indeed the MO state can be realized for any U, if $J_H$ is small enough. This state can be considered as orbital selective (23), because only d orbitals provide local moments, and electrons on c orbitals form spin singlet. For a finite U the simple estimates such as Eq. 5 do not hold anymore, and the critical value $J_H^c$ needed to stabilize the DE state is much smaller than for $U=0$, because the Coulomb repulsion modifies the ground-state wave function for c electrons from real molecular orbital to the Heitler–London, or rather Coulson–Fisher-like, with an increased weight of the ionic terms (with respect to homopolar ones) (24). The transition from one state to another is discontinues, since they are characterized by different quantum numbers ($S_{tot}=3/2$ for DE state vs. $S_{tot}=1/2$ for MO state), and corresponding terms do not hybridize, but simply cross.

Fig. 3.

Phase diagram for a dimer with two orbitals (c and d) per site and three electrons in U (onsite Hubbard repulsion) and $J_H$ (Hund’s rule coupling) coordinates; c orbitals form molecular orbitals (corresponding hopping is $t_c$), and d orbitals stay localized ($t_d=0.1t_c$, the same as in Fig. 4). Results of the exact diagonalization at $T=0$ K. We restrict ourselves only by the repulsive Coulomb potential, which in the Kanamori parameterization corresponds to $U>3J_H$.

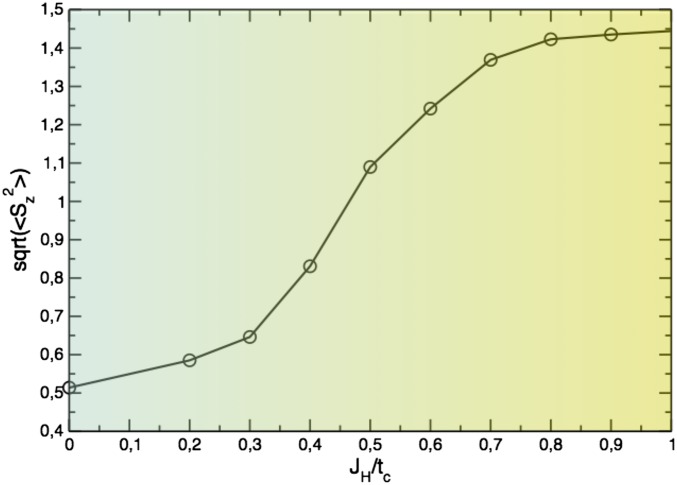
We can generalize this treatment onto larger systems, which we did for a dimerized chain with 2 orbitals and 1.5 electrons per site. The calculations have been performed using a cluster version of the dynamical mean-field theory (DMFT) (25). The cluster DMFT was shown to provide a very accurate description of the one-dimensional chain (25). The results of the cluster DMFT calculations for a dimerized chain at a fixed U are shown in Fig. 4. We see that indeed the MO-like state with $S_{tot}=1/2$ survives for realistic values of $J_H$ (for 4d–5d materials) (20, 21) and the DE can be suppressed for small $J_H$ even in an extended system. The transition to this MO state is not discontinuous now, but is broadened, because of two factors: temperature (which is one of the parameter in our cluster-DMFT calculations) and formation of bands, or in other words the presence of the finite electron hoppings between dimers. As it was explained above, the critical Hund’s rule coupling strongly depends on U. If U is small, then $J_H$ competes with the difference of hopping parameters, $t_c-t_d$, which defines the energy of the MO. In contrast, with increasing U we quickly arrive at the Heitler–London type of the wave function for c electrons with the energy gain $\sim t_c^2/U$ in the MO state.

Fig. 4.

Dependence of $\sqrt{\langle S_{tot,z}^2\rangle }$ on the $J_H/t_c$ ratio at fixed $U=6t_c$ for a dimerized chain with 1.5 electrons and with 2 orbitals per site at T = 1,100 K. Intradimer hopping parameter for d orbitals was taken to be $0.1t_c$, and interdimer hopping $t_c^{\prime }=t_d^{\prime }=0.05t_c$; Results of the cluster DMFT calculations.

Role of the Spin–Orbit Coupling

As the effects discussed in this paper are met mainly in $4d$ and $5d$ compounds (although not exclusively, see the discussion about CrO₂), it is important to address the possible role of spin–orbit coupling (SOC), which is strong in these systems. It turns out that the effect of SOC is not universal and depends on a specific situation.

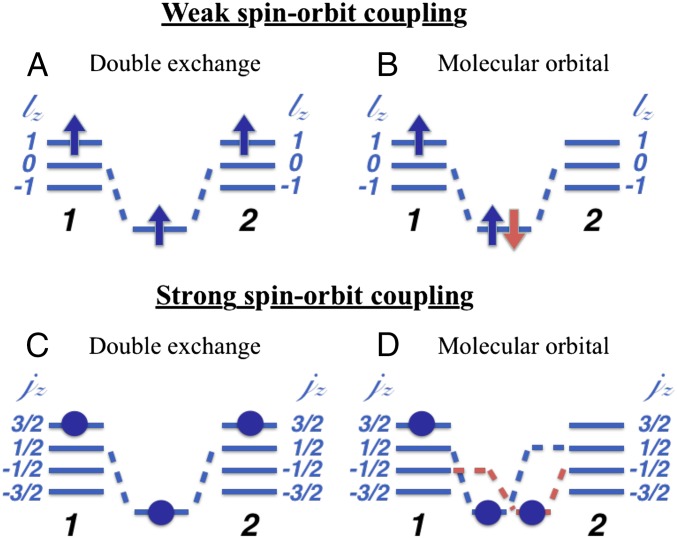
Consider first the same situation with three electrons per dimer and threefold degenerate $t_{2g}$ orbitals, which now can be labeled by value of z projection of the effective orbital moment $l=1$, i.e., $|l^z=0\rangle \equiv |0\rangle$ and $|l^z=\pm 1\rangle \equiv |\pm 1\rangle$. For the sake of simplicity here and below we consider SOC on the one-electron level, i.e., $H_{SOC}=-{\displaystyle {\sum }_m\zeta {\overrightarrow{l}}_m{\overrightarrow{s}}_m}$ (here m numerates orbitals). Then for weak SOC, $\zeta \ll \left(t_c,J_H\right)$, we can again have two situations: that of the DE, with the maximum spin for a dimer possible, here $S_{tot}=3/2$, Fig. 5A, and the state with the singlet MO and the total spin $S_{tot}=1/2$, Fig. 5B. To gain at least some SO energy, we put localized electrons with spin $\uparrow$ on the orbital $|+1\rangle$. Because in the most geometries such as edge and face sharing the orbitals with $l_z=0$ ($xy$ and $a_{1g}$ orbitals, respectively) strongly overlap, we put itinerant electrons on the bonding orbital $\frac{1}{\sqrt{2}}\left({|0\rangle }_1+{|0\rangle }_2\right)$, where 1 and 2 are site indexes. The energy of the DE state in this case is

$$E_{weak-SOC}^{DE}=\hspace{0.17em}-\hspace{0.17em}{t}_c\hspace{0.17em}-\hspace{0.17em}{J}_H\hspace{0.17em}-\hspace{0.17em}\zeta ,$$ [7]

(cf. Eq. 1), because here for localized electrons only the “classical” part of the SOC contributes in lowest order, −$\zeta \langle 1,\uparrow |l^z{s}^z|1,\uparrow \rangle =-\zeta /2$ per site, and in the lowest order the bonding states with $l_z=0$ do not give energy gain due to SOC (it will appear due to “quantum” terms $l^{+}{s}^{-}$, etc., in the second order in $\zeta /t_c$). Similarly, the energy of the MO state of Fig. 5B is

$$E_{weak-SOC}^{MO}=\hspace{0.17em}-\hspace{0.17em}2t_c\hspace{0.17em}-\hspace{0.17em}{J}_H/2\hspace{0.17em}-\hspace{0.17em}\zeta /2,$$ [8]

(cf. Eq. 4). Comparison of these expressions shows that in this case SOC stabilizes magnetic DE state: the condition for low-spin MO state is now, instead of Eq. 5,

$$2t_c\hspace{0.17em}>\hspace{0.17em}{J}_H\hspace{0.17em}+\hspace{0.17em}\zeta .$$ [9]

This agrees with results of ref. 26, where the case of the weak SOC was considered.

Fig. 5.

Two competing electronic configurations for a dimer—DE and MO in the case of weak (A and B) and strong (C and D) spin–orbit coupling, three $t_{2g}$ orbitals per site and three electrons.

However, the situation is very different for strong SOC, $\zeta \gg \left(t_c,J_H\right)$. In this case we can project relevant states onto a quartet $j=\frac{3}{2}$, with the states $|j^z=\frac{3}{2}\rangle =|1,\uparrow \rangle$, $|j^z=\frac{1}{2}\rangle =\sqrt{\frac{2}{3}}|0,\uparrow \rangle +\sqrt{\frac{1}{3}}|1,\downarrow \rangle$, $|j^z=-\frac{1}{2}\rangle =\sqrt{\frac{2}{3}}|0,\downarrow \rangle +\sqrt{\frac{1}{3}}|-1,\uparrow \rangle$, $|j^z=-\frac{3}{2}\rangle =|-1,\downarrow \rangle$. Then the “DE” state with the maximum total moment j of a dimer 7/2 is the state shown in Fig. 5C, with localized d electrons on sites 1 and 2 in states $|j^z=3/2\rangle$, and a “mobile” electron—on a bonding orbital $\frac{1}{\sqrt{2}}\left({|j^z=1/2\rangle }_1+{|j^z=1/2\rangle }_2\right)$. For such state the effective hopping is reduced, as only the $|0\rangle$ component “hops” to a neighbor, $\langle j^z=\pm \frac{1}{2}|\widehat{t}|j^z=\pm \frac{1}{2}\rangle =\frac{2}{3}\langle 0|\widehat{t}|0\rangle =\frac{2}{3}{t}_c$, and the total energy of such state turns out to be

$$E_{strong-SOC}^{DE}=-\frac{2}{3}{t}_c-\frac{3}{2}\zeta -\frac{2}{3}{J}_H$$ [10]

(SOC energy in any state of the quartet $j=\frac{3}{2}$ is $-\zeta /2$ per electron; the calculation of the Hund’s energy contribution is quite straightforward, but somewhat tedious). We treat the Hund’s energy in a mean-field approximation, using the “recipe” described for example in ref. 2: the Hund’s energy is equal to $J_H\times$(number of parallel spins, see Eq. S1). More accurate treatment of the Hund’s coupling, including quantum effects in it, would somewhat change numerical coefficients, but would not change qualitative conclusions. In our numerical and ab initio calculations presented below the Hund’s rule coupling is taken into account in a more rigorous way, including quantum effects in it.

Similarly, an analog of the MO state is shown in Fig. 5D. In this state we put one electron on a localized state $|j^z=\frac{3}{2}\rangle$, say on a site 1, and two electrons on bonding orbitals $\frac{1}{\sqrt{2}}\left({|j^z=\frac{1}{2}\rangle }_1+{|j^z=\frac{1}{2}\rangle }_2\right)$ and $\frac{1}{\sqrt{2}}\left({|j^z=-\frac{1}{2}\rangle }_1+{|j^z=-\frac{1}{2}\rangle }_2\right)$. The energy of this state, calculated similarly to that of the DE state in this regime, is

$$E_{strong-SOC}^{MO}=-\frac{4}{3}{t}_c-\frac{3}{2}\zeta -\frac{13}{18}{J}_H.$$ [11]

We see that in this regime (strong SOC) the MO state is definitely favored over the DE state: the contribution from the SOC in any state of a quartet is the same, and in the MO state both the bonding and even Hund’s energies are lower.

Summing up, in the case of three electrons per dimer weak SOC acts in favor of the magnetic DE state, but strong SOC, instead, stabilizes the MO state with reduced moment. This is related to the fact that the energy of the bonding orbital (the lowest curve in Fig. S1) rapidly decreases with the increase of SOC, which makes the MO state (in which this orbital is occupied twice) more favorable.

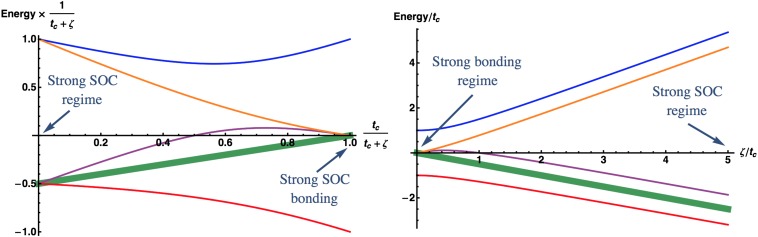
Fig. S1.

Level diagram for a dimer with three orbitals per site taking into account spin–orbit coupling on the one-electron level, i.e., as $-\zeta {\displaystyle {\sum }_m{\overrightarrow{l}}_m{\overrightarrow{s}}_m}$, and hopping $t_c$ for $l_z=0$ orbital. There are 12 spin orbitals in a dimer with three $t_{2g}$ orbitals per site. Degeneracy of each level except bold one is two. Bold level is fourfold degenerate. One may trace evolution of the electronic structure with increase of the ζ starting from the strong bonding regime ($\zeta \to 0$) with one bonding, one antibonding, and four nonbonding orbitals to the case of the strong spin–orbit coupling ($\zeta \to \infty$) with $j=3/2$ and $j=1/2$ states. This is easier to see in Left. Right shows energy dependence in more “natural” variables E vs. ζ. One may see that bonding orbital in the case of $\zeta =0$ continuously transforms to, again lowest in energy, $j=3/2$ quartet as the spin–orbit coupling increases. This results in stabilization of the MO state for moderate and large ζ, see Fig. 6.

The analytic treatment presented above is confirmed by the exact diagonalization results for the dimer with three orbitals per site. The resulting phase diagram is shown in Fig. 6. We see that it agrees with our analytical results for limiting cases of $\zeta \to 0$ and $\zeta \to \infty$ presented above, and it has a “reentrant” character: for certain values of parameters the increase of SOC can initially transform system into the magnetic DE state, but for larger ζ - back to the MO state.

Fig. 6.

Phase diagram for a dimer with three $t_{2g}$ orbitals per site and three electrons, which takes into account spin–orbit coupling on the one-electron level. Results of the exact diagonalization at $T=0$ K.

One may expect that for the weak SOC the situation is similar also not for three electrons, but for three holes in $t_{2g}$ levels [situation typical, for example, for a dimer of, formally, Ir⁴⁺($d^5$) and Ir⁵⁺ ($d^4$)]. However, for strong SOC we do not have anymore the electron–hole symmetry: as is well known (2, 27), these states can be projected onto a Kramers doublet $j=1/2$ without any extra orbital degeneracy, and for the situation with $d^4/d^5$ occupation (nine electrons per dimer) only the analog of a low-spin state with the total moment 1/2 is possible. Thus, in this case the qualitative phase diagram would again have the form similar to the one shown in Fig. 6, with weak SOC stabilizing magnetic DE state, but strong SOC suppressing total moment—although mathematical description is different from the case with three d electrons.

However, for example one can show that the situation is qualitatively different for five electrons per dimer: in this case the treatment similar to that for three electrons above, shows that both strong and weak SOC works in favor of a less-magnetic MO state, i.e., the corresponding curve separating MO and DE states in the phase diagram, similar to that of Fig. 6, would increase already at small ζ, without reentrant behavior. Thus, we see that, in contrast to the Hund’s coupling, which always competes with the electron hopping and tends to stabilize a “more magnetic” state, the SOC can work differently in different situations.

One more important factor, which can change the interplay of SOC with the Hund’s exchange and electron hopping, is a possible contribution of not only the direct d–d hopping, considered in our treatment, but also of the hopping via p orbitals of ligands, e.g., oxygens. To take into account all these effects, for real materials it is probably better to rely on ab initio calculations, the results of some of which are presented in the next section.

Suppression of the Double Exchange and Magnetic Moment in Real Materials

We now turn to real materials and show that the physics described above (strong reduction of magnetic moment and eventual suppression of double exchange, due to formation of orbital-selective covalent bonds between TM) indeed works in real materials and allows us to explain the behavior of many $4d$ and $5d$ systems. The first example of such a system is the recently synthesized oxyfluoride Nb₂O₂F₃ (28) (see its structure in Fig. S2 and the results of our ab initio calculations in Supporting Information). Although, according to the chemical formula there has to be three d electrons per Nb dimer, i.e., $S_{tot}=3/2$, the experimental effective magnetic moment is consistent with $S_{tot}=1/2$ per dimer (28). The band-structure calculations show that the bonding–antibonding splitting for the $xy$ orbitals pointing to each other in the common edge geometry (cf. Fig. 1A) is very large here, $2t_c\sim 4$ eV—much larger than the Hund’s rule energy estimated to be $J_H\sim$ 0.5 eV for Nb (21).

Fig. S2.

(A) The crystal structure of Nb₂O₂F₃. Niobium (large green balls) ions form dimers, sharing common edge. Oxygen ions shown as red and fluorine as gray balls. (B) The level splitting in the Nb₂ dimer in high-temperature phase of Nb₂O₂F₃. Crystal structure was plotted using VESTA software (39).

According to the results of our model cluster DMFT calculations, see above, for $J_H/t_c\sim 0.25$ the DE is largely suppressed, which agrees with the experimental findings (28). However, parameters $t_d$, $t\prime$, U in Nb₂O₂F₃ can be very different from what we used in the model calculations, so that comparison with the results (see Fig. S3) of the generalized gradient approximation (GGA) should be more appropriate. These results are summed up in Supporting Information, and indeed show that the value of the local magnetic moment in the high temperature phase is ${\mu }^{theor}\sim 1{\mu }_B$ per dimer, which agrees with the experimental value of the effective moment (28, 29).

Fig. S3.

Results of the nonmagnetic GGA calculation for high-temperature phase of Nb₂O₂F₃. The bonding–antibonding splitting for $xy$ orbitals pointing to each other in neighboring Nb₂O₂F₃ octahedra is shown. The Fermi energy is set to zero.

We have discussed so far how covalent bonding competes with Hund’s rule coupling. However, as discussed above, for $4d$ and $5d$ TM compounds also another “player” can enter the game: the spin-orbit coupling, which is known to be strong enough in heavy $4d/5d$ metals and has been already demonstrated to cause very unusual physical effects (30–32). On our second example, Ba₅AlIr₂O₁₁, we show that this interaction may indeed take part in the competition between intra-atomic exchange and covalent bonding.

The crystal structure of Ba₅AlIr₂O₁₁ consists of [Ir-Ir]⁹⁺ dimers (Fig. S4A) with nine electrons or three holes per dimer, so that this is exactly the example of a system, considered in the first part of our paper, where the DE and MO states could compete. Indeed, the effective magnetic moment in the Curie–Weiss law ${\mu }_{eff}\sim 1{\mu }_B$/dimer, measured at high temperatures, indicates substantial suppression of the magnetic moment (33). However, our GGA calculations show that accounting for covalency and exchange splitting is not sufficient to explain this small ${\mu }_{eff}$; they give ${\mu }^{GGA}\sim 2{\mu }_B$. It is the spin–orbit coupling, that, by additional splitting of d levels, conspires with the covalency and finally helps to suppress the DE in this system, see Supporting Information. However, as stressed in the previous section, this is not a general conclusion: depending on the filling of the d shell and on a specific geometry, the spin–orbit interaction can act against the DE or support it.

Fig. S4.

(A) The crystal structure of Ba₅AlIr₂O₁₁. Iridium ions are in oxygen octahedra (red balls), and aluminum ions are in tetrahedra. The crystal structure was plotted using VESTA software (39). (B) The level scheme of Ir dimer (without spin–orbit coupling).

Until now we have considered real materials in which the structure provides relatively well-separated dimers. As we saw, e.g., in our cluster DMFT calculations, the effect of suppression of the DE can survive even for solids, without well-defined dimers. In some of such systems singlet covalent bonds can form spontaneously, also acting against DE (cf. ref. 34).

One such example seems to be given by CrO₂—a classical DE system (35). In CrO₂ one of the two 3d electrons is localized in the $xy$ orbital on each Cr site, and another one occupies a broad $xz/yz$ band, stays itinerant and actually makes this system ferromagnetic (35). In contrast to VO₂, having the same rutile structure, but one d electron per V, CrO₂ does not dimerize at zero pressure.

Apparently, in normal conditions in this system the hopping via oxygens is more important, and in effect DE wins and provides ferromagnetism with large Curie temperature. However, under high pressure the situation can change: the direct d–d hopping can begin to dominate, the bonding–antibonding splitting even in this 3D system can become comparable with what we have in $4d$ and $5d$ TM compounds at normal conditions, in which case our physics could come into play. Indeed, accurate band-structure calculations (36) have found a cascade of structural transitions in CrO₂ with pressure, with the formation of the dimerized monoclinic structure for P $\sim$ 70 GPa. As in the case of the Jahn–Teller distortions, it is not clear whether the lattice or electronic subsystem triggers the structural transition, but once the dimerization starts they go hand in hand and destabilize the DE state by lowering the energy of the $xy$ molecular orbital. At some point two out of four d electrons in the Cr–Cr dimer occupy this molecular orbital, and the remaining two electrons provide metallicity and eventual paramagnetism, similar to what is observed in MoO₂ at normal conditions (37) or expected in MoCl₄ at moderate pressure (38). We thus see that even some $3d$ systems could in principle be tuned to the MO regime, in particular under pressure, which increases d–d overlap and hopping, making such systems more similar to the $4d$ and 5d ones.

It is also possible that some other factors, such as charge ordering (29), could modify the situation. The external perturbations, such as temperature or pressure, can drive a system from the DE to the MO state, so that the phase diagrams of systems with competing DE and MO states can be rather rich and their physical properties can be highly unusual.

Conclusions

In conclusion, we demonstrated in this paper that the standard approach to describe the magnetism in solids with strongly correlated electrons, proceeding from the isolated ions in their ground state, and adding electron hopping between ions perturbatively, may break down in certain situations, especially for $4d$ and $5d$ systems. In particular, due to large d–d hopping orbital-selective covalent bonds, or singlet molecular orbitals between transition metal ions may form in this case. This would lead to a strong suppression of the effective magnetic moment, and, for fractional occupation of d shells, can strongly reduce or completely suppress the well-known double exchange mechanism of ferromagnetism. Several examples of real material considered in our paper indeed demonstrate that this mechanism is very efficient in suppressing the double exchange in a number of $4d$ and $5d$ compounds, and can even operate in some $3d$ systems. Spin–orbit coupling, especially relevant for $4d$ and $5d$ compounds, can also play an important role and in many cases it works together with electron hopping to suppress magnetic state, although in some situations it can also act in opposite direction. Our results show yet one more nontrivial effect in the rich physics of systems with orbital degree of freedom, especially those close to Mott transition.

Details of the Exact Diagonalization and Cluster DMFT

To study suppression of the DE we considered dimers and dimerized chain, described by the Hamiltonian, which reads as

$$H\hspace{0.17em}=\hspace{0.17em}{H}_0\hspace{0.17em}+\hspace{0.17em}{H}_{inter}\hspace{0.17em}+\hspace{0.17em}{H}_U,$$ [S1]

where $H_0$ noninteracting intradimer part, $H_{inter}$ interdimer part (only for chain), and $H_U$ is the interaction, defined by intraorbital Hubbard repulsion U and Hund’s rule exchange $J_H$:

$$\begin{array}{c}{H}_0=-{\displaystyle \sum _i\left(t_c{c}_{i,2}^{†}{c}_{i,1}+t_d{d}_{i,2}^{†}{d}_{i,1}+H.c.\right)}\\ H_{inter}=-{\displaystyle \sum _i\left(t_c\prime c_{i,2}^{†}{c}_{\left(i+1\right),1}+t_d\prime d_{i,2}^{†}{d}_{\left(i+1\right),1}+H.c.\right)}\\ H_U=\frac{1}{2}{\displaystyle \sum _{\stackrel{j}{mm\prime \mathit{\sigma }}}{U}^{mm\prime }{n}_{j,m}^{\sigma }{n}_{j,m\prime }^{-\sigma }+\frac{1}{2}{\displaystyle \sum _{\stackrel{j}{\langle mm\prime \rangle \mathit{\sigma }}}\left(U^{mm\prime }-J^{mm\prime }\right)n_{j,m}^{\sigma }{n}_{j,m\prime }^{\sigma }}}\end{array}.$$

Here, $m,m\prime$ are orbital, and σ - spin indexes, 1 and 2 are labels of two ions in a dimer, i numerates dimers and j all sites in the lattice. Here, $t_c$ and $t_d$ are corresponding hoppings between c and d orbitals in the dimer, $t_d^{\prime }$ and $t_c^{\prime }$ are interdimer hoppings, $n_{j,m}^{\sigma }-$ the occupation number operator at site j for orbital m and spin σ.

In numerical calculations we used the Kanamori parameterization of $U^{mm\prime }$ and $J^{mm\prime }$, so that $U^{mm}=U$, $U^{mm\prime }=U-2J_H$, if $m\ne m\prime$, and $J^{mm\prime }=J_H$.

We used the exact diagonalization technique to treat a dimer and cluster DMFT (25) with Hirsch–Fye solver (40) to study dimerized chain.

Details of the Ab Initio Calculations

All ab initio band structure calculations were performed within the GGA (41) and full-potential linearized augmented plane wave method using Wien2k code (42). The crystal structure of Nb₂O₂F₃ were taken from ref. 28 and for Ba₅AlIr₂O₁₁ from ref. 33. The parameter of the plane-wave expansion was chosen to be $R_{MT}{K}_{max}=7$, where $R_{MT}$ is the smallest atomic sphere radii and $K_{max}$ the plane wave cutoff.

Muffin-tin (MT) radii were chosen to be $R_{Nb}=1.95$, $R_F=1.83$, and $R_O=1.73$ a.u. for Nb₂O₂F₃ and $R_{Ir}=1.91$ a.u., $R_{Ba}=2.35$ a.u., $R_{Al}=1.63$ a.u., and $R_O=1.63$ a.u. for Ba₅AlIr₂O₁₁. We used following k meshes for the Brillouin-zone integration: 7 $\times$ 6 $\times$ 7 for Nb₂O₂F₃ and 3 $\times$ 10 $\times$ 5 for Ba₅AlIr₂O₁₁.

Nb₂O₂F₃

The crystal structure of Nb₂O₂F₃ consists of Nb–Nb dimers, which are formed by two NbO₃F₃ octahedra sharing their edges, see Fig. S2A. Nb ions are inside octahedra formed by O (red balls) and F (gray balls) ions. As a result the $xy$ orbitals in a dimer (in the local coordinate system with axes directed along Nb–O bonds; cf. Fig. 1A) point to each other.

The density of states (DOS) plot obtained in the nonmagnetic GGA calculations for the high temperature phase is presented in Fig. S3. Analysis of the partial contributions to the total DOS shows that the bonding–antibonding splitting for the $xy$ orbital is $\sim$4 eV. Because of such large splitting two electrons with opposite spins are stabilized on the bonding molecular orbital made of lowest $xy$ orbital, and single unpaired electron occupies $xz/yz$ orbital, as shown in Fig. S2B. As a result the total spin and the double exchange turn out to be suppressed in this situation.

Ba₅AlIr₂O₁₁

The main structural element of Ba₅AlIr₂O₁₁ is isolated Ir–Ir dimers. Here, Ir ions are in the IrO₆ octahedra, which share their faces, see Fig. S4A. Here, in contrast to Nb₂O₂F₃, the bonding–antibonding splitting is not large enough to stabilize the state with the lowest total spin. This is clearly seen in the ferromagnetic GGA calculations, where the ground state corresponds to configuration shown in Fig. S4B with the spin moment ${\mu }_s\sim 2{\mu }_B$/Ir, slightly reduced due to hybridization with oxygen. However, this disagrees with the experimental finding that the effective magnetic moment obtained from the fitting of the high-temperature tail to the Curie–Weiss law is ${\mu }_{eff}\sim 1{\mu }_B$/dimer (33).

Theory and experiment become consistent if one includes the spin–orbit coupling (SOC), which additionally splits antibonding Ir $5d$ states and which finally results in the total moment ${\mu }^{GGA+SOC}\sim 0.8{\mu }_B$/Ir. Thus, in this case the strong relativistic spin–orbit coupling conspires with the covalency to suppress DE magnetism, in agreement with the results presented in the main text.

Details of Model Calculations with Spin–Orbit Coupling

To study effect of the spin–orbit coupling we considered isolated dimer with three electrons and three $t_{2g}$ orbitals, where hopping $t_c$ was allowed only between the $l_z=0$ orbitals. The spin–orbit coupling was taken into account in one-electron approximation as $H_{SOC}=-\zeta {\displaystyle {\sum }_m{\overrightarrow{l}}_m{\overrightarrow{s}}_m}$, where ${\overrightarrow{l}}_m$ is effective orbital moment for a given $t_{2g}$ orbital, ${\overrightarrow{s}}_m$ is its spin and m numerates these orbitals. Corresponding level diagrams are given in Fig. S1.

In the calculations of the phase diagram, given in Fig. 6, we took into account the intra-atomic Hund’s exchange as $J_H\times$(number of parallel spins). In these numerical calculations we compared the states shown in Fig. 5, but did not consider other possible configurations.