Extracting multistage screening rules from online dating activity data

Significance

Online activity data—for example, from dating, housing search, or social networking websites—make it possible to study human behavior with unparalleled richness and granularity. However, researchers typically rely on statistical models that emphasize associations among variables rather than behavior of human actors. Harnessing the full informatory power of activity data requires models that capture decision-making processes and other features of human behavior. Our model aims to describe mate choice as it unfolds online. It allows for exploratory behavior and multiple decision stages, with the possibility of distinct evaluation rules at each stage. This framework is flexible and extendable, and it can be applied in other substantive domains where decision makers identify viable options from a larger set of possibilities.

Abstract

This paper presents a statistical framework for harnessing online activity data to better understand how people make decisions. Building on insights from cognitive science and decision theory, we develop a discrete choice model that allows for exploratory behavior and multiple stages of decision making, with different rules enacted at each stage. Critically, the approach can identify if and when people invoke noncompensatory screeners that eliminate large swaths of alternatives from detailed consideration. The model is estimated using deidentified activity data on 1.1 million browsing and writing decisions observed on an online dating site. We find that mate seekers enact screeners (“deal breakers”) that encode acceptability cutoffs. A nonparametric account of heterogeneity reveals that, even after controlling for a host of observable attributes, mate evaluation differs across decision stages as well as across identified groupings of men and women. Our statistical framework can be widely applied in analyzing large-scale data on multistage choices, which typify searches for “big ticket” items.

Vast amounts of activity data streaming from the web, smartphones, and other connected devices make it possible to study human behavior with an unparalleled richness of detail. These “big data” are interesting, in large part because they are behavioral data: strings of choices made by individuals. Taking full advantage of the scope and granularity of such data requires a suite of quantitative methods that capture decision-making processes and other features of human activity (i.e., exploratory behavior, systematic search, and learning). Historically, social scientists have not modeled individuals’ behavior or choice processes directly, instead relating variation in some outcome of interest into portions attributable to different “explanatory” covariates. Discrete choice models, by contrast, can provide an explicit statistical representation of choice processes. However, these models, as applied, often retain their roots in rational choice theory, presuming a fully informed, computationally efficient, utility-maximizing individual (1).

Over the past several decades, psychologists and decision theorists have shown that decision makers have limited time for learning about choice alternatives, limited working memory, and limited computational capabilities. As a result, a great deal of behavior is habitual, automatic, or governed by simple rules or heuristics. For example, when faced with more than a small handful of options, people engage in a multistage choice process, in which the first stage involves enacting one or more screeners to arrive at a manageable subset amenable to detailed processing and comparison (2–4). These screeners eliminate large swaths of options based on a relatively narrow set of criteria.

Researchers in the fields of quantitative marketing and transportation research have built on these insights to develop sophisticated models of individual-level behavior for which a choice history is available, such as for frequently purchased supermarket goods. However, these models are not directly applicable to major problems of sociological interest, like choices about where to live, what colleges to apply to, and whom to date or marry. We aim to adapt these behaviorally nuanced choice models to a variety of problems in sociology and cognate disciplines and extend them to allow for and identify individuals’ use of screening mechanisms. To that end, here, we present a statistical framework—rooted in decision theory and heterogeneous discrete choice modeling—that harnesses the power of big data to describe online mate selection processes. Specifically, we leverage and extend recent advances in change point mixture modeling to allow a flexible, data-driven account of not only which attributes of a potential mate matter, but also where they function as “deal breakers.”

Our approach allows for multiple decision stages, with potentially different rules at each. For example, we assess whether the initial stages of mate search can be identified empirically as “noncompensatory”: filtering someone out based on an insufficiency of a particular attribute, regardless of their merits on others. Also, by explicitly accounting for heterogeneity in mate preferences, the method can separate out idiosyncratic behavior from that which holds across the board, and thereby comes close to being a “universal” within the focal population. We apply our modeling framework to mate-seeking behavior as observed on an online dating site. In doing so, we empirically establish whether substantial groups of both men and women impose acceptability cutoffs based on age, height, body mass, and a variety of other characteristics prominent on dating sites that describe potential mates.

Modeling Noncompensatory, Heterogeneous, Multistage Choice Processes: An Application to Online Mate Choice

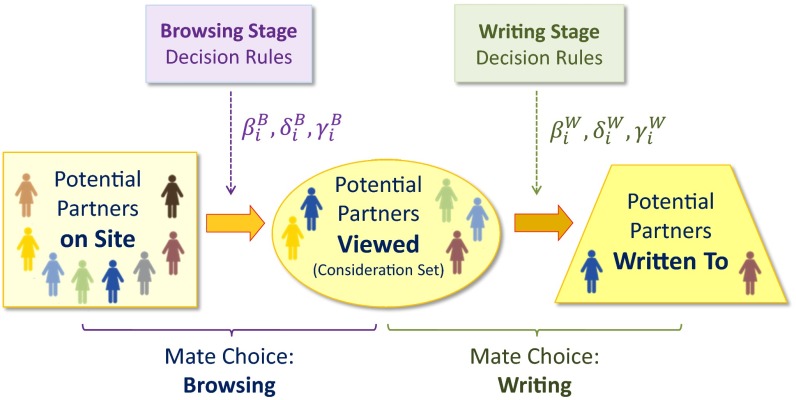
Fig. 1 provides an overview of how mate choice unfolds online. The pool of potential partners includes all relevant users active on the site. Thus, a mate seeker must first decide whom to “browse”—that is, which subset of profiles to consider—and then, among those browsed, to whom to write. Informative features of mate choice behavior are revealed at each stage, and choices made at the browsing stage restrict which alternatives are subsequently available. One may, for example, browse a narrow band of ages and then be relatively indifferent to age thereafter when writing. Empirical studies suggest that the choice process commences using cognitively undemanding, cutoff-based criteria operating on a small number of attributes (e.g., “locals only” or “no one over 40”); decision makers then carefully balance a wider range of attributes after the choice set has been reduced to a manageable size (3, 5, 6).

Fig. 1.

The multistage mate choice process.

Our proposed framework can accommodate an arbitrary number of sequentially enacted winnowing stages. Here, we focus on two intrinsic to the medium: browsing and writing. At each stage, choice is governed by one or more possible decision rules, which are uncovered by the model. For example, users may adopt a “compensatory” approach, arriving at a carefully balanced index for each potential mate and browsing all profiles with indices that surpass a user-specific acceptability threshold. Alternately, they may impose noncompensatory screening rules, in which they browse only those profiles meeting some threshold of acceptability on one or more attributes. Decision theorists distinguish screeners that are conjunctive (deal breakers) from those that are disjunctive (deal makers); the former indicates a set of qualities where all must be possessed, and the latter indicates a set of qualities where any one suffices.

Even sophisticated modeling approaches in social research (7, 8), although offering great flexibility to fit data well, typically encode two procedures at odds with how actual humans seem to process large amounts of information. First, they require that all attributes be somehow accounted for and combined into an index of the quality of each item; second, they compare and/or rank these indices across all items. Ironically, decision rules that are intrinsically demanding—in terms of amassing large quantities of information, recalling it at will, and weighting it judiciously (that is, computationally)—for the decision maker are easier to model and estimate statistically than simpler, more “cognitively plausible” strategies. For example, the compensatory model can be readily estimated using standard regression-based techniques; even allowing for the existence of different groups or “latent classes” of respondents is straightforward with standard software. However, noncompensatory decision rules that allow for (i) abrupt changes in the (relative) desirability of potential partners as an attribute passes outside an acceptability threshold and (ii) an attribute to have a disproportionate effect on choice outcomes over some region of values lack anything approaching a turnkey solution.*

We model each choice as a realized outcome of an underlying utility model: browsing a profile (or subsequently, writing) suggests that the profile’s attributes are relatively desirable. We use piecewise linear splines to identify potential “discontinuities” in the slope of individuals’ utility functions (9). Such splines consist of linear functions joined at specific points called knots. If knot positions are known in advance—for example, a downturn in utility for men under a given height—estimating the slopes of each of the component linear functions is straightforward and quick; however, here, we seek to identify both the slopes and the knots themselves, which are highly nontrivial (10). The key impediment to efficient estimation is that the space of all possible knots is typically very large (for our final model, on the order of 10⁶² in fact), and therefore, brute force exhaustive search is out of the question. Thus, one needs a powerfully efficient way to explore potential knot configurations (Materials and Methods).

Experimentation with our data and prior empirical work (11) suggest that “trilinear” splines—which have (up to) three distinct linear components—typically suffice to capture nonlinearities in discrete choice applications; moreover, the usual linear utility formulation is a testable parametric restriction. Utility functions for each activity (browsing and writing) are decomposed into three portions: an intercept, a two-knotted piecewise linear spline for each continuous (or “continuizable”) attribute (e.g., age), and dummy variables for intrinsically categorical attributes (e.g., ethnic group). Specifically, in standard notation (9, 11), utility ($V_{ij}^B$) for user i browsing (B superscript; an analogous formulation holds for writing W) potential mate j is

$$V_{ij}^B={\mathrm{\beta }}_{0i}^B+{\displaystyle \sum }_{k=1}^K\left[{\mathrm{\beta }}_{1ik}^B{x}_{ijk}^B+{\mathrm{\beta }}_{2ik}^B{\left(x_{ijk}^B-{\mathrm{\delta }}_{1ik}^B\right)}_{+}+{\mathrm{\beta }}_{3ik}^B{\left(x_{ijk}^B-{\mathrm{\delta }}_{2ik}^B\right)}_{+}\right]+{\displaystyle \sum }_{l=1}^L{\mathrm{\gamma }}_{il}^B{x}_{ijl}^B,$$

$${\text{where}\hspace{0.17em}\mathrm{\delta }}_{1ik}^B\le {\mathrm{\delta }}_{2ik}^B\hspace{0.17em}\text{and}\hspace{0.17em}{\left(y\right)}_{+}=\{\begin{array}{c}y\hspace{0.17em}\text{if}\hspace{0.17em}y\ge 0\\ 0\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}y<0\end{array}\hspace{0.17em}.$$ [1]

Thus, utility is additive with three components: (i) ${\mathrm{\beta }}_{0i}^B$ (intercept), (ii) sum of utilities of K continuous splined attributes (coefficients $\left\{{\mathrm{\beta }}_{1ik}^B,{\mathrm{\beta }}_{2ik}^B,{\mathrm{\beta }}_{3ik}^B\right\}$, knots $\{{\mathrm{\delta }}_{1ik}^B,\hspace{0.17em}{\mathrm{\delta }}_{2ik}^B\}$, and covariates $x_{ijk}^B$), and (iii) sum of utilities of L discrete attributes (coefficients ${\mathrm{\gamma }}_{il}^B$ and covariates $x_{ijl}^B$). Setting ${\mathrm{\beta }}_{2ik}^B={\mathrm{\beta }}_{3ik}^B=0$ means that all three slopes for spline k are identical, and therefore, it yields the standard linear-additive utility model. Large (positive or negative) slope values—any of β₁, (β₁+β₂), or (β₁+β₂+β₃)—indicate potential noncompensatory behavior, including deal breakers. With V on a logit scale, a difference of three represents a difference in odds (and thereby, probability) on the order of being 20 times less likely that the potential match will be browsed or written to, which may be large enough that no other attribute combination can overcome it: a deal breaker.

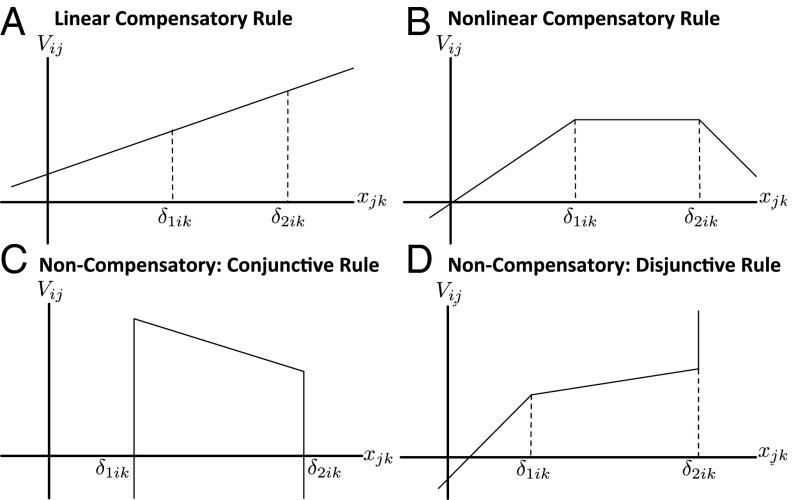
Fig. 2 illustrates how the utility model (Eq. 1) captures specific decision rules. For a continuous attribute $k$, if any of the three estimated component slopes is “large” (i.e., ideally but impractically $\pm \mathrm{\infty }$), it represents a noncompensatory rule, such as in Fig. 2 C and D. In reality, imposing a slope of $\mathrm{\infty }$ is somewhere between meaningless and too harsh: practically speaking, if the utility slope is large enough to render all other attributes and their differences irrelevant, a nonlinear but ostensibly compensatory rule can function as deal breaker or deal maker. Similar logic applies to the L categorical attributes: the dummy slope coefficient ${\mathrm{\gamma }}_{il}^B$ determines whether the attribute $l$ functions as deal breaker or deal maker. [For categorical attributes, the binary dummy coefficients need to be compared with an average and not merely with adjacent ones, because “adjacent” is not meaningful for purely categorical variables (e.g., ethnicity).]

Fig. 2.

Illustration of how choice model captures alternative decision rules. A depicts a linear compensatory rule; B depicts a nonlinear but compensatory one. C is a conjunctive rule where being outside of the range (${\mathrm{\delta }}_{1ik}$ and ${\mathrm{\delta }}_{2ik}$) acts as a deal breaker, and D is a disjunctive rule where being greater than ${\mathrm{\delta }}_{2ik}$ acts as a deal maker.

In summary, the model accommodates three key constructs: (i) nonlinear, even noncompensatory, evaluative processes; (ii) heterogeneity across individuals; and (iii) multistage choice behavior. For our specific application to online dating, it allows for distinct but statistically intertwined accounts of both the browsing and writing stages and explicit quantification of the relative importance placed on observable attributes included in online profiles. Importantly, decision rules need not be prespecified: the number of preference profile “types” and where the cutoffs enter are handled nonparametrically (that is, of a degree of complexity driven by the data). The model also accommodates exploratory and stochastic behavior, thus guarding against a deal breaker on, say, age being tautologically inferred as the oldest (or youngest) value observed for each individual.^† Latent classes allow for heterogeneity—that groups of people have distinct preferences—without imposing it, so that true commonalities in both preferences and deal breakers can stand out.

Data and Results

Our data consist of over 1.1 million browsing and writing decisions made by 1,855 deidentified, randomly selected individuals from the New York metropolitan area joining an established, marriage-oriented, subscription-based dating site (SI Appendix, Section S2) (N_Men = 696; N_Women = 1,159).^‡ Analysis focuses on attributes revealed in users’ profiles, including three continuous attributes [height, body mass index (BMI), and age] as well as categorical predictors, including marital status, children, smoking, and education. For categorical attributes, dummies capture potential interactions. To maintain parsimony and accord with findings from prior studies (12–14), continuous attributes of potential mates are coded relative to the seeker’s baseline. Differences likely matter more at low vs. high values: a 5-y gap matters far more at 23 y old than at 53 y old, and there is likely a wider “margin of acceptance” among people with high BMIs. Both BMI and age are, therefore, accommodated as differences on a log scale [e.g., $\ln \left({\text{Age}}_{\text{user}}\right)-\text{ln}\left({\text{Age}}_{\text{potential}\hspace{0.17em}\text{match}}\right)$].

Table 1 reports the fits of two-stage models with and without heterogeneous decision rules (latent classes) as well as models that allow for conventional representation of continuous covariates (i.e., no splines). Based on standard fit metrics [Bayesian Information Criterion (BIC) and L²], the proposed model with five latent classes for both men and women fits the data better than all nested models (e.g., homogeneous and linear utility) and nonnested ones with polynomial representation of continuous covariates, and those differences are statistically significant. To safeguard against overfitting, we also assess goodness of fit using a holdout sample consisting of 181 men and 318 women who joined the site immediately after the estimation period. These out of sample estimates reaffirm that a model allowing for nonsmooth response and heterogeneity outperforms other more traditional specifications. In addition to superior fit, our model captures features of decision processes that are distorted by traditional approaches. Additional details are in SI Appendix, Section S4.

Table 1.

Fit statistics for proposed, nested, and alternate models

	Men				Women
	L2	df	BIC	L2 holdout	L2	df	BIC	L2 holdout
One-class model
Linear	394,182	658	385,686	55,473	658,900	1,121	643,747	111,325
Quadratic	343,782	652	335,363	48,188	547,755	1,115	532,683	92,173
Cubic	342,704	646	334,363	47,929	547,644	1,109	532,653	91,237
Splines	341,783	646	333,442	47,708	544,956	1,109	529,965	90,609
Five-class model
Linear	347,897	502	341,415	48,381	575,977	965	562,933	96,426
Quadratic	321,296	472	315,201	44,790	525,351	935	512,712	88,157
Cubic	320,390	442	314,683	44,754	524,280	905	512,047	87,867
Splines	319,956	442	314,249	43,777	523,108	905	510,875	86,835
No. of users	696			181	1,159			318
No. of observations	405,249			56,900	742,250			121,357

Although our models produce many results, we focus here on key features of mate choice behavior that would be, as a whole, inaccessible with alternative modeling approaches: (i) different rules at different decision stages, (ii) sharp cutoffs in what attribute values are desired or acceptable, (iii) invocation of deal breakers, and (iv) heterogeneity in behavior. All results reported in the main text are significant at the 0.01 level or greater; details are in SI Appendix, Tables S3 and S4.

Different Rules at Different Stages.

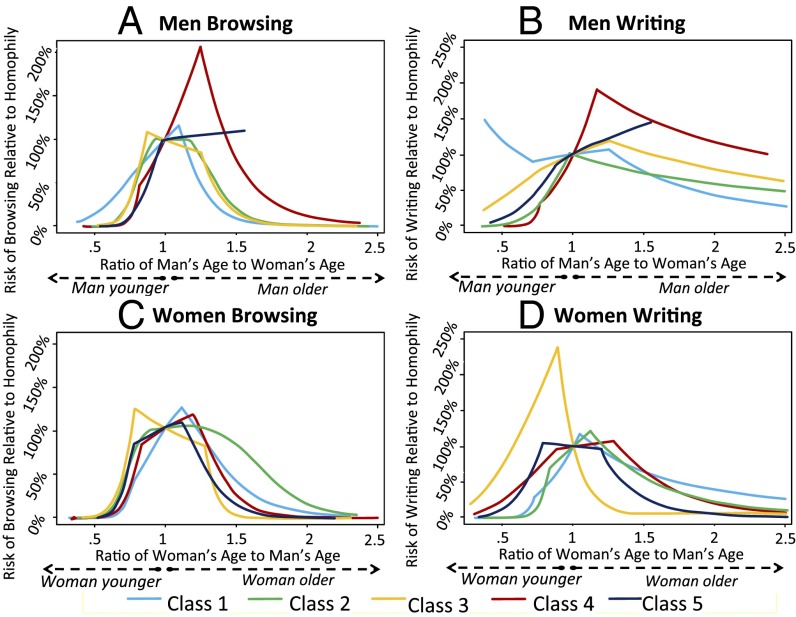
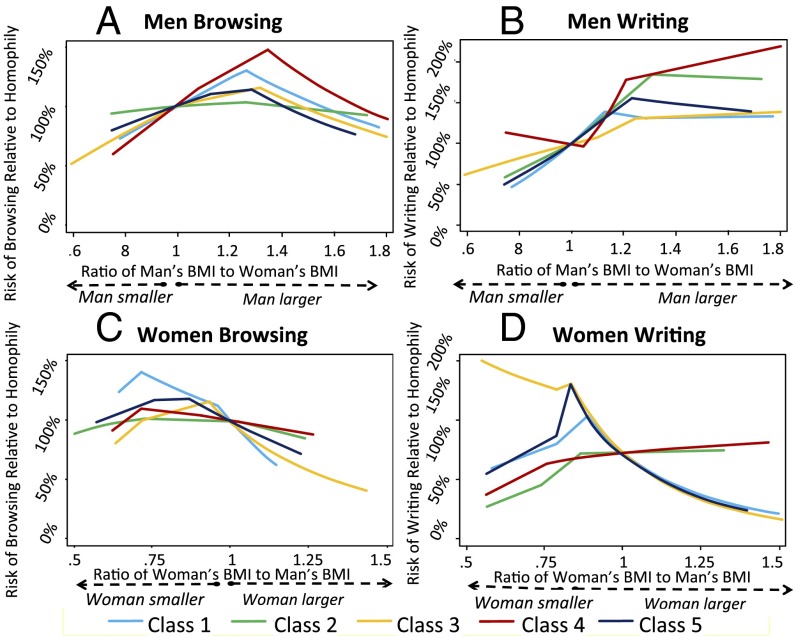
Distinct subsets of attributes are implicated at the browsing and writing stages. For example, when men select among women, age plays a greater role in the browsing stage. Consider Fig. 3 A and B: the portions to the right of one (denoting equal age) suggest that men tend to browse women of their own age or somewhat younger; however, conditional on browsing, men are mostly indifferent to increasingly younger women. Among women, age matters in both browsing and writing, but its effects can vary across stages. For example, as we see in Fig. 3 C and D, whereas class 3 women—whose median age is around 40 y old—do browse profiles of younger men, they almost never write to them (i.e., the sharp drop off for this class for age ratio above 1). BMI also figures differently into browsing and writing decisions. Fig. 4 A and B suggests that men across the board prefer to browse women with lower BMIs than their own. Intriguingly, nearly all contours reach their maximum when men’s BMIs are around 30% higher (i.e., ratio of 1.3). Thus, it seems that women can never be too thin (to write to; conditional on browsing).

Fig. 3.

The probability of browsing and writing someone of a given value of age relative to the probability of browsing or writing someone of equal age. A and B show results for men, and C and D show results for women (n = 1,855 users; estimates based on 1,147,499 browsing and writing observations). The x axis displays the ratio of the user’s attribute value to that for potential matches. The y axis shows the associated probability ratio for both browsing and writing. Outliers are trimmed (top and bottom 1%); all variables except for the focal attribute are held at their mean values.

Fig. 4.

The probability of browsing and writing someone of a given value of body mass relative to the probability of browsing or writing someone of equal body mass. A and B show results for men, and C and D show results for women (n = 1,855 users; estimates based on 1,147,499 browsing and writing observations). The x axis displays the ratio of the user’s attribute value to that for potential matches. The y axis shows the associated probability ratio. Outliers are trimmed (top and bottom 1%); all variables except for the focal attribute are held at their mean values.

Sharp Cutoffs.

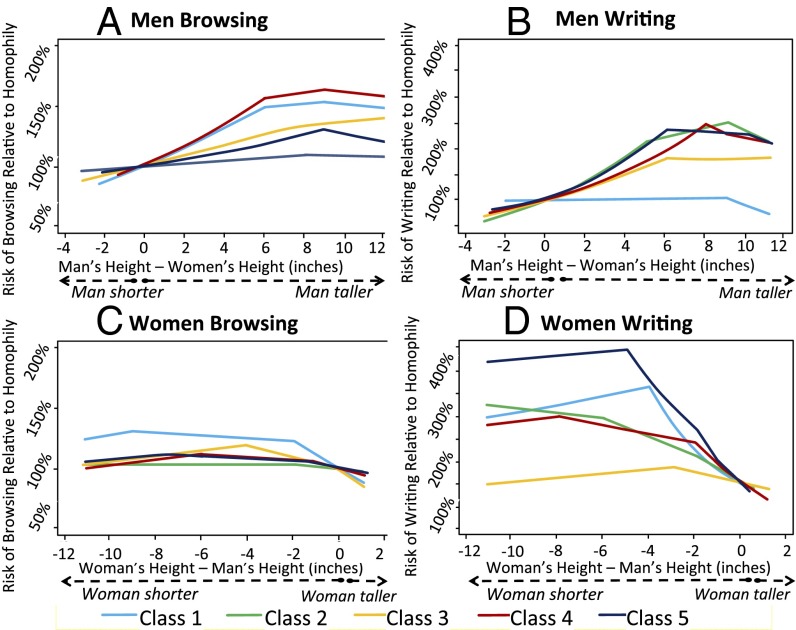
By identifying sharp cutoffs in acceptability criteria, the model can identify norms or rules that would be difficult to extract using traditional methods. The results for height, as shown in Fig. 5, provide one illustration of what we can learn from a model that allows for sharp cutoffs in attribute utilities rather than smooth changes. Overall, women seem to prefer men who are 3–4 in taller across the board, with substantial drop offs for men below this cutoff. This finding is consistent with prior research showing that women prefer a partner who is not taller than she is in heels (15). With regard to age (Fig. 3), we also see that some men (e.g., class 4) impose sharp cutoffs in their decisions to browse a particular profile, focusing their attention primarily on women who are 30% younger than they are. Given that these men are, on average, 39 y of age, this guideline puts them within 1 y of the conventional acceptability criteria: the youngest person one can appropriately date is “half-your-age-plus-seven” (16). Any such crisp criteria would be smoothed over in a model that captured nonlinearities via polynomial specifications.

Fig. 5.

The probability of browsing and writing someone of a given value of height relative to the probability of browsing or writing someone of equal height. A and B show results for men, and C and D show results for women (n = 1,855 users; estimates based on 1,147,499 browsing and writing observations). The x axis is height difference (in inches) between the user and potential match. The y axis shows the associated probability ratio. Outliers are trimmed (top and bottom 1%); all variables except for the focal attribute are held at their mean values.

Deal Breakers.

Age differences are the biggest deal breaker. Even within the bulk of observations (i.e., excluding elderly outliers), women can be up to 400 times less likely to browse someone with an undesirable value of age (all else equal). The model can also locate deal breakers in categorical covariates, although this is not unique to its framework. In online dating, one that stands out is not demographic but an act of omission: failing to provide a photo. Both men and women are roughly 20 times less likely to browse someone without a photo, even after controlling for all other attributes in the model (age, education, children, etc.). Nearly as strong is smoking behavior: among those who do, nonsmokers are nearly 10 times less likely to be browsed and, therefore, smoking is evidently a decisive screen. In short, we find clear evidence of deal-breaking behavior, although the strength of effects varies across the revealed classes. Note that, although none of these may be truly inviolable, they are practically insurmountable within the observed range of available covariates.

Heterogeneous Behavior.

By allowing for unobserved heterogeneity, we can both assess what behaviors hold across the board and identify subclasses of users pursuing unique mate selection strategies. Fig. 3 shows that, although men and women adhere to the same basic criteria in identifying an appropriately aged partner—the man is somewhat but not excessively older than the woman—there is a great deal of variation in where cutoffs occur. For example, although most women pursue partners who are slightly older than they are, class 3 women tend to pursue men who are substantially older. The median woman in this class is around 40 y old; she is 2.5 times more likely to write to a man who is 50 y old compared with a man her own age. Our model also reveals a nontrivially sized class of men—class 4, which is 22% of the male user population—who seem to be attracted to women very different from themselves. These men are, on average, overweight and older (mean BMI = 25.0; mean age = 39.2 y old) but tend to pursue much younger, slimmer women.

In our final set of results, we show that analogous analyses can be distorted by traditional statistical modeling approaches. Because unobserved heterogeneity is standard in most statistical software packages, an appropriate comparison is between our model and a single-stage choice model for either browsing or writing conditional on browsing with a polynomial representation of nonlinearity plus unobserved heterogeneity.

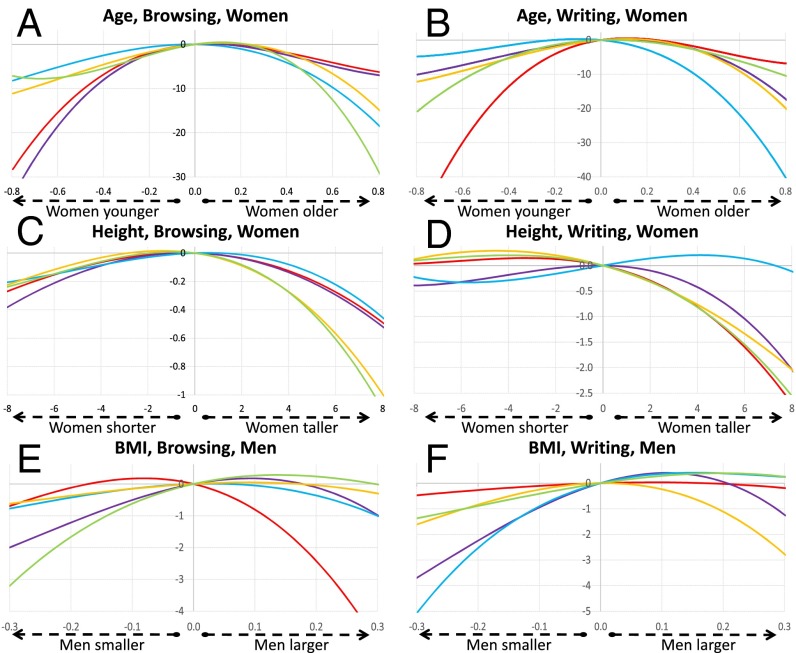
Fig. 6 illustrates what such a conventional model infers about how men and women respond to age, BMI, and height differences. Selected results are shown; a complete set of panels is available in SI Appendix, Section S4. First, we see that, although different rules apply at different stages—and there is clear heterogeneity in behavior across classes—class-specific behavior cannot be linked across the two stages (that is, a particular class in browsing does not uniquely correspond to any of the revealed classes in writing). Also, we see that the cubic functions smooth out all sharp cutoffs, making it difficult to identify potential “rules” that people are using to select mates. However, most critically, because the whole range of data—not just local information—drives the shape of the cubic (or indeed, any polynomial), we observe a number of substantively erroneous results. For example, the red line in Fig. 6B suggests that one class of women is most likely to write to men who are substantially younger than they are. Similarly, in Fig. 6D, the blue line implies that one class of women pursues men who are around 5 in. below their own height. Odd maxima also emerge in the results for men (e.g., the red line in Fig. 6E suggests that there is a class of men who prefer women who are 8 to 10% heavier than they are). These results appear as artifacts of the cubic needing to get the asymptotics correct at the expense of accurately representing other, substantively salient features of the response curve, such as the modally optimal height, BMI, or age within class.

Fig. 6.

Selected effects of age, height, and body mass on log odds of browsing and writing in conventional models for men and women (n = 1,855 users; estimates based on 1,147,499 browsing and writing observations). A and B show the log odds of women (A) browsing or (B) writing a potential mate as a function of age. C and D show the log odds of a women (C) browsing or (D) writing a potential mate as a function of height. E and F show the log odds of men (E) browsing or (F) writing a potential mate as a function of body mass. In all cases, the two stages of the mate choice process, browsing and writing conditional on browsing, are modeled separately. Nonlinearities in response to age, height, and body mass are represented by a cubic specification. Colors denote latent classes consistent within stage (browsing and writing) but not across them.

Discussion

Online activity data throw open a new window on human behavior. These data offer not only unprecedented temporal- and unit-level (i.e., person) granularity but also the ability to observe how eventual choices unfold in stages. However, to take full advantage of the richness of these data requires quantitative methods capable of capturing human cognitive processes and not merely capturing associations among variables or making accurate forecasts. The proposed statistical framework is based on decision strategies compatible with people’s observed mate choices and can be estimated using only observed behavioral data. Efficient parallelized estimation of heterogeneous, “knotted” preference curves uncovers both distinct screening strategies for men vs. women and browsing vs. writing and commonalities that span these dimensions. It also allows a quantification of various deal breakers: who uses them, when they operate, and how difficult they are to surmount.

Our results illustrate the types of insights that can be gained from a model that aims to better represent underlying choice processes. This approach is flexible and extendable, and it can be applied to a wide swath of activity data, such as in housing search (e.g., Trulia and Zillow), job search (e.g., Monster), and other sites allowing people to browse and select among potential choices. Such big data are intriguing, because they are actual behavior and not merely self-reports, and as such, they allow us to observe at very high granularity the results of search strategies, contact or application processes, learning, and other sociologically relevant activities that unfold over time.

Although this analysis focuses on online activities, a large body of work shows that—both online and offline—people invoke noncompensatory decision rules as a strategy for managing the complexity of decision problems. For example, employers routinely screen potential job candidates based on experience, references, and other attributes (17, 18). College admissions officials impose a cutoff on grades or Scholastic Aptitude Test (SAT) scores, below which they will not give an application additional consideration (19, 20). Potential movers only search for housing in a small set of areas that fit their criteria with regard to affordability and location (21, 22). All of these decision rules involve cutoffs on a small number of focal attributes rather than complex tradeoffs across all salient attributes of choice alternatives. Our approach provides a flexible framework for capturing such decision processes.

Closer attention to the strategies that people use to learn about and evaluate choice options may also suggest new policies that target particular stages of the decision process (23). Although this possibility has only recently been raised among academics and policymakers, the idea is well-known in marketing research that tries to tailor its “interventions” to capitalize on nuances in how people perceive and respond to their environment. Case studies and field experiments reveal that investment in products has little effect on purchasing behavior if consumers are prone to exclude them from consideration (24). Extending this insight to social policy, an intervention that targets the criteria that people use to decide what options to consider may be more efficacious than an intervention that affects how people assess their alternatives under consideration.

Materials and Methods

We describe two key features of our modeling strategy: first, how we allow for multiple decision stages; and second, our strategy for estimating the model coefficients.

Modeling Multiple Decision Stages.

We model each site user’s behavior as a sequence of browsing and writing decisions. In the first stage, the probability that the ith mate seeker will consider (browse) the jth option (at a particular time, which for simplicity, we leave unsubscripted) can be written as a binary choice model, which we operationalize as softmax (i.e., logit):

$$p_{ij}^B=\frac{\text{exp}\left(V_{ij}^B\right)}{1+\text{exp}\left(V_{ij}^B\right)},$$ [2]

where $V_{ij}^B$ is the systematic component of utility derived from browsing profile j. In the second stage, writing behavior (conditional on browsing) is similarly specified as a binary logit model. The probability that user i writes to user j is, therefore,

$$p_{ij}^W|\text{browsing}=\frac{\text{exp}\left(V_{ij}^W\right)}{1+\text{exp}\left(V_{ij}^W\right)},$$ [3]

where $V_{ij}^W$ is the systematic component of utility derived from writing to the jth potential mate. It is not necessary that all salient attributes of potential partners be involved in both the browsing and writing stages of the model. Note that we allow for separate decision rules at each stage but link the two stages together using latent classes. This procedure provides a joint account of multiple decision phases: here browsing and writing behavior. For example, one strategy may be to only consider a narrow age range in the browsing stage but—among all profiles that meet the age criterion—be relatively indifferent to potential mates’ age in the writing stage.

Model Estimation.

Estimation of knots using such “mixture regression with change point” models is known to be computationally demanding (25), and even more so with discrete outcomes, repeat observations, and multiple stages that span latent classes. Because no general purpose method scales to data of the complexity used here, we use a parallelized local grid search strategy using commercial software as an engine to extract latent classes, which quantify differences in preference across site users and span both stages. Our method is generalizable and replicable, and it leverages two specific software packages^§ to break the statistical model into two parts: generating random “nearby” candidate knot configurations (carried out in Matlab) and assessing discrete heterogeneity in resulting parameters (carried out in Latent Gold). We then use a combination of stochastic- and gradient-based methods to iterate between estimating the two-stage, latent class models for a given set of knots and exploring the space of possible knots. (Details about the algorithm are available in SI Appendix, Section S1.)

Human Subjects.

This study was approved by the University of Michigan’s Institutional Review Board (HUM00075042). It makes use of observational data on browsing and writing behavior. Users give their informed consent when they register for the site; they must check a box that acknowledges that their deidentified data will be used for research purposes.

SI Appendix.

SI Appendix has additional description of the data, details about model specification and estimation strategy, supplementary results, and comparison with conventional approaches.