Configuration of the thermal landscape determines thermoregulatory performance of ectotherms

Significance

Environmental temperatures drive major ecological processes, largely because the physiology of any organism depends on its temperature. For this reason, many animals behave in ways that prevent their body temperatures from fluctuating, even as climate changes dramatically. Using a combination of computer simulations and controlled experiments, we show that thermoregulation depends not only on the mean and variance of operative environmental temperatures but also on the spatial arrangement of these temperatures. Our results have further implications for ecological models that rely on estimates of activity to predict the responses to climatic change.

Abstract

Although most organisms thermoregulate behaviorally, biologists still cannot easily predict whether mobile animals will thermoregulate in natural environments. Current models fail because they ignore how the spatial distribution of thermal resources constrains thermoregulatory performance over space and time. To overcome this limitation, we modeled the spatially explicit movements of animals constrained by access to thermal resources. Our models predict that ectotherms thermoregulate more accurately when thermal resources are dispersed throughout space than when these resources are clumped. This prediction was supported by thermoregulatory behaviors of lizards in outdoor arenas with known distributions of environmental temperatures. Further, simulations showed how the spatial structure of the landscape qualitatively affects responses of animals to climate. Biologists will need spatially explicit models to predict impacts of climate change on local scales.

The rapid warming of many environments has generated great concern about the potential impacts on biodiversity (1). Genetic changes in response to anthropogenic warming seem rare (2) or limited (3), and many species have shifted habitats over space and time (4–7). Indeed, facultative behavioral strategies are the primary means by which many species cope with changing environments (8). In a warming world, behavioral thermoregulation could enable most organisms to maintain body temperatures that promote physiological performance (9–11). However, excessive warming constrains thermoregulation, potentially leading to extinction of populations. At local scales, recent warming apparently caused numerous extinctions by limiting the duration of foraging by lizards (12). According to mechanistic models, thermal constraints on activity will play a major role in biological invasions and local extinctions (13–16). Given constraints on thermoregulatory behaviors, some have predicted that global warming could eliminate more than 40% of lizard species by 2080 (12).

Such projections, although dire, underestimate the impacts of climate change by failing to consider costs of thermoregulation that are imposed by environmental heterogeneity (10, 17, 18). Most models assume that an animal can access either unshaded michrohabitats or shaded microhabitats without using energy to search for and move between them (14, 19). As long as the animals prefers a body temperature within the range of operative environmental temperatures, an animal can thermoregulate by shuttling between microhabitats at no cost. Given this assumption, researchers combine meteorological data and biophysical equations to calculate the expected performance of an organism in specific climates. However, thermoregulatory behaviors impose costs such as energy loss, predation risk, and missed opportunities for foraging and breeding (20), which researchers have ignored when modeling the biological impacts of climate change. Therefore, biologists would benefit greatly from a theory that weighs costs and benefits of behavioral thermoregulation.

The prevailing theory of behavioral thermoregulation focuses on the energetic costs and benefits of locating preferred microclimates (20). Presumably, organisms must move more when these microclimates become rare, increasing the energetic cost of thermoregulation. Given this assumption, the thermoregulatory performance of an organism depends on the frequency distribution of microclimates in its environment (21). Such distributions have been quantified by the index d_e, which equals the absolute difference between an animal’s preferred temperature and the mean operative temperature of its environment (22). To describe the quality of an environment, researchers typically average samples of d_e over space or time (23); a greater mean of d_e reflects lower thermal quality. Although animals in an environment with a greater d_e should thermoregulate less accurately, comparative analyses uncovered the opposite relationship (24). This discord between theory and data arose because the statistical distribution of operative temperatures carries no information about the spatial distribution. However, the statistical and spatial distributions of thermal resources interact to determine whether an organism can thermoregulate and the cost that it incurs when doing so (25, 26).

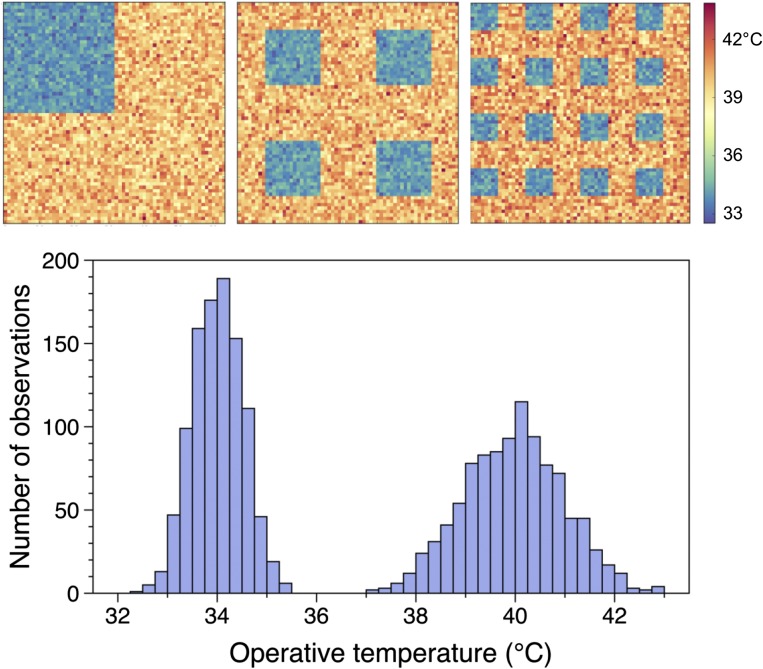
To illustrate how the spatial distribution of thermal resources affects thermoregulatory performance, we simulated movements of ectothermic animals in 2D landscapes. Simulated individuals moved through a 64- × 64-m grid, in which each cell (1 m²) had an operative temperature drawn from a bimodal distribution (Methods). Holding this statistical distribution constant, we configured the thermal landscape in various ways, comprising a set of spatial distributions ranging from clumped to dispersed (Supporting Information and Fig. S1). For each environment, we simulated behavioral thermoregulation and estimated the energetic cost of movement. The spatial structure of the environment dramatically affected the accuracy and cost of thermoregulation; regardless of the mean environmental temperature, virtual animals thermoregulated more accurately, moved shorter distances, and expended less energy in dispersed environments (Fig. 1). More movement was necessary in a clumped landscape because many positions lay far from preferred microclimates. In a dispersed environment, however, an individual was always close to a preferred microclimate regardless of its position in the landscape. These simulations show how the spatial structure of a thermal landscape affects thermoregulation, especially when animals must choose between microhabitatst that promote thermoregulation and those that promote other functions. Such tradeoffs are probably common considering that animals must move to locate food, defend territories, and avoid predators.

Fig. S1.

Bimodal distributions of operative temperatures were distributed in three different ways to create thermal landscapes ranging from clumped to dispersed. From left to right, these three maps exemplify the structure of the three types of landscapes for a common distribution (plot beneath maps).

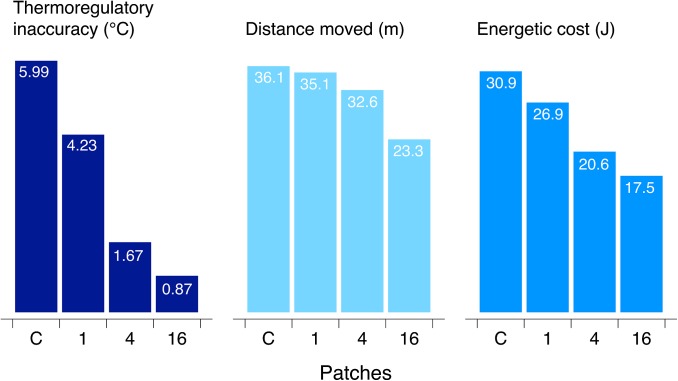
Fig. 1.

Virtual animals thermoregulated less accurately but moved more and expended more energy when preferred microclimates were clumped. Here, thermoregulatory inaccuracy is the absolute difference between body temperature and the preferred temperature. Thermoregulation was simulated in landscapes containing 1, 4, or 16 patches within the preferred range of operative temperatures. The structure of the thermal landscape had no impact on the performance of animals that moved randomly with respect to temperature (labeled C for control). See Supporting Information for details about the simulations.

We tested our theory of thermoregulation in large, outdoor arenas at the Sevilleta National Wildlife Refuge (Socorro, NM; Fig. 2). In each arena, we used a canopy of shade cloth (80%) to create landscapes ranging from a clumped to a dispersed distribution of operative temperature (1, 4, or 16 patches; each replicated three times). In some arenas, another uniform layer of shade cloth (30% or 50%) covered the entire area, including the first layer of shade cloth. This additional shading broadened the range of mean temperatures among arenas without affecting the level of dispersion. Lizards (Sceloporus jarrovi) experienced each level of dispersion for 2 d in a random order. In clumped arenas, a lizard had to choose between foraging widely and minimizing the cost of shuttling between sun and shade. In dispersed arenas, a lizard could explore its environment while shuttling. Every 10 min, the body temperature of each lizard was recorded automatically by a miniature device (Thermochron iBat; Alpha Mach), surgically placed in the coelomic cavity. Operative temperatures in shaded and unshaded patches were measured with hollow copper electroforms designed to mimic the radiative and convective properties of a lizard (9, 27).

Fig. 2.

Outdoor arenas (400 m²) were used to manipulate thermal landscapes. Each arena represented a combination of spatial dispersion from clumped to dispersed (1, 4, or 16 patches of shade) and background shade (0%, 30%, or 50%).

To predict thermoregulatory performance in each arena, we simulated movements and temperatures of virtual lizards under the specific conditions of our experiment (Supporting Information). We predicted microclimates at 1-min intervals using a cubic spline, fit to the time-series of operative temperatures in our experiment. To optimize the thermoregulatory strategy, parameters defining rules for movement evolved through a genetic algorithm. We chose a fitness criterion that maximized thermoregulatory performance, quantified as the absolute difference between the body temperature of a lizard and its median preferred temperature (34 °C; Supporting Information). Parameters were optimized over all levels of dispersion (1, 4, and 16 patches).

Results and Discussion

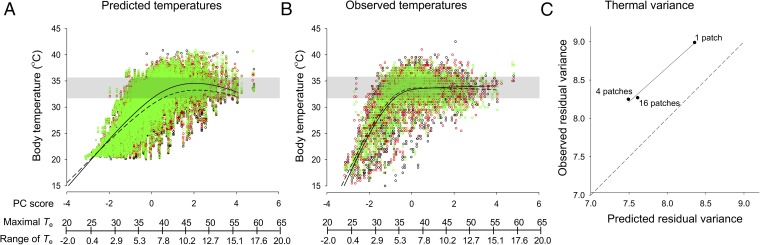
In our simulations and in the experiment, lizards thermoregulated more accurately when preferred microclimates were dispersed. Consistent with our simulations in described in Fig. 1, virtual lizards in a clumped landscape experienced 9% more variance of body temperature than those in dispersed landscapes with either 4 or 16 patches (Fig. 3A). Because mean temperatures generally fell within the range of preferred temperatures, the smaller variance of body temperature in more dispersed landscapes reflected a better thermoregulatory performance. Additionally, the mean body temperature for a given operative temperature was about a degree closer to the preferred range in the most dispersed landscape (effect of treatment: F = 6.31, P = 0.0001), particularly under colder conditions. We observed similar patterns in our field experiment. Real lizards in arenas with 1 patch experienced either 12% or 10% more variance of body temperature than did real lizards in arenas with either 4 or 16 patches, respectively (Fig. 3B). The variances of body temperature observed among thermal landscapes correlated strongly with those predicted by our simulations (adjusted r² = 0.96; Fig. 3C). Moreover, the mean body temperature for a given operative temperature differed significantly between the most and least dispersed arenas (effect of treatment: F = 8.63, P = 0.0001). The match between predicted and observed patterns of thermoregulatory performance suggests that our model effectively captures the impact of thermal landscapes on behavior.

Fig. 3.

Body temperatures of virtual lizards in computer simulations (A) and those of real lizards in outdoor arenas (B) are plotted against a principal component of environmental temperatures. As PC1 increases, so does the maximum operative temperature and the range of temperatures (between sun and shade) (Table S2). The variance of body temperatures depended on the frequency and dispersion of operative temperatures (1, 4, and 16 patch treatments are represented by red, black, and green circles, respectively). For both simulated and real lizards, the variance of body temperatures in the clumped landscape (1 patch) exceeded those in dispersed landscapes (4 or 16 patches). (C) The observed variance of body temperature correlated strongly with the variance predicted by our individual-based model (r² = 0.99). For context, shaded regions on the plots show the central 50% of temperatures selected by lizards in a thermal gradient.

Our approach to the study of thermoregulation confers significant advantages over other approaches. Previous models focused only on the mean or range of operative temperatures, ignoring how environmental structure shapes the cost of reaching preferred microclimates (20, 23, 28). By explicitly mapping operative temperatures, we accounted for their statistical and spatial distributions, revealing how the structure of the landscape impacts behavior. We can also consider spatial covariations between temperature and other factors, such as food, water, and predators. These spatial covariations ultimately determine the costs of predation risk and missed opportunities. Finally, our model elevates the significance of organismal properties such as perception, mobility, and memory to the same level as size, shape, and color (Supporting Information).

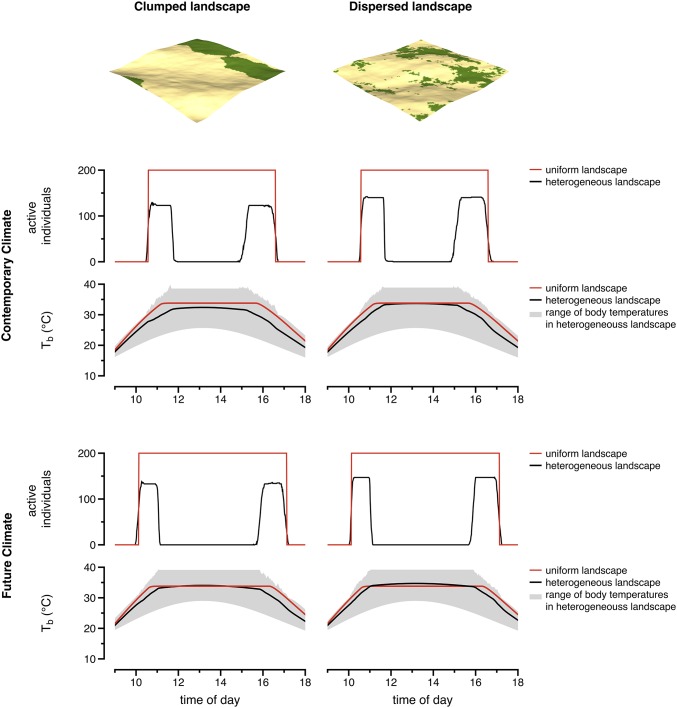
We can directly apply this theory to understand or predict biological impacts of climate change (12, 29). Researchers simplify their models by assuming that animals can access the full range of microclimates at any point in space (14, 19). Nevertheless, warming of a heterogeneous landscape will alter the spatial distribution of preferred microclimates (10). We can appreciate the significance of this effect by comparing thermoregulatory performances of lizards in different landscapes (Fig. 4). In a thermally homogeneous landscape, all individuals in a population commence or cease activity at the same time. In a heterogeneous landscape, however, individuals commence or cease activity at different times, such that only a fraction remain active at any point. Consequently, the simulation in a homogeneous landscape grossly overestimates activity throughout the day, primarily because animals have access to shade and sun at all positions on the landscape. In heterogeneous landscapes, individuals cease activity during midday when preferred microclimates become too rare to locate without overheating. As the spatiotemporal structure of thermal landscapes change during climate warming, ectotherms that rely on behavioral thermoregulation could lose more time for activity than previously expected (10, 12, 21, 30, 31).

Fig. 4.

Ignoring the spatial distribution of thermal resources causes one to grossly overestimate the duration of activity. Virtual lizards in heterogenous landscapes had fewer opportunities for activity and experienced qualitatively different impacts of climate change than those in a spatially uniform landscape. Comparisons were made with two heterogenoeus landscapes, one with a clumped distribution of shade (Left Column) and another with a dispersed distribution (Right Column). Black and red lines depict thermoregulatory performances (in terms of achieved body temperatures) of individuals in heterogeneous and uniform landscapes, respectively; gray shading depicts the range of body temperatures in heterogeneous landscapes. Note, no variation in body temperature is exhibited in homogeneous environments. A warming of air temperature by 3 °C (future climate) increased activity in the uniform landscape but reduced activity in the heterogeneous landscapes. Activity is shown as the number of individuals (of 200) that were active at a given time. For both contemporary and future scenarios of climate, individuals in the dispersed landscape were more likely to be active and thermoregulated more accurately (compare black lines between plots in Left and Right Columns). Further, the spatially implicit and explicit approaches make qualitatively different predictions with regard to climate. With the spatially implicit approach, the activity time is predicted to not only be greater at present but also to increase following climate change. In our spatially explicit approach, the activity time is predicted to decrease in the future.

By integrating our knowledge of biophysics, energetics, and behavior, we initiated a theory of physiological ecology that connects organisms to landscapes. Despite being considerably more complex than previous models, our individual-based model possesses greater generality. For instance, one can easily change the values of parameters to predict behaviors of other species. One can even add a function that incorporates metabolic sources of heat to yield a spatially explicit model of endothermic thermoregulation. Thus, individual-based modeling should become a common approach to answering questions about behavioral thermoregulation. This spatially explicit perspective on physiological ecology will become increasingly important as biologists start to explore how anthropogenic factors will shape thermal heterogeneity at the local scale (12, 29).

Methods

Construction of Thermal Arenas.

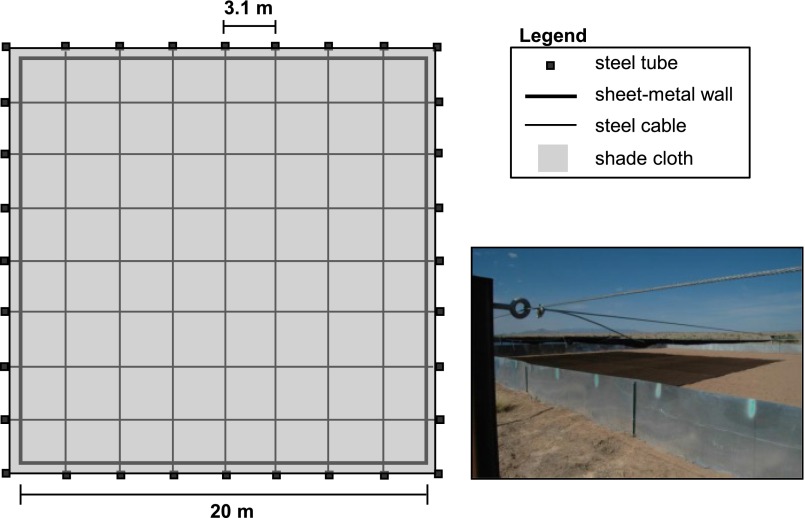
We designed nine thermal arenas to independently manipulate the statistical and spatial distributions of operative temperatures (Fig. S2). These arenas were arranged in a square matrix on a level plateau ∼1 km west of the Sevilleta Field Station. All arenas were oriented east-to-west, such that the sun moved parallel to northern and southern walls. The walls of each arena (20 × 20 m) were constructed from sheet metal (0.5 mm thick), buried 20 cm below the surface and extending 71 cm above the surface. Joints between the adjacent sheets of metal were bolted to metal posts at 10-m intervals. To homogenize the surface within and among arenas, all vegetation was removed, and the substrate was raked. The interior of each wall was painted a flat gray to minimize the reflection of solar radiation near edges.

Fig. S2.

Schematic of an arena and a photograph of an arena with a clumped distribution of thermal resources (one patch).

To manipulate the thermal landscape, each arena was covered by a canopy of shade cloth supported by a scaffold of steel cable. The cables (diameter = 0.4 cm) were fastened to steel tubes (5 cm × 5 cm × 2 m) positioned at regular intervals along the perimeter of the arena. The resulting scaffold supported the canopy at a height of 1.2 m and extended beyond the edge of the arena to prevent solar radiation from entering laterally. The canopy consisted of two superimposed layers designed to manipulate the spatial and statistical distributions of operative temperatures, respectively. The first layer consisted of 16 patches (3 × 3 m) of 80% black knitted shade cloth (Greenhouse Megastore). These patches were distributed spatially within an arena according to one of three designs: 1 large patch (12 × 12 m, consisting of 16 contiguous small patches), 4 medium patches (each 6 × 6 m, consisting of 4 contiguous small patches), or 16 small patches (each 3 × 3 m). Because we had nine arenas, each of these spatial arrangements was replicated three times. Importantly, the total shaded area of this first layer remained constant among arenas, despite the variation in spatial distribution. The second layer was designed to shift the statistical distribution of operative temperatures in some arenas; therefore, this layer consisted of either no cloth (0% shade) or a uniform piece of cloth (30% or 50% shade) that spanned the entire arena. A uniform layer of shade lowered the mean temperature of the ‘sunny’ areas while not affecting the temperatures of the already shaded areas. Further, the unfiroem layer of shade did not affect the spatial distribution of warm and cool patches, although the temperature differences between sunny and shaded patches was reduced in the overall shaded treatments. The nine arenas enabled us to use a factorial combination of the three spatial and three statistical distributions. The levels of these treatments were pseudorandomly assigned to arenas such that each row of arenas within the matrix received all levels of each treatments (Fig. 2).

Measuring Set-Point Temperatures in Artificial Thermal Gradients.

To calculate the accuracy of thermoregulation, we needed to compare the body temperatures of lizards in our thermal arenas to the body temperatures that lizards seek to maintain, usually referred to as preferred temperatures (22). Body temperatures in our arenas were logged automatically by miniature sensors implanted in each lizard (in Measuring Body Temperature in Thermal Arenas). Preferred temperatures were estimated in an artificial thermal gradient before our field experiment.

Artificial thermal gradients consisted of plastic containers (36 × 91 cm) filled with ∼1 cm of sand. A 250-W infrared bulb (Exo-Terra) was suspended above one end of each container. Using rheostats (Exo-Terra), we adjusted the heat generated by the bulbs such that operative temperatures within each container ranged from 23 °C to 45 °C. During measurements, the gradients were illuminated uniformly by fluorescent lights.

After fasting lizards for 24 h, we placed each one in a gradient and gave it the remainder of the day to explore its new environment. At 0700 hours on the next day, fluorescent lights were turned on to stimulate activity. Between 0800 and 1600 hours, body temperatures were recorded every 2 h with a cloacal thermometer (T-4000; Miller & Weber). After the measurement at 1600 hours, each lizard was placed in a clean terrarium to await surgery.

On the same day, we surgically implanted a temperature logger (iBat; Alpha Mach) in the peritoneal cavity of each lizard. Before surgery, the loggers were coated in rubber epoxy and dipped in food-grade paraffin. We recorded the masses of the coated loggers to ensure that each lizard received a logger that was less than 10% of its body mass. The loggers were soaked in 70% ethanol for 1 h before surgery. We anesthetized lizards with isoflurane, which was delivered through a mask attached to a squeeze bottle. Once anesthetized, each lizard was marked for permanent identification by clipping a unique combination of toes. After sterilizing the ventral surface of a lizard, we made small incisions (∼ 1 cm) in the skin and peritoneum of the abdomen. The logger was inserted into the peritoneal cavity, and the incision was closed with sutures and adhesive (Gluture; Abbott Laboratories). After each surgery, the lizard was returned to its terrarium and was monitored until recovery. Generally, lizards recovered consciousness and mobility within 1 h of surgery and accepted food within 48 h.

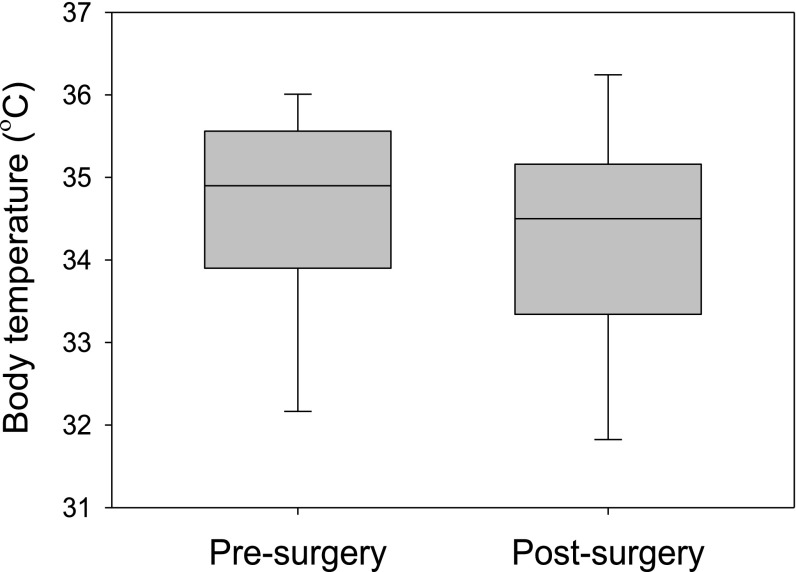
To see whether surgery altered the behaviors of lizards, we remeasured preferred temperatures on the eighth day after surgery (Fig. S3). Two days before this point, we withheld food from the lizards as we did for the measurements before surgery. We used general linear mixed modeling to estimate the effects of surgery (before vs. after) and time (0800–1600 hours) on set-point temperature. Body mass was included as a covariate, and lizard was included as a random factor. We started with a model that included all possible main effects and interactions. We then simplified this model by eliminating the highest-order term and used Akaike’s information criterion (AIC) to judge whether the simpler model described the data better. We repeated the process until further simplification failed to yield a model with a lower value of AIC. Analyses were performed using the nlme library of the R Statistical Package (32). Because median temperatures chosen before and after were nearly identical (Fig. S3), the most likely model excluded the surgical state (pre- vs. postsurgery) as a factor. When interpreting results from our field experiment, we assumed that the preferred range of temperatures equaled the central 50% of mean body temperatures selected after surgery (32.7–34.9 °C; Fig. S4).

Fig. S3.

Lizards preferred a median body temperature between 34 °C and 35 °C before and after surgery. Box and whiskers denote the central 50% and 80% of all measurements of body temperature in an artificial thermal gradient.

Fig. S4.

Distribution of mean body temperatures preferred by lizards was centered around a median of 34 °C. Each datum is the mean body temperature selected by a lizard in an artificial gradient, 1 wk after surgery.

Measuring Body Temperatures in Thermal Arenas.

We used a Latin square design, in which the movements and temperatures of each lizard were recorded in three of the nine arenas. Each lizard was randomly assigned to three arenas with the constraint that it would experience all levels of thermal patchiness (1, 4, and 16 patches of shade in the first layer of the canopy) and all levels of background shade (0%, 30%, and 50% shade in the second layer of the canopy). The order in which lizards experienced these arenas was also randomized.

The same procedure was used for each trial in an experimental arena. A trial lasted 48 h, except in rare cases where precipitation caused us to extend our observations by a day. Lizards were placed in their assigned arena in the afternoon of the first day. At this time, each lizard was provided a wooden shelter covered with sheet of aluminum to reflect solar radiation. Lizards were left undisturbed until the next morning. At ∼0700 hours, we removed the shelters from the arenas, forcing lizards to explore their environment. From that point on, we recorded the operative temperature in full sun and under 80% shade cloth using hollow copper electroforms of lizards (27); temperatures of models were highly correlated with body temperatures of live lizards tethered to a fixed location (range = 27–39 °C; slope = 1.06, intercept = −2.51, R² = 0.96). Body temperatures of lizards in our arenas were recorded every 12 min by the implanted loggers after shelters were removed; because a lizard the size of S. jarrovi has a thermal time constant of ∼5 min, the longer duration between measurements decreased the dependence between samples. To ensure that our arenas presented the same proportions of shade throughout each trial, we analyzed only those body temperatures recorded between two points in the day. The starting point occurred when the sun rose sufficiently to cast an equal area of shade on each arena. The ending point occurred either when one or more patches of shade moved out of the arena or when the minimal temperature in the hottest arena reached 37 °C, which is a few degrees below the critical thermal maximum (33). At this time, we returned the shelters to the arenas and placed each lizard within its shelter. On the third day, we followed the same procedure to generate a second day of observations. At the end of this day, the lizards were removed from the arenas and were returned to the laboratory until their next trial. Arenas were raked between trials to eliminate olfactory cues.

To enhance efficiency, we completed the experiment in two temporal blocks, with each block comprising three sets of nine lizards (n = 54 lizards). Within each block, only one set of lizards occupied the arenas for a given trial, whereas the other sets remained in the laboratory. Because each set occupied the arenas for 48 h at a time, each lizard rested 96 h between successive trials. During this period of rest, lizards had water and food for the first 3 d but were fasted on the fourth day. The entire block of measurements took ∼27–30 d, depending on the weather.

After each block, we surgically removed the temperature loggers from the lizards. The coating was carefully removed from each logger, and the data were downloaded to a computer. Lizards remained in the laboratory for a week following surgery and then were returned to their sites of capture.

Modeling Costs of Thermoregulation.

We used a spatially explicit, individual-based model (detailed by ref. 26) to simulate the thermoregulatory behavior of a 20-g lizard (Fig. 1). This simulation was conducted for several environments that differed in the spatial structure of operative temperatures. Each environment comprised a grid of cells (64 × 64). Operative temperature remained homogeneous within cells but varied among cells. For 25% of the cells, operative temperatures were drawn from a normal distribution with a mean of 34 °C and an SD of 0.5 °C to represent temperatures within an individual’s preferred range. For the remaining 75% of cells, operative temperatures were drawn from a normal distribution with a mean of 45 °C and an SD of 1 °C. Consequently, each grid contained a wide range of operative temperatures offering opportunities for behavioral thermoregulation.

Once operative temperatures were assigned, the cells were arranged into a specific configuration. Preferred microclimates were placed into a number of contiguous patches that summed to the same area: 1 large patch, 4 medium patches, or 16 small patches. These patches were uniformly spaced throughout the grid (Fig. S1). Importantly, all configurations were characterized by the same mean and variance of operative temperature, despite differing in spatial structure. During simulations, grids were tiled such that the spatial configuration of operative temperatures repeated indefinitely through space. The spacing between contiguous patches should determine the energetic cost of thermoregulation, whereas the mean temperature of the environment constrains the accuracy of thermoregulation (because individuals can only attain body temperatures within the range of operative temperatures).

During a simulation, an animal sampled its environment for a microclimate that offered an operative temperature (27) that permitted a body temperature between 32 °C and 36 °C. At the start of a simulation, the animal was placed in a randomly selected position and assigned a body temperature of 34 °C. Every minute, a binomial probability described whether the animal remained in its current position. This probability depended on the animal’s temperature relative to its preferred range of temperatures: p₁, p₂, and p₃ when the animal’s temperature fell within, above, or below its preferred range, respectively. For the simulations summarized in Fig. 1, we chose values of 0.9, 0.1, and 0.1 for p₁, p₂, and p₃, respectively. Note, these probabilities are independent of one another.

When moving, the animal searched for better microclimates within ranges of distances and angles to simulate how an animal might look for a favorable patch when the number of behavioral decisions is limited for any given time period. The distance and angle were drawn from beta and von Mises distributions, respectively. The β function

$$f\left(x|\alpha ,\beta \right)=\frac{\Gamma \left(\alpha +\beta \right)}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{x}^{\alpha -1}{\left(1-x\right)}^{\beta -1}\hspace{0.17em},$$

required two parameters, α and β. This function was multiplied by the maximal distance to determine how far an animal would sample locations. Importantly, some values of α and β yielded a nonzero chance that the animal could sample its current position. We set α and β to 1 and 4, respectively, such that locations were sampled at a higher intensity and a close proximity, up to a maximal distance of 8 cells.

The von Mises function

$$f\left(x|\mu ,\kappa \right)=\frac{e^{x\hspace{0.17em}\text{cos}\left(x-\mu \right)}}{2\pi I_0\left(\kappa \right)},$$

also required two parameters, κ and μ. The parameter κ determines the concentration and range of angles; for instance, when κ = 0, the animal sampled with equal probability over a range of 2π radians, but searches concentrated toward 0 (or straight forward) as κ increased. The parameter μ determined the precise angle with reference to a forward-facing direction. Both μ and κ were set to 0 such that animals oriented straight ahead and searched at any angle between +π or −π radians with equal probability. This behavior mimics the shuttling behavior observed in many animals that thermoregulate by basking. The final term, I₀, equals the modified Bessel function of zero order.

Once a sampling location was determined, the animal evaluated the body temperature that would result from spending 1 min in that location. This body temperature (T_b2) was given by the following equation:

$$T_{b2}=T_e+e^{\left(-\frac{t}{\tau }\right)}\left(T_{b1}-T_e\right),$$

where T_b1 equals the current body temperature, T_e equals the operative temperature, t equals the duration at the T_e (1 min), and τ equals the thermal time constant of the animal. The value of τ depended on the animal’s mass and whether the animal was heating or cooling; we estimated values from equations in ref. 34. Each minute, the animal evaluated 12 locations and chose the one that brought its body temperature closest to 34 °C; when multiple locations would confer the same body temperature, the closest location was chosen.

After determining the animal’s new body temperature, we calculated the energy spent to reach its new location. Energy expenditure was estimated from equations in ref. 35, modified to account for the cost of locomotion. We assume that energy expenditure increased by a factor of 1 + (d/d_max), where d equals the distance moved and d_max equals the maximal distance. Thus, when the animal moved the maximal distance, its metabolic rate doubled. Note, this energetic expenditure includes resting metabolism.

We simulated 60 min of activity for each animal, recording thermoregulatory performance, distance moved, and energy expenditure. One thousand simulations were run for each combination of spatial arrangement and mean operative temperature. For comparison, we simulated 1,000 thermoconforming animals in the same environments. In these simulations, all parameters were the same as they were for our simulations of thermoregulation except that 90% of the time, regardless of body temperature, the animal moved to a new location chosen randomly with respect to operative temperature. For all simulations, we recorded the accuracy of thermoregulation, the distance moved, and the energy expended.

Simulating Body Temperatures of Lizards in Thermal Arenas.

We used our individual-based model (described in Modeling Costs of Thermoregulation) to predict the body temperatures of lizards during our experiment. Because we did not know (a priori) how to parameterize behavioral decisions for S. jarrovi, we used a genetic algorithm (36) to optimize p₁, p₂, p₃, α, β, μ, κ, and d_max (see the section that follows for details). Once we obtained the optimal parameters (Table S1), we simulated the experiment with five lizards in each combination of thermal patchiness (1, 4, and 16 patches) and background shade (0%, 30%, and 50% shade). Although we simulated behavior at an interval of 1 min, body temperatures were recorded every 10 min as we did in our field experiment. Unlike our previous simulations, we imposed a physical boundary around the landscape (i.e., the grid was not tiled) to mimic the walls of our arenas.

Table S1.

Optimal values of parameters for functions that determine searching distances and angles for each strategy

Parameter	Strategy 1	Strategy 2	Strategy 3	Strategy 4
p1	0.779	0.015	0.142	0.019
p2	0.853	0.399	0.809	0.618
p3	0.570	0.709	0.410	0.293
⍺	1.75	4.94	3.79	4.50
β	1.56	4.09	4.25	2.13
μ	0.0	0.0	0.0	0.0
κ	0.185	0.150	0.577	0.649
dmax	31.61	21.33	3.95	21.75
αbelow	—	—	5.76	3.28
βbelow	—	—	2.83	5.74
μbelow	—	—	0.0	0.0
κbelow	—	—	0.0	3.06
dmax,below	—	—	12.42	30.64
αabove	—	—	3.75	5.18
βabove	—	—	1.17	4.25
μabove	—	—	0.0	0.0
κabove	—	—	0.384	5.53
dmax,above	—	—	19.97	30.54

Strategy 1 includes thermally insensitive parameters and is error prone. Strategy 2 includes thermally insensitive parameters is not error prone. Strategy 3 includes thermally sensitive parameters and is error prone. Strategy 4 includes thermally sensitive parameters and is not error prone. For strategies 3 and 4, the initial parameters represent values used when the animal’s body temperature fell within its preferred range.

Because, we did not know how lizards might move in the context of our movement model a priori, we modeled several strategies of thermoregulation, which differed in how lizards perceived and responded to their environments. For all strategies, parameter estimates were optimized with our simple genetic algorithm (Supporting Information) to maximize thermoregulatory performance, i.e., lizards minimized the cumulative deviation between their body temperature and their preferred range (32.7–34.9 °C). For our model optimization, we considered whether parameter estimates were temperature sensitive (or not) and whether lizards were prone to making errors (or not). With respect to thermal sensitivity, we (i) optimized parameters (α, β, μ, κ, d_max) such that parameter estimates were insensitive to body temperature and (ii) optimized the same parameters such that that they were sensitive to body temperatures (i.e., each parameter estimate depended on whether the lizard was below, within, or above the preferred rage of temperatures). With regard to making errors, we either (i) allowed lizards to choose and move to the first location where it’s resulting body temperature would be within its preferred range of body temperatures (up to six decisions, moving randomly if a suitable location could not be found) or (ii) choose six locations and then move to the one with would best allow the lizard to keep its body temperature within or closest to its preferred range. All four possible combinations of thermal sensitivity and error making were run to determine optimal parameter estimates and determine the best fit model to be used to simulate the experiment.

Climate Change and Thermoregulation in Spatially Explicit Landscapes.

To examine how thermal heterogenity affects the performance of organisms in a changing climate, we applied our optimized model of behavioral thermoregulation to simulated landscapes with realistic topographies (Fig. 4). We randomly distributed 200 virtual lizards on each landscape, keeping track of body temperature, movement, and metabolic costs as described for our previous simulations. Each landscape comprised a 100- × 100-m grid with an elevational relief of 5 m and a fractal dimension of 1.6. Twenty-five percent of the landscape was covered with vegetation (80% shade), with fractal dimensions of 1.6 (clumped landscape) and 2.6 (dispersed landscape). Daily climates were reconstructed on a minute-by-minute basis from historical data collected by the East Entrance weather station at Zion National Park. For this exercise, we simulated the 120th day of the year. Although these landscapes experienced the same climates and had the same mean and variance of temperature, individuals starting at different position in the landscape experienced different opportunities for thermoregulation. To appreciate the impacts of thermal heterogeneity on thermoregulatory performance, we also modeled lizards in a uniform landscape that offered individuals access to either sun or shade at any position. The latter scenario equates to conditions frequently assumed by researchers who model the impacts of climate change on activity time and thermoregulatory performance.

Collection and Care of Lizards.

In the summer of 2009, we collected adult males of S. jarrovi (mean SVL = 92 mm) in the Chiricahua Mountains of Arizona, at elevations between 1,500 and 2,500 m. Lizards were brought to the Sevilleta Field Station of the University of New Mexico, where our experiment was conducted. Lizard were housed individually in plastic terraria (30 × 50 cm) lined with paper towels. The floor of each terrarium was heated on one side, such that operative temperatures ranged from 23 °C to 39 °C (determined using hollow copper models of a lizard). Before the experiment, lizards were fed adult crickets (Acheta domestica) and larval beetles (Zophobas morio) daily. Food was coated with a powder containing vitamins and minerals. Lizards were kept under these conditions for at least a week before the experiment began and were returned to these conditions whenever they were not in a thermal arena.

Modeling Operative Temperatures Within Arenas.

To know whether lizards were thermoregulating in the arenas, we needed to estimate the operative temperatures during each trial. Traditionally, operative temperatures would be estimated with hollow copper electroforms that mimic the size, shape, and color of a lizard. However, we were reluctant to place physical models of lizards in the arenas, because these models might have affected the behavior of real lizards. Therefore, we placed miniature temperature loggers, iButton Thermochrons (Maxim Integrated Products), under each combination of shade cloth in the arenas; the thermochrons were painted white to alter the reflective properties. We also placed one copper electroform in the open and another under a piece of shade cloth (80%). The temperatures recorded by the thermochrons and electroforms were used to estimate operative temperatures under all combinations of shade.

First, we related the difference between the temperatures of thermochrons to the difference between the temperatures of electroforms

$${\mathit{L}}_0\mathrm{-}{\mathit{L}}_{80}\mathrm{=}0.930\times \left({\mathit{T}}_0\mathrm{-}{\mathit{T}}_{80}\right),$$

where L₀ and L₈₀ equal the temperatures of electroformed lizards under 0% and 80% shade, respectively, and T₀ and T₈₀ equal temperatures of thermochrons under 0% and 80% shade, respectively. Given the strength of this relationship (r² = 0.966; P < 0.001), the difference between temperature of thermochrons at different shade levels can be used to predict operative temperature at one level of shade levels from operative temperature at another level of shade.

For example, the difference between thermochrons under 30% and 80% shade was strongly related to that between thermochrons at 0% and 80% shade (r² = 0.947; P < 0.001)

$${\mathit{T}}_{30}\mathrm{-}{\mathit{T}}_{80}\mathrm{=}0.627\times \left({\mathit{T}}_0\mathrm{-}{\mathit{T}}_{80}\right),$$

where T₃₀ equals the temperature of a thermochron under 30% shade. Similarly, the difference between thermochrons at 50% and 80% shade was strongly related to the difference between thermochrons at 0% and 80% shade (r² = 0.954; P < 0.001)

$${\mathit{T}}_{50}\mathrm{-}{\mathit{T}}_{80}\mathrm{=}0.494\times \left({\mathit{T}}_0\mathrm{-}{\mathit{T}}_{80}\right),$$

where T₅₀ equals the temperature of a thermochron under 50% shade.

Because the differences are proportional, the following relationships must hold:

$$L_{30}\mathrm{-}{L}_{80}\mathrm{\propto }{\mathit{T}}_{30}\mathrm{-}{\mathit{T}}_{80},$$

or

$${\mathit{L}}_{30}\mathrm{-}{\mathit{L}}_{80}\mathrm{=}0.627\left({\mathit{T}}_0\mathrm{-}{\mathit{T}}_{80}\right).$$

By substitution, we arrive at the following equation:

$${\mathit{L}}_{30}\mathrm{-}{\mathit{L}}_{80}\mathrm{=}0.627\left({\mathit{L}}_0\mathrm{-}{\mathit{L}}_{80}\right)/0.930,$$

or

$${\mathit{L}}_{30}=0.674\left(L_0\mathrm{-}{\mathit{L}}_{80}\right)+{\mathit{L}}_{80}.$$

Using the same logic, we can conclude that

$${\mathit{L}}_{50}\mathrm{-}{\mathit{L}}_{80}\mathrm{\propto }{\mathit{T}}_{50}\mathrm{-}{\mathit{T}}_{80},$$

or

$${\mathit{L}}_{50}\mathrm{-}{\mathit{L}}_{80}=0.494\left({\mathit{T}}_0\mathrm{-}{\mathit{T}}_{80}\right).$$

By substitution, we obtain the following:

$${\mathit{L}}_{50}\mathrm{-}{\mathit{L}}_{80}=0.494\left({\mathit{L}}_0\mathrm{-}{\mathit{L}}_{80}\right)/0.930,$$

or

$${\mathit{L}}_{50}=0.531\left({\mathit{L}}_0\mathrm{-}{L}_{80}\right)+L_{80}.$$

Using these equations, we calculated the operative temperatures of lizards under 30% and 50% shade (L₃₀ and L₅₀, respectively) from our estimates of operative temperatures under 0% and 80% shade (L₀ and L₈₀, respectively).

Optimization of Parameters Using a Genetic Algorithm.

Optimal strategies of behavioral thermoregulation were determined using a genetic algorithm, a population-based method of optimization inspired by the principle of natural selection. Each individual in the population was represented by a real-valued vector, or chromosome, X_n. Each locus of the chromosome corresponded to a parameter, $X_n^P,$ to be optimized for individual n. Thus, the nth individual in the population was described by

$$X_n=\left[x_n^1,x_n^2,\dots ,x_n^p\right],$$

where p equals the number of parameters and $x_n^p$ represents loci along the chromosome. Each individual had a fitness that corresponded to its thermoregulatory performance. As simulated generations passed, the mean fitness of the population increased and the parameters converged on an optimal or near-optimal strategy for the simulated environment. Parameters were optimized for all three levels of dispersion, because we had no a priori reason to believe that one of these landscapes predominates in nature. Simulations were stopped after 12 generations, but parameter values did not change appreciably after five generations.

Parameters for individuals in the population were initialized by Latin hypercube sampling, an efficient and robust method of stratified sampling. For each parameter, the allowable range of values was divided into N intervals, where N was the number of individuals in the population (here, n = 256). A random value in each interval was generated and assigned to an individual such that each interval was sampled once. This procedure was repeated until all individuals possessed values within a unique Latin hypercube of parameter space. Once initialized, all individuals thermoregulated in each thermal environment to determine their initial fitnesses.

Subsequent generations were produced through selection, cross-over, and mutation. All individuals in the population, regardless of fitness, were considered for reproduction. Mating pairs were chosen through k-tournament selection (k = 2), where the individual possessing the phenotype with the highest fitness was designated as the dominant parent. Tournament selection is less prone to premature convergence on a local optimum than are other methods of selection (37). Each mating produced a single offspring, whose genotype depended on the maternal genotypes and the frequency of crossing over. With no crossing over, the offspring inherited the phenotype of the dominant parent. Crossing over between the parental chromosomes occurred with a probability of 0.6 at each locus. Intermediate cross-over for the pth parameter ($x_{offspring}^p$) is given by

$$x_{offspring}^p=x_{parent\hspace{0.17em}1}^p+R\times \left(x_{parent\hspace{0.17em}1}^p-x_{parent\hspace{0.17em}2}^p\right),$$

where R equals a uniformly distributed random number between −1 and 1. If mutated, each locus was considered for uniform neighborhood mutation with a probability of 0.05. The new value of the locus ($x_n^{p\prime }$) was found by

$$x_n^{p\prime }=x_n^p+r_m\times R\times \left(x_n^{p_{upper}}-x_n^{p_{lower}}\right),$$

where R equals a uniformly distributed random number between −0.5 and 0.5, $x_n^{p_{upper}}$ and $x_n^{p_{lower}}$ equal the upper and lower bounds of the pth parameter, and r_m equals the mutation radius. This radius decays over generations

$$r_m=\frac{g_{\max }-g}{g_{\max }}\hspace{0.17em}\times \hspace{0.17em}0.1,$$

where g and g_max equal the current and final generation. After selection, cross-over, and mutation, each locus was checked to ensure a reasonable value within the range for the parameter. The entire procedure was repeated until all individuals in the population were replaced by offspring. Subsequent generations proceeded in the same manner.

Comparing Predicted and Observed Body Temperatures.

We used generalized additive mixed modeling (GAMM) to detect patterns in the observed and simulated body temperatures. To obtain a single variable that characterized the thermal environment of each arena at each time, we used a principal component analysis to generate a linear combination of two highly correlated variables: maximal operative temperature and the range of operative temperatures. The first principle component (PC1) captured 90% of the variation in these thermal variables (Table S2). We then used GAMM to estimate the effects of PC1 (a continuous factor) and dispersion (a fixed factor with three levels) on body temperature (the dependent variable). We analyzed variation in body temperature rather than variation in d_b, a common index of thermoregulatory performance (22). This decision was necessary to obtain a satisfactory fit to the statistical model, because the value of d_b often equals zero (see ref. 38 for details on the problems associated with zero-inflated models). Nevertheless, plots of the fitted models enable one to visualize values of d_b (Fig. 3). To avoid pseudoreplication, the identity of each lizard was included as a random factor. A correlation structure was added to describe variation in body temperature within and among days. Analyses were performed with the mgcv and nlme libraries of R (39).

Table S2.

Principal components describing the covariation between operative environmental temperatures

Variable	PC1	PC2
Maximal operative temperature	0.71	−0.71
Range of operative temperature	0.71	0.71
Eigenvalue	1.80	0.20
% of variance	90.1	9.9
Cumulative	90	100

Because our individual-based model predicted that the variance of body temperature decreases with increasing dispersion (Fig. 1), we used AIC to compare a model with one variance parameter to a model with three variance parameters, one for each level of dispersion: 1, 4, and 16 patches. For both simulated data and observed data, the best model (∆AIC = 0) included three variance parameters. These variances constitute indices of thermoregulatory performance, because large variances of body temperature reflect less inaccurate thermoregulation. The next best models, comprising only a single error term, provided substantially poorer fits to simulated and observed data (ΔAIC = 448 and 34, respectively).

To evaluate our individual-based model, we compared the variances of body temperatures collected in our field experiment to those of body temperatures simulated with the optimal parameterization of the model; the optimal parameterization minimized the simulated variance of body temperature summed for the three landscapes (see above). If our model captures behavioral thermoregulation, the observed data and simulated data should reveal similar patterns of thermoregulatory performance within and among landscapes.