A Tutorial on Pharmacodynamic Scripting Facility in Simcyp

INTRODUCTION

The Simcyp Simulator provides a framework for mechanistic Physiologically‐Based Pharmacokinetic/Pharmacodynamic modeling of potentially interacting drugs. It also provides a scripting facility, using the Lua language, for developing customized pharmacodynamic and toxicity models driven by drug concentrations at the site of action.

We present an overview of the scripting facility including the scripting language, the editor, and how scripts are embedded within the Simulator. Examples incorporating differential equations and including inter‐individual variability on parameters are presented.

BACKGROUND

The Simcyp population‐based Simulator is a widely used platform for predictive simulation of pharmacokinetic/pharmacodynamic (PKPD) parameters and profiles, and drug‐drug interaction (DDI) based largely on the extrapolation of a limited set of physicochemical properties and in vitro experimental data, such as the clearance and transport of a drug by one or more metabolizing enzymes and transporters.1, 2

In a clinical setting, several predictive variable factors, i.e. covariates, may be measured in an individual patient or volunteer and used to improve a PKPD model prediction and describe the observed variability. To incorporate inter‐individual variability, the Simcyp Simulator generates virtual populations of individuals from models incorporating structural correlation of multiple factors (including demographics, genetic and disease status) generating an individual subject with its own set of parameters.1 A more mechanistic simulation approach can incorporate model components that account for and predict individual covariates. The Simcyp Simulator uses such mechanisms benefiting from both “bottom‐up” and “top‐down” paradigms, called by some the “middle out approach”.1, 3

While prediction of PBPK involves a certain level of modeling complexity, the extension of such predictions to PD outcomes requires an even more complex layer. Linking PD to the PBPK model allows the possibility of deriving the response (pharmacological or toxicological) by the organ concentration.

The Simulator provides common empirical and semi‐mechanistic “Built‐In” pharmacometric building‐blocks to ease construction of quite complex models by picking and mixing such building blocks, in a flexible environment, to various input tissue/organ concentrations to drive the response. These built‐in PD models have been described earlier,1 but are defined further here to fully understand the architecture of the environment that includes the scripting features.

Briefly, the architecture of the Simcyp PD module presents a number of different model‐building blocks called PD Response Units (Figure 1). Such units can be linked together to develop more complex responses via certain “transduction” options offered by the platform (for the basics of transduction see4). There are two types of PD Response unit; a PD Basic unit and a PD Link unit.1 The PD Basic unit offers the most commonly used simple response models that include, linear, exponential and sigmoidal/Hill,5 providing an option to link them to an effect compartment. These models can represent a kinetic receptor binding model and be transduced to a stimulus response model in a subsequent PD Basic unit. The PD Link unit includes transform link models, which are simple transforms to convert response to a probability or event count rate, and parameterised link models which include indirect response models6 and survival models.7 The PD Link unit does not include the effect compartment or kinetic receptor binding links as these models are available in the PD Basic unit. PD Response units are subdivided into a sequence of steps with associated model choices from unit input to unit output. Each step calculates values according to a chosen model for that step and passes its result to the next step in the sequence. Applications of linking PBPK and these PD models to predict the impact of genotypic variability, formulation differences, differences in target binding capacity and target site drug concentrations on drug responses and variability have been described previously.8

Figure 1.

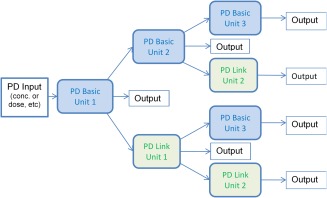
Simcyp PD response unit structure and interconnections enabling various combinations of PD units up to three layers.

Since a Simcyp PD model is linked onto the PBPK simulation model for a specific compound via a chain of response units and each unit comprises a number of built‐in steps in a data flow, this design gives an opportunity for replacing a step within a unit by a custom model (Figure 2). In the same way as for a built‐in model, the custom model connects to its input and passes on its output. By this mechanism, the input of the custom model acts in the same manner as the input into the processing step it replaces, and the custom step output feeds back into the sequence of PD processing step in the same way that the output from the step it replaces would have done. Thus, the flow of the PD units is maintained in a sequential manner. The step replacement is represented by a Step function which substitutes a built‐in function with a user‐scripted function in the Simulator's C++ code. If the PD Custom step is on the first step occurrence in a chain of PD response steps (for example on PD Basic 1), the input to the PD Custom step can be a drug (total or free) concentration or amount in plasma, blood, effect compartment, or any other tissue in the PBPK model. It can be the total dose of the drug, if no PK model is assumed. If the PD Custom step is preceded by one or more PD steps, then the input to the PD Custom step is the output from the preceding step. The output response will be the response in the last step in the PD chain returned by the user, however when the codes contain ODEs, the output will also report all state variable profiles. More than one built‐in step can be replaced by a custom step allowing more than 20 places across the various compound types to be used, however replacing only one step can be enough, depending on the PBPKPD model settings.

Figure 2.

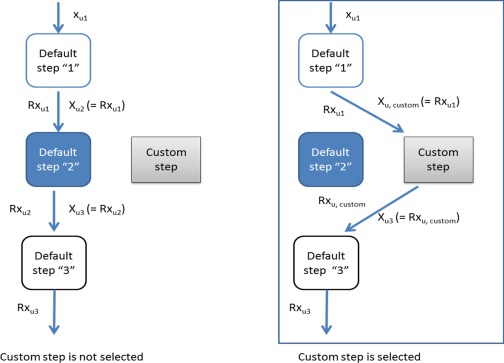
General scheme shows the Custom PD Step within the PD Units Chain. The figure shows how the Custom Step replaces a default PD Step. Each figure block can be equivalent to a single script containing one or more functions. The output function, Rx_u1, from an upstream step “1” is considered as an input function to the PD Custom Step, X_u,custom, while the output from the custom step, Rx_u,custom, is considered as an input function, X_u3, to a subsequent step “3”.

ENVIRONMENT CONSIDERATIONS

The scripting language – Lua

Lua is a high‐level freely available, very lightweight, and flexible scripting language (www.lua.org). It can easily be embedded in other programs with no need to run an external compiler, and scripts are run seamlessly as part of a “live simulation.” Lua is a relatively new language for PKPD scientists and modellers but it has been used extensively, particularly in computer games where very fast script execution is required. While advanced features in the Lua language are very powerful, the basics of Lua are rather easy to learn. There is extensive online documentation (www.lua.org/docs.html). Details of this documentation are beyond the scope of the current paper.

Mathematical functions available in Standard Lua library are supported, for example logarithm, exponential, random distribution … etc. (www.lua.org/manual/5.1/manual.html#5.6). Only functions that are not required or potentially unsafe for the purposes of a modeling script were disabled. In addition to the requirement of valid Lua Syntax in a script, there are additional rules imposed for valid script execution in the Simcyp environment. Most of these are enforceable through a validation tool linked to the script editor; others through limited access provided by Simcyp Lua Library functions; a few by the user interface itself. The scripting editor is based on generic text editing components from the Scintilla project (www.scintilla.org) but is adapted for Simcyp PD scripting.

Simcyp call‐back functions

When a simulation is executed, different branches of the simulator (trial design, population library, and compound library) are initiated in order and connected to generate individual values for the compound and population type under study. The engine then starts to run PKPD calculations and reports the results. A summary scheme of these processes have been provided in the supplementary material (Appendix A).

Within a script, there are named script functions (e.g. “Step” and “Setup” functions) which are called by the Simulator platform at specific points in the simulation. Such functions are generically known to programmers as “call‐back” functions. Simcyp maintains the signatures of these call‐back functions and uses them to give controlled access to inputs and parameters through function arguments and the values to be passed onto as the function's return value. The particular function names are reserved and a particular signature is required for the function to be valid. Coding of Lua scripts is supported by a “Functions” dropdown menu, which provides templates for calls to Simcyp Library functions (calls to Simcyp C++ code available as Lua script functions) as well as function definition templates for user‐coded Lua Setup and Step functions (Figure 3; see also Supplementary Materials for additional functions in the dropdown menu).

Figure 3.

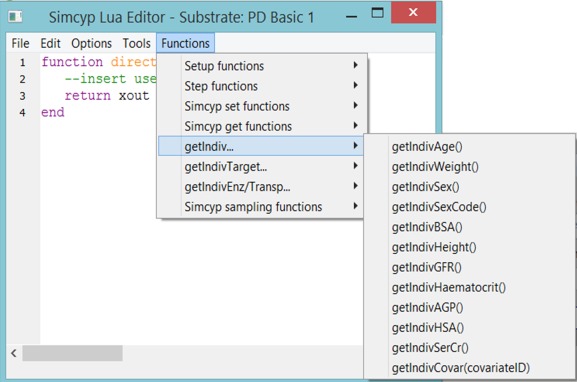
A screenshot of the Simcyp Lua Editor shows the Functions dropdown menu. The expanded menu shows how to access various get functions templates to get individual covariates.

Generally, Setup functions map onto execution of simulation contexts and called once a certain simulation context is reached, where Simcyp Library set and get functions can be used to manipulate data stores (see Figure 4). In order to control the information passage, the Simcyp data store provides four types of storage space to support PD custom scripting, namely: stores for values scoped at the simulation‐population, compound, individual, and individual‐compound data levels with one Setup function corresponding to each scoping level (Figure 4).

Figure 4.

Simcyp datastores for persistence of script variables at the different scoping levels, together with the Setup, Step, and Simcyp library (sc:) functions and Lua code that can access or modify them. Higher level stores can provide default parameters for lower level access when a requested value is not available at the same level as the get call. The set functions typically set store values at the same level as the function call. sc:sampleIIVDistribution generates individual values from the parameter distribution stored at the next higher level.

The Step functions are used to code the model in algebraic or ODE equations. All step functions operate at the individual‐compound specific level. They are called for each individual per active compound and could be for each time point if the model contains ODE. Most step functions have read access to an array of parameters (P) which are individualised model parameters specific to that step for a particular compound type (see the warfarin example below). Details of these functions are available in Simcyp help documentation.

While PBPKPD applications using the Simcyp PD module with customized features have been published,9, 10, 11 the aim of this tutorial is to provide a description of the underlying structure and feature of the scripting environment and to demonstrate a case example of coding a PD model step by step.

Case Examples

Example – Warfarin PD model

The case example presented here is based on the PD response model to warfarin in a Chinese population12 as this model has different coding features. The PK model is not of interest in this tutorial, since the plasma concentration is instead taken from the PBPK model and used as an input to the PD model. The PD model we are interested in here is depicted next:

$$\frac{{dNPT}_{ij}}{dt}=Kin·\left(1-\frac{I_{\text{max}} ·{Cp\left(S\right)}_{ij}}{{mIC}_{50} + {Cp\left(S\right)}_{ij}}\right)-Kout ·{NPT}_{ij}$$

$${INR}_{ij}={INR}_{Base}+ {INR}_{Max}·{\left(1-\frac{{NPT}_{ij}}{{NPT}_0}\right)}^{m\_\gamma }$$

As the equations show, the time course of normal prothrombin (NPT) concentration in response to an increase in the S‐warfarin plasma concentration (Cp(S)) after warfarin administration was described by an indirect model to express the time delay between Cp(S) and NPT, in which NPT synthesis was assumed to be inhibited by the E_max model. NPT_ij represents the NPT in the ith individual at the jth observation, Kin is expressed as Kout multiplied by NPT₀ (baseline NPT before warfarin administration), I_Max is the maximum decrease in NPT concentration assumed to be 1.0 (complete inhibition of NPT synthesis), Cp(S)_ij is the Cp(S) in the ith individual at the jth time point, and IC50 is the Cp(S) that inhibits NPT synthesis at 50% of I_Max.

The time course of international normalized ratio (INR) in response to a decrease in the plasma concentration of NPT after warfarin administration was described based on the percentage inhibition of NPT₀. INR_ij represents the INR in the ith individual at the jth observation, and INR_Base and NPT₀ represent the baseline INR and NPT before warfarin administration, respectively. INR_Max is the maximum INR increase from the baseline, which was set at 5 (the maximum INR_ij was fixed at 6) because the observed maximum INR_ij in 97.3% of the study patients was less than 6. The exponent Gamma ( $\gamma$) accounts for the nonlinear relationship between NPT inhibition and the increase in INR by warfarin and modified by inter‐individual variability in an exponential manner ( $m\_\gamma )$ after centring on the median value of NPT₀ (119 µg/ml).

The model parameter values are:

Cp(S)_ij is the S‐warfarin plasma concentration

NPT₀ (µg/ml) = 118.2 ± 22.1 (mean ± SD)

INR₀ = 1.05 ± 0.10 (mean ± SD)

Kout (1/hr) = 0.0138 (CV=44%)

Kin = Kout · NPT₀

I_max = 1 (fixed)m_IC₅₀= IC₅₀*(2.07 ^ VKORC1), where IC₅₀ (µg/ml) = 0.072 (equivalent to 0.233 µM) (CV =37%) and VKORC1 code was 0 for VKORC1 *2/*2 and 1 otherwise.

INR_Max = 6 (Fixed)

m_Gamma ( $m\_\gamma$) = Gamma * e^(0.005886 * ^{(NPT0 – 119)}, where Gamma = 3.48 (CV=23%).

The Simcyp Lua code of this model is provided in Figure 5. To code this model, one needs functions that define and handle the structural model, define parameters and their distribution and covariate, generate individual values and sampling function. The first function is the popSimSetup function

Figure 5.

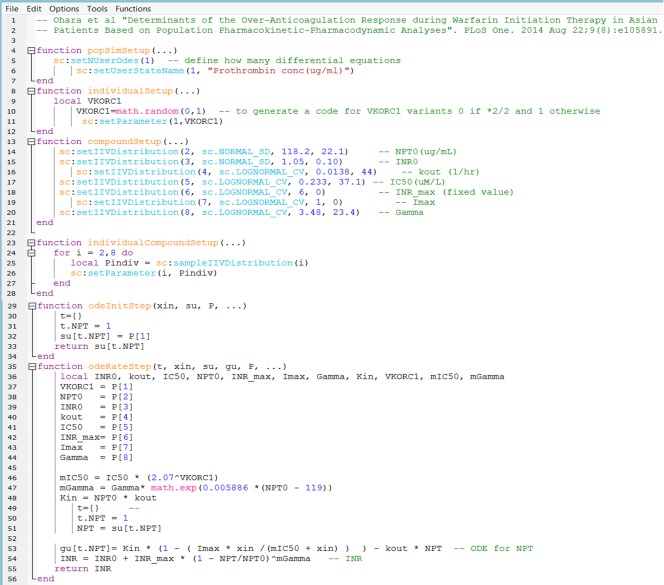
Simcyp Lua code for INR model after warfarin administration (based on Ref. 12).

function popSimSetup(…)

sc:setNUserOdes(1)– define how many differential equations

sc:setUserStateName(1, “Prothrombin conc(µg/ml)”)

end

The popSimSetup function has the widest context. We have defined here the number of ODE in the whole workspace. In our case we have only one ODE for the parent compound. It is recommended to assign values that are kept constant for all compounds and individuals so this function does not need to be called repeatedly at lower level of storage. The second line in our code is to label the state variable, but other parameters, including covariates, can be labelled here as well. The popSimSetup function operates at the population and simulation level and is called only once per simulation. Iteration through all active scripts for a call to popSimSetup will occur in order of compound (i.e., substrate then inhibitors then metabolites) and step sequence within compound.

Next, we need to start coding on either an individual or compound level. We will start with coding individual level and then compound level information. However, the reverse is also permitted. The function that writes on individual level is called individualSetup function as below:

function individualSetup(…)

local VKORC1

VKORC1=math.random(0,1)

sc:setParameter(1,VKORC1)

end

We have coded here a covariate that was found to affect IC50. The code for this covariate is either 1 or 0 for each individual (VKORC1*2 rs9923231 (−1639 G>A). Carriers of this allele will have a code of 0 (see the original model)). Therefore we have to declare this variable as local and use a Lua standard function math.random(lower, upper) to generate an individual value for this categorical covariate. For sake of code simplicity, here we have assumed 50% of the population have the code 1 and 50% have the code 0, but other frequency can be coded. The individualSetup function is called once for each individual subject to assign individual parameter values. We have used this function to set up a covariate (other examples of using Simcyp covariates are given in the Survival example in Appendix B). In the last line of the step function we used a set function to store and index this parameter. This is the first parameter in our model.

Now, we need to code compound parameters with their distribution types on the compound level. The function that writes to that level is called compoundSetup function. This function is called once for each active compound per response step combination in the following order; substrate, then inhibitors, then metabolites.

function compoundSetup(…)

sc:setIIVDistribution(2, sc.NORMAL_SD, 118.2, 22.1) – NPT0 (µg/mL)

sc:setIIVDistribution(3, sc.NORMAL_SD, 1.05, 0.10) – INR0

sc:setIIVDistribution(4, sc.LOGNORMAL_CV, 0.0138, 44) – kout (1/hr)

sc:setIIVDistribution(5, sc.LOGNORMAL_CV, 0.233, 37.1) – IC50(µM/L)

sc:setIIVDistribution(6, sc.LOGNORMAL_CV, 6, 0) — INR_max

sc:setIIVDistribution(7,sc.LOGNORMAL_CV, 1, 0) – Imax

sc:setIIVDistribution(8, sc.LOGNORMAL_CV, 3.48, 23.4) – Gamma

end

We have an arithmetic mean and SD for INPT₀ and INR₀ as baseline before administration of warfarin. We will code them as parameters that have normal distribution with the reported mean and SD. For the rest of the parameter a lognormal distribution with CV was assumed. More details on the distribution are given later in this tutorial. The input to the PD model is the total plasma concentration of S‐warfarin. The simulator takes PD input as total or free concentration or total amount in molar units. Since the input concentration is in µM, the IC50 is changed from µg/ml to µM. We have started indexing these parameters from 2, because we have already the first index for VKORC1. Please note that INR_max and Imax were fixed, therefore they will not have any CV.

After defining the compound parameters and their distribution types, we need in the next step to sample from these distribution types and assign parameter values to each individual. To do this we need to use a function called individualCompoundSetup function. This function operates at the individual‐compound level and is called once for each individual per active compound and response step combination. Values which depend on both compound type and individual, for example an individual clearance value of a drug, can be manipulated here.

function individualCompoundSetup(…)

for i = 2,8 do

local Pindiv = sc:sampleIIVDistribution(i)

sc:setParameter(i, Pindiv)

end

end

In our model we have sampled for the seven parameters, indexed previously under CompoundSetup function, using the distribution associated to each of them and we pass individual values down to the lowest level “step” function to be used for the calculation. We have one differential equation with initial condition and one algebraic function. We will start coding the initial condition for the NPT parameter using a function called odeInitStep function. This function can be ignored if the initial condition is zero, otherwise it is required. Here we simply can write it as:

function odeInitStep(xin, su, P, …)

su[1] = P[2]

return su[1]

end

The table type in Lua implements associative arrays that can be indexed not only with numbers, but also with strings or any other value of the language, except nil. Therefore to make the code clearer we can use names instead of numbers by constructing a table and assigning it to a variable “t” as below:

function odeInitStep(xin, su, P, …)

t={}

t.NPT = 1

su[t.NPT] = P[1]

return su[t.NPT]

end

The su is a reference to arrays or associative arrays representing a reserved block of user state variables reserved by Simcyp.

After coding the initial condition, we can now code the block of differential equations using a function called odeRateStep (t, xin, su, gu, P, …) function. This is similar to using the ODE block in other software such as $DES in NONMEM or $DIFF in WinNonlin. The argument xin and the returned value, represent respectively the input (e.g. drug concentration or amount from the PBPK model, such as unbound concentration in the liver or kidney). In our example xin represents total plasma concentration of S‐warfarin. The argument P is a reference to a generic input parameter array. The su and gu are references to arrays or associative arrays representing a reserved block of user state and user gradient variables reserved by Simcyp by subscripting, so gu[1] and gu[2] will correspond to su[1] and su[2]. Alternatively, names can be used instead of numbers as shown earlier.

The variables used within the scope of this function will be declared as local. In our example, the IC50 is assumed to be dependent on individual VKORC1 variant and Gamma is influenced by individual NPT values, according to the original code. The math.exp expression is the Lua standard library function for exponent.

function odeRateStep(t, xin, su, gu, P, …)

local INR0, kout, IC50, NPT0, INR_max, Imax, Gamma, Kin, VKORC1

NPT0 = P[1]

INR0 = P[2]

kout = P[3]

IC50 = P[4]

INR_max = P[5]

Imax = P[6]

Gamma = P[7]

VKORC1 = P[8]

mIC50 = IC50 * (2.07 ^VKORC1)

mGamma = Gamma* math.exp(0.005886 *(NPT0 ‐ 119))

Kin = NPT0 * kout

t={}

t.NPT = 1

NPT = su[t.NPT]

gu[t.NPT]= Kin*(1‐(Imax * xin/(mIC50 + xin))) ‐ kout* NPT

INR = INR0 + INR_max * (1 ‐ NPT/NPT0)^mGamma

return INR

end

Currently, up to 25 ODEs can be coded in all activated custom models. The user needs to make sure that the correct indices or names are used by each script. Another code example for this function is given in the viral model code example (Appendix C). The total number of user ODEs should be set up at the start of a simulation via a sc:setNUserOdes(number) call within the popSimSetup function. The odeRateStep may also contain simple algebraic formulae assigned to other local variables.

It is also possible to directly access the ODE state variables like substrate or inhibitor concentration. Therefore it is possible to connect/combine the impact of different compounds, for instance, metabolite and the parent compounds (substrate or inhibitor) simultaneously.

If the scripted model does not contain ODEs, such as simple linear or E_max models, then one can select a different Step function from the Function dropdown menu called directAlgebraicStep(xin, P, …) function (see example below). Indirect PD models6 or survival models7 in their algebraic forms can be coded using a different function called indirectAlgebraicStep(t, xin, P, …) function to use the simulation time (t) as the independent variable. A code example of this function is given for a survival model in Appendix B in the supplementary document.

So far we have clarified the concept of the Setup and Step functions of the Simcyp Lua script and we have seen many Simcyp Library Functions such as set functions and some for distribution functions without providing details of their roles. These will be discussed below before we go to the next examples.

Simcyp library script functions

The Simcyp Library consists of a number of Lua function calls (prefixed by sc:) implemented within the Simcyp C++ code, as well as some pre‐supplied named values (prefixed by sc.) for use as function arguments. These facilities allow and control the passing of information between the Simcyp simulator and Lua scripts, and are one of three main types.

1. Simcyp set functions (to set/write values e.g., sc:setParameter)

2. Simcyp get functions (to get/read stored values e.g., sc:getIndivAge)

3. Simcyp sampling functions (to sample from a random distribution, e.g., sc:sampleRandomDistribution)

The sc:set functions: Most custom Step functions have read‐only access to an array of individual parameters P specific to the step model for a given compound. Lua code in Setup functions may define model parameter values and store a value in P with the sc:setParameter (index, value) function as we did for the VKORC1 variable. Then the stored value can be retrieved with sc:getParameter(index)function. For additional examples see the survival model code (Appendix B). Such sc:set functions store values at the same scoping level as the function within which they occur (Figure 4). The sc:get functions try the same level and if the parameter information is not found, go to the next higher scoping level to find the information.

Some sc:set functions need a value only as argument such as the one we used at the top of the code for setting the total number of ODEs in the simulation. At the same place we used a function to label the state variable and other parameters, if we wish to do so. For example:

function popSimSetup(…)

sc:setNUserOdes(1) – define how many differential equations

sc:setUserStateName(1, “Prothrombin conc(µg/ml)”)

sc:setParameterName(1, “VKORC1”)

sc:setParameterName(2, “NPT0”)

end

Additional code examples are given in the supplementary material (Appendices B & C). Parameter labels are stored and used for the output of inter‐individual variability distributions and individual values.

The sc : get functions: This function can be used to retrieve any values stored temporarily for the current script or can be used to call any covariates within the Simcyp Population Library. The Simcyp Library provides read only access to different covariates generated as part of its virtual population to obtain an individual value by calling one of many sc:get functions, such as sc:getIndivAge(), sc:getIndivEnzCovar(), sc:getIndivWeight(), sc:getIndivSexCode() from a setup or step function. A code example for using these functions is given in the next example as well as in the supplementary document (Appendix B). The range of covariates includes demographic and physiological details amongst enzyme/transporter/receptor phenotypes, abundances, and turnover. The drop‐down menus shown in Figure 3 give an idea of the range of covariates available. The advantage of accessing covariates assigned as part of the PBPK model is that a covariate that is also used by the PD model will be given the same value for the same individual as is used in the PBPK model.

The set function can be used to allocate extra storage. Extra storage is provided at the simulation‐population level (Xtra) and at the individual (IndivXtra) levels through the sc:setXtra(index, value) and sc:setIndivXtra (index, value) function, respectively. The extra storage allows additional values or variables to be set and stored for later use independent of the step function. Information for different compounds may be stored at different indices. Both individualSetup, individualCompoundSetup functions write to indivXtra storage, while compoundSetup and popSimSetup functions write to Xtra storage (Figure 4). Read access is possible for Xtra at all levels with sc:getXtra(index), but indivXtra is readable only for the same individual through sc:getIndivXtra(index) in individualSetup, individualCompoundSetup and Step functions as different individuals may be simulated on different execution threads. More examples are in the Survival code (Appendix B).

In our warfarin example, different parameters for an inter‐individual statistical distribution that is used to generate individual P values were set up with sc:setIIVDistr(parameterIndex, distrName, mean, dispersion). This will be discussed below under the Random Distributions and Parameter Dispersion section.

Random distributions and parameter dispersion

Currently, there are five types of predefined random distributions available for PD Custom scripting which are selectable from the editor menu, namely lognormal (mean, CV %), converted lognormal (meanln, sdln), normal (mean, SD), zero truncated normal (mean, CV), and uniform (min, max). A distribution for inter‐individual variability of model parameters can be specified through the function sc:setIIVDistr(parameterIndex, distrName, mean, dispersion) in the compound setup function. We have previously defined in the warfarin model two types of distribution, normal and lognormal. Then in individualSetup function, there was a call via sc:sampleIIVDistr(parameterIndex) to sample from that distribution. The individual value is passed as argument P[index] to a step function.

Alternatively, a user can sample from any of the aforementioned distribution types via the library function sc:sampleRandomDistribution(distrName, mean, dispersion) without reference to a step‐model parameter. Such calls will use the same pseudorandom number generator coded within Simcyp as the sampleIIVDistribution function but the value can be assigned and used however the user intends, not necessarily for inter‐individual variability.

A Simcyp simulation runs with a particular pseudorandom number generator type. Currently, a user may select from a linear congruential generator13 or a Mersenne Twister generator14 with a master seed fixed by a user or system‐set from a clock time. This initial sequence will however be used to seed several other generators so that parallel individual simulations can proceed independently. PD simulation of an individual is also set up with a generator seeded with very large offset from the original PK generator. This approach maintains repeatability of various random elements of a simulation from a fixed seed even when some elements in a model have changed. Calls to Simcyp Library distribution functions will insert calls in the pseudorandom number generators specific to the PD context in which the script is placed, but will not change the random number sequences of purely PK – based sampling.

A user also has the option of generating random distributions using facilities in the Lua standard library for accessing the American National Standards Institute (ANSI) standard C library (uniform) random number generator, notably the math.random, math.randomseed functions. Since such calls are independently seeded, there is no direct reference to any built‐in Simcyp pseudorandom sequence. Thus, the user will have to consider carefully the effect of calls from multiple scripts.

Example ‐ E_max model

This example shows a simple pharmacodynamic model commonly known as the E_max model, subtracted from a baseline response, and inserted into a typical nonlinear mixed effects population model. Let us code a subtractive E_max model from a baseline that is age‐dependent in Simcyp using Lua script that is structurally equivalent to a NONMEM code in NMTRAN (shown below).

$PROB PD_E_MAX MODEL WITH AGE AS A COVARIATE ON BASELINE

$INPUT ID TIME CONC RESP=DV AGE WT

$DATA E_MAX_PD.txt IGNORE=#

$PRED

TVE0 = THETA(1) ‐ THETA(4)*(AGE‐45)

E0 = TVE0 + ETA(1)

EC50=THETA(2)*EXP(ETA(2))

E_MAX=THETA(3)*(1+ETA(3))

RESPONSE = E0 ‐ (E_MAX * CONC/(EC50 + CONC))

Y = RESPONSE + EPS(1)

$THETA 50, 7, 15, 0.1

$OMEGA 5, 0.1, 1

$SIGMA 1

$SIMULATION

The concentration used as the PD input is not defined here, however it can come from the PK model section or as part of the data set file.

Pharmacometricians familiar with NONMEM NM‐TRAN terminology will recognize this code as defining a nonlinear effects model through a set of structural parameters (the THETA's) modulated by certain independent normal random variables (the ETA's) representing inter‐individual variability; with structural parameter values given in a $THETA block and (diagonal) elements of the random variable's covariance matrix given in a $OMEGA block. Adding ETA(1) to THETA(1) thus makes the E0 parameter normally distributed, and multiplication of THETA(2) by EXP(ETA(2)) makes the EC50 parameter lognormally distributed. The prediction includes an added residual random error represented by an (EPS‐ilon) and another standard normal variable with a fixed variance defined in the $SIGMA block.

An equivalent PD model can be scripted in Lua, whereby the PD model parameter (labelled E0, EC50, E_max ‐ parameters specific to a compound) and their associated inter‐individual random distribution are defined in a compoundSetup function. Similar to the previous example, the Simcyp Simulator can be told to sample individual values from each such distribution in an individualCompoundSetup function and save the individual values appropriately in the underlying Simcyp datastore. The individual values will then be available to a parameterised step function as elements of parameter array P.

function compoundSetup(…)

sc:setIIVDistribution(1, sc.NORMAL_SD, 100, 5) – E0

sc:setIIVDistribution(2, sc.LOGNORMAL_CV, 7, 4) – EC50

sc:setIIVDistribution(3, sc.NORMAL_SD, 45, 0) – E_max

sc:setIIVDistribution(4, sc.NORMAL_SD, 0.1, 0) – effect of age

sc:setIIVDistribution(5, sc.NORMAL_SD, 0, 1) – used as ETA

end

function individualCompoundSetup(…)

for i=1,5 do

localP_indi = sc:sampleIIVDistribution(i)

sc:setParameter(i, P_indi)

end

end

function directAlgebraicStep(xin, P, …) local E0, EC50, E_MAX, CONC, AGEF, E0_AGE, EPS_1

E0 = P[1]

EC50 = P[2]

E_MAX = P[3] * (1+ P[5])

AGEF = P[4]*(sc:getIndivAge() ‐ 45) – effect of age on baseline response

CONC = xin – PD input (conc in the X (tissue) compartment)

EPS_1 = sc:sampleRandomDistribution(sc.NORMAL_SD, 0, 1) – to add residual error

E0_AGE = E0 ‐ AGEF

RESPONSE = E0_AGE ‐ (CONC * E_MAX/(CONC + EC50)) ‐ ‐ response model

Y = RESPONSE + EPS_1 ‐ ‐ overall response

end

A residual variability (as in NM‐TRAN for EPS/SIGMA) can alternatively be added through a Simcyp Trial Design built‐in facility. The Trial Design input screens include a feature called “Analytical error” where this additive (or other) error term can be entered as the standard deviation rather than variance.

Another example of Simcyp PD Custom scripting has already been published in this journal as part of an investigation of factors affecting response to the drug rosuvastatin.9 That study involved investigation of the role of OATP1B1 transporter phenotypes on the change in cholesterol synthesis rate using a scripted indirect PKPD response model incorporating a circadian rhythm. Details of the code are included in that publication's Supplementary Material.

Many additional examples of scripts are pre‐supplied and available upon installation of the Simcyp Simulator. These examples allow users to become familiar with the scripting language, Syntax and provide a basis for users to modify the script.

Additional examples that show different elements of the code such as antiviral and survival models where a user can add individual covariates or enzyme phenotypes, or use the extra storage options, are provided in the supplementary document.

The model parameter distributions are not correlated by default; however the user can code the correlation. An example of Simcyp Lua script for bivariate normal distribution is provided in the supplementary document (Appendix D).

REMARKS AND FUTURE GOALS

The first implementation of this scripting facility has focused on supporting the simulation of custom PD models using the scripting language Lua. Several well‐known PKPD software applications have their own coding language using named blocks of code which are selected and executed as determined by the software, for examples DIFF or $DES respectively for differential equations in PKPD software WinNonlin (http://www.certara.com) or NONMEM (http://www.iconplc.com). In some cases, the application provides flags for user code to test for a particular context and so conditionally executes a user code section. For example, a user may wish to perform specific tasks once in the whole simulation or assign specific parameters to each individual. The NONMEM population modeling program, when used with its PREDPP Population Pharmacokinetic library, calls user code represented say by a $PK block in the associated NMTRAN control file to define algebraic equations for a PK model prediction, and supplies a value to the NEWIND flag that differentiates a first overall call from a first subsequent call for a new individual. Simcyp also recognises these two different contexts, and defines specific Lua setup functions for each, namely: popSimSetup for once‐per‐overall‐simulation execution and individualSetup executed once‐per‐each‐individual. Lua variables are places that store values and are by default global in a script. They may however be declared local to a particular function with the local keyword. It is good practise to declare variable local to scope them within their relevant block. Unlike global variables, local variables have their scope limited and a short lifetime to the block where they are declared. As shown in the examples, the Simcyp Library includes a number of sc:set functions to store variables within the C++ application across different script calls and sc:get functions to access them.

Parameter estimation facilities have not as yet been extended to include custom‐scripted parameters. Nevertheless parameter estimation can still be used for built‐in PKPD model parameters when a user script is part of the model. Furthermore, a freely available R library package has recently been developed to enable a user to run Simcyp directly from the R environment, commonly used for statistical scripting (a similar interfacing facility has been developed for the Matlab environment).15 This will allow further manipulation of Simcyp parameters from these computing platforms and so could potentially be used for fitting Lua‐coded models as well.

The current Simcyp architecture of PD response chains allows the replacement of built‐in models seamlessly and is in principle expandable to more complex networks of response units. Feedback of drug response on some physiological and biological parameters like gastric pH have been enabled.

Recently, the Simcyp Lua scripting features have been extended to allow the user to modify individual age‐height‐weight covariance relationships in the demographics section as part of the population library that generates virtual individuals. This is potentially useful if the user wants to define these covariates differently for a special population of interest, such as for a new disease or a particular obesity profile.

Lua custom scripts may also help in the sharing of model components with external model repositories as part of an enhanced interoperability capability. For example Innovative Medicines Initiative's DDMoRe project (www.ddmore.eu) has been developing a repository of annotated PD‐related disease models, elements of which might be translated into Lua scripts. A command line console has been added which supports the DDMoRe Project Interoperability Framework. This new functionality allows DDMoRe partners with a Simcyp Simulator license to run simulations in scripted workflows with other software such as NONMEM and PSN, Monolix, PFIM, and PopED using PharmML.16 Further, the console allows use of the Simulator's databases of populations, compounds, and PBPK models through other platforms such as Matlab and R.

CONCLUSIONS

A scripting facility for customising PD response models within the Simcyp Simulator has been developed, whereby a user can replace the built‐in model for a given PD step with a script using a dedicated editor. The editor supplies a library of Simcyp functions for storing variables in the Simulator and for accessing or manipulating elements of the PK and PD simulation. In addition it facilitates the implementation of complex PD models defined using ODEs with limited computational overheads. Further, the Simcyp platform handles the compilation of the Lua code allowing less experienced users to access advanced modeling capabilities.

Abbreviations

ADME

Absorption Distribution Metabolism and Excretion

ANSI

American National Standards Institute

DDI

Drug‐Drug Interaction

gu

Time‐gradient of a user‐state variable in the Custom differential equation model

GUI

Graphical User Interface

NONMEM

Nonlinear Mixed Effects Modeling software

NMTRAN

NONMEM Translator

ODE

Ordinary Differential Equation

P

Array of parameter for a Response Model

PREDPP

NONMEM PRED Population PharmacokiNetics subroutine library

PBPKPD

Physiologically Based Pharmacokinetic/Dynamic [model]

PD

Pharmacodynamic

PK

pharmacokinetic

PKPD

Pharmacokinetic‐Pharmacodynamic

R_X

Response as input: terminology to identify a PD response in a chain of transduction/link processing as an input in the current context

R_y

Response as output: terminology to identify a PD response in a chain of transduction/link processing as an input in the current context

su

A (user‐) state variable in the custom PD ordinary differential equation model

X

General input

x_in

Incoming functions into a PD step. (x_{in , custom} in case of custom PD model input)

x_out

 = leaving functions into a PD step (x_{out , custom} in case of custom PD model input).

Supporting information

Supporting Information

Supporting Information