Levofloxacin‐Induced QTc Prolongation Depends on the Time of Drug Administration

Abstract

Understanding the factors influencing a drug's potential to prolong the QTc interval on an electrocardiogram is essential for the correct evaluation of its safety profile. To explore the effect of dosing time on drug‐induced QTc prolongation, a randomized, crossover, clinical trial was conducted in which 12 healthy male subjects received levofloxacin at 02:00, 06:00, 10:00, 14:00, 18:00, and 22:00. Using a pharmacokinetic‐pharmacodynamic (PK‐PD) modeling approach to account for variations in PKs, heart rate, and daily variation in baseline QT, we find that the concentration‐QT relationship shows a 24‐hour sinusoidal rhythm. Simulations show that the extent of levofloxacin‐induced QT prolongation depends on dosing time, with the largest effect at 14:00 (1.73 (95% prediction interval: 1.56–1.90) ms per mg/L) and the smallest effect at 06:00 (−0.04 (−0.19 to 0.12) ms per mg/L). These results suggest that a 24‐hour variation in the concentration‐QT relationship could be a potentially confounding factor in the assessment of drug‐induced QTc prolongation.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ The propensity of new drugs to prolong the QTc interval is typically assessed in a clinical trial in which drug administration occurs at a fixed time of the day. Many factors, including time of day, may influence the relationship between the concentration of a drug and the extent of QTc prolongation.

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ The objective of this study was to investigate the effect of dosing time on the extent of levofloxacin‐induced QTc prolongation.

• WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ The relationship between the levofloxacin concentration and the extent of QTc prolongation varies systematically over the course of the day. Dosing time is a potentially confounding factor in the assessment of drug‐induced QTc prolongation.

• HOW THIS MIGHT CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR CLINICAL THERAPEUTICS

☑ To accurately assess a drug's effect on the QTc interval, an approach is required that takes into account the time of drug administration.

Over the past decades, several noncardiac drugs have been withdrawn from the market or their use has been restricted because of their propensity to delay ventricular repolarization.1 This potentially serious side effect is manifested as a prolonged heart rate‐corrected QT (QTc) interval on the electrocardiogram (ECG). The most common mechanism by which drugs cause QTc prolongation is through blockade of the hERG channel, a potassium channel that underlies the rapid component of the delayed rectifier potassium current (I_Kr) in cardiomyocytes.2 Reduced I_Kr delays cardiac repolarization and, often in combination with other predisposing factors, such as genetic polymorphisms or hypokalemia, may lead to the occurrence of early afterdepolarizations and Torsades de Pointes.3

Much effort has been put into the identification of the different sources of variability that affect the extent of drug‐induced QTc prolongation, including gender, age, ethnicity, comorbidity, and comedication.4 Moreover, it is well known that the baseline QTc interval shows 24‐hour variation.5, 6 Based on the 24‐hour variations in various physiological processes, such as serum potassium levels7 and cardiac ion channel expression,8, 9, 10, 11 it has also been suggested that the magnitude of the effect of a drug on the QTc interval may depend on the time of day.12, 13 However, this hypothesis has not been investigated directly. In fact, current approaches to evaluate drug‐induced QT prolongation during drug development include one time‐point of drug administration and exclude night‐time recordings,14 thereby relying on the implicit assumption that delayed ventricular repolarization does not depend on dosing time.

To test this assumption, we investigated whether the sensitivity to drug‐induced QTc prolongation varies during the 24‐hour period, using levofloxacin as a model compound. Levofloxacin is a fluoroquinolone antibiotic that blocks hERG channels.15, 16 Causing a slight but significant prolongation of the QTc interval,17, 18, 19 it was shown previously that levofloxacin can be used as a positive comparator in thorough‐QT (TQT) studies.17 In this study, we used pharmacokinetic‐pharmacodynamic (PK‐PD) modeling to characterize the relationship between levofloxacin concentration and the extent of QTc prolongation after oral administration to 12 healthy male subjects at six different time‐points during the day and night.

METHODS

Study design

Data used for model development were obtained from a clinical trial that was described previously.20 Briefly, 67 occasions were completed by 12 healthy subjects (10 subjects completed 6 occasions, 1 subject completed 3 occasions, and 1 subject completed 4 occasions). In each occasion, the subjects received an oral dose of 1,000 mg levofloxacin (Aurobindo Pharma B.V., Zwijndrecht, The Netherlands) at a different time of day (t = 0 at 02:00, 06:00, 10:00, 14:00, 18:00, and 22:00). The occasions were separated by at least 1 week and each subject was randomly allocated to a sequence of dosing times. Subjects fasted from t = −2 hours until t = 6 hours. At t = 6 hours and t = 10 hours, subjects were allowed to eat a maximum of four slices of bread and a small snack, respectively. Twelve‐lead ECGs were recorded at t = 0, 0.5, 1, 1.5, 2, 2.5, 3, 4, 6, 8, and 12 hours after dosing using a Marquette MAC 5500 (GE Healthcare, Milwaukee, WI) and stored using the MUSE Cardiology Information System (GE Healthcare). The ECG parameters (RR and QT intervals) were calculated automatically and each ECG recording was manually reviewed by a physician. Blood samples to measure levofloxacin and potassium concentrations were drawn via an indwelling intravenous catheter immediately after each ECG recording and at t = 5 and 10 hours. The concentration of levofloxacin in these samples was analyzed by a liquid chromatography mass spectrometry method.20 The study was approved by the Medical Ethics Committee of the Leiden University Medical Centre and registered in the European Clinical Trials Database (EudraCT Number: 2013‐001976‐39). All subjects gave written informed consent before the study.

Data exploration

For data exploration, drug concentrations, and the change from the pre‐dose QT interval, corrected for heart rate by the Fridericia formula (ΔQTcF), was stratified by time of drug administration and plotted over time as mean and 95% confidence intervals. The relationship between observed levofloxacin concentrations in plasma and ΔQTcF was also stratified by dosing time. Linear mixed effects modeling to assess this relationship was performed with the NLME package (version 3.1.118) in R (version 3.1.221), using ΔQTcF as the dependent variable, drug concentration, and dosing time as fixed effects (including interaction) and subject as random effect.

Pharmacodynamic modeling

Population modeling was performed using NONMEM version 7.3 (Icon PLC, Dublin, Ireland).22 R, Pirana (version 2.8.2), PsN (version 3.7.6), and Xpose (version 4) were used for evaluation and graphical representation of the models.23 First‐order conditional estimation with interaction was used throughout the analysis and interindividual variability (IIV) and interoccasional variability (IOV) in model parameters were assumed to be log‐normally distributed. Additive and proportional error structures were considered to describe the residual error. A sequential modeling approach was used: first, a baseline model was developed based on the pre‐dose QT data; second, the concentration‐effect relationship was modeled using pre‐ and post‐dose QT data.

Baseline model

To describe the relationship between the QT and RR interval as well as potential 24‐hour variation in the QT interval in the absence of levofloxacin, a baseline model was developed, as described previously,24 using Eq. (1).

$$Q{T}_{baseline}(t)=Q{T}_0\hspace{0.17em}\text{*}\hspace{0.17em}R{R}^{\alpha }+{\displaystyle \sum }_{n=1}^N\left[A_n\text{*}\cos (\frac{2\pi \text{*}n\text{*}\left(t-{\phi }_n\right)}{24})\right]$$ (1)

where QT₀ represents the intercept of the QT‐RR relationship in ms, RR is the observed RR interval in s, α is the correction factor for RR, N is the total number of harmonics included in the model, A_n is the amplitude of the 24‐hour variation of the nth harmonic in ms, φ_n is the acrophase (time of peak) of the nth harmonic in hours after midnight, and t is the time of the observation in hours after midnight. The number of harmonic terms was determined by the criteria for statistical significance, as explained below. Because sleep may affect the QT‐RR relationship,6, 25 the use of a separate value of α during sleep (between 23:30 and 07:30) was investigated. A linear mixed effects model (as described above) was used to investigate whether the α estimated by the final baseline model adequately removed the dependency of the QTc interval on RR, using QTc as the dependent variable, RR as fixed effect, and interaction between dosing time and RR, and subject as random effect.

Drug effect model

The concentration‐dependency of QTc (PD) and the temporal relationship between PK and PD effects was modeled using the pre‐ and post‐dose ECG recordings. Individual PK parameters were fixed to their estimates from a previously reported population PK model20 and used to predict individual concentration‐time profiles for PK‐PD modeling. Briefly, the PK model was a one‐compartment model with one transit compartment to describe the absorption phase. The transit rate constant was equalized to the absorption rate constant, which both showed 24‐hour variation that was modeled as a cosine function with a fixed period of 24 hours.

Throughout development of the drug‐effect model, the fixed‐effect estimates of QT₀, α, A, and φ were fixed to the values obtained in the baseline model, whereas the concentration‐effect parameters as well as IIV and IOV were estimated. Initially, a linear model was appended to the baseline model shown in Eq. (1) to describe the concentration‐effect relationship as follows:

$$QT\left(t\right)={QT}_{baseline}\left(t\right)+Slope*C$$ (2)

where ${QT}_{baseline}\left(t\right)$ is the model described in Eq. (1), slope is a linear term to describe the concentration‐QT relationship (in ms per mg/L), and C is the levofloxacin concentration in plasma (in mg/L). Because it has been reported that a 1,000 mg oral dose of levofloxacin may transiently increase heart rate,17, 26 which could affect the relationship between the QT and RR interval, inclusion of a separate α for off‐ and on‐drug data was considered as recommended previously.27

A sequential modeling strategy was applied to investigate whether the effect of levofloxacin on the QT interval is influenced by time of day. First, IOV was included on the slope parameter, with the different dosing times representing the different occasions. Second, it was investigated whether any bias in the distribution of the occasion‐specific random effects could be reduced by estimating separate values for slope for each of the 24 hours or by describing slope as a cosine function with one or more harmonic terms and a principal period of 24 hours (Eq. (3)).

$$Slope=Slope\_Mesor+{\displaystyle \sum }_{n=1}^N\left[Slope\_A_n\text{*}\cos (\frac{2\pi \text{*}n\text{*}\left(t-Slope\_{\phi }_n\right)}{24})\right]$$ (3)

The use of these approaches was possible because the data were collected evenly across the 24‐hour period with an average of 30 ECG recordings per hour (range, 24–36 observations).

Potassium levels in plasma were considered as a covariate on QT₀ or slope as follows:

$$P_{i,j,t}={\theta }_P+{\theta }_{pot}*({Potassium}_{i,j,t}-{Potassium}_{Median})$$ (4)

With parameter P_i,j,t as a function of θ_P (typical parameter value), θ_POT (linear change in P per unit of potassium), and the difference between the potassium concentration in the i^th individual on the j^th occasion at sampling time t and the median concentration of potassium in the population (4 mmol/L).

Model evaluation

Model selection was based on objective function value (OFV), plausibility and precision of the parameter estimates, and goodness‐of‐fit plots. The fit of nested models was compared using the likelihood ratio test with the significance level set at P = 0.01, corresponding to a drop in OFV of at least 6.63 points upon inclusion of one additional parameter, assuming that the difference in OFV is χ² distributed. The fit of non‐nested models was compared using the Akaike information criterion.28

Because the baseline parameters were fixed to the values obtained with a limited pre‐dose dataset during development of the drug‐effect model, we determined whether misspecification of the baseline model affects the estimated concentration‐QT relationship in the final model by fixing the 24‐hour variation in the baseline QTc to values reported in the literature.24, 29, 30, 31, 32 Additionally, the bias and precision of the parameter estimates of the final model, with all (baseline and drug‐effect) parameters estimated, were evaluated using a bootstrap analysis with 500 resampled datasets. The parameter estimates returned by the bootstrap were summarized as medians and 95% prediction intervals of the parameters.

Clinical trial simulation

The fixed and random parameter estimates of the PK‐PD model were used to simulate clinical trials in which concentration and QTc profiles were obtained in 24 subjects receiving a placebo, therapeutic dose (500 mg), and supratherapeutic dose (1,500 mg) in a crossover design. Five hundred clinical trials with PK and PD sampling at t = 0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 8, 12, 16, 20, and 24 hours post‐dose and additional PD sampling at t = −2 and −1 hour were simulated per dosing time (02:00, 06:00, 10:00, 14:00, 18:00, and 22:00) and were re‐estimated with two alternative PK‐PD models: (1) a model that did not include a concentration‐effect relationship and (2) a model that did include a linear concentration‐effect relationship. The PK component of the alternative models was simplified versions of the final PK model (no covariance between CL and V, no cosine and IIV on absorption rate constant, and no transit compartment) to accommodate the simpler study design. A significant drug effect was observed if the OFV returned by alternative model 2 was more than 3.84 points (significance level α = 0.05) lower than the OFV in alternative model 1. These simulations and re‐estimations were performed using the stochastic simulation and estimation tool in PsN. The output was used to compute: (1) the slope of the drug effect; (2) the percentage of studies in which a significant drug effect was observed; and (3) the percentage of studies in which the upper limit of the two‐sided 90% confidence interval of the ΔQTc at the population predicted peak plasma concentration (C_max) exceeded 10 ms in alternative model 2.

RESULTS

Data exploration

The concentration‐time profiles of levofloxacin in plasma and the change from pre‐dose QT interval ΔQTcF after administration of a 1,000 mg oral dose at six different time‐points are shown in Figure 1 a,b. There was a significant interaction between the effect of levofloxacin concentration and the effect of dosing time (P = 0.0319; linear mixed effects model), indicating that dosing time influences the relationship between levofloxacin concentration and ΔQTcF (Figure 1 c).

Figure 1.

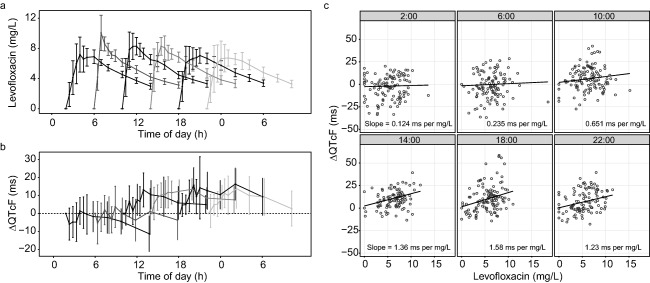
Concentration time profiles of levofloxacin in plasma (a) and the change from pre‐dose QT interval corrected for heart rate by the Fridericia formula (ΔQTcF) over time (b) after dosing at six different clock times. Data are presented as mean ± 95% confidence intervals. Concentration time profiles were published previously.20 (c) The relationship between levofloxacin concentration and ΔQTcF after dosing at six different clock times, in which dots represent observed data points; lines and numbers show the estimated regression coefficients from a linear mixed effect model.

Baseline QT model

To correct for potential 24‐hour variation in the baseline QT interval and for study‐specific dependency of the QT interval on heart rate, a baseline model was developed. The parameter estimates of this model are shown in Supplementary Table S1. A proportional error structure was used to describe the residual error. IIV and IOV were included on the intercept of the QT‐RR relationship (QT₀). A one harmonic cosine function with a period of 24 hours best described the variation in the baseline QT interval over the course of the day (ΔOFV −15; P < 0.01; 2 df). Inclusion of an additional harmonic with a period of 12 hours did not further improve the fit of the model (ΔOFV −3.1; P > 0.05; 2 df vs. model with 24‐hour cosine). Accounting for this 24‐hour variation in the baseline QT interval decreased the IOV on QT₀ from 3% to 2.3% and removed a bias observed in the conditional weighted residuals over time of day (Supplementary Figure S1). Estimation of a separate value of α during sleep did not significantly improve the fit of the model (ΔOFV −6.2; P > 0.01; 1 df). This baseline model adequately removed the dependency of the QTc interval on the RR, as evidenced by the nonsignificant effect of RR on QTc (P = 0.49; linear mixed effects model), and described the 24‐hour variation in the QTc intervals of the baseline data (Figure 2).There was no indication that the relationship between the QT and RR interval depends on the time of day (Supplementary Figure S2).

Figure 2.

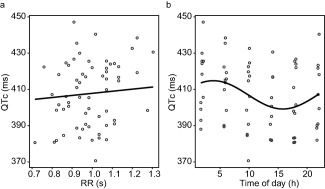
(a) The relationship between the RR interval and the QTc interval in pre‐dose electrocardiogram (ECG) recordings after correction for heart rate with the coefficient estimated by the baseline model (α = 0.216). The line shows the regression coefficient estimated by a linear mixed effect model. (b) Variation in pre‐dose QTc interval over the time of day. The line shows the shape of the cosine function estimated by the baseline model. (a and b) The dots show observed data.

Drug effect model

The development process of the drug‐effect model and corresponding changes in OFV are shown in Table 1. A linear function best described the relationship between drug concentration and the QT interval, but a bias was observed in conditional weighted residuals vs. the time of day (Figure 3 a). Additionally, the distribution of the IOV on the concentration‐QT relationship depended on the time of drug administration (Figure 3 b). These biases could be corrected by estimating a separate value for the concentration‐QT relationship for each of the 24 hours (Figure 3 c,d). Alternatively, describing the concentration‐QT relationship by a cosine function with two harmonic terms with periods of 24 and 12 hours significantly improved the fit of the model and also corrected the bias in conditional weighted residuals over time of day and IOV (Figure 3 e,f). IOV was reduced to 0.3% and no longer affected the fit of the model.

Table 1.

Changes in objective function values during model development

Model no.a	Reference model	Description	d.f.b	OFV	ΔOFV
01		Baseline model with linear C‐QT		3,910
02	01	C‐QT as Emax function	1	3,904	−6
03	01	Separate α for on‐drug measurements	1	3,909	−1
04	01	IIV on C‐QT	1	3,903	−7
05	01	IOV on C‐QT	1	3,898	−12
06	05	IIV and IOV on C‐QT	2	3,898	0
07	05	Estimation of C‐QT per hour	24	3,754	−144
08	05	C‐QT as cosine with 24‐hour period	3	3,860	−38
09	08	C‐QT with additional 12‐hour cosine	5	3,786	−74
10	09	No IOV on C‐QT	4	3,786	0
11	10	Potassium as covariate on QT0	5	3,773	−13
12	10	Potassium as covariate on C‐QT	5	3,779	−6
13	11	Potassium as covariate on QT0 and C‐QT	6	3,773	0
Final model	10	All parameters estimated	‐	3,783	‐

C‐QT, concentration‐QT relationship; d.f., degrees of freedom; E_max, maximum effect; IIV, interindividual variability; IOV, interoccasional variability; OFV, objective function value; ΔOFV, change in OFV compared to reference model.

^aQT₀, α, ϕ_baseline and amplitude_baseline were fixed to the values of the baseline model; pre‐ and post‐dose data included.

^bCompared to model 1.

Models shown in bold were selected for subsequent modeling steps.

Figure 3.

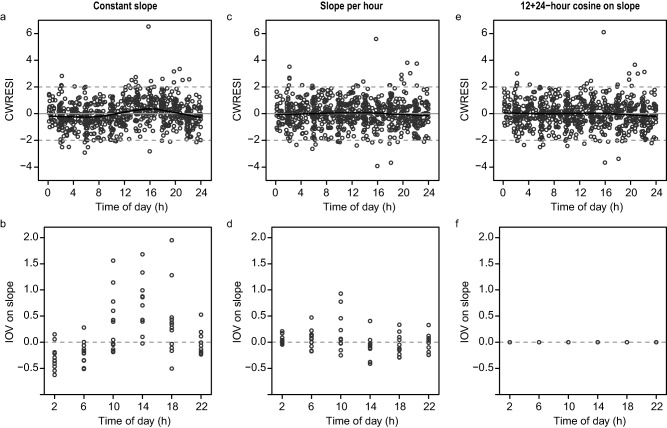
Distribution of the conditional weighted residuals with interaction (CWRESI) and of interoccasional variability (IOV) on slope vs. time of day in a model in which the linear concentration‐effect relationship is constant over the 24 hours (a,b), includes 24 estimates of slope depending on the time of the electrocardiogram (ECG) recording (c,d), and is described by a cosine function with two harmonics with periods of 24 and 12 hours (e,f). Black lines in panels a, c, and e: nonparametric regression line (loess curve with span 0.6).

Inclusion of potassium as a covariate on QT₀ significantly improved the model fit (see Table 1). It was found that for a 1 mmol/L increase in potassium levels, QT₀ decreased by 5.7 ms. However, the uncertainty in the parameter estimate was large (65%), whereas other parameter estimates were minimally affected. Potassium levels varied over the 24‐hour period within a narrow physiological range (Supplementary Figure S3), so the observed effect of potassium on the QT interval is of limited clinical relevance in this study. Therefore, this parameter was not further included in the model.

Model evaluation

The values of the concentration‐QT relationship from the model in which this relationship was estimated independently for each of the 24 hours had a low level of precision, but followed a sinusoidal‐like pattern over time, with higher values in the afternoon and lower values in the early morning (Figure 4, dots). This pattern was closely matched by the model in which the concentration‐QT relationship was described by a two harmonic cosine function (Figure 4, line). The cosine model was selected over the model with 24 separate estimates because of a lower Akaike information criterion (Δ Akaike information criterion = −6), indicating a better trade‐off between model complexity (number of model parameters) and fit of the data. Additionally, providing a continuous description of the variation in the concentration‐QT relationship over the 24‐hour period, the cosine model has more predictive value than the other model.

Figure 4.

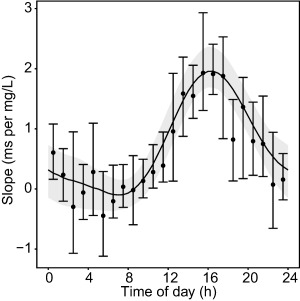
Twenty‐four‐hour variation in slope. Dots: median ± 95 prediction intervals derived from 500 bootstrap runs of the model in which a separate value for slope was estimated for each of the 24 hours. Solid black line: estimated cosine function from the model with fixed baseline parameters, with the light gray area representing the 95% prediction interval derived from 500 bootstrap runs.

Of note, comparable parameter estimates and a similar shape of the cosine function were obtained when QT₀, α, A, and φ were estimated with the full (on‐ and off‐ drug) dataset instead of fixed to the values of the baseline model (Table 2 and Supplementary Figure S4). Additionally, we found that, regardless of the baseline model used, the shape of the estimated 24‐hour variation in the concentration‐QT relationship was characterized by a peak in the late afternoon and a trough in the early morning (Supplementary Figure S4).

Table 2.

Parameter estimates of the final QT model with fixed baseline parameters and estimated baseline parameters

Parameter	Value (RSE)(fixed baseline parameters)	Value (RSE)a(estimated baseline parameters)	Bootstrap median (95% CI)
OFV	3786	3783
QT0 (ms)	407b	409 (1%)	409 (399–419)
α	0.216b	0.211 (6%)	0.210 (0.190–0.243)
A (ms)	7.8b	6.27 (24%)	6.28 (3.54–9.28)
φ (hours from midnight)	3.84b	4.11 (11%)	4.05 (3.16–4.93)
Slope
Mesor (ms per mg/L)	0.73 (19%)	0.73 (18%)	0.73 (0.49–1.04)
A1 (ms per mg/L)	0.977 (10%)	0.763 (25%)	0.772 (0.409–1.12)
φ1 (hours from midnight)	16.7 (1%)	17.3 (3%)	17.3 (16.3–19.0)
A2 (ms per mg/L)	0.274 (21%)	0.269 (22%)	0.285 (0.159–0.395)
φ2 (hours from midnight)	15.8 (3%)	15.8 (4%)	15.8 (14.7–16.9)
IIV QT0 (CV%)	4.3% (23%)	4.3% (22%)	4.1% (2.3–5.9)
IOV QT0 (CV%)	1.4% (10%)	1.4% (10%)	1.3% (1.1–1.6)
Proportional residual error (CV%)	1.8% (5.8%)	1.8% (6%)	1.8% (1.6–2.0)

CI, confidence interval; IIV, interindividual variability; IOV, interoccasional variability; OFV, objective function value; QT₀, intercept of QT‐RR relationship; α, correction term for RR interval; A, amplitude of the 24‐hour variation in QT; RSE, relative standard error; slope, C‐QT relationship; Slope_Mesor: rhythm‐adjusted mean of the slope; slope_A₁ and slope_A₂, amplitude of the first and second harmonic of slope, respectively; slope_ φ₁ and slope_ φ₂, phase of the first and second harmonic of slope, respectively; φ: acrophase (time of peak) of the 24‐hour variation in QT.

^aAll parameters were estimated simultaneously using the full pre‐ and post‐dose dataset.

^bValues fixed to parameter estimates from the baseline QT model.

The parameter estimates of the final model, in which the baseline and concentration‐effect parameters were simultaneously estimated, showed good precision (relative standard error values between 1 and 25%; Table 2) and the population and individual predicted data were in agreement with the observed data (Supplementary Figure S5). The parameter estimates returned by bootstrap analysis were similar to the parameter estimates of the final model, indicating the robustness of the model (Table 2).

Clinical trial simulations

Our findings suggest that the concentration‐QT relationship changes over time during a study occasion, whereas in a typical clinical trial this relationship is characterized by a single, linear, slope estimate. The predicted effect of dosing time on levofloxacin‐induced QT prolongation is illustrated by clinical trial simulations (Table 3). We found that dosing time affects the linear concentration‐QT relationship, the proportion of trials in which a significant drug effect was detected, and the proportion of trials in which the upper two‐sided 90% confidence bound of ΔQTc at C_max exceeded 10 ms.

Table 3.

Results of clinical trial simulations in which oral doses of 0, 500, and 1,500 mg levofloxacin were administered to 24 subjects in a crossover design

Dosing time	Slope (ms per mg/L) (median (95% PI))	Trials with significant drug effect (%) [95% CI]	Trials with upper limit 90% CI of ΔQTc >10 ms (%) [95% CI]
02:00	0.27 [0.11–0.44]	85 [82–88]	0 [0–0.8]
06:00	−0.04 [−0.19 to 0.12]	5.2 [3.6–7.5]	0 [0–0.8]
10:00	0.71 [0.55–0.88]	100 [99–100]	44 [40–49]
14:00	1.73 [1.56–1.90]	100 [99–100]	100 [99–100]
18:00	1.08 [0.88–1.29]	99 [98–100]	96 [94–97]
22:00	0.50 [0.33–0.69]	99 [98–100]	0 [0–0.8]

CI, Wilson confidence interval; PI, prediction interval; ΔQTc, change from the baseline QT interval corrected for heart rate.

Five hundred clinical trials were simulated per dosing time.

DISCUSSION

In this study, we explored the implicit assumption that drug‐induced QTc prolongation is not influenced by dosing time. Our results show that the relationship between the concentration of levofloxacin and the extent of QTc prolongation systematically varies over the course of the day. Using the developed PK‐PD model to simulate clinical trials in which a therapeutic and a supratherapeutic dose of levofloxacin are administered, we show that dosing time would consequently influence the probability that a significant drug effect is detected. Likewise, the probability that the upper 90% confidence limit of the ΔQTc exceeds 10 ms would depend on dosing time. Hence, if the developed model from this study on levofloxacin also applies to other drugs, dosing time influences the probability to detect drug‐induced QT prolongation.

Our PK‐PD model predicts that the largest drug effect occurs at 16:15, when the QTc interval increases by 1.7 ms per mg/L of levofloxacin, whereas the drug effect is virtually absent at 7:00. In a typical clinical trial, a linear slope is calculated to determine the concentration‐QT relationship. Our model suggests that this slope estimate depends on the range of slope estimates that is present over time across the study period, but is most heavily influenced by the slope around the C_max. For a clinical trial starting in the morning at 6:00 or 10:00, our simulations predict that the estimated concentration‐QT relationship is −0.04 ms per mg/L and 0.71 ms per mg/L, respectively. This range of drug effects encompasses the value of 0.36 ms per mg/L that was found in a previous study that investigated the relationship between levofloxacin concentration and QTc interval in healthy subjects that was presumably started in the morning.17

Variation in PDs can only be correctly analyzed if the variation in PKs is properly accounted for. The concentration‐time profiles of levofloxacin used in this study were derived from a PK model in which 24‐hour variation in the PK parameters was implemented.20 Because this PK model was built using the same dataset as the current study, we used the individual post‐hoc parameter estimates from this model as input for our PK‐PD model. Therefore, the variation in the relationship between levofloxacin concentration and the QT interval can be attributed to variation in the sensitivity to levofloxacin, rather than to an artifact introduced by incorrect description of its PKs.

Various physiological mechanisms may underlie the 24‐hour variation in the extent of levofloxacin‐induced QTc prolongation. We investigated whether variation in potassium levels may provide an explanation for our findings. Potassium levels showed 24‐hour variation with higher levels during the day and lowest levels during the night, which is in line with previously published potassium profiles.7, 33, 34 However, we found that the variation in potassium cannot account for the 24‐hour variation in the concentration‐QT parameter. Another explanation may be 24‐hour variation in the expression of ion channels in cardiomyocytes, which has been reported in experimental animal models.8, 9, 10, 11 It remains to be elucidated if rhythmic expression of cardiac ion channels affects the QT‐prolonging potential of a drug and to what extent this applies to humans.

By showing that the sensitivity to the QTc prolonging effects of a drug varies systematically over the day and night, our study calls into question the implicit — but untested — assumption that the relationship between a drug and the QTc interval is independent of the time of day. This assumption is the basis of most clinical research on drug‐induced QTc prolongation. For example, the current International Conference on Harmonisation E14 guidelines require the conduct of a TQT study for every new drug under development.35 In a TQT study, dosing typically occurs at the same clock time in every occasion in order to perform time‐matched baseline subtraction. This approach assumes a constant concentration‐effect relationship over time, whereas our findings indicate that this relationship varies considerably over the course of the 24‐hour period. Using clinical trial simulations, we show that the extent of drug‐induced QT prolongation may thus depend on the time of day that it is investigated. This finding is relevant in the current debate on the utility of the TQT study, in which it has been proposed that data from early phase clinical trials, combined with integrated PK‐PD analysis, is a more informative approach to evaluate the QT prolonging potential of new drugs.24, 37, 38, 39 By showing that potentially clinically relevant effects on the QT interval cannot be detected within the strict design of a TQT study, which is commonly limited to dosing in the morning, our study offers a strong argument in favor of assessing these effects by a more sophisticated design in which the dosing time is taken into account.

As this study was exploratory in nature, several limitations need to be considered. First, the study population was relatively small and homogenous, consisting of healthy men between the ages of 21 and 48 years, and factors, such as food intake and sleep/wake rhythms, were strictly standardized.20 Hence, to what extent our findings can be extrapolated to other populations and to real‐life conditions remains to be investigated.39 Second, the use of continuous ECG recordings or triplicate recordings may have resulted in a richer dataset. Nevertheless, the high precision of the parameter estimates and the results of the bootstrap analysis suggest that the parameters could be precisely estimated with our dataset. Last, we did not include a placebo arm in our study, because the aim of the study was to investigate the effect of time of day on drug‐induced QTc prolongation, and, as such, the subjects served as their own controls. Notwithstanding, we obtained sufficient pre‐dose data in order to build a baseline model with precise parameter estimates that are comparable to previously published baseline models.24 Additionally, applying previously published baseline models to our dataset results in a similar shape of the 24‐hour variation in the concentration‐QT relationship, further reducing the likelihood that our baseline model is misspecified.

An important question is to what extent our results are applicable to other drugs with QTc‐prolonging potential. As the mechanism by which levofloxacin prolongs the QTc interval, namely blockade of the hERG channel is shared by most other QTc‐prolonging drugs,3 it is unlikely that the observed time‐of‐day dependency is a drug‐specific property. Nevertheless, future research is warranted to extend our findings to other drugs that prolong the QTc interval. In this light, it will be useful to retrospectively and prospectively assess the effect of dosing time on the extent of drug‐induced QTc prolongation in clinical studies with multiple daily dosing.

In conclusion, the tacit assumption that a drug's effect on the QTc interval is constant over the course of the day should not be taken for granted, as we show that the probability of detecting a significant drug effect depends on the time that a clinical trial is carried out, at least within the constraints of our study design. Future research into the relevance of our findings for other types of drugs as well as for other (patient) populations is crucial from both a regulatory as well as clinical perspective.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information