Population Pharmacokinetics and Pharmacodynamics of the Calcimimetic Etelcalcetide in Chronic Kidney Disease and Secondary Hyperparathyroidism Receiving Hemodialysis

Abstract

Etelcalcetide is a novel calcimimetic in development for the treatment of secondary hyperparathyroidism (SHPT). A population pharmacokinetic/pharmacodynamic (PK/PD) model was developed relating etelcalcetide exposures to markers of efficacy (parathyroid hormone [PTH]) and safety (calcium) using data from three clinical studies. The semimechanistic model was developed that included allosteric activation pharmacology and understanding of calcium homeostasis. The temporal profiles for all biomarkers were well described by the model. The cooperativity constant was 4.94, confirming allosteric activation mechanism. Subjects with more severe disease (higher PTH baseline) were predicted to experience less pronounced reduction in PTH (percentage change from baseline), but more reduction in calcium (Ca; percentage change from baseline). There was no evidence that dose adjustment by any covariate was needed. Model‐based simulations provided quantitative support to several elements of dosing, such as starting dose, monitoring, and titration timing for registration trials.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Etelcalcetide is a novel calcimimetic used in the treatment of SHPT. PK/PD models that quantitatively describe the relationships between drug exposure, PTH and Ca and identify significant predictors of drug effect have not been reported.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ This is the first study to describe the PK/PD relationship in the target population between etelcalcetide exposure and PTH/Ca system using allosteric modulation, investigate potential predictors of effect, and provide quantitative support for the design of future trials.

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ With 5 mg etelcalcetide TIW, subjects with more severe disease (higher baseline PTH) were predicted to have a less pronounced relative reduction in PTH, but more reduction in Ca levels. No covariates were considered as predictors of drug response. Quantitatively integrating key components of the PTH/Ca homeostatic system supported the design of future titration studies.

HOW THIS MIGHT CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS

☑ This model can be generally applied to calcimimetic. Analysis results suggested that dose adjustment are warranted only based the measured responses.

Mineral and bone disorder in patients with chronic kidney disease (CKD) is a complex disorder associated with endstage renal disease. The impairment of bone mineral homeostasis (calcium [Ca] and phosphorus) and vitamin D (vitD) metabolism lead to excessive parathyroid hormone (PTH) levels that result in a secondary hyperparathyroidism (SHPT). Elevated PTH levels further exacerbate Ca and phosphorus imbalances. These imbalances are linked to pathological effects in a variety of organ systems, including osteodystrophy, vascular calcification, left ventricular hypertrophy, and increased risk for cardiovascular events.1, 2, 3, 4 Such cardiovascular events are known to be the leading cause of morbidity and mortality (approximately 66% 5‐year mortality) in patients with CKD. The importance of the appropriate management of SHPT is underscored by the clinical practice guidelines promulgated by different foundations.5, 6

PTH secretion by the parathyroid gland is primarily controlled by the action of the calcium‐sensing receptor (CaSR) surface of the parathyroid cells. Thus, one approach to control SHPT involves the use of CaSR agonists/modulators to enhance the interaction between ionized Ca and CaSR, which consequently reduces PTH production. This has been suggested as the mechanism of action of cinacalcet and etelcalcetide (formerly known as AMG 416).7, 8

Etelcalcetide is a novel peptide that allosterically activates the CaSR.9 When administered as an i.v. bolus, etelcalcetide reduced PTH levels in normal animals as well as in models with impaired renal function and significantly elevated PTH.7 In the first‐in‐human phase I study, etelcalcetide also showed intact PTH lowering effect in healthy subjects.10 Due to the variations in the effects of etelcalcetide on PTH and Ca and the potential side effects of lowering Ca severely, the drug is intended to be administered according to a dose titration algorithm based on PTH and serum Ca levels after treatment. The titration scheme aims at lowering PTH and Ca levels while minimizing safety risks that may result from extremely low serum Ca levels. In the design of registration trials, patients with SHPT start on 5 mg etelcalcetide thrice weekly (TIW) for 4 weeks. On week 3, measurements of PTH and Ca are taken. At week 5, based on the PTH and Ca levels, doses can be uptitrated (up to a maximum of 15 mg), or downtitrated (or suspended) according to a complex titration algorithm. Subsequent titrations are allowed on weeks 9, 13, and 17. The primary outcome measure is set as the proportion of subjects with >30% reduction from baseline in predialysis intact PTH upon long‐term administration (efficacy assessment between weeks 20 and 27).

The pharmacokinetics (PKs) of etelcalcetide was evaluated in several clinical studies. After TIW i.v. administration in patients on hemodialysis (HD), etelcalcetide plasma exposure (maximum PK concentration peak plasma concentration [C_max] and area under the curve over 48 hours) increased proportionally with the dose. With 4 weeks of 5 mg TIW dosing, approximately twofold and threefold accumulation in C_max and area under the curve over 48 hours were achieved, respectively. A linear three‐compartment model with an additional on‐HD clearance adequately described the PK of etelcalcetide in patients with SHPT who received etelcalcetide at the end of TIW HD.11

A number of model‐based approaches for describing PTH,12, 13 Ca dynamics,14, 15, 16, 17, 18, 19 and the PTH‐Ca axis20, 21, 22, 23, 24, 25, 26 have been proposed. The models vary in degree of complexity and address different mechanisms of action.

The objectives of this semimechanistic population pharmacokinetic/pharmacodynamic (PK/PD) analysis for etelcalcetide in subjects with SHPT were: (i) to develop a population PK/PD model relating etelcalcetide exposure to markers of efficacy (PTH) and safety (Ca), including physiological interaction between the markers and the quantification of interindividual and residual variability; (ii) to evaluate effects of subjects’ demographic covariates and other disease‐ and treatment‐specific characteristics on the PK/PD of etelcalcetide; and (iii) to use model‐based simulations to quantitatively support certain elements of dosing regimens built into the designs of future registration trials. These elements include usage of 5 mg as a starting dose, as well as dosing and titration frequencies.

MATERIALS AND METHODS

Study design and treatment

This etelcalcetide population PK/PD analysis was performed on pooled data from one phase I study (20130139) and two phase II studies (2a: 20120330 and 2b: 20120331) in subjects with SHPT receiving HD TIW. Characteristics of each clinical study are summarized in Table 1. In the phase I and phase IIa studies, fixed doses of etelcalcetide (5 to 60 mg for up to 12 weeks) were administered as single or multiple TIW i.v. doses. In the phase IIb study, the TIW i.v. doses (2.5–20 mg for up to 12 weeks) were titrated based on responses of PTH and Ca.27 In all studies, doses were administered at the end of HD. All studies were sponsored by KAI Pharmaceuticals (a wholly owned subsidiary of Amgen), conducted in accordance with principles for human experimentation, as defined in the Declaration of Helsinki and International Conference on Harmonisation Good Clinical Practice guidelines, and approved by the respective Institutional Review Boards. Informed consent was obtained from each subject, given the investigational nature of the study.

Table 1.

Summary of clinical studies conducted in patients with CKD with SHPT receiving HD

Study	Phase	Etelcalcetide dose in mg (no. of subjects planned)	PTH and Ca sampling scheme		No. of subjects	Population
Study I: 20130139 (KAI‐4169‐002)	I	Placebo only (n = 9)	Predose, at 10, 30 min, and at 1, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36, 42, and 48 h postdose		28	ESRD subjects with SHPT
		Placebo/etelcalcetide fixed dose (cross over):
		5 mg (n = 4)
		10 mg (n = 3)
		20 mg (n = 4)
		Etelcalcetide fixed dose only:
		40 mg (n = 4)
		60 mg (n = 4)
Study II: 20120330 (KAI‐4169‐003)	IIa	Placebo: 38	Predialysis samples for Ca were obtained at screening, days −2, 1, 3,6, 8, 10, and 13 of the study	Predialysis samples for PTH were obtained at screening, days −2, 1, 3, 6, 8, 10, 13, 15, 20, 27, and 41 of the study	78	HD subjects in SHPT
		Etelcalcetide fixed dose: 5 mg (2 wk) (n = 6)
		5 mg (4 wk) (n = 13)
		10 mg (4 wk) (n = 21)
Study III: 20120331 (KAI‐4169‐005)	IIb	Etelcalcetide doses titrated ranging from 2.5–20 mg (n = 37)	Predialysis samples for Ca were obtained at prescreening (weekly), wk 2, 3, 4, 6, 7, 8, 10, 11, 12, and 13 of the study or upon early terminationa	Predialysis samples for PTH were obtained at screening, wk 1–12, 85, 99 ± (3 d), and 113 ± (3 d) of the study or upon early terminationa	37	HD subjects in SHPT

Ca, corrected serum calcium levels; CKD, chronic kidney disease; ESRD, endstage renal disease; HD, hemodialysis; PTH, parathyroid hormone; SHPT, secondary hyperparathyroidism.

^{a a}Unscheduled laboratory assessments were performed on each visit when etecalcetide dose was withheld due to cCa concentration <7.5 mg/dL or symptoms of hypocalcemia to inform resuming dosing. Samples were submitted to the central laboratory.

Blood sampling

PTH and Ca sampling were relatively rich in all three studies, with 11–24 planned Ca samples and 14–26 planned PTH samples per subject. Details on sampling schemes in each of these three studies are provided in Table 1.

Bioanalysis

For all of the studies used in this analysis, serum samples were analyzed for levels of intact PTH using the Advia Centaur assay (Covance). The intra‐assay and inter‐assay precision was <10% coefficient of variation and the accuracy was −9% to 23.6% coefficient of variation. The validated assay range was from 2.5–1,900 ng/mL. Ca was measured using standard calcium quantification method. Ca was measured as serum corrected Ca and was converted to ionized Ca²⁺ through multiplying Ca by 0.45 (the average fraction of total calcium that is unbound).

In this report, unless otherwise noted, all references to ionized Ca will use the term (Ca²⁺), corrected Ca, and all references to intact PTH will be using the term “PTH.”

Population PK modeling

The population PK model was previously developed for the same subjects.11 A three‐compartment PK model with linear disposition (including a clearance term due to HD) adequately described the time‐course of etelcalcetide concentrations after i.v. administrations of TIW doses in these subjects with SHPT receiving HD. The resulting individual empirical Bayes estimates of PK parameters were used to predict the individual etelcalcetide serum concentration‐time profiles, which were used as an input function for the population PK/PD model.28

Population PK/PD structural model

Different direct and indirect effect model structures were examined. The selected PK/PD model structure was based on the current understanding of the mechanism of action, physiological interactions, and findings from exploratory graphical analyses. The model structure is depicted in Figure 1. In this model, Ca production was stimulated by increases in PTH from baseline through a linear relationship, whereas PTH production was inhibited by increases in CaSR receptor occupancy from baseline. Ca and PTH were eliminated through first‐order processes.

Figure 1.

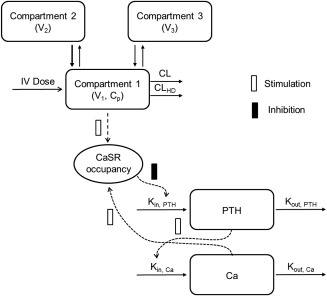
Schematic of the pharmacokinetic/pharmacodynamic (PK/PD) model structure. K_in,PTH and K_out,PTH: the zero‐order production rate of parathyroid hormone (PTH) and the first‐order elimination rate constant for PTH, respectively. ρ₀: the calcium (Ca)/calcium‐sensing receptor (CaSR) occupancy at baseline λ: a constant determining the strength of the effect of changes in ρ on PTH production K_in,Ca and K_out,Ca: the zero‐order production rate of Ca and the first‐order elimination rate for Ca, respectively. S, the slope relating changes in PTH from baseline to Ca production; K_i, the equilibrium dissociation constant for etelcalcetide at the CaSR; K_D, the equilibrium dissociation constant for Ca at the CaSR; α, the cooperativity constant; C_p, etelcalcetide plasma concentration.

In the absence of drugs, fractional occupancy of CaSR by Ca²⁺ was described as:

$$\rho = \frac{C{a}^{2+}}{K_D+{Ca}^{2+}}$$ (1)

where K_D is the equilibrium dissociation constant of calcium (assumed to be 1.2 mM).29

The fractional change in CaSR occupancy from baseline drives PTH production, and PTH turnover was described by the differential equation as follows:

$$\frac{dPTH}{dt} = K_{in,PTH }·{\left(\frac{\rho }{{\rho }_0}\right)}^{\lambda }- K_{out,PTH }·PTH$$ (2)

where, K_in,PTH is the zero‐order production rate of PTH, ρ₀ is the Ca/CaSR occupancy at baseline, λ is a constant determining the strength of the effect of changes in ρ on PTH production, and K_out,PTH is the first‐order elimination rate constant for PTH. As an increase in receptor occupancy is expected to lead to a decrease in PTH production rate, λ is expected to be negative.

Ca turnover is described by the following differential equation:

$$\frac{dCa}{dt}= K_{in,Ca}·\left(1+s·\left(PTH-{PTH}_0\right)\right)-K_{out,Ca}·Ca$$ (3)

where K_in,Ca is the zero‐order production rate of Ca, s is the slope relating changes in PTH from baseline to Ca production, PTH₀ is baseline PTH, and K_out,Ca is the first‐order elimination rate for Ca.

Etelcalcetide is an allosteric activator.7, 10, 30 Allosteric modulators modify either the affinity of the receptor for the endogenous ligand, and/or the intrinsic efficacy of the endogenous ligand.31 Etelcalcetide was assumed to increase CaSR occupancy by Ca²⁺ and stimulation of PTH production for the same Ca concentration. By combining the Ehlert model for receptor allosterism32 and the operational model of agonism,33 a model was obtained that characterizes modulation on endogenous ligand effect.26, 33 In the presence of etelcalcetide, this model can be presented as a closed form solution in which Eq. 1 is replaced with the following:

$$\rho =\frac{\frac{C{a}^{2+}}{K_D}\cdot (1+\frac{\alpha \cdot C_p}{K_i})}{\frac{C{a}^{2+}}{K_D}\cdot (1+\frac{\alpha \cdot C_p}{K_i})+\frac{C_p}{K_i}+1}$$ (4)

where K_i is the equilibrium dissociation constant for etelcalcetide on the CaSR, α is the cooperativity constant, and C_p is the etelcalcetide plasma concentration. As such, if α is less than unity, the interaction is negatively cooperative, but if α >1, the interaction is positively cooperative (i.e., the affinity of the CaSR for Ca²⁺ is increased).

The baseline Ca and PTH values, Ca₀ and PTH₀, were estimated and K_in,Ca and K_in,PTH were calculated as:

$$K_{in,Ca }= {Ca}_0 · K_{out,Ca }$$ (5)

and

$$K_{in,PTH }= {PTH}_0 · K_{out,PTH }$$ (6)

Statistical model

Interindividual variability (IIV) in the PK and PD model parameters was assumed to follow a log‐normal distribution and is described as follows:

$$P_j=P · e^{\left(\eta j\right)}$$ (7)

where P_j is the model parameter for the j^th individual; P is the population typical value for the model parameter; η_j is a random IIV effect and it is assumed to be a random Gaussian variable with zero mean and variance ω² that distinguished the j^th individual's model parameter from the population typical value, P.

Residual variability was evaluated using an additive error model using a logarithmic transformation of both sides approach for both Ca and PTH34 as follows:

$${\ln \left(C_{obs}\right)=\ln (C}_{pred})+ \epsilon$$ (8)

where C_obs is the observed PTH or Ca concentrations; C_pred is the corresponding model predicted PTH or Ca concentrations (separate ε were used for PTH vs. Ca), and ε is the residual departure of the natural logarithm of the observed PTH or Ca concentration from the predicted PTH or Ca concentration in serum, which is assumed to follow an independent Gaussian distribution with mean zero and variances σ₁² (PTH) or σ₂² (Ca).

Covariate analysis

The influence of the following covariates on relevant model parameters (Ki, s, baseline C, and baseline PTH) was tested: age, body weight, sex, race, time on dialysis, baseline phosphorus, and vitD usage. Categorical covariates were tested in NONMEM only if data in each category were collected were >10% of the subjects in the dataset. For parameter variances with low shrinkage (≤30%), covariate relationships with model parameters were explored graphically and tested only if significant trends were apparent. For parameter variances with high shrinkage (>30%), covariate effects were formally tested in NONMEM on relevant parameters. Stepwise covariate analysis35 was carried out using standard forward selection (P = 0.01), followed by backward elimination (P = 0.001). If the covariate inclusion resulted in a <20% change in typical parameter value, the covariate was considered not clinically relevant and was excluded from the model. The clinical relevance criteria were further confirmed via typical value simulations. The effects of continuous covariates were explored using a power function, whereas the effects of categorical ones were tested using additive or proportional shifts in parameters.

Model evaluation

Model fit was evaluated using standard goodness‐of‐fit criteria, reduction of patterns in normalized prediction distribution errors over time and range of predicted values, reduction in the objective function value, and obtaining acceptable precisions on estimates.

The model predictive performance was evaluated using baseline‐adjusted visual predictive checks (VPCs).

Software

Nonlinear mixed effects modeling for the population PK analysis of etelcalcetide was performed using NONMEM version 7.2 (ICON Development Solutions, Ellicott City, MD) implemented in a high performance computing system. The ADVAN 13 subroutine and first‐order conditional estimation with interaction were used. Graphical data visualization, postprocessing evaluation of NONMEM outputs, and graphical model comparisons were conducted using S‐Plus version 8.2.0 (TIBCO Software, Palo Alto, CA) and R version 3.0.2.

Model‐based simulations

Stochastic simulations were carried out to investigate the adequacy of 5 mg as a starting dose and verify the appropriateness of the titration and dosing frequencies. The time courses for Ca and PTH for 2,000 subjects after TIW administration of 5 mg etelcalcetide were simulated for 1 month, representing the first dosing period prior to the first titration in pivotal studies. The median and 95% prediction interval were calculated and presented.

Additional simulations were carried out to explore the effect of disease severity, as described by PTH baseline, on Ca and PTH responses. Time courses for Ca and PTH for 500 subjects following 8 weeks of 5 mg TIW treatment were simulated for 8 weeks, followed by 2‐week follow‐up. For graphing purposes, the PTH baseline levels were used to group simulated subjects into tertiles of low, moderate, and high baseline PTH.

RESULTS

Population PK/PD structural model

The analysis consisted of 2,824 serum PTH and 2,358 corrected Ca samples from 143 subjects receiving single or multiple TIW i.v. doses ranging from 2.5–60 mg of etelcalcetide. The ages ranged from 20–86 years (median 55 years), and body weight ranged from 53–154 kg (median 85 kg). Approximately 60% were white. The baseline PTH values ranged from 19–421 pmol/L, with medians of 75, 57, and 69 pM for studies I, II, and III, respectively. Ca baselines ranged from 1.98–2.96 mM, with medians of 2.43, 2.33, and 2.54 mM, respectively.

The model shown in Figure 1 provided the best fit to PTH and Ca time‐course data. In initial PK/PD models, the baselines of PTH and Ca were estimated using one parameter across the three different studies. However, an improvement in the goodness‐of‐fit was noted when the baselines were estimated separately for each study.

IIV was successfully estimated for s, K_i, PTH₀, and Ca₀. The estimated extent of IIV was moderate for s, K_i, baseline PTH, and low for baseline Ca. Additionally, estimating IIVs on the residual error magnitude for Ca and PTH resulted in a clear improvement in model fit. The covariance between IIV estimated on PTH₀ and Ca₀ was included in the model and resulted in improvement of fit. All PD parameters were estimated with good precision (relative standard error % <30%). The shrinkage on s, K_i, baseline PTH, and baseline Ca were 33%, 24%, 1.8%, and 3.5%, respectively. Parameter estimates and the corresponding precisions are provided in Table 2. Figure 2 shows the goodness‐of‐fit plots for the base structural model. There was acceptable agreement between the observed and the predicted concentrations. The conditional weighted residuals and normalized prediction distribution errors suggested the absence of time‐dependent PTH and Ca change. Residual variability was low (<20%) for Ca, but moderate for PTH (∼50%). Higher IIV was estimated for the remaining PD parameters (slope and K_i).

Table 2.

Final population PK/PD model parameters

Model parameters (unit)	Definition	Typical value (%RSE)	Variabilitya (%RSE)
s (1/pM)	Slope relating Ca production to the change in PTH from baseline	0.00405 (7.8)	53.7 (23)
λ	Power relating PTH production to the relative change in CaSR binding from baseline	−6.30 (6.8)
Kout,PTH (h−1)	PTH elimination rate constant	2.83 (5.7)
Kout,Ca (h−1)	Ca elimination rate constant	0.032 (11)
Ki (ng/mL)	Equilibrium dissociation constant for etelcalcetide	629 (30)	61.4 (23)
Α	Cooperativity constant	4.94 (25)
KD (mmol/L)	Equilibrium dissociation constant for Ca	1.2 (FIXED)
PTH0,study I (pmol/L)	PTH baseline (study I)	59.7 (16)	44.9 (11)
PTH0,study II (pmol/L)	PTH baseline (study II)	61.9 (6.1)
PTH0,study III (pmol/L)	PTH baseline (study III)	71.5 (8.8)
Ca0,study I (mmol/L)	Ca baseline (study I)	2.43 (1.0)	4.69 (14)
Ca0,study II (mmol/L)	Ca baseline (study II)	2.31 (0.6)
Ca0,study III (mmol/L)	Ca baseline (study III)	2.50 (0.9)
SDPTH	Additive SD on log scale for PTH	0.274 (5.2)	45.2 (16)
SDCa	Additive SD on log scale for Ca	0.04 (3.8)	33.9 (17)

Ca, corrected serum calcium levels; CaSR, calcium‐sensing receptor; PTH, parathyroid hormone; RSE, relative standard error.

^{a a}Estimates are apparent coefficients of variation for the interindividual variability.

Figure 2.

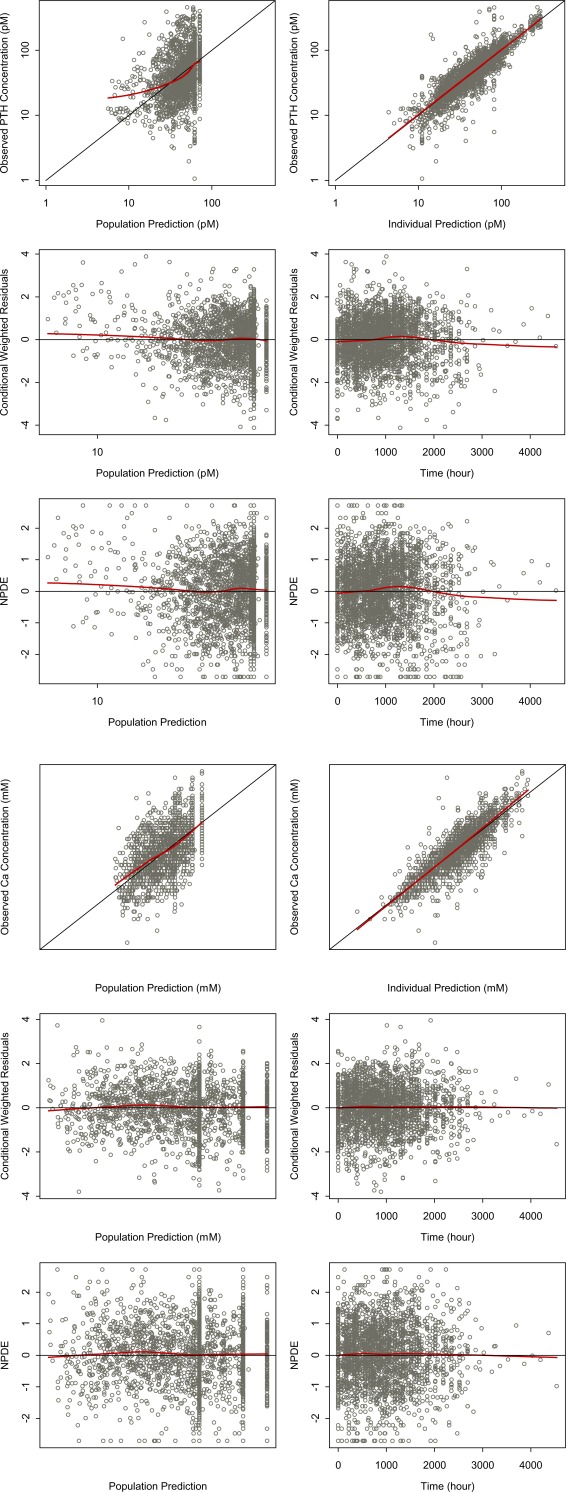
Goodness‐of‐fit plots for the final pharmacokinetic/pharmacodynamic (PK/PD) model. (a) Parathyroid hormone (PTH) and (b) calcium (Ca). In both cases: upper left, observed vs. population predicted concentrations; upper right, observed vs. individual predictions; middle left, conditional weighted residuals vs. population predicted concentrations; middle right, conditional weighted residuals vs. time; bottom left, normalized predicted distribution errors vs. population predicted concentrations; and bottom right, normalized predicted distribution errors vs. time.

The effects of subject‐specific covariates on key PD parameters were explored. The relationships with obvious trends in these plots were tested statistically. At the end of the covariate screening, no covariates were deemed as significant predictors of K_i and baseline PTH and Ca.

Model evaluation

This model was subsequently evaluated internally using simulation‐based VPC. Examples of the VPCs are shown in Figure 3, both for the first few days after a single dose of etelcalcetide in study I, and for the long‐term treatment effects after repeated dosing in study III. The bulk of the data was included within the prediction interval. The VPCs confirm acceptable predictive performance for PTH and Ca. Collectively, model evaluation confirmed the stability and predictive ability of the developed model.

Figure 3.

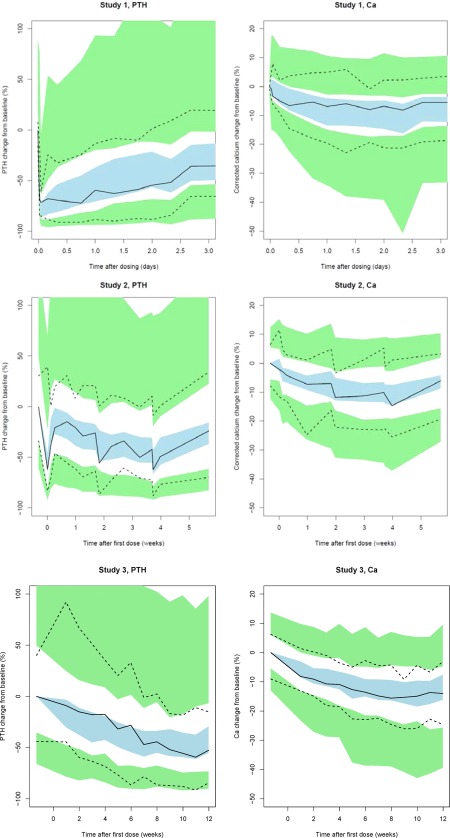
Visual predictive check based on the final population pharmacokinetic/pharmacodynamic (PK/PD) model for change from baseline in parathyroid hormone (PTH; top left) and corrected calcium (Ca; top right) after administration of a single dose of etelcalcetide in study I, and for PTH (bottom left) and corrected Ca (bottom right) after repeated administration of etelcalcetide in study III. In all panels, lines represent median (solid line), 5th and 95th percentile (dashed lines) of observed change from baseline. Shaded areas represent the 95% prediction interval of the median (blue) or 5th and 95th percentile (green) from the simulations.

Model‐based simulations

The effects of etelcalcetide administration on PTH and Ca following 5 mg TIW administration for 1 month are shown in Figure 4. Following the administration of multiple doses, a significant drop (median approximately ∼50%) in PTH from baseline was predicted. The pattern and extent of PTH reduction were predicted to be maintained upon repeated TIW administration (Figure 4 a). Delayed and less pronounced patterns of response in Ca levels to etelcalcetide repeated administration were predicted. After the first dose, <5% change in Ca from baseline is predicted. Upon TIW administration, a gradual reduction in Ca levels from baseline is predicted. On a median level, <8% change in Ca levels was predicted at the end of 1 month of TIW administration. Moreover, simulations suggested minimal differences in the changes in predialysis Ca and PTH from baseline levels are predicted on weeks 3 and 4.

Figure 4.

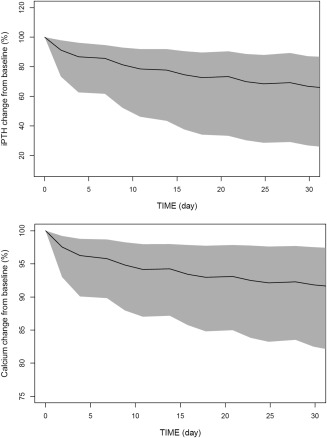
Simulated time courses of change from baseline in parathyroid hormone (PTH; top) and calcium (Ca) upon postdialysis administration of 5 mg etelcalcetide three times a week for 1 month. Shaded areas represent the 95% prediction interval of the median (black) from the simulations.

The effect of baseline PTH, as a measure of disease severity, on the PTH and Ca responses following treatment with etelcalcetide is highlighted in Figure 5. Subjects with more severe disease (higher PTH baseline) were predicted to experience less pronounced reduction in PTH, but more reduction in Ca.

Figure 5.

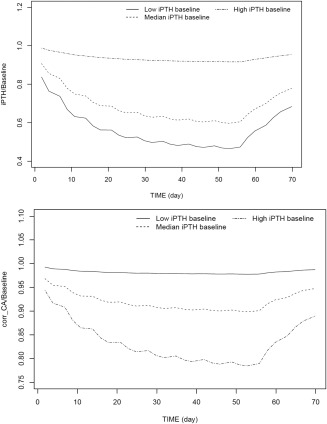
Effect of disease severity (measured by parathyroid hormone [PTH] baseline) on responses to etelcalcetide treatment: time courses of of PTH (left) and calium (Ca; right) in typical subjects with varying disease severity in response to treatment with 5 mg etelcalcetide three time a week for 8 weeks.

DISCUSSION

The population PK/PD approach discussed herein is used to describe the complex interplay among etelcalcetide exposure, PTH, and Ca based on single and multiple dose PD‐guided titration data from phase I and II clinical studies. This approach allows the analysis of PD data from titration schemes that are otherwise hard to interpret using conventional approaches. These analyses can help evaluate dose titration regimens and inform designs of clinical studies, including switching to other agents.36

The physiological system that maintains Ca homeostasis in humans comprises a large number of regulatory components and a complex network of molecular and cellular interactions.22 Current knowledge identifies Ca and PTH as key components of such a complex system, along with a number of other factors, such as phosphorus, vitD, bone metabolism, and kidney function. A number of mathematical and systems models have been built that take many of these factors and their interactions into consideration in healthy subjects, subjects with bone disease, and/or CKD.23, 24, 25, 37 Although such models describe the complex system of Ca homeostasis and bone physiology, using the population approach described herein provides complimentary and direct information related to residual and IIV in system and drug effect parameters. Additionally, the current model is mechanistically and physiologically relevant, while being supported by the available data. Similar models have been reported in literature to describe the time course of PTH and/or Ca.20, 38 However, these models did not include the mechanism‐based components of allosteric activation in the case of etelcalcetide and the physiologic feedback mechanisms described in the current model.

Even though Ca is introduced into the circulation in a number of ways, by absorption of ingested Ca, by release of immediately available calcium from the bone, from bone resorption, and by reabsorption in the kidneys,39 these mechanisms are primarily under the influence of PTH, directly or through vitD activation. Consistent with the current understanding of the pathophysiology, allowing PTH to have a direct stimulatory effect on Ca production provided a good fit to the data. The effect of Ca on PTH was modeled through a receptor‐binding model, in which the innate ligand Ca interacts with CaSR to inhibit PTH secretion. This is in agreement with the known mechanism of regulation of PTH secretion.30, 40

In the current analysis, we allowed etelcalcetide to affect the PTH‐Ca system through an allosteric effect on the CaSR, increasing the binding to Ca, and, as a result, increasing the relative functional occupancy. This mechanism provided a better fit to the data than allowing etelcalcetide to have a direct stimulatory effect on Ca production (Δ objective function value >80 points). A value of the cooperativity constant α >1 indicates that an allosteric modulator has the ability to increase the binding of CaSR to the endogenous ligand. The estimate of α for etelcalcetide was 3.41, which confirms the proposed mechanism of action of etelcalcetide as an allosteric activator. Low IIV estimates of <10% on baseline Ca were expected, given the fact that Ca levels are known to be tightly regulated. To facilitate this tight regulation, PTH is allowed to have considerable variability, which is reflected in the differing magnitude of the inhibitory effects of Ca on PTH secretion (via the CaSR), and of stimulatory effect of PTH on Ca production. This is reflected in the relative sizes of the scaling factors for the two effects, the high negative value of the power parameter (−6.3) for the effect of Ca on PTH production and the small linear slope (0.00405 pM⁻¹) for the effect of PTH on Ca production.

The typical PTH elimination rate constant, K_out,PTH, was estimated to be 2.83 h⁻¹. This corresponds to a half‐life of ∼15 minutes. This is slightly longer than the 5 minutes reported for healthy volunteers following etelcalcetide administration,40 but in general agreement with the approximate 24 minutes reported in the literature for subjects with CKD.38 At the time of the first PTH sample (0.5 hours after dosing), the decrease in PTH levels was near maximal,30 indicating that several PTH elimination half‐lives had passed and, thus, making the determination of the true half‐life difficult. The VPCs indicate that the observed decrease in PTH immediately after dosing was well described by the model.

For Ca, the elimination rate was estimated to be much lower, with a K_out,Ca of 0.03 h⁻¹, corresponding to a half‐life of ∼22 hours. The difference in the half‐lives for PTH and Ca are reflected in the very rapid reduction observed in PTH with treatment, followed by a slower reduction in Ca. The magnitude of the feedback parameter (−6.3) is comparable in magnitude (=11.7) to the feedback component parameter reported by Riggs et al.39 as well as the slope of the relationship between transformed Ca and PTH concentrations (=10.5) reported by Goodman et al.41

The final PK/PD model was used to assess starting dose and titration schema. At the end of the first week of 5 mg TIW administration, model‐based simulations suggested that an ∼50% reduction in PTH levels from baseline. PTH levels return to baseline as the drug is eliminated. Ca response was predicted to be delayed and less pronounced (<8%). Because ∼50% of the drug is eliminated by TIW HD,10 replacement is achieved by etelcalcetide postdialysis administration. Collectively, these results support the selected 5 mg dose as a safe and efficacious starting dose, as well as the TIW dosing frequency in registration trials that target >30% change in PTH from baseline with treatment. Moreover, between titrations, minimal changes in predialysis Ca and PTH were predicted beyond week 3. This supports the selection of the monitoring sample (week 3) and titration decision timing (week 4).

Additionally, subjects with more severe disease (higher baseline PTH) were to experience less pronounced reduction in PTH (percentage change from baseline), but more reduction in Ca levels (percentage change from baseline). This is in agreement with the clinical experience that patients with more advanced disease (i.e., higher PTH levels) tend to show less PTH suppression.42 This highlights the need for dose titration based on PTH and Ca markers.

The current model is capable of describing the PTH‐Ca homeostasis and the pharmacology of positively modulating CaSR and provides a simple platform for analysis of molecules targeting the PTH‐Ca axis and effects of changes in dosing regimen. However, the model does not fully account for all the factors involved in PTH control and Ca homeostasis. These include the actual levels of vitD and its activated form (calcitriol), systemic phosphorus levels, and comorbidities.

In conclusion, a model has been developed incorporating key components of the PTH/Ca physiological homeostatic system, in which etelcalcetide acts through allosteric activation of CaSR. Model‐based simulation implemented provided supportive evidence for the initial dosing, monitoring, and titration schema to be implemented in registration trials. This model may also be useful for clinical trial simulation to explore the effects of relevant factors not previously explored, assess drug combinations, and compare dosing regimens. Further development of model components based on longer‐term data in larger number of subjects is warranted.

Supporting information

Supporting Information