The forward and backward stepping processes of kinesin are gated by ATP binding

Abstract

The kinesin motor converts the chemical energy from ATP turnover into mechanical work, which produces successive 8-nm steps in the forward and backward direction along a microtubule. A key problem for kinesin mechanochemistry is explaining how ATP turnover is coordinated with mechanical work. We investigated this by measuring the ATP dependent properties of kinesin forward and backward steps using optical trapping nanometry. The results showed that the rate for both forward and backward steps are ATP-dependent, indicating that ATP binding to kinesin triggers both forward and backward steps. This suggests that ATP turnover in kinesin is not rigidly coupled to total mechanical work at high load.

Kinesin is an ATP-driven molecular motor that transforms the chemical energy from ATP turnover into mechanical work1–4. Up to a load of approximately 5–7 pN, kinesin takes successive 8 nm steps almost entirely toward the plus end (forward direction) of a microtubule5. At loads exceeding 5–7 pN, the preferred stepping direction becomes ambigious due to an increase in the frequency of backward steps6.

It is essential to understand how ATP turnover is coordinated with the production of forward and backward steps so as to understand the mechanism underlying the mechanochemical conversion in kinesin. It has been shown that the mean kinesin displacement per one ATP turnover is 8 nm at zero load7,8, which suggests that each 8-nm forward step is coupled to each ATP turnover. On the other hand, it remains unclear whether the backward steps are also coupled to ATP turnover.

Previous studies have investigated the kinetics of backward stepping by using an optical trapping nanometry system6,9. This system applies variable loads on a kinesin molecule moving along a microtubule and is capable of measuring the displacement with nanometer precision, enabling quantitative analysis of forward and backward steps. These studies found that the dwell times for both steps are identical and equally decrease as [ATP] is increased, suggesting that the forward and backward steps occur kinetically in parallel. However, ATP coupling to backward stepping is still controversial. Assuming that forward and backward steps occur in parallel with rates of k_f and k_b respectively10, ensemble averages of dwell times for each are equally described by (k_f + k_b)⁻¹. Therefore, given that k_f is ATP dependent, the ATP dependence for the dwell time can be explained whether k_b is ATP dependent or not.

In this study, we examined the ATP coupling of kinesin steps by determining the [ATP] and mechanical load dependence of the stepping rates in both directions. Results showed that the rate for both forward and backward steps equally increased with increasing [ATP]. This confirms that the production of both forward and backward steps are coupled to the kinesin ATP binding reaction.

Materials and methods

Sample preparation

Kinesin and tubulin were obtained from bovine brains as described11. Tubulin was labeled with tetramethylrhodamine succinimidyl ester and then polymerized into microtubules. Assays were performed in a solution containing 2 mM MgCl₂, 1 mM EGTA, 10 μM Taxol, 0.2 mg/ml casein, 80 mM PIPES (pH 6.8), antiphotobleaching reagents (10 mM glucose, 9 μg/ml catalase, 50 μg/ml glucose oxidase and 0.5% 2-mercaptoethanol) and 1 mM or 10 μM ATP. Carboxylate-modified polystyrene beads (0.22 μm in diameter) were precoated with 10 mg/ml casein and mixed with kinesin at a kinesin:bead molar ratio of 1:1. To confirm that the displacements of the beads were caused by single kinesin molecules, the probability that beads bind and move processively along the microtubule as a function of the bead/kinesin molar ratio was examined. The experiments described here used a kinesin/bead ratio low enough so that less than 33% of the beads were moving. Assuming Poisson statistics, >95% of the moving beads were estimated to be driven by a single kinesin molecule12. The experimental temperature was regulated at 25°C by an air conditioner with an accuracy of 1°C.

Optical trapping and data analysis

We used an optical trap nanometry system with dark-field illumination as described13. The displacement of the beads was measured using a quadrant photodiode and recorded at a sampling rate of 40 kHz with a bandwidth of 20 kHz. The raw traces of the bead were passed through a low-pass filter with a bandwidth of 1 kHz, which could discriminate individual 8-nm steps with a minimal number of unobservable events (<0.2%). The kinesin force was calculated from the bead displacement multiplied by the trap stiffness (0.02–0.06 pN nm⁻¹), which was determined from the variance of the thermal fluctuations of a trapped bead according to the equipartition theorem of energy11. The step size was defined as the difference between the average kinesin position over a 5-ms interval before and after the step. The measured steps were grouped into three categories14: forward steps, backward steps (step size <14 nm = (the peak value of backward step histogram) + (3×s.d. of the peak distribution)) and detachments (>14 nm). The dwell time was measured as the point in time when the first step was half completed to the point in time when the next step was half completed. The distribution of dwell times assuming a one- or two- rate-limiting transition scheme for steps is given by: nbt₁⁻¹ exp(−τ/t₁) or nb(t₁t₂(1/t₂ − 1/t₁))⁻¹(exp(−τ/t₁) - exp(−τ/t₂)), where τ is the dwell time, n is the number of steps, b is the bin width, and t₁ and t₂ are the time constants. The number of total steps analyzed was 1780 and 1868 at 1 mM and 10 μM ATP, respectively. 1 mM data reported in a previous paper is included in these data14. All parameter errors were estimated according to the law of propagation of uncertainty while the method of constant chi-square boundaries determined confidence limits.

Results and discussions

Kinesin 8-nm steps at different [ATP]s

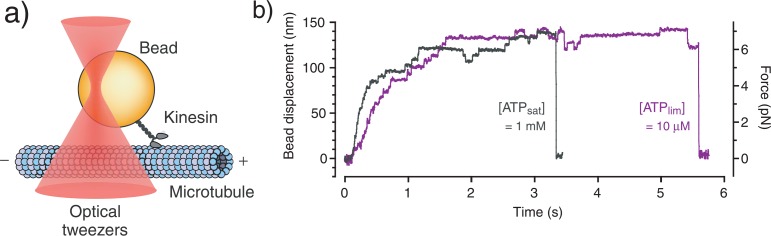
Optical trapping nanometry was used to directly detect mechanical steps of single kinesin molecules along microtubules12,13 (Fig. 1a). Typical recordings predictably showed a distinctive 8-nm stepwise pattern in the forward and backward directions (Fig. 1b). When the ATP concentration decreased from a saturating concentration ([ATP_sat] = 1 mM) to a limiting concentration ([ATP_lim] = 10 μM), the velocity of the movement decreased as reported in previous studies6,9. In addition, the trapping force acted as an external load against kinesin movements. As the load increased, the stepping speed decreased and backward steps occurred more frequently.

Figure 1.

Nanometry of single kinesin molecules. (a) The optical trapping nanometry system (not to scale). The kinesin-coated bead captured by the optical tweezers was used as a probe to measure the kinesin displacement. (b) A typical displacement record by a single kinesin molecule at saturating ([ATP_sat] = 1 mM) and limiting ([ATP_lim] = 10 μM) ATP concentrations. The external load, calculated from the trap stiffness (0.05 pN nm⁻¹), is indicated on the right.

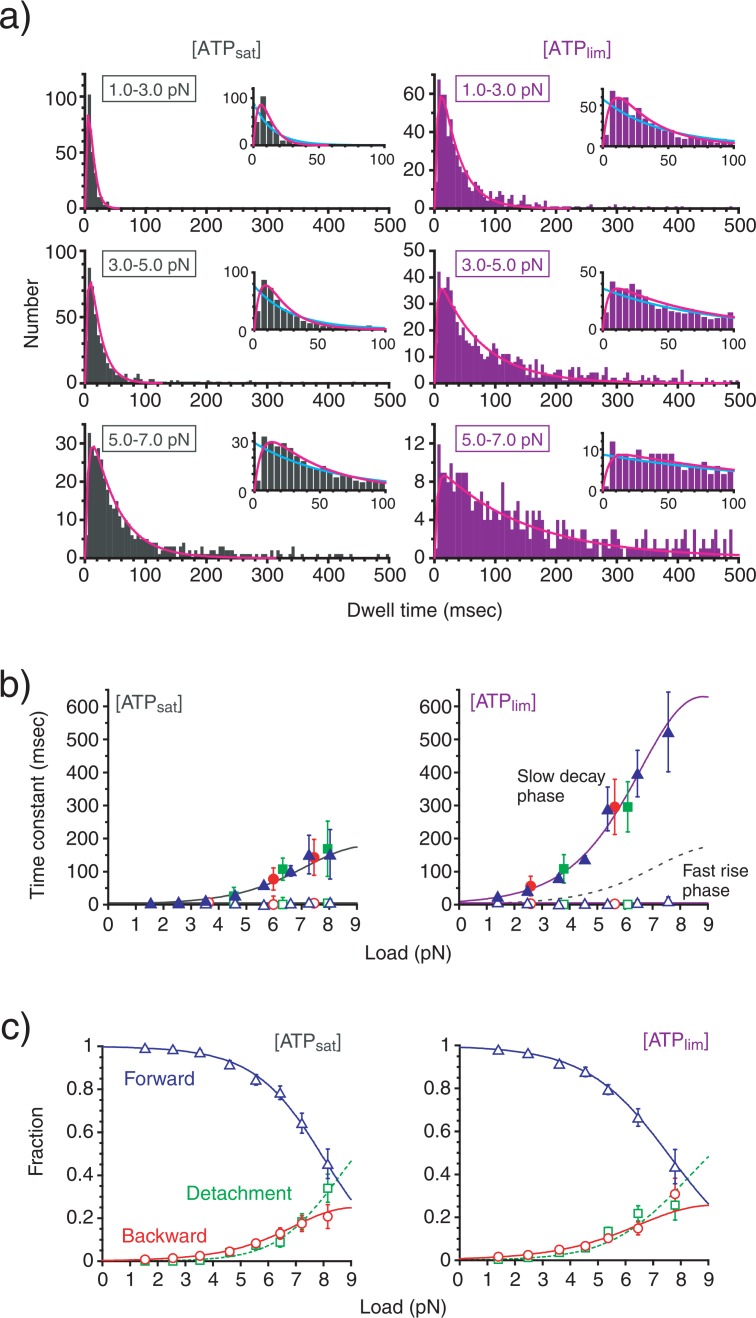
To examine the ATP-dependent kinetics of the kinesin steps, the distribution of dwell time between steps was analyzed. The distribution showed an exponential decay with the rise phase occurring over a short time range (Fig. 2a). The distributions was fitted significantly better to a two rate-limiting transition scheme (χ²(98)=90.1, P>0.1, at 10 μM ATP and 5–7 pN; for example, see Fig. 2a) than a one rate-limiting transition scheme (χ²(98)=170.3, P<0.005, for the same data set). Similar results were obtained from the dwell-time distributions for all loads and ATP concentrations. We obtained time constants corresponding to two transitions from the fitting. The results showed that one time constant increased with load while the other remained constant (Fig. 2b). This indicates that one of the two rate-limiting transitions is a load-dependent mechanical transition and the other is a load-independent biochemical transition14,15. In addition, a decrease in the ATP concentration did not affect the load-independent transition but did make the load-dependent transition slower. This indicates that the load-dependent transition originates in the ATP binding reaction. Furthermore, these time constants were unchanged even if the analyzed data was limited to just one of forward steps, backward steps or detachments (Fig. 2b), indicating that these three events occured in parallel.

Figure 2.

Dwell time and step directionality. (a) Histogram of dwell times between steps at different [ATP]s. Inset, an expansion of the histogram around a shorter time range. The curves are one (light blue) or two (pink) rate-limiting transition scheme fits. (b) Load-dependence of the time constants (mean±s.e.m) obtained from the dwell time distribution for forward steps (blue), backward steps (red) and detachments (green). The time constants obtained for the slow decay phase of the histogram (τ_m, closed symbols) and for the fast rise phase (τ_c, open symbols) were plotted. (c) Load dependence of the proportion (mean±s.e.m) of forward steps (p_f, blue), backward steps (p_b, red) and detachments (p_d, green). The curves are calculated as: p_f= k_f/(k_f+ k_b+ k_d), p_b= k_b/(k_f+ k_b+ k_d) and p_d= k_d/(k_f+ k_b+ k_d) using the kinetic parameters summarized in Table 1.

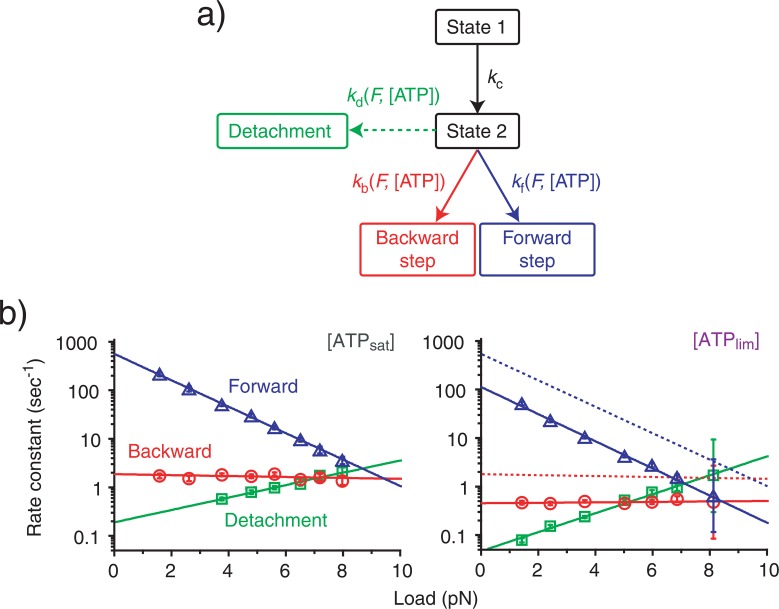
We further analyzed the directionality of stepping by examining the propagation of forward steps, backward steps and detachments as a function of load and [ATP] (Fig. 2c). The proportion of forward steps exponentially decreased from almost 1 at zero load to 0.5 at about 7–8 pN, while both backward steps and detachments increased. We obtained similar results for all ATP concentrations studied. Attributing the load-dependence of stepping direction to the load dependent transition14 (Fig. 3a), the rate constants for forward steps (k_f), backward steps (k_b) and detachments (k_d) can be given by: k_ζ = p_ζ/τ_m / (ζ=f, b, d), where p_ζ are the proportion of forward steps (f), backward steps (b) and detachments (d), and τ_m is the time constant of the load-dependent mechanical transition.

Figure 3.

Kinetic analysis of kinesin steps. (a) Kinetic pathway of kinesin steps. Forward steps, backward steps, or detachments occur by passing through a sequence of load-independent transitions (state 1 to state 2) and a load-dependent transition (state 2 to forward step, backward step or detachment). (b) Load-dependence of rate constants (mean±s.e.m) for the forward steps (k_f, blue), backward steps (k_b, red) and detachments (k_d, green) at different [ATP]s. The lines are best fits to equation (1). All kinetic parameters determined are listed in Table 1. The dotted lines in the right ([ATP_lim]) are the data from the left ([ATP_sat]) and are included for comparison.

ATP dependence of stepping rates in the forward and backward direction

We plotted the rate constants for forward steps, backward steps and detachments as a function of load (Fig. 3b). The rate constant for forward steps decreased with load in an exponential manner. However, it was independent of load for backward steps and only slightly increased with load for detachments. The exponential manner of load (F) dependence was described by a Boltzmann-type relationship:

$$\text{ln}{k}_{\zeta }\left(F,\left[\mathit{ATP}\right]\right)=\text{ln}{k_{\zeta }}^0\left(\left[\mathit{ATP}\right]\right)-\frac{{\mathit{Fd}}_{\zeta }\left(\left[\mathit{ATP}\right]\right)}{k_{\text{B}}T},$$ (1)

where ζ =f, b, or d, k_B is the Boltzmann constant and T is the experimental temperature. k⁰_ζ ([ATP]) and d_ζ ([ATP]) are the rate constants at zero load and the characteristic distances16, respectively. These parameters can be determined from a line fit to the plot (Table 1).

Table 1.

Kinetic parameters of kinesin steps. Mean±s.e.m. T=25°C. *Rate constants for the biochemical transition (k_c) are described by: k_c= 1/τ_c, where τ_c is the time constant of the load-independent transition in Fig. 2b.

	[ATPlim] (=10 μM)		[ATPsat] (=1 mM)
	kζ0 (s−1)	dζ (nm)	kζ0 (s−1)	dζ (nm)
Forward step (f)	106±8	2.7±0.1	528±49	2.6±0.1
Backward step (b)	0.39±0.04	0.0±0.1	1.81±0.17	0.1±0.1
Detachment (d)	0.05±0.01	−1.8±0.2	0.18±0.03	−1.2±0.1
Biochemical* (c)	212±28	N/A	207±13	N/A

We examined ATP dependence of the rate constants at zero load and the characteristic distances. The rate constants for forward steps at zero load declined by a fator of 5.0±0.6 when [ATP] was reduced from saturating to limiting levels reflecting an increase in the ATP binding time for kinesin7. For the backward steps, the rate constants decreased in a similar fashion (factor of 4.6±0.6), indicating that ATP binding to kinesin triggered the occurrence of backward steps as well as forward steps. In addition, the time constants for detachments at zero load decreased in a similar fashion with a decrease in the concentration of ATP (factor of 4.1±1.2), which suggests that detachments at low loads also involve ATP binding. In contrast, the characteristic distances for the forward and backward steps were independent of ATP concentration. This strongly suggests that the ATP binding frequency between the forward and backward steps is maintained over a wide range of loads.

Mechanochemistry of kinesin forward and backward steps

The analysis above indicates that both forward and backward steps are equally coupled to ATP binding. This suggests that the backward step is not driven by an optical trap forcing a simple detachment from the microtubules. Rather, it is a component of the kinesin’s mechanochemistry and comprises an aspect of work fundamental to kinesin. Below we reconsider kinesin’s mechanochemical coupling in terms of kinesin-induced backward stepping.

Previous ensemble ATPase studies have shown that the ATP turnover reaction to kinesin at zero load obeys Michaelis-Menten kinetics7,8, which is described by: 1/k⁰=1/k⁰_cat + K⁰_M/k⁰_cat/[ATP], where k⁰ is the total ATPase reaction rate, k⁰_cat and K⁰_M are the ATP catalysis rate and the Michaelis-Menten constant, respectively, and the superscript 0 denotes “zero load”. Our results describe k⁰ by using the rate constants for forward steps (k_f), backward steps (k_b), detachments (k_d) and biochemical reactions (k_c) as follows,

$$\frac{1}{k^0\left(\left[\mathit{ATP}\right]\right)}=\frac{1}{k_c}+\frac{1}{k_f^0\left(\left[\mathit{ATP}\right]\right)+k_b^0\left(\left[\mathit{ATP}\right]\right)+k_d^0\left(\left[\mathit{ATP}\right]\right)}$$ (2)

Furthermore, k⁰_cat and K⁰_M are given by: k⁰_cat= k⁰([ATP_sat]) and K⁰_M= [ATP_lim](k⁰([ATP_sat])/k⁰([ATP_lim])− 1) (ref. 9). In addition, the equivalency in the ATP binding between forward steps, backward steps and detachments is represented by the relationship:

$$\frac{k_f^0\left(\left[{\mathit{ATP}}_{\mathit{sat}}\right]\right)}{k_f^0\left(\left[\mathit{ATP}\right]\right)}=\frac{k_b^0\left(\left[{\mathit{ATP}}_{\mathit{sat}}\right]\right)}{k_b^0\left(\left[\mathit{ATP}\right]\right)}=\frac{k_d^0\left(\left[{\mathit{ATP}}_{\mathit{sat}}\right]\right)}{k_d^0\left(\left[\mathit{ATP}\right]\right)}=c\left(\left[\mathit{ATP}\right]\right),$$ (3)

where c([ATP]) is a constant. Equations (2) and (3) can be transformed into: c=1+K⁰_M/(1 – k⁰_cat/k_c)/[ATP], indicating that k⁰_f, k⁰_b and k⁰_d all obey Michalis-Menten kinetics with a common Michaelis-Menten constant, K⁰_M′ = K⁰_M/(1 – k⁰_cat/k_c). Further introducing this equation into the rate of reaction at a given load, k(F), defined by: 1/k=1/k_c + 1/(k_f exp(−Fd_f/k_BT) +k_b exp(−Fd_b/k_BT) + k_d exp(−Fd_d/k_BT)), the rate of reaction can then be transformed into Michaelis-Menten form, indicating the above two relationships assure the formation of Michaelis-Menten kinetics even in loaded conditions. This conclusion is consistent with a previous observation15. The ATP catalysis rate, k_cat(F), and the Michaelis-Menten constant, K_M(F), at a given load are defined as:

$$k_{\text{cat}}(F)={\left[\frac{1}{k_c}+\frac{1}{\sum _{\zeta }^{f,b,d}{k}_{\zeta }^0\left(\left[{\mathit{ATP}}_{\mathit{sat}}\right]\right)\text{exp}\left(\frac{{\mathit{Fd}}_{\zeta }}{k_{\text{B}}T}\right)}\right]}^{-1}$$ (4)

$$K_{\text{M}}(F)={{K^0}_{\text{M}}}^{\prime }\left[1-\frac{1}{1+\frac{k_c}{\sum _{\zeta }^{f,b,d}{k}_{\zeta }^0\left(\left[{\mathit{ATP}}_{\mathit{sat}}\right]\right)\text{exp}\left(-\frac{{\mathit{Fd}}_{\zeta }}{k_{\text{B}}T}\right)}}\right].$$ (5)

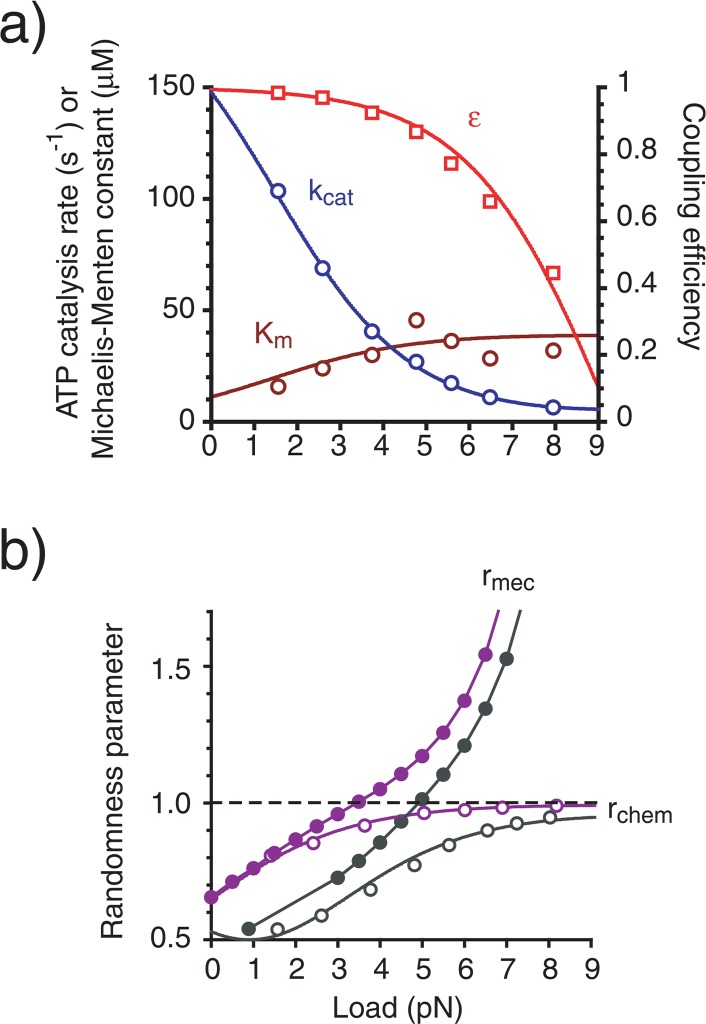
We plotted these parameters as a function of load (Fig. 4a). The ATP catalysis rate decreased exponentially as load increased, whereas the Michaelis-Menten constant increased slightly.

Figure 4.

Envisaged properties of kinesin mechanochemical coupling. (a) The enzymatic rate of ATP catalysis (blue), Michaelis-Menten constant (dark red) and coupling efficiency (red). (b) The randomness parameter for mechanical (closed symbols) and chemical (open symbols) reactions at [ATP_sat] (black) and [ATP_lim] (purple). Each curve is calculated using the parameters from Table 1 and equations (2)–(7). Plots are calculated from those in Figs. 2 and 3.

Ensemble mechanical properties of kinesin mechanochemial coupling can also be obtained using this model. The velocity (V), work (W) and power (P) are given by: V=(8 nm)k(k_f − k_b)/(k_f+ k_b), W = (8 nm)F(k_f− k_b)/(k_f+ k_b) and P=(8 nm)kF(k_f − k_b)/(k_f + k_b), when it has been assumed that the detachment does not result in movement9. In this case, the coupling efficiency between the chemical reaction and work production ε is given by: ε=(k_f − k_b)/(k_f+ k_b). This value showed an exponential decrease as the load increased (Fig. 4a), suggesting that the ATPase reaction and total work production of kinesin are not rigidly coupled at high load conditions.

Randomness of kinesin mechanochemistry

Revelations of stochastic stepping processes in single kinesin molecules also involves an understanding of the noise properties in the kinesin mechanochemical reactions. The probability density function of finding a kinesin molecule at a given position X=(8 nm)n at a time t is represented as:

$$\begin{array}{l}P\left(X=8n|T=t\right)\\ =\sum _{r=0}^{\infty }\left(\begin{array}{c}n+2r\\ r\end{array}\right)p_f^{n+r}{p}_b^r\underset{0}{\overset{t_2}{\int }}\underset{0}{\overset{t_3}{\int }}\cdots \underset{0}{\overset{t_{n+2r}}{\int }}\underset{0}{\overset{t}{\int }}p(\tau =t_1)p(\tau =t_2-t_1)\cdots \\ \cdots p(\tau =t_{n+2r}-t_{n+2r-1})p(\tau \ge t-t_{n+2r})d{t}_{1}d{t}_2\cdots d{t}_{n+2r-1}d{t}_{n+2r}.\end{array}$$ (6)

p(τ) is the dwell time distribution: p(τ=t)=(k_mk_c/(k_m− k_c)) (exp(−k_ct) - exp(−k_mt)), where, k_m is the rate constant of the mechanical transition (k_m= 1/τ_m), t_i is the time of the occurrence of the ith step and r is the number of backward steps occuring between time 0 and t. Applying the Laplace transform and the residue theorem transforms this equation into an explicit form:

$$\begin{array}{l}P\left(X=8n|T=t\right)=\sum _{r=0}^{\infty }\frac{p_f^{n+r}{p}_b^r}{\left(n+r\right)!r!}\frac{{\left(k_m{k}_c\right)}^{n+2r+1}}{{\left(k_m-k_c\right)}^{2n+4r+1}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \left[\left(n+2r\right)\left\{\frac{{J\text{'}}_0\left(-t\right)}{k_c{e}^{k_{c}t}}-\frac{{J\text{'}}_0\left(t\right)}{k_m{e}^{k_{m}t}}\right\}-\left\{\frac{{J\text{'}}_1\left(-t\right)}{k_m{e}^{k_{c}t}}-\frac{{J\text{'}}_1\left(t\right)}{k_c{e}^{k_{m}t}}\right\}\right],\end{array}$$ (7)

where ${J\text{'}}_s\left(t\right)=\sum _{i=0}^{n+2r+s}{\left(-1\right)}^{n+2r-s}{\left\{\left(k_m-k_c\right)t\right\}}^i\frac{\left(2n+4r-1-i\right)!}{\left(n+2r-s-i\right)!i!}.$ A quantitative way to evaluate the noise of mechanical movements is to investigate the randomness parameter17 of the movement (r_mec), which can be defined by: r_mec= (〈x²〉-〈x〉²)/〈8x〉, where 〈x^m〉 is the mth moment of P(X=8n|T=t). This parameter showed a monotonic increase with an increase in load and decreased as [ATP] increased (Fig. 4b). Alternatively, it is also possible to define the randomness parameter as a characteristic of noise in the ATP reactions (r_chem) as described by: r_chem = (〈τ²〉-〈τ²〉)/〈τ²〉 ={(1/k_c)² + 1/(k_f +k_b +k_d)²}/(1/k_c+ 1/(k_f+k_b + k_d))² where 〈τ^m〉 is the mth moment of p(τ). The randomness parameter for the ATP reactions was similar to that for the mechanical movements at near zero load, but the two became distinct at higher loads (Fig. 4b).

Deduced models

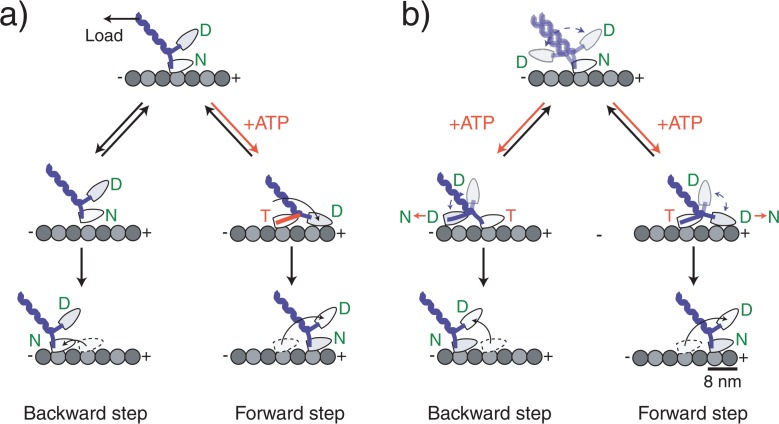
Recent studies support that kinesin moves in a walking manner using alternate microtubule-binding heads18–21. One interpretation is that ATP binding to the nucleotide-free, microtubule-bound head relieves stress allowing the unbound head with ADP bound to land on either of the adjacent microtubule binding sites18,22 (Fig. 5b). The landing direction of the unbound head is biased to the forward direction, possibly by the effect of one or a combination of the neck linker docking23, a strain-based gating mechanism24 or an asymmetric steric effect14. The search by the head to the binding site is powered by the energy from Brownian motion, which causes loose coupling between the ATPase reaction and the total mechanical work done by kinesin. The molecular mechanism behind this may be explained by several physical models including the Feynman’s ratchet model25, the flashing ratchet model26, or the classical Huxley scheme27, where, along with coupling to the mechanical movment, chemical reactions induce non-directional fluctuations or dramatic changes in the energy landscapes. Consequently, the backward steps are not caused by a simple slippage along the microtubule (Fig. 5a) but are coupled to the ATPase reaction. This will be inconsistent with the entire tight mechanochemical coupling mechanism in F₁-ATPase28, in which the process of backward steps couple to the ATP synthesis reaction. Futhermore, our results indicate that the detachment of kinesin from the microtubule is an ATP-dependent process. We imagine that most observed detachments were caused by an ATP-bound, attached head undergoing phosphate release before the unbound head attached to a microtubule binding site. The phosphate release caused the attached head to change from strong to weak binding29,30, which in turn would facilitate detachment.

Figure 5.

Molecular models of kinesin stepping. Kinesin moves in a walking manner using its two head domains. (a) A model in which the backward steps is not coupled with ATP binding. ATP binding to the nucleotide-free head that is attached directly to the microtubule coerces a forward-directed mechanical change in the neck domain forcing the partner head to the forward direction. After the detached head has landed, the alternate head releases from the microtubule as a result of an internal strain between the heads completing the forward step. Backward steps occur because load causes the head to briefly detach, but it quickly reattaches at a nearby backward site. (b) A model in which the backward step is coupled with ATP binding. ATP binding to the nucleotide-free head does not make an ATPase-coupled mechanical change. Instead it relieves the inhibition which allows the partner head to search for adjacent binding sites on the microtubule by undergoing a microtubule-activated ADP release of the partner head. The direction of the step is biased to the forward direction by an asymmetric free energy landscape such as a rachet-like structure or an asymmetric steric effect. The originally bound head releases after the detached head attaches. Letters in the circle at the head represent the prospective binding nucleotide: T=ATP, D=ADP, Pi=phosphate.

Overall, we conclude that both forward and backward kinesin steps are gated by ATP binding. This suggests that kinesin steps can be regarded as a random walk along a linear rail, but with a bias to the forward direction that can be altered by an external load. The efficiency at which the kinesin mechanochemistry uses Brownian motion is of interest in future studies.