Mechanism of muscle contraction based on stochastic properties of single actomyosin motors observed in vitro

Abstract

We have previously measured the process of displacement generation by a single head of muscle myosin (S1) using scanning probe nanometry. Given that the myosin head was rigidly attached to a fairly large scanning probe, it was assumed to stably interact with an underlying actin filament without diffusing away as would be the case in muscle. The myosin head has been shown to step back and forth stochastically along an actin filament with actin monomer repeats of 5.5 nm and to produce a net movement in the forward direction. The myosin head underwent 5 forward steps to produce a maximum displacement of 30 nm per ATP at low load (<1 pN). Here, we measured the steps over a wide range of forces up to 4 pN. The size of the steps (∼5.5 nm) did not change as the load increased whereas the number of steps per displacement and the stepping rate both decreased. The rate of the 5.5-nm steps at various force levels produced a force-velocity curve of individual actomyosin motors. The force-velocity curve from the individual myosin heads was comparable to that reported in muscle, suggesting that the fundamental mechanical properties in muscle are basically due to the intrinsic stochastic nature of individual actomyosin motors. In order to explain multiple stochastic steps, we propose a model arguing that the thermally-driven step of a myosin head is biased in the forward direction by a potential slope along the actin helical pitch resulting from steric compatibility between the binding sites of actin and a myosin head. Furthermore, computer simulations show that multiple cooperating heads undergoing stochastic steps generate a long (>60 nm) sliding distance per ATP between actin and myosin filaments, i.e., the movement is loosely coupled to the ATPase cycle as observed in muscle.

Just a half-century ago, H. E. Huxley & Hanson1 and A. F. Huxley & Niedergerke2 independently discovered that muscle contraction is caused by the relative sliding of actin and myosin filaments. The myosin heads project from the myosin filaments, forming links between actin and myosin filaments. These links are referred to as cross-bridges. The cross-bridges cyclically attach and detach from actin filaments, a process coupled to the biochemical cycles of ATP hydrolysis. H. E. Huxley3 and A. F. Huxley & Simmons4 proposed “the cross-bridge swinging model”, in which the actin filament is pulled by the swing of the cross-bridges. This model had been widely accepted as a working hypothesis for analyzing experimental data. About ten years later, however, polarized fluorescence microscopy5 and EPR spectroscopy6 showed that the ATP binding site and the SH1 domain, which are located in the motor domain of the myosin head, did not change their orientations during muscle contraction. An intramolecular bending model7–10 was proposed as an alternative to the cross-bridge tilting model, in which the motor domain remains unchanged while the light chain binding domain (neck domain), far from the actin binding site, bends. In the early 1990’s, the crystal structure11–13 of the myosin head was solved showing the neck domain attached to the motor domain of the head changed its angle relative to the motor domain depending on the form of the bound nucleotide. Based on these findings, the cross-bridge swinging model has been refined to the “lever-arm swinging model”. Here the neck domain acts as a lever arm and a small conformational change in the motor domain results in swinging the lever arm causing large displacements of 5 to 10 nm14. In the conventional view of muscle contraction, chemical energy from the hydrolysis of a single ATP is converted into mechanical work in a single step, i.e., the biochemical cycle of ATP hydrolysis is tightly coupled to the mechanical cycle in a one to one fashion15,16. However, it was shown that the sliding distance (>60 nm) between actin and myosin filaments per ATP during the shortening of muscle at no load was much larger than the displacement expected during a single step of the mechanical cycle17,18. Thus, two critical questions concerning muscle contraction mechanism are: “Is the conformational change of the neck domain (lever-arm swing) the origin of the generated force in muscle?” and “Is the mechanochemical coupling tightly coupled one to one or loosely coupled to ATP hydrolysis?”.

Since it was demonstrated that single actin filaments labeled with fluorescent phalloidin could be observed stably in solution19,20, techniques to directly investigate the elementary processes of force generation of the actomyosin motor in vitro have greatly advanced. Sliding movements of single actin filaments were observed on a myosin-coated surface21 and forces were measured by manipulating single actin filaments with a microneedle22. Furthermore, highly sensitive photo detectors enable displacement and force measurements at nanometer and piconewton resolutions, respectively23. Finally, in vitro motility assays have been extended to investigate the mechanical24,25 and chemical26,27 processes of the actomyosin motor directly at the single molecule level.

Using these assays, displacements of single myosin molecules have been measured to be 4 to 25 nm per ATP28. In order to examine the underling mechanism of movement, it is essential to investigate the process driving the displacement. However, past experiments have not resolved the rising phase of the displacements due to a poor signal to noise ratio. This is because the displacements were measured by observing the movement of actin, not myosin, and thus the compliance (1/stiffness) of the linkage between the optically trapped beads or microneedle and the actin filament damped the signal to noise ratio. To overcome this problem, we have developed a more direct method of measuring the displacements of the myosin head by using a scanning probe29 (Fig. 1). The series stiffness during acto-S1 interaction significantly increased to >1 pN/nm, compared to that obtained with optical trapping experiments (0.05–0.2 pN/nm)30,31. Resulting thermal fluctuations of the probe, namely, the noise of the measurements, was reduced from 4–9 to <2 nm r.m.s. This improvement was critical to resolve the process generating these ∼10–20 nm displacements. Furthermore, the myosin head rigidly attached to a relatively large scanning probe could steadily interact with actin without diffusing away from the actin filament as it does in muscle (H. E. Huxley, personal communication). Using this improved method, we demonstrated that the displacements did not take place abruptly but instead developed in a stepwise fashion. The size of the steps during the rising phase was 5.3 nm, which coincided with the actin monomer pitch (5.5 nm), and the number of steps per displacement was distributed in the range of one to five. Since each displacement corresponded to one biochemical cycle of ATP turnover, the result shows a step is not tightly coupled to the ATP turnover in a one to one fashion. This one-to-many coupling between the ATP turnover and the mechanical event is in accordance with a loose-coupling mechanism17,32.

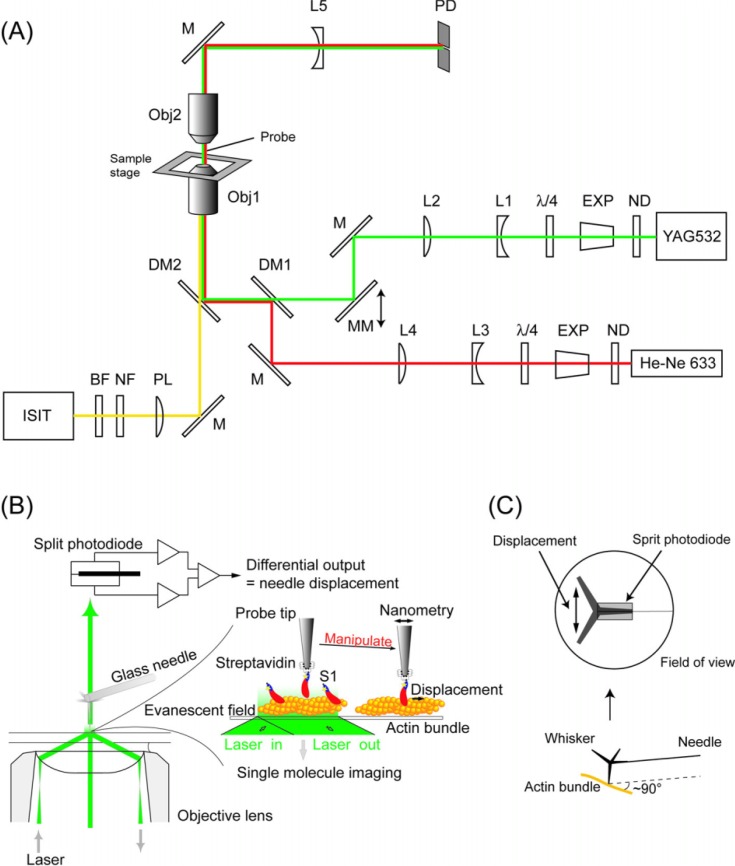
Figure 1.

(A) Schematic drawing of the experimental apparatus. The system was built on an inverted microscope. A green laser (YAG532) was used as the light source for both single molecule imaging (objective-type TIRFM) and nanometry (bright field illumination) by changing the incident angle of the laser by moving the mirror, MM. The fluorescent image of single Cy3-BDTC-S1 molecules was collected by the lower objective (Obj1), magnified by a projection lens (PL), and detected by an intensified-SIT camera (ISIT) under TIR illumination mode. The magnified image of the probe was obtained by the upper objective (Obj2) and a concave lens (L5) under bright field illumination mode. Displacement of the needle was monitored using a split-photodiode (PD). The red laser (He-Ne 633) was used for monitoring the probe position during single molecule manipulation (See text for details). ND, neutral density filters; Exp, beam expanders; λ/4, quarter-wave plates; L1&3, concave lens; L2&4, convex lens; DM1&2, dichroic mirrors; NF, notch filter; and BF, bandpass filter. (B) Imaging and nano-manipulation of single S1 molecules. A single S1 molecule, which had been biotinylated and fluorescently labeled by Cy3 at its regulatory light chain, was specifically attached to the tip of a scanning probe through a biotin-streptavidin bond and observed as a single fluorescent spot. The displacement produced when the S1 molecule was brought into contact with an actin bundle bound to a glass surface in the presence of ATP was determined by measuring the position of the needle with sub-nanometer accuracy. The S1 was rigidly attached to a fairly large scanning probe, so it was assumed to stably interact with an actin filament without diffusing away just like in muscle. (C) The schematics of the measurement geometry. A ZnO whisker crystal, whose length was 5–10 µm and radius of curvature of the tip was ∼15 nm, was attached to the tip of a very fine glass microneedle, 100 µm long and 0.3 µm in diameter. The glass needle was set perpendicular to the longitudinal axis of the actin bundle (Lower). The magnified image of the whisker + needle was projected onto the split-photodiode to measure the nanometer displacement (Upper).

Whole muscle preparations contain a huge number of molecules. Thus, one could only deduce the elementary process of force generation and mechanochemical coupling from the average value of ensemble measurements. Single molecule detection techniques have allowed important insights into the mechanical properties and the mechanochemical coupling of individual actomyosin motors to be directly obtained. Although these techniques provide invaluable information on the mechanism of the individual actomyosin motors, our final goal is to elucidate the mechanism of the more complex system, the muscle. Thus, our first aim is to compare the properties of the individual acto-myosin motors with those of muscle. Two of the most important comparable parameters in the systems are the force-velocity relationship and the thermodynamic efficiency. The force-velocity curve of individual actomyosin motors has not been previously obtained. In this study, we have analyzed the stepwise movement produced by single S1 molecules at various force levels. The size of the elementary steps was constant, 5.5 nm, and independent of the force level. However, the number and rate of steps in the rising phase decreased as the load increased. The velocity at various forces was obtained by dividing the step size (5.5 nm) by the dwell time. The basic components of the force-velocity curve for individual actomyosin motors were comparable to those of muscle. The maximum thermodynamic efficiency of energy transduction of single S1 molecules was also similar to that of muscle. Thus, the mechanical and thermodynamic features of muscle result from the intrinsic properties of individual motors.

The myosin head stepped back and forth, stochastically, but biased in one direction. Based on the analysis of the stochastic nature of mechanical steps, we propose a stepping model based on preferential landing of the heads due to a steric effect. Computer simulations of biased Brownian particles described by a Lanvegin equation33 shows that this model can be extended to explain the long (>60 nm) sliding distance between actin and myosin filaments per ATP, i.e., the loose mechanochemical coupling observed in muscle17,18,34 and in vitro35.

Materials and methods

Proteins

Biotinylated and fluorescently-labeled S1 (Cy3-BDTC-S1) and fluorescent actin bundles were prepared as previously described29,36 with some modifications. The single cystein residue of the recombinant fusion protein, which consisted of chicken gizzard myosin regulatory light chain and biotin-dependent transcarboxylase (BDTC-RLC), was labeled with a fluorescent dye molecule, Cy337. The extinction coefficient of BDTC-RLC at 280 nm is fairly low (<0.2 (mg/ml)⁻¹cm⁻¹) and thus the amount of Cy3-BDTC-RLC was determined by PAGE analysis. For instance, the concentration of the Cy3-BDTC-RLC was determined as 0.041 mg/ml, i.e., 0.041/33,500 (calculated molecular weight) = 1.22 µM, and the concentration of Cy3 in the Cy3-BDTC-RLC as determined by the absorption at 552 nm (extinction coefficient = 150,000 M⁻¹cm⁻¹) was 1.25 µM (data not shown). This indicated that the labeling ratio of Cy3-BDTC-RLC was 1.02. We only proceeded with the following steps if the labeling ratio had been determined to be within 0.98–1.02.

The endogenous RLC of S1 was then exchanged for the Cy3-labeled BDTC-RLC. Thus, the single Cy3-BDTC-S1 molecules had single Cy3 molecules attached to their RLC region. The labeling ratio of Cy3-BDTC-S1 was determined spectrophotometrically as >0.95 using the extinction coefficients of 0.83 (mg/ml)⁻¹cm⁻¹ at 280 nm for S1. To test whether the suspension was a mixture of S1 molecules which bound none, one or more than one fluorescent Cy3 molecule, we measured the fluorescence intensity and photo-bleaching of individual S1 molecules bound to a glass surface by total internal reflection fluorescence microscopy (TIRFM)26,37.

Actin bundles were prepared by dialyzing G-actin (0.02 mg/ml) against the assay buffer (25 mM KCl, 20 mM HEPES pH 7.8, 5 mM MgCl₂) containing 1/10 of equimolar α-actinin overnight at 4°C and were fluorescently labeled by incubating with BODIPY FL-phallacidin (Molecular Probes, USA) for >2 hours at 0°C. Actin bundles were freshly prepared just before use to avoid the formation of large aggregates due to long-time incubation. The thickness of the bundle measured from the fluorescence image was approximately 1 µm and the number of the actin filaments in a bundle was estimated to be 10–100 from the fluorescence intensity compared with that of single actin filaments.

Preparation of the scanning probe

The scanning probe consisted of a thin glass needle and a ZnO whisker crystal. The thin glass needle, with diameter ∼0.3 µm and length 50–100 µm, was prepared according to the method previously described38. A ZnO whisker crystal, which has a tetrapod-like structure with legs typically of 5–10 µm in length and a tip radius of ∼15 nm (M.T., unpublished), was used as the tip of the scanning probe. The crystal was first amino-silanized by 3-aminopropyltriethoxysilane (Shin-etsu chemicals, Japan)39,40 and then biotinylated by biotin-(AC₅)₂-Osu (Dojin, Japan)29. The biotinylated ZnO whisker crystal was attached to the tip of the glass needle with epoxy resin with one of the legs pointed downward using a micromanipulator under a binocular microscope (Fig. 1). The bending stiffness (spring constant) of the needles was calibrated by measuring the mean square of their thermal fluctuations using the principle of energy equipartition or by crosscalibration against stiffer, calibrated needles38. The bending stiffness of the ZnO whisker crystal, which was estimated from its shape and material constants as ∼2 N/m (J. Yoshida, Personal communication), was >10,000-fold larger than that of the glass needle. Therefore, the bending of the whisker crystal should not affect the estimated S1 displacement. The compliance added by the torsion of the glass needle was calculated to be 0.5–1 nm/pN for the typical dimensions of the most flexible needle and was not significant.

Microscope apparatus

The setup was based on an epi-fluorescence microscope (IMT-2; Olympus, Japan), sitting on an air table in a soundproof and air-conditioned chamber to minimize vibration and thermal drift (Fig. 1A). A diode pumped frequency doubled Nd: YAG laser (λ=532 nm; Model 142; LightWave electronics, USA, or HK-5526; Shimadzu, Japan) was used as the light source for both nanometry (transmitted light illumination) and single molecule imaging (TIRFM). A divergent and linearly polarized beam from the laser was collimated and expanded to an appropriate beam width by a beam expander (Exp), and converted into circularly polarized beam by a quarter-wave plate (λ/4). A telescope, a combination of concave (L1, L3) and convex (L2, L4) lenses with adjustable apertures, was used to focus the beam at the back focal plane of the objective lens (Obj1; PlanApo 100X 1.40 oil; Olympus, Japan), achieving Köellar illumination. A motorized mirror (MM) was used to change the angle of incidence for TIRFM. The size of the field of view was adjusted to ∼30 µm in diameter by changing the size of the aperture. The laser power at the nosepiece was ∼5 mW. A He-Ne laser (λ=632.8 nm, Melles Griot, USA) was used as the illumination light source for monitoring the movement of the probe during the single molecule capturing procedure to suppress the photobleaching of Cy3-BDTC-S1 (See Next section). The beam from the He-Ne laser was also expanded and combined with the green laser via a dichroic mirror (DM1; DM605; Asahi-Spectra, Japan), and focused at the back focal plane of the objective lens. Both the green and red lasers were introduced into the objective lens (Obj1) using a custom-made dual wavelength reflecting dichroic mirror (DM2; Sigma Koki, Japan).

Single molecule fluorescence from Cy3 was collected by Obj1 and passed through the dichroic mirror (DM2). Background fluorescence and scattered incident laser light were rejected by a holographic notch filter (HNPF-532AR-1.0; Kaiser Optical Systems Inc., USA) and an interference bandpass filter (BF; 585DF30; Omega Optical Inc., USA). The fluorescence image was magnified by a projection lens (PL; PE5; Olympus) and detected by an ISIT camera (ISIT), which consists of an image intensifier (VS4-1845; Video Scope International Ltd., USA) and an SIT camera (C2400-08; Hamamatsu Photonics, Japan).

The brightfield image of the probe was formed by a long working distance objective lens (Obj2; Plan 60 DIC/LWD; Nikon, Japan) and magnified by a concave lens (L5) to the final magnification of ∼300×. The magnified image of the probe was projected onto a split-photodiode (PD; S2721-02; Hamamatsu Photonics), and the displacement of the needle was measured as the differential output of the photodiode. The photocurrents of the photodiodes were amplified and converted into a voltage signal and the difference was calculated by a custom-made amplifier system (Sentech, Japan). The output signal was acquired for online monitoring by a PC with a DAQ board (16 bit A/D conversion at 100 kS/sec; PCI-MIO-16XE-10; National Instruments Co., USA) using a LabVIEW (National Instruments) based custom program. The data was also recorded on digital audiotape (DAT) with 14 bits resolution at 24 kHz (RD-120T; TEAC, Japan) for offline analysis.

The position of the sample (coverslip) and the scanning probe was controlled by a closed-loop piezo-driven stage with 1 nm accuracy (P-730.20 for XY movement of sample and P-753.11C for Z (vertical) movement of the scanning probe; Physik Instrumente, Germany).

Observation and manipulation of single S1 molecules

Cy3-labeled BDTC-S1 (Cy3-BDTC-S1) was visualized under an improved epi-fluorescence microscope equipped for both an objective-type TIRFM37 and a nanometer-pico-newton measurement system38. Fluorescence intensity and photobleaching of single S1 molecules were measured under the same measurement conditions as described previously29. The S1 was captured onto the tip of the probe with a slightly modified capturing procedure. Both the Cy3-labeled S1 and BODIPY FL-labeled actin bundles were excited by the green laser41.

A solution containing the actin bundles was applied to two separated areas on a glass surface, cleaned and then coated with α-actinin (0.1 mg/ml). Unbound bundles were washed out with the assay buffer. ∼10⁻¹⁶ mole of Cy3-BDTC-S1 in assay buffer without ATP was then applied to one of the actin bundle coated regions. After one minute of incubation, unbound Cy3-BDTC-S1 was washed out. The surface was then washed with assay buffer containing 0.5% 2-mercaptoethanol and an oxygen-scavenging system to reduce photobleaching35. The tip of the probe was coated by streptavidin and then brought into contact with a Cy3-BDTC-S1 bound to an actin bundle in the absence of ATP for ∼5 second. This procedure was repeated 5 times without scanning the probe, avoiding damage to the S1 by scanning the probe. Contact of the probe to the surface was monitored by observing thermal fluctuations of the needle under He-Ne laser (λ=632.8 nm) illumination. The green laser was turned off during this part of the procedure to suppress photobleaching. Then, the fluorescence intensity and single-step photobleaching at the tip of the probe were observed under 532 nm illumination to determine if a single S1 molecule had bound. During the time required (∼5 min.) to complete all preparations prior to checking for single S1 capture, Cy3 bound to S1 photobleached on a glass surface was negligible. There was no difference in the number of the fluorescent spots between with and without illumination either by the red laser or room light. Thus, it is unlikely that the photobleaching of the Cy3 occurred before the green laser illumination.

If no S1 molecule was captured, this procedure was repeated at a new position on the coverslip until an S1 molecule was successfully captured. If more than one S1 were captured as determined by the fluorescence (<5% of total trials), the probe was replaced by a new one and the procedure was repeated. All these manipulations were achieved by careful manipulation of the probe, minimizing damage to the S1.

Displacement measurements

After the S1 molecule was captured on the probe tip, ATP was added to the medium. The S1 was then brought into contact with a fresh actin bundle bound to another region of the same coverslip without S1 as indicated in Fig. 1B. The angle between the needle and the actin bundle was set at ∼90° (Fig. 1C). The interaction between the single S1 molecule and the actin filaments was monitored by measuring deflections of the glass microneedle with sub-nanometer resolution using a split-photodiode. The response time (rise time from 0 to 63%) of a free needle with the stiffness (k_needle) of 0.01 to 0.6 pN/nm was 0.3–5 ms, as determined from the corner frequency (f_c = 30–570 Hz) of the power spectrum of the needle’s thermal fluctuations, τ=1/(2πf_c). However, during displacement generation, the stiffness of the probe-S1-actin linkage (k_S1) increased to ∼1 pN/nm, so that the response time (τ) needed to be calculated according to the equation, τ=ζ/(k_S1+ k_needle), where ζ was the friction coefficient. τ is calculated to be <0.2 ms at k_S1 of ∼1 pN/nm. This response time was enough to observe millisecond steps in the rising phase of displacements. Thermal fluctuations of a free needle were large when the stiffness was small, e.g., r.m.s. amplitude of ∼15 nm at k_needle=0.01 pN/nm, but decreased during the acto-S1 interactions due to the increased stiffness. Eventually, the fluctuation of the needle during displacement generation becomes smaller than 2 nm when k_S1 is 1 pN/nm as calculated using the principle of energy equipartition, <Δx²>^1/2=(k_BT/(k_S1 + k_needle))^1/2, where k_B is the Boltzmann constant and T is the absolute temperature (293 K).

Data analysis

The probe position data was digitized at a sampling rate of 24 kHz and stored on DAT and analyzed offline. The acquired data was passed through a digital recursive Chebyshev type I or Butterworth filter with a 2 kHz bandwidth (DADiSP, DSP Development Corp., USA). Before the pairwise distance analysis, the rising phase of the displacements was further filtered using a non-linear median filter of rank 242. The pairwise distance was calculated as the difference between all the data points in the rising phase of the displacements. The histograms of the pairwise distance were fit with the sum of several Gaussian distributions by the Levenberg-Marquardt algorithm using Origin (OriginLab Corp., USA).

Fluorescence images of single Cy3-BDTC-S1 were stored on a digital videotape and analyzed using a personal computer (PowerMac G4, Apple computer Japan, Japan) using NIH Image software (NIH) with a custom macro program.

The data presented are mean±standard deviation, unless stated otherwise.

Computer simulation of biased Brownian steps of myosin heads

The movements of myosin heads were simulated as Brownian movement under a periodic and asymmetric sawtooth shaped potential and traced by numerically solving the Langevin equation as previously described33.

Results

Fluorescence from single Cy3-labeled S1 molecules captured onto the tip of a probe

S1 molecules were labeled at the RLC with a fluorescent dye complex (Cy3-BDTC) in an almost one (0.95) to one molar ratio (see Methods). The number of S1 molecules captured onto the probe tip was determined from the fluorescence intensity and photobleaching behavior. The fluorescence was observed by TIRFM26,37 (Fig. 2).

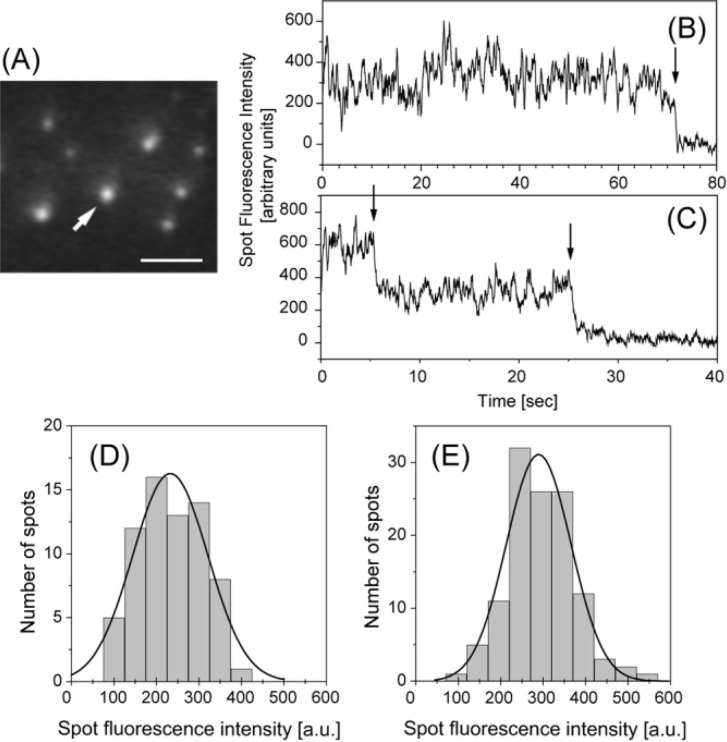
Figure 2.

Imaging of single Cy3-labeled S1 (Cy3-BDTC-S1) molecules captured on the tip of the scanning probe under TIRFM. (A) Fluorescence image of a Cy3-BDTC-S1 molecule captured on the tip of the probe (arrow). The S1 molecules were clearly observed as fluorescent spots. Bar=5 µm. (B and C) Typical time trajectories of the fluorescence intensity of a single (B) and double (C) Cy3-BDTC-S1 molecule captured onto the tip of the probe. Arrows indicate photo-bleaching. (D and E) Distributions of fluorescence intensities from Cy3-BDTC-S1 captured onto the tip of the probe (D) and adhering to the glass surface (E) were well fitted with Gaussian distributions centered at 230±88 and 290±76 (mean±s.d.), respectively.

The Cy3-BDTC-S1 molecules could be clearly observed as fluorescent spots using evanescent field illumination (Fig. 2A). The Cy3-BDTC-S1 molecule was captured on the tip of a probe at its biotinylation site of BDTC through a biotin-streptavidin bond (indicated by an arrow in Fig. 2A). Figures 2B and C show typical fluorescence time trajectories of Cy3-BDTC-S1 molecules captured on the tip of the probe, in which the fluorescence intensities decreased in a single step and double steps, respectively. The histograms of the intensity of the fluorescent spots of single Cy3-BDTC-S1 molecules captured on the tip of the probe and bound to the glass surface, which showed single step-photobleaching behavior, were both characterized by single Gaussian distributions centered at 230±88 (n=69) and 290±76 (n=119), respectively (Fig. 2D and E). These results indicate that we could count the number of S1 molecules on the tip of the probe. For example, the number of Cy3-BDTC-S1 molecules on the tip of the probe in Fig. 2B and C was judged to be one and two, respectively. Only the data for single molecules were used for the following analysis.

Displacements and forces

To minimize damage to the S1 molecules caused by the interaction with the surface of the probe, the S1 molecule was specifically attached to the tip of a probe at its tail end via a biotin-streptavidin bond29,36. After the number of S1 molecules on the probe tip was confirmed to be one by fluorescence, the captured S1 molecule was brought into contact with an actin bundle fixed to the glass surface in the presence of ATP (Fig. 1B). Displacements produced by single S1 molecules were measured with a high stiffness needle (0.1–0.6 pN/nm) which was up to 10-fold stiffer than those (0.01–0.1 pN/nm) used in previous experiments29.

Figure 3A shows a typical time course of displacements at high needle stiffness. The S1-actin interactions could be clearly identified by an increase in stiffness calculated from the reciprocal of the variance of the fluctuations of the probe43. Thermal fluctuations occurred when S1 dissociated from the actin bundle and their amplitude was dependent on the stiffness of the probe. During S1-actin attachments, the fluctuations decreased to an r.m.s. amplitude of 1.4–2.9 nm which corresponded to a stiffness of 0.5–2 pN/nm. The highest value of stiffness during attachments (∼2 pN/nm) was as large as that of an actomyosin crossbridge in muscle44.

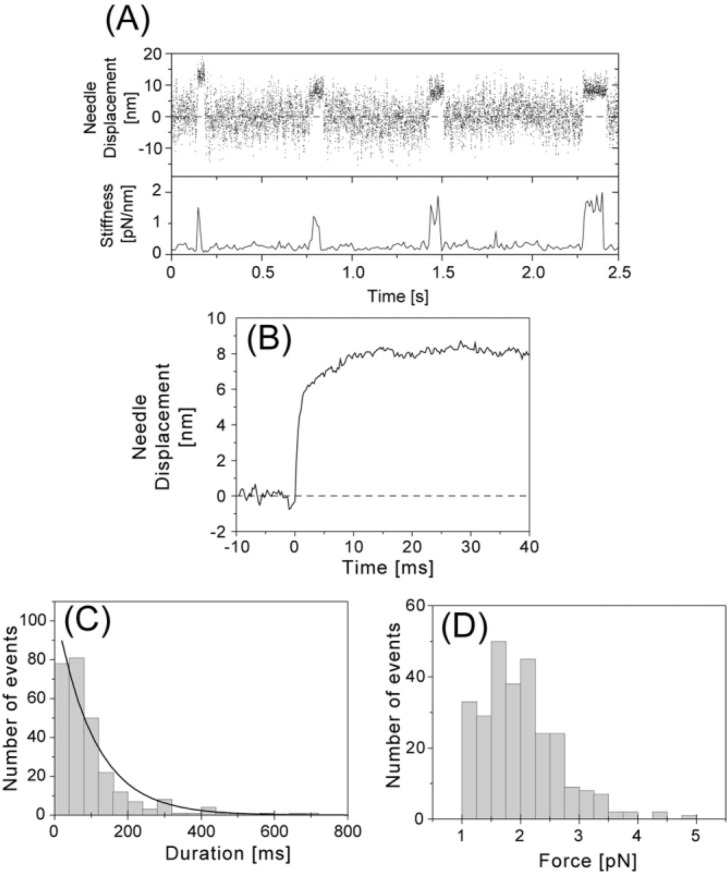
Figure 3.

Displacements and forces produced by single S1 molecules at high needle stiffness (0.1–0.6 pN/nm). (A) Representative recording of the generation of displacements by a single S1 molecule (Upper, 2 kHz bandwidth) and changes in the stiffness (Lower). The stiffness was calculated from the variance of the fluctuations of the needle. The stiffness of the needle was 0.21 pN/nm at 1 µM ATP and 20°C. (B) Needle displacement averaged over all observed events at high needle stiffness (n=274). The rising phases of the displacements were synchronized at the starting position by eye and the data at each sampling point was averaged. Mean needle displacement was 8.1 nm and when corrected to S1 displacement, 9.2 nm. (C) Histogram of displacement duration. The solid line shows a single exponential fitted to the distribution by a least squares fit. Time constant was 110 ms. (D) Histogram of forces. The forces were obtained by multiplying the stiffness of the needle by the individual needle displacements. Mean force at the plateau was 2.0 pN. Forces less than 1 pN were excluded in the histogram and from the averaging process.

Since the dispacement of S1 was attenuated by the system compliance, the displacement of S1 was obtained by correcting the displacement of the needles for system compliance. The displacement of S1 was calculated as D_S1=D_p× K_a/(K_a−K_p), where D_S1 and D_p are the displacements of an S1 and the probe, respectively, K_p is the stiffness of the probe and K_a is the stiffness during the attachment of S1 to actin30,45. Each displacement was corrected for stiffness before and during the attachment. The above equation for correction, however, is only applicable if the system stiffness is approximately linear. Previous single molecule studies, which measured the displacement through the actin filament using optical tweezers, have shown that the system stiffness is likely highly nonlinear mainly due to the compliance resulting from the linkage between the actin filament and the bead31,46. Therefore, we first determined whether the system stiffness was linear or nonlinear. Figure 4 shows one example of the stiffness during acto-S1 attachment at the dwell time between steps, plotted against the amplitude of displacement (n=43). The system stiffness changed little over the range of individual displacements from −4 to 15 nm in our measurements. This result strongly suggests a linear force-extension relationship for the observed displacement range (<20 nm). The correction factor, K_a/(K_a−K_p), was calculated to be 1.05–2.5.

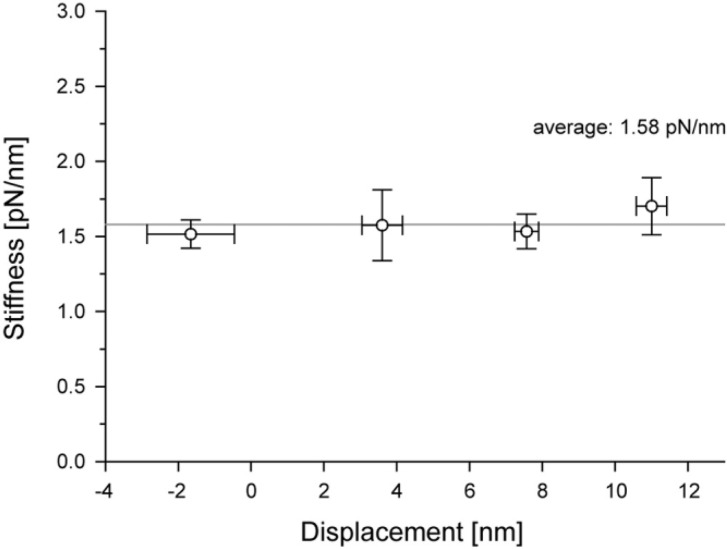
Figure 4.

Stiffness during the attachment of an acto-S1. The system stiffness was measured for individual displacements and the mean vaules were plotted against the plateau levels of displacements (see Fig. 1A). The data represents mean±s.e.m. Note that the system stiffness is constant over the range of displacement observed.

The mean displacement of S1 was determined by averaging observed events (n=274, Fig. 3B). The mean displacement was 8.1 nm (before correction) and 9.2 nm (after correction) at high needle stiffness (0.1–0.6 pN/nm), whereas it was 13 nm (before correction) at low needle stiffness (0.01–0.1 pN/nm)29. The duration of displacements in the presence of 1 µM ATP at 20°C was distributed exponentially with a mean of 0.11 sec at high needle stiffness (Fig. 3C), which was shorter than that at low needle stiffness (0.22 sec)29. The second-order rate constant for the dissociation of S1-actin by ATP was deduced from the mean duration and found to be 4–5×10⁶ M⁻¹s⁻¹ at low needle stiffness29. This value was consistent with the values obtained in solution15 and in optical trapping experiments27,30. These results indicate that each displacement corresponds to one cycle of ATP turnover29. At high needle stiffness, each displacement would also correspond to no more than one ATP turnover cycle because the mean duration of displacements was shorter than that at low needle stiffness. Since it has been shown that load accelerates the dissociation of an acto-S1 rigor complex47, the observed shorter duration is likely due to a larger load created by higher needle stiffness.

Maximum (peak) forces exerted by single S1 molecules were calculated by multiplying the spring constant of the needle by the peak (uncorrected) needle displacements (Fig. 3D). Mean force was 2.0 ± 0.7 pN (n = 274). This value is similar to the force (∼2 pN) obtained for single S1 molecules using optical tweezers43. The mean work done per displacement, which was calculated from the mean of the uncorrected displacement and force as 0.5 × 8.1 nm × 2.0 pN = 8.1 pNnm, was one-third the maximum value obtained for muscle fibers4,34.

Polarity of actin filaments in a bundle

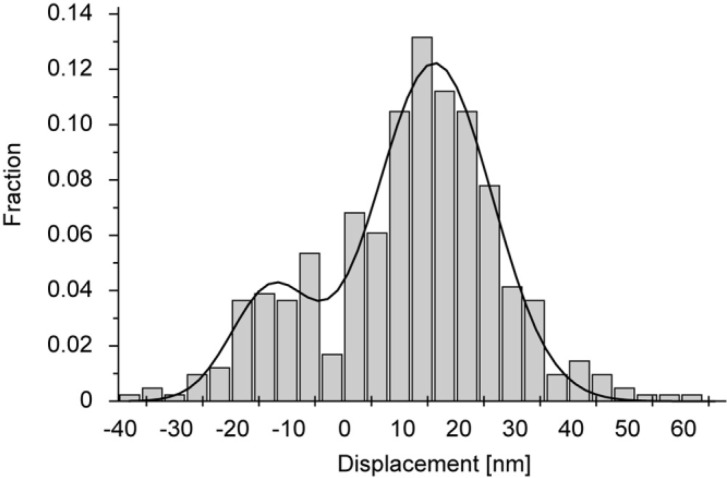
We used actin bundles formed by α-actinin, in which actin filaments might be randomly incorporated. To investigate the polarity of actin filaments in a bundle, we observed movement of myosin filaments along actin bundles. Myosin filaments moved in both directions, indicating that some actin filaments in a bundle were oriented anti-parallel to the majority of the filaments (data not shown). Furthermore, in most cases, the histogram of all displacements of an S1 molecule interacting with the same actin bundle showed a bimodal distribution (Fig. 5). The distribution was well fit to a double Gaussian distribution, with centers in the positive and negative displacement regions which were almost equidistant relative to zero displacement. Furthermore, the spread of each Gaussian distribution was similar to that of the thermal fluctuation of the free needle. Therefore, the double Gaussian distribution should be due to an S1 molecule interacting with both parallel and anti-parallel actin filaments in the bundle. Judging from the number of displacements in the positive and negative regions (Fig. 5), about 20% or less of the actin filaments were anti-parallel.

Figure 5.

A histogram of needle displacements caused by single S1 molecules at low needle stiffness (n=135). The solid line indicates a double Gaussian with peaks at 14 nm and −13 nm fit to the data. The standard deviation of each Gaussian was similar to that of the thermal vibration of the needle used in solution.

To determine the direction of the displacements, we counted the number of displacements in each direction relative to the equilibrium position of the freely moving needles and defined the direction with the majority of displacements as positive.

Considering the molecular size of α-actinin, the gap between actin filaments crosslinked to each other through α-actinin is expected to be approximately 20 nm. The bending stiffness of a whisker was ∼2 nN/nm and the stiffness of the needle in the longitudinal direction should be large, so the thermal fluctuation of an S1 attached to the probe should be <1 nm in the direction perpendicular to the actin bundle. Therefore, it is unlikely that an S1 molecule interacted with more than one actin filaments in a bundle during each displacement.

Steps within a displacement at various loads

Analysis for displacements and forces produced by single S1 molecules showed that the mean work done per displacement was significantly smaller than that measured in muscle. This implies that it is rather difficult to interpret the molecular mechanism of muscle contraction only by investigating the mean value of single molecule displacements and forces. To overcome this difficulty, we scrutinized the elementary process of the displacement generation.

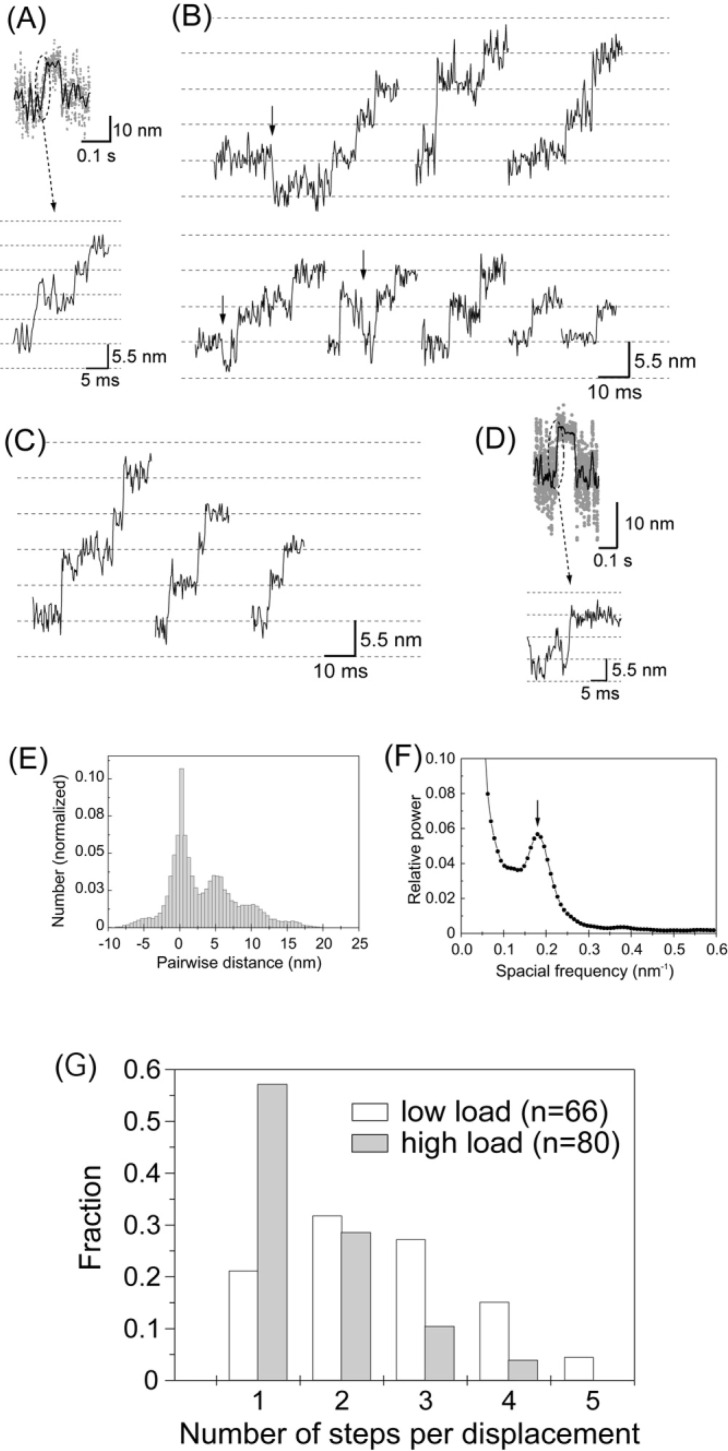
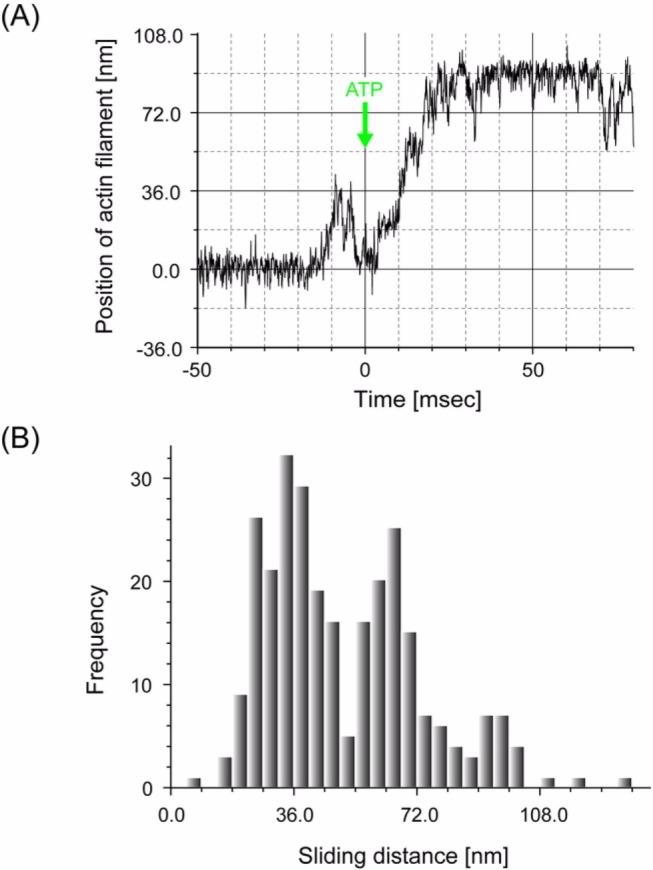
Figures 6A and B show the rising phases of the displacements at high needle stiffness on an expanded time scale. Displacements were not abrupt but took place in a stepwise fashion as observed previously at low needle stiffness (Fig. 6C). Most steps occurred in the forward direction but a small number were also recorded in the backward direction (indicated by arrows in Fig. 6B). Such stepwise motion was observed in the rising phase of approximately 30% of the total number of displacements observed (80 out of 274 displacements in 20 independent experiments for high needle stiffness). The probability such stepwise motion was observed was similar for low needle stiffness (66 out of 190 displacements)29. Clear steps were not observed for all displacements. In one group, the stiffness during the attachment did not increase sufficiently (<0.5 pN/nm. r.m.s. fluctuations of a needle >3 nm), so that the signal to noise ratio was not high enough to resolve the steps (65 displacements). The possibility exists that the actin filament may not have been rigidly fixed to the actin bundle on the glass surface. In another group (129 displacements), the stiffness was high enough to resolve the steps during the plateau after generating displacements. However, the displacements probably took place so rapidly that the steps in a displacement could not be reliably identified (Fig. 6D). Reliable identification of the start positions of displacements required that the myosin head attached to the actin for >3 ms and the stiffness was large29. Since the mean dwell time between the 1st and 2nd steps in displacements was approximately 5 ms, the fraction of displacements with the high-stiffness period of >3 ms before developing displacements was calculated to be <45%. Thus, first steps may have been missed in >50% of displacements, even if the stiffness increased. Furthermore, if the 2nd and 3rd steps took place within 3 ms, we could observe no steps in many displacements. Therefore, it is reasonable that we could observe no steps in many displacements (Supplement Table 1).

Figure 6.

Stepwise movements in the rising phase of the displacements. (A) The rising phase of the displacement record plotted on an expanded timescale. (B) Representative traces of stepwise movements in the rising phase at high needle stiffness (2 kHz bandwidth). Some backward steps were observed as indicated by arrows. (C) Stepwise movements in the rising phase at low needle stiffness (0.01–<0.1 pN/nm) from Kitamura et al.29. (D) The rising phase of the displacement that took place so rapidly that the steps were unclear. (E) Histogram of the pairwise distance for all the data points of stepwise movements in the rising phase at high needle stiffness (number of rising phases=80). (F) Power spectrum of the histogram of pairwise distance shown in (E). An obvious peak was observed at 0.18 nm⁻¹ corresponding to the spatial periodicity of 5.6 nm in the histogram. (G) Histogram of the number of steps per displacement. The steps were counted by eye. Steps of ∼5.5×N nm were counted as N steps. White and gray bars indicate the results obtained at low and high needle stiffness, respectively.

The size of the steps was determined by computing the histogram of pairwise distances of all the data points of the stepwise movements in the rising phases at high needle stiffness42 (Fig. 6D). The stepwise data were corrected by the stiffness after the displacements reached the plateau (maximum) according to the method earlier described. This is because the stiffness of an acto-S1 complex during the rising phases could not be determined quantitatively due to the short dwell phase of the steps, and the stiffness in the rising phase was assumed to be the same as on the plateau. The power spectrum of the histogram had an obvious peak at 0.18 nm⁻¹ (Fig. 6E). This corresponded to the periodicity of the peaks in the histogram with a spacing of 5.6 nm. The histogram of pairwise distances had a small peak near −5.5 nm, corresponding to steps in the backward direction. The size of the steps (5.6 nm) at high needle stiffness was almost the same as that (5.3 nm) at low needle stiffness. That is, the size of the steps was independent of the load, although the overall displacement decreased at high needle stiffness due to a decrease in the total number of steps.

Figure 6F shows histograms of the number of steps per displacement at low and high needle stiffness. As previously reported, the number of steps in a displacement varied from 1 to 5 with an average of 2.5 steps at low needle stiffness. At high needle stiffness, the number of steps decreased 1 to 4 with an average of 1.6 steps.

Force dependence of the velocity of stepping

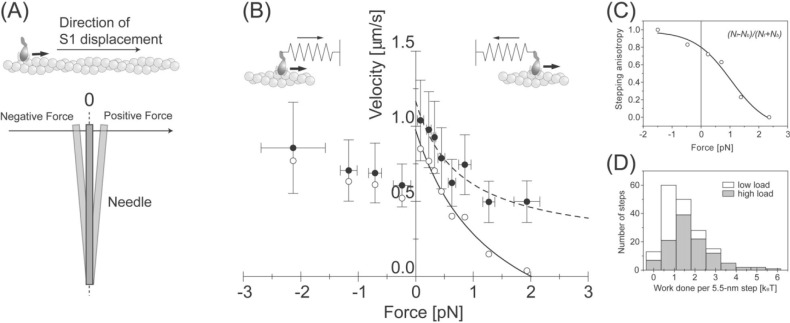
Though high needle stiffness leads to higher forces, the data at high needle stiffness included the dwell times over all force levels. To quantitatively compare the mechanical properties of individual actomyosin motors with those of muscle, their force-velocity curve was investigated. As mentioned above, displacements started at various force levels due to thermal fluctuations of a needle and thus steps also took place at various force levels. Force levels were measured at the dwell times of the steps and the direction of the force was defined as depicted in Figure 7A. The equilibrium position of the needle was taken as the zero level of force, and the force was defined as positive when the S1 pulled the needle. When S1 was pushed by the needle, the force was defined as negative. The velocity was obtained by dividing the step size (∼5.5 nm) by the dwell time, and the forces were obtained from the recorded force levels.

Figure 7.

Load dependent properties of the 5.5-nm steps. (A) The definition of the direction of the forces. When the S1 was pulled by the needle against its proceeding direction, determined by the direction of major displacement as shown in Fig. 4, the force was defined as positive. (B) Force-velocity curve of individual S1 molecules. The velocity was obtained by dividing the step size, 5.5 nm, by the dwell time (Filled circles). Bars indicate the standard deviations for 10–30 steps. Open circles indicate the velocity corrected by the anisotropy of the stepping direction. The solid line shows the Hill’s curve fitted to the corrected velocity. (C) Load dependence of the stepping anisotropy. (D) Histogram of work done by each 5.5-nm step at low (white bars) and at high needle stiffness (gray bars). Average work done per 5.5-nm step at higher needle stiffness was 1.8 k_BT.

Figure 7B (filled circles) shows the force-velocity curve obtained from the step size and the dwell time of single S1 molecules. The velocity did not reach zero but some positive value at a large positive force, which is different from that of muscle. This is most likely because the backward steps were not considered in the analysis. Backward steps took place more frequently at larger forces, thus the backward steps need to be considered when calculating the velocity of individual S1 molecules. The anisotropy of the stepping direction was defined as (N_f − N_b)/(N_f + N_b), where N_f and N_b are the number of steps in the forward and backward directions at each force level, respectively (Fig. 7C). The values were corrected by multiplying the velocities by the anisotropy of the stepping direction (Fig. 7B, open circles). The positive force regions of this curve were in close agreement to the data obtained in muscle48.

The work done per 5.5-nm step (W_step) was defined as the energy needed to pull a linear spring (spring constant of a needle, k) over a distance of 5.5-nm from an initial position x such that $W_{\mathit{step}}=\frac{1}{2}k\left({\left(x+5.5\right)}^2-x^2\right)$. We measured the position, x, during the dwell time of the step from the equilibrium position of the needle. Figure 7D shows histograms of W_step at low (blank bars) and high needle stiffness (full bars). The mean of W_step was 7.4 pNnm (=1.8 k_BT) and 4.0 pNnm (=1.0 k_BT) at high and at low needle stiffness, respectively.

Discussion

Evidence for single molecules

We confirmed that the observed events were indeed due to single S1 molecules, based on several observations. First, we checked if S1 molecules were specifically labeled at the RLC with single Cy3 molecules. The fluorescence intensity and photobleaching of individual S1 molecules bound to a glass surface have been measured as described previously37. 169 out of 179 fluorescent spots corresponding to S1 molecules photobleached in one-step, and the other 10 spots photobleached in two-steps, probably because two S1 molecules were in close proximity on the surface. The histogram of the fluorescence intensity showed a single Gaussian, and the photobleaching lifetime could be well fit to a single exponential. These results indicate that most (>95%) of the S1 molecules were specifically labeled with a single Cy3 molecule. Second, to test if additional S1 molecules bound to the tips of the probes during displacement measurements, we observed the tips by TIRFM under experimental conditions a continuous period longer than that of the displacement measurements (ca. ∼10 min). We did not observe binding of additional S1 molecules to the tips of the probes.

As we observed bound fluorophores rather than S1 molecules, the possibility that the probe may have bound extra non-fluorescent S1 molecules either unlabeled or with photobleached fluorophores should be considered. However, this is unlikely for various reasons. First, S1 molecules, labeled with fluorophores at a molar ratio >0.95 to 1, were attached to the tip of the probe under red light illumination preventing the photobleaching during the procedures prior to the measurement (see Methods). Illumination with green laser light was then used to check that single S1 molecules were captured. At this point in time more than 95% of the S1 molecules should fluoresce, so most instances of multiple S1s would have had a higher fluorescence intensity. Furthermore, as for the probability of capturing more than one S1 molecule was <5%, as determined by the fluorescence (see Methods), and the fraction of contaminating, non-fluorescent S1 molecules in the preparation was <10%. Therefore, the likelihood that the probe bound one fluorescent S1 molecule and one or more non-fluorescent S1 molecules is <0.5%. Third, if multiple steps are caused by multiple S1 molecules, each producing a single step for each ATP utilized, then the velocity in the rising phase should have been much smaller at 1 µM ATP than the actomyosin sliding velocity at saturating ATP concentration. This is because, at low ATP, the myosin head forms a rigid long-lived rigor complex with actin that limits the rate of movement.

In conclusion, the condition that S1 molecules are fluorescently labeled with a one to one molar ratio and individual fluorescent dyes bound to S1 are correctly observed without photobleaching was sufficiently verified and thus the observed events should be indeed due to single S1 molecules.

Are observed steps active?

The observed steps might be merely due to the fluctuation and the noise of the measurement or artifacts of data analysis. As described in our previous paper, we first tested if the non-specific interaction between actin and the probe (and/or S1) would produce the 5.5-nm steps. When the probe with and without attached S1 interacted with an actin bundle on a glass surface in the absence of ATP and the stage was moved smoothly at a velocity similar to that in the rising phase of the displacements, the pairwise distance histogram showed a single Gaussian peak and no auxiliary peaks with a spatial periodicity near 5.5 nm. As the stage could not be moved in 5.5-nm steps rapidly enough to simulate the active step displacements, simulated data with stochastic 5.5-nm steps and Gaussian noise were processed the same way as the experimental data. The pairwise distance histogram of the simulated data showed a spatial periodicity near 5.5 nm, similar to Fig. 6 (data not shown). Additionally we tested if the filtering method might lead to deformation — ringing — of the data so that the 5.5-nm steps in the rising phases of the displacements could be the artifacts of data analysis. Since the ripple of the Chebychev filter was small, 0.01 dB, the overshoot at the roll-off frequency (2 kHz) was minimum and thus artifacts should be unlikely. We further examined the data passing through a Butterworth filter, which has no ripple in the passband but has slower roll-off than the Chebychev filter. The traces after passing through both filters gave essentially the same results, thus the type of filtering method in the analysis should not change the results.

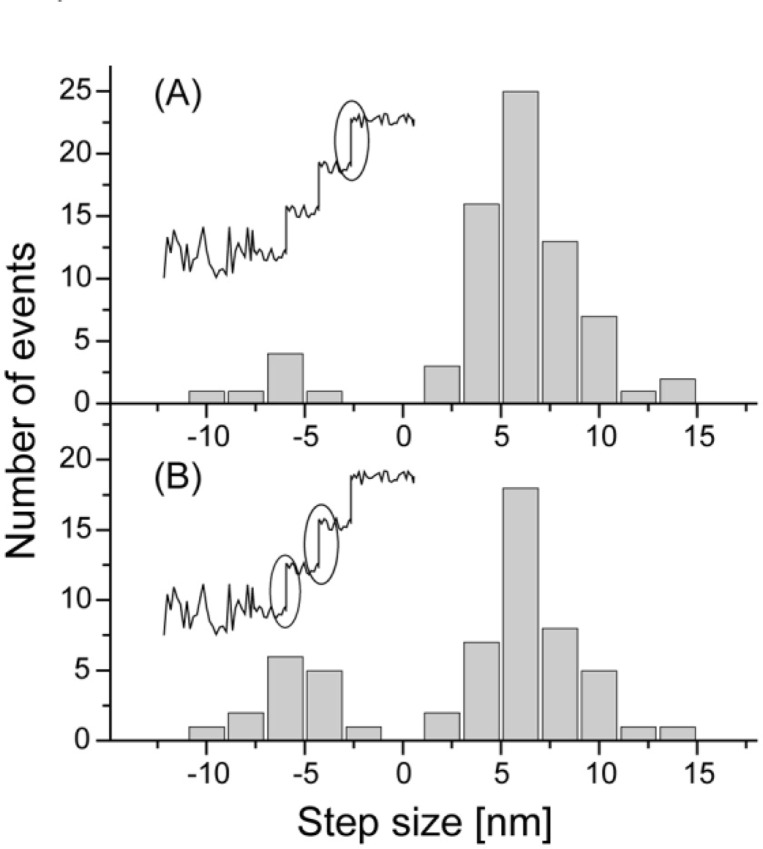
It may be possible that the multiple steps observed in the rising phase of the displacement resulted from two distinct events, i.e., thermal (passive) forward and backward jumps on the discrete binding site on an actin filament and active powerstrokes. According to the commonly accepted lever-arm theory, the powerstroke would be produced when the transition from a weakly-bound to a strongly-bound state occurred. Resting on this assumption, the step just before the final plateau should be an “active” powerstroke and its size should be equal to the amplitude of the average displacement (9.2 and 13 nm at high and low needle stiffness, respectively). We measured the size of the steps which occurred just before the final plateau (Fig. 8A) and the remainder of the steps of the rising phase (Fig. 8B). The histograms were indistinguishable and the peaks in both of them were around 6 nm. Therefore, all steps in the rising phase of displacements should be equivalent. Thus, this result excludes the possibility that only the last step in a displacement is caused by an active powerstroke and others are caused by passive fluctuations due to Brownian motion.

Figure 8.

Histograms of the step size just before the final plateau (A) and the remaining steps at the rising phase (B). Plateaus were determined as the greatest displacement achieved before myosin detaches from actin causing the displacement to return to zero.

All these results indicate that each 5.5-nm step in the rising phase of displacements is due to an “active” step, probably produced by biased Brownian motion.

Chemomechanical coupling

Multiple 5.5-nm steps were observed in the rising phase of the displacement and the number of 5.5-nm steps in each displacement decreased as the force applied to the S1 increased (Fig. 6). As each displacement corresponds to no more than one ATP turnover cycle, the result shows that the number of steps (mechanical events) during one biochemical cycle of ATP hydrolysis varies depending on the load. Thus, actomyosin is a load dependent loose-coupling motor.

The step size coincided with the distance between adjacent actin monomers in an actin filament (5.5 nm). These results strongly suggest that the myosin head walks along actin filament monomers. The S1 was fixed at its tail end to the probe tip and thus is expected to rotate when moving along the actin filament because of the actin filament’s helical structure. Evidence from EM studies suggests that the linkage between the catalytic and neck domains of S1 is flexible49,50. Therefore, the S1 could rotate when undergoing 5 continuous steps. This distance corresponds to 5 actin monomers, i.e., a rotation of ∼130°. However, the S1 did not undergo more than 5 successive steps. The maximum number is most likely limited by the helical structure of the actin filament and our experimental configurations.

Force velocity curve

The velocity corrected for the stepping anisotropy had a hyperbolic dependence with the positive force applied. The data were well described by Hill’s equation (solid line in Fig. 7B; (P + a)(V + b) = (P₀ + a)b. P: load; V: velocity; P₀: isometric force; a and b: constants having the dimensions of force and velocity, respectively). Maximum velocity (V_max), isometric force (P₀) and the curvature of the hyperbola (a/P₀) were determined to be 1.0 µm/s, 2.0 pN and 0.7, respectively. V_max at zero load was similar to the sliding velocity of actin filaments in vitro at 20°C35 and P₀ was consistent with the mean peak force (Fig. 3D). However, the value of a/P₀, which is a measure of the curvature of the force-velocity curve, was significantly larger than that of shortening muscle (0.2–0.4)48. One possible explanation for this difference is that the force generating step and other steps of the ATPase cycle, such as association and dissociation of actin and myosin, are all involved during measurements of a shortening muscle, giving the steeper force-velocity curve. In individual actomyosin motors, however, only the force generating step is measured.

The force-velocity relationship at negative forces was also obtained (Fig. 7A). Interestingly, the velocity decreased to two thirds (0.6 µm/s at −0.2 pN, n=18) the value at near zero loads (0.9 µm/s at 0.1 pN, n=15) when the S1 was pulled by the needle (P<0.04, Student’s t-test). In the case of negative forces, the velocity increased gradually with an increase in negative force. While this feature is different from the force-velocity curve of shortening muscle51, it is consistent with that of in vitro force-movement assays, in which the movement of myosin coated beads along actin bundles was measured under centrifugation52. The discontinuity of the force-velocity curve of single actomyosin molecules may be attributed to the asymmetries in the structures and/or the binding of an actomyosin molecule.

The mean work done per 5.5-nm step was determined as 7.4 pNnm (=1.8 k_BT) at high needle stiffness (Fig. 7D). The number of steps per displacement was distributed from one to four, hence the maximum work done during one ATPase cycle was measured as 31 pNnm (=7.2 k_BT). This result indicates that single S1 molecules could convert chemical energy into mechanical work with the maximum efficiency of ∼36% (energy liberated by ATP hydrolysis ∼20 k_BT). This value is similar to the maximum efficiency of contracting muscle fibers34. The similarities of the force-velocity curve and thermodynamic efficiency of single actomyosin molecules to ensemble systems such as muscle suggest that the major mechanical and thermodynamic properties of muscle are essentially the effect of intrinsic characteristics of individual actomyosin motors.

Stochastic properties of biased Brownian steps

The stepping motion of an S1 molecule was not always smooth and sometimes moved towards the opposite direction along an actin filament. The size of the steps was ∼5.5 nm for steps in both the forward and backward directions. This step size coincides with the distance between adjacent actin monomers in one strand of an actin filament (Fig. 9A). Furthermore, the number of steps ranged randomly from one to five during no more than one ATP hydrolysis cycle, i.e., the 5.5-nm steps were not tightly coupled to the ATP hydrolysis cycle. The stochastic features of this stepping motion and the step size strongly suggest that the myosin head walks or slides along the actin monomer repeat driven by Brownian motion. Because the majority of steps occurred in one direction, they should not result from pure thermal diffusion but rather be biased in one direction (forward), i.e., this process is active, not passive.

Figure 9.

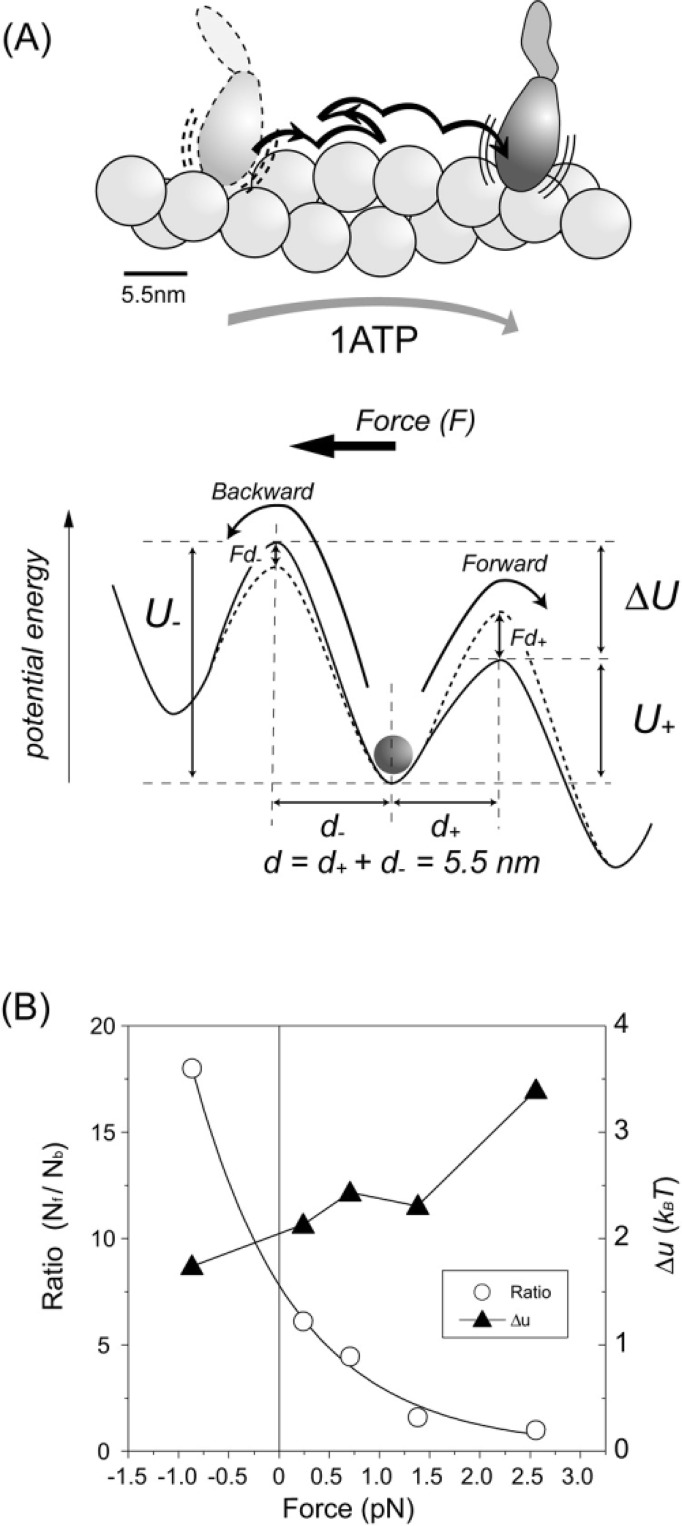
Potential profile for biased Brownian steps. (A) Biased Brownian steps of a myosin head along an actin filament (Upper) and asymmetric potential of the activation energy (Lower). (B) Ratio of forward and backward steps at various loads (open circles) and difference between the maximum potential barriers for forward and backward steps, Δu (filled triangles) (Supplement Movie 1).

In order to clarify this point quantitatively, the number of forward (N_f) and backward (N_b) steps were counted at low force levels and the (N_f /N_b) ratio was calculated. The ratio of the number of forward and backward steps near zero force (0–0.5 pN) was 55/9≈6. Thus the likelihood that the 55 forward steps out of total 64 steps were due to pure Brownian motion could be calculated as $\frac{64!}{55!9!}{\left(1/2\right)}^{55}{\left(1/2\right)}^9\approx {10}^{-9}$. In this calculation, it was assumed that no external force was applied to the S1. The S1, however, underwent steps against a force, thus, the actual likelihood should be much less. Therefore, the observed steps cannot be due to pure Brownian motion. Rather, Brownian steps of S1 are likely biased towards the forward direction.

Applying the asymmetric potential model53 presented in Fig. 9A, we analyzed the S1 Brownian steps. The activation energy of the forward and backward directions can be described by u₊ + Fd₊ and u₋ − Fd₋, respectively, where u₊ and u₋ are the heights of the potential barrier maximum at zero load, and d₊ and d₋ are the characteristic distances. Assuming the Boltzmann energy distribution, the rates in the forward and backward directions will be proportional to exp[−(u₊ + Fd₊)/k_BT] and exp[−(u₋ − Fd₋)/k_BT], respectively. Differences between the potential barriers for forward and backward steps at the load F is given by Δu − Fd = k_BTln(N_f /N_b), where Δu=u₊− u₋ and d=d₊+ d₋= 5.5 nm. Fig. 9B (open circles) shows the ratios of N_f to N_b at various loads. Using these ratios, Δu is calculated to be 2–3 k_BT (filled triangles). Thus, Brownian steps are biased by the potential energy of 2–3 k_BT at zero load. At N_f = N_b, F is calculated to be 2.5 pN, which gives the maximum force at zero velocity, consistent with that directly measured (Fig. 3D). However, this maximum force is smaller than that estimated from isometric force of muscle. Conformational changes in the myosin head coupled to Pi release may cause additional force54 as discussed later.

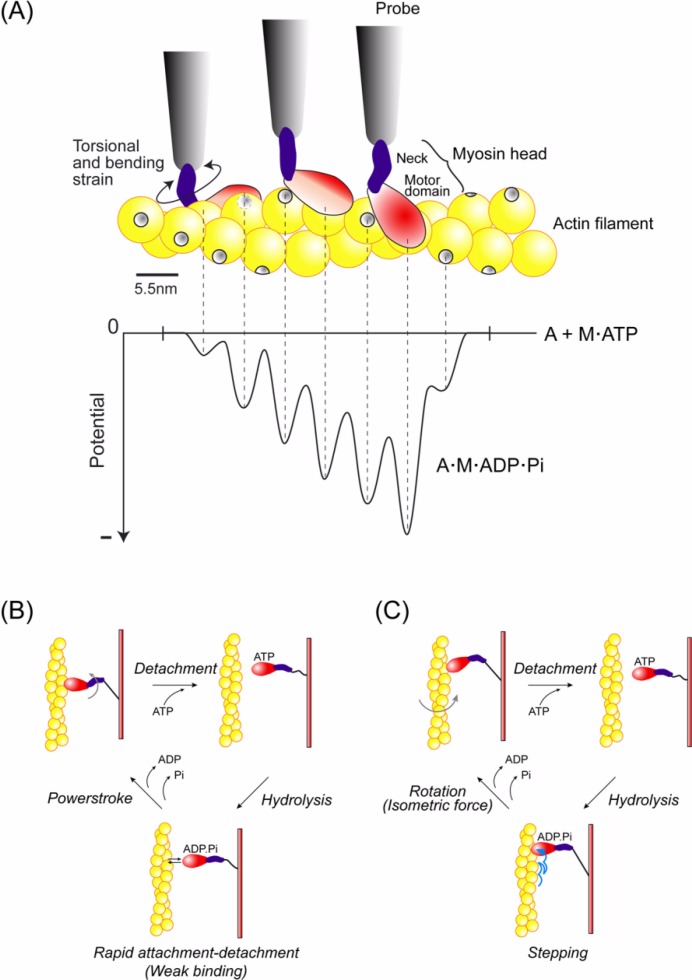
Stepping model based on preferential landing of the head

How do the myosin steps define the potential? So far, several models have been proposed33,55,56. Here, we propose a simple model assuming more realistic situations in which the potential slope is produced by a steric compatibility between the orientations of the binding sites of actin and the myosin head. The actin filament has a double helical structure and the protofilament contains 7 monomers and rotates by 180° per half helical pitch. The tail (neck domain) of the myosin head is not rigid, so the myosin head attached to the probe can move along the actin helical pitch. However, the binding sites of actin monomers rotate along the helix relative to the myosin head attached to the probe and hence the steric compatibility between the orientations of the binding sites of the myosin head and the actin should change depending on their relative positions. Thus, this steric compatibility should result in a potential slope along the actin helical pitch. If the binding site of the head faces the right side of the actin filament fixed on a glass surface, the head could favorably bind to the actin on the right side of the filament but it would be unfavorable for the head to bind to the other sides (up and left sides) of the actin filament because the head would be required to bend and rotate (Fig. 10A, Upper). Thus, the potential slope that declines along the forward direction is produced along the half helical pitch (Fig. 10A, Lower). The idea of preferential landing was originally proposed by A. F. Huxley57 while the idea of preferential landing due to such a steric effect has been also argued for myosin55,58 (Iwaki et al., personal communication) and kinesin (Taniguchi et al., personal communication).

Figure 10.

Stepping model based on preferential landing of the myosin head. (A) Potential slope along the actin half helical pitch due to the steric compatibility between the orientations of the binding sites of actin and the myosin head (see text for detail). (B) Mechanochemical coupling for the conventional model. The myosin head undergoes rapid attachment-detachment cycles with actin after ATP hydrolysis and then swings its neck domain (lever arm) to perform a powerstroke, coupled to Pi release77. (C) Mechanochemical coupling for the present model. The myosin head undergoes steps in the forward direction during attachment-detachment cycles. Coupled to Pi release, the head rotates the actin filamen60–64 (see Fig. 11) and stops the step, and isometric force may be generated7,54.

Finally, we consider the coupling between the mechanical and ATPase cycles. The myosin head dissociates from actin upon binding ATP and the bound ATP is hydrolyzed into ADP and Pi. The myosin head with ADP and Pi bound undergoes rapid attachment and detachment cycles with actin59. The myosin head steps toward the forward direction during the attachment and detachment cycles according to the potential slope along the actin helical pitch. When the head releases Pi to form the rigor complex with actin, the movement stops (Fig. 10B and C). Coupled to the Pi release, conformational changes in the myosin head take place, which rotates the actin filament and probably causes isometric force7,64 (see below).

Cooperative action of multiple myosin heads undergoing stochastic steps

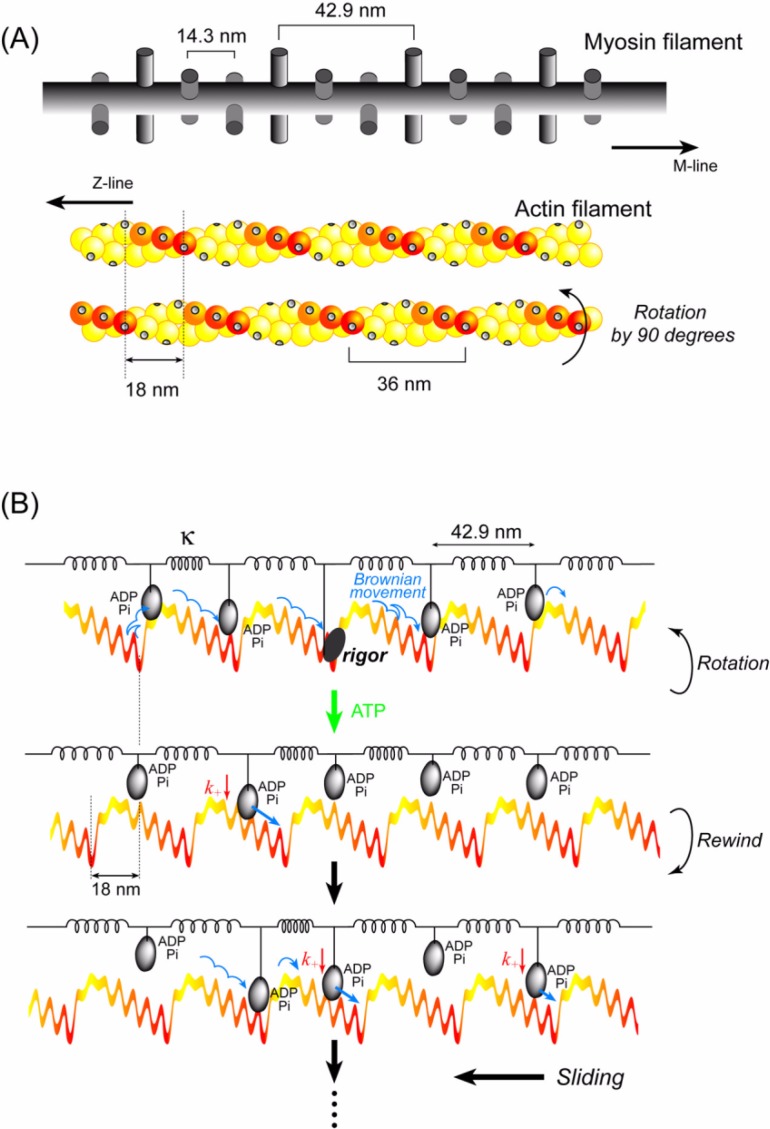
The sliding distance between actin and myosin filaments per ATP was observed to be >60 nm at zero load in muscle17,18. It is unlikely that a single myosin head continuously moves >60 nm beyond the half helical pitch of an actin filament. The maximum displacement (30 nm) per ATP observed here was actually shorter than the half helical pitch (36 nm). In muscle, however, multiple myosin heads interact with an actin filament. Therefore, we hypothesize that cooperative action of multiple heads would cause a longer sliding distance per ATP.

We assume that multiple myosin heads are bound to ADP and Pi during most of the ATPase cycle; are tethered to a myosin filament via elastic elements (neck domain and S2); and move along the actin helical pitches due to the potential slope generated by the steric compatibility (Fig. 11A). At some point in time, one of these heads releases Pi to form a rigor complex with actin (Fig. 11B Top). It has been demonstrated that the actin filament is rotated during sliding in vitro60–62 and during force generation in muscle63,64. Since the actin filament is rotated by approximately 90° in muscle64, we assume that the actin filament is rotated by 90° due to the formation of a rigor complex. The energy for rotating one end of the actin filament 1 µm long by 90°, whose other end is fixed to the z-line, is estimated to be 16–32 k_BT based on its torsional rigidity (2.6–6.7×10⁻²⁶ Nm²)65, which is similar to the free energy (20 k_BT) driven by the hydrolysis of one ATP molecule. Then, an ATP molecule binds to the rigor head to dissociate it from actin and the actin filament rewinds to its original orientation because one end of the actin filament is fixed to the z-line (Fig. 11B Middle). The myosin heads with ADP-Pi bound that have interacted with actin, of which most should be near the bottom end of the potential slope, dissociate from the actin and then gradually interact with new actin monomers. Since the potential slope is shifted by about three actin monomers — corresponding to a 90° rotation of the actin filament — the heads previously located at the potential bottom can move the actin filament again according to the new potential slope (Fig. 11B Middle and Bottom).

Figure 11.

Cooperative action of multiple heads undergoing stochastic steps. (A) Schematic diagrams of actin and myosin filaments in skeletal muscle78. The actin filament has a helical structure with a half pitch of 36 nm. The myosin filament also has a helical structure with a pitch of 43 nm and a subunit repeat of 14.3 nm. Myosin heads on a myosin filament project toward an actin filament at 43 nm intervals. In skeletal muscle, the actin and myosin filaments are arranged in a hexagonal lattice and one actin is surrounded by three myosin filaments. Therefore, the number of myosin molecules project toward one actin filament 0.7 µm long (length when fully overlapped with myosin filaments) is approximately 50. When the actin filament is rotated 90°64, the relative position between the actin helical pitches and the myosin heads shifts by approximately 3 actin monomers. The actin slopes along the actin helical pitches are represented by a color gradient. (B) Qualitative explanation of the cooperative action of myosin heads on a thick filament. The myosin filament is equivalently represented by a row of myosin heads connected with springs at intervals of 43 nm. The actin filament is represented by straight, periodic, saw-tooth shape potentials along the half helical pitches as shown in Fig. 10. Cooperative action of the myosin heads causes a long (>60 nm) sliding distance of an actin filament per ATP (see text for detail).

Based on these features, we first make a qualitative explanation of the long sliding distance in muscle. To simplify the explanation, we consider that after the rewinding of the actin filament, at first, one head interacts with the actin filament and moves it until the head moves to the bottom end of the potential slope (Fig. 11B Middle and Bottom). Then two or three heads, dissociated from actin by its rotation, interact with the actin filament and exert force on the actin filament in the forward direction (Fig. 11B Bottom). Since the potential energy produced by two or three heads is sufficient to move the first head at the potential bottom to the next forward helical pitch, the actin filament is moved further. After that, if more than four heads interact with the actin filament, it would be moved again. Thus, the actin filament can be moved more than >60 nm per ATP by cooperative action of multiple heads.

When actin filaments move on a myosin-coated surface in vitro, they rotate without limitation because their ends are free. Since the essence of the present model is that the actin filament is rotated and the potential slope is shifted relative to the myosin heads, it could be applied to the in vitro system. In the present model, each ATP turnover corresponds to rotation of 90° of an actin filament. Therefore, the sliding distance of an actin filament per rotation of 360° in vitro is given as (sliding distance/ATP)×(360°/90°). The sliding distance per ATP is obtained to be 200 nm in vitro35, so the sliding distance per rotation of 360° is 200 nm×4=800 nm, which is consistent with the results (∼1000 nm per revolution) reported in vitro61,62.

In order to test this model quantitatively, we performed computer simulations of cooperative action of multiple myosin heads undergoing biased Brownian motion along the actin helical pitches. The long (>60 nm) sliding distance per ATP could be successfully simulated by the present model (Fig. 12).

Figure 12.

Computer simulation of multiple head cooperative activity undergoing stochastic steps. We simulated cooperative action of myosin heads under a periodic and asymmetric potential as shown in Fig. 11B by numerically solving the Langevin equation,

$$0=-\rho d{x}_i/dt-dU(x_i,t)/dx+F(t)-A_i,$$

where x_i is the position of i-th myosin head; ρ is a drag coefficient; F(t) is the random force obeying a Gaussian white noise characterized by the ensemble average, <F(t)>=0 and <F(t)F(s)>=2 k_BTδ(t−s); A_i is the interaction force between the neighboring heads described as κ(x_i−x_i−1)−κ(x_i+1−x_i), where κ is the spring constant connecting the heads. The potential slope along the actin helical pitch (Fig. 10B) was simplified to be a straight saw-tooth shaped potential. Instead, the drag coefficient was set to be larger than it is in solution so that the velocity of the heads was equal to the maximum velocity in Fig. 7. Other parameters were chosen such that 1) the spring constant (κ) connecting the head was 0.1 pN/nm, which is approximately one tenth as large as that of a rigor crossbridge; 2) the ratio of potential rise to decline was 1 to 6 and the depth of the potential at the bottom was 2 k_BT; 3) the pitch of the potential and the average intervals of myosin heads were 36 nm and 43 nm, respectively; 4) the number of heads interacting with the actin filament was 11 (∼20% overlap between actin and myosin filaments); 5) the rotation angle of the actin filament was 90°; and 6) the rate constant (k₊) that the heads rebind to actin after the rewinding of the actin filament was 100 s⁻¹head⁻¹. The potential slope was assumed to be smaller than that estimated in the present experiment (see Fig. 10). The strain exerted on the neck domain would be much smaller during free shortening at zero load in muscle because the head is tethered to the myosin filament via a flexible α-helix (S2), while the head is directly attached at its tail end to the probe in the present measurement system. Thus, the potential slope depending on the strain would be smaller. (A) A typical time course of the movement of an actin filament. (B) Histogram of the sliding distance of actin filaments per ATP. The average sliding distance of actin filaments was 58.4 nm per ATP.

Comparison with other work

There has been a large body of evidence regarding conformational changes in the neck domain of the myosin head in crystals13 and in solution66 depending on the form of bound nucleotides. Furthermore, recent studies of muscle67 have suggested that the neck domain changes its angle during contraction. The observed conformational changes may contribute to the generation of isometric force at large loads but may not cause the sliding movement at smaller loads. In our stepping model (Figs. 10, 11), the conformational change in the neck domain coupled with Pi release is not the direct cause of the movement. The lever arm model hypothesizes that the neck domain swings parallel to the longitudinal axis of the actin filament to directly produce displacements in the forward direction. However, several studies using electron microscopy have suggested that the direction of the neck domain swing is not parallel but perpendicular to the longitudinal axis of actin filament7,68. Therefore, the conformational changes in the neck domain coupled to Pi release may cause the rotation of the actin filament, consistent with our model (Fig. 11).

Tsiavaliaris and his colleagues69 have demonstrated, using protein engineering, that the orientation of movement is reversed when the orientation of the neck domain is reversed. They have argued that this result strongly supports the lever arm swinging model, but this result is also consistent with our model because the direction of the myosin binding sites relative to the actin helical pitch is reversed and so the potential slope is also reversed.

Several in vitro studies using optical trapping nanometry have shown that the displacements are proportional to the length of the myosin head’s neck domain70–72. These results appear to support the lever arm swinging model. The problem with these experiments is that the reported values were not directly measured but just determined as an average of a large number of independent experiments. In these experiments, the starting positions of the displacements cannot be determined because the position of an actin filament manipulated by dual optical traps fluctuates with an amplitude much larger than that of myosin displacements due to Brownian motion. Therefore, individual displacements cannot be measured directly. The displacement can be obtained only by averaging many mechanical events generated by many heads, assuming that the starting position averaged over many events is zero43. For example, if some of heads are damaged while interacting with the surface of the glass stage or incorrectly oriented relative to the actin filament, they would not produce full displacements and hence the mean value would be underestimated. The observed proportional relationship between the neck length and displacement may be due to this effect because the effects of damage during interaction with a glass surface and incorrect orientation of heads likely decrease as the neck length increases. Individual displacements of processive, unconventional myosins can be directly measured. While some results show this proportionality71–73, others do not74–76. Furthermore, these myosins are two-headed and their movements are too complicated to analyze the relationship between step size and neck length.

Conclusions

Investigation of the load dependence of the stepping movements produced by single myosin heads revealed new aspects of the mechanism of actomyosin motors. First, the force-velocity relationship of individual actomyosin motors is similar to that of muscle. The mechanical properties of muscle are essentially the result of the intrinsic properties of individual molecules rather than whole ensembles of many molecules. Second, the actomyosin motor does not overcome thermal fluctuation (noise) but rather utilizes it to operate at an energy level as small as the average thermal energy (=∼k_BT) with a relatively high energy conversion efficiency. Third, the loose coupling between the mechanical and chemical cycles observed in muscle can be explained by the cooperation between multiple myosin heads operating in a stochastic manner. Thus, the stochastic nature of individual actomyosin motors is important for the dynamic and adaptive operation of muscle because it can adapt to the every changing demands of the muscle.

Abbreviations:

S1

Myosin Subfragment-1

RLC

regulatory light chain

BDTC

biotin-dependent transcarboxylase

TIRFM

total internal reflection fluorescence microscopy