Ubiquity of log-normal distributions in intra-cellular reaction dynamics

Abstract

The discovery of two fundamental laws concerning cellular dynamics with recursive growth is reported. Firstly, the chemical abundances measured over many cells were found to obey a log-normal distribution and secondly, the relationship between the average and standard deviation of the abundances was found to be linear. The ubiquity of these laws was explored both theoretically and experimentally. By means of a model with a catalytic reaction network, the laws were shown to exist near a critical state with efficient self-reproduction. Additionally, by measuring distributions of fluorescent proteins in bacteria cells, the ubiquity of log-normal distribution of protein abundances was confirmed. Relevance of these findings to cellular function and biological plasticity is briefly discussed.

The search for universal statistics with regards to fluctuations in cellular dynamics is an important topic in biophysics. Generally, the molecule numbers of the various chemical species (e.g., proteins) change from cell to cell. Since many intra-cellular reaction processes are finely tuned to specific functions, one would initially expect the number distributions of the involved chemical species to be sharp in order to suppress fluctuations. In reality, however, they are far from sharp, and large fluctuations do occur. In order to understand how cells can function nonetheless, it is essential to gain an insight into the statistics of chemical abundances.

Indeed, fluctuations in cellular processes have been extensively studied in stochastic gene expressions and signal transduction recently1–5. In particular, significant advances have been made in the study of their distributions using fluorescent proteins6,7. In light of these recent advances, it is important to look for general laws that hold for such distributions.

Previously, by using a simple reaction network model, we found a universal power-law distribution in the average abundances of chemicals in cells8. The theoretical conclusions were confirmed with the help of large-scale gene expression data8–10. The above power-law concerned an average over all chemical species and formed a first step in the study of universal statistics in cellular dynamics. As for the next step, it is important to explore universal characteristics with regards to the distribution of each chemical over the cells.

Here, we report two basic laws for the number distributions of chemicals in cells that grow recursively. The first law is a log-normal distribution of chemical abundances measured over many cells, and the second law is a linear relationship between the average and standard deviation of chemical abundances. We give a heuristic argument as to why these laws should hold for a cell with steady growth, and demonstrate the laws numerically using a simple model for a cell with an internal reaction network. Lastly, the results of an experimental study confirming the two laws are presented.

Indeed, the log-normal distribution is clearly different from the Gaussian distribution normally adopted in the study of statistical fluctuations, and has a much larger tail for greater abundances. Hence the generality of the laws we report is of considerable significance for all the statistical studies of cellular fluctuations, and is essential to understanding cellular function, adaptation, and evolution.

Heuristic argument

Cells contain huge numbers of chemicals that catalyze each other and form complex networks. For a cell to replicate itself recursively, a set of chemicals has to be synthesized from nutrients supplied from the outside through biochemical processes driven by the same set of chemicals. Consequently, it is natural to consider an auto-catalytic process as the basis of biochemical dynamics within replicating cells.

As a very simple illustration, let us consider an auto-catalytic process where a molecule (or a set of molecules) x_i is replicated with the aid of other molecules. Then, the growth of the number n_i(t) of the molecule species x_i is given by dn_i(t)/dt=An_i(t) with A describing the rates of the reaction processes that synthesize the molecule x_i. Clearly, this kind of synthetic reaction process depends on the number of the molecules involved in the catalytic process. At the same time, however, all chemical reaction processes are inevitably accompanied by fluctuations arising from the stochastic collisions of chemicals. Thus, even when the reactions that synthesize a specific chemical to subsequently convert it to other chemicals are balanced in a steady state, fluctuation terms will remain. Consequently, the above rate A has fluctuations η(t) around its temporal average ā such that dn_i(t)/dt = n_i(t)(ā + (t)), and hence we obtain

$$d\text{log}{n}_i(t)/dt=\overline{a}+\eta (t).$$ (1)

In other words, the logarithm of the chemical abundances shows Brownian motion around its mean, as long as η(t) is approximated by random noise. Accordingly, one would expect the logarithm of the chemical abundances (i.e. molecule numbers) to obey a normal (Gaussian) distribution (this kind of a distribution is known as a log-normal distribution)11. In contrast to the Gaussian distribution, the log-normal distribution has a longer tail, representing the higher frequencies of greater abundances when plotted in the original scale without taking the logarithm.

In general, at each step of the auto-catalytic process, a multiplicative stochastic factor η(t)n_i can appear. Consequently, a log-normal distribution of chemical abundances, rather than a Gaussian distribution, may be common for cells that reproduce recursively.

Of course, the above argument is too simplistic to describe the dynamics of actual cells. For example, fluctuations may be suppressed since an increase in chemical abundance does not continue forever due to cell divisions, which may thus alter the form of the distribution. Furthermore, in a complex biochemical reaction network, several reaction processes may work in parallel for the replication of a chemical. This leads to the addition of fluctuation terms, and the central limit theorem of probability theory could imply that the distribution becomes Gaussian.

Hence it is far from clear whether the simple argument to support the log-normal distribution is valid or not. Nevertheless, since the log-normal distribution is rather different from the standard Gaussian distribution, its universality is of great importance for understanding the fluctuations in cells and stochastic gene expressions. Here we will confirm the validity of the law both theoretically and experimentally.

Model study with catalytic reaction network

In order to search for universal laws of replicating cells which are independent of details, we employed a simple reaction network model following Ref. 8. Consider a cell consisting of a variety of chemicals. The internal state of the cell can be represented by a set of numbers (n₁, n₂, ..., n_k), where n_i is the number of molecules of the chemical species i with i ranging from i=1 to k. We chose a randomly generated catalytic network among these k chemicals, where each reaction from some chemical i to some chemical j was assumed to be catalyzed by a third chemical l, that is (i+l → j+l). For simplicity all the reaction coefficients were chosen to be equal, while the connection paths of this catalytic network were chosen randomly, such that the probability of any two chemicals i and j to be connected is given by the connection rate ρ.

Some chemicals diffuse between the cell and the environment with the diffusion coefficient D. Among the penetrable chemicals, nutrients without catalytic activity are supplied by the environment. Through the catalytic reactions to synthesize impenetrable chemicals, the total amount of chemicals N=∑_in_i in a cell increases, and when the total amount of chemicals is beyond some threshold N_max, the cell divides into two. This growth and division process is repeated. In the numerical simulations, we randomly picked up a pair of molecules in a cell, and transformed them according to the reaction network. In the same way, diffusion through the membrane was also computed by randomly choosing molecules inside the cell and nutrients in the environment (see Ref. 8 for details of the model).

As the diffusion coefficient D increases, the growth speed of the cell increases up to a critical value D_c after which the cell ceases growing because the flow of nutrients from the environment is so fast that the internal reactions transforming them into chemicals sustaining its ‘metabolism’ cannot keep up. As discussed in Ref. 8, the intra-cellular dynamics at D≈D_c is biologically relevant due to the efficient recursive growth for this value, and its statistical property of chemical abundances, i.e., the power-law distribution with exponent-1 was confirmed experimentally for almost all the cells we investigated. Accordingly, this simple model captures enough basic properties of a cell to adequately reflect universal statistical properties and we therefore chose it to measure the distribution of each chemical’s abundance over many cells, by sampling them over a large number of divisions.

Results of simulations

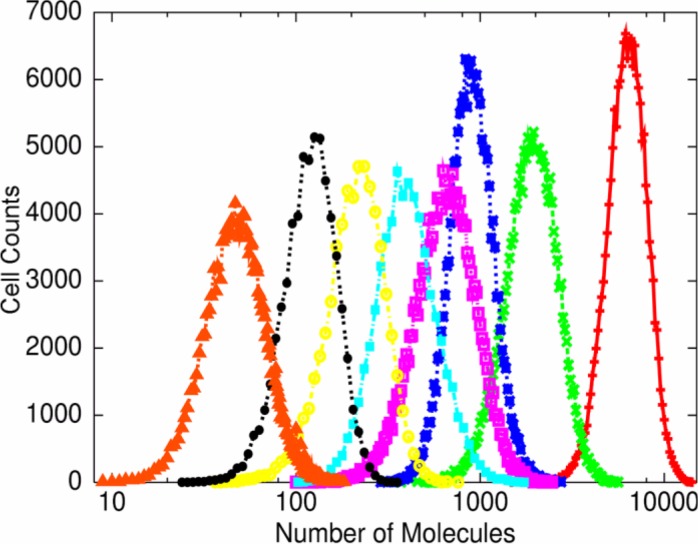
In Fig. 1, the number distributions of several chemicals for D≈D_c were plotted*1. Here we measured the number of molecules of each chemical when a cell divides into two and the distribution indeed was nearly log-normal. i.e.

$$P(n_i)\approx \mathit{exp}\left(-\frac{{\left(\text{log}{n}_i-\text{log}{\overline{n}}_i\right)}^2}{2\sigma }\right),$$ (2)

where n̄_i indicates the average of n_i over the cells.

Figure 1.

The number distribution of the molecules of chemical abundances of our model. Distributions were plotted for several chemical species with different average molecule numbers. The data were obtained by observing 178800 cell divisions.

This log-normal distribution holds for the abundances of all chemicals except for those that are supplied externally as nutrients which obey the standard Gaussian distribution. In other words, those molecules that are reproduced in a cell obey a log-normal distribution, while nutrients that are just transported from the outside of a cell follow a Gaussian distribution.

Why would the log-normal distribution law generally hold, in spite of the fact that the central limit theorem implies that the addition of several fluctuation terms should lead to a more Gaussian distribution? This can be understood by considering that the recursive production process is a cascade reaction near the critical state D≈D_c8. At this point, a small part of au the possible reaction pathways is dominant and organized in a cascade of catalytic reactions, so that a chemical in the j-th group is catalyzed by a chemical in the (j+1)-th group. In other words, a “modular structure”, with groups of successive catalytic reactions, is self-organized in the network. In this cascade of catalytic reactions, fluctuations propagate “multiplicatively”; for example, the concentration fluctuation of a chemical in the (j+2)-th group influences multiplicatively that of the (j+1)-th group, which then influences multiplicatively that of the i-th group, and so forth. The result of this multiplicative effect is the log-normal distribution of n_i*2. Note that, at the critical state with which we are concerned, this cascade of catalytic reactions continues over all chemical species that are reproduced, and that the log-normal distribution holds firm. The importance of cascade processes for a log-normal distribution is also studied in the theory of turbulence12, where an energy cascade leads to a multiplicative creation of vortices. In the present case, a cascade in the catalytic reaction is essential for a log-normal distribution.

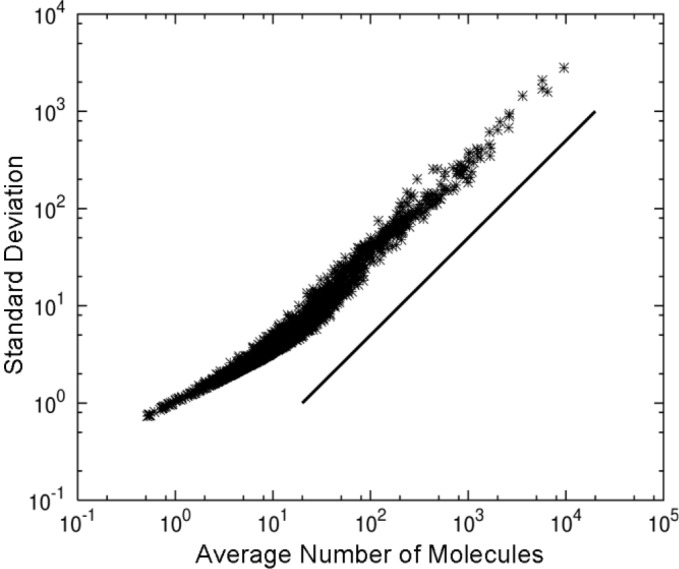
The width of the distribution for each chemical, shown in Fig. 1, looks almost independent of its average. This suggests a connection between the fluctuations and the averages of the chemicals. We therefore plotted the standard deviation of each chemical $\sqrt{\overline{{\left(n_i-\overline{n_i}\right)}^2}}$ as a function of the average n̄_i in Fig. 2, and indeed found a linear relationship between the standard deviation (not the variance) and the average number of molecules. This can be understood by considering the steady growth and cascade structure of the catalytic reactions. Take two chemicals i and j, one of which (j) catalyzes the synthesis of the other in the cascade. During the steady growth phase of a cell, the synthesis and conversion of chemical i should be balanced, i.e., n_j × A−n_i× B=0, where A and B are average concentrations of other chemicals involved in the catalytic reaction. The average concentration then satisfies n̄_j /n̄_i = A/B. Taking into account that the relation remains satisfied as n_i, n_j, ... increase while the cell grows, it is natural to assume that the relationship holds for the fluctuations of the average as well: $<\delta n_j{>}^2/<\delta n_i{>}^2={\left(A/B\right)}^2={\overline{n_j}}^2/{\overline{n_i}}^2$. Hence the variance is expected to be proportional to the square of the mean, yielding the linear relationship between the mean and the standard deviation.

Figure 2.

Standard deviation versus average number of molecules. Using the same data set and parameters as for Fig. 1, the relationship between the average and standard deviation was plotted for all chemical species. The solid line is for reference.

A linear relationship was also found with regard to the variation of the chemical abundances when changing the external conditions. For example, we computed the change from n̄_i to ${\overline{n^{\prime }}}_i$ by varying the concentrations of the supplied nutrients. The variation $\left|{\overline{n^{\prime }}}_i-{\overline{n}}_i\right|$ was again found to be proportional to n_i for each chemical i, similar to the data plotted in Fig. 2.

Through extensive simulations of a variety of related models, we confirmed that the discovered laws hold generally and do not rely on the details of the model, such as the kinetic rules of the reactions, or the structure of the reaction network, including networks with heterogeneous path connectivity as scale-free topology. They are universal properties of replicating cellular systems near the critical state D≈D_c.

Of course, the arguments for the two laws thus far are based on the recursive production of a cell. In general, there can be deviations from the two laws if the steady growth condition for a cell is not satisfied. In the present case, for example, recursive production is not possible when the parameter D is much smaller than D_c, as all the possible reaction pathways occur with similar weights, or if the cascade of catalytic reactions is replaced by a random reaction network. In this case, the fluctuations of the molecule numbers were highly suppressed, and the distributions were close to normal Gaussian. The multiplicative stochastic process supported by the cascade of catalytic reaction was replaced by several parallel catalytic processes, and the central limit theorem for the addition of stochastic processes would lead to a Gaussian distribution of chemicals.

Furthermore, we confirmed numerically that the variance (not the standard deviation) increases linearly with the average concentrations. In other words, the “normal” behavior expected from the central limit theorem is observed.

Experiment

Here, we report experimental confirmations of the two basic laws on the distributions of abundances. Recalling that these laws are expected to hold for the abundances of a protein synthesized within cells with recursive (steady) growth, we measured the distribution of protein abundances in Escherichia coli that are in an exponential phase of growth, i.e., in a stage of steady growth*3. To obtain the distribution of protein abundances, we introduced fluorescent proteins with appropriate promoters into the cells, and measured the fluorescence intensity by flow cytometry. To demonstrate the universality of the laws, we carried out several sets of experiments, by using a variety of promoters and also by changing the places were the reporter genes were introduced (i.e., on the plasmid or on the genome).

The detailed experimental procedures are as follows.

Method

Plasmids and strains

Reporter plasmids were constructed by subcloning tetA promoter from pASK-IBA3 (Sigma Genosys) and egfp gene (BD Biosciences Clontech) into pPROTet.E 6xHN (BD Biosciences Clontech) and dsred.t4 gene coding red fluorescence protein (RFP)13 into pTrc99A (Amersham Biosciences). E. coli strain OSU2, a derivative of DH5α that lacks glutamine synthetase gene, was transformed with these reporter plasmids. E. coli strain OSU5 was constructed by replacing glnA gene with tetA promoter and gls-h14 fused with gfpuv515 gene by homologous recombination16.

Culture and measurements.

Cultures of strain OSU2 with the reporter plasmid were grown in LB medium with 100 μg/ml ampicillin for 6 h at 37°C. To obtain a high expression level of RFP, the culture was grown to mid-exponential growth and then induced with 1 mM isopropyl-β-D-thiogalactoside (IPTG) for 3 h at 37°C. E. coli OSU5 was grown in a minimal medium (0.1 M Sodium L-Glutamate Monohydrate, 4 g/l glucose, 10.5 g/l K₂HPO₄, 4.5 g/l KH₂PO₄, 50 mg/l MgSO₄7H₂O, 50 mg/l thiamine HCl, 10 μM FeSO₄7H₂O, 0.5 μM CaCl₂, micronutrient solution17, 25 μg/ml kanamycin) for 24 h at 37°C. All expression data were collected using a COULTER^®EPICS^®ELITE flow cytometer with a 488-nm argon excitation laser and bandpass filter at 525±25 nm for GFP fluorescence and 600-nm dichroic filter for RFP fluorescence. For each culture, 10,000 events were collected. We confirmed that the flow cytometer was within its dynamic range, by using commercialized beads with a known amount of fluorescent dye. All flow data were converted to text format using WinMDI Version 2.8.

Results

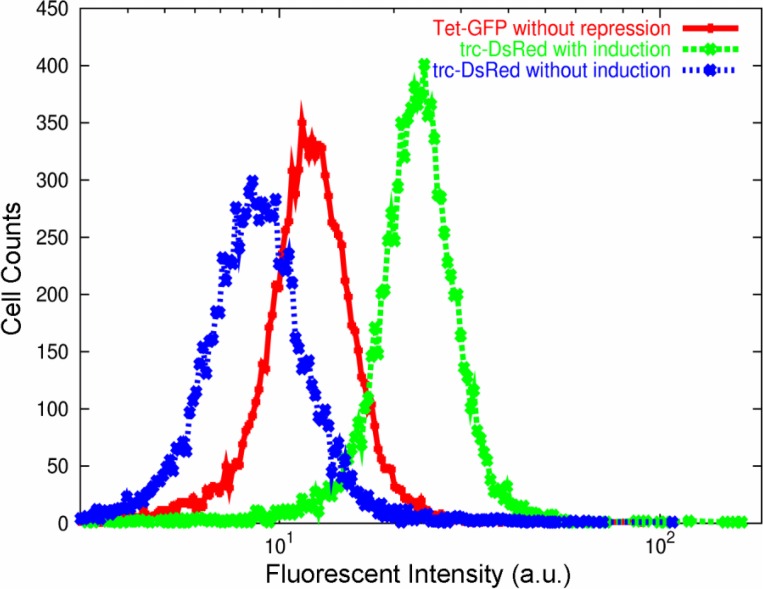
In Fig. 3, we plotted the distributions of the emitted fluorescence intensity from Escherichia coli cells with reporter plasmids containing either EGFP (enhanced green fluorescent protein) under the control of the tetA promoter without repression, or dsRed.t4 (monomeric red fluorescent protein) under the control of the trc promoter with and without IPTG induction18. In general, the fluorescence intensity (the abundance of the protein) increased with the cell size. To avoid the effect of variation in cell size, which may also obey log-normal distribution, we normalized the fluorescence intensity with the volume of each cell. Here we adopted the forward-scatter (FS) signal from the flow cytometry to estimate cell volume. Infact, by plotting data of the fluorescence intensity versus FS signal, the two were proportional in general. (The data points were distributed around the proportionality line between the two, as was generally observed in the plot of fluorescence intensity made by flow cytometry). Thus, we normalized the fluorescence intensity by dividing it with the FS signal. Fig. 3 is the distribution of this normalized fluorescence intensity. Note that all these data fit well with log-normal, rather than Gaussian, distributions, even though each of the expressions is controlled by a different condition of the promoter.

Figure 3.

The number distribution of the proteins measured by fluorescence intensity, normalized by the cell volume. Distributions were obtained from three Escherichia coli cell populations containing different reporter plasmids (see text). Note that, although the IPTG induction changes the average fluorescence intensity, both the distributions (with and without the induction) can be fitted to log-normal distributions well.

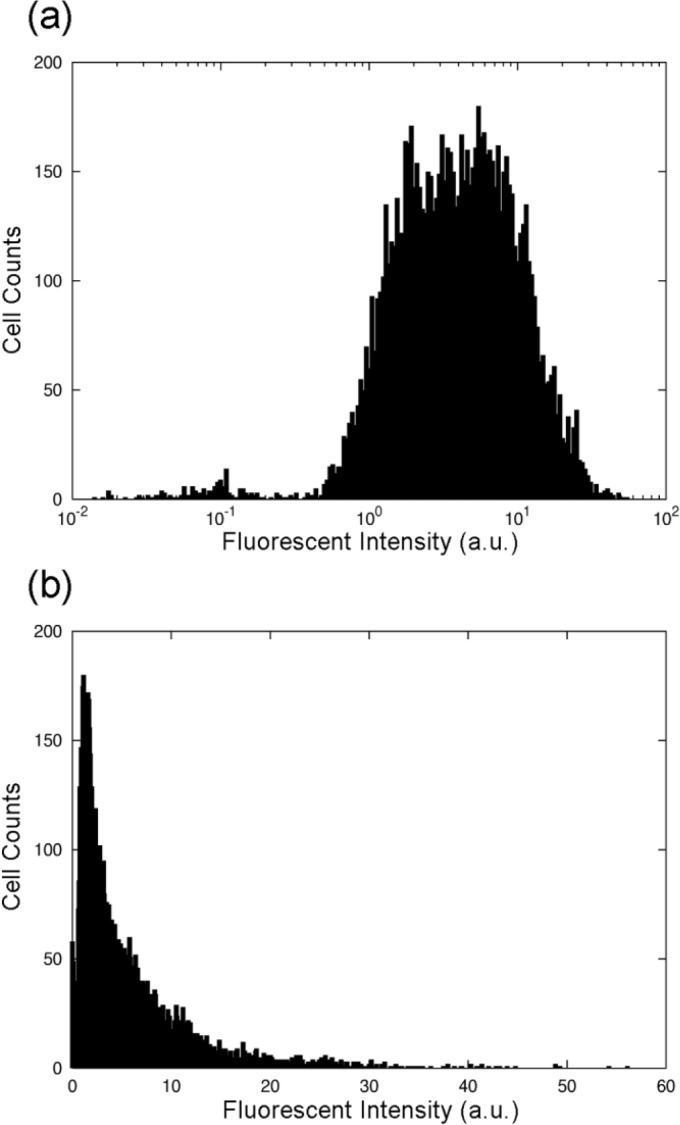
To clarify the existence of a larger tail for greater abundances of proteins, in Fig. 4, we plotted the distribution of protein abundances both in a logarithmic scale and in a normal scale. The abundances of fluorescent protein expressed from the chromosome was also found to obey the log-normal distribution, as shown in Fig. 4. Here, the data was obtained from Escherichia coli cells with an expression of glutamine synthetase (GS) fused to GFP in the chromosome, whose expression is controlled by an upstream tetA promoter. In Fig. 4, the distribution of fluorescence intensity, again normalized by cell volume, is plotted. As can be seen, when using the logarithmic scale (a), the distribution is roughly symmetrical and close to Gaussian, while when using the normal scale (b), the distribution has a larger tail on the side of greater abundances. The fact that a log-normal distribution was also observed when genes were located on the genome indicates that the nature of the log-normal distribution was not due to a variation in plasmid copy number. We also examined several other cases using different reporter genes both on the plasmids and on the genome, and obtained similar results supporting the universality of log-normal distributions. It is furthermore interesting to note that the abundances of fluorescent proteins, reported in the literature so far, have been often plotted with a logarithmic scale7.

Figure 4.

The distribution of the fluorescence intensity normalized by the cell volume, plotted (a) with a logarithmic scale and (b) with a normal scale. Data were obtained from a population of isogenic bacterial cells with an expression of GFP-GS fusion protein in the chromosome. It is clear that the distribution with the logarithmic scale is symmetric and close to a Gaussian form.

It should be noted that the log-normal distribution of protein abundances is observed when the E. coli are in the exponential phase of growth, i.e., when the bacteria are in a steady growth stage. For other phases of growth without steady growth, the distribution often deviates from a log-normal distribution, and sometimes shows distribution with double peaks, as will be reported in the future. Note that this theory supports the log-normal distribution for the steady growth case only.

As for the linear relationship between the variation and the average, Banerjee et al.19 recently reported that the standard deviation of gene expressions in cell population is proportional to the average expression level, which supports the relationship discovered in our study. However, using a different system, Ozbudak et al.20 showed that the standard deviation of gene expression is not proportional to its average, but that the variance increases linearly with the average. However, in these studies, the dynamic ranges of the measurements were relatively narrow and the growth conditions of cells were not kept precisely in the log phase, so that the conditions for the steady growth were not satisfied. To confirm the linear relationship between the standard deviation and the average, further experimental studies with a wide dynamic range of measurements and precise control of the steady cellular growth are required.

Discussion

To sum up, we report universal laws on the distributions of chemical abundances in cells with steady growth. Firstly, the distribution of chemical abundance obeys a log-normal distribution due to the multiplicative propagation of fluctuations. Secondly, there is a linear relationship between the average and standard deviation of chemical abundances. Since the laws generally appear near the critical state D≈D_c, and the dynamics at the critical state provides a faithful and efficient self-reproduction of a cell8, it is natural to conclude that cells generally hold these laws. We have also shown experimental confirmations of the law using E. coli cells, where the number distribution of fluorescent proteins obeys the log-normal distribution, independent of the conditions of promoters and locations of reporter genes. The ubiquity of the discovered log-normal distributions can be a solid basis for the study of fluctuations in cells. It should be stressed that a log-normal distribution of chemical abundances implies that the average magnitude of the fluctuations is much larger than what one would observe for a normal distribution. However, at the present time, analysis of cellular heterogeneity mostly relies on a Gaussian distribution in the abundance of chemicals. Hence, our discovery for the ubiquity of log-normal distribution sets drastic and essential changes to future studies concerned with fluctuations in cellular dynamics.

Clearly, these laws bear relevance to adaptation and evolution21, since the role of phenotypic fluctuations cannot be neglected. With these two laws in mind, it is important to study how cells maintain their functions and replicate themselves successfully, despite being subjected to such large fluctuations, and to search for possible relationships between the topology of the reaction networks and the fluctuations in intra-cellular reaction dynamics. Likewise, the search for some ‘exceptional’ chemicals that do not follow the log-normal distribution that may be located at specific positions in the network will be of interest. Indeed, the log-normal distribution appears as a result of multiplicative propagation of noise in cascade catalytic reaction processes, and the distribution could be sharpened by an interference of parallel reaction processes, including a negative feedback loop.

Finally, we note again that the observed laws hold for a cell that grows recursively. For cells undergoing a change of state, the distribution may be distorted or have double peaks, as was observed when the condition of the culture was changed or in the course of cell differentiation. The present two laws could be a basis for studying such a change of distribution as a measure of biological plasticity.