Ratio of membrane proteins in total proteomes of prokaryota

Abstract

The numbers of membrane proteins in the current genomes of various organisms provide an important clue about how the protein world has evolved from the aspect of membrane proteins. Numbers of membrane proteins were estimated by analyzing the total proteomes of 248 prokaryota, using the SOSUI system for membrane proteins (Hirokawa et al., Bioinformatics, 1998) and SOSUI-signal for signal peptides (Gomi et al., CBIJ, 2004). The results showed that the ratio of membrane proteins to total proteins in these proteomes was almost constant: 0.228. When amino acid sequences were randomized, setting the probability of occurrence of all amino acids to 5%, the membrane protein/total protein ratio decreased to about 0.085. However, when the same simulation was carried out, but using the amino acid composition of the above proteomes, this ratio was 0.218, which is nearly the same as that of the real proteomic systems. This fact is consistent with the birth, death and innovation (BDI) model for membrane proteins, in which transmembrane segments emerge and disappear in accordance with random mutation events.

In the course of evolutionary time, a wide variety of biological systems have formed that combined various types of proteins. Therefore, the numbers or ratios of particular kinds of proteins in a proteome characterizes the life strategy of a biological organism1,2. Since membrane proteins are located at the boundary between the external environment and the cell, and thus have very important functions, the ratio of membrane proteins to total proteins in currently existing genomes provides us with an important clue about how membrane proteins have evolved under various environmental conditions.

Two models of the evolution of the protein world have been proposed: the stochastic birth, death and innovation model2–4, and the duplication and recombination model1,5. In the former, members of protein families shift between different families, due to random mutation, and the kinds of proteins spontaneously increase over time. In the latter, the most important factor driving the complexity of proteomes is domain duplication and recombination. It is important to note here that both models originally were proposed on the basis of the incomplete classification of proteins, in the sense that the classification was based on the homology of sequences to known, experimentally investigated proteins. It is well known that about a half of proteins which are coded in total genomes are not homologous to any known proteins. Therefore, the behaviors of half of proteins in total proteomes cannot be discussed at all, if the analysis depends on the sequence homology. Thus, a complete classification of proteins in total proteomes is necessary for obtaining a meaningful conclusion concerning the relative contributions of the two models to the evolution of the proteins world.

Previously, we developed a high performance membrane protein predictor, SOSUI, on the basis of the following physicochemical parameters: hydrophobicity and amphiphilicity of amino acids, and size of proteins6–8. The accuracy of this system is better than 95%. The SOSUI system has two advantages over other systems: (1) the probability of the false-positive prediction of membrane proteins by the SOSUI system is much lower than those of other methods: The false positive prediction for SOSUI system is smaller than 7%, while the corresponding values for other systems that are now available through internet are larger than 10%. Therefore, SOSUI currently provides the best estimation of the ratio of membrane proteins to soluble ones, an important parameter that is necessary for properly analyzing the stochastic birth, death and innovation model; (2) domain duplication and recombination introduce higher order into an amino acid sequence. The control data used for the duplication and recombination model are completely random amino acid sequences. However, other prediction systems that use a database approach cannot properly handle this control data. In contrast, because SOSUI is a physics-based system, it is applicable to unknown sequences and even to completely random sequences.

In this study, we estimated the numbers of membrane proteins in the total proteomes of 248 prokaryota, and also generated randomized sequences of all proteins for these proteomes. The results showed that the ratios of membrane proteins to total proteins were almost constant for all real proteomes. The corresponding ratios for random sequences were also constant for all proteomes, but the proportionality constant for real proteomes was three times larger than that of the random sequences, when the probability of occurrence of all kinds of amino acids was set to 5%. However, when the amino acid composition of the actual proteomes was used for the simulation, the membrane protein/total protein ratios were close to the actual values for the real proteomes. The contribution of the two models to the evolution of the protein world is discussed, based on a comparison of the membrane protein ratios in the real and randomized genomes.

Results

Number of membrane proteins in proteomes

All amino acid sequences from the total genomes of 248 biological organisms were analyzed for estimation of the ratio of membrane proteins to total proteins in total proteomes. The number of membrane proteins is plotted as a function of the number of all proteins for 248 prokaryote organisms in Figure 1A. In this analysis, we first predicted membrane proteins using the software system SOSUI, and then secretory proteins were removed from the resulting membrane protein set by using the signal peptide predictor SOSUIsignal; both predictors are sufficiently accurate for reliable statistical analysis (the accuracy of SOSUI system is better than 95%). The linearity between the numbers of predicted membrane proteins to that of all proteins in the proteomes was surprisingly good, as seen in Figure 1A, and the R²-value of the correlation was 0.933. The coefficient was 0.228, indicating that about a quarter of amino acid sequences code membrane proteins and that the deviation from the average ratio was small for all biological organisms. When the proportionalities for eubacteria and archaea were analyzed independently, the results were nearly the same: the ratio for eubacteria and archaea were 0.228 and 0.229, respectively, and the corresponding R²-values were 0.930 and 0.927. The fact that the membrane protein/total protein ratio is nearly constant for all organisms suggests the existence of a general mechanism for the conservation of the number of membrane proteins.

Figure 1.

Ratio of membrane proteins to total proteins for various organisms was estimated by prediction systems SOSUI and SOSUIsignal, leading to an average constant value of 0.23. (A) Number of membrane proteins is plotted as a function of total ORFs for 248 prokaryota. The solid blue line was obtained by least square deviation analysis: y=0.228x, with an R²-value of 0.933. (B) The distribution of the deviation from the constant ratio calculated by equation (4) is shown for all organisms. A Gaussian distribution fitted to the data points is represented as a solid blue line. Skewness, kurtosis and standard deviation of distribution are 0.347, 2.404 and 1.561, respectively.

The deviation from the average membrane protein/total protein ratio provides information indicating whether or not the elementary process in determining the constant ratio of membrane proteins is random. If the elementary process is random, the distribution of the deviation around the average ratio must be a Gaussian distribution. The distribution of the deviation analyzed using equation (4) can be very well fitted to a Gaussian distribution (Fig. 1B). Here, we used the deviation normalized by the square root of the number of amino acid sequences in the proteome. The observed standard deviation of 1.561 indicates that the linearity is very good. For example, the standard deviation for an organism with an ORF number of 10000 is about 140, which is only 1.4% of the total number of sequences. The skewness and the kurtosis of the Gaussian distribution were 0.347 and 3.404, respectively9. These values indicate that the deformation of the distribution is very small, since these values are very similar to the skewness and the kurtosis of the ideal Gaussian distribution, 0.0 and 3.0, respectively.

Although the mechanism of the elementary process behind the evolutionary birth and death of membrane proteins as specific types of protein cannot be identified only by this kind of analysis of real proteomes, very important conclusions are obtained from Figures 1A and 1B. First, the universally constant membrane protein/total protein ratio, at least for this set of proteomes, strongly suggests a common mechanism for the development of the protein world. Second, the Gaussian distribution of this ratio around the average value leads to the hypothesis that the mechanism of the constant ratio of membrane proteins contains some random processes.

Simulation of point mutations in total proteomes

The most general mechanism for the change in amino acid sequences is the point mutation. Therefore, we thought it would be interesting to use simulated point mutations to study the effect of randomizing amino acid sequences on the membrane protein/total protein ratio. To accomplish this, we carried out a simulation of 1000 mutational steps, in which point mutations were introduced at the rate of one mutation per 100 residues at each step. We carried out three kinds of simulations, with each simulation defined by using a specific type of amino acid composition for the protein sequences of a proteome. It should be pointed out that only the point mutations in amino acid sequences are considered and the creation of membrane proteins is not in the scope of this simulation.

In the first simulation, the probability of the occurrence of amino acids was set to the constant value of 5%. In Figure 2A, the variation in the membrane protein/total protein ratio is shown as a function of the number of mutational steps for the case of Escherichia coli K12. For clarification purposes, the variation to the 1000-th step is shown. The membrane protein/total protein ratio decreased monotonically until a plateau was reached at around 300 steps of the simulation. Because one step includes 1% of mutation, the appearance of the plateau means that the sequences were completely randomized after about 300 steps. Therefore, a ratio of membrane protein to total protein of about 8% at the plateau must be a characteristic of completely random sequences. The decrease of about 0.15 in Figure 2A by the extensive mutations is much lower than the fluctuation of the ratio. We also estimated the systematic error due to the false positive and false negative prediction by SOSUI system. The result showed that the systematic error is about 0.04 which is much smaller than the change in Figure 2A. Therefore, the decrease of about 0.15 is clearly beyond various types of errors.

Figure 2.

Ratio of membrane proteins to total proteins for randomized proteomes also was found to be constant for all organisms, but the average value was 0.085, which is much smaller than the corresponding value for the real proteomes. (A) The solid green line represents the variation in this ratio for Escherichia coli K12, plotted as a function of the randomized simulation up to the 1000-th step. The dotted green line represents the average of the set of membrane protein/total protein ratios of E. coli K12, from mutation steps 300 to 1000, this value being 0.084. (B) Numbers of membrane proteins at the 400-th mutational step are plotted as a function of the numbers of all proteins coded in total genomes. The solid green line is obtained by least square deviation analysis: y=0.085x, with an R²-value of 0.985. Gray closed triangles and solid line indicate the result of Fig. 1A for comparison. (C) The distribution of the deviation from the constant ratio at the 400-th mutational step is shown for all organisms. A Gaussian distribution fitted to the data points is represented as a green line. Skewness, kurtosis and standard deviation of distribution are 0.177, 3.106 and 0.362, respectively. Gray closed triangles and solid line indicate the result of Fig. 1B for comparison.

It is remarkable that the membrane protein/total protein ratio remains almost constant throughout the entire set of organisms (Fig. 2B). Although an essentially constant ratio was maintained even after complete randomization, the proportionality constant, as well as the standard deviation from the average values, were different. For complete randomization, this ratio and the R²-value were 0.085 and 0.985, respectively, at the 400-th mutational step (green line in Fig. 2B), while the standard deviation was 0.362. In comparison to the values for the real proteomes (blue line in Fig. 1A, gray line in Fig. 2B), both the ratio and the standard deviation were three times smaller. Since the skewness and the kurtosis were 0.177 and 3.106, respectively, the deformation from the Gaussian distribution was very small (Fig. 2C).

The second simulation also introduced random mutations, but used the amino acid compositions of the real proteomes. Figure 3A shows the variation in the membrane protein/total protein ratio for the E. coli K12 proteome, starting from the real sequences to the 1000-th mutational step. The result of the simulation presented in Figure 3A is clearly different from that shown in Figure 2A. The membrane protein/total protein ratio in the simulation based on the amino acid composition of the real proteome was nearly constant throughout the entire simulation process. Figure 3B show the numbers of predicted membrane proteins at the 400-th step of mutation for every organism as a function of the numbers of proteins in the proteomes, while Figure 3C is the distribution of the deviation from the average value of the membrane protein/total protein ratio. Surprisingly, the membrane protein/total protein ratio for the sequences that were randomized starting from the amino acid compositions of the real proteomes was nearly the same as that of the real proteomes, suggesting that the natural selection in the real organisms dose not influence the ratio so much. Moreover, the distribution of the deviation for these random sequences was also the same as that of the real proteomes. Taken together, these results revealed that the membrane protein/total protein ratio and the standard deviation depend on the amino acid compositions. Furthermore, the membrane protein/total protein ratio in the real proteomes seems to be determined by the amino acid composition.

Figure 3.

The average membrane protein/total protein ratio for randomized proteomes, using the amino acid compositions observed in the real proteomes, was 0.22. (A) The solid red line represents the variation of this ratio for the case of Escherichia coli K12. A dotted green line represents the average the set of membrane protein/total protein ratios in the simulation of the point mutations for the proteome of E. coli K12, this value being 0.247. The result of the simulation in Fig. 2A is shown with solid and dotted gray lines for comparison. (B) Numbers of membrane proteins at the 400-th mutational step is plotted as a function of the numbers of total proteins. The solid orange line was obtained by the least square deviation analysis: y=0.218x, with an R²-value of 0.891. Gray closed triangles and solid line indicate the result of Fig. 1A for comparison. (C) The distribution of deviation from the constant ratio at the 400-th mutational step is shown for all organisms. A Gaussian distribution fitted to the data points is represented by an orange line. Skewness, kurtosis and standard deviation of distribution are −0.040, 3.897 and 1.715, respectively. Gray closed triangles and solid line indicate the result of Fig. 1B for comparison.

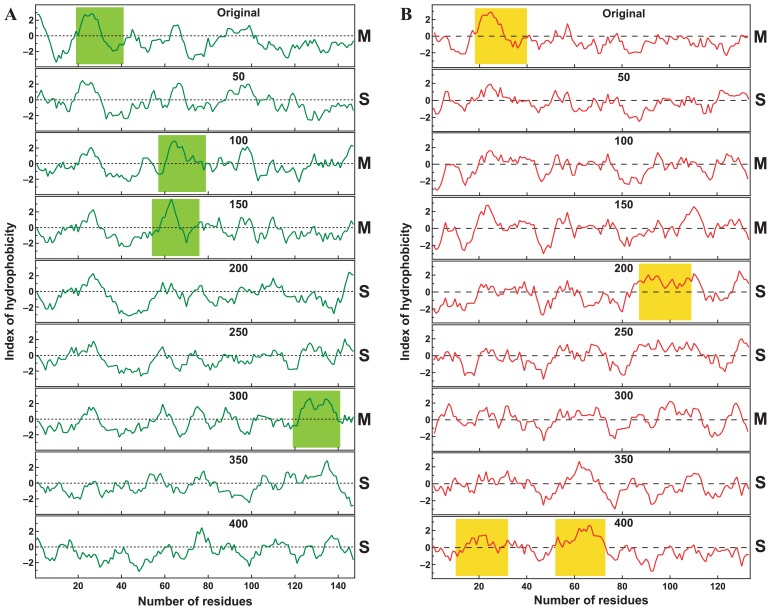
It should be pointed out that amino acid sequences are completely randomized during the simulation of 400 steps. Since we analyze only the existence of transmembrane helices in this work, a single amino acid sequence can change from the membrane protein to the soluble one and vice versa during the simulation. The time dependences of the hydropathy plots for amino acid sequences from E. coli K12, the accession number of RefSeq NP_417851.3 and NP_417093.1, are shown in Figures 4A and 4B, respectively. Figure 4A is an example of the simulation for the uniform amino acid composition (Fig. 2), and Figure 4B is an example of the simulation for the real amino acid composition (Fig. 3). The dynamic transformation of proteins is clearly demonstrated by the examples. This fact indicates that the good correlation between the number of membrane proteins and the total number of proteins in proteomes is not due to the conservation of initial transmembrane regions and that membrane protein/total protein ratio is determined by the dynamical process of the appearance and disappearance of transmembrane regions in the course of the complete randomization of sequences.

Figure 4.

Time dependences of the hydropathy plots for amino acid sequences during the simulations. Amino acid sequences which RefSeq accession numbers are NP_417851.3 and NP_417093.1 were used for the hydropathy plots of (A) and (B), respectively. Indexes of hydropathy for amino acid sequences were plotted using seven residues windows.

In order to confirm the strong correlation between the amino acid composition and the membrane protein/total protein ratio, we carried out a third simulation, this time changing the amino acid composition according to equation (2). The numbers of membrane proteins after 400 mutational steps for the entire set of organisms are plotted in Figure 5A as a function of the numbers of proteins in the total proteomes. As the fraction of the real amino acid composition decreased, the ratio of membrane proteins to total proteins monotonically decreased (Fig. 5C). In accordance with the change in this ratio, the distribution of the deviation became gradually sharper (Fig. 5B). The distributions of hydrophobic and amphiphilic amino acids changed according to the variation in the fraction of the real amino acid compositions, as shown in Figures 6A and 6B, respectively. These results indicate that the membrane protein/total protein ratio in the simulations is determined by the amino acid compositions through variation of the hydrophobicity and the amphiphilicity, both physicochemical properties.

Figure 5.

Ratio of membrane proteins to total proteins (A) and the distribution of the deviation from this constant ratio (B) are shown for five sets of proteomes of varying amino acid compositions. The values at the 400-th mutational step of the simulations were used for the analysis. (A) The average membrane protein/total protein ratio decreased in accordance with the decrease in the contribution of the amino acid composition from the real proteomes. The factor α in equation (5), which represents the contribution of the real proteomes, was varied in order to study the relationship between the membrane protein/total protein ratio and the amino acid composition. The results for α values 0.00, 0.25, 0.50, 0.75 and 1.00 are represented by red, orange, green, sky-blue and blue lines, respectively. The average ratios for α values 0.00, 0.25, 0.50, 0.75 and 1.00 were 0.218, 0.183, 0.148, 0.114 and 0.085, respectively, and the corresponding R²-values were 0.891, 0.930, 0.959, 0.981 and 0.985, respectively. (B) Distributions of deviation from these (essentially constant) ratios are shown for α values 0.00, 0.25, 0.50, 0.75 and 1 by the corresponding colors to the graph of (A). All of the distributions could be fitted well with a Gaussian distribution, and the values of the standard deviations increased gradually in accordance with the increase in α: standard deviations of 0.359, 0.465, 0.864, 1.251 and 2.038 were observed for α values 0.00, 0.25, 0.50, 0.75 and 1, respectively. (C) The average membrane protein/total protein ratio and the standard deviation of the distribution from the average ratio are plotted as a function of the factor α of the real proteomes to the amino acid compositions. Membrane protein ratio and standard deviation are indicated by the green closed circle and blue closed triangles, respectively. The standard deviation is shown in the logarithmic scale. The observation of a very good correlation indicates that the membrane protein/total protein ratio is determined by the amino acid composition.

Figure 6.

The number density of hydrophobic amino acids (A) and amphiphilic amino acids (B) were calculated for five sets of proteomes. It is already known that hydrophobic and amphiphilic clusters in amino acid sequences directly affect the membrane translocation of proteins. The distribution of both parameters systematically changed according to the variation of the factor α. Hydrophobic amino acids in this diagram include isoleucine, leucine, methionine, phenylalanine and valine, and amphiphilic amino acids are arginine, glutamine, glutamate, histidine and lysine. Because both types contain five amino acids, the probability of occurrence of both types of amino acids is 0.25 for the system of the uniform amino acid composition.

Discussion

In the present work, we estimated the number of membrane proteins, using the SOSUI prediction software systems, in proteomes of 248 prokaryotic organisms. The results are summarized to the following four points. (1) Real genomes of prokaryota code membrane proteins at an almost constant ratio of about 23%, despite the large variation in amino acid composition. (2) When the amino acid sequences were randomized, maintaining the size distribution of the proteins but changing the given amino acid composition (in this case to a uniform value), the constancy of the membrane protein/total protein ratio was preserved. (3) However, the specific value of this ratio itself changed greatly, and apparently depended on the given amino acid composition. (4) When the amino acid compositions of the real proteomes were used as starting points for the randomization, the membrane protein/total protein ratio in the subsequent randomized proteomes was very similar to the value for the real proteomes. All these results are compatible with the very simple model for the evolution of the proteins world: the stochastic birth, death and innovation (BDI) model2–4.

In the case of membrane proteins, the model can be described by Figure 7. When mutations are introduced into the amino acid sequence, a protein transforms from a membrane protein to a soluble protein and vice-versa. If the current proteomes have been formed by such reversible reactions during the process of extensive mutations, then our results support the idea that these proteomes have already reached an equilibrium state. If so, the numbers of soluble proteins N_s and membrane proteins N_m are related by the following equation,

Figure 7.

Changes in an amino acid sequence gives rise to the transformation between soluble and membrane proteins. The rate constants, k_m→s and k_s→m, can be defined as the numbers of transformations from soluble to membrane proteins and of the inverse process per a given number of mutations, respectively.

$$k_{\text{m}\to \text{s}}{N}_{\text{m}}=k_{\text{s}\to \text{m}}{N}_{\text{s}}$$ (1)

where the rate constants of the transformation between the two classes of proteins are represented by k_m→s and k_s→m. The equilibrium constant K_m↔s is related to the rate constants and the numbers of the two classes of proteins according to the equation,

$$K_{m\leftrightarrow s}=\frac{k_{m\to s}}{k_{s\to m}}=\frac{N_s}{N_m}$$ (2)

The ratio of membrane proteins to total proteins is, therefore, represented by the equilibrium constant

$$R=\frac{N_m}{N_m+N_s}=\frac{1}{1+\frac{N_s}{N_m}}=\frac{1}{1+K_{m\leftrightarrow s}}=\frac{k_{s\to m}}{k_{s\to m}+k_{m\to s}}$$ (3)

It should be pointed out that the equilibrium constant K_m↔s is not for the translocation of a protein through a membrane but for the reversible change of the two types of proteins, soluble and membrane, by mutations occurring in evolutionary time.

We have analyzed this set of total proteomes from the artificial proteomes produced by the extensive mutations in silico as well as the real genome information. In all simulations using different given amino acid compositions, the membrane protein/total protein ratio was constant at the equilibrium state. This universal behavior of the proteomes in the face of extensive mutation can be explained by a very simple mechanism. If the equilibrium constant for the change in the types of proteins, i.e., between soluble and membrane proteins, in evolutionary time does not change among various biological organisms, the ratio of membrane proteins to total proteins inevitably becomes constant, as shown in equation (3). The fact that this ratio for real proteomes is nearly constant strongly suggests that the same mechanism for achieving constancy that works for the simulation systems also is applicable to the real proteomes. It is well known that there are molecular machineries, e.g., Sec machinery and translocon, for membrane translocation whose characteristics are common to various biological organisms. Therefore, it seems reasonable that the nearly constant equilibrium K_m↔s leads to the nearly constant membrane protein/total protein ratio.

The dependence of this ratio in proteomes on the amino acid compositions was quite systematic, as shown in Figure 5C. In the simulations, when the given amino acid compositions were changed from the uniform composition to those of the real proteomes, the membrane protein/total protein ratio linearly increased from about 0.08 to 0.23. Furthermore, this ratio was nearly the same between the proteomes derived from real genomes and the completely randomized amino acid sequences, the compositions remaining unchanged. This result further supports our hypothesis that random mutation, as an the elementary process, is the most plausible reason for the constancy of this ratio.

However, several questions remain to be answered. (1) Why is the membrane protein/total protein ratio of about 23% maintained for such a wide variety of prokaryota? (2) The accuracy of the SOSUI system is better than 95% which is high enough for the statistical analysis of the membrane protein/total protein ratio. However, a question about the fine structure of membrane proteins, e.g. the number of transmembrane helices, which is closely related to their functions is not discussed in this work. The former question is very interesting from the viewpoint of the evolution of the protein world. The results of this work indicate that the ratio is determined by the amino acid composition. Therefore, the question can be rewritten as follows, “How are the current amino acid compositions formed by the mutation of DNA?” We have to analyze the codon usages extensively in order to answer this question; this analysis will be described elsewhere.

The latter question about the number distribution of transmembrane helices is closely related to the living strategy of biological organisms. The algorithm of the membrane protein predictor SOSUI is also useful for the statistical analysis of the number distribution of transmembrane helices. If the algorithm of the predictor is based on a particular kind of sequence homology or motif, it will not be applicable to completely new or artificial sequences. However, the SOSUI predictor is based only on the following physicochemical parameters: the hydrophobicity and amphiphilicity of amino acids, and the size of proteins. Therefore, it is applicable to randomized sequences that do not occur in natural proteins. We will describe elsewhere the simulations of the change in the fine structure of membrane proteins by the extensive mutations.

Methods

Genome data

Genome data of 248 prokaryota were obtained from the FTP server of NCBI, RefSeq release12 (ftp://ftp.ncbi.nih.gov/genomes/Bacteria/). The data set included 226 eubacteria and 22 archaea.

Prediction of the membrane proteins

We predicted membrane proteins by using SOSUI and SOSUIsignal. The SOSUI system was used for the prediction of membrane proteins and the signal peptide were predicted by SOSUIsignal6,10. Accuracy of the prediction systems is approximately 95% and 90% for SOSUI and SOSUIsignal, respectively. The membrane proteins predicted by SOSUI include secretory proteins. Therefore, the single spanning membrane proteins, whose transmembrane region predicted by the SOSUI system coincides with the region of a signal peptide, were assumed to be secretory proteins. We estimated the real number of membrane proteins by this procedure.

Deviation from the average ratio of membrane proteins

The ratio of the number of membrane proteins to that of all proteins in a proteome is nearly constant among the various organisms that were analyzed in this work. However, the ratio for each organism showed a small deviation from the average value. The distribution of the deviation contains some information about the mechanism involved in the constancy of the ratio. The deviation from the average number of membrane proteins was normalized by the square root of the total number of amino acid sequences in a proteome, as shown by the following equation.

$$X=\frac{M_{total}-AN}{\sqrt{N}}$$ (4)

where M_total represents the number of membrane proteins in a proteome, A is the average ratio of 0.239 and N is the total number of amino acid sequences in the proteome. The normalization factor of $\sqrt{N}$ was introduced for comparing various genomes with different numbers of amino acid sequences.

Simulation of random point mutations for total proteomes

The effect of random point mutations on the ratio of membrane proteins was analyzed for all proteins in the 248 prokaryota. The flow chart of the simulation is shown in Figure 8. The initial sequences are the real amino acid sequences of total proteomes. Mutations are randomly introduced into sequences at the rate of one mutation per 100 residues at each step of the simulation. New amino acids were randomly selected at the position of mutation according to the given probabilities of occurrence of amino acids. Then, at each step of the simulation, we estimated the membrane protein/total protein ratio.

Figure 8.

Flow chart of the simulation of point mutations for total proteomes.

Amino acid compositions in sequence simulation

The membrane protein/total protein ratio depends on the amino acid composition. Therefore, we carried out three kinds of simulation by changing the given amino acid composition as follows: (1) a uniform amino acid composition, in which the probabilities of occurrence of all amino acids are 0.05, (2) the given amino acid compositions are those of the real proteomes studied, (3) the given amino acid compositions are those calculated by the additivity of the uniform and the real compositions, as expressed by the following equation,

$$c_i=0.05+\mathrm{\alpha }(p_i-0.05)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(0\le \mathrm{\alpha }\le 1)$$ (5)

in which c_i represents the amino acid composition and p_i represents the probability of occurrence of amino acids in each proteome. The coefficient α is the contribution of the real composition in the simulation. The values of α used for the simulation were 0.75, 0.5 and 0.25.