X-ray fiber diffraction modeling of structural changes of the thin filament upon activation of live vertebrate skeletal muscles

Abstract

In order to clarify the structural changes of the thin filaments related to the regulation mechanism in skeletal muscle contraction, the intensities of thin filament-based reflections in the X-ray fiber diffraction patterns from live frog skeletal muscles at non-filament overlap length were investigated in the relaxed state and upon activation. Modeling the structural changes of the whole thin filament due to Ca²⁺-activation was systematically performed using the crystallographic data of constituent molecules (actin, tropomyosin and troponin core domain) as starting points in order to determine the structural changes of the regulatory proteins and actin. The results showed that the globular core domain of troponin moved toward the filament axis by ∼6 Å and rotated by ∼16° anticlockwise (viewed from the pointed end) around the filament axis by Ca²⁺-binding to troponin C, and that tropomyosin together with the tail of troponin T moved azimuthally toward the inner domains of actin by ∼12° and radially by ∼7 Å from the relaxed position possibly to partially open the myosin binding region of actin. The domain structure of the actin molecule in F-actin we obtained for frog muscle thin filament was slightly different from that of the Holmes F-actin model in the relaxed state, and upon activation, all subdomains of actin moved in the direction to closing the nucleotide-binding pocket, making the actin molecule more compact. We suggest that the troponin movements and the structural changes within actin molecule upon activation are also crucial components of the regulation mechanism in addition to the steric blocking movement of tropomyosin.

In vertebrate skeletal muscles, the troponin-tropomyosin complexes are bound to F-actin in the thin filaments to inhibit interaction between actin and myosin in the absence of Ca²⁺ ions, but they undergo structural changes upon binding of Ca²⁺ ions to troponin to allow actin-myosin interaction for muscle contraction1. The regulatory protein troponin (TN) with a molecular mass of ∼80 kDa consists of three subunits: troponin C (TNC) is the Ca²⁺-binding subunit, troponin I (TNI) is the inhibitory subunit of actin-activated ATPase, and troponin T (TNT) is the tropomyosin binding subunit. Tropomyosin is a two-chain, α-helical coiled-coil protein with a length of 400 Å and a molecular mass of ∼35 kDa that links end-to-tail to form a continuous strand, and lies along the grooves of F-actin. Each tropomyosin molecule interacts with seven actin molecules of F-actin by electrostatic interactions2,3. Troponin on tropomyosin also binds to actin by electrostatic interaction but its structural organization on the thin filament is just started to investigate. There is one troponin associated with each tropomyosin molecule. Upon binding of Ca²⁺ ions to TNC, TNI which links the TN globular domain to actin in a low Ca²⁺-state, detaches from actin, and tropomyosin changes its position around F-actin, making the myosin-actin interaction possible. This is the so-called ‘steric blocking mechanism’ for muscle regulation, whereby tropomyosin controls actomyosin interaction by virtue of its position on actin (see a review by Brown and Cohen (2005)3). Recently, the atomic structures of the troponin globular core domain consisting of TNC, partial TNI and TNT with and without Ca²⁺ ions in vertebrate skeletal muscle were solved by X-ray crystallography4. The C-terminal region of TNT (TNT2) connects to TNC and TNI in the globular core domain whereas the N-terminal tail of TNT (TNT1) may associate laterally with tropomyosin. As the atomic structures of the essential constituent proteins of the thin filament have now been elucidated, it is essential to derive the structure of the thin filament at close to atomic resolution in order to discuss the regulation mechanism at an atomic level of detail. Using the atomic models of F-actin proposed by Holmes et al.5, tropomyosin2 and the troponin core domain4, we constructed a model of the thin filament structure, refined it by fitting the calculated X-ray fiber diffraction intensity distributions to the observed ones, and modeled the structural changes of the thin filament upon activation of skeletal muscles. With our systematic simulation, it was not possible to explain all the observed changes in the diffraction pattern just by moving the regulatory proteins without changing the F-actin structure. A conformational change of actin, which has been often ignored in X-ray fiber diffraction analysis as well as electron microscope (EM) image reconstruction analysis, was needed to obtain a better fit to the layer line intensity changes upon activation. In this article we describe the dispositional changes of troponin and the structural changes within the actin molecules in addition to the movement of tropomyosin upon activation of muscle that were necessary to explain the observed intensity changes.

Materials and Methods

Specimen preparation

Bullfrogs (Rana catesbeiana) were killed by decapitation, followed by destruction of the spinal chord. Live semi-tendinosus muscles were dissected and used for the X-ray diffraction studies. They were mounted vertically in a specimen chamber with the ends of tendon connected to a force transducer and to the clip. The chamber was continuously perfused with chilled (10°C) frog Ringer’s solution (115 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl₂, 0.85 mM NaH₂PO₄, 2.15 mM Na₂HPO₄, pH adjusted to 7.2). The chamber had a pair of silver plates, which were placed along the two sides of the muscle to induce field stimulation. After the muscle at the full-filament overlap length was tested to exert full isometric tension by stimulation, the sarcomere length of muscle was then stretched, adjusted to ∼4.0 μm by using the optical diffraction of He-Ne laser light. Overstretched muscles were stimulated for 1.3 s with trains of 3 ms supra-maximal current pulses at 33 Hz, and the development of very small tension which originated from the ends of muscle fibers was monitored. Finally, the effect of stimulation of muscles was ensured by the intensification of the second thin filament-based layer line reflection around ∼1/40 Å⁻¹ along the equator.

X-ray diffraction measurements

X-ray experiments by synchrotron radiation from the storage ring operated at the energy of 2.5 GeV with the ring current of ∼350 mA were done using the small-angle diffractometer6 installed at the beamline 15A1 at the Photon Factory, Tsukuba, Japan. X-ray energy was 8.0 keV. Two-dimensional X-ray diffraction patterns from the relaxed and activated states of overstreched muscles were recorded with an image plate (a storage phosphor area detector, Fuji Film Co., Japan)7 at a specimen-to-detector distance of ∼2.4 m to measure the low- to medium-angle layer lines and at that of ∼0.9 m to measure the medium- to high-angle layer lines. The size of the X-ray beam was 0.3 mm vertically and 0.6 mm horizontally at the specimen. X-ray diffraction patterns were recorded in the relaxed and activated phases of the same muscle for 1.0 s each by 1.3-s stimulation for activation with resting intervals of 90 s between activations. The measurements were repeated twenty times while shifting the position of muscle vertically after every 5 s of X-ray exposure, and the data in each phase were accumulated in the same image plate. In order to measure a high-angle meridional reflection at 1/13.7 Å⁻¹, the fiber axis of muscle was tilted by ∼3° so as to bring it into the reflection position on the Ewald sphere.

Analysis of X-ray Intensity data

X-ray diffraction data collected on the image plates were read out with a read-out scanner (BAS2500, Fuji Film Co., Japan) using a pixel size of 100 μm. After determining the origin and correcting for the inclination angle of the image, the four quadrants of the patterns were folded and averaged. The intensity data from relaxed and activated muscles in pairs were normalized to each other by the total intensity of the diffraction pattern, except for the strong equatorial region and the part around the beam stop8. The intensities of the thin filament-based layer lines were carefully measured by radial integration over an appropriate width of stripes parallel to the meridian in appropriate radial ranges, and the intensity distributions across the several layer lines were obtained in the axial direction. The background was determined by assuming an exponential function connecting two minima at the both sides of the reflection peaks and subtracted. The intensity profile was deconvoluted to obtain the intensities and peak positions of individual reflections by modeling them as overlapping Gaussian functions. Since the first thin filament layer line at ∼1/360 Å⁻¹ was broad and overlapped by the myosin first layer line at ∼1/430 Å⁻¹, they were separated by assuming two Gaussian functions centered at 1/360 Å⁻¹ and 1/430 Å⁻¹. The integrated intensity of each reflection was plotted as a function of the reciprocal radial coordinate R, defined by 2sinθ/λ (where θ is the Bragg angle and λ is the X-ray wavelength used (8 keV)) and finally sampled with an interval of 1.6×10⁻³ Å⁻¹, comparable to ∼1/2D where D is a diameter of the filament.

Model calculations

The crystal structures (atomic coordinates) of the constituent molecules in the thin filament were used: actin, PDB ID: 1ATN; tropomyosin, PDB ID: 2TMA; troponin core domain, PDB ID: 1YV0. To reduce computation time, a set of several atoms in a molecule was grouped from their N-terminal end and approximated by one equivalent sphere of a different radius located at different places, which produced a model of actin consisting of 224 spheres with radii less than 8 Å, tropomyosin with 17 spheres of radii less than 8 Å, and the troponin core domain with 60 spheres of radii less than 15 Å. The troponin T1 (TNT1) tail part having a length of ∼160 Å and a molecular weight of ∼18 kDa was represented as a single α-helical chain, consisting of 21 spheres with a radius of 8 Å. In the calculation, the density of each sphere was expressed as a Gaussian function. A correlation coefficient between the computed Fourier transform of the thin filament model as described above and that of the all atom model was higher than 0.99 within the region used for present intensity fitting.

The precise helical symmetry of the thin actin filament of the frog skeletal muscle was 80 subunits/37 turns in the relaxed state and 106 subunits/49 turns in the activated state9. Although these symmetries are slightly different from the conventional one (13 subunits/6 turns)5, there was no significant difference in the calculated intensities. We therefore adopted the 13/6 symmetry for the model calculation in both states. The axial repeat of the F-actin helix (∼360 Å) is shorter than that of the tropomyosin-troponin helix (∼384 Å) in vertebrate skeletal muscles. As this difference is important for modeling, we took it into account in the calculations.

All calculations were made in cylindrical coordinates (r,ϕ,z) in real space where the z-axis is parallel to the fiber axis. The Fourier transform F(R,Φ,Z) of the helical filament in cylindrical coordinates in reciprocal space was calculated using the following equation10:

$$F(R,\Phi ,Z)={\mathrm{\Sigma }}_n{F}_n(R,Z)\text{exp}(\mathit{in}\Phi ),$$ (1)

where F_n(R,Z) is written by:

$$F_n(R,Z)={\mathrm{\Sigma }}_j\text{exp}\left\{\mathit{in}(\pi /2-{\varphi }_j)\right\}{f}_j(R,Z)J_n(2\pi r_{j}R)\text{exp}(2\pi z_{j}Z),$$ (2)

in which f_j(R,Z) is the atomic scattering factor of jth atom, r_j,ϕ_j,z_j are cylindrical coordinates of the jth atom and J_n(2πr_jR) is the nth order Bessel function of the first kind with an argument 2πr_jR. As the myofilaments in muscle fibers have a random azimuthal orientation, the cylindrically averaged intensity is then calculated as the sum of the squares of the absolute values of the Fourier transform10:

$$I(R,Z)=<I(R,\mathit{\Phi },Z){>}_{\Phi }=\mathrm{\Sigma }{\left|F_n(R,Z)\right|}^2.$$ (3)

Since it is known that the stoichiometric ratio of actin, troponin and tropomyosin in the thin filament is 7:1:1, we assumed the structural unit consisting of one tropomyosin molecule per seven actin monomers and designated this structure factor as F_an(R,Z). Two troponin molecules bound to two tropomyosins in the thin filaments are staggered by ca. 27 Å every 384 Å11. We designated the structure factor of the unit consisting of two troponin molecules on two tropomyosins as F_rn(R,Z). The total intensity is written by:

$$I(R,Z)={\mathrm{\Sigma }}_n{\left|F_{an}(R,Z)+F_{rn}(R,Z)\right|}^2.$$ (4)

The sum over n was taken from the selection rule, l=−6n + 13m with a repeat of 360 Å (C_a) for F-actin and 384 Å (C_r) for the regulatory proteins. Then the intensity of lth layer line is expressed by:

$$I(R,l/C_a)={\mathrm{\Sigma }}_n{\left|F_{an}(R,l/C_a)+F_{rn}(R,l/C_a)\right|}^2.$$ (5)

Using the atomic coordinates of the constituents molecules in the thin filament, the intensity of lth layer line is given by:

$$\begin{array}{l}I(R,l/C_a)=\\ \hspace{0.17em}\hspace{0.17em}|{\mathrm{\Sigma }}_j{f}_{aj}(R,l/C_a)J_n(2\pi r_{aj}R)\text{exp}\left\{\mathit{in}(\pi /2-{\varphi }_{aj})+2\pi i{z}_{aj}l/C_a\right\}\\ {+{\mathrm{\Sigma }}_k{f}_{rk}(R,l/C_a)J_n(2\pi r_{rk}R)\text{exp}\left\{in(\pi /2-{\varphi }_{rk})+2\pi i{z}_{rk}l/C_a\right\}|}^2,\end{array}$$ (6)

where only the first term of n from the selection rule was used in the present radial range of the layer lines. As mentioned above, several atoms were grouped and each group was approximated by one sphere with a weight w_j and a radius rd_j (={5Σ_kw_k(c_k² 3rd_k²/5)/3Σ_kw_k}^1/2 where c_k is the distance between jth and kth atoms) in the calculation. The value of rd_j was changed from sphere to sphere within a molecule in order to fill the space as much as possible. The scattering factor f_j (R,Z) of the jth sphere consisting of several atoms was expressed by a Gaussian function as follows:

$$f_j(R,Z)=w_j\text{exp}\left(-{\sigma }^2{u}^2/2\right)\text{exp}\left(-B{u}^2/4\right),$$ (7)

where $\sigma ={rd}_j/\sqrt{}5$ and $u=2\pi \sqrt{}\left(R^2+Z^2\right)$. The correction factor for the solvent effect was given as the negative temperature factor (exp(−Bu²/4)), and w_j was calculated by using the atomic scattering factor in the solvent12. Both corrections were addressed in the structure analysis of DNA13.

The most probable values of the parameters used in the calculation were evaluated by searching for the best fit between the calculated and observed intensities of the layer lines in order to minimize the following R_f -factor:

$$\begin{array}{l}{R}_f={\mathrm{\Sigma }}_i\left|\sqrt{}{I}_{i,\mathit{obs}}(R,Z)-k\sqrt{}{I}_{i,\mathit{calc}}(R,Z)\right|/{\mathrm{\Sigma }}_i\sqrt{}{I}_{i,\mathit{obs}}(R,Z),\\ k={\mathrm{\Sigma }}_i\sqrt{}{I}_{i,\mathit{obs}}(R,Z)/{\mathrm{\Sigma }}_i\sqrt{}{I}_{i,\mathit{calc}}(R,Z),\end{array}$$ (8)

where k is a scale factor, and the summation of i was performed over all thin filament layer lines (N=8 in the relaxed and activated states).

It is unlikely that the constituent molecules of the thin filament are positioned with no form of disorder. Since the effect of disorder introduced by small random motions is just to reduce the intensities of the layer lines, the model described here contains no provision for disorder effects.

Results and Discussion

Figure 1 shows the low- to moderate-angle (A) and the moderate- to high-angle (B) X-ray diffraction patterns from live frog skeletal muscles at non-filament overlap length by using synchrotron X-rays, in which the diffraction patterns in the relaxed state and upon activation are compared with the meridional axes coincident. The layer line reflections from the thick and the thin filaments are observed with different periodicities, and the representative reflections from the thin filaments are marked by the letters T and A in Fig. 1. Figure 2 shows the comparison of the intensity data of the thin filament-based layer lines in the relaxed state and upon activation of non-filament overlapped muscle. The intensity changes of the thin filament reflections occurring upon activation were much smaller than those during contraction of muscle at full-filament overlap length9. The first and the second thin filament-based layer lines exhibited distinct intensity changes upon activation; the first layer line intensity decreased by ∼39% and the second layer line intensity rose from nearly zero level at rest to ∼16% of the 59 Å layer line intensity. The 59 Å and the 51 Å layer lines, whose axial spacings correspond to the pitches of the left and the right-handed genetic (1-start) helices, exhibited a small increase in intensity upon activation: the intensity increment of the main peak of the 51 Å layer line was ∼22%, greater than that of the 59 Å layer line which was almost the same, and the main peak of the 51 Å layer line shifted slightly away from the meridian. The second peak intensity of the 29 Å layer line markedly decreased by ∼40%, and that of the 27 Å layer line, whose spacing corresponds to the axial repeat of actin subunits, shifted away from the meridian. The reciprocal intensity change of the first and the second layer lines implicates that the four-fold rotational symmetry nature of the thin filament structure is strengthened in the activated state, because the Bessel function J₄ contributes to the second layer line and J₂ contributes to the first layer line. There were also small intensity changes observed for other layer lines. The first and the second troponin-associated meridional reflections with a repeat distance of 384 Å increased their intensities but the intensity of the third one decreased upon activaion9,14. Since they were modulated due to a confounding sampling effect, they were not used for the present modeling. There is no interaction of myosin heads with actin filaments in the overstretched muscle, and thus small but distinct intensity changes of the layer lines upon activation are ascribed solely to the structural changes within the thin filaments by the calcium-regulation mechanism.

Figure 1.

X-ray diffraction patterns from live frog skeletal muscles at non-filament overlap length. (A) A comparison of diffraction patterns in the low- to medium-angle region between the relaxed and the activated states, and (B) a comparison of those in the medium- to high-angle region between them. The meridional axis (M) is coincided. E is the equatorial axis. The letter T with an index of the 384 Å repeat denotes the troponin-associated meridional reflections and the letter A with the axial spacing in Ångstrom unit, the representative thin filament-based layer lines.

Figure 2.

The measured intensity distributions of the thin filament-based layer lines in the relaxed state (blue) and upon activation (green). The layer lines (A1 to A26) are indexed to the basic repeat of ∼360 Å and the number in the parenthesis denotes the axial spacing.

Modeling of the thin filament

The high-resolution modeling was performed by using eight observed thin filament-based layer line intensities up to a resolution of ∼1/13.7 Å⁻¹, which corresponds to the second meridional reflection from the F-actin structure (Fig. 2). The atomic model of F-actin derived by Holmes et al.5 was used as a starting model. Hereinafter, we cite this F-actin model as “the Holmes model”. In this model, the crystal structure of actin in a complex with the DNase I15 is assembled with a minimal change, forming F-actin with a helical symmetry of 13 subunits/6 left-handed turns and a repeat of ∼360 Å. The atomic models of tropomyosin2 with a length of 400 Å and a diameter of ∼20 Å were linked with one another in a head-to-tail manner and were wound into the grooves between two long-pitch helices of F-actin with the known stoichiometry (one tropomyosin molecule per seven actin molecules)3, and that of the troponin core domain4 with a predicted troponin tail part (TNT1 part) was placed at the interface of tropomyosin molecules every after seven actin subunits. The effect of the small head-to-tail overlap between the neighboring tropomyosin molecules was practically small and was therefore neglected in the calculation. Thus the form factor of tropomyosin contributes solely to the low-angle layer lines (i.e., the first and the second ones). The mass of missing chains within the troponin core domain (arm part of troponin I (TNI) and part of T2 (TNT2)) corresponding to ∼1.8 kDa was correctly weighted but their structures were not considered. As the TNT1 part is known to be a long α-helical structure3, it was approximated as a single α-helix with a length of ∼160 Å and a mass of 18 kDa. Two troponin molecules bound to the thin filaments were staggered by ca. 27 Å every 384 Å11.

The model calculations were systematically performed by the procedure as follows. In the first step, the TNT1 parts were arranged along tropomyosin molecules so that their C-termini can be connected to the N-termini of TNT2 parts (see Fig. 3B). At present there is no evidence that the TNT1 part, which is a calcium-insensitive anchor, is separated from the tropomyosin strands16. The optimal disposition of the tropomyosin molecule with the TNT1 part, which is located initially at the appropriate position, was searched by moving around the periphery of F-actin and radially (Fig. 3A) to obtain good fits of the calculated intensities of the first and the second layer lines to the observed intensities in the relaxed state. The range and the step sizes for the angular (θ) and radial (r) parameters are given in Table 1A. It was not possible to obtain a good fit to the observed intensities of these low-angle layer lines solely by the rotation of the tropomyosin + TNT1 tail around the initial F-actin model.

Figure 3.

Searching parameters used in the model calculation. (A) Parameters for the optimal positioning of tropomyosin (white) around the fiber axis which is denoted by a star mark. r and θ are the radial distance and the azimuthal angle of tropomyosin around the fiber axis, respectively. The zero positions for the parameters are defined in the text. The positive direction of r is away from the fiber axis and the clockwise rotation is positive for θ. (B) Parameters used for the optimal positioning of the troponin core domain (left). r and θ are the radial distance and the azimuthal angle of the troponin core domain around the fiber axis, respectively. The parameters α, β and γ are the rotation angle around the x, y and z Cartesian coordinates, respectively. The N-terminus of the troponin core domain is located so that it connects with the C-terminus of TNT1 (right). The loci of these termini are depicted by red circles. The variable range of each parameter is given in Table1. F-actin is shown by blue balls, in which four subdomains of an actin molecule15 are colored by red (subdomain 1), orange (subdomain 2), magenda (subdomain 3) and pink (subdomain 4). Tropomyosin is shown by the two strands of white balls and the troponin three subunits are shown by light blue (TNC), green (TNI) and yellow balls (TNT).

Table 1.

(A) The searching range and the step sizes of the parameters (r and θ) used for the tropomyosin movement in the modeling. (B) Those of the parameters used for positioning of the troponin core domain in the modeling.

(A)
Parameter	Searching range	Step
r	25 Å ≤ r ≤ 40 Å	5 Å
θ	0° ≤ θ ≤ 330°	30°
(B)
Parameter	Searching range	Step
α	0° ≤ α ≤ 330°	30°
β	0° ≤ β ≤ 330°	30°
γ	0° ≤ γ ≤ 330°	30°
r	25 Å ≤ r ≤ 40 Å	5 Å
θ	0° ≤ θ ≤ 330°	30°
z	25 Å ≤ z ≤ 40 Å	10 Å

In the second step, the troponin core domain was introduced based upon observation in the immuno-electron micrographs17 and by connecting the N-terminus of TNT2 part to the C-terminus of TNT1 part on tropomyosin molecules. The orientation of the core domain was varied around the N-terminus of TNT2 so as not to break the connecting portion between the C-terminus of TNT1 and the N-terminus of TNT2 where tropomyosin is adjacent. Its optimal disposition of the troponin core domain on tropomyosin including the TNT1 part was searched by varying the rotation angles (α, β, γ) around three axes of the Cartesian coordinate, the radial (r), angular (θ) and axial (z) coordinates of the core domain (Fig. 3B) without changes of the subunit arrangement within the core domain to obtain a better fit of the calculated intensities to the observed ones of the first and the second layer lines including the 51 Å and the 59 Å layer lines. The variable ranges and the step sizes for these parameters are given in Table 1B. The position r = 0 corresponds to that where the TNT2 N-terminus contacts with tropomyosin, and the position θ = 0 corresponds to that where the line connecting the N- and the C-termini of TNT2 in the core domain is parallel to the tropomyosin strand. Four optimal models for the disposition of the TN core domain were obtained with similar values of R_f. The intensities of the 51 Å and the 59 Å layer lines are not in fact affected by the movement of the tropomyosin + TNT1 tail. The orientation of the TN core domain in the two representative models depicted in Fig. 4, which yielded similar intensity fits, was in the opposite direction with each other. Unfortunately, we could not determine the correct orientation of the TN core domain with respect to the F-actin and the tropomyosin polarity by X-ray fiber diffraction, and therefore two types of models with either orientation remain possible. However, the orientation of the troponin core domain in the model of Fig. 4A, in which the apex (taper end) of the V-shaped core domain orients toward the barbed end of F-actin, was consistent with that shown by the recent EM single-particle image analysis18. The troponin core domain placed over subdomain 1 of actin and lay at a radius of 54 Å. This model was also consistent with the result suggested from distance measurements between the amino acid residues in reconstituted thin filaments obtained by fluorescence resonance energy transfer (FRET) method19. In addition, the D/E helix linker of TNC was oriented almost perpendicularly to the filament axis. This orientation was consistent with the data from fluorescence polarization measurement from the TN core domain20,21. Considering these features, we adopted the model depicted in Fig. 4A and refined it further, although firm evidence for the correct orientation is still under investigation (see below). As seen in Fig. 4, the fit to the observed data, however, was poor for the low-angle layer lines, suggesting that the F-actin model used here may not be compatible with the structure of F-actin in frog skeletal muscle thin filament. We therefore refined the initial F-actin model against the observed diffraction data by changing the conformation of actin molecule consisting of four subdomains in the crystal structure15.

Figure 4.

Modeling thin filaments with an unchanging Holmes F-actin. (A) A model with the V-shaped troponin core domain is oriented toward the pointed/M-line end of the actin filament. (B) A model with the troponin core domain is oriented toward the barbed/Z-band end of the actin filament. The upper side is toward the pointed/M-line end. The color assignment for the constituent molecules is the same as in Fig. 3. The calculated and observed layer line intensities are compared in the relaxed state (C) and in the activated state (D).

In the third step, the actin conformation was altered by changing the relative dispositions of four subdomains (Fig. 5A). The optimum dispositions of four subdomains together with the tropomyosin + TNT1 tail and the TN core domain were examined using the simulated annealing method22. The intensities of the first, second, 59 Å, 51 Å, 29 Å and 27 Å layer lines were used for fitting. The parameters for each actin subdomain were translations along x, y and z Cartesian coordinates, and those for the tropomyosin + TNT1 tail and the TN core domain were the same as in the above. Each subdomain was moved as a rigid body with a step of 0.2 Å within 3 Å so as to avoid collision. The azimuthal and radial parameters for the tropomyosin + TNT1 tail and the TN core domain were altered with 1° and 0.2 Å step, respectively. As the results, four subdomains of actin tended to move to close the nucleotide-binding cleft, making an actin molecule compact along the filament axis. Together with this subdomain movement in actin, the position of the tropomyosin + TNT1 tail and the orientation of the TN core domain altered, resulting in a reasonable fit to the observed low- to medium-angle intensity data. This fact indicates that movements of regulatory proteins alone on the Holmes F-actin model without changing the actin structure are insufficient to account for the low- to medium-angle intensity data. This conclusion may be in line with the simulations by Al-Khayat et al. (1995)23, Squire and Morris (1998)24 and Iwamoto et al. (2003)25. However, the fits to the high-angle intensities beyond the 29 Å layer line, which are dominated by the actin structure in F-actin, were still poor. The intensities of the high-angle layer lines could not be explained by global movements of four subdomains in the actin structure. We needed to introduce finer movements within the actin molecule to obtain a better fit to the high-angle intensity data.

Figure 5.

Four subdomains of an actin molecule and division of 16 segments used in the modeling. (A) An actin molecule consists of four subdomains by Kabsch et al. (1990)15. Subdomains 1, 2, 3 and 4 are colored in red, orange, magenda and pink, respectively. (B) The division of the actin molecule into 16 segments. The sequential number of amino acid residues in the boundary between neighboring segments is written above the color bar and the corresponding segment number is written below the bar. (C) The surface display of the actin molecule devided into 16 segments. The number of the segments is indicated, and the color assignment for them is the same as in (B). The right panel is the view with the left one rotated by 180° around the vertical axis.

In the final step, in order to obtain the better fit to the high-angle intensity data as well as the medium- to low-angle intensity data, the actin molecule was further divided into 16 segments while retaining the secondary structures (Fig. 5B). Although such segmentation is a bit arbitrary, the movable loci were determined by observing the crystal structure of actin (Fig. 5C). Subdomain 1 consists of five segments (1, 10, 11, 15, 16), subdomain 2 consists of two segments (2, 12), subdomain 3 consists of three segements (3, 13, 14) and subdomain 4 consists of six segments (4, 5, 6, 7, 8, 9). Each actin segment was moved as a rigid body and their optimal dispositions together with the regulatory proteins were determined to fit to all the observed layer line intensities by the simulated annealing procedure. The searching parameters of each segment in an actin molecule were translations along x, y and z Cartesian coordinates and those of the tropomyosin + TNT1 tail and the TN core domain were the same as in the above. The step size of the parameter variation was 1° for the angular component and 0.2 Å for the translation component. By varying all parameters consisting of 48 for actin, 6 for the TN core domain and 2 for the tropomyosin + TNT1 tail using eight observed layer line data, the best-fit model was obtained via the minimization of the R_f-factor between the calculated and the observed intensity data (see Materials and Methods) in both states. In the present simulation, as the number of observables by inclusion of the peak shape information was larger than that of the fitting parameters by a few times, ensuring that the overall fitting process was not under-determined.

Refinement simulation of the thin filaments was performed using the 16-segmented model of actin in the relaxed and activated states. Here the crystal structure of the TN core domain without Ca²⁺ ions (PDB ID: 1YV0) was commonly used for modeling because there was no significant change in the subunit arrangement in the absence and presence of Ca²⁺ ions4. Figure 6 shows the best-fit model of the thin filament in both states. It is evident that the best-fit model of the thin filament yielded nice fits to the observed X-ray diffraction data in each state (Figure 7); the R_f-factor was ∼11% in the relaxed model and ∼13% in the activated model for the observed layer line data. Although in the high-angle region the fits of intensity profiles near the meridian of the 29 Å, 27 Å and 13.7 Å layer lines were not satisfactory, the fits of the low- to the medium-angle data were excellent, and the discrepancy between the experimental and the calculated intensities seen in Fig. 4 was greatly improved. Note that when we attempted to fit the data in the activated state just by changing the orientation/disposition of the regulatory proteins using the best-fit model obtained in the relaxed state without changing the F-actin structure, it was unsuccessful. Our simulation results indicate that a conformational change of actin was inevitably needed to obtain satisfactory fits to all layer line intensities upon activation.

Figure 6.

The best-fit models of the thin filament structure in the relaxed and the activated states. (A) The model of the relaxed state and (B) the model of the activated state. The upper panel is a side view and the lower panel is a top view seen from the pointed/M-line end. Changes in the orientation and dispositions of the molecules upon activation are directed by arrows with the amount of changes. TM, tropomyosin and TN, troponin. The color assignment for the constituent molecules is the same as in Fig. 3.

Figure 7.

Comparison of the calculated intensities from the best-fit models and the observed intensities of the thin-filament-based layer lines. (A) The relaxed state and (B) the activated state. The layer line intensities of the 71 Å, 19.9 Å, 17,7 Å, 16.9 Å and 14.2 Å were mostly too weak to measure. They are denoted by small dotted curves. R_f for the eight layer lines in total was ∼11% in the relaxed state and ∼13% in the activated state.

Conformational changes of actin in the thin filament upon activation

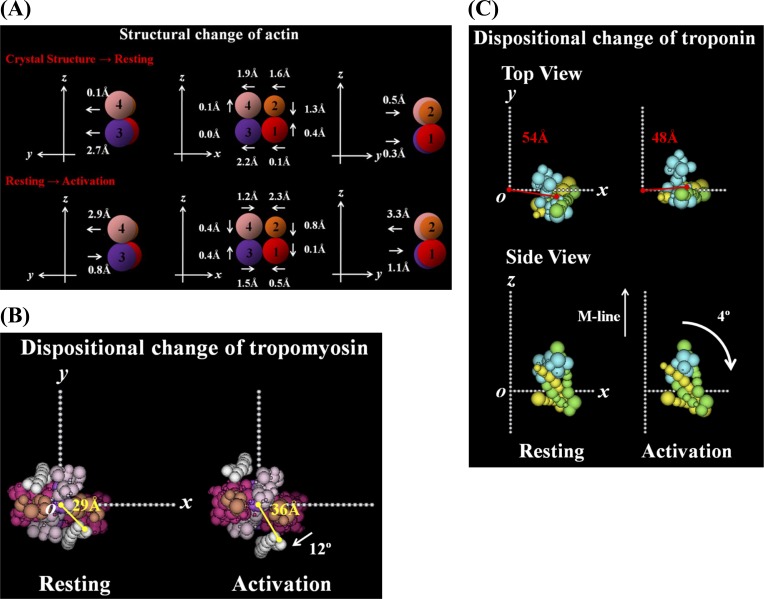
The changes in the center of gravity of each of four subdomains were calculated from the small movements of the segments within each subdomain of actin (Fig. 8A). The positional differences of the actin subdomains in the relaxed model from their positions in the Holmes model are depicted in the upper panel in Fig. 8A. All subdomains moved toward the filament axis from the positions in the Holmes model, and subdomains 1 and 2 moved close to each other. The largest may be the motion of subdomain 3 along the x and y axes. This is the actin conformation in the thin filament of frog skeletal muscle in the relaxed state.

Figure 8.

Dispositional changes of actin, tropomyosin and the troponin core domain in the best-fit models. (A) Structural change in actin. The central figure is viewed along the fiber axis (z axis), and the left and right ones are rotated by ±90° around the fiber axis. Subdomains 1, 2, 3 and 4 are colored as in Fig. 5. The top panel shows the changes from the Holmes actin in the best-fit model in the relaxed state. The bottom panel shows the changes in the transition of the relaxed state to the activated state. The direction of change of subdomains in actin is depicted by an arrow. (B) The positional change of tropomyosin (viewed from the pointed/M-line end). The left is in the relaxed state and the right is in the activated state. In each state, the radial distance of tropomyosin from the filament axis is indicated by yellow. In the activated state, the azimuthal angle change of tropomyosin around the filament axis is denoted by an arrow. (C) The dispositional and orientation changes of the troponin core domain. The left is in the relaxed state and the right is in the activated state. The top panel (“Top View”) is viewed from the pointed/M-line end, and the bottom panel (“Side View”) is viewed perpendicular to the filament axis (y axis). In the top panel, the radial distance of the troponin core domain from the filament axis is indicated by a red line. In the bottom panel, the change in the rotation angle around the y axis is denoted by a curved arrow. The color assignment for the constituent molecules is the same as in Fig. 3.

In the transition from the relaxed to the activated state (the bottom panel of Fig. 8A), all subdomains moved in the direction to closing the nucleotide-binding pocket. Subdomains 1 and 2, and subdomains 3 and 4 moved respectively in the opposite directions from each other along the y axis. Along the z axis, subdomains 1 and 2 moved toward the minus direction in a concerted manner, and subdomains 3 and 4 moved in the opposite direction from each other. By these small movements the actin molecule in F-actin became more compact upon activation in the axial direction, consistent with the modeling result on the thin filaments during activation of live mouse muscle25. This compaction of the actin molecule may weaken the interaction between the neighboring subunits along the long-strand of the actin helix, causing to increase a filament flexibility of F-actin26.

Dispositional changes of tropomyosin and troponin upon activation

As mentioned above, we could not determine the unique polarity for the troponin core domain along the tropomyosin/F-actin axis by X-ray fiber diffraction. We adopted the best-fit model in each state that was consistent with the FRET analysis of Kimura-Sakiyama et al. (2008)19 and the 3D-EM image analysis of Pirani et al. (2006)18. The main feature of the models was that the long axis of the TN core domain was oriented mostly parallel to the F-actin axis and was inclined against the tropomyosin strands. The apex (taper end) of the V-shaped TN core domain was oriented toward the barbed/z-band end of F-actin in the sarcomere (see Fig. 6).

As depicted in Fig. 8B, in the relaxed state tropomyosin molecules were located at a radial position of about 29 Å and near subdomain 1 of actin where the binding sites of myosin heads reside, and tropomyosin can inhibit the interaction between actin and myosin heads sterically. Upon activation, tropomyosin strands moved azimuthally toward the inner domains of actin by ∼12° from the relaxed position to partially open the binding moiety of myosin heads and sat at the radial position of ∼36 Å.

As depicted in Fig. 8C, the TN core domain sat at a radius of ∼54 Å and can cover the myosin binding site of actin subdomain 1 in the relaxed state. In the transition from the relaxed state to the activated state, it moved toward the F-actin filament axis by ∼6 Å and rotated around the filament axis by ∼16° in the opposite direction against the rotation of tropomyosin. The inner shift of the TN core domain makes the intensity of the 51 Å layer line away from the meridian (see Fig. 2). According to a neutron scattering study of the native thin filaments in solution27, the center of gravity of TNC within the core domain moved inward by ∼4 Å upon activation, which was consistent with the present inner shift of TNC in the core domain. In addition, the TN core domain moved slightly along the filament axis toward the pointed end of F-actin and rotated around the x axis by −14°, around the y axis by −4° and around the z axis by −31°. Thus the TN core domain rotated around the F-actin surface in the opposite direction against the tropomyosin movement. Such movements of the regulatory proteins strengthen the fourfold rotational symmetry nature of the thin filament structure upon activation. On the other hand, in the relaxed state the positions of tropomyosin and troponin yield a strong twofold rotational symmetry nature of the thin filament (see Fig. 6).

In the present modeling, the TNT1 tail remained closely associated with the tropomyosin strands and moved together with them. Independent movements of the tropomyosin and TNT1 tail strands did not yield good fits to the observations.

We calculated the intensity profiles of the meridional reflections with a repeat of 384 Å from the troponin structures in the best-fit models in both states and compared with those observed in the X-ray diffraction patterns from the oriented sols of the native thin filaments in the absence and presence of Ca²⁺ ions (Oda, unpublishied data) using a method developed by Makino, Oda and Maeda (manuscript in preparation). Figure 9 shows the comparison of the intensity profiles of the first to the third order troponin-associated meridional reflections. Reasonable fits to the radial profiles were obtained in both states but the determination of the whole troponin structure is needed for further refinement.

Figure 9.

Comparison of the calculated intensities from the best-fit models and the observed ones of the three troponin-associated meridional reflections with the repeat of 384 Å. The observed data were measured from the highly orientated sols of native thin filaments (Oda, unpublished data). (A) The relaxed state/in the absence of Ca²⁺ ions and (B) the activated state/in the presence of Ca²⁺ ions. The intensity normalization is made so that the total intensities of the three reflections in each state are indentical.

Comparisons with other models

Oda et al. (2009) refined an atomic model of F-actin using X-ray diffraction data from a highly oriented sol of F-actin by the normal mode analysis28. They reported that conformational changes took place during the globular (G)-fibrous (F) transformation of actin. The angle between the line connecting the centers of gravity of subdomains 1 and 2 and the line connecting those of subdomains 3 and 4 is ∼20° in the G-actin crystal. According to their analysis, this angle became close to 0° in the F-actin form, by which the actin molecule forms a flatter structure. This alteration predicts that subdomains 2 and 4 approach each other along the y axis in F-actin, but such alteration was not observed in our modeling of the thin filament in the relaxed state (see Fig. 8A). This difference may be attributed to the difference between free F-actin in solution and constrained F-actin in the thin filament.

The layer line intensities have been calculated for several actin filament models with bound regulatory proteins, showing that the intensity ratio of the 59 Å and 51 Å layer line reflections as well as the maximum intensity of the 360 Å layer line are much larger than in observations from vertebrate skeletal muscles29. These discrepancies could be much reduced by allowing alterations of the actin structure. Such alterations in actin have not been considered in previous single particle analysis studies of EM images or even in X-ray fiber diffraction analyses29–31.

In the muscle thin filament, the structure of the actin filament is constrained by the bound regulatory proteins. Wakabayashi et al. (1994)32, Huxley et al. (1998)33 and Takezawa et al. (1998)34 reported that the thin filament in frog skeletal muscles shortened with some change in the helical twist upon activation. The change of actin into a more compact structure along the filament axis by Ca²⁺ binding to troponin may lead to the shortening of F-actin in the thin filament upon activation of muscle. Twisting change of F-actin32,34 may affect the electrostatic interaction between regulatory proteins and actin molecules underlying the tropomyosin movement.

In the present modeling of muscle thin filament, the radial position of tropomyosin shifted outward by ∼7 Å (29 Å→36 Å) with an azimuthal movement of ∼12° from the relaxed position upon activation. Previous modeling by Al-Khayat et al. (1995)23 for live frog muscle thin filaments at non-overlap length revealed that the radial shift was ∼4 Å (41 Å→37 Å) and that the azimuthal shift was ∼15°. Additionally, there were small movements of subdomains 1 and 2 in actin. The modeling by Poole et al.30 for the thin filament in skinned rabbit skeletal muscle at non-overlap length suggested that the radial position of tropomyosin with an apparently higher mass kept at ∼42 Å and the azimuthal shift was ∼15° from the EGTA position. The former authors did not take troponin into account, and the latter authors did not consider the TNT1 tail part and the actin conformation remained unchanged. Our favored orientation of the troponin core domain on the F-actin/tropomyosin is with the globular head bound closer to the pointed end of the actin filament and with the TNT1 tail pointing toward the barbed end (Fig. 4A). However, most recently Paul et al. (2009)35 reported by the single-particle analysis of EM images that the polarity of the troponin complex in the thin filament was reversed with respect to the current EM image analysis, similar to the model in Fig. 4B. The reverse orientation of the TN core domain on the actotropomyosin filament had been preferred by Narita et al. (2001)36 (see also Murakami et al. (2005)37). Although the reverse polarity did not affect significantly the conformational changes of tropomyosin and actin described here, a correct polarity of troponin on the thin filament would be important when considering the mechanism of regulation. Further studies will be needed to clarify this crucial point.

Relations to the regulation mechanism

A three-state model in terms of the tropomyosin positioning has been proposed from solution kinetics for the regulation mechanism of striated muscles³⁸. In the Ca²⁺-free ‘blocked’ state, troponin may bind strongly to actin, holding tropomyosin in a blocking position on actin subdomain 1. Binding of Ca²⁺ ions to TNC may release troponin from actin and allow a partial movement of tropomyosin but still inhibit strong binding of myosin heads to actin (‘closed’ state). In the ‘open’ state, tropomyosin may move further across the thin filament and switch the filament fully on, allowing maximal crossbridge cycling and increased ATPase activity. The thin filaments in the relaxed state (in the absence of Ca²⁺ ions) may correspond to the blocked state, and those in the activated state (in the presence of Ca²⁺ ions) may correspond to the closed state. In our modeling, tropomyosin molecules are located between subdomains 1 and 3 in the relaxed state, and myosin heads may not be able to bind to actin. In the transition from the relaxed to the activated state, tropomyosin rotates by ∼12° in the direction to opening the myosin binding sites, and the actin conformation alters; subdomains 1 and 2 and subdomains 1 and 3 become closer to each other, possibly increasing the affinity of myosin heads to actin. Since tropomyosin shifts across the surface of the actin filament, possibly from a position in the off-state to a position in the on-state away from subdomain 1, the steric blocking mechanism appears to be valid. According to the preliminary analysis of the thin filament in a contracting muscle at full-filament overlap length by Sugimoto et al. (2008)9, tropomyosin rotated further by more than 10° from the activated position, completely opened the myosin binding sites, and subdomains of actin became even closer together. This state may correspond to the ‘open’ state. More detailed results from this modeling will be presented elsewhere (manuscript in preparation). Thus, our modeling results are in line with the three-state model for regulation. However, the steric blocking mechanism alone would not explain the whole regulation mechamism. Additional factors such as movements within the troponin molecule including the motion of segments in the inhibitory subunit TNI37,39,40 and structural changes within the actin molecule as described above may also play important roles, and should be included in schemes for thin filament regulation.

In summary

Systematic modeling of structural changes of the thin filaments upon activation using the atomic data of the constituent molecules revealed the distinct changes in actin conformation as well as orientational changes of the globular core domain of troponin, the dispositional changes of tropomyosin upon activation of muscle. The structural changes of regulatory proteins and actin in the thin filament occur initially in response to Ca²⁺-binding to troponin and may be completed as a result of actomyosin interaction. In addition to the steric blocking mechanism, troponin subunit motions and alteration of actin structure should be considered as possible participants in the regulation mechanism of muscle contraction.