Modeling a synthetic multicellular clock: Repressilators coupled by quorum sensing

Abstract

Diverse biochemical rhythms are generated by thousands of cellular oscillators that somehow manage to operate synchronously. In fields ranging from circadian biology to endocrinology, it remains an exciting challenge to understand how collective rhythms emerge in multicellular structures. Using mathematical and computational modeling, we study the effect of coupling through intercell signaling in a population of Escherichia coli cells expressing a synthetic biological clock. Our results predict that a diverse and noisy community of such genetic oscillators interacting through a quorum-sensing mechanism should self-synchronize in a robust way, leading to a substantially improved global rhythmicity in the system. As such, the particular system of coupled genetic oscillators considered here might be a good candidate to provide the first quantitative example of a synchronization transition in a population of biological oscillators.

Organisms are biochemically dynamic. They are continuously subjected to time-varying conditions in the form of both extrinsic driving from the environment and intrinsic rhythms generated by specialized cellular clocks within the organism itself. Relevant examples of the latter are the cardiac pacemaker located at the sinoatrial node in mammalian hearts (1) and the circadian clock residing at the suprachiasmatic nuclei in mammalian brains (2). These rhythm generators are composed of thousands of clock cells that are intrinsically diverse but nevertheless manage to function in a coherent oscillatory state. This is the case, for instance, of the circadian oscillations exhibited by the suprachiasmatic nuclei, the period of which is known to be determined by the mean period of the individual neurons making up the circadian clock (3–7). The mechanisms by which this collective behavior arises remain to be understood.

Individual clock cells are known to operate through biochemical networks comprising multiple regulatory feedback loops (8). The complexity of these systems has hindered a complete understanding of natural genetic oscillators. Synthetic genetic networks, on the other hand, offer an alternative approach aimed at providing a relatively well controlled test bed in which the functions of natural gene networks can be isolated and characterized in detail (9). In this direction, a synthetic biological oscillator, termed the “repressilator,” was developed recently in Escherichia coli from a network of three transcriptional repressors that inhibit one another in a cyclic way (10). Spontaneous oscillations were observed in individual cells within a growing culture, although substantial variability and noise was present among the different cells. Recently, another synthetic genetic circuit was designed and built, exhibiting damped oscillatory responses to perturbations in culture (11).

A natural next step in this design effort would be to include a mechanism of intercell coupling that would globally enhance the oscillating response of the system. However, coupling among oscillators is not, in general, sufficient to achieve synchronization, and many ensembles of coupled oscillators exhibit phase dispersion rather than a synchronized state [because either the oscillators actively resist synchronizing (12) or coupling is too small or nonexistent (13)]. Therefore, the collective behavior of a population of coupled oscillators must be analyzed carefully. Here we propose a potential means of achieving such a collective response on the basis of cell-to-cell communication through quorum sensing (14).

Quorum sensing has lead recently to programmed population control in a bacterial population (15). In another recent study, McMillen et al. (16) have demonstrated theoretically that quorum sensing can lead to synchronization in an ensemble of identical genetic oscillators. The oscillators considered there were assumed to be of a relaxational type (that is, with spike-like waveforms), analogous to neural oscillators. The repressilator, on the other hand, is sinusoidal rather than relaxational. Furthermore, in the experimental implementation of the repressilator (10), individual cells were found to oscillate in a “noisy” fashion, exhibiting cell–cell variation in period length, as well as variation from period to period within a single cell.

Accordingly, it seems natural to consider the effect of intercell signaling on a population of nonidentical and noisy repressilators coupled by quorum sensing. Using computational modeling, we show here that a diverse population of such oscillators is able to self-synchronize, even if the periods of the individual cells are broadly distributed. The onset of synchronization is sudden, not gradual, as a function of varying cell density. In other words, the system exhibits a phase transition to mutual synchrony. Although the existence of this phase transition was predicted and studied theoretically several decades ago in general models of coupled phase oscillators (12, 17), only recently has it been confirmed experimentally by using an electrochemical system (18). No corresponding confirmations exist in biological systems (19). We believe that the system proposed here could provide a favorable arena for such a test.

Our results indicate that coupling also has a second beneficial effect: it reduces the noisiness of the system, effectively transforming an ensemble of “sloppy” clocks into a very reliable collective oscillator (20–22). Noise dominates biochemical systems with a small number of molecules (as is the case in transcriptional regulation systems) because of the intrinsically stochastic nature of the reactions involved. In that context, the robustness of genetic oscillators to noise is a topic of current interest (23–25). Our findings suggest that the constraints that local cell oscillators have to face to be noise-resistant could be relaxed in the presence of intercell coupling, because coupling itself provides a powerful mechanism of noise resistance.

Model

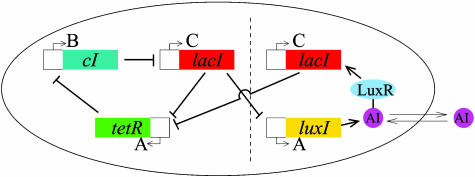
The repressilator is a network of three genes, the products of which inhibit the transcription of each other in a cyclic way (10). Specifically (see Fig. 1), the gene lacI (from E. coli) expresses protein LacI, which inhibits transcription of the gene tetR (from the tetracycline-resistant transposon Tn10). The product of the latter, TetR, inhibits transcription of the gene cI (from λ phage), the protein product CI of which in turn inhibits expression of lacI, completing the cycle. We propose a modular addition to this design, with the aim of coupling a population of cells containing this network. To that end, we make use of the quorum-sensing system of the bacterium Vibrio fischeri, a bioluminescent organism that lives in symbiosis with certain marine hosts forming part of specialized light organs (14). These bacteria exhibit cell-to-cell communication through a mechanism that makes use of two proteins, the first one of which (LuxI) synthesizes a small molecule known as an autoinducer (AI), which can diffuse freely through the cell membrane. When a second protein (LuxR) binds to this molecule, the resulting complex activates transcription of various genes, including some coding for light-producing enzymes.

Fig. 1.

Scheme of the repressilator network coupled to a quorum-sensing mechanism. The original repressilator module is located at the left of the vertical dashed line, and the new coupling module appears at the right. The letters A, B, and C correspond to the notation used in the text. The coupling module can be added to existing repressilator strains.

In the spirit of ref. 16, we propose to incorporate this intercell signaling apparatus into the repressilator by placing the gene that encodes LuxI under the control of the repressilator protein LacI, as shown in Fig. 1. Additionally, a second copy of another repressilator gene (such as lacI) is inserted into the genetic machinery of the E. coli cell in such a way that its expression is induced by the complex LuxR–AI. The result is the appearance of a feedback loop in the repressilator, which is reinforced the more similar the levels of LacI are among neighboring cells. (Simulations indicate that this scheme, in which the gene activated by the AI is the same one that represses LuxI, provides the best synchronization of the three possible arrangements of the feedback loop within the repressilator.)

To model the dynamics of gene expression in the cell population, one must keep track of the temporal evolution of all mRNA and protein concentrations from every cell in the network. To describe the behavior of the system, we formulate differential equations in the standard way. However, it is not clear yet whether this formalism is appropriate for the intracellular environment, nor is it clear what the effective biochemical constants are.

The mRNA dynamics is governed by degradation and repressible transcription for all three genes of the repressilator plus (according to the coupling mechanism explained above) transcriptional activation of the additional copy of the lacI gene:

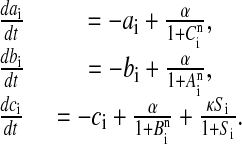[1]

Here a_i, b_i, and c_i are the concentrations in cell i of mRNA transcribed from tetR, cI, and lacI, respectively, and the concentration of the corresponding proteins are represented by A_i, B_i, and C_i (note that the two lacI transcripts are assumed to be identical). The concentration of AI inside each cell is denoted by S_i. A certain amount of cooperativity is assumed in the repression mechanisms by the Hill coefficient n, whereas the AI activation is chosen to follow a standard Michaelis–Menten kinetics. The model is rendered dimensionless by measuring time in units of the mRNA lifetime (assumed equal for all genes) and the protein levels in units of their Michaelis constant, i.e., the concentration at which the transcription rate is half its maximal value (also assumed to be equal between all three genes). The AI concentration S_i is also scaled by its Michaelis constant. α is the dimensionless transcription rate in the absence of repressor, and κ is the maximal contribution to lacI transcription in the presence of saturating amounts of AI.

The protein dynamics is given by

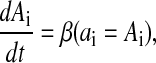[2]

and is given similarly for B_i (with b_i) and C_i (with c_i). The parameter β is the ratio between the mRNA and protein lifetimes, and the mRNA concentrations have been rescaled by their translation efficiency (proteins produced per mRNA, assumed equal for the three genes).

Finally, the dynamical evolution of the intracellular AI concentration is affected by degradation, synthesis, and diffusion toward/from the intercellular medium. Assuming equal lifetimes of the TetR and LuxI proteins, their dynamics are identical, and hence we will use the same variable to describe both protein concentrations. Consequently, the synthesis term of the AI rate equation will be proportional to A_i:

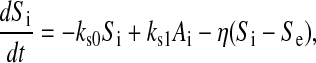[3]

where 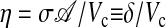measures the diffusion rate of AI across the cell membrane, with σ representing the membrane permeability, 𝒜 its surface area, and V_c the cell volume. The parameters k_s0, k_s1, and η have been made dimensionless by the time rescaling. S_e represents the extracellular concentration of AI, the dynamics of which is given by

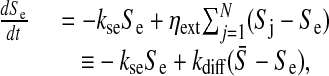[4]

where η_ext = δ/V_ext, with V_ext being the total extracellular volume, and 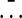indicates average over all cells. The diffusion rate is given by k_diff = η_extN and the degradation rate is given by k_se.

The modeling approach described above ignores variations in cell density (caused by cell growth and division, for example) and assumes a uniform AI concentration throughout the cell culture. These approximations are standard in quorum-sensing modeling (16, 26) and describe reasonably well the situation encountered in a well controlled chemostat.

In the quasi-steady-state approximation (16, 26), the extracellular AI concentration can be approximated by

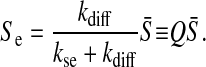[5]

From the definition of k_diff given above, we note that Q depends on the cell density N/(V_ext + V_c) ≈ N/V_ext according to∥

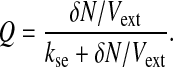[6]

In other words, Q is linearly proportional to the cell density provided δN/V_ext is sufficiently smaller than the extracellular AI degradation rate k_se. In the following, we analyze the effect of quorum-sensing coupling on the collective behavior of the model in Eqs. 1–3, with S_e defined by Eqs. 5 and 6, considering Q (and hence the cell density) as a control parameter.

Transition to Synchronization

In the hypothetical case of infinite cell dilution (Q → 0), the system consists of a population of uncoupled limit-cycle oscillators. Each individual cell clock is an extension of the original repressilator (10), where a new degree of freedom has been added to the original six-dimensional phase space to represent the intracellular AI dynamics defined by Eq. 3. The resulting dynamical system exhibits limit-cycle oscillations in a wide region of parameter space. The characteristic oscillations of the repressilator (10) do not change qualitatively in the presence of the AI dynamics. In particular, the shape of the waveform does not vary; only its amplitude is modified, but by <20% for the parameters chosen here (see also Fig. 2b).

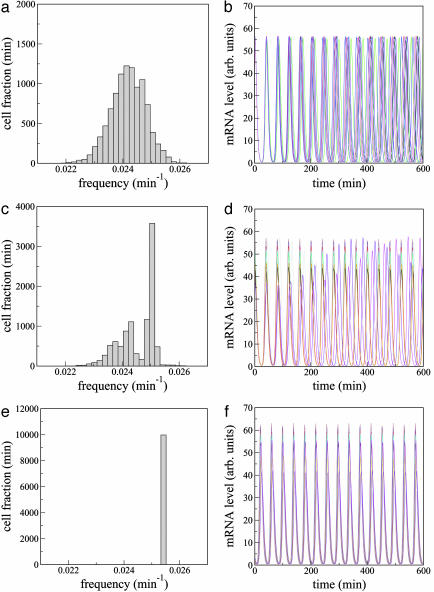
Fig. 2.

Frequency histogram (a, c, and e) and time evolution of b_i(t)(b, d, and f) for 10 cells and increasing cell density. (a and b) Q = 0.4. (c and d) Q = 0.63. (e and f) Q = 0.8. Other parameters are n = 10⁴, α = 216, κ = 20, n = 2.0, k_s0 = 1, η = 2.0, and k_s1 = 0.01. The lifetime ratio β in the different cells is chosen from a random Gaussian distribution of mean 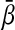and standard deviation Δβ = 0.05. In the plots (b, d, and f), the oscillators are allowed to evolve from an initially synchronous state. We note, however, that synchronization also arises from initially unsynchronized cultures. arb., Arbitrary.

The oscillator population will likely contain substantial differences from cell to cell [e.g., extrinsic noise (27)], giving rise to a relatively broad distribution in the frequencies of the individual clocks at any given time. In the case of Eqs. 1–3, the parameter that affects most markedly the oscillation frequency is the lifetime ratio β. Accordingly, we model the variability in the cell population by considering that β is nonuniformly distributed among the repressilators following a Gaussian law with standard deviation Δβ. The corresponding frequency distribution of a group of 10⁴ uncoupled cells for Δβ/β = 0.05 is shown in Fig. 2a. The temporal evolution of the cI mRNA concentration in 10 of those cells is plotted in Fig. 2b, showing how the global operation of the system is completely disorganized such that no collective rhythm can exist under these conditions.

As the cell density increases, diffusion of extracellular AI molecules into the cells provides a mechanism of intercell coupling, which leads to partial frequency locking of the cells (Fig. 2 c and d). Finally, when the cell density is large enough (Fig. 2 e and f), perfect locking and synchronized oscillations are observed. In that case the system behaves as a macroscopic clock with well defined period, although it is composed of a widely varied collection of oscillators. The parameters used in these simulations (given in the Fig. 2 legend) generally match those in ref. 10. Experimental attempts to achieve β = 1, corresponding to equal decay times of mRNA and protein, were made in ref. 10, although actual values of β remain unknown. Furthermore, we have chosen the parameters of all three genes identical for mathematical and computational convenience, but the same results are obtained for the more realistic case of nonidentical genes (including differences in the Hill coefficient n). As for the value of Q, earlier experimental work has reported (29) that the equilibration time between extracellular and intracellular AI (1/k_diff in Eq. 4) is clearly <20 s. Assuming that k_diff ≈ 1 s^–1 and k_se ≈ 10 min^–1, we can estimate Q to be ≈0.8.

The results shown in Fig. 2 indicate that a transition from an unsynchronized to a synchronized regime exists as the strength of coupling increases (caused by an increase in cell density). This transition was predicted theoretically in the mid-1960s (12), but no quantitative experimental realization of this phenomenon has been reported thus far in coupled biological oscillators (19). To characterize quantitatively the transition to synchronization in this system, it is convenient to define a quantity (an “order parameter”) with value that changes abruptly at the transition point as a certain “control parameter” (in this case the cell density) varies. To that end, we compute the average signal 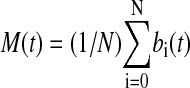, the temporal behavior of which in the synchronized case (Fig. 2f) will be similar to each one of the local signals b_i(t), i.e., it will display large-amplitude oscillations corresponding to the limit-cycle repressilator dynamics. On the other hand, in the unsynchronized situation (Fig. 2b), the individual signals b_i(t) are completely out of step with respect to each other, and their sum will be averaged out to an approximately constant value at all times (identically constant in the limit of an infinite number of cells). Accordingly, we define the order parameter R as the ratio of the standard deviation of the time series of M(t) to the standard deviation of b_i averaged over i,

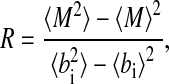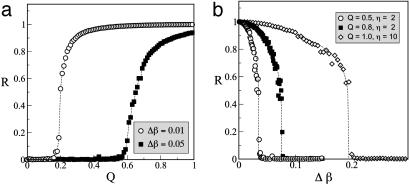
where 〈.〉 denotes time average, and indicates average over all cells. In this way, in the unsynchronized regime, R ≈ 0, whereas R ≈ 1 in the synchronized case. A sudden change between these two limiting values indicates that a phase transition has occurred. Such a signature is shown in Fig. 3a, which plots the dependence of R on the coupling strength Q for two different values of the parameter distribution width Δβ.

Fig. 3.

Synchronization transition for increasing Q (a) and Δβ (b). Parameters are the same as those described for Fig. 2. The dashed lines are guides for the eye.

Fig. 3a shows that the more similar the individual repressilators are, the smaller the threshold coupling for synchronization is. Furthermore, the maximum level of coherence in the synchronized regime (as measured by the plateau in R for large coupling) decreases as the difference between the oscillators increases. In fact, the diversity of the repressilators can be used as a control parameter of the transition as well, similar to what happens in general models of coupled oscillators (30). Fig. 3b shows how the system loses synchronization as Δβ increases. For Q = 0.8, the cutoff value of Δβ_c for which synchronization is lost (≈0.07, for which R = 0.5) corresponds to a range of periods of ≈3.5%. This period range increases above 10% for larger coupling strength Q and AI diffusion η, as shown by the open diamonds in Fig. 3b, where Δβ_c ≈0.2 for Q = 1 and η = 10, which are realistic parameter values.

The behavior shown in Fig. 3 is similar to that found in general models of coupled phase oscillators such as the Kuramoto model (30). In particular, the order parameter R of the transition displays a characteristic scaling as the transition point is approached. Whether the corresponding scaling form is the same as in Kuramoto's case is still an open question.

Coherence Enhancement Caused by Coupling

Previous experimental implementations of the repressilator have shown that there is not only substantial variability between cells in the growing population but also a noticeable irregularity in the oscillatory behavior of each individual cell (10). This irregularity may be caused by noise intrinsic or extrinsic to gene expression (27, 28), plasmid copy-number variability (31), or other extrinsic effects. Although its origin is not clear yet, systematic simulations of Eqs. 1–3 show that oscillatory behavior is most sensitive to parameter β. Therefore, we study the effects of extrinsic noise by substituting in Eq. 2 β by β_i + ξ_μi(t) for cell i (with μ = a, b, c representing each of the three genes of the repressilator). Many types of extrinsic noise are expected to be correlated on a time scale of one cell cycle (27). Hence, ξ_μi(t) is taken to be a Gaussian correlated noise of Ornstein–Uhlenbeck type, with zero mean and correlation 〈ξ_μi(t)ξ_νj(t′)〉 = δ_μνδ_ij(D/τ) exp(–|t – t′|/τ). Thus, the noise is considered to be uncorrelated between cells (and between genes in each cell), its intensity is given by D, and its autocorrelation time is given by τ. The resulting stochastic differential equation system has been numerically integrated by means of the Heun algorithm (32).

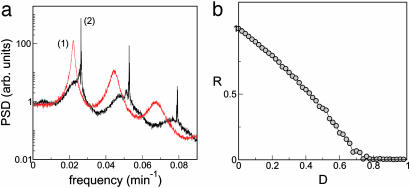
The effect of fluctuations in β are shown in Fig. 4a, which displays the power spectrum of the time series of the mRNA concentration b_i(t) averaged over 100 repressilators. In the absence of coupling (curve 1), peaks corresponding to the main oscillation frequency and its harmonics are clearly visible and are substantially broadened because of noise. When the cell density increases, coupling induces synchronization of the oscillators as described in the previous section. In that situation, synchronization enhances the spectral peaks and reduces strongly the irregularity in the oscillatory dynamics (see Fig. 4a, curve 2). In other words, coupling improves the reliability of the synthetic biochemical clocks. Synchronization, and hence coherence enhancement, disappears for strong noise, as shown in Fig. 4b. The cutoff value of D for which R = 0.5 (D ≈ 0.4, which incidentally is the value of D used in Fig. 4a) corresponds to a period dispersion similar to that given by the cutoff in Δβ defined above.

Fig. 4.

Effects of colored noise on the power spectrum and coherence of a population of coupled repressilators. (a) Power spectral density (PSD) averaged over a population of 100 repressilators for the case of Q = 0 (curve 1) and Q = 1 (curve 2), with D = 0.4. (b) Coherence parameter R vs. noise intensity D. In both plots, the noise correlation time is τ = 15 min, the AI diffusivity is η = 10, and Δβ = 0. Other parameters are the same as those described for Fig. 2. arb., Arbitrary.

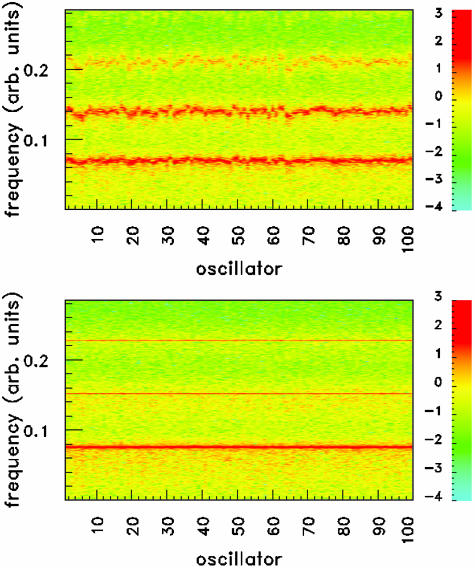
The double role of coupling in reducing the diversity and irregularity of the cell population is shown in Fig. 5, where the power spectral density of 100 cells is simultaneously shown. For small coupling (Fig. 5 Upper), the position of the spectral peaks (and their harmonics) is scattered over a relatively large range, and a sizeable amount of power is distributed between the peaks. In the synchronized case (Fig. 5 Lower), on the other hand, the peak location is the same for all oscillators (corresponding to the result shown in Fig. 2e), and the spectral power is concentrated at the peaks.

Fig. 5.

Spectrogram showing the power spectral density (in logarithmic scale; decade indexes are shown on the right) of 100 coupled repressilators, for Q = 0.2 (Upper) and Q = 1.0 (Lower). The noise intensity is D = 0.04, and the standard deviation in β is Δβ = 0.04. Here the noise is taken to be white, namely τ = 0. Other parameters are the same as those described for Fig. 2. arb., Arbitrary.

Discussion

Earlier experimental studies have shown that a large degree of variability prevents the observation of macroscopic rhythms in a population of synthetic genetic oscillators (10). On the other hand, it is well known that natural multicellular clocks operate on mean periods resulting from averaging over the diverse individual cells (3–7). We have proposed a modular coupling mechanism through quorum sensing that leads to synchronization under realistic conditions in an ensemble of existing synthetic repressilators (or optimized variants of them). By its design, the communication module can be added directly to existing repressilator strains. Earlier attempts to synchronize repressilators in this way have been made by D. Endy and coworkers (see http://parts.mit.edu).

In a recent theoretical study, McMillen et al. (16) have shown that this type of intercell signaling produces synchronized behavior in populations of identical genetic relaxation oscillators. In contrast to the repressilators studied in the present article, which only make use of negative feedback and in which all biochemical species have similar decay rates, relaxation oscillators are based on both positive and negative feedback, and their dynamics are governed by two (at least) widely different time scales. These features lead to oscillations characterized by abrupt changes in the chemical concentrations (dynamically similar to the spiky behavior of neural oscillators). In our case, on the other hand, oscillations are approximately sinusoidal, with no abrupt jumps or decays of the dynamical variables, similar to what happens in the phase oscillators that have long been used to model biological rhythms (12, 19).

In the spiky relaxation oscillators, coupling occurs in the form of so-called fast threshold modulation (21), which generally is believed to lead to synchronization faster than phase oscillators. McMillen et al. (16) found that perfect synchrony was achieved within two oscillation periods, starting from an ensemble of oscillators with randomly distributed phases. We examined whether synchronization of repressilators requires much longer time windows. Our results (not shown) indicate that synchronization can be achieved in a few cycles, i.e., in time windows of the same order of magnitude as those required by fast threshold modulation in relaxation oscillators. We checked that this rate is relatively independent of the coupling strength by varying this parameter over 2 orders of magnitude. These results may indicate that the speed of synchronization is related more to the type of coupling than to the nature of the individual oscillators. A realistic description of intercell communication, such as the one considered here through quorum sensing, can be expected to lead to efficient synchronization even among phase oscillators.

Besides its efficiency, the synchronization reported here has been seen to lead to the generation of a global rhythm in a highly heterogeneous ensemble of genetic oscillators. The resulting clock behavior is seen to be highly robust to random phase drifts of the individual oscillators because of noise. In light of these results, one might speculate whether natural biological clocks have evolved in this same way, i.e., by using intercell communication to couple an assembly of originally independent sloppy clocks. The positive effects of coupling are also relevant in synthetic gene networks, given the experimental difficulties usually encountered when dealing with populations of oscillating repressilators (10). The present proposal adds just one small communication module to an existing synthetic genetic circuit (see Fig. 1); hence, the results reported here lead us to expect that the experimental observation of a synchronizing transition in biological phase oscillators (19) is within reach.

Finally, we close with two remarks about the limitations of our work, first with respect to its biological implications and then with respect to its mathematical aspects.

Throughout this article, we have drawn inspiration from the example of naturally occurring biological clocks. However, one must not take the analogy too strictly, given the important differences between the various multicellular clocks found in vivo and the synthetic system studied here. For example, consider the diversity of coupling mechanisms that nature uses to enforce synchrony among cells. In the sinoatrial node of the heart, the coupling is electrotonic and mediated by gap junctions. In the suprachiasmatic nuclei of the mammalian circadian pacemaker, the early evidence suggested that neither gap junctions (33) nor synaptic communication (34) were essential for synchrony, leading to the proposal that the coupling was provided instead by diffusion of the inhibitory neurotransmitter γ-aminobutyric acid (3, 35) or some other diffusible substance. More recent experiments, however, seem to indicate a crucial role for action-potential propagation and synaptic coupling in the suprachiasmatic nuclei (36). Thus, neither the cardiac nor the circadian pacemaker are likely to be coupled by the sort of diffusive mechanism assumed in our model. Perhaps the closest analog to our system in nature is the metabolic synchrony observed in a well mixed suspension of yeast cells, in which the glycolytic oscillations of millions of cells are mutually synchronized by diffusive exchange of acetaldehyde (37, 38).

On the mathematical side, the governing equations assumed here provide interesting challenges for the analysis of collective synchronization. Our simulation results suggest that this system should undergo a phase transition to mutual synchronization of the same sort seen in the Kuramoto model, but we have not proven that analytically. Such a calculation may be possible, perhaps by applying phase-reduction methods in the limit where the individual repressilators are weakly coupled and close to a Hopf bifurcation (39) or by adapting the methods recently developed by Ott et al. (40) for globally coupled systems.