Origin of the neighboring residue effect on peptide backbone conformation

Abstract

Unfolded peptides in water have some residual structure that may be important in the folding process, and the nature of the residual structure is currently of much interest. There is a neighboring residue effect on backbone conformation, discovered in 1997 from measurements of ³J_HNα coupling constants. The neighboring residue effect appears also in the “coil library” of Protein Data Bank structures of residues not in α-helix and not in β-structure. When a neighboring residue (i – 1 or i + 1) belongs to class L (aromatic and β-branched amino acids, FHITVWY) rather than class S (all others, G and P excluded), then the backbone angle φ of residue i is more negative for essentially all amino acids. Calculated values of peptide solvation (electrostatic solvation free energy, ESF) predict basic properties of the neighboring residue effect. We show that L amino acids reduce the solvation of neighboring peptide groups more than S amino acids. When tripeptides from the coil library are excised to allow solvation, the central residues have more negative values of 〈φ〉 but less negative values of 〈ESF〉 with L than with S neighbors. The coil library values of 〈³J_HNα〉, which vary strikingly among the amino acids, are correlated with the neighboring residue effect seen by ESF. Moreover, values for the “blocking effect” of side chains on the hydrogen exchange rates of peptide NH protons are correlated with ESF values.

Short peptides, too short to form any structure that is stabilized by peptide H bonds, nevertheless have significant structure. The first clear demonstration was the 1997 discovery by Penkett et al. (1) of a neighboring residue effect. The ³J_HNα coupling constant in NMR studies of peptides is directly related to the backbone angle φ by the Karplus relation (2). The φ value of residue X is more negative when its preceding neighbor is class L (aromatic and β-branched, FHITVWY) rather than class S (all other amino acids, Gly and Pro omitted) (1). This behavior is found for all amino acids, except that Gly and Pro are omitted for reasons given below. The physical cause of the neighboring residue effect is unknown. We show here that peptide backbone solvation and the shielding from water of peptide groups by adjacent side chains are the probable causes.

The coil library of residue structures from the Protein Data Bank, not in α-helix and not in β-sheet, was used as a working model of the backbone conformations of residues in unfolded peptides (3–8). In the coil library, average values of the backbone angle φ and also of 〈³J_HNα〉 calculated from φ differed substantially among the amino acids (3–8). The same values of 〈³J_HNα〉 were found in the coil library as in NMR studies of unfolded peptides, within error (5, 8). The coil library is said to reveal the true propensities of different amino acids to form various backbone conformations (3–6). It is widely accepted that protein structures are made from “low-energy parts” (9), and consequently peptide structures provide values not only for bond angles and distances and prevalence of the trans peptide bond but also for the most probable side chain rotamers (9). Here we turn this hypothesis around and use protein structures to provide the distributions of backbone angles φ and ψ in unfolded peptides. Because peptide H bonds constrain the backbone angles in α-helices and β-sheets, we omit residues from these secondary structures and use the coil library instead of the “all” residue library. Protein structures are tight-packed, including residues in the coil library, but unfolded peptides are not. This distinction suggests that use of the coil library to model unfolded peptides should be restricted to data from single residues or perhaps pairs of residues. Because the neighboring residue effect appears in both unfolded peptides (1) and the coil library, it seems that the coil library models at least pairs of unfolded residues.

Our thesis is that solvation of the peptide backbone, with side chain shielding of peptide groups from water, has the properties needed to explain the neighboring residue effect. Electrostatic solvation results from the interaction between water and partial charges on the peptide NH and CO groups, and we argue that electrostatic solvation free energy (ESF, also known as the Born term) is responsible for the neighboring residue effect. delphi was used here to calculate ESF. The structure of the molecule must be known accurately, but other parameters are not adjustable (10). The PARSE parameter set of delphi (10) has been calibrated against experimental solvation free energies of model compounds, including amides. Thus, calculated values of ESF are based on experimental solvation free energies. Solvation is a stabilizing interaction between the peptide group and water, and ESF values are free energies with a negative sign and are reported here in kcal/mol.

A self-evident property of ESF is that it exhibits a neighboring residue effect. The properties of this effect are investigated here with two different systems. The first system is a model peptide system, acetyl-A₄XA₄-amide, where X is any amino acid and the peptide has the extended β conformation (–120°, 120°). The peptide length was chosen to avoid end effects. The second system is the coil library, used here as a putative model of backbone conformations in denatured proteins. Tripeptides (with blocking groups added) were excised from 1,476 high-resolution structures to allow solvation to occur. The effects of L and S neighbors on the values of 〈φ〉 and of 〈ESF〉 of the various amino acid types are studied.

Finally, we look for a possible correlation between the neighboring residue effect seen by ESF and certain experimental quantities suggested by the model peptide results. The first quantity is the coil library value of 〈³J_HNα〉, which varies strikingly among the amino acids (3–8). The second quantity is the “blocking effect” observed in measurements of hydrogen exchange rates in dipeptides (11, 12); the amino acid side chains shield adjacent peptide NH protons from exchange with solvent.

Methods

Representation of peptides, calculation of ESF from peptide structure, and calculation of ³J_HNa from φ were performed as described (8). 〈³J_HNα〉 was found from φ values in the coil library by first calculating ³J_HNa and then averaging. “PARSE-neutral” charges were used in delphi calculations of ESF, and the side chains were treated as uncharged. To obtain the ESF of individual atoms (at the peptide CO and NH groups), equation 13 of ref. 13 was used. The dssp program (14) was used to obtain the coil library residues from the Protein Data Bank structures. Note that the coil library thus includes residues in β-turns. Selective filters were used to eliminate some residues for ESF calculations. The backbone conformation of residue 5 in the (Ala)₉ calculations was changed from approximately extended β (–120°, 120°) to approximately polyproline II (PPII) (–70°, 150°) in five steps of 10° in φ,6° in ψ. For the (Ala)₉ electrostatic calculations, the delphi grid had 61 × 61 × 61 points, one focusing step was performed, and the final mesh size of the grid was 0.4 Å. The value of ΔG*(HX), the blocking effect in hydrogen exchange, was calculated as –2.303RT log(A+B)/2, as described by Bai and Englander (12); the values of A and B (which are negative) are given in table 2 of ref. 11.

Results

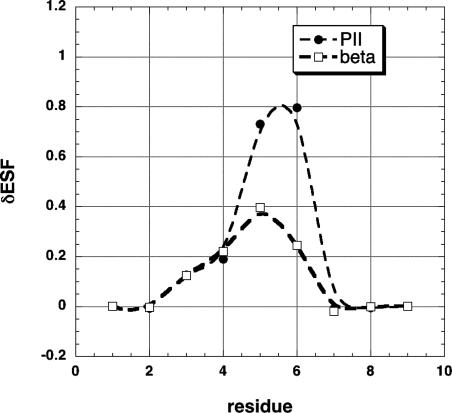
Changes in ESF at Neighboring Peptide Groups for Amino Acid Substitutions in an Alanine Host Peptide. Fig. 1 shows δESF, the change in ESF at each residue position, for a nine-residue alanine peptide (extended β conformation), resulting from the substitution Ala→Val at residue 5. There are several points of interest. First, individual values of δESF are as large as 0.8 kcal/mol. Substitution of the more bulky Val side chain for Ala reduced the –ESF values of nearby peptide groups and thus the substitution is destabilizing. Second, substantial values of δESF are found not only at the substitution site, residue 5, but also at the neighboring residues 4 and 6, and δESF is significant even at residue 3. Third, values of δESF are roughly twice as large when residue 5 is in the PPII conformation as opposed to the β conformation. Finally, the curve of δESF versus residue number is not symmetrical about the substitution site. The curve of δESF versus residue number may shift as well as changing shape when the rotamer of residue 5 varies. Thus, we use the sum of all δESF changes (ΔESF) when correlating the neighboring residue effect of X with an experimental quantity that involves averaging over different rotamers of X.

Fig. 1.

The change in ESF (δESF) resulting from amino acid substitution, plotted against residue number. The host peptide is a nine-residue alanine peptide, and the substitution is Ala→ Val at residue 5. The units of ESF are kcal/mol. At all residues except the substitution site, the alanine host peptide has the extended β backbone conformation (φ, ψ = –120°, 120°). At the substitution site, the residue (either Ala or Val) has either the extended β or an approximate PPII (φ, ψ = –70°, 150°) conformation.

Evidently the substitution Ala→Val produces large enough δESF values to be the cause of the neighboring residue effect. Penkett et al. (1) reported the neighboring residue effect only for residues that precede X. Fig. 1 shows that an ESF change occurs also at the residue after X and even at residue 3, two peptide groups away from the substitution site. The plot of ESF versus residue number for the (Ala)₉ peptide is a horizontal line (ESF = –8.53 kcal/mol) for residues 3–7, whereas the ESF values of the two end residues 1 and 9 are more negative because of increased solvent accessibility (15).

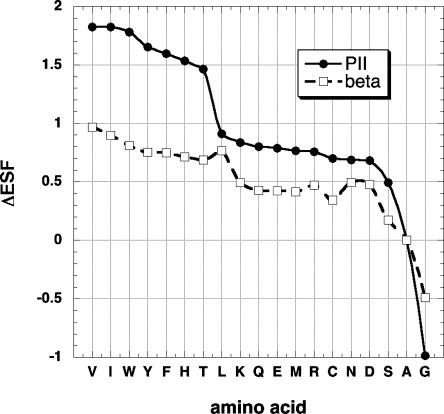
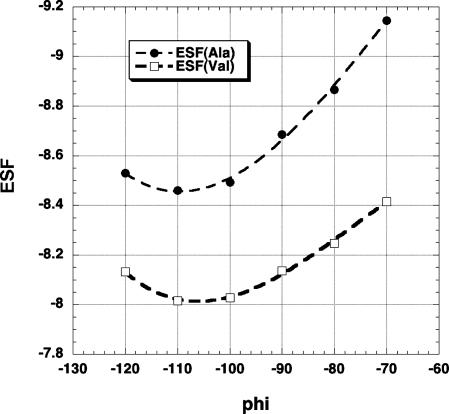
The sum of the δESF changes at all residue positions (ΔESF) is shown in Fig. 2 for various amino acid substitutions. There are two points of interest. First, ΔESF is substantially larger when the substituted amino acid is in the PPII rather than the extended β conformation. Second, one group of amino acids (FHITVWY) shows values of ΔESF that are almost twice as large as the others (G and P excluded) when residue 5 is in the PPII conformation. These two side chain groups correspond to the class L and class S amino acids of Penkett et al. (1). Fig. 3 shows how the ESF values of Ala and Val at residue 5 change with φ between extended β (–120°, 120°) and a conformation close to PPII (–70°, 150°). Ala is more solvated than Val at all values of φ and, as –φ decreases, –ESF increases for –φ < 105°.

Fig. 2.

The overall change in ESF (ΔESF, kcal/mol) produced by an amino acid substitution in an (Ala)₉ peptide (see legend to Fig. 1) plotted against amino acid type. The first seven amino acids (VIWYFHT) belong to group L, as defined earlier (1), whereas the other amino acids (except for Gly) belong to group S.

Fig. 3.

Residue 5 [the substitution site in the (Ala)₉ peptide of Fig. 1] is made to undergo a transition from extended β (–120°, 120°) to approximately PPII (–70°, 150°) in steps of 10° in φ and 6° in ψ. The value of ESF (in kcal/mol) at residue 5 is plotted against φ for the substituted residue, Ala or Val.

The two amino acids Gly and Pro are excluded from class S for different reasons. The behavior of Gly in response to a neighboring residue is unpredictable because of the large allowed regions in the φ, ψ map for Gly; moreover, in Fig. 2 Gly shows a large ΔESF value with the opposite sign from other amino acids. Pro is excluded because the proline ring fixes the value of φ for Pro, which cannot show a substantial neighboring residue effect.

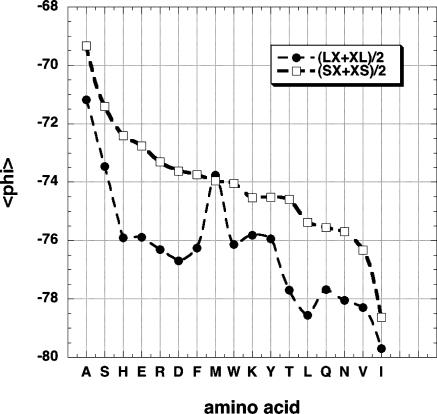
Neighboring Residue Effect in the Coil Library. Fig. 4 shows the neighboring residue effect (L versus S neighbors) in the coil library given by 〈φ〉 values of the various amino acids within the PPII window (–100° > φ >–40°, 90° < ψ < 180°). On average, residues with L neighbors have more negative 〈φ〉 values than residues with S neighbors by –2.2°. Only residues within the PPII window are included because, if instead the entire φ, ψ map is included, sparsely populated conformations with positive φ values are likely to give misleading results. (This problem can be minimized by comparing values of 〈³J_HNα〉 instead of 〈φ〉, but it is of interest to determine the different 〈φ〉 values caused by L versus S neighbors.) Gly and Pro are omitted for reasons explained above, and Cys is also omitted from coil library data because of the very small number of entries for free Cys residues. Met is an outlier in Fig. 4 in not showing 〈φ〉 to be more negative with L than S neighbors, but the number of entries for Met is small. The neighboring residue effect in the coil library (Fig. 4) is much like the one found by Penkett et al. (1), who analyzed the “all” library.

Fig. 4.

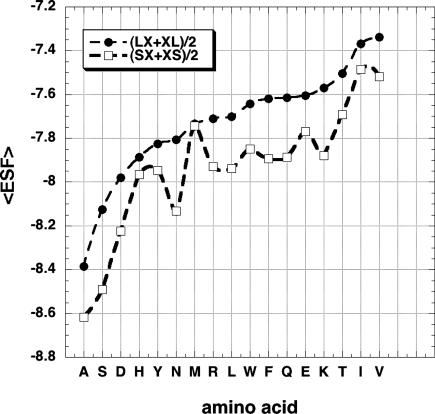
The neighboring residue effect seen by plotting 〈φ〉 for the central residues of tripeptides excised from the coil library; the neighboring residues are either L or S. Only backbone conformations contained in the PPII window (–100° > φ > –40°, 90° < ψ < 180°) are counted. The average of the values found for preceding (LX or SX) and following (XL or XS) neighbors is shown. The amino acids are ordered by the 〈φ〉 values of residues with S neighbors.

The effect of L versus S neighbors on the 〈ESF〉 values (central residues) for the 35,310 coil library tripeptides present in the PPII window (–100° > φ >–40°,90° < ψ < 180°) after filtering is shown in Fig. 5. There is a consistent difference with L versus S neighbors, as expected from Figs. 1 and 2. On average, the 〈ESF〉 values are less negative by 0.21 kcal/mol with L than with S neighbors. In summary, when a given amino acid type in the coil library has L rather than S neighbors, it has on average a more negative value of 〈φ〉 by 2.2° but a less negative value of 〈ESF〉 by 0.21 kcal/mol.

Fig. 5.

The neighboring residue effect shown by ESF values in tripeptides excised from the coil library. 〈ESF〉 is the average ESF of the central residue (type X) when the neighbors of X are either L or S; average results for preceding and following neighbors are shown. The amino acids are ordered by the 〈ESF〉 values of residues with L neighbors.

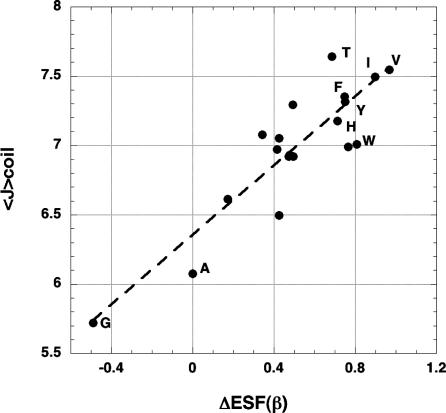
ESF Correlates with the Variation in 〈³J_HNa〉 Among the Amino Acids. The first clear evidence for significant structure in unfolded peptides came from the variation in φ with amino acid type, evidenced by ³J_HNa coupling constants in unfolded peptides and their agreement with coil library 〈³J_HNα〉 values computed from data for φ (3–8). The different φ, ψ maps of the amino acids in the coil library have been interpreted as revealing the intrinsic propensities of the amino acids in unfolded peptides to assume different backbone conformations (3–8). If, as expected from Figs. 1 and 2, the variation in φ with amino acid type in the coil library is caused chiefly by peptide solvation (ESF), then the coil library values of 〈³J_HNa〉 computed from φ should be correlated with ΔESF values for amino acid substitutions in an (Ala)₉ host peptide. This correlation is shown in Fig. 6: the correlation coefficient is 0.89. Note that class L amino acids (FHITVWY) have larger values of 〈³J_HNa〉 than class S amino acids, as expected.

Fig. 6.

The average coupling constant (〈³J_HNα〉 in Hz) of an amino acid in the coil library plotted against calculated values of the neighboring residue effect (extended β conformation, ΔESF in kcal/mol) for the various amino acids in an (Ala)₉ host peptide (see Fig. 2). The class L amino acids are labeled, and also Ala and Gly for reference.

Peptide Solvation (ESF) Correlates with the Blocking Effect in Hydrogen Exchange. In hydrogen exchange studies with dipeptides (11), the bulkiness of a nonpolar side chain affects the rate of hydrogen exchange of the adjacent peptide NH proton. The side chain reduces the access of solvent to the peptide group, whereas the solvent species that takes part in the exchange reaction (the OH^– ion in base-catalyzed exchange and the H⁺ ion in acid-catalyzed exchange) is highly solvated. Thus, Val has a 4-fold-lower hydrogen exchange rate than Ala in both the base- and acid-catalyzed exchange reactions (11). The electron-withdrawing effect of a nonpolar side chain is negligible and the pH minimum for exchange is the same for different nonpolar side chains, because the acid- and base-catalyzed rates are affected to the same extent by the side chain. Then the blocking effect is measured by the reduction in exchange rate (compared with Ala) at the pH minimum. For polar side chains, whose electron-withdrawing effects are not negligible, the pH minimum shifts and the blocking effect is measured from the reduction in exchange rate at the shifted pH minimum (11, 12).

Hydrogen exchange is considered to be a diffusion-controlled proton transfer reaction, to a close approximation (16–18), and its exchange rate (k_HX) is given by

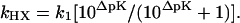[1]

In Eq. 1, k₁ is the diffusion-controlled rate for proton transfer in water (≈10¹⁰ M^–1·s^–1), and the factor in brackets gives the fraction of productive encounters between proton donor and acceptor. Thus, the hydrogen exchange rate depends on the equilibrium pK difference (ΔpK, which is always negative) between the proton donor (water) and acceptor (peptide); 10^ΔpK is usually ≪1, so that ln k_HX is proportional to ΔpK. Thus, the effect of varying the nonpolar side chain at C_α on the pK of the peptide group should determine the blocking effect in hydrogen exchange. The change in ΔpK caused by an amino acid substitution is determined directly from the change in ESF of the ionized peptide species for the base- or acid-catalyzed reaction. Note that the pK values (25°C) of acetic acid (side chain 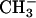; pK 4.756) and propionic acid (side chain 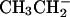; pK 4.874) (19) differ significantly. McCammon and coworkers (18) have used pK prediction to compare, with good success, predicted and observed exchange rates in dipeptides for amino acids that contain electron-withdrawing substituents.

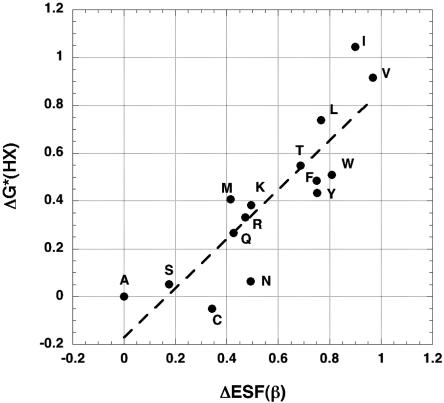
Because the blocking effect is the same in the acid- and base-catalyzed reactions (11, 12), whereas the ionized peptide group has opposite charges in the two reactions, we used the neutral form of the peptide and compared the blocking free energy with the relative changes in ESF of the different amino acids in the (Ala)₉ peptide. Fig. 7 shows a good correlation between ΔESF and blocking free energy for the left peptide group in dipeptides; the correlation coefficient is 0.87 and the slope is 1.03. The slope is not predictable at present. According to ESF calculations, the exchange rate should depend on the peptide backbone conformation and also on the rotamer conformation of the amino acid, and the measured exchange rate represents an average over all conformations present. On the other hand, the ESF calculations were made for a single fixed conformation, because the actual backbone and side chain conformations are still a subject of research. The slope in Fig. 7 increases almost to 2 if ΔESF values for the PPII conformation, instead of the extended β conformation, are used. However, the slope decreases substantially if the value for δESF at residue 5 (which corresponds to the measured exchange rate) is used instead of ΔESF for the whole peptide.

Fig. 7.

The “blocking effect” of the side chain (11, 12) on the hydrogen exchange rate of the adjacent peptide NH proton plotted against the neighboring residue effect (extended β conformation, ΔESF in kcal/mol, Fig. 2) for that amino acid in an (Ala)₉ host peptide. The blocking effect is given as an apparent free energy in kcal/mol (see text).

Glu, Asp, and His are not included in Fig. 7 because their blocking effects are not known accurately, because their ionization states are changing at their respective pH minima for exchange. Gly is not included because the apparent blocking free energy difference between Ala and Gly is not the same in the acid- and base-catalyzed exchange reactions (11).

Bai and Englander (12) correlated the blocking free energy in hydrogen exchange with thermodynamic β structure propensities measured by Kim and Berg (20) at a solvent-exposed site within the β-hairpin of a zinc finger protein. Likewise, Avbelj and Baldwin (21) correlated Kim and Berg's β-structure propensities with ESF values of the 20 aa, using structures computed for the substitution site in the zinc finger protein. Interestingly, the correlation between β-structure propensities and blocking free energy is inverse, not direct (12), as is the correlation between β-structure propensities and ESF (21). The inverse correlation was explained by arguing that the blocking effect in hydrogen exchange (12) should be larger when the zinc finger is unfolded than when it is folded, and the same argument was made with the ESF correlation (21).

Discussion

The ESF Approach to Peptide Solvation. The landmark experiment of Wolfenden (22) showed in 1978 that amides have solvation free energies of approximately –10 kcal/mol and demonstrated that peptide solvation is an important but neglected factor in the energetics of protein folding. Makhatadze and Privalov (23) then incorporated estimates of peptide solvation into their analysis of folding energetics. Honig and coworkers (10) were able to fit the experimental solvation free energies of 67 small polar molecules with electrostatic calculations based on delphi, after taking into account the nonelectrostatic factors that also contribute to solvation free energy by using a simple, approximate, experimentally based procedure.

Only recently have detailed ESF calculations been made for peptides (8, 13, 15, 21). The results emphasize that the ESF of a peptide group depends strongly on its accessibility to water. If the peptide is buried out of contact with water, its ESF falls to zero and ESF calculations cease to be informative (21). The study of unfolded peptides in water is an optimal case in which the assumptions made in calculating ESF values correspond reasonably well with reality. As discussed earlier (8), the most direct test at present of how well ESF calculations compare with reality is to compare the simulated distributions of backbone conformations in denatured proteins with the coil library distributions. The simulations involve two additional physical factors besides ESF (see below). Some success has been reported (8), but the agreement between the coil library distributions and the simulated distributions is not yet fully quantitative.

ESF calculations on peptides have been used to discuss the following topics: the nature of helix propensities (13, 15) and β-structure propensities (13, 21), the desolvation penalty for burying a H bonded peptide group (15, 21, 24), and the contribution of ESF to the enthalpy change for forming an alanine peptide helix (24). Note that for amides, the free energy and the enthalpy of interaction of the polar groups (NH and CO) with water are practically equal, according to experimental data (15). ESF calculations provide an important part of the electrostatic screening model (ESM), which has been used to predict the cooperative formation of β-strands in denatured proteins (13) and to simulate libraries of backbone conformations for the different amino acids in denatured proteins (8).

Neighboring Residue Effect Seen via ESF. The neighboring residue effect seen via ESF (Figs. 1 and 2) has correct properties to explain why 〈φ〉 values in the coil library depend on whether the adjacent residues are class L or S. First, the size of the neighboring residue effect seen by ESF is large. For the substitution Ala→Val in an extended (Ala)₉ peptide, the energetic cost of the substitution is nearly 2 kcal/mol if the substituted residue is in the PPII conformation, or ≈1 kcal/mol if it is in the extended β conformation (Fig. 2). Second, when the ESF changes caused by amino acid substitutions are divided into two classes, large and small (Fig. 1), the same two classes of amino acids appear as in the neighboring residue effect studied by Penkett et al. (1). Third, the dipole–dipole interactions in the peptide backbone determine that ESF depends directly on φ, as illustrated in Fig. 3, and the dependence has the correct sign to account for the neighboring residue effect. The magnitude also appears reasonable.

Simulations of backbone conformations in denatured proteins, using the ESM, provide insight into the neighboring residue effect. In the ESM, the distribution of backbone conformations, g(φ), for φ values between β and PPII, depends chiefly on three factors: ESF, E_local, and V(φ). E_local is the local electrostatic potential in the peptide backbone, and V(φ) is the torsional potential about φ. Both V(φ) and E_local depend only on peptide backbone geometry, whereas ESF depends on the type and rotamer conformation of neighboring side chains (Figs. 1 and 2) as well as on peptide backbone geometry. V(φ) has its maximum (destabilizing) value at φ = –120° and consequently V(φ) acts to destabilize extended β more than PPII. On the other hand, E_local has its maximum (stabilizing) value at φ = –120° because the peptide dipoles are antiparallel in this conformation (25, 26), and therefore E_local acts to stabilize extended β more than PPII. ESF, which represents a stabilizing interaction of the peptide group with water, changes strongly with φ (Fig. 3), and the behavior of ESF is critical in determining g(φ) because ESF depends directly on the side chain type (Figs. 2 and 3). Although ESF is proportional to E_local (13, 26), the change in ESF with φ has the opposite sign to the change in E_local with φ (13). Thus, each of these three physical factors [ESF, E_local, and V(φ)] has its own distinctive effect in determining g(φ), the distribution of φ values between extended β and PPII. There are striking differences among the coil library g(φ) distributions of the 20 aa (8), with Ala and Val representing opposite extremes: Ala is highly populated at PPII whereas Val favors extended β.

The slope (σ) of ESF versus φ (at each φ value considered) is a critical parameter determining how the backbone conformations (φ values) of a given amino acid are distributed between extended β and PPII. When the amino acid becomes less well solvated, the value of –σ decreases as the –ESF value decreases. Thus at φ =–75° in Fig. 1, the values of σ for Ala (which is well solvated) and Val (which is less well solvated) are –0.028 and –0.017 kcal/mol per degree. For any coil library residue X, –σ is smaller if X has L neighbors than S neighbors (data not shown). This dependence of σ on the extent of solvation is the origin of the neighboring residue effect according to the ESM. The coil library difference between 〈ESF〉 values of residues with L and S neighbors is –0.21 kcal/mol (Fig. 5), and the difference between 〈φ〉 values is 2.2° (Fig. 4). The ratio is –0.095 kcal/mol per degree, which is roughly similar in magnitude to the values of σ given above.

F.A. and S. Golic-Grdadolnik (unpublished work) found that electrostatic coupling among neighboring peptide NH and CO dipoles in the backbone induces cooperative formation of β-strands in unfolded ubiquitin. The neighboring residue effect and the formation of β-strands are different manifestations of the same phenomenon: stronger electrostatic interactions when large or bulky side chains are nearby.

Implications of the ESF Neighboring Residue Effect. A basic conclusion from our work is that peptide solvation provides a connecting link between the backbone conformations of adjacent residues in unfolded peptides. Class L side chains cause substantial decreases in the –ESF values of neighboring peptide groups, whereas class S side chains produce smaller decreases. This behavior has the potential to be important in directing the folding process at initial stages of folding.

Erman and coworkers (27) looked for possible sequence-dependent correlations between successive pairs of φ, ψ angles in structures from the Protein Data Bank and used the results to test for preferences for native backbone conformations in an unfolded polypeptide. After excising tripeptides from protein structures (using the all library, not the coil library), they used the tripeptides to construct a knowledge-based potential of mean force. Then they used the rotational isomeric states model (28) to describe the unfolded polypeptide chain of the well studied small protein CI2. They compared the backbone conformations in the unfolded chain predicted by the knowledge-based potential and by a potential based on rejecting conformations showing steric clash. They concluded that the knowledge-based potential has significant success in choosing native backbone conformations for unfolded CI2, whereas the potential based on steric clash does not. Our results suggest that peptide solvation is probably a major contributor to correlations between successive pairs of φ,ψ angles and to the success of the knowledge-based potential in predicting native backbone conformations.

The neighboring residue effect influences the φ, ψ maps of the amino acids because it broadens the distribution of residue conformations in each type of backbone conformation. In the coil library g(φ) distributions, g(φ) for amino acid X in LX pairs is shifted relative to g(φ) for X in SX pairs (data not shown, but this is evident from Fig. 4), and so the sum of the two g(φ) distributions is broadened compared to either one separately. The φ, ψ maps, or Ramachandran maps, of the amino acids are often said to reflect their folding properties. However, the neighboring residue effect shows that the φ, ψ maps also depend on the properties of pairs of residues; see also ref. 27.

Related Work on the Energetic Origin of the PPII Conformation in Alanine Peptides. The recent reports by several laboratories, using various approaches, that PPII is the major backbone conformation present in alanine peptides containing seven or fewer residues (for review, see ref. 29; see also a dissenting view, ref. 30) has sparked an interest in finding the energetic origin of this preference (31–34). There is general agreement that solvation should be a key factor in determining the preference of alanine peptides for the PPII conformation, which is an open extended structure not stabilized by peptide H bonds. A key point is that the unsolvated PPII conformation in an alanine peptide is not predicted to be stable in the gas phase, although it is predicted to be stable in water (33). As discussed above, the ESM predicts that the preference of alanine for the PPII conformation arises chiefly from the electrostatic interactions between peptide NH and CO dipoles and screening of these interactions by water, which is shielded only slightly by alanine but more strongly by bulky side chains such as those of valine and isoleucine.

Monte Carlo simulations of the interaction between water and polyalanine, using the charm 22 force field, have been reported recently by Mezei et al. (34). Their simulations used explicit water molecules, and they were able to examine the H bonding interactions made between water and the peptide backbone. Overall, their results show good agreement with our results for alanine in the (Ala)₉ peptide. They found that the apparent interaction enthalpy between water and the alanine peptide is significantly stronger in the PPII than in the extended β conformation, and examination of the H bonds made between water and the peptide group did not provide an obvious explanation. Although the ESF values in Fig. 3 refer to the free energy of the interaction between water and the peptide group, the ESF is approximately equal to the enthalpy of the interaction, according to experimental data for amides (15).

Molecular dynamics simulations of backbone conformation for the alanine dipeptide (containing a single alanine residue with acetyl and amide blocking groups) have been made for five different force fields by Hermans and coworkers (35). The results show that the five different force fields give quite different φ, ψ maps, presumably because the energy differences between backbone conformations are smaller than the errors of these force fields. As a result, modifications of two of these force fields have been reported recently, made with the specific aim of obtaining agreement either with experimental data on alanine peptides (36) or with the all library φ, ψ maps of the different amino acids (37).

The rationale for our approach to problems of backbone conformations in unfolded peptides, where the energy differences are small, is this. By studying only the small number of physical factors necessary to reproduce the data, as compared with the large number of physical factors represented in a force field, it may be possible to determine factors such as V(φ) directly and to check the reliability of the calculations used to determine ESF and E_local.