The dynamics of genomic-length DNA molecules in 100-nm channels

Abstract

We show that genomic-length DNA molecules imaged in nanochannels have an extension along the channel that scales linearly with the contour length of the polymer, in agreement with the scaling arguments developed by de Gennes for self-avoiding confined polymers. This fundamental relationship allows us to measure directly the contour length of single DNA molecules confined in the channels, and the statistical analysis of the dynamics of the polymer in the nanochannel allows us to compute the SD of the mean of the extension. This statistical analysis allows us to measure the extension of λ DNA multimers with a 130-nm SD in 1 min.

The location of landmark restriction sites on chromosomal-length DNA molecules is a powerful way to guarantee that the assembled DNA sequences in shotgun DNA sequencing represent the native genome faithfully. The restriction sites can be determined by measuring the length of restriction fragments by gel electrophoresis (1). Alternatively, they can be located by using optical mapping of stretched DNA molecules trapped on a surface (2). To measure the contour length of a single molecule by using optical techniques directly, it is necessary to extend the polymer such that a one-to-one mapping can be established between the spatial position along the polymer and position within the genome.

Confinement elongation of genomic-length DNA has several advantages over alternative techniques for extending DNA, such as flow stretching and/or stretching relying on a tethered molecule. Confinement elongation does not require the presence of a known external force because a molecule in a nanochannel will remain stretched in its equilibrium configuration, and hence, the mechanism is in equilibrium. Second, it allows for continuous measurement of length.

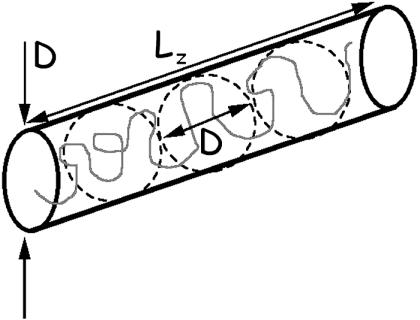
Some fundamental statistical mechanical problems are associated with confinement of a polymer in a channel whose width D is much less than the radius of gyration of the unconfined polymer, such as (i) the dependence of the end-to-end length L_z of the confined polymer on the length L of the polymer and (ii) the dependence of the effective spring constant k of the confined polymer on the length L. The spring constant sets the scale of end-to-end length fluctuations for the confined polymer because of thermal effects. For the measurement process, an understanding of the relaxation time τ is also crucial. A key element for understanding these questions is the influence of the self-avoiding nature of random walk of the polymer in the channel, as we show in Fig. 1.

Fig. 1.

When the DNA polymer is confined to a channel of diameter D, the polymer must elongate to some end-to-end distance L_z(D). In a confining tube, the polymer must elongate as a series of “blobs,” which cannot interpenetrate because of self-avoidance. Thus, in a tube of diameter D, we have .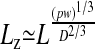

The effect of self-avoidance on flexible polymers that are freely coiled in solution was first understood by Flory (3) and later generalized to the semiflexible case by Schaefer et al. (4). The rms radius of gyration R_g of a self-avoiding persistent polymer in solution scales according to Flory–Pincus with the persistence length p, molecule width w, and contour length L, such that (pw)^1/5L^3/5. Compare this form with the result expected for an ideal, non-self-avoiding polymer R_g ≈ (pL)^1/2. Thus, self-avoidance for a freely coiled polymer has the following two effects: it adds a weak dependence on the molecule width and it “puffs out” the coil slightly by giving rise to a stronger dependence on the contour length. These equations are, in fact, roughly in agreement with existing data for freely coiled DNA (5). Benzothiazolium-4-quinolinium dimer (TOTO-1)-dyed DNA molecules in the range of 309–4.36 kbp are well fit by the form R_g = 80 nm·n[kbp]^0.6. Compare this experimentally measured prefactor to the prefactor predicted by the Flory–Pincus result, which turns out to be ≈90 nm if we use a DNA diameter of 2 nm, a persistence length of 60 nm (6), and a base pair spacing of 0.34 nm (7).

Things change dramatically if the polymer is confined in a channel whose width D is less than its free-solution radius of gyration R_g. Self-avoidance increases the scaling exponent for the contour length because the polymer is prevented from back-folding. As de Gennes demonstrated (8), self-avoidance effectively divides the confined polymer into a series of noninterpenetrating blobs, distributing the polymer mass along the channel in such a way that the monomer density is uniform. Consequently, the extension of the polymer in the channel L_z must scale linearly with the contour length L. Assuming that the rms end-to-end length of each blob follows the Flory–Pincus scaling, de Gennes showed that

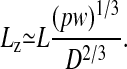[1]

Note that this formula gives us a numerical estimate of how much a DNA molecule should stretch in a nanochannel, given that the stretching is purely due to self-exclusion. For example, in a 100-nm-wide channel, we would expect an extension factor, defined as the ratio ε = L_z/L, of ≈0.20; in a 400-nm-wide channel, we would expect ε ≈ 0.15. It is not clear, however, that the de Gennes theory actually holds in the regime in which the channel width is on the order of or less than the persistence length, and hence we do not attempt to predict extension factors for channels <100 nm in width.

The polymer extension also exhibits thermal fluctuations δL_z around the mean value L_z. Fluctuations set the lower bound for the error in a single “snapshot” of the polymer extension. The de Gennes scaling theory can be adopted to predict how the rms fluctuation 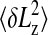should scale with L and D. We use the free energy of a confined polymer, also predicted by the de Gennes theory, to derive an effective spring constant k for small fluctuations around L_z. We find that

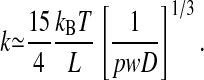[2]

The rms length variance 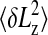is then given by the following equation:

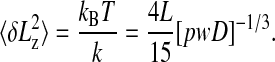[3]

The SD of 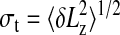, and defining the resolving power ℛ as the ratio L_z/σ_t, we obtain the following equation:

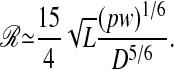[4]

Thus, we expect ℛ to increase with the square root of the length of the polymer L, and we should expect a greater resolving power for narrower channels.

Averaging of independent measurements of L_z allows one to compute the SD of the mean length L_z and, thus, achieve even higher resolution. In order for a measurement to be independent from a previous measurement, it is necessary to wait a time t_wait longer than the mean relaxation time of the length fluctuations. The de Gennes theory can be used to show how the polymer relaxation time should scale with the channel width and length (9). De Gennes argued that the friction factor of the chain can be written as follows: ξ ≃ 6 πηL_z, where η is the viscosity of the solvent. The relaxation time for the lowest vibrational mode should scale as ξ/k, so we expect the following:

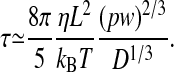[5]

This formula can be used to make a direct numerical estimate of the relaxation time of confined DNA. For λ-DNA, assuming a channel diameter of 100 nm and a buffer viscositity of 1 mPa, we get a relaxation time of ≈1.6 s.

Experimental Methods

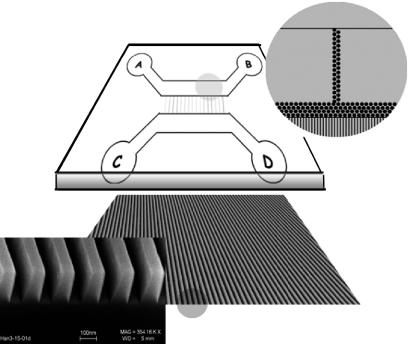
The nanochannels that were used in this experiment were 100 nm in width with a depth of 200 nm. The channels were nanofabricated on fused silica wafers by using the imprinting technique of Chou and coworkers (10). Fig. 2 shows a cross section of the channel array after imprinting. The channels were then sealed with fused silica plates by a combination of the surface-cleaning protocol (RCA) (11), room-temperature bonding, and annealing at 1,000°C. As channel dimensions approach the nanoscale, it is important to use sealing techniques that leave the interior of the channels highly uniform. Otherwise, nonuniformities in the channel width or height give rise to variability in the polymer extension. Microfeatures were etched in the adjoining quartz plates to allow for high-throughput access of the DNA molecules to the nanochannels. Fig. 2 shows a cross section of the channel array and the mating quartz plate with etched microfeatures.

Fig. 2.

The assembly of a sealed 100-nm-wide nanochannel array with a microfabricated coverslip. The nanoimprinted chips were made in fused silica (thickness, 1 mm) obtained from ValleyDesign (Westford, MA). The cover chips were patterned by using standard UV-lithographical techniques and reactiveion etching. Access holes were defined by using sand blasting. The cover chips were made in fused silica obtained from Hoya (Tokyo). DNA molecules from the gel were moved along the path from well A to well B, and a driving voltage was used to transfer molecules into wells C and D through the nanochannels on the mating nanoimprinted quartz wafer. Posts of 1 μm in diameter that were separated by 2 μm were used to prestretch the genomic length molecules to facilitate entry into the nanochannels and decrease the entropic barrier (20, 21).

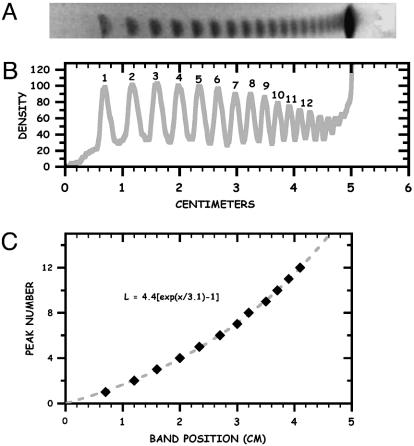
We used a λ-ladder consisting of concatemers of the 48.5-kbp-long λ monomer (cI857 ind1 Sam7) embedded in low-melting-point agarose (product no. N0340S, New England Biolabs) as a DNA standard to test the feasibility of the nanochannel technique (Fig.3). The total contour length of a λ monomer is 16.3 μm (12). The intercalating dye at our concentration increases the contour length to 22 μm (13–15). The DNA molecules were extracted from the gel plug directly on the chip by using electrophoresis from a 10-mm³ piece of gel. When the molecules were extracted from the gel, a second set of electrodes was used to move molecules into the nanochannels.

Fig. 3.

Analysis of pulsed-field gels. (A) Gel of the λ-ladder used in this experiment. (B) Scanned density of the gel lane, with N-mer labeling. An applied electric field of 5 V/cm was used, with the field direction switching ±60° to the average direction, with a period that was linearly ramped from 5–120 s over the entire run (≈18 h). (C) Result of curvefiting the peak number n from B to the empirical relation β [exp(χ/γ) – 1] = L, with L = 0 set by the predicted position of the n = 0 effective solvent front, with a β value of 4.4 and a γ value of 3.1 cm. Positions of the peaks are shown by diamonds, and the curve fit is shown by the dashed line.

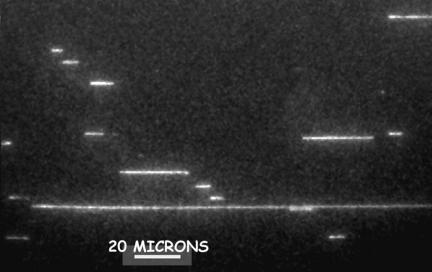
The λ-ladder DNA was moved by electrophoresis into the imprinted channel array, the electrophoretic field was turned off, and 100-ms-duration frames from the camera were captured to memory. Fig. 4 shows a typical frame capture. The intensity I(z) of the elongated molecule was assumed to be a convolution of a step function I_o of length L_z, with a Gaussian point-spread function 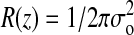, yielding the following fitting function:

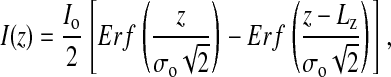[6]

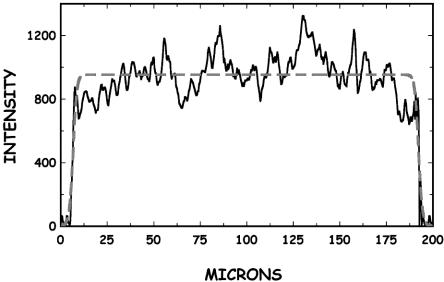
where Erf is the error function and L_z and σ_o are fitting parameters denoting the true end-to-end distance and the point-spread function resolution of the optics, respectively. The resolution σ_o of the ×60 numerical aperture 1.4 oil-immersion objective was determined by curve fitting to be 0.4 μm. An example of such a fit is shown in Fig. 5.

Fig. 4.

Typical digital camera frame with a 0.1-s exposure time. The camera was an iPentamax ICCD (Roper Scientific, Trenton, NJ) on a Eclipse TE300 microscope (Nikon) and a ×60 PlanApo (Nikon) numerical aperture 1.4 oilimmersion objective. A laser beam from an argon–krypton laser (Coherent Radiation, Palo Alto, CA) was raster scanned over the wafer by using a orthogonal pair of servocontrolled mirrors (Cambridge Scientific, Cambridge, MA) so that excitation density over the wafer was highly uniform. The protocol was to turn on an electrophoretic field for ≈2 s, remove previously measured molecules, and bring in a new set of molecules. The camera took ≈20 frames at 10 Hz, the frames were digitally stored to a disk, and the process was repeated. The running buffer contained 5 μM benzothiazolium-4-quinolinium dimer (TOTO-1) dye, Tris·EDTA buffer with boric acid (0.5× TBE), antibleaching agent DTT, and 0.1% POP6 (Applied Biosystems) to suppress any electroendosmosis.

Fig. 5.

Intensity vs. length of a confined DNA molecule with L_z = 185 μm. The dashed line is the fit of the data.

Results and Discussion

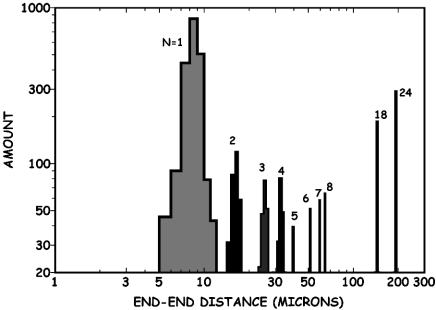
The end-to-end distances L_z of molecules on a frame-by-frame basis were histogrammed by length. The amount of DNA was determined by multiplying the end-to-end distance of the molecules L_z by the number of molecules measured at that length (this operation was done later to compare the intensity results from a nanochannel experiment, which directly measures the size of a polymer, with a gel, which measures the density of stained bases as a function of position in the gel). The resulting histogram of the amount of DNA vs. end-to-end distance L_z is plotted in Fig. 6.

Fig. 6.

A histogram of end-to-end distances L_z of molecules observed in 2 min of running DNA molecules into 100-nm-width nanochannels vs. the amount of DNA is shown, as described in the text. The assignment of the single DNA molecules to n = 5–8 is based on the assumption that L_z ≃ L.

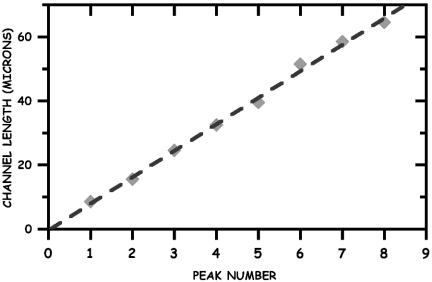
There are clear maxima in the histograms for the first four peaks observed at L_z = 8 ± 1 μm (n = 1), 16 ± 1 (n = 2) μm, 24 ± 1 μm (n = 3), and 32 ± 1 μm (n = 4). Because L = 22 μm [for λ-DNA dyed with benzothiazolium-4-quinolinium dimer (TOTO-1)] (14) and L_z = 8 μm, the extension factor is ε = 0.36 for monomers in 100-nm-wide channels. Ligation numbers of n = 5, 6, 7, 8, 18, and 24 were assigned to the additional peaks under the assumption that a λ monomer in a 100-nm-wide nanochannel has a end-to-end length L_z of 8 μm. The linear relation between L_z of the observed histogram maxima for n = 1–4, as shown in Fig. 7, indicates that L_z ≈ L, as predicted by the de Gennes theory for self-avoiding confined polymers (8).

Fig. 7.

Observed end-to-end distance vs. the N-mer ligation value. The data are shown as diamonds, and a linear fit is shown by the dashed line.

We now address issues of resolution by exploiting the single-molecule nature of a nanochannel measurement and the fact that the molecule can undergo fluctuations in the length. The gel scan shown in Fig. 3 demonstrates the key drawback to the pulsed-field technique if ensemble averages are used, namely, loss of resolution at high molecular weights because of the nonlinear decrease of mobility with increasing molecule length L. However, the resolution of the ensemble average due to the optical resolution σ_o of Eq. 6 is not the limit for single-molecule techniques because the uncertainty in the ensemble average (i.e., the SD of the mean) is not limited by the width of the point-spread function σ_o of Eq. 6. By collecting enough photons, the location of a point source of light can be determined to arbitrary precision (16, 17). We do not look at point sources of light here but, rather, extended molecules. In this case, thermal fluctuations of the end-to-end distance of the molecule allow us to overcome the pixelation error that is inherent in any digital technology for imaging. Thus, the SD of the mean end-to-end distance of a single molecule can, in principle, be made arbitrarily small.

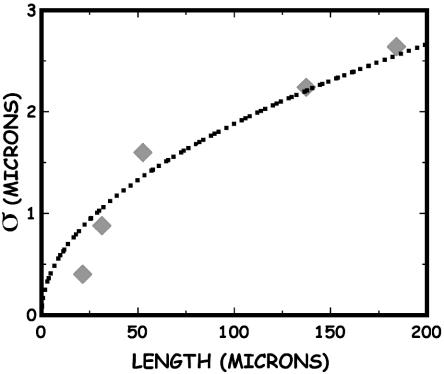
The fluctuations set the error in a single snapshot of the polymer extension. We first test the predictions of Eq. 3, namely, that the SD σ_t of the length of a confined molecule should vary as the square root of the contour length L. Fig. 8 gives a plot of the observed SD of single molecules of known length L as a length fit to an L^1/2 length dependence. The SD of the mean extension 〈L_z〉 of a given molecule should scale as 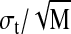after M independent measurements, where the σ_t refers to the SD due to thermal fluctuations of the individual molecule and is shown in Fig. 8. This analysis allows us to determine the mean length 〈L_z〉 of a molecule in a nanochannel to arbitrary precision simply by making enough measurements. For example, in Fig. 9 we show a histogram made of measurements of the fluctuating end-to-end distance of a single confined λ monomer. A Gaussian fit yields a σ_t of 0.6 μm. After 20 measurements, or a measurement time on the order of 1 min, the SD of the mean extension (8.38 μm) is ±0.15 μm. This means that we know the extension of the λ monomer to an accuracy of ±400 bp within 1 min of observation.

Fig. 8.

The observed SD in the length of a confined channel of width 100 nm vs. the length of the molecule. The dashed line is a fitofEq. 3 to the data.

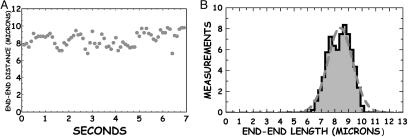
Fig. 9.

The end-to-end dynamics of a confined DNA molecule. (A) End-to-end distance of a λ monomer confined in a 100-nm-wide channel as a function of time. (B) Histogram of the observed end-to-end distances L_z of the monomer data. The SD of the mean length of 8.38 μm is 0.15 μm, as determined by the Guassian curve fit (dashed line).

Conclusions

We have extended genomic-length molecules of >1 million bp in arrays of imprinted nanochannels. We have shown that the de Gennes scaling theory for self-avoiding walks can explain the linear dependence of the polymer extension on the contour length. We have also shown that the de Gennes theory can be used to show how the rms variation in the extension due to thermal fluctuations should scale with contour length. Last, we have demonstrated that nanochannel-based measurements of DNA length have advantages over current techniques for the sizing of genomic length molecules. We have shown (10) that these channels can be made substantially smaller than the 100-nm channels used here. Although it is challenging to introduce molecules into these channels, such channels will push the statistical mechanics analysis beyond the de Gennes analysis used here, requiring a more detailed analysis based on the work of Odijk (18) in the D « P limit and including the possibility that the polymer can undergo highly nonlinear “kinks” in the backbone configuration (19).