Modelling water use efficiency in a dynamic environment: An example using Arabidopsis thaliana

Highlights

• •A model scaling stoma behaviour at leaf level is proposed.
• •The model is tested by reproducing natural variations of light intensity.
• •Stomatal aperture and photosynthesis decrease as a function of sugar accumulation.
• •Leaf anatomy influences the rapidity of stomatal conductance.
• •The model dissects intrinsic water use efficiency into traits of interest.

Abstract

Intrinsic water use efficiency (W_i), the ratio of net CO₂ assimilation (A) over stomatal conductance to water vapour (g_s), is a complex trait used to assess plant performance. Improving W_i could lead in theory to higher productivity or reduced water usage by the plant, but the physiological traits for improvement and their combined effects on W_i have not been clearly identified. Under fluctuating light intensity, the temporal response of g_s is an order of magnitude slower than A, which results in rapid variations in W_i. Compared to traditional approaches, our new model scales stoma behaviour at the leaf level to predict g_s and A during a diurnal period, reproducing natural fluctuations of light intensity, in order to dissect W_i into traits of interest. The results confirmed the importance of stomatal density and photosynthetic capacity on W_i but also revealed the importance of incomplete stomatal closure under dark conditions as well as stomatal sensitivity to light intensity. The observed continuous decrease of A and g_s over the diurnal period was successfully described by negative feedback of the accumulation of photosynthetic products. Investigation into the impact of leaf anatomy on temporal responses of A, g_s and W_i revealed that a high density of stomata produces the most rapid response of g_s but may result in lower W_i.

Nomenclature

A

Net CO₂ assimilation

A_G

Gross CO₂ assimilation

R_d

Mitochondrial respiration

g_s

Stomatal conductance to water vapour

g_m

Mesophyll conductance to CO₂

g_b

Boundary layer conductance to water vapour

g_t

Total conductance to CO₂

W_i

Intrinsic water use efficiency

C_a

Atmospheric CO₂ concentration

C_i

CO₂ concentration in the intercellular airspaces

C_c

CO₂ concentration at the site of carboxylation

a

Stomatal pore area

a_s

Steady state target of stomatal pore area

a_min

Minimum stomatal pore area

a_max

Maximum stomatal pore area

α_L

Slope of the relationship

θ_L

Curvature factor of the curve

k_i

Time constant for an increase in a

k_d

Time constant for an decrease in a

L

Percentage of efficiency

SD

Stomatal density

D

Diffusivity of water in air

V

Molar volume of air

l

Depth of stomatal pore

P_a

The atmospheric pressure

S_a

Factor representing the influence of the rate of accumulation of sugars

S_e

Factor representing the influence of the rate of export of sugars

Vc_max

Maximum Rubisco activity

J_max

Maximum electron transport activity

α

Proportion of light absorbed by PSII

1. Introduction

In order to meet the projected demand for cereal production by 2050, crop yields must improve by 1.16–1.31% each year; however, current estimates are well below this required rate [1]. The primary determinant of crop yield is the cumulative rate of photosynthesis over the growing season and is determined by the ability of the plant to capture light and CO₂, use this energy to convert the CO₂ to biomass, and how much of this biomass ends in usable yield. Improving photosynthetic efficiency is recognised as an important but unexploited avenue to increase yield potential in crop plants [2]. Increasing photosynthetic efficiency is accompanied by a higher CO₂ demand, which can be limited by the resistance of CO₂ diffusion into the leaf. Any attempt to decrease this resistance greatly increases the water loss by transpiration from the leaf.

Photosynthetic productivity is linked to water consumed by the plant and often measured as water use efficiency (WUE). WUE can be defined at different scales of time and space and, at the leaf level, it is often assessed as the ratio of CO₂ fixed per unit of H₂O transpired (E). Intrinsic water use efficiency (W_i) is defined when stomatal conductance to water vapour (g_s) is used instead of E. The use of g_s to describe the stomatal control on the rate of E facilitates the comparisons between different leaves and environmental conditions. The photosynthetic capacity of the leaf determines the net CO₂ assimilation (A) as a function of the variation in the micro-climate surrounding the leaf. Over the diurnal period, A is mainly determined by the irradiance absorbed by the leaf and the limitation of CO₂ imposed by stomatal control. Under field conditions, environmental variables that affect both photosynthesis and stomatal behaviour are rarely constant. For example, light intensity (and spectral quality) alters in time scales of seconds to hours to which A and g_s must respond. The temporal response of A and g_s to a fluctuating environment are asynchronous, with g_s response often an order of magnitude slower than A, which results in rapid variations of W_i. Thus, it is important when describing the kinetic response of W_i to use an approach that considers responses by A and g_s simultaneously.

Intrinsic water use efficiency (W_i) is dependent on the anatomy (e.g. stomatal size and density) and the physiology (e.g. behaviour) of stomata as well as the leaf biochemistry (e.g. activity of the Calvin cycle), all of which interact to determine the kinetics of CO₂ and H₂O gaseous exchange between the leaf and atmosphere. The dynamic nature of the interactions between the different components that determine W_i are not fully understood and need to be addressed if we are to successfully improve both A and W_i under dynamic field conditions.

It is possible to conceptualise the inherent complexity of gas exchange over a fluctuating light regime through modelling, which will improve our understanding of the W_i response by simulating a number of gas exchange scenarios (e.g. changes in light intensity and humidity) that would normally be difficult to assess in a reasonable amount of time using experimental approaches. Current models focus on predicting g_s in steady state [3] and cannot be used to infer the impact of stomatal behaviour on A or W_i under dynamic conditions. Although temporal responses of g_s have previously been described using a dynamic model [4], [5], the relationship between stomatal response and leaf level gas exchange was not clearly described. We propose to use a model that will take into consideration the anatomy and physiology of stomata to more accurately represent the stomatal control of W_i.

To scale stomatal responses to leaf level g_s, the two most important stomatal characteristics are aperture and density [6], [7], [8]. A high stomatal density does not necessarily result in a higher g_s as stomata ultimately control their aperture depending on the guard cell responses to the external (e.g. light intensity) and internal (e.g. mesophyll demand for CO₂) stimuli [9]. To link stomatal behaviour to leaf level gas exchange responses, we propose a ‘big stoma’ approach that consists of simulating the response of one stoma that is representative of the heterogeneous response of many stomata and scaling the response to the leaf level. This approach was incorporated in an enhanced version of the multi compartments model described by Noe and Giersch [10] to predict A and W_i. Scaling up the dynamic of the stomatal response to the leaf level, with the improved model for CO₂ diffusion inside the leaf, will help to dissect W_i into traits of interest and predict potential gains in W_i.

The objective of this study was to develop a new model combining our most recent knowledge of kinetics in stomatal behaviour and photosynthesis to describe the temporal response of W_i over the course of a day with natural dynamic variations in irradiance. All the parameters of the model described here incorporate a trait of interest for W_i and were adjusted using Bayesian inference. The model was validated using a dataset with a different irradiance pattern to assess the predictive power of the model. A sensitivity analysis was finally performed to show the interaction among the parameters and display the potential gain in W_i in the case of one or two parameters changing. We used the output of the model to understand how temporal responses in g_s impacts A and W_i.

2. Material and methods

2.1. Dynamic modelling of photosynthesis and stomatal conductance

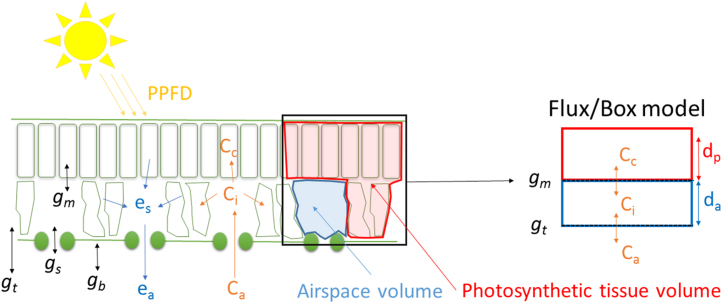
The model essentially consists of four differential equations describing the diffusion of CO₂ between different compartments represented by the atmosphere, the intercellular air spaces and the photosynthetic tissues (Fig. 1). The exchanges between these compartments are dependent on the stomatal aperture and the resistance of diffusion in the mesophyll cells. In addition, the model took into account the limitation of photosynthesis and stomatal aperture that appeared during a period of light.

$$\{\begin{array}{c}\hfill \frac{da}{dt}=\frac{a_s-a}{k_i}ifa<a_s\hfill \\ \hfill \frac{da}{dt}=\frac{a_s-a}{k_d}ifa\ge a_s\hfill \end{array}$$ (1)

Fig. 1.

Schematic of the diffusion of gas exchange between the leaf and atmosphere compared to the conceptual version used in the model. The total conductance to water vapour (g_t) controlling the gradient of H₂O from leaf to atmosphere was composed by the stomatal conductance (g_s) and the boundary layer conductance (g_b). The gradient of CO₂ from the atmosphere to the site of carboxylation was also dependent on mesophyll conductance (g_m). The H₂O concentrations inside and outside the leaf were represented by e_s and e_a respectively. The CO₂ concentrations in three compartments were considered: in the atmosphere (C_a), in the intercellular airspaces (C_i) and at the sites of carboxylation (C_c). The different compartments of the leaf were represented as a standardized volume defined by the thickness of the intercellular airspace (d_a) and the photosynthetic tissues (d_p).

The first differential equation (Eq. (1)) described the temporal variations of the stomatal pore area (a) with a_s the steady state target followed by a and two time constants, k_i and k_d, for an increase or a decrease of a respectively. Considering the spatial heterogeneity of the stomatal response, a top-down approach was used, signifying that the model simulated the response of one stoma representative of the sum of the individual stomatal responses and scaled it to leaf level instead of trying to integrate the response of each stoma.

The steady state target of a (a_s) as a function of the light intensity (PPFD) was predicted using a non-rectangular hyperbola [4]:

$$a_s=\left[a_{min}+\frac{{\alpha }_{L}PPFD+\left(a_{max}-a_{min}\right)-\sqrt{{\alpha }_{L}PPFD+{\left(a_{max}-a_{min}\right)}^2-4{\theta }_L{\alpha }_{L}PPFD\left(a_{max}-a_{min}\right)}}{2{\theta }_L}\right]\cdot L$$ (2)

with a_min and a_max the minimum and maximum stomatal pore area, α_L the slope of the relationship, θ_L the curvature factor of the curve and L the percentage of efficiency (see below).

$$\frac{d{C}_i}{dt}=\left[g_t\left(C_a-C_i\right)-g_m\left(C_i-C_c\right)\right]\frac{R{T}_l}{d_a{P}_a}$$ (3)

Eq. (3) described the variation of the CO₂ concentration in the intercellular airspaces (C_i) with C_a the atmospheric CO₂ concentration and C_c the CO₂ concentration at the sites of carboxylation.

The resistance of CO₂ diffusion from the air to the leaf was represented by the total conductance to CO₂ (g_t):

$$g_t=1/\left(1.6/g_s+1.37/g_b\right)$$ (4)

with g_b the boundary layer conductance to water vapour estimated in the gas exchange chamber.

The stomatal conductance to water vapour (g_s) was derived from a using the equation of Dow et al. [7]:

$$g_s=\frac{SD\cdot D\cdot a}{V\left(l+\frac{\pi }{2}\sqrt{\frac{a}{\pi }}\right)}$$ (5)

with SD the stomatal density, D the diffusivity of water in air, V the molar volume of air and l the depth of the stomatal pore.

The resistance of CO₂ diffusion in the mesophyll cells (g_m) was calculated following the equations described by Von Caemmerer et al. [11] and the values given for Arabidopsis thaliana. As the temperature of the leaf was regulated during the experiment, g_m was considered stable.

The last part of the equation $\frac{R{T}_l}{d_a{P}_a}$ was used to convert the fluxes (μmol m⁻² s⁻¹) between the two compartments (leaf and atmosphere) into concentrations of CO₂ (μmol mol⁻¹) contained in the volume represented by the intercellular airspaces (See the Appendix in Noe and Giersch [10] for more information), with R the gas constant, T_l the leaf temperature, P_a the atmospheric pressure, and d_a the depth of the intercellular airspaces (d_a = leaf thickness (m) • airspaces (%)).

$$\frac{d{C}_c}{dt}=\left[g_m\left(C_i-C_c\right)+R_d-A_{G}L\right]\frac{R{T}_l}{d_p{P}_a}$$ (6)

Eq. (6) described the variation of C_c with R_d the mitochondrial respiration during the day, A_G the gross CO₂ assimilation and L the efficiency coefficient of a_s and A_G (see below). The gross assimilation was calculated using C_c at the current state of the solver and the equations of Farquhar et al. [12]. The net CO₂ assimilation A was calculated at the end of the simulation as: A = A_G − R_d. In the last part of the equation d_a is replaced with d_p representing the depth of the photosynthetic tissues (d_p = leaf thickness (m) •[1 − airspaces (%)]).

$$\frac{dL}{dt}=S_e\left(1-L\right)-S_a{A}_{G}L$$ (7)

The last equation (Eq. (7)) described the negative feedback of sugar accumulation on a_s (Eq. (2)) and A_G during a period of light, with S_a being a factor representing the influence of the rate of accumulation of sugars, and S_e a factor representing the influence of the rate of export of sugars.

Originally in Noe and Giersch [10], this equation only described the negative feedback of sugar export on A. The equation was modified to allow recovery of the response of A_G in the absence of light$\left(S_e\left(1-L\right)\right)$ and tested using the diurnal data sets described below. The initial simulations showed that the model was able to reproduce the slow decrease of A during the day but not the similar decrease observed for g_s. Eq. (2) was therefore modified to include a decrease in g_s during the diurnal period similar to that for A.

2.2. Solving differential equations

The differential equations were solved using the function lsodes from the R package deSolve (v1.12). The initial absolute tolerance was set to 0.01 for all the outputs and decreased by 10 each time the solver failed to converge. The initial values of the differential equations were chosen based on the observed data. For the pore area, the initial aperture was calculated by solving Eq. (5) for the first recorded g_s.

2.3. Parameterization of the model

Parameter values known to impact the diurnal variation of gas exchange were adjusted using the Bayesian inference (see below) to fit the observed data. During the diurnal period, gross CO₂ assimilation (A_G) was determined by maximum Rubisco activity (Vc_max), maximum electron transport activity (J_max) and the proportion of light absorbed by PSII (α). The day respiration in presence of light (R_d) was used to calculate the net CO₂ assimilation (A). The stomatal conductance to water vapour (g_s) was determined as described above by a_min, a_max, α_L and k_i/k_d. The diurnal variation of A and g_s were linked by the negative feedback of sugar export described by S_a and S_e.

Parameter values known to remain unchanged during the diurnal period of measurement or that could be assigned a priori were treated as constants in the model, to facilitate the adjustment, and were chosen from the literature or measured on Arabidopsis thaliana (see below). The Michaelis constants and the temperature responses of the Farquhar model were parameterized using values from Walker et al. [13]. The thickness of the leaf was set to 200 μm [14], [15] and the ratio of airspace in the leaf was set to 0.255 [14], [16]. The value of θ_L in equation 2 was chosen at 0.7 by analogy with the similar equation describing the electron transport rate [17]. The boundary layer conductance (g_b) and atmospheric pressure (P_atm) were set to the values provided by the LI-6400XT: 9.29 mol m⁻² s⁻¹ and 101.8 kPa respectively. Estimates of g_b are computed as a function of leaf area and fan speed (LI-6400XT Instruction Manuals, page 3–93). The parameter values describing the membrane properties required to estimate g_m followed that of Von Caemmerer et al. [18]. Stomatal density (SD) was assessed on plants grown under the same environmental conditions, on both faces of the leaf (section 1.9). As the model simulated the average response of both faces, the densities of both faces were added and set to 400 mm⁻². In equation 5, 5.89 μm was used for the depth of the stomatal pore (l) [7], the diffusivity of water in air at 25 °C (D) was 24.2e⁻⁶ m² s⁻¹, the molar volume of air at 25 °C (V) was 0.02446533 m³ mol⁻¹ [19].

2.4. Bayesian inference

The parameter values were estimated using Bayesian inference by comparing the model outputs to recorded gas exchange data [20]. The inference was performed on two objective functions as A and g_s were adjusted simultaneously and in this case, there was a risk of bimodal posterior distributions. Monte Carlo Markov Chain (MCMC) using inter-chain adaptation were previously able to sample from bimodal distributions and this technique was thus used to adjust our model (INCA, [21], [22]). To remove any adaptive effect, the final algorithm used to sample the posterior distributions was the random walk metropolis (RWM) with the covariance matrix estimated previously with INCA as an input. The use of Bayesian Inference allowed us to use prior information available in the literature and shown in Table 1. The results of the inference were posterior estimates describing the probability density of the possible parameter values considering the error of prediction and the sensitivity of the model for these parameters and their inter-correlation. The posteriors were represented using quantiles of the posterior distribution at 2.5% and 97.5%, also called credible intervals (similar to a confidence interval). The medians were also shown as the most representative set of parameter values. Two chains with 30,000 iterations were thinned every 2 samples and tested for different criteria: the acceptance rate greater than 15% (to achieve a rapid mixing of the chain), the Effective Sample Size (ESS) > 100 (which is usually enough to describe 95% probability intervals) and the convergence using Monte Carlo Standard Error (MCSE) less than 6.27% (which allows the true mean to be within 5% of the area under a Gaussian distribution around the estimated mean; [23]). The algorithms used to perform the Bayesian inference were implemented using the R software (R Core Team, 2015, v3.2.2).

Table 1.

Parameters of the dynamic gas exchange model adjusted with Bayesian inference: mean and standard deviation (SD) of the prior values estimated from the literature (see footnotes) and quantiles at 2.5%, 50% and 97.5% of the credible interval of each posterior distribution estimated using Bayesian inference.

	unit	Prior		Posterior
		Mean	SD	2.5%	50%	97.5%
amin1	μm2	3.56	0.2	4.03	4.16	4.27
amax2	μm2	100	10	72.15	93.24	113.87
αL	$\frac{\mathrm{\mu }{\text{m}}^2}{\mathrm{\mu }\text{mol}{\text{m}}^{-2}{\text{s}}^{-1}}$	0	10	0.742	0.767	0.793
ki	s	100	1e4	1290	1430	1580
kd	s	100	1e4	463	541	627
Vcmax3	μmolm−2s−1	65.5	22.6	89.8	99.3	128.8
Jmax3	μmolm−2s−1	102.4	21.9	180.5	186.4	193
Rd	μmolm−2s−1	0	10	0.01	0.14	0.37
α	$\frac{\mathrm{\mu }\text{mol}\left(electron\right)}{\mathrm{\mu }\text{mol}\left(photon\right)}$	0	1	0.177	0.183	0.192
Se		0	10	0.263e−6	8.486e−6	32.904e−6
Sa		0	10	0.207e−6	0.280e−6	0.385e−6

1. Parameter estimated using the observed stomatal conductance under dark conditions.

2. Parameter estimated from Dow et al. [7]

3. Parameter estimated by averaging published values for Col-0 by Flexas et al. [42], Tholen et al. [14], Heckwolf et al. [43], Cousins et al. [44], Sade et al. [45].

The accuracy of the model outputs compared to the observed data was assessed using the Root Mean Square Error (RMSE):

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{t=1}^n{\left(x_{obs,t}-x_{mod,t}\right)}^2}{n}}$$ (8)

where x_obs and x_mod represents the observed and modelled values to be compared, and n the number of observations.

2.5. Sensitivity analysis

The sensitivity analysis was performed using the same data set and parameter values estimated previously using Bayesian inference. Each parameter value was altered by ±50%, the impact on the model outputs was summarized by using the daily mean of A and g_s divided by the corresponding values obtained using the original parameters values. This resulted in a factor centred on 1 representing the positive or negative impact of the parameter alterations on A and g_s (e.g. a factor of 1.1 corresponds to an increase of 10% in the original parameter value).

2.6. Plant material

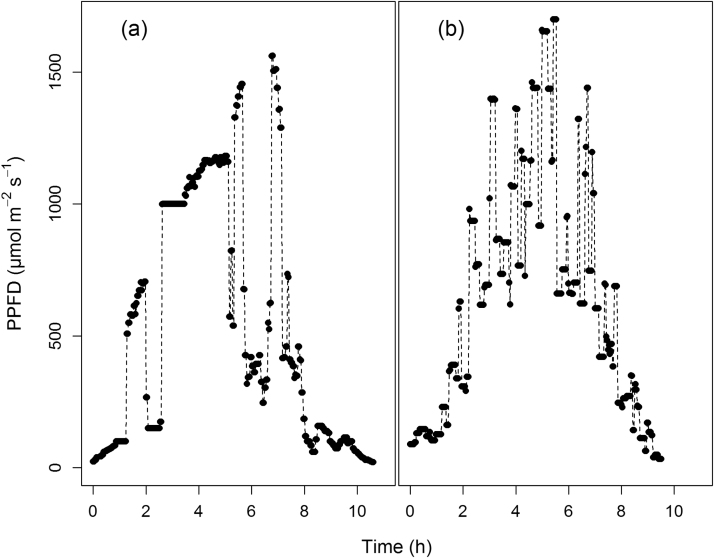
Arabidopsis thaliana ecotype Col-0 plants were grown in a controlled environment under fluctuating light conditions provided by a Heliospectra LED light source (Heliospectra AB, Göteborg, Sweden). The fluctuating light regime was reconstructed from natural variations in light intensity recorded during a day in July 2013 at the University of Essex, UK (Fig. 2a) assuming a constant spectral distribution. The growth environment was maintained at a relative humidity of 55–65%, a temperature of 21–22 °C and a CO₂ concentration of 400 μmol mol⁻¹. Plants were well watered, and positioning under the Heliospectra light was altered daily. Measurements were taken on the youngest fully expanded leaf.

Fig. 2.

Light regimes a recorded from natural variations at the University of Essex, UK, July 2013, and b simulated using a Gaussian altered with random variations.

2.7. Model simulations of step change of light

Using the set of parameter values previously estimated, the model was used as a simulator to assess the diversity of the temporal response of g_s after a step change of light. The step change was performed by initially setting the light to an intensity of 100 μmol m⁻² s⁻¹ for 30 min followed by a step increase in intensity to 1000 μmol m⁻² s⁻¹ for 2 h. All other environmental conditions were kept constant, with the [CO₂] maintained at 400 μmol mol⁻¹ and a leaf temperature of 25 °C. Parameter values of SD, k_i and α_L were increased or decreased by a factor of 2 to illustrate their impact on temporal responses of g_s, A and W_i. The rate of change of g_s was estimated using a linear regression on the first 10 min of the variation. The impact of the temporal response of g_s on A and W_i was characterised by calculating the percentage of variation of the mean A and W_i during the 2 h after the step change of light.

2.8. Leaf gas exchange

Photosynthesis gas exchange parameters (A and g_s) were measured using a Li-Cor 6400XT portable gas exchange system (Li-Cor, Lincoln, Nebraska, USA), with dew point and vapour pressure deficit maintained via a Li-Cor 610 portable dew point generator. Throughout the measurement cuvette, conditions were maintained at a CO₂ concentration of 400 ppm (corresponding to ambient growth), leaf temperature of 25 °C, and a leaf to air water vapour pressure deficit of 1 (±0.2) kPa. The largest fully expanded mature leaf was used, with A and g_s allowed to stabilize under the controlled cuvette conditions for a minimum of 30 min. At this point, the automatic 12 h light program (mirroring that of the growth conditions, Fig. 2a) was started, with A and g_s recorded every 2 min. W_i was calculated as A/g_s. For the model validation, the same measurement conditions were used in the cuvette with the exception of the light that reproduced a different pattern of light intensity (Fig. 2b).

2.9. Stomatal density

Following the dental impression methods of Weyers & Johansen (1985), negative impressions of the ab- and ad-axial leaf surface were made using Xantoprene Polysiloxane precision material (Heraesus Kulzer Ltd). Positive impressions were produced by coating nail varnish on the dry polymer and used to count the number of stomata in 9 field of view using an Olympus BX60 light microscope (Olympus Europa, Southend-On-Sea, UK). The area of view was measured using an eyepiece graticule to express the number of stomata by mm⁻². Stomatal impressions of the leaf surface were taken on the same leaves as gas exchange measurements were conducted.

3. Results

3.1. Bayesian inference

The two chains (describing the posterior distributions) resulting from the Bayesian inference successfully converged and were used to calculate the credible intervals of each parameter shown in Table 1. The credible interval of a_min was significantly higher and not overlapping the prior distribution, which was not the case for a_max, suggesting that the observed data were informative for a_min but not for a_max. The model estimated α_L precisely, despite the fact that the prior distribution covered a large range of possible values, suggesting that the model was particularly sensitive to this parameter. The time constants, k_i and k_d, displayed a strong asymmetry with values almost 3 times higher for k_i compared to k_d. Vc_max and J_max values were sensibly higher than the prior means estimated from the literature, however the prior distribution and the credible interval overlapped, suggesting that these values were still in the range observed in the literature.

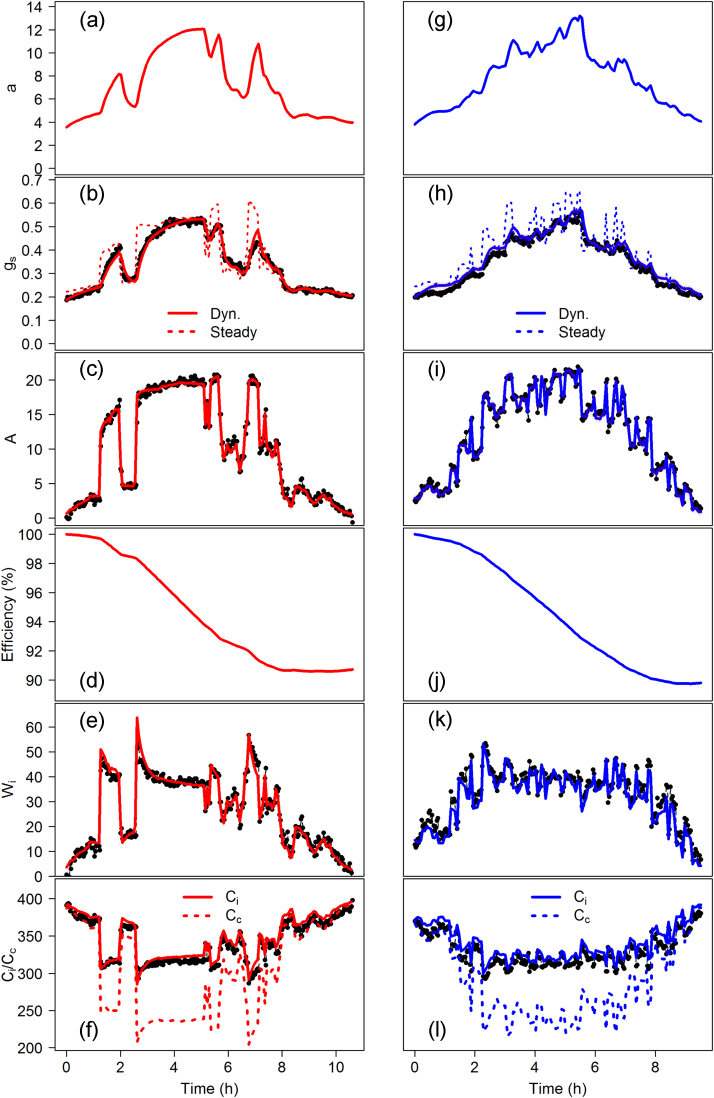
The medians of the posterior estimates shown in Table 1 were used to represent the most representative prediction of the model (Fig. 3a–f). Under a diurnal fluctuating light regime, our dynamic model accurately described g_s (Fig. 3b, RMSE: 0.014 mol m⁻² s⁻¹; Suppl. Fig. S1a, R²:0.984) and A (Fig. 3c, RMSE: 0.6 μmol m⁻² s⁻¹; Suppl. Fig. S1b, R²:0.993). Consequently, the rapid variations of W_i were also accurately reproduced (Fig. 3e, RMSE: 2.58 μmol mol⁻¹; Suppl. Fig. S1c, R²:0.97). By adjusting the model to the observed g_s, our ‘big stoma’ approach allowed us to predict the average behaviour of the stomata with a variation of the pore area from 4 to 14 μm² (Fig. 3a). Under these environmental conditions A and g_s displayed a decrease in efficiency of approximately 8% at the end of the diurnal period (Fig. 3d), which was described by S_e and S_a. The model seemed to be less sensitive to S_e as the credible interval was much larger than the one of S_a. The model successfully describes the variation of C_i but also predicts the variations of C_c that showed a larger variation compared to C_i due to low g_m (Fig. 3f).

Fig. S1

Modelled (Mod.) vs observed (Obs.) stomatal conductance to water vapour (g_s, mol m⁻² s⁻¹), net CO₂ assimilation (A, μmol m⁻² s⁻¹) and intrinsic water use efficiency (W_i, μmol(CO₂)/mol(H₂O)) measured under: a–c light regime described in Fig. 2a for the model parameterization, d–f light regime describe in Fig. 2b for the model validation. Solid lines and dashed lines represented the 1:1 lines and linear regressions respectively. The coefficient of determination (R²) was derived from the linear regression.

Fig. 3.

Modelled (solid & dashed lines) and observed (black circles) diurnal variations in gas exchange under two different light regimes (Fig. 2). a–f Modelled data (red lines) were fitted to observations (black circles) using Bayesian inference to estimate the most credible set of parameter values under the light regime described in Fig. 2a. g-l Modelled data (blue lines) were simulated using the same set of parameter values and the light regime describe in Fig. 2b. The red and blue dashed line in b and h represented the steady state g_s target (Steady) if conditions remained constant, whilst solid lines represent the dynamic outputs. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.2. Model validation

To validate the model, the same plant and set of parameter values (Table 1) were used to predict A, g_s and W_i under a different light regime (Fig. 2b). Our dynamic model was able to accurately predict the observed gas exchanges (Fig. 3g-l): g_s (Fig. 3h, RMSE: 0.023 mol m⁻² s⁻¹; Suppl. Fig. S1d, R²:0.983), A (Fig. 3i, RMSE: 0.69 μmol m⁻² s⁻¹; Suppl. Fig. S1e, R²:0.988) and W_i (Fig. 3k, RMSE: 2.95 μmol mol⁻¹; Suppl. Fig. S1f, R²:0.961). Compared to the rapidity of the stomatal response (k_i: 24 min and k_d: 9 min), the light variations were too fast (on average a change every 8 min) to observe the complete stomatal response and, as a consequence, a followed the general tendency of the light intensity (Fig. 3g). The efficiency of A and g_s during the diurnal period showed a decrease of around 10% similar to that of the estimate during the other diurnal period (Fig. 3j).

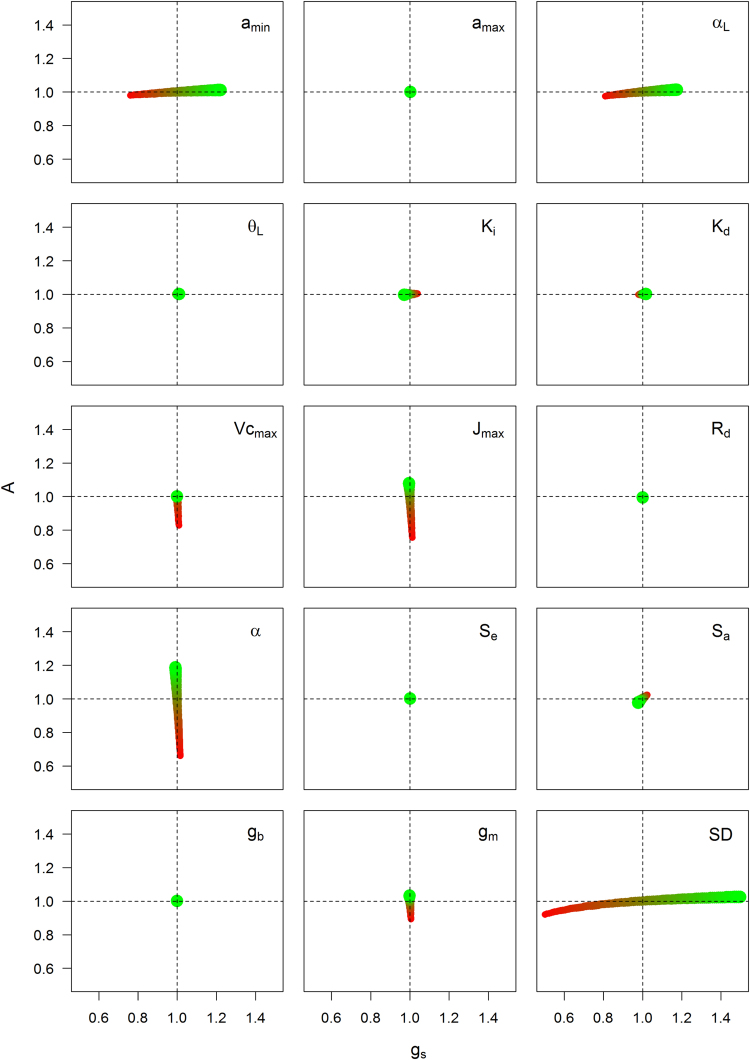
3.3. Sensitivity analysis

A sensitivity analysis of the model was undertaken to illustrate the impact of varying individual parameters on A and g_s (Fig. 4). The parameters that displayed the most sensitivity for g_s were (ordered by importance): SD, a_min, α_L, k_i, and S_a. For A, the parameters were (ordered by importance): α, J_max, Vc_max, g_m, SD, a_min, α_L and S_a, showing the interdependence of A and g_s. Even if the model was sensitive to the variation of a parameter, this variation would not necessarily improve W_i. For example, Vc_max only displayed variation in A that resulted in a decrease in W_i suggesting that under the conditions used here A is not limited by CO₂ diffusion. The greatest impact on both A and g_s was observed when SD was decreased, while increasing photosynthetic capacity (Vc_max and J_max) by 50% only improved A by 10% under the environmental conditions used here.

Fig. 4.

Relative variation of the daily mean net assimilation (A) and daily mean stomatal conductance to water vapour (g_s) using parameter values ranging ±50% around the estimated parameters from Table. 1. The size and the colour of the circles are proportional to the deviation of the parameter values (small and red circles correspond to decreased parameter values whilst large green circles correspond to increased parameter values). The length and direction are relative to the impact of the parameter on A and g_s.The simulated daily mean of A and g_s for each parameter set was divided by the mean values of A and g_s determined using the parameters in Table 1. The (1,1) coordinate showed similar daily mean values of A and g_s compared to values simulated using the parameter set described in Table 1. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.4. Impact of stomatal characters on g_s, A and W_i temporal responses

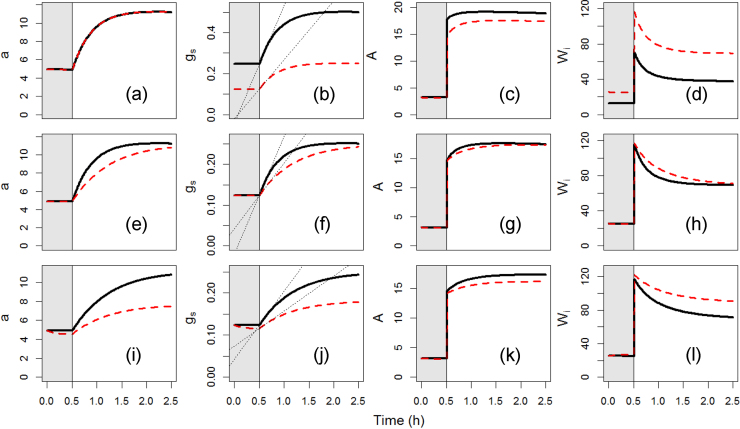
In order to determine the impact of stomatal characters on the temporal response of g_s, A and W_i, the influence of the rapidity of the stomatal response (k_i) and the steady states g_s (SD, α_L) to a step increase in light intensity were examined (Fig. 5). The initial slope of the g_s response displayed large differences (e.g. 0.58–0.29 mol m⁻² s⁻², Fig. 5b) even if the rapidity of increasing stomatal aperture did not change (Fig. 5a). The different temporal responses of g_s driven by SD, k_i and α_L limited A by 8.8% (Fig. 5c), 2% (Fig. 5g) and 6.1% (Fig. 5k) respectively. The impact on W_i was due to a larger decrease in g_s rather than A following the step increase in light intensity, with an increase of W_i by 82% (Fig. 5d), 7.4% (Fig. 5h) and 19.2% (Fig. 5l) respectively.

Fig. 5.

Simulation of the temporal response of a, g_s, A and W_i with different alterations on SD, k_i, and α_L under a step change of light from 100 (shaded area) to 1000 (white area) μmol m⁻² s⁻¹. a-d Impact of a variation of the stomatal density (SD) from 400 (black line) to 200 mm⁻² (red dashed line). e-h Impact of a variation of the time constant for stomatal aperture (k_i) from 1430 (black line) to 2860s (red line). i-l Impact of a variation of the slope of the relationship between the pore area and the light (α_L) from 0.77 (black line) to 0.38 μm²/μmolm⁻²s⁻¹(red line). The dotted lines on (b, f, j) represent the rates of g_s variation for the first 10 min of the step change estimated by linear regression. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

Over different diurnal light regimes, our new dynamic model was able to incorporate the rapid fluctuations in light and accurately predicted g_s, A and W_i. To our knowledge, this is the first attempt to model stomatal behaviour and scale it up to leaf level to predict gas exchange under dynamic light regimes. This ‘big stoma’ approach to model g_s provides a direct estimation of the rapidity of the stomatal response, whereas most current models consider only an instantaneous response [3]. Moreover, the simulated average pore area (a) predicted by the model was in a similar range to those previously reported in the literature [24], [25]. Previous studies have attempted to directly model temporal responses of g_s [4], [5], but our approach models the speed of increasing pore area rather than the speed of g_s increase, and is therefore more mechanistic and biologically relevant when describing the dynamics of gas exchange. Although we have validated the model using responses to fluctuations in light intensity, other environmental variables (e.g relative humidity) could be included in the future and would greatly improve the predictive power of the model.

Our model also incorporates negative feedback on A and g_s that revealed a 10% decrease in both by the end of the diurnal period. Noe and Giersch [10] suggested that the accumulation of sugars from photosynthesis could negatively regulate A. The decrease in g_s and therefore subsequent decrease in guard cell turgor, could be related to the decrease of A [26], [27], [28]. Such mechanisms for negative feedback are not well documented but are important for breeders, as any increase in photosynthetic capacity could lead to a great decrease in efficiency over the diurnal period. By accurately predicting diurnal gas exchange and dissecting W_i into the key parameters controlling dynamic responses, we believe our model will provide an important tool for future breeding strategies to identify targets for improved W_i under different environmental conditions.

Previous studies have shown spatial heterogeneity in stomatal distribution and behaviours [29], [30], [31], [32] that have not been included in the model. Instead, the model predicted the behaviour of a stoma that is representative of the sum of individual stomatal responses over the entire leaf surface. This simplification did not appear to impact on the quality of the predictions and it is difficult to assess the temporal and spatial heterogeneity in stomatal response; therefore, further investigations would be required to determine if and how such variations would impact model outputs.

Stomatal density (SD) was shown to be the most sensitive stomatal parameter for improving W_i, with decreases in SD resulting in a substantial reduction in g_s but minimal impact on A. This is in agreement with the work of Franks et al. [33], who showed significant variation of W_i in Arabidopsis mutants with different SD. The Bayesian inference and the sensitivity analysis revealed that the model was not sensitive to changes in a_max, as this value was not reached at any point over the diurnal period. In contrast, a_min and α_L were important determinants of W_i but are rarely reported or examined in this context in the literature. The model predicts that, under dark conditions, a_min is statistically greater than zero resulting in significant nocturnal transpiration, which has been reported previously [34] and has implications for overall plant water use. As SD cannot change over the diurnal period, α_L could be an important determinant of plant water use by adjusting the magnitudes of change in g_s as a function of the environment.

Although the coefficient of light absorption by PSII (α) was an important determinant of A and W_i in the field, this parameter does not show a large diversity; therefore, Vc_max, J_max and g_m are the most promising targets for improving A. The model predicts that increasing g_m could lead to similar improvements in A and W_i [35] as those observed when Vc_max and J_max were increased through manipulating enzymes associated with the Calvin cycle (e.g. [36]).

The sensitivity analysis performed here should be seen as a tool to determine the key parameter(s) for improving W_i under specific environmental conditions (e.g. fluctuating light intensity). Indeed, the parameter values estimated with the Bayesian inference are specific for this study and the variation around the determined parameter may change between individuals and/or species. For example, an individual with different photosynthetic capacity (Vc_max, J_max) or SD will exhibit different thresholds of A limitations (Fig. 5c) and the results of the sensitivity analysis may also vary. To generalize the sensitivity analysis, ranges of biologically possible parameter values and the interactions between them (e.g. relationship between size of the pore and SD) should be used; however, to our knowledge, this information is not yet fully available in the literature.

Our model simulations clearly showed that the temporal response of g_s is the product of several parameters (SD, α_L and k_i/k_d), and the rapidity of the stomatal response cannot be interpreted by comparing the initial slope of variation in g_s, as is often reported in the literature [37], [38]. Changes in the initial slope of the g_s response are correlated with SD, α_L and k_i/k_d and therefore are not only indicative of the speed of changes in stomatal aperture. In terms of gas diffusion, stomatal size constrains the maximum pore area but the observed pore area also depends on the sensitivity of the guard cell (α_L) responses to light intensity. As a result, it is theoretically possible to have large stomata that even at high light retain a small pore area. Considering the relationship between stomatal size and density [39], our results suggest that having a high density of small stomata will result in fast changes in g_s but also in a high average g_s value through the diurnal period, decreasing W_i.

The model simulations also revealed large variations in W_i (>80%) when the parameter values controlling the temporal response of g_s were altered. Indeed, the decrease in A due to greater limitation of CO₂ diffusion was minimal compared to the improvement in W_i. The importance of the temporal response of g_s was highlighted previously [40], [41], but not the importance of the additive effects of parameter interactions on A and W_i as revealed by our model. Therefore, our model could be used to find the optimal parameter set that would decrease g_s without impacting A and maximizing W_i to direct future breeding and research programmes to identify plants with reduced water usage, but the same or greater productivity.

5. Conclusion

We assessed and validated a new dynamic model of leaf gas exchange that accurately predicts g_s, A, and W_i under fluctuating light regimes such as those experienced by plants in the field. The model uses a unique framework that takes into account leaf anatomy, biochemistry and the physiological responses of stomata on W_i. The model revealed important negative feedback controls on A and g_s towards the end of the diurnal period that resulted in decreases in A with implications for overall plant productivity. Importantly, the model enabled W_i to be dissected into key parameters such as stomatal sensitivity to light (α_L) and minimal pore area under dark conditions (a_min) that have previous been neglected and could provide new and realistic targets for future improvements in crop water use efficiency.