Computational simulation of platelet interactions in the initiation of stent thrombosis due to stent malapposition

Abstract

Coronary stenting is one of the most commonly used approaches to open coronary arteries blocked due to atherosclerosis. Stent malapposition can induce thrombosis but the microscopic process is poorly understood. The objective of this study was to determine the platelet-level process by which different extents of stent malapposition affect the initiation of stent thrombosis. We utilized a discrete element model to computationally simulate the transport, adhesion, and activation of thousands of individual platelets and red blood cells during thrombus initiation in stented coronary arteries. Simulated arteries contained a malapposed stent with a specified gap distance (0, 10, 25, 50, or 200 μm) between the struts and endothelium. Platelet-level details of thrombus formation near the proximal-most strut were measured during the simulations. The relationship between gap distance and amount of thrombus in the artery varied depending on different conditions (e.g., amount of dysfunctional endothelium, shear-induced activation of platelets, and thrombogenicity of the strut). Without considering shear-induced platelet activation, the largest gap distance (200 μm) produced no recirculation and less thrombus than the smallest two gap distances (0 and 10 μm) that created recirculation downstream of the strut. However, with the occurrence of shear-induced platelet activation, the largest gap distance produced more thrombus than the two smallest gap distances, but less thrombus than an intermediate gap distance (25 μm). A large gap distance was not necessarily the most thrombogenic, in contrast to implications of some computational fluid dynamics studies. The severity of stent malapposition affected initial stent thrombosis differently depending on various factors related to fluid recirculation, platelet trajectories, shear stress, and endothelial condition.

1. Introduction

Coronary stenting is one of the most commonly used approaches to open coronary arteries blocked due to atherosclerosis, but stent failure continues to occur in 10%–20% of patients, though significant progress has been made over the last decade [1–3]. Stent thrombosis is a leading cause of stent failure, which can be fatal [4]. Stent thrombosis can occur at any time, from within 24 h of stent implantation up to several years after implantation, and may be due to vascular injury during stent implantation, thrombotic risk factors of the patient, inhibited re-endothelialization, endothelial expression of prothrombotic factors, platelet activation, or stent malapposition [5–9]. Among these factors, stent malapposition, which is the occurrence of gaps between the vessel wall and stent struts, occurs in up to 33% of implanted drug-eluting stents and up to 75% of patients with very late stent thrombosis (VLST) [7, 10]. Stent malapposition may occur acutely due to unsatisfactory stent deployment [11] and later due to excessive fibrin deposition, positive vascular remodeling, or inflammation [7]. Stent thrombosis in association with malapposition has been observed clinically in patients [8, 12] and in autopsy settings [7, 13]. Therefore, it is of importance to further study the mechanism of stent thrombosis associated with malapposition.

Previous studies of malapposed stents have suggested that thrombosis may be initiated at the location of stent separation from the wall and initiated by altered hemodynamics due to malapposition [8, 12, 14]. Computational fluid dynamics (CFD) studies, some of which also included experimental testing, examined the fluid flow field near malapposed struts. One such study by Kolandaivelu et al [15] found that slight and severe stent malapposition in vitro produced more thrombus mass than intermediate malapposition. This result was explained by complementary CFD simulations that revealed that as malapposition became more severe, the size of the recirculation zone adjacent to the distal side of the strut increased, then decreased, and then increased again [15]. The CFD component of a study by Foin et al [16] noted that the maximum shear rate and the size of regions with high shear rates increased with increasing severity of malapposition. With this result and results of the retrospective study component of this work, the authors suggested that high shear stress induced by malapposed struts could affect neointimal healing and increase platelet activation and thrombi aggregation, and that thrombogenicity of struts may be a function of malapposition severity [16]. A purely CFD study by De Santis et al [17] showed that in a patient-specific artery, stent malapposition co-localized with low wall shear stress on the non-gap side of the stent and on the endothelium between strut interconnections and co-localized with profiles of the vessel that were concave prior to stenting. Hence, the authors suggested that malapposition did not necessarily induce low wall shear stress [17]. In contrast, another purely CFD study by Chen et al [18] found that endothelial shear stress near malapposed struts was significantly reduced compared with that of an unstented vessel. The authors proposed that this low endothelial wall shear stress due to malapposition may be a culprit of stent thrombosis [18].

While current studies including those discussed above indicate that stent malapposition leads to fluid flow disturbances and stent thrombosis, the conclusions were generally inferred by comparing CFD results, which did not include platelets, to either corresponding in vitro results or to general observations of stent thrombosis. Because platelets are the main cellular components of arterial thrombi [19], it is necessary to include platelets in simulations to determine how their interactions with fluid flow disturbances lead to thrombosis. In addition, the effect of malapposition severity on stent thrombosis has not been investigated thoroughly [16]. Hence, it is necessary to delineate how the severity of stent malapposition induces flow disturbances that affect (1) the incidence of platelet activation (due to high shear stress or due to thrombogenic conditions from dysfunctional endothelium in low shear stress regions), (2) the occurrence of platelet adhesion to the endothelium, and (3) platelet trajectories. Additionally, contributions of strut thrombogenicity and vessel injury or inhibited re-endothelialization caused by struts need to be incorporated into computational models of stent thrombosis due to malapposition in order to understand the interaction of stent malapposition with these factors.

Accordingly, the objective of this study was to determine the microscale processes and platelet-level mechanisms by which stents initiate thrombosis due to malapposition. We first simulated stent malapposition in a tube and compared results of platelet deposition to experimental observations from a previous study to validate our model. Next, we simulated and analyzed the effect of different levels of malapposition on the initiation of thrombosis in coronary stenting.

2. Methods

The transport, collision, activation, adhesion, and aggregation processes of thousands of individual red blood cells (RBCs) and platelets were numerically simulated near stent struts in coronary arteries by a mesoscale, discrete element method for adhesive blood cells. In this section, the computational simulation conditions are described first, followed by descriptions of the models of platelet activation and of endothelium dysfunction. Details of the discrete element method have been previously published [20–23], with a brief description provided in appendix A.

2.1. Computational simulation conditions

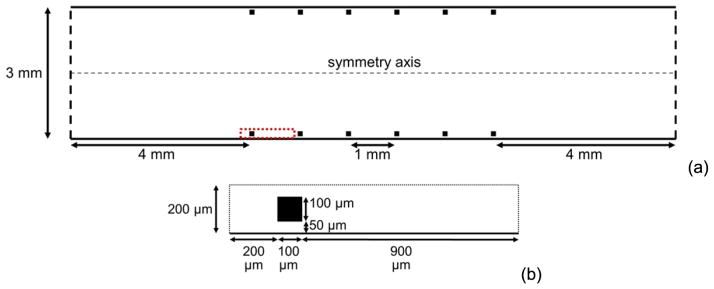
We performed two sets of simulations, one for model validation by comparison with experiments with malapposed stents (validation simulations) and one for investigation of malapposition (malapposition simulations). For each simulation, a stented segment with six square struts was modeled as a two-dimensional (2D) channel in which fluid flow was computed (e.g., see figure 1 for geometry of a malapposition simulation with gap distance of 50 μm between walls and struts).

Figure 1.

Geometry of a stented segment, within which fluid flow is solved on the half plane (a), and the local computational domain (boxed by the red dashed lines in (a)) within which cell interactions are simulated (b). The dashed box in (a) encompasses the region depicted in (b). The case with a gap distance of 50 μm is shown. For all malapposition simulations of different gap distances, all dimensions other than gap distance are the same.

Validation simulations were performed as closely as possible to a previous in vitro study in collagen-coated tubes with different gap distances between the wall and each strut of a malapposed, bare metal stent under pulsatile flow [15]. Each square strut had a dimension (thickness) of 81 μm. Gap distances were set as 30 μm (mild malapposition), 180 μm (intermediate malapposition), and 357 μm (severe malapposition) to correspond with those in the in vitro study, which were 0–60 μm (mild malapposition), 150–210 μm (intermediate malapposition), and 350–400 μm (severe malapposition). Platelet deposition was measured along the wall starting 200 μm upstream of the first strut and ending at the upstream edge of the third strut, which comprised a length of 2.4 mm. Additional conditions of validation simulations are given in table 1.

Table 1.

Simulation conditions.

Property	Value or Condition
	Validation simulations	Malapposition simulations
Artery or tube diameter (D)	3.18 mm	3 mm
Strut height and width	81 μm	100 μm
Gap distance	30, 180, or 375 μm	0, 10, 25, 50, or 200 μm
Spacing between struts	1 mm	1 mm
Distance from first (last) strut to inlet (outlet)	4 mm	4 mm
Strut thrombogenicity	Non-thrombogenic	Non-thrombogenic or thrombogenic
Mean fluid velocity (U)	0.42 m s−1	0.38 m s−1a
Fluid density (ρf)	1060 kg m−3	1030 kg m−3
Fluid dynamic viscosity (μ)	0.0035 kg m−1 s−1	0.0035 kg m−1 s−1
Reynolds number (ρfUD/μ)	404	335
Boundary condition at inlet	Poiseuille velocity profile	Poiseuille velocity profile
Boundary condition at outlet	Zero-pressure	Zero-pressure
Boundary condition at solid wall	No-slip	No-slip
Boundary condition at centerline	Symmetry	Symmetry
Platelet count at inlet	300 000 mm−3	300 000 mm−3
Area fraction of RBCs at inlet	0.40	0.40
Platelet volume	7.1 μm3	7.1 μm3
RBC volume	94 μm3	94 μm3
Platelet diameter	2.4 μm	2.4 μm
RBC diameter	5.6 μm	5.6 μm
Density of platelet or RBC	1063 kg m−3	1063 kg m−3

^aTypical peak diastolic coronary artery velocity.

Malapposition simulations were performed to model thrombosis in stented coronary arteries. Each square strut had a dimension (thickness) of 100 μm. Strut thickness values of commercially available stents generally range from 50 to 140 μm, with most being closer to 100 μm [2, 15, 24–26]. Gap distance was varied for different simulations as 0, 10, 25, 50 and 200 μm. Thrombus formation near the first strut closest to the inlet was examined. Some clinical observations have shown thrombus in the proximal segment of the stent [27, 28] and have shown that malapposed struts were more frequently located at the two edges of the stent, especially at the proximal edge [29]. We chose the first strut for these reasons and also because this strut is the first location at which platelets encounter altered shear stress that may influence platelet activation. Table 1 gives additional conditions of malapposition simulations.

For all simulations, fluid flow was solved for Newtonian, incompressible, steady, fully developed flow in the x–y plane. A second-order finite-volume method [30] with the PISO algorithm [31] was used to solve the Navier–Stokes equations of fluid flow in the absence of blood cells. The implication of this one-way coupling is discussed later in this section. Fluid flow was computed on structured meshes that were manually constructed with a higher concentration of nodes near struts and walls. A mesh sensitivity study was performed with four meshes of increasing resolutions (coarse, medium, fine, and finest) with a strut gap distance of 50 μm, as listed in table 2. The maximum errors for measurements at specific locations and for each velocity component were 18%, 8%, and 2% for the coarse, medium, and fine meshes, respectively. Hence, meshes similar to the tested fine mesh (161 nodes along strut dimension and 989 319 total nodes) were used for simulations with non-zero gap distances. With zero gap distance, a mesh sensitivity study of our previous work [32] found that a less fine mesh than required with malapposition was appropriate (41 nodes along strut dimension and 330 721 total nodes).

Table 2.

Mesh resolutions with strut gap distance of 50 μm for malapposition simulations.

Mesh type	Number of nodes along strut dimension	Number of nodes within gap in vertical direction	Number of mesh nodes	Maximum errora
Coarse	11	6	74 680	18%
Medium	41	21	330 057	8%
Fine	161	81	989 319	2%
Finest	231	116	1295 661	—

^aMaximum error is the maximum error compared with the next finer grid for all measured locations and for each component of velocity.

For computational efficiency, a local computational domain near the first strut was used for simulation of platelet and RBC interactions. The same local computational domain was used with all gap distances, as shown, for example, for the 50 μm gap distance in figure 1(b). Platelets and RBCs were modeled as three-dimensional (3D) spheres for computational efficiency, similar to previous computational studies of thrombus formation that utilized spheres or circles [33–35]. This approximation was expected to have a small effect on the relative results between different gap distances. Although unactivated platelets are discoid, activated platelets are spheroidal [36]. Hence, the approximation of spherical platelets was justified because this work focused on thrombus formation with activated platelets. Even though RBCs are deformable with non-spherical shapes under flow, the approximation of rigid, spherical RBCs in the current work was justified because RBCs were still expected to collide with platelets to force them toward the wall and strut surface just as physiological RBCs would. Centroids of 3D spherical cells remained the x–y plane in the 2D flow because forces on cells in the spanwise direction (z-direction) were zero, and the only nonzero torques on cells were in the z-direction. The volume of each cell was set to the physiological value in humans (see table 1).

We assumed that cells entered at the inlet with an initial velocity equal to the local fluid velocity at the location of the cell centroid. Platelets were initially unactivated. Activated platelets could aggregate with each other and adhere to thrombogenic struts, the collagen-coated tube wall in validation simulations, and dysfunctional or denuded endothelium in malapposition simulations. RBCs could aggregate only with each other. A platelet and an RBC could not aggregate with each other, and RBCs could not adhere to struts, the tube wall, or the endothelium. Initial positions of platelet centroids at the inlet were within 15 μm of the endothelium, without platelets touching the endothelium. Initial positions of RBC centroids were within the region that was greater than 15 μm from the endothelium. These initial positions assumed that platelet and RBC distributions at the inlet were those expected in a straight tube or artery. After the initial location of a cell was set, the cell was subjected to no further restrictions on its location.

For computational efficiency, the fluid flow and cell motion were one-way coupled such that the fluid flow affected cell motion and cell motion did not affect fluid flow. In arteries, whole blood can be considered to be a single-phase, Newtonian fluid with an apparent viscosity that is mainly due to the presence of RBCs [37, 38]. The viscosity of plasma is ~1.2 cP, while the higher apparent viscosity of whole blood is ~3.5 cP. Hence, to account for the macroscale effect of RBCs on the fluid flow, the fluid flow was solved with the apparent viscosity of whole blood using CFD without cells. In simulations, RBCs did not further affect fluid flow and were included because RBCs are known to force platelets toward vessel walls. Due to the low volume fraction of platelets (0.2%), the effects of platelets, aggregates, and thrombi on the fluid flow were also neglected. This assumption is reasonable since the focus of this work was the initial formation of thrombus, rather than later possible thrombotic occlusion of an artery. To account for the effects of the fluid between cells near each other, a model was incorporated that accounted for increased drag force on a cell due to increased apparent viscosity from cell crowding in the vicinity of the cell [39].

In validation simulations, the number of platelets in mural thrombi (thrombogenicity) was measured for comparison with the measure of thrombogenicity in the previous in vitro study [15], which was the amount of lactate dehydrogenase present, which was a measure of platelet and cell adhesion. To quantify results in malapposition simulations, a thrombus was defined as a group of two or more platelets in contact with each other. A platelet was considered to be part of a mural thrombus if the platelet was in contact with the endothelium or if the platelet was part of a thrombus that was in contact with the endothelium. One measure of thrombosis, activation count, was defined as the cumulative count of the number of platelets that had become activated since the start of the simulation and so represented platelets that had entered the artery whether or not they were still within the artery at the specified time. Another measure of the amount of thrombus, number of platelets in mural thrombi, included only platelets in the artery at the specific time.

Simulations were run to a final time (t_f = 1.58 s) at which the increase in activation count reached a state of statistical equilibrium for each gap distance, and activation count due to contact with the endothelium mainly reached a plateau for each gap distance for malapposition simulations. Malapposition simulation cases are listed in table 3. Each simulation was performed as a serial (non-parallel) program on a 3.0 GHz node having either four or eight processing cores, with 2 GB of RAM per core. Simulations were run simultaneously on these processing cores.

Table 3.

Simulation cases for malapposition simulations.

Case	Gap distance (μm)	Platelet activation model	Endothelial condition	Strut thrombogenicity
A	0	Shear-history	Denuded	Non-thrombogenic
B	10	Shear-history	Denuded	Non-thrombogenic
C	25	Shear-history	Denuded	Non-thrombogenic
D	50	Shear-history	Denuded	Non-thrombogenic
E	200	Shear-history	Denuded	Non-thrombogenic
F	0	Shear-history	Denuded	Thrombogenic
G	10	Shear-history	Denuded	Thrombogenic
H	25	Shear-history	Denuded	Thrombogenic
I	0	Shear-history	Low shear dysfunction	Non-thrombogenic
J	10	Shear-history	Low shear dysfunction	Non-thrombogenic
K	25	Shear-history	Low shear dysfunction	Non-thrombogenic
L	50	Shear-history	Low shear dysfunction	Non-thrombogenic
M	200	Shear-history	Low shear dysfunction	Non-thrombogenic
N	0	Critical-shear	Denuded	Non-thrombogenic
O	10	Critical-shear	Denuded	Non-thrombogenic
P	25	Critical-shear	Denuded	Non-thrombogenic
Q	50	Critical-shear	Denuded	Non-thrombogenic
R	200	Critical-shear	Denuded	Non-thrombogenic
S	0	Critical-shear	Intact	Non-thrombogenic
T	10	Critical-shear	Intact	Non-thrombogenic
U	25	Critical-shear	Intact	Non-thrombogenic
V	50	Critical-shear	Intact	Non-thrombogenic
W	200	Critical-shear	Intact	Non-thrombogenic

2.2. Platelet activation model

The shear stress magnitude and exposure time have both been shown to affect shear-induced platelet activation in vitro [40–42]. We employed two different models of shear-induced platelet activation in simulations. The first model, called the critical-shear model, was the shear-induced platelet activation model as developed in our previous work [23]. It is commonly known that normal platelets are not activated under normal, physiological conditions. Hence, this model assumed that a platelet became activated if it experienced shear stress higher than a critical shear stress (i.e., 6 Pa), which was greater than the normal, physiological shear stress in an unstented vessel (i.e., 2.66 Pa for our specific vessel). The critical-shear model possessed two attributes that were not necessarily apparent in other existing models: (1) The critical-shear model ensured that a platelet would not become activated by experiencing normal, physiological shear stress, irrespective of exposure time, while some other existing models assumed long enough exposure time could lead to activation [40, 43–46]. (2) The critical-shear model clearly indicated the point at which an individual platelet became activated, which was unclear in some other existing models. We used one of these other models as the second shear-induced platelet activation model, which was the model of Soares et al [43]. We called this model the shear-history model because it accounted for both magnitude of and exposure time to shear stress. Details of this model are provided in appendix B.

In addition to shear-induced platelet activation, a platelet was assumed to become activated if it contacted another activated platelet, which represented activation of the platelet by chemical agonists released by other activated platelets, similar to simulations of Kamada et al [35]. In specified simulation cases, a platelet was also assumed to become activated if it contacted denuded or dysfunctional endothelium or if it contacted a thrombogenic strut. Only activated platelets were subjected to adhesion and aggregation, and activation was considered irreversible. Activated platelets could adhere only to denuded or dysfunctional endothelium or to a thrombogenic strut.

2.3. Endothelial dysfunction model

Simulations assumed that activated platelets were subjected to adhesion only with those segments of endothelium that were either dysfunctional or denuded, which could be due to events such as injury during stent implantation [6, 13, 47] or inhibited re-endothelialization due to either drug-eluting stents [6] or penetration of struts into a necrotic core [7]. In simulation cases, the condition of the endothelium was such that (1) the entire endothelium was denuded, (2) the entire endothelium was intact, neither denuded nor dysfunctional, or (3) only specific locations of the endothelium were assumed to be dysfunctional due to low wall shear stress, termed low shear dysfunction. Dysfunctional endothelial segments were determined as follows. To indicate the local significance of platelet interactions with intact endothelium, Longest and Kleinstreuer [48] proposed a surface reactivity factor (SR) given by SR = τ_w,mean/τ_mean, where τ_w,mean is mean wall shear stress of the vessel, and τ_mean is local time-averaged wall shear stress. The authors did not model endothelial dysfunction per se but noted that a constant value of SR greater than unity could be used to approximate an increased likelihood of platelet adhesion to a surface compared with normal endothelium. Hence, we assumed that the endothelium was dysfunctional at a specific location if the local SR was greater than a critical value of SR_crit = 2. Thus, with τ_w,mean = τ_w,0 = 2.66 Pa, segments of endothelium that were subjected to shear stresses less than 1.33 Pa were considered dysfunctional, while remaining segments were not. Obviously, for denuded endothelium, 100% of the endothelium was assumed dysfunctional.

3. Results

3.1. Effects of gap distance in validation simulations

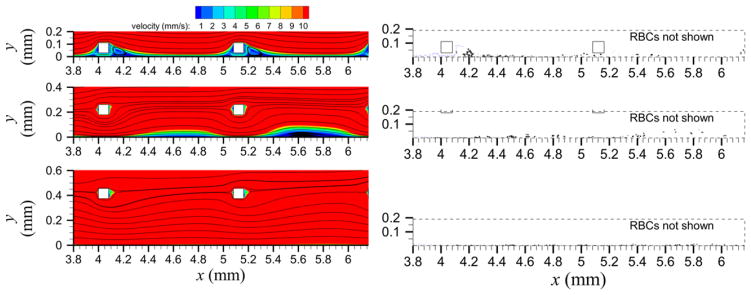
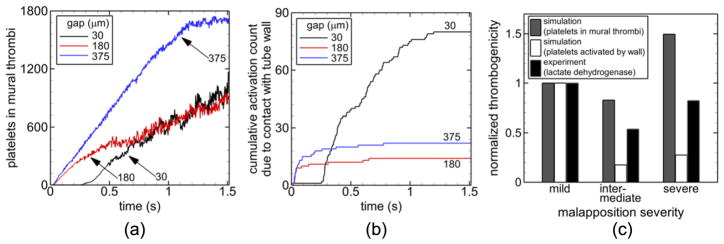
For the validation simulations, mild malapposition (30 μm gap distance) produced recirculation nearly immediately distal to each of the six struts and adjacent to the tube wall (shown for the first two struts in figure 2 top-left panel). Intermediate malapposition (180 μm gap distance) produced recirculation distal to all but the first strut, which was adjacent to the tube wall and somewhat centered between struts (figure 2 middle-left panel). Severe malapposition (375 μm gap distance) did not produce recirculation (figure 2 bottom-left panel). Initially, the number of platelets in mural thrombi (the measure of thrombogenicity) was larger with a larger gap distance (figure 3(a)). At approximately time t = 0.68 s and later, mild and intermediate malapposition yielded similar numbers of platelets in mural thrombi while severe malapposition maintained the largest value (figure 2 right panels and figure 3(a)). At the final time, mild malapposition yielded the largest number of platelets activated due to contact with the collagen-coated wall (rather than contact with another activated platelet), and intermediate malapposition yielded the smallest number (figure 3(b)). Because thrombogenicity was measured by two quantities in simulations (number of platelets in mural thrombi and number of platelets activated by contact with the wall) and by a different quantity in previous experiments (lactate dehydrogenase) [15], normalized thrombogenicity, as defined by the measured quantity divided by the measured quantity of the mild malapposition case, was used to compare between simulation and experimental results. It was seen that normalized thrombogenicity was larger with mild malapposition than with intermediate malapposition at the final time (figure 3(c)). Among the tested malapposition levels, intermediate malapposition generated the smallest normalized thrombogenicity with the measured quantity as platelets activated by the wall (figure 3(c)). The previous in vitro experimental results [15] used for validation showed similar trends, in agreement with our simulations as shown in figure 3(c).

Figure 2.

Velocity contours and streamlines (left panels) and platelet locations (right panels) near the first two struts for validation simulations. Gap distances (from top to bottom) are 30, 180, and 375 μm. In right panels, unactivated platelets (blue) and activated platelets (black) are shown, but RBCs are removed for clarity.

Figure 3.

Results of validation simulations including time variations of number of platelets in mural thrombi (a), time variations of cumulative number of platelets activated by contact with the collagen-coated tube wall (b) and comparison of thrombogenicity normalized by thrombogenicity of the case of mild malapposition at the final time with experimental data from [15] (c).

3.2. Effects of gap distance on fluid flow

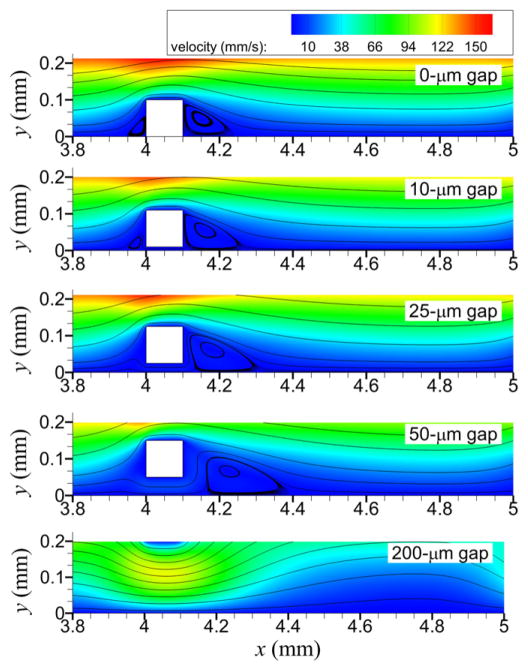
As gap distance increased, recirculation regions generally reduced in number, decreased in length upstream of the strut, increased in length downstream of the strut, and moved farther away from the sides of struts (figure 4). With the well-apposed strut (0 gap distance), recirculation regions were adjacent to upstream and downstream sides of each of the six struts. With the 10 μm gap distance, recirculation regions were slightly detached from each side of each strut, with the detachment more enhanced for the upstream, rather than downstream, recirculation region. For each of the six struts with the 25 and 50 μm gap distances, upstream recirculation regions were not present and detachment of the downstream recirculation region was more enhanced with increased gap distance. With the 200 μm gap distance, recirculation regions formed on the endothelium downstream of only the last five struts (and not the first strut), and the regions were about equidistant from each strut.

Figure 4.

Streamlines and contours of velocity for the local computational domain for different gap distances.

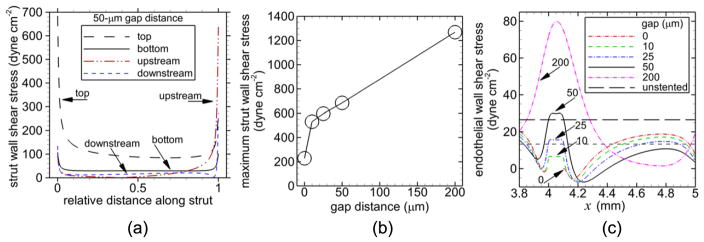
From this point forward, results refer to the first strut, which was the strut within the local computational domain (or above the local computational domain with the 200 μm gap distance). The highest wall shear stress on the strut occurred on the top, horizontal side of the strut with the next highest value occurring on the upstream, vertical side of the strut, for a given gap distance as shown in figure 5(a) for the 50 μm gap distance. The maximum wall shear stress on the strut was smallest for the well-apposed strut and increased nearly linearly with gap distance for malapposed struts (figure 5(b)). Regions with lower than physiological endothelial wall shear stress were produced by all gap distances (figure 5(c)). The largest two gap distances (50, 200 μm) also produced regions with higher than physiological endothelial wall shear stress that were mainly centered below the strut.

Figure 5.

Magnitude of shear stress including shear stress on the indicated surfaces of the first strut (a), maximum shear stress on the strut versus gap distance (b), and endothelial wall shear stress for each gap distance (c). Relative distance along the strut in (a) is measured from either the upstream side or bottom side, and the gap distance is 50 μm.

3.3. Effects of gap distance on endothelial function

Our results showed that, due to low wall shear stress (<1.33 Pa), the amount of dysfunctional endothelium increased with increasing gap distance, excluding the largest gap distance (200 μm). 45%, 59%, 66%, 84%, and 49% of the endothelium was dysfunctional for gap distances of 0 μm, 10 μm, 25 μm, 50 μm, and 200 μm, respectively.

3.4. Effects of gap distance on thrombosis

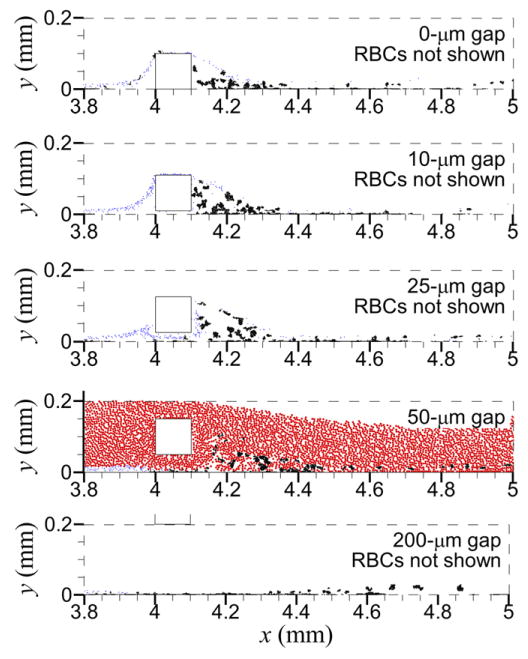
For almost all cases, no cells (platelets and RBCs) entered the upstream recirculation regions with the gap distances that produced upstream recirculation (0, 10 μm), except for one unactivated platelet in Case S and about ten unactivated platelets in Case T (see figure 6 for Cases A–E. With the 10 μm gap distance, most platelets traveled over the top of the strut, while only a few platelets (e.g., 1% of platelets for Case B) traveled through the gap between the strut and endothelium; no RBCs traveled through this gap. With the 25 μm gap distance, a few platelets (e.g., two platelets for Case C) traveled over the top of the strut; most platelets traveled through the gap, along with some RBCs. With the 50 and 200 μm gap distances, due to the large distance from the locations of platelets near the endothelium, no platelets traveled over the top of the strut or came in contact with the strut. For cases with the shear-history platelet activation model, no shear-induced platelet activation occurred due to the short exposure time to high shear stress. For cases with the critical-shear platelet activation model, shear-induced platelet activation occurred for all but the 50 μm gap distance because platelets did not travel over the top of the strut, which was the only location where shear stress exceeded the critical value. Although with the critical-shear platelet activation model and 200 μm gap distance platelets did not travel over the top of the strut, platelets were activated by high shear stress located near the endothelium below the strut (see wall shear stress in figure 5(c)).

Figure 6.

Locations of unactivated platelets (blue) and activated platelets (black) at the final time for each gap distance with a non-thrombogenic strut, denuded endothelium, and shear-history platelet activation model. RBCs (red) are present as shown in the panel with 50 μm gap distance but not shown in other panels for clarity.

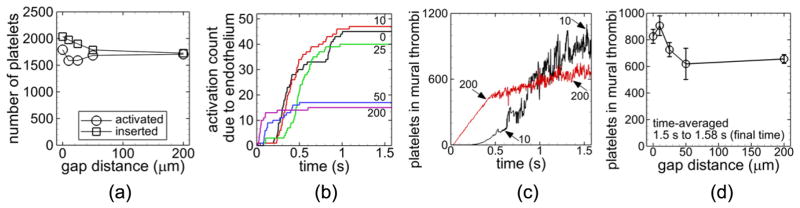
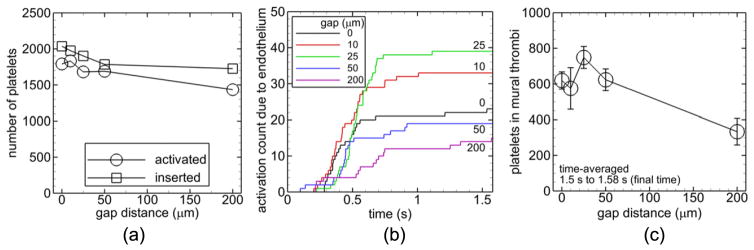
Number of platelets inserted into the flow decreased as gap distance increased for a given set of cases (figures 7(a), 8(a), 9(a), 10(a)). Number of inserted platelets varied depending on whether an existing platelet was near the inlet due to fluid flow patterns or due to platelet adhesion at the inlet that delayed insertion of a new platelet to avoid overlap with existing platelets. For all cases with a given non-intact endothelial condition (denuded or dysfunctional due to low shear stress) and a given strut thrombogenicity (non-thrombogenic or thrombogenic), the largest gap distance (200 μm) yielded a lower activation count at the final time than the well-apposed strut (0 μm gap distance) and in some cases the other gap distances (figures 7(a), 8(a), and 9(a)). With shear-history platelet activation, a given non-intact endothelial condition, and a given strut thrombogenicity, the largest gap distance (200 μm) yielded a lower number of platelets in mural thrombi time-averaged near the final time between t = 1.5 s and t_f = 1.58 s than the well-apposed strut and in some cases the other gap distances (figures 7(d), 8(c), and 9(c)), while with critical-shear platelet activation the opposite was true (figure 10(b)).

Figure 7.

Measures of thrombosis for cases with a non-thrombogenic strut, denuded endothelium, and shear-history platelet activation model. Number of platelets inserted into the flow (squares) and activated (activation count, circles) during the simulation versus gap distance (a). Activation count due to contact of platelets with the endothelium versus time for the indicated gap distances in μm (b). Number of platelets in mural thrombi versus time for the indicated gap distances in μm (c). Number of platelets in mural thrombi time-averaged between t = 1.5 s and the final time t = 1.58 s versus gap distance with error bars representing standard deviation (d).

Figure 8.

Measures of thrombosis for cases with a thrombogenic strut, denuded endothelium, and shear-history platelet activation model. Number of platelets inserted into the flow (squares) and activated (activation count, circles) during the simulation versus gap distance (a). Activation count due to contact of platelets with the endothelium (circles) and strut (squares) versus gap distance at the final time (b). Number of platelets in mural thrombi time-averaged between t = 1.5 s and the final time t = 1.58 s versus gap distance with error bars representing standard deviation (c).

Figure 9.

Measures of thrombosis for cases with a non-thrombogenic strut, low shear dysfunctional endothelium, and shear-history platelet activation model. Number of platelets activated (activation count, circles) and inserted into the flow (squares) during the simulation versus gap distance (a). Activation count due to contact of platelets with the endothelium versus time for the indicated gap distances (b). Number of platelets in mural thrombi time-averaged between t = 1.5 s and the final time t = 1.58 s versus gap distance with error bars representing standard deviation (c).

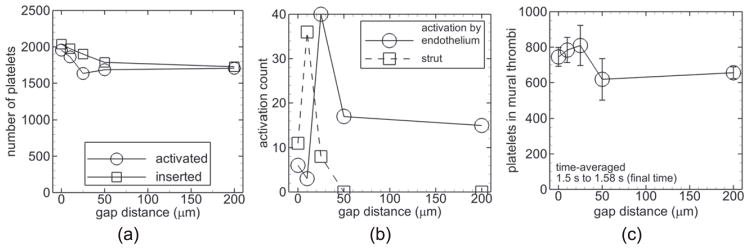
Figure 10.

Measures of thrombosis for cases with a non-thrombogenic strut, denuded endothelium, and critical-shear platelet activation model. Number of platelets activated (activation count, circles) and inserted into the flow (squares) during the simulation versus gap distance (a). Number of platelets in mural thrombi time-averaged between t = 1.5 s and the final time t = 1.58 s versus gap distance with error bars representing standard deviation (b).

3.4.1. Non-thrombogenic strut, denuded endothelium, and shear-history platelet activation

With a non-thrombogenic strut, denuded endothelium, and the shear-history platelet activation model (Cases A–E), activation count slightly increased with increasing gap distance of malapposed struts (figure 7(a)). Activation count due to platelets contacting the denuded endothelium reached a plateau for each gap distance and was at least twice as large with the smallest three gap distances (0, 10, 25 μm) compared to the larger gap distances (50, 200 μm) at the final time (figure 7(b)). Activation count due to endothelial contact was two orders of magnitude smaller than the overall activation count with each gap distance. Number of platelets in mural thrombi increased on average with time with a given gap distance. With the 200 μm gap distance, this value quickly increased initially compared with the other gap distances, as shown in figure 7(c) for the 10 μm and 200 μm gap distances. Averaged near the final time, this value was largest with the smallest malapposed gap distance (10 μm), which appeared to be significantly larger than that of the other malapposed gap distances (25, 50, 200 μm) (figure 7(d)).

3.4.2. Thrombogenic strut, denuded endothelium, and shear-history platelet activation

With the two largest gap distances (50, 200 μm), platelets did not contact the strut such that results with a thrombogenic strut, denuded endothelium, and the shear-history platelet activation model were the same as those in the previous subsection with a non-thrombogenic strut (Cases D and E). Activation count was smallest with the 25 μm gap distance (Case H) (figure 8(a)). Activation count due to platelets contacting the denuded endothelium or the thrombogenic strut was two orders of magnitude smaller than the overall activation count with a given gap distance (figure 8(b)). The 25 μm gap distance produced at least double the activation count by endothelial contact compared with the other gap distances, and the 10 μm gap distance (Case G) produced at least double the activation count by strut contact compared with the other gap distances (figure 8(b)). Number of platelets in mural thrombi time-averaged near the final time did not show large differences between gap distances considering the variation (figure 8(c)).

3.4.3. Non-thrombogenic strut, low shear dysfunctional endothelium, and shear-history platelet activation

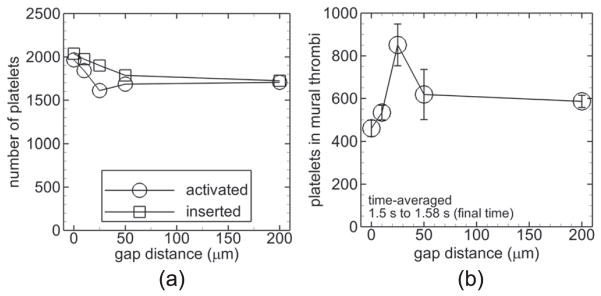
With a non-thrombogenic strut, low shear dysfunctional endothelium, and the shear-history platelet activation model (Cases I–M), the 200 μm gap distance yielded a much lower activation count compared with the other gap distances (figure 9(a)). Activation count due to platelets contacting the dysfunctional endothelial segments was two orders of magnitude smaller than the overall activation count with each gap distance and was largest with the smallest two nonzero gap distances (10, 25 μm) compared with the other gap distances at the final time (figure 9(b)). Number of platelets in mural thrombi time-averaged near the final time was smallest for the largest gap distance (200 μm) (figure 9(c)).

3.4.4. Non-thrombogenic strut, denuded or intact endothelium, and critical-shear platelet activation

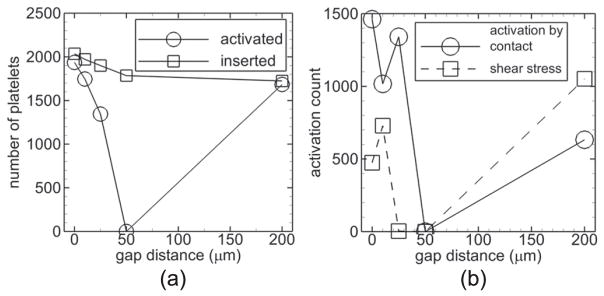
With a non-thrombogenic strut, the critical-shear platelet activation model, and denuded endothelium (Cases N–R), activation count for a given gap distance was nearly the same as that with a thrombogenic strut, the shear-history platelet activation model, and denuded endothelium (figure 10(a)). Number of platelets in mural thrombi time-averaged near the final time was largest with the 25 μm gap distance (figure 10(b)). This value with the 200 μm gap distance was slightly larger than that with the 0 and 10 μm gap distances.

With a non-thrombogenic strut, the critical-shear platelet activation model, and intact endothelium (Cases S–W), the largest activation counts occurred with the smallest two gap distances (0, 10 μm) (figure 11(a)). As described earlier, shear-induced activation did not occur with the 50 μm gap distance. Activation count due to contact with an activated platelet was larger than that due to shear stress with the smaller gap distances (0, 10, 25 μm); the opposite was true with the 200 μm gap distance (figure 11(b)).

Figure 11.

Measures of thrombosis for cases with a non-thrombogenic strut, intact endothelium, and critical-shear platelet activation model. Number of platelets activated (activation count, circles) and inserted into the flow (squares) during the simulation versus gap distance (a). Activation count due to contact of platelets with an activated platelet (circles) and by shear stress above the critical value (squares) versus gap distance at the final time (b).

3.5. Effects of endothelial condition on thrombosis

The effects of endothelial condition were determined by comparing cases that included the shear-history platelet activation model (Cases A–M). These effects are discussed in the following two sub-subsections.

3.5.1. Comparison of trends with respect to gap distance

Activation count with the largest gap distance (200 μm) was smaller than with the other gap distances with low shear dysfunctional endothelium (figure 9(a)) unlike that of cases with denuded endothelium (see figures 7(a), 8(a), 9(a) and 10(a)). Also unlike cases with denuded endothelium, with low shear dysfunctional endothelium, number of platelets in mural thrombi time-averaged near the final time was noticeably smaller with the 200 μm gap distance than with the other gap distances. On the other hand, with either denuded endothelium or low shear dysfunctional endothelium, a non-thrombogenic strut, and shear-history platelet activation, the number of platelets activated by contact with dysfunctional or denuded endothelium at the final time was largest for the three smallest gap distances (0, 10, 25 μm) compared with the larger two gap distances (50, 200 μm) (see figures 7(b) and 9(b)).

3.5.2. Comparison of thrombosis measures with a given gap distance

With all but the largest gap distance (200 μm), activation count with low shear dysfunctional endothelium was larger or the same as that with denuded endothelium with a non-thrombogenic strut with shear-history platelet activation (figures 7(a) and 9(a)). With these cases, the percent changes of activation count between low shear dysfunctional and denuded endothelium were 0%, 16%, 6%, 0%, and −16% for gap distances of 0 μm, 10 μm, 25 μm, 50 μm, and 200 μm, respectively. Number of platelets in mural thrombi time-averaged near the final time was much smaller for most gap distances with low shear dysfunctional endothelium compared with denuded endothelium with a non-thrombogenic strut with shear-history platelet activation (figures 7(d) and 9(d)). The percent changes of this value between low shear dysfunctional and denuded endothelium were −25%, −37%, 3%, 1%, and −49% for gap distances of 0 μm, 10 μm, 25 μm, 50 μm, and 200 μm, respectively.

4. Discussion

4.1. Qualitative validation of model

The previous in vitro study used for validation [15] found that mild malapposition was the most thrombogenic and intermediate malapposition was the least thrombogenic. The validation simulations agreed with the previous in vitro study in that thrombogenicity was larger with severe malapposition compared with intermediate malapposition (figure 3(c)). In contrast to the in vitro study, severe malapposition was the most thrombogenic in simulations. However, the ordering of levels of malapposition was the same when comparing thrombogenicity in the in vitro study with the number of platelets activated due to wall contact in the simulations. This order from most to least thrombogenic was mild, severe, and intermediate malapposition.

Differences between simulations and the in vitro study may be due to differences in time and length scales. The in vitro experiments were completed after four minutes while simulations were completed after 1.58 s due to computational cost. As well, thrombosis within the entire stent was considered in the in vitro study, while thrombosis below two struts was computationally feasible in simulations. Additionally, the in vitro study indirectly measured the amount of thrombus using the amount of lactate dehydrogenase while simulations directly measured mural thrombi. Considering (1) the partial agreement in the relative effect of gap distance on overall thrombogenicity between the in vitro study and simulations, (2) the similarities in the relative effect of gap distance on number of platelets activated by the collagen-coated wall in simulations and thrombogenicity in the in vitro study, and (3) the validation of the model by our previous work [32] with respect to locations of platelet deposition between well-apposed struts, the computational model is capable of qualitatively simulating the relative effects of gap distance on thrombosis.

The computational model gave results that are in good agreement with clinical observations. Clinical data and observations have been used to associate the presence of stent malapposition with the presence of stent thrombosis; however, such clinical studies generally have not compared the severity of malapposition with the amount of thrombus and hence are difficult to use to directly validate our results. Nevertheless, results of our malapposition simulations were in general agreement with clinical studies that showed that a zero gap distance did not necessarily produce zero thrombus [10, 14]. For example, in an observational study at ten months follow-up after coronary stent implantation of a sirolimus-eluting stent, optical coherence tomography (OCT) revealed thrombus with both well-apposed and malapposed (defined as a gap distance >160 μm) stents, while the proportion of struts with an incidence of new thrombus was significantly greater with malapposed than well-apposed struts [14]. Additionally, in a five-year follow-up study of patients with coronary drug-eluting stents, intra-vascular ultrasound revealed that malapposed struts were associated with higher rates of thrombosis than were well-apposed struts [10]. Some cases with malapposed stents in our simulations produced more thrombus than the well-apposed stent, depending on thrombogenic conditions and gap distance, in agreement with these clinical observations. As well, in a retrospective study of patients who received coronary stents (drug-eluting and bare-metal) and subsequently died within 30 days, the number of histological sections with malapposed struts was significantly larger in sections with thrombus compared with patent sections, and malapposition was shown to be a risk factor associated with stent thrombosis [13]. Histology of a representative patient showed that several stent struts were malapposed and were surrounded by thrombus, with thrombus also along the vessel wall [13]. Our simulations with a malapposed thrombogenic strut similarly produced thrombus on both the strut and vessel wall.

4.2. Thrombus formation did not necessarily increase with increased gap distance

With denuded endothelium and the shear-history platelet activation model, more thrombus formed with the well-apposed strut than with the largest gap distance, which may have been due to recirculation regions with the well-apposed strut, which were absent with the largest gap distance. The downstream recirculation region of the well-apposed strut might have increased thrombus formation by directing platelets toward denuded endothelium or toward adhered activated platelets.

With denuded endothelium and the critical-shear platelet activation model, the two smallest gap distances produced less thrombus than the largest gap distance, unlike with the shear-history model. With each model of shear-induced platelet activation, thrombus amounts remained about the same with the largest gap distance. However with the two smallest gap distances, because almost every platelet passed over the top of the strut where shear stress exceeded the critical shear stress, these platelets became activated with the critical-shear model and hence were more likely to form aggregates than with the shear-history model. Visualization of the simulations showed that unattached, single, unactivated platelets present with the shear-history model were more likely to adhere to the wall than aggregates present with the critical-shear model, such that the critical-shear model produced less thrombus amount with the two smallest gap distances.

With low shear dysfunctional endothelium, the fact that the largest gap distance yielded a lower thrombus amount than the other gap distances was partly due to the largest gap distance producing a considerably smaller percent of endothelium that was dysfunctional compared with other malapposed struts, such that fewer locations were available for platelets to adhere to the endothelium. In contrast, with the well-apposed strut, a slightly smaller percent of endothelium was dysfunctional (45%) compared with that of the largest gap distance (49%). Unlike with the largest gap distance, with the well-apposed strut, thrombus may have been promoted by recirculation regions and dysfunctional endothelium being located mainly within the proximal half of the domain near the strut.

Both our study and the previous study of Foin et al [16] used CFD to show that shear stress on and near struts increased with increasing gap distance. Foin et al [16] suggested that thrombogenicity possibly increased as gap distance increased based on the fact that high shear stress can activate platelets. However, our study simulated the cellular interaction and revealed that the largest gap distance tested was not necessarily the most thrombogenic gap distance. One reason for this result was that platelet activation factors other than high shear stress (i.e., dysfunctional or denuded endothelium, thrombogenic strut, or other activated platelets), as well as recirculation regions, also affected thrombosis. Another reason was that, because platelets were concentrated near the endothelium, platelets did not experience increasingly higher shear stresses on and near struts with larger gap distances. As well, shear stress did not activate platelets for cases with the shear-history platelet activation model; however shear stress affected the amount of dysfunctional endothelium of cases with low shear dysfunctional endothelium. Instead, our results were consistent with in vitro results of Kolandaivelu et al [15] that showed a larger gap distance did not necessarily yield a larger thrombus amount.

4.3. Clinical relevance

Stent malapposition occurs due to unsatisfactory stent deployment [11] or later due to excessive fibrin deposition, positive vascular remodeling, or inflammation [7], causing stent thrombosis in patients [8, 12]. Clinical observations in patients have suggested that stent malapposition caused VLST within both bare-metal stents [8] and drug-eluting stents [12]. For example, after treatment of the occurrence of VLST within the left anterior descending artery in a patient with a bare-metal stent, intravascular ultrasound and OCT showed malapposition at the proximal and distal sites of the stent with residual thrombus at these sites [8]. Because neointimal plaque and lipid-laden neointimal tissue that may induce thrombosis were not observed within the stent, the authors of this case study determined malapposition to be a possible cause of VLST, possibly due to deposition of fibrin and platelets at locations of malapposition, though the specific mechanisms were unclear in this case. In a different patient with drug-eluting stents, after treatment of the first occurrence of VLST within the left anterior descending artery, coronary angiography and OCT revealed stent malapposition despite a preserved stent expansion [12]. The authors of this case study suggested that VLST may have been partly due to thrombus initiation at the location of stent separation from the artery wall, as well as due to discontinuation of clopidogrel, which was part of dual antiplatelet therapy (DAPT) with clopidogrel and picotamide. The authors also suggested that had OCT been performed after initial stent placement, possible stent malapposition could have been detected and corrected, and it would have been known whether this stent malapposition developed later instead. Similar to these two case studies, in our study, thrombus formed at locations of malapposition, which was due to dysfunctional or denuded endothelium. Though thrombus also formed with well-apposed struts, had we assumed well-apposed struts were associated only with intact endothelium, thrombus would not have formed on the endothelium.

Additionally, in a study with patients whom each received a drug-eluting coronary stent, OCT at 10 month follow-up revealed that stents with late-acquired malapposition (gap distance >160 μm) were associated with significantly more thrombus development than were well-apposed stents [14]. The authors suggested this result might be due to an increase in exposed surface area with malapposed struts compared with well-apposed uncovered struts and possible local flow disturbance due to malapposed struts. Because of their study, the authors noted that DAPT with aspirin and clopidogrel is necessary for at least 12 months. Our results in which shear-induced platelet activation occurred similarly showed more thrombus amount with the 200 μm gap distance compared with the well-apposed strut.

4.4. Study limitations

For computational efficiency, our study focused on one of the six simulated struts, which was the proximal-most strut because this strut created the first location at which cells experienced flow disturbances and the endothelium experienced possible denudation or dysfunction. As noted above, with the 200 μm gap distance, flow recirculation did not occur downstream of the first strut as it did for the other five struts and as it did for all struts with the other gap distances. The first two struts will be examined in future studies. We expect that the additional recirculation region for the 200 μm gap distance may direct platelets toward the endothelium to increase thrombus amount relative to that of the other gap distances, though whether the value will be greater than that of the other gap distances is unclear.

Our study assumed that agonist-induced platelet activation and aggregation could occur (e.g., due to other activated platelets, thrombogenic strut, or dysfunctional endothelium). However, for one year or more after stent implantation, patients generally receive DAPT (aspirin and clopidogrel), which reduces agonist-induced platelet activation and aggregation [49, 50]. Hence, our results with cases that lacked shear-induced platelet activation may better represent situations with either inadequate or discontinued DAPT. On the other hand, because neither aspirin nor clopidogrel prevents shear-induced platelet activation [51, 52], our results with cases that yielded shear-induced platelet activation characterize situations both with and without adequate DAPT [50].

Endothelial condition was assumed to be the same with both well-apposed and malapposed struts in a given set of cases. With non-intact endothelium in our study, the well-apposed strut yielded thrombus formation, which in some cases exceeded that with the largest gap distance. If we assumed that re-endothelialization occurred and that the endothelium was dysfunctional or denuded only at the site from which the strut separated from the wall, in accordance with indications from the clinical studies described in section 4.3 [8, 12], then the well-apposed strut would not produce thrombus because platelets would not adhere to the sustained intact endothelium. Hence, the well-apposed strut would be the least thrombogenic.

While activation of platelets by chemical agonists was represented by contact of an unactivated platelet with an activated platelet or with dysfunctional endothelium (similar to a previous model [35]), the process of platelet activation by chemical agonists was not described in our current model. In future work, we will incorporate a model of agonist-induced platelet activation into our current model, for example an activation model based on that of Flamm et al [53] that simulates platelet release of ADP and thromboxane and simulates dynamic concentration fields of these agonists.

For computational efficiency, fluid flow was assumed to be 2D, rather than 3D, which would be infeasible due to the much larger number of cells, cell collisions, and platelet adhesions. The assumption of 2D flow was similar to that in many previous studies of thrombosis, cell adhesion, or stented vessels [16, 33, 34, 54–56]. Although secondary flow cannot be captured in 2D, because our previous works have shown similar characteristics in aggregate size distributions of RBC aggregates in 2D simulations compared with 3D [57] and have demonstrated the same locations of thrombus initiation in vessels in 2D simulations as an in vivo study [23], we expected that platelet aggregates and thrombus initiation locations in our 2D simulations would be similar to 3D. Due to the above justifications regarding fluid flow, platelet aggregates, and thrombus initiation, results of our 2D simulations were expected to be qualitatively, if not quantitatively, similar to 3D results. In future work, we will extend the model to efficiently simulate flows of cells in 3D cylindrical vessels.

The flow was assumed to be steady with the inlet mean fluid velocity equal to a typical peak diastolic coronary velocity. Previous CFD studies with pulsatile flow demonstrated similar recirculation regions as in our study with well-apposed struts. It was found that recirculation regions were largest at peak velocity for a case with recirculation downstream of a single strut [26] and for a case with two recirculation regions between two struts [54]. The length of the recirculation region downstream of the single strut was 20% larger at the peak velocity, compared to the minimum velocity [26]. Because our study utilized a peak velocity, we would expect that our downstream recirculation regions would represent the peak size during a cardiac cycle under pulsatile flow. Additionally, thrombus growth rate within in vitro coronary stenoses have been shown to be similar with either steady or pulsatile flow, though thrombosis was initiated earlier with steady flow [58]. Similarly, we would expect that, compared with pulsatile flow, our simulations would initiate thrombosis earlier while nonetheless yielding similar thrombus growth patterns and locations. Furthermore, we would expect that the dysfunctional endothelial segments produced under the low shear dysfunctional endothelium model in our steady flow simulations would be the same segments that would be periodically subjected to sufficiently low shear stress (or SR_crit > 2) under pulsatile flow. Thus, the same segments of endothelium would become dysfunctional in pulsatile flow, and results would be similar to our steady flow simulations. Although some differences would exist in results between steady and pulsatile flow, the relative effects of gap distance were expected to be similar.

5. Conclusions

We simulated the transport, adhesion, and activation of thousands of individual platelets and RBCs during thrombus initiation in stented coronary arteries with stent malapposition through our discrete element model. Results agreed with an in vitro study that showed a larger gap distance was not necessarily more thrombogenic. Depending on several conditions (e.g., amount of dysfunctional endothelium, shear-induced activation of platelets, and thrombogenicity of the strut), the largest gap distance produced less thrombus than the smallest two gap distances in some cases. In other cases under different conditions, the opposite was true.

Our work was the first to include individual cells in computational simulations of stent thrombosis with malapposed struts, to the best of our knowledge. Previous CFD studies without cells postulated a higher thrombogenicity as gap distance increased due to results that showed increased shear stress on the tops of struts, which could activate platelets. Our study furthered knowledge gained by previous CFD studies to show that platelets did not travel over the tops of struts in some cases; hence, thrombogenicity did not necessarily increase with increased gap distance. Our study revealed that the process of initial stent thrombosis was multifactorial and depended not only on the severity of stent malapposition, but also on various factors related to fluid recirculation, platelet trajectories, shear stress, and endothelial condition.

Appendix A. Discrete element method

The transport, collision, activation, adhesion, and aggregation of thousands of individual platelets and RBCs were simulated in stented coronary arteries by a mesoscale, discrete element method for blood cells. Details of the computational model have been previously published [20–23]. A brief description of the model is given here.

The computational model followed the motion of each spherical cell due to interactions with the fluid, vessel walls, struts, and other cells. The model solved the linear and angular momentum equations of each cell, which included forces and torques due to the fluid (i.e., drag force, added mass force, and fluid rotation torque) and due to collision with adhesion effects (i.e., force due to elastic deformation of a cell from collision, force due to energy dissipation from collision, sliding resistance force, sliding resistance torque, and rolling resistance torque). Forces and torques were determined using equations given in the literature, except for the force due to elastic deformation, which was determined, as described below, based on the theory of Johnson et al [59].

Upon collision, cells were assumed to retain their shapes except within a flattened circular region of contact, in accord with the model of cell–cell contact of Bell et al [60]. Receptor–ligand bonds that formed within the contact region were modeled as springs following Bell et al [60]. Under our model assumptions, receptor–ligand binding took a form that was mathematically analogous to van der Waals adhesion with a time-dependent adhesive surface energy density u(t) given by

$$u(t)=-\frac{\sigma }{2}{(x_b-x_{\mathrm{e}})}^2{\int }_0^1{N}_b(t-t_0(s))s\mathrm{d}s,$$ (A.1)

where σ is spring constant, x_b is length of the bond, x_e is equilibrium length of the bond, N_b is number density of bonds, and s is radial position within the contact region divided by the radius of the contact region. The variation of N_b with time was given by a kinetics equation of Bell [61] that accounted for forward and reverse reactions of bond formation given by

$$\frac{\mathrm{d}{N}_{\mathrm{b}}}{\mathrm{d}t}=k_f(N_{L0}-N_b)(N_{R0}-N_b)-k_{\mathrm{r}}{N}_b,$$ (A.2)

where k_f and k_r are respectively forward and reverse reaction rate coefficients, and N_L0 and N_R0 are respectively initial ligand and receptor densities. The reaction rate coefficients were given by Dembo et al [62]

$$\begin{array}{ll}{k}_f\hfill & =k_{f0}exp\left[-\frac{{\sigma }_{ts}{(x_b-x_e)}^2}{2kT}\right],\hfill \\ k_r\hfill & =k_{r0}exp\left[\frac{(\sigma -{\sigma }_{ts}){(x_b-x_e)}^2}{2kT}\right],\hfill \end{array}$$ (A.3)

where k_f0 and k_r0 are respectively initial forward and reverse equilibrium reaction rates, σ_ts is transition state spring constant, k is the Boltzmann constant, and T is absolute temperature. Values of parameters in equations (A.2) and (A.3) were taken from the literature. For platelets, N_L0 = N_R0 = 1.195 × 10¹² cm⁻² and for RBCs equaled 4.798 × 10⁹ cm⁻². For both platelets and RBCs, k_f0 = 10⁻⁷ cm² s⁻¹, k_r0 = 10⁻⁵ s⁻¹, x_e = 100 nm, x_b = 90 nm, σ = 2.2 dyn cm⁻¹, σ_ts = −5 dyn cm⁻¹, and T = 310 K. Number density of bonds in equation (A.2) was obtained using the solution given by Chesnutt and Marshall [20]. For simulations in the current work, the time scale for bond formation was much less than the time scale for elastic response of two colliding cells. Thus, number density of bonds was approximated by its equilibrium value N_b (∞), such that adhesive surface energy density simplified to a constant value, given by

$$u(t)=-\frac{\sigma }{4}{(x_b-x_e)}^2{N}_b(\infty ),$$ (A.4)

where calculations yielded u(t) = −4 × 10⁻¹ dyn cm⁻¹ for platelets and −1 × 10⁻⁴ dyn cm⁻¹ for RBCs. The adhesive surface energy density for platelets yielded an effective spring constant at the equilibrium contact region radius that was on the same order of magnitude as that determined by Filipovic et al [63] from computational simulations by comparison with experiments. The adhesive surface energy density for RBCs was previously shown to be in good agreement with in vitro aggregation experiments [20].

Because of the analogy with van der Waals adhesion, we used the theory of Johnson et al [59] for adhesive elastic particles to approximate elastic deformation forces acting between two colliding cells, given by

$$\begin{array}{ll}\frac{F_{ne}}{F_c}\hfill & =4{\left(\frac{a}{a_0}\right)}^3-4{\left(\frac{a}{a_0}\right)}^{3/2},\hfill \\ \frac{{\delta }_n}{{\delta }_{\mathrm{c}}}\hfill & =6^{1/3}\left[2{\left(\frac{a}{a_0}\right)}^2-\frac{4}{3}{\left(\frac{a}{a_0}\right)}^{1/2}\right],\hfill \end{array}$$ (A.5)

where a(t) is contact region radius, and δ_n is normal overlap distance of cell surfaces. Critical force F_c and critical overlap δ_c can be written in terms of contact region radius at equilibrium a₀ as

$$F_{\mathrm{c}}=3\pi uR,{\delta }_{\mathrm{c}}=\frac{a_0^2}{2(6^{1/3})R},a_0={\left(\frac{9\pi u{R}^2}{E}\right)}^{1/3},$$ (A.6)

where R and E are respectively effective radius and effective elastic modulus of the two cells.

Appendix B. Shear-history model of platelet activation

The shear-history model of shear-induced platelet activation was that of Soares et al [43], which accounted for both magnitude of and exposure time to shear stress. A brief description of the model is given as follows. The model measured the degree of platelet activation or platelet activation state (PAS) in the interval between 0 and 1, where PAS = 0 represented unactivated platelets and PAS = 1 represented fully activated platelets. Because PAS can only asymptote to unity, the current simulations assumed a platelet became activated if its PAS value reached 1–10⁻⁶ (or 0.999 999). Platelet activation state is given as

$$\frac{\text{dPAS}(t)}{\mathrm{d}t}=K_0[\text{PAS},{\tau }^{(t)}(s)](1-\text{PAS}),$$ (B.1)

where K₀ is the rate of stress-induced platelet activation given PAS = 0, and τ is shear stress. The rate of stress-induced platelet activation is given as

$$K_0[\text{PAS},{\tau }^{(t)}(s)]=S(\text{PAS},H_{\tau })+F(\text{PAS},\tau )+G(\text{PAS},\stackrel{.}{\tau }).$$ (B.2)

The first term in equation (B.2) accounts for platelet sensitization to activation given as

$$S(\text{PAS},H_{\tau })=S_r\text{PAS}·H_{\tau },$$ (B.3)

where S_r = 1.5701 × 10⁻⁷ is a constant determined by experiments, and H_τ is stress accumulation given as

$$H_{\tau }={\int }_0^t\tau (s)\mathrm{d}s.$$ (B.4)

The second and third terms in equation (B.2) are nonlinear rates of activation that depend on stress and stress rate, respectively, given as

$$\begin{array}{l}F(\text{PAS},\tau )=C^{\frac{1}{\beta }}\beta {\text{PAS}}^{\frac{\beta -1}{\beta }}{\tau }^{\frac{\alpha }{\beta }},\\ G(\text{PAS},\stackrel{.}{\tau })=C_r^{\frac{1}{\delta }}\delta {\text{PAS}}^{\frac{\delta -1}{\delta }}{\mid \stackrel{.}{\tau }\mid }^{\frac{\gamma }{\delta }},\end{array}$$ (B.5)

where τ̇ is the time derivative of shear stress, and C = 1.4854 × 10⁻⁷, α = 1.4854, β = 1.4401, C_r = 1.3889 × 10⁻⁴, γ = 0.572, and δ = 0.5125 are constants determined by experiments.