Prefrontal Cortex Networks Shift from External to Internal Modes during Learning

Abstract

As we learn about items in our environment, their neural representations become increasingly enriched with our acquired knowledge. But there is little understanding of how network dynamics and neural processing related to external information changes as it becomes laden with “internal” memories. We sampled spiking and local field potential activity simultaneously from multiple sites in the lateral prefrontal cortex (PFC) and the hippocampus (HPC)—regions critical for sensory associations—of monkeys performing an object paired-associate learning task. We found that in the PFC, evoked potentials to, and neural information about, external sensory stimulation decreased while induced beta-band (∼11–27 Hz) oscillatory power and synchrony associated with “top-down” or internal processing increased. By contrast, the HPC showed little evidence of learning-related changes in either spiking activity or network dynamics. The results suggest that during associative learning, PFC networks shift their resources from external to internal processing.

SIGNIFICANCE STATEMENT As we learn about items in our environment, their representations in our brain become increasingly enriched with our acquired “top-down” knowledge. We found that in the prefrontal cortex, but not the hippocampus, processing of external sensory inputs decreased while internal network dynamics related to top-down processing increased. The results suggest that during learning, prefrontal cortex networks shift their resources from external (sensory) to internal (memory) processing.

Introduction

As we learn about items in our environment, it is hard to see them the same way ever again. Neural processing induced by them becomes increasingly enriched with “internal” information, such as associated semantic knowledge and memories. Seeing a hammer, for example, might elicit recall of associated objects, such as nails, and memories of recent home-improvement projects. The learning of these associations depends on both the prefrontal cortex (PFC) and the hippocampus (HPC). Damage to either causes deficits in associative learning, especially if implicit memory (e.g., familiarity, priming) cannot be used (Scoville and Milner, 1957; Cohen and Squire, 1980; Gutnikov et al., 1997; Squire et al., 2004; Farovik et al., 2008). Both regions are activated when humans form explicit (declarative) memories (Sperling et al., 2001; Kim, 2011). Neural correlates of associative learning in the PFC and HPC have now been documented in monkeys and (especially) rodents. Of course, neurons in these areas also reflect incoming sensory information (Constantinidis et al., 2001; Takeda and Funahashi, 2002), which provides the building blocks of memories. But less well documented is what happens to sensory processing as new memories are formed. Are the memories simply grafted onto the same networks that processed the sensory inputs? Or is the processing of sensory inputs affected by acquiring memories about them?

We sought to answer these questions by examining data from a recent experiment on the interactions between the PFC and HPC during object–object associative learning, a nonhuman primate model of human explicit memory. We previously reported that only PFC spiking activity reflected learning while HPC neurons, as well as synchronous oscillations between both regions, reflected feedback about whether trial-and-error guesses were correct or incorrect. Here, we compare and contrast learning-related associative activity with that specifically related to sensory inputs. We also examine how learning affects sensory-evoked potentials, compared with internally generated network rhythms. These analyses independently point to the same conclusion: with learning, neural processing—particularly in the PFC—shifts from emphasizing feedforward sensory inputs to stressing internally generated associated signals.

Materials and Methods

Behavioral task

Two adult rhesus macaques (Macaca mulatta), one male and one female, were trained to perform an object paired-associate learning task requiring them to rapidly learn arbitrary associations between pairs of objects. Both monkeys were experimentally naive at the start of this study. For each daily recording session, six completely novel objects were chosen; four were randomly designated as cue objects and the remaining two as associate objects, and each cue was randomly paired with an associate (Fig. 1A). The resulting many-to-one (4:2) mapping from cues to associates distinguished neural activity related to the cues from the learned associates (see below, Data analysis), and encouraged prospective recall of the associate before its appearance (Rainer et al., 1999). The monkeys' task was to learn, through trial-and-error guessing, which associate was paired with each cue object.

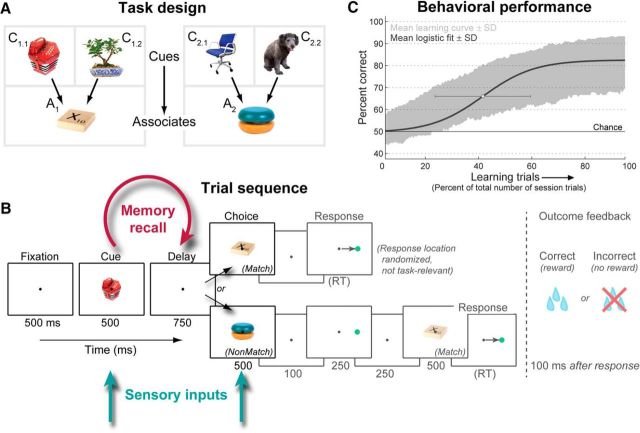
Figure 1.

Paired-associate learning task. A, Task design. Each session, six novel objects were randomly chosen. Four objects were designated as cue objects, and each was arbitrarily paired with one of two associate objects. The monkeys' task was to learn this associative pairing through trial and error. B, Task trial sequence. After central fixation, a cue object was presented, followed by a short memory-recall delay and then a choice object. If it was that cue's paired associate, the monkeys had to saccade to a target (whose varied location was not task-relevant); otherwise, they were required to withhold response until the correct associate was presented. Correct choices were rewarded with juice; incorrect choices resulted in no reward and a 3 s “time-out.” Task period durations given in milliseconds below panels (RT, reaction time). In previous work (Brincat and Miller, 2015), we focused on neural activity and interactions during the post-trial feedback period (grayed out); here we examine sensory and mnemonic-related activity during the trial proper (cue, delay, and choice periods). C, Learning performance. Shaded area, Mean ± SD of percent correct performance across all 348 associations (87 sessions), plotted as a function of the percentile of each session's trials (mean ± SD trials per session: 1117 ± 125). Blue curve, Average sigmoidal learning curve fit to each association. White dot, Mean ± SD of fit curve centers.

Each trial (Fig. 1B) started when the monkey acquired fixation of a white dot at the center of the stimulus screen. After a blank fixation baseline, one of the four cue objects was presented, followed by a blank delay interval in which the monkey was expected to recall its paired associate from memory. This was followed by a choice object, which could be either the correct paired associate for the given cue (50% of trials) or the other associate object for that session (which was not paired with the given cue; 50% of trials). The correct associate mandated a saccadic response to a subsequent target; otherwise, the monkeys had to withhold response through an additional delay until the correct associate was shown. The location (left vs right) of the response target following each associate was randomized and unrelated to task performance, so that a specific motor plan could not be formed until the target was shown, and procedural (stimulus–response) learning (Cohen and Squire, 1980) could not be used to correctly perform the task. Responses to the correct associate were rewarded with juice, while incorrect choices were punished by withholding reward and extending the subsequent 3 s intertrial interval by an additional 3 s.

Each session began with a block of 36 trials where the cue and associate objects for that day were passively presented to the monkey under fixation control (passive viewing task; three objects per trial at 500 ms each, 750 ms blank interstimulus interval), and a block of 96 identity match-to-sample task trials in which each object was matched to itself, rather than to an arbitrary associate (same timing as learning task). These trials familiarized the monkeys with the stimuli and eliminated any contribution of novelty-based or familiarity-based memory processes (Miller et al., 1991; Li et al., 1993; Anderson et al., 2008) to our results. For the analysis of these tasks in Figure 12, the first passively viewed object and the sample object were compared with the learning task cue, and the second passively viewed object and the match/nonmatch object were compared with the learning task choice object. Note that the relatively few trials for these tasks precluded reliable analysis of across-trial dynamics or between-condition information, and we thus focus on analyses that pool together all trials of each task.

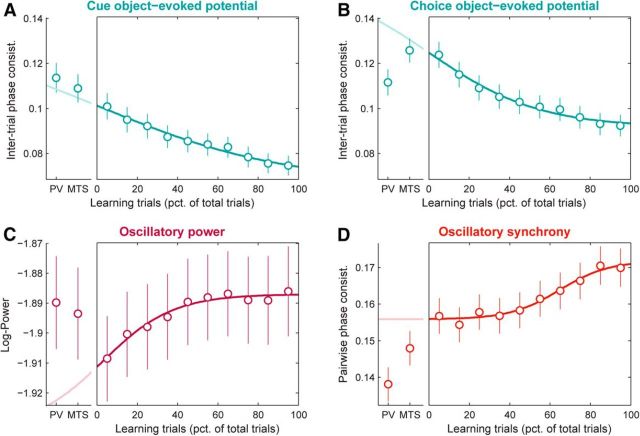
Figure 12.

PFC network learning effects cannot, in general, be explained by processes arising before learning. Each panel shows, on the right, PFC population mean (±SEM) LFP signals across learning (measured in nonoverlapping windows, each with a width of 10% of session trials). Overlaid are logistic functions fit to each neural signal during learning (darker lines). For comparison, on the left of each panel are the same LFP signals pooled across all trials for each of two prelearning control tasks with the same set of objects: passive stimulus viewing (PV) and identity match to sample (MTS). Overlaid is the extrapolation (lighter lines) of the fitted function to the prelearning tasks, based on their average timing relative to the learning task. If learning-related changes in neural signals simply reflect a continuation of changes arising during the control tasks, then the control task values should be well predicted by the extrapolated curves. A, Cue object-evoked potentials (ITPC; pooled over 2–64 Hz and 0–250 ms after cue onset). B, Choice object-evoked potentials (ITPC; 2–64 Hz and 0–250 ms after choice onset). C, Beta-band power (log-transformed; 11–27 Hz and 150–1350 ms after cue onset). D, Beta-band synchrony (PPC; 11–27 Hz and 150–1350 ms after cue onset). While control task values for cue-evoked potentials (A) do fall within the predictions based on the learning task, values for the other signals (B–D) fall well outside these predictions, arguing against the idea that the changes we observe during learning are likely, in general, to be due to familiarity or other passive processes that develop continuously through the entire session.

Eye position was monitored using an infrared pupil tracking system (EyeLink II, SR Research; RRID:SCR_009602), and was required to be maintained within a 1.5° window around the fixation dot through the entire trial; fixation breaks terminated the trial without reward. The National Institutes of Health Cortex real-time control system (RRID:SCR_006837) handled the task control and stimulus display on a CRT monitor with a 100 Hz refresh rate.

All procedures followed the guidelines of the Massachusetts Institute of Technology Committee on Animal Care and the National Institutes of Health.

Neurophysiological methods

For each daily experiment, ≤16 microelectrodes were inserted through the intact dura into the PFC, and ≤4 electrodes were inserted through transdural guide tubes into the HPC. All PFC, and most HPC, recordings were performed with epoxy-coated tungsten electrodes (FHC). Some HPC recordings used 24-channel linear probes with 300 μm spacing between adjacent platinum-iridium recording contacts (U-Probes, Plexon).

The ground-referenced neural signal from each electrode was amplified by a high-input-impedance headstage (HST/8o50-G1, Plexon), split, and filtered to extract spiking activity (250–8000 Hz) and local field potentials (LFPs; 0.7–300 Hz), and then digitized and stored using an integrated multichannel recording system (MAP, Plexon; RRID:SCR_003170). The spiking signal was threshold-triggered to separate neuronal spikes from background noise, and individual spike waveforms were manually sorted off-line into isolated neurons (Offline Sorter, Plexon; RRID:SCR_000012). To minimize any sampling bias of neural activity, we did not prescreen activity for responsiveness or task selectivity. Neurons were included in analyses only for the duration of time in which they were well isolated from background noise and other neurons. LFPs were recorded continuously at 1 kHz, and corrected off-line for filtering-induced phase shifts (FPAlign Utility, Plexon). Only LFPs from electrodes recording ≥1 neuron (isolated or multiunit) were used for all analyses, to ensure they were in the appropriate cell layer.

Electrodes were targeted using custom Matlab software that coregistered each monkey's implanted recording chambers and structural MRIs in stereotaxic coordinates. Recordings targeted the dorsolateral and ventrolateral PFC (parts of areas 46, 45, and 8), and all subregions (dentate gyrus/CA4, CA3, CA2, CA1, and subiculum) of approximately the anterior three-quarters of the HPC formation (Brincat and Miller, 2015, their Fig. 2). For the results reported here, no robust differences were observed across HPC subregions or its anterior–posterior extent; therefore all HPC recordings were pooled together. Across all sessions meeting our inclusion criteria (see below, Data analysis, General), we sampled a total of 319 PFC and 199 HPC neurons; 250 PFC and 166 HPC LFPs; and 649 PFC–PFC, 694 HPC–HPC, and 970 PFC–HPC LFP pairs.

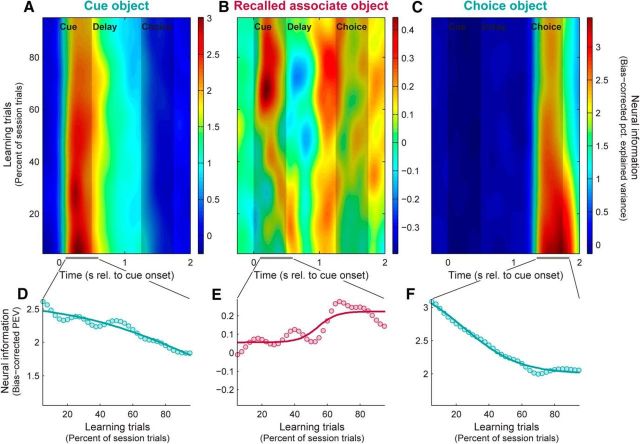
Figure 2.

PFC neurons shift from emphasizing sensory to mnemonic information with learning. A–C, Population mean neural information (bias-corrected PEV) in PFC spiking activity reflecting cue objects (A), paired-associate objects recalled from memory (B), and choice objects (C), plotted across time within trials and learning session trials. Shaded areas represent duration of cue and choice object presentations. D–F, Summary of learning-related changes in neural information about cue (D), associate (E), and choice objects (F). Dots, Neural information (PEV) pooled within factor-appropriate time epochs (A–C, bottom, gray bars). Curves, Bounded logistic function fits. With learning, PFC neurons carry decreasing sensory information about the presented cue and choice objects, and increasing information about the learned associate objects.

Data analysis

General.

Only trials where the monkey made a valid response to the correct or incorrect associate were analyzed, thus excluding trials where the monkey broke fixation or failed to respond. To restrict analysis to only those sessions with successful learning, we set a learning criterion of 32 correct responses over the final 50 trials of each association (p ≈ 0.01; binomial test). Only sessions where all four associations were learned to criterion were included in the reported analyses (61 of 87 sessions).

Changes in behavior and neural activity across learning were measured by performing analyses independently in sliding trial windows, each defined by a percentile of the total number of session trials to normalize for differences in session length. For analysis of behavioral and spiking data, window width was 10% of session trials, stepped in 2.5% increments; for most LFP analyses, window width and step were both 33%. All analyses were performed using custom code written in Matlab (MathWorks), with the exception of wavelet decomposition, which used code provided by C. Torrence and G. Compo (Torrence and Compo, 1998) and available at http://atoc.colorado.edu/research/wavelets/.

Behavioral analyses.

Behavioral learning curves (Fig. 1C, dark curve) were estimated by fitting binary (correct/incorrect) outcomes across trials with a bounded logistic curve as follows:

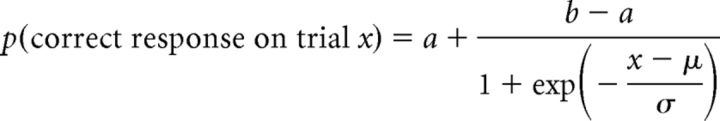where the probability p of a correct response on each trial is estimated as a sigmoidal learning curve with center μ, width σ (inversely related to learning rate), initial guess rate a (∼0.5 for our two-choice task), and post-learning asymptote b. These four parameters were fitted for each learned association using nonlinear least-squares estimation with reasonable parameter bounds based on the data.

Spike-rate analyses.

For analyses of spiking activity, spike trains were converted into smoothed rate (spike density) functions via convolution with a Hann function of half-width 175 ms (nearly identical to a 70 ms SD Gaussian, but with finite spread).

To measure the strength of spike-rate signals reflecting task factors of interest—the identity of the presented cue and choice objects and the recalled associate object on each trial—we performed a regression analysis on the spike densities. A linear model was fit to spike rates separately for each neuron, time point, and trial window and was used to compute the percentage of variance explained (PEV) by each factor, using the bias-corrected ω-squared formulation (Olejnik and Algina, 2003). A primary goal of this analysis was to identify population information specifically reflecting learning of the paired associates, while eliminating any potential contribution of sensory responses related to the presented cue objects. To do so, we took advantage of our experimental design in which two of the four cue objects were linked through learning to a single paired-associate object, and the other two cues were linked to the other paired associate. This 4:2 mapping enabled us to partition neural variance expected from sensory selectivity to the cues per se from that expected due to the learning-related linkages between the pairs of cues that map to the same paired associate. Based on this mapping, we derived a correction (described in detail below) that ensured that, at the single-neuron level, a neural response to only a single cue object would not contribute to the learning effect, and at the population level, a random equal mix of neurons responding to task-relevant and nontask-relevant cue pairs would cancel out, resulting in no net population learning effect. In a standard uncorrected regression model, both of these situations could contribute.

We fit a model with the following form: Rate = β_AssocX_Assoc + β_Control1X_Control1 + β_Control2X_Control2 + β_ChoiceX_Choice + β₀ + ε.

The first regressor X_Assoc reflected the actual learned task-relevant grouping of cue objects that were paired with the same associate object. It contrasted trials on which either of the cue objects that was mapped to the first paired associate appeared (Fig. 1A, C_1.1, C_1.2) to those in which either cue mapped to the other paired associate appeared (C_2.1 or C_2.2). The following two regressors X_Control1 and X_Control2 were controls used for our correction procedure, and reflected both possible nontask-relevant groupings of the cue objects (i.e., pairs of cue objects not mapped to the same associate): {C_1.1, C_2.1} vs {C_1.2, C_2.2}, and {C_1.1, C_2.2} vs {C_1.2, C_2.1}. We quantified neural information reflecting the associate objects (i.e., the learning effect; Figs. 2B,E, 4B,E) as the PEV for the associate regressor, corrected by subtracting the average PEV for the two control regressors. At the single-neuron level, any spurious contribution to the learning effect due to activation by only a single cue object is eliminated as the expected PEV for all three regressors is equal, thus resulting in a corrected PEV ≈ 0. At the population level, any spurious contribution due to a random mix of neurons responding to task-relevant and nontask-relevant pairs of cue objects would be avoided because a response to any pair of cues will result in expected PEV > 0 for exactly one regressor (i.e., the one that groups together the pair of cues eliciting responses). For task-relevant cue pairings (i.e., those linked though learning to the same paired-associate object), this PEV value will be unchanged by our correction procedure (remaining, say, at PEV = x). For nontask-relevant cue pairings, the corrected PEV will have an expected value of the following: $0-\frac{0+x}{2}=-\frac{x}{2}$. Thus, a population with an equal mix of similar-strength responses to each of the six possible pairs of cues will result in an average corrected PEV of $\frac{1}{6}\left(x+x-\frac{x}{2}-\frac{x}{2}-\frac{x}{2}-\frac{x}{2}\right)=0$, whereas a population average corrected PEV > 0 indicates a population bias toward neurons responding to the task-relevant cue pairing. To confirm these theoretical results, we performed extensive simulations exploring different patterns, strengths, and underlying distributions of neural responses across the set of four cue objects. These confirmed that the expected value for the corrected associate PEV was >0 for simulated neurons activated by recall of a specific associate object, but ≤0 for all simulated populations with any nontask-relevant selectivity for ≥1 cue objects.

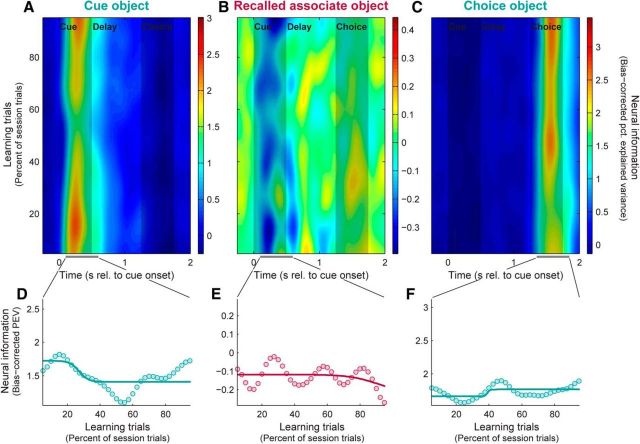
Figure 4.

HPC neurons exhibit constant sensory information across learning. A–C, Population mean neural information in HPC spiking activity reflecting cue objects (A), recalled paired-associate objects (B), and choice objects (C). Each plot has the same color scale as the corresponding plot for the PFC in Figure 2. D–F, Summary of neural information (dots), with logistic fits (curves), reflecting cue (D), associate (E), and choice objects (F). Each plot has the same y-axis range as the corresponding plot for the PFC in Figure 2. HPC neurons show little evidence of acquiring information about learned associations, and relatively constant sensory information across learning, despite having a similar strength of sensory information to the PFC.

If the set of four cue objects is considered as a four-dimensional vector space, these three regressors, along with the intercept term β₀, form a basis for the space. This means that any possible set of neural responses to the cue objects can be expressed as a linear combination of these regressors, and hence they capture all variance reflecting cue selectivity. Therefore, we quantified sensory neural information reflecting the cue objects (Figs. 2A,D, 4A,D) as the sum of the PEV for all three of these regressors. Finally, the model also included a fourth regressor reflecting which of the associate objects was actually presented during the choice period. Sensory neural information reflecting the choice objects (Figs. 2C,F, 4C,F) was simply quantified as the PEV for this term.

For display purposes only, all spike information plots were smoothed with a 2D Gaussian with SDs equal to 5% of session length and 50 ms, and interpolated to a finer sampling grid.

LFP analyses.

Before power and synchrony analyses, evoked potentials were removed from each LFP by subtracting its across-trial mean from each individual trial (Kalcher and Pfurtscheller, 1995); this isolated the contribution of spontaneous and “induced” LFP components not phase-locked to trial events. This preprocessing step was not performed for analyses of evoked potentials themselves.

LFPs were transformed into the time–frequency domain by a continuous wavelet transform with complex Morlet wavelets (wavenumber, 6; evaluated at 0.25 octave intervals from 1 to 128 Hz). Wavelet power was computed separately for each electrode, trial window, frequency, and time point. The resulting values were log-transformed to render them approximately normally distributed. To enhance visualization of band-specific signals relative to the well known 1/frequency distribution of LFP power, log power at each frequency was normalized for display purposes only: logPowerNorm (x) = logPower (x) + log (f).

The strength of neural synchrony was quantified by the pairwise phase consistency (PPC), a measure of the degree to which LFP pairs maintain the same phase relationship across repeated trials, independent of their individual absolute phases and amplitudes (Vinck et al., 2010). PPC is related to the traditional phase-locking value (PLV) measure of phase synchrony (Lachaux et al., 1999), squared and corrected to remove bias due to the number of trials [note that this characterization and the associated formula given below have been shown (Aydore et al., 2013) to be equivalent to the original definition put forth by Vinck and colleagues]. Like PLV, PPC is based on the length of the across-trial vector average of the relative phase between an electrode pair, expressed as follows:

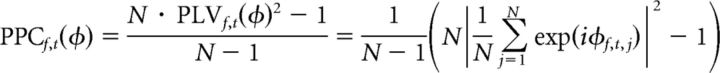where j indexes trials 1 to N, and φ_f,t,j = angle(x_f,t,j) − angle(y_f,t,j) is the relative wavelet phase between a pair of electrodes x and y on trial j, for frequency f and time point t. Phase synchrony corresponds to clustering of these relative phases around a specific value, and thus to a larger magnitude mean vector and PPC, with a maximal PPC of 1 indicating perfect consistency across trials. Lack of phase synchrony corresponds to a random (uniform) distribution of relative phases across trials, and thus to a smaller magnitude mean vector and PPC ≈ 0. This statistic was computed separately for each electrode pair, trial window, frequency, and time point. Similar results were obtained using the phase-locking value or coherence instead of PPC.

To analyze evoked potentials in the time–frequency domain, previous authors (Tallon-Baudry et al., 1996; Delorme and Makeig, 2004; Lakatos et al., 2009) have employed an analog of the PLV statistic—variously termed “intertrial coherence” or “phase-locking factor”—which computes the across-trial vector mean of the phase of an individual LFP, rather than the relative phase of a pair of LFPs. Large values of this statistic, which has a maximum value of 1, indicate consistent clustering of the LFP phase around a specific value at a given time point relative to trial events, as observed during evoked potentials. Smaller values indicate a random distribution of LFP phases, as is typically observed in periods between external sensory events. Like the phase-locking value for LFP pairs, this statistic is independent of LFP amplitude and absolute phase, facilitating pooling of results across sites with often quite different evoked potential shapes. However, also like the phase-locking value, this statistic is biased by the number of trials included in the analysis. We therefore propose a novel intertrial phase consistency statistic (ITPC) that is simply a bias-corrected version of (the square of) the traditional intertrial coherence statistic, a relationship exactly analogous to that between LFP-pair statistics PPC and PLV. As such, ITPC has the same formula as that shown above for PPC, but with φ_f,t,j = angle(x_f,t,j) representing instead the phase of a single LFP x on trial j, for frequency f and time point t. This statistic was computed separately for each electrode, trial window, frequency, and time point. Similar results were obtained using intertrial coherence or the power of wavelet-transformed evoked potentials.

Two complementary methods were used to measure learning-related changes in LFP signals (evoked potentials, power, and synchrony). Both analyses were performed separately at each time–frequency point. A d′ statistic quantified the overall signal change across learning as the difference between the means of the distributions of signal values across the population of LFPs or LFP pairs during the late (final 33% of session trials) and early (first 33% of trials) learning stages, normalized by their pooled SD. To more directly measure the relationship between LFP signals and behavioral learning, we also computed the Spearman rank correlation between trial-windowed neural signals and behavioral task performance (percent correct), across all trial windows and LFPs or LFP pairs. For this analysis, a trial window width equal to 10% of session trials, stepped in 10% increments, was used for both the neural and behavioral data. We focus our interpretation on clusters of time–frequency points showing conjunctive significance for both analyses, that is, neural signals that both significantly change during learning and are significantly correlated with behavior. Results on learning-related signal changes were confirmed using summary statistics on signals pooled within time–frequency regions of interest (ROIs) based on the patterns observed in the overall across-trial mean signals (see Fig. 6A–C, gray bars). For the evoked potentials, which show broadband increases during the stimulus presentations, we used a cue epoch ROI (2–64 Hz, 0–250 ms after cue object onset) and a choice epoch ROI (2–64 Hz, 0–250 ms after choice object onset). For power and synchrony, we used an ROI that encompassed their beta-band peak (11–27 Hz) and extended through the full trial time period, conservatively spanning the full temporal extent of either signal (−400–1750 ms after cue onset).

Figure 6.

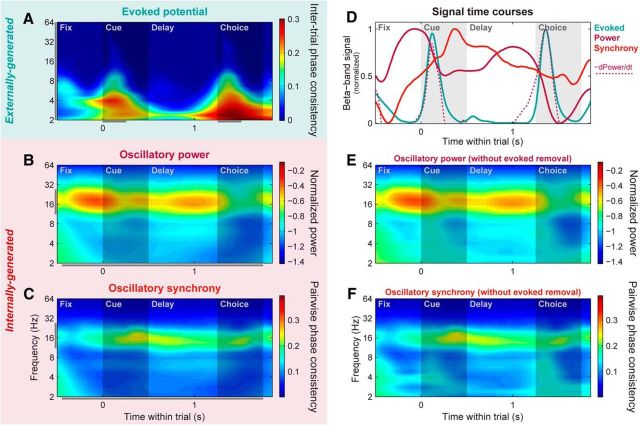
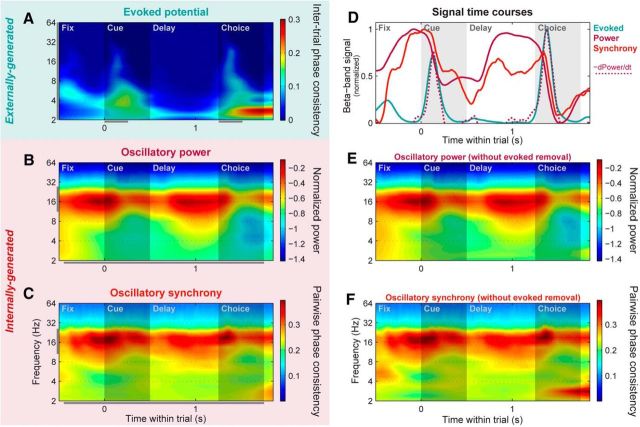
PFC networks switch from a locally to globally synchronized state at cue onset. A, Population mean evoked potential strength across all individual PFC LFP sites, pooled across all trials. Evoked potential strength was quantified by the ITPC of wavelet-transformed raw LFP signals. This method highlights time–frequency locations where potentials had a consistent phase relative to trial events across trials, independent of their sign and amplitude. B, Population mean power across all individual PFC LFP sites, pooled across all learning session trials. Evoked potentials phase-locked to trial events were removed from each LFP before spectral decomposition and power calculation, and the resulting power values were log-transformed to normalize them. To enhance visualization of band-specific signals relative to the well known 1/frequency distribution of LFP power, power at each frequency was normalized by 1/frequency for display purposes only. C, Population mean synchrony across all pairs of PFC LFP sites, pooled across all trials. Synchrony strength was quantified using PPC, which highlights time–frequency locations where an LFP pair had a consistent relative phase across trials, independent of their amplitude. Evoked potentials locked to trial events were removed from each LFP before PPC calculation. D, Within-trial time courses of evoked potential (blue line), power (solid magenta line), and cross-electrode synchrony (orange) signals, pooled within the beta band (11–27 Hz; A–C, gray bars; note that for this plot the same range is used for evoked potentials, despite their more broadband nature, to match the wavelet time resolution of the other signals). Beta power is strongest before the onsets of the cue and choice objects. The rapid power decrease at object onset—quantified here by the negative of the time-derivative of the power time course (dotted magenta line)—is closely paralleled by the transient evoked potential signals. Synchrony is strongest following the cue-evoked potential, when the monkey is required to map the cue onto its paired associate. E, F, PFC mean power (E) and synchrony (F) computed without removal of trial-locked evoked potential signals, plotted in same color scale as B and C for comparison. Removing the evoked potentials had only minor effects at lower frequencies, and had virtually no effect on the beta-band signals of interest here.

All time–frequency plots were linearly interpolated to a finer sampling grid for display purposes only.

Statistics.

Significance testing was conducted using random resampling methods that make no assumptions about the underlying data distribution. To generate significance values for paired-sample tests and confidence intervals, we used a bootstrap (Efron and Tibshirani, 1994). To generate significance values for two-sample tests and correlations, we used permutation tests (Manly, 2007). At least 10,000 iterations were performed for each test. Where appropriate, Bonferroni corrections for multiple comparisons were performed.

Additional methodological details can be found in our previous report on this dataset (Brincat and Miller, 2015).

Results

PFC spiking activity shifts from sensory to memory information with learning

We have previously shown that, as monkeys learn new object–object or object–saccade associations, associative cues elicit progressively more information about their anticipated pair in the PFC (Asaad et al., 1998; Pasupathy and Miller, 2005; Brincat and Miller, 2015) but not the HPC (Brincat and Miller, 2015). This learning-related increase in recalled information in the PFC about anticipated object paired associates was reported by Brincat and Miller (2015) and is also shown in Figure 2B. Note that as the monkeys gradually learned which associate object was paired with each cue object, PFC neurons conveyed increasing information about the anticipated paired associate (Fig. 2B,E; across-trial Spearman rank correlation between associate information and behavioral learning curve: r = 0.59, p = 0.004; two-sided permutation test).

Here we report that this increase in memory information is accompanied by a decrease in sensory information. Figure 2A plots the sensory information about the cue object presented at the start of the trial. Information about the cue is primarily limited to the time it was visible, consistent with it being sensory-driven. Figure 2D plots the average of this information as a function of learning. It shows that in contrast to mnemonic information, sensory information decreased with learning (r = −0.85, p = 0.004). Figure 2C plots another type of sensory information. This type of sensory information is about the choice object seen at the end of the trial. Note that this is distinct from information about the paired associate because on half of the trials the choice object was not the associate object anticipated by the monkey (i.e., it was a nonmatch). Thus, the information plotted in Figure 2C reflects sensory information about the choice object that was actually seen and, like the cue information, it is primarily restricted to the time the object was visible. Figure 2F plots the average sensory information about the choice object as a function of learning. Like the cue object, sensory information about the choice object decreases with learning (r = −0.96, p = 10⁻⁵). It should be noted that sensory neural information about the cue and choice objects is overall considerably stronger than mnemonic information about the recalled associate. This should perhaps not be surprising when viewed as a comparison between actual physical stimuli with sharp temporal dynamics, and newly acquired, internally generated cognitive constructs with some degree of uncertainty and likely variable temporal dynamics.

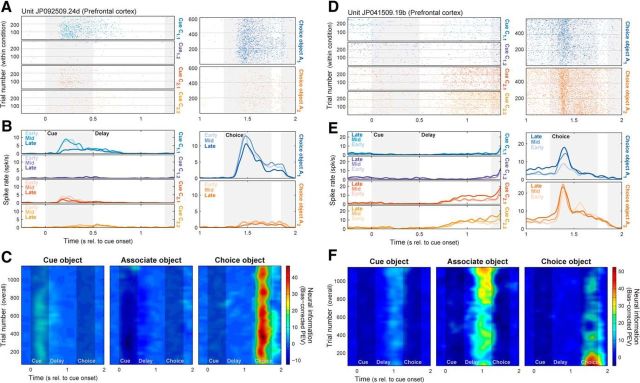
Though we focus here on characterizing the PFC neural population, these effects could also be observed within single neurons. Figure 3A–C shows spike rasters (Fig. 3A) and densities (Fig. 3B) for each task condition, and the corresponding neural information (Fig. 3C), for a PFC neuron that conveyed information about the cue object during the cue period and about the choice object during the choice period. With learning, responses to the preferred cue and choice objects diminished (Fig. 3A,B, blue rasters and densities), resulting in decreases in cue and choice object information (Fig. 3C). Figure 3D–F shows another PFC neuron carrying associate information during the delay period and choice object information during the choice period. With learning, responses increased for the preferred associate object (Fig. 3D,E, red and yellow rasters/densities) but also for the nonpreferred choice object, resulting in increasing associate information but decreasing choice information (Fig. 3F). Thus, at both the single-neuron and population levels, PFC neurons de-emphasized exogenous sensory inputs as internally generated mnemonic signals increased. These example neurons also highlight the highly heterogeneous, context-dependent nature of PFC neural responses (Jun et al., 2010; Rigotti et al., 2013). Little to no correlation was observed between selectivity for different task factors, and while some associate-selective neurons—like the one in Figure 3D–F—also responded when the preferred associate was actually presented as a choice object, nearly equal numbers carried no information about the choice object (p = 0.16, binomial test) or preferred the other choice object (p = 0.33).

Figure 3.

Basic spiking results could be observed in individual PFC neurons. A–C, PFC neuron with decreasing neural information about cue and choice objects with learning. A, Spike rasters across all trials for each of four cue (left) and two choice (right) objects. Horizontal gray lines indicate divisions between early, middle, and late learning stages. B, Spike densities for same cue (left) and choice (right) objects. Light-to-dark colors correspond to successive learning stages (early, middle, and late). With learning, responses to the preferred cue (blue) and choice (blue) objects diminish. C, Information conveyed (PEV) in this neuron's spiking rate about cue (left), associate (middle), and choice (right) objects. Cue and choice object information both decrease with learning. D–F, PFC neuron with learning-related decrease in choice object and increase in associate object information. D, Spike rasters. E, Spike densities. With learning, responses increase in the delay period when the preferred associate object is cued (red, yellow), and in the choice period when the nonpreferred choice object is shown (blue). F, Neural information (PEV). With learning, delay-period associate information increases, while choice-period choice object information decreases.

HPC neurons show little or no change with learning

We performed the same analysis on spiking activity recorded from the HPC. The average sensory information about the cue and choice objects and mnemonic information about the anticipated paired associate is plotted in Figure 4. As reported by Brincat and Miller (2015), HPC neurons did not reflect the anticipated paired associate object and this did not change with learning (Fig. 4B,E; r = −0.21, p = 0.56).

HPC neurons did convey sensory information about the cue object (Fig. 4A) and choice object (Fig. 4C), albeit at a weaker level than that seen in the PFC. But in contrast to the PFC, sensory information in the HPC was stable across learning. This can be seen in both sensory information about the cue object (Fig. 4A,D; r = 0.05, p = 0.89) and sensory information about the choice object (Fig. 4C,F; r = 0.30, p = 0.41).

In addition to conveying information about the object stimuli, HPC neurons were also activated by them. This can be seen both in the raw spiking rates across all HPC neurons (Fig. 5B) and in the normalized rates (z-scored relative to the across-trial rate mean and SD during the intertrial interval) for neurons whose responses increased (Fig. 5D) and decreased (Fig. 5F) relative to baseline. In all cases, HPC neurons showed clear spiking responses to the cue and choice objects, of comparable magnitude to PFC responses (Fig. 5A,C,E). Thus, the lack of learning-related changes in the HPC are not due to a lack of HPC activation or selectivity for our object stimuli, but specifically to a lack of reliable modulation of this selective activity with learning.

Figure 5.

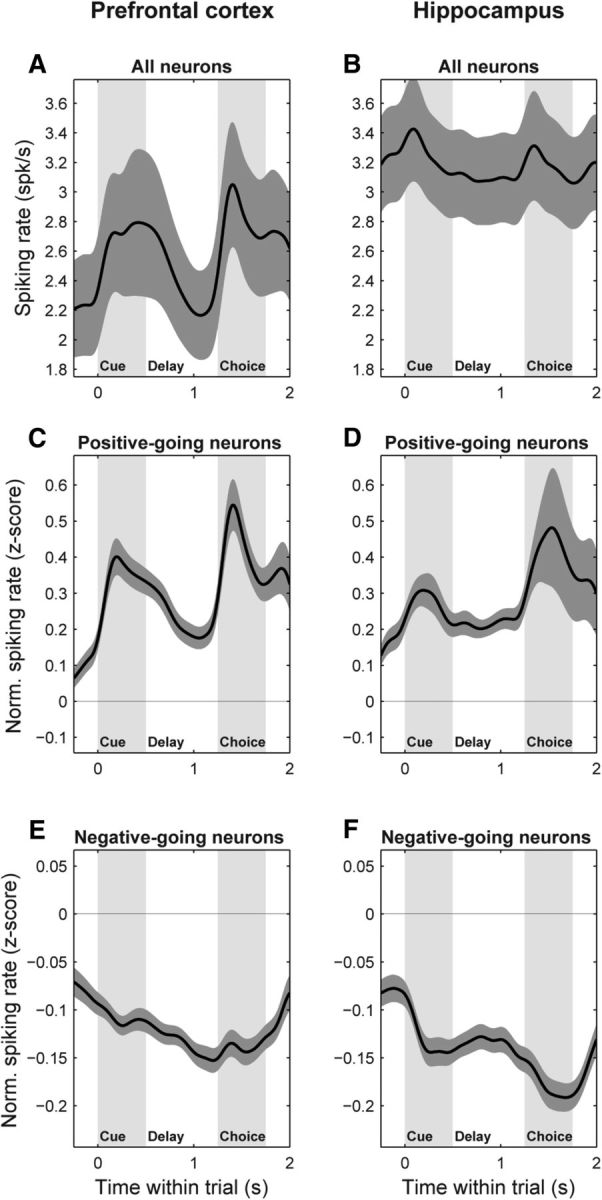
PFC and HPC neurons are both responsive to object stimuli. A, B, Population mean raw spiking rate (±SEM), pooled across all trials, for all sampled neurons in the PFC (A) and HPC (B). C–F, Population mean normalized spiking rate (±SEM), expressed as z-scores relative to the mean and SD of the intertrial interval (−1000 to −500 ms) baseline rate. C, D, PFC (C) and HPC (D) neurons whose average rate during the full trial period (0–1750 ms) was greater than baseline. E, F, PFC (E) and HPC (F) neurons whose average rate during the full trial period was less than baseline. Both areas show clear spiking responses to the cue and choice objects of comparable magnitude.

PFC networks exhibit distinct externally and internally generated signals

We next examined network-level activity in the PFC during associative learning. We extracted three different signals—with distinct putative sources—from PFC LFPs. Evoked potentials were analyzed in the time–frequency domain using an ITPC statistic (cf. Tallon-Baudry et al., 1996; Vinck et al., 2010; see Materials and Methods), which isolated LFP components that exhibit a consistent phase locking to the timing of trial events across trials. This revealed broadband potentials occurring at short latency after the onset of both the cue and choice objects (Fig. 6A), similar to those found in other cortical regions (Lakatos et al., 2009). Thus, they likely reflect feedforward inputs from lower-level visual areas and can ultimately be traced back to the sensory periphery. Because of their likely ultimate origin external to the cortex, we will refer to these evoked potentials as “externally generated.” Oscillatory power on each electrode was measured by first subtracting out its mean evoked potential (raw LFP averaged across trials) from each individual trial (Kalcher and Pfurtscheller, 1995), before computing the LFP power. These signals therefore include only LFP components not phase-locked to external trial events. They showed a prominent peak in beta-band frequencies (∼11–27 Hz), as well as a smaller peak in the theta band (∼3–7 Hz), and—in contrast to the evoked potentials—they were sustained across long periods with no visual stimulus (Fig. 6B). This all suggests they are the result of internal network dynamics, and we therefore refer to them as “internally generated.” Finally, we measured oscillatory synchrony between electrode pairs using PPC of the relative phase between pairs of LFPs (Vinck et al., 2010). This was also computed with evoked potentials removed from each electrode before analysis to isolate nonevent-locked components. PFC synchrony also showed a prominent beta-band peak, as well as a smaller peak at theta-band frequencies (Fig. 6C). Again, both were sustained across long periods with no visual stimulus, suggesting this signal also reflects internal network dynamics.

These three signals (externally generated evoked potentials, internally generated oscillatory power and synchrony) had distinct, but interrelated, within-trial time courses (Fig. 6D). Beta-band power (Fig. 6D, solid magenta line) peaked at the start of the trial just before presentation of the cue object, and again during the memory delay just before choice object presentation. For both the cue and choice objects, visual stimulus onset led to low-latency evoked potentials, as well as rapid decreases in beta power (Fig. 6D, blue line), commonly observed—but poorly understood—effects of bottom-up stimulation in the visual cortex. In fact, the timing of evoked potential peaks closely matched the time course of power decreases (Fig. 6D, dotted magenta line; Spearman rank correlation of time courses: r = 0.51, p ≤ 10⁻⁴), suggesting that the externally generated potentials may play a role in shutting off internally generated oscillations. Note that these stimulus-induced dips in beta power were not an artifact of removing the evoked potentials before spectral analysis, as they persisted virtually unchanged when analysis was performed on the raw LFP signals (Fig. 6E; similar results for beta-band synchrony are shown in Fig. 6F). Although beta-band synchrony (Fig. 6D, orange line) was present throughout most of the trial, it was strongest immediately following the cue object-evoked potential (and associated power decrease), with a time course uncorrelated with that of oscillatory power (r = 0.03, p = 0.63). These results suggest that cue-evoked potentials may switch PFC networks from a locally synchronized (strong beta power) state to a more globally synchronized state (strong beta across-site synchrony) right around the time when the cue must be mapped onto its learned associate.

PFC networks shift from feedforward inputs to internal dynamics with learning

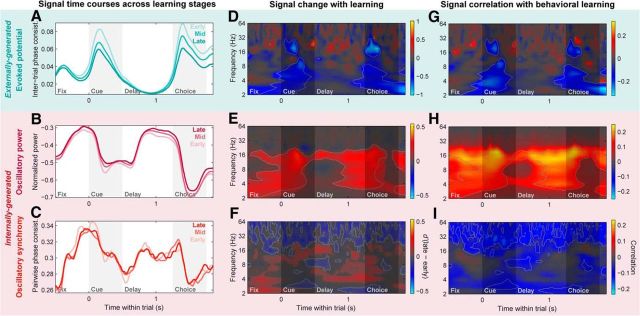
To quantify changes in network dynamics with learning, we calculated two complementary measures. A d′ statistic quantified the overall signal change across learning as the difference between the means of the population distribution of LFPs or LFP pairs during the late (final 33% of session trials) and early (first 33% of trials) learning stages, normalized by their pooled SD (Fig. 7D–F; red colors reflect an increase during learning; blue colors reflect a decrease). To more directly measure the relationship between network dynamics and behavioral learning, we also computed the Spearman rank correlation between trial-windowed neural signals and behavioral task performance (percent correct) across all trial windows and LFPs or LFP pairs (Fig. 7G–I; red colors reflect positive correlation with performance; blue colors reflect negative correlation). We focus our interpretation on time–frequency points showing conjunctive significance for both analyses (Fig. 7, gray outline), that is, neural signals that both significantly change during learning and are significantly correlated with behavior.

Figure 7.

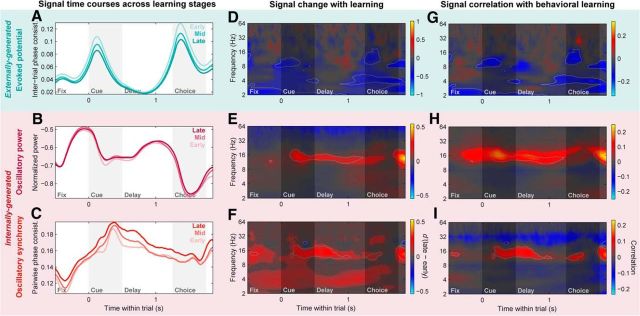
PFC networks shift from feedforward to internally generated signals with learning. A–C, Population means of PFC LFP signal time courses during the early, middle, and late learning stages (first, second, last 33% of session trials; light to dark colors). A, Evoked potentials (intertrial phase consistency) pooled across 2–64 Hz. B, Log-transformed LFP power pooled across the beta band (11–27 Hz). C, Beta-band LFP–LFP synchrony (PPC) between distinct PFC sites. D–F, Change in PFC evoked potentials (D), LFP power (E), and LFP–LFP synchrony (F) with learning, quantified with a d′ statistic between population distributions of their values in the late and early learning stages, computed at each frequency and within-trial time point. Warm colors indicate increases with learning, cool colors indicate decreases, and time–frequency points failing to meet a significance criterion (p < 0.05, Bonferroni corrected, two-sided permutation paired t test) are displayed with a desaturated gray mask. Light gray outlines delineate points meeting significance criteria for both this analysis and the correlation analysis in G–I. G–I, Correlation of PFC evoked potentials (G), LFP power (H), and LFP–LFP synchrony (I) with behavioral performance, measured as the Spearman-rank correlation between LFP signals (at each frequency and within-trial time) and task percent correct, each measured within nonoverlapping trial windows with a width of 10% of session trials. Warm colors indicate positive correlation with behavior, cool colors indicate negative correlation, color saturation indicates significant time–frequency points for this analysis (p < 0.05, Bonferroni corrected, two-sided permutation test), and light gray outlines delineate points showing conjunctive significance for both the correlation and d′ analyses. PFC evoked potentials (A, D, G) exhibit broadband decreases with learning primarily during the cue and choice periods. LFP power (B, E, H) and LFP–LFP synchrony (C, F, I) both show reliable increases with learning in the low-beta band (∼11–20 Hz), primarily during the cue and recall delay periods.

PFC evoked potentials significantly decreased with learning (Fig. 7A), especially around the time of stimulus presentations, when they were strongest. In the time–frequency domain, these decreases were somewhat broadband in nature (Fig. 7D), like the evoked potentials themselves, though with peaks in the low-beta/alpha band (∼8–16 Hz) particularly for the behavioral correlation analysis (Fig. 7G). These results were confirmed with summary statistics evaluated within time–frequency ROIs set based on the pattern of the raw, trial-pooled evoked potentials (Fig. 6A, gray bars), for both the d′ statistic [cue epoch d′: −0.15; 95% CI (−0.18, −0.13); p ≤ 10⁻⁴; choice epoch d′: −0.17; 95% CI (−0.20, −0.14); p ≤ 10⁻⁴, bootstrap test] and the behavioral correlation statistic (cue epoch r: −0.09, p ≤ 10⁻⁴; choice epoch r: −0.09, p ≤ 10⁻⁴, permutation test).

By contrast, both internally generated beta-band signals—oscillatory power (Fig. 7B,E,H) and synchrony (Fig. 7C,F,I)—significantly increased with learning and were significantly correlated with behavior. For both signals, the effects were strongest in the low-beta band (∼11–20 Hz). These results were again confirmed with ROI-based (Fig. 6B,C, gray bars) summary statistics (power d′: 0.07; 95% CI (0.02, 0.12); p = 0.005; synchrony d′: 0.08; 95% CI (0.06, 0.11); p ≤ 10⁻⁴, bootstrap test; power r: 0.12, p ≤ 10⁻⁴). Although the correlation analysis failed to reach significance when pooled within the full beta ROI (11–27 Hz; r: 0.02, p = 0.14), this was clearly due to opposing positive correlations in the lower frequencies of the beta ROI (11–20 Hz; r: 0.04, p = 9 × 10⁻⁴) and negative correlations in the high-beta/low-gamma band (∼25–40 Hz) that were captured in the higher end of our standard beta-band ROI (20–27 Hz; r: −0.07; p ≤ 10⁻⁴; Fig. 7I). Although this gamma-band synchrony decrease—as well as the broadband gamma (>∼40 Hz) decrease observed for the PFC power d′ statistic (Fig. 7E)—might seem contrary to our overall interpretation, many lines of evidence suggest gamma oscillations may mediate feedforward cortical processing (see Discussion); thus their trend toward decreasing with learning is consistent with a downregulation of feedforward signals. Additionally, intra-PFC synchrony showed significant learning-related increase in the theta band (∼3–7 Hz) only for the d′ statistic. Taken together, these results suggest that, with learning, PFC networks shifted from externally generated sensory signals to internally generated dynamics, paralleling the shift in spiking activity from sensory to memory information.

Noteworthy was the time course of the learning-related changes in internal dynamics. While internally generated beta-band power and synchrony within the PFC showed distinct within-trial temporal profiles on average (Fig. 6D), their learning-related increases exhibited similar time courses (correlation of d′ time courses: r = 0.22, p = 7 × 10⁻⁴). Both were strongest and most reliable during the late cue and memory delay periods (Fig. 7E,F,H,I), similar to the overall average temporal profile of synchrony (Fig. 6D, orange; correlation of power d′ and mean synchrony time courses: r = 0.39, p ≤ 10⁻⁴; synchrony d′ and mean synchrony: r = 0.37, p ≤ 10⁻⁴), but distinct from the average temporal profile of power (Fig. 6D, magenta; correlation of power d′ and mean power time courses: r = −0.57; p ≤ 10⁻⁴; synchrony d′ and mean power: r = −0.26; p ≤ 10⁻⁴). In other words, while overall beta-band oscillatory power and synchrony waxed and waned very differently over the course of a trial, they both showed increases that correlated with learning behavior primarily during the period when the cue object must be used to retrieve its paired associate, and when overall prefrontal network synchrony was strongest.

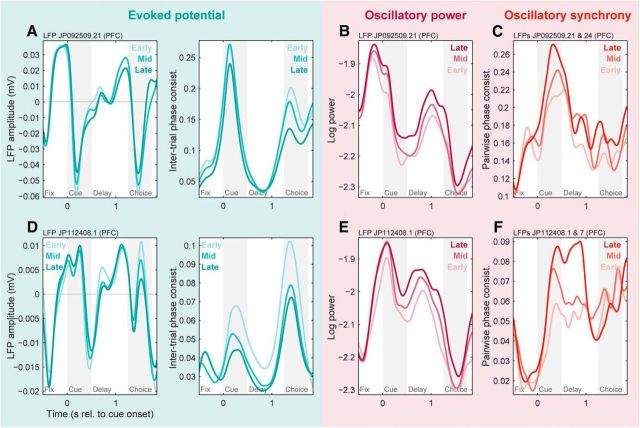
Learning-related changes in PFC evoked potentials, beta-band power, and beta-band synchrony could readily be observed in individual LFPs (Fig. 8A,B,D,E) and LFP pairs (Fig. 8C,F).

Figure 8.

Basic network-level results were observed in individual PFC LFPs and LFP pairs. A, Evoked potentials from an example prefrontal LFP site during early, middle, and late learning stages (light to dark colors). Left, Raw evoked potentials (across-trial mean LFP). Right, Intertrial phase consistency metric of evoked potential strength, pooled from 2 to 64 Hz. Both plots show decreasing evoked potentials with learning, primarily during the cue and choice periods. B, Log-transformed beta-band (11–27 Hz) power from the same LFP site during early, middle, and late learning stages. Beta power increases with learning, particularly during the cue and delay periods. C, Beta-band (11–27 Hz) synchrony (PPC) between this site and a distinct PFC LFP site ∼3 mm away. Beta synchrony increases with learning, particularly during the cue period. D–F, Similar results for evoked potentials (D), power (E), and synchrony with a site ∼7 mm away (F) from another example LFP. Note the consistent decrease in evoked potential strength despite its different shape (compare A, D).

HPC networks exhibit weaker and more broadband changes with learning

HPC LFPs showed similar externally generated evoked potentials to the PFC (compare Figs. 6A, 9A). Again, these were broadband in frequency and strongest at short latency after stimulus presentation. Internally generated beta-band power was overall significantly stronger in the HPC than in the PFC (Figs. 6B, 9B; log power pooled within full-trial ROI: −1.71 for HPC, −1.91 for PFC; p ≤ 10⁻⁴, two-sided permutation test), but with a similar time course—peaks just before cue and choice object onset and decreases that strongly correlated with the evoked potential time course (r = 0.41, p ≤ 10⁻⁴). Internally generated beta-band synchrony was also significantly stronger overall in the HPC than in the PFC (Figs. 6C, 9C; PPC pooled within full-trial ROI: 0.29 for HPC, 0.15 for PFC; p ≤ 10⁻⁴), but exhibited distinct temporal dynamics. In contrast to the PFC, where the temporal profiles of oscillatory power and synchrony were uncorrelated (Fig. 6D), in the HPC these two signals showed highly correlated profiles (Fig. 9D; r = 0.71, p ≤ 10⁻⁴), both peaking in the fixation period just before the cue presentation and in the delay period just before the choice object presentation, and decreasing at the onset of both stimuli.

Figure 9.

HPC networks exhibit similar dynamics for local and global oscillations. Plotting conventions and color scale ranges are the same as for corresponding plots in Figure 6. A, Population mean evoked potentials (intertrial phase consistency) across all individual HPC LFP sites, computed across all trials. B, Population mean log-transformed power across all individual HPC LFP sites, pooled across all learning session trials. C, Population mean synchrony (PPC) across all pairs of HPC LFP sites, pooled across all trials. D, Within-trial time courses of evoked potential (blue line), power (solid magenta line), and cross-electrode synchrony (orange) signals, pooled within the beta band (11–27 Hz). Like the PFC, HPC LFP power peaked before the onsets of the cue and choice objects, and rapidly decreased (dotted magenta line) nearly simultaneously with the transient stimulus-evoked potentials. In contrast to the PFC, oscillatory synchrony across HPC sites exhibited a time course similar to power, also peaking before the stimulus onsets. E, F, HPC mean power (E) and synchrony (F) computed without removal of trial-locked evoked potential signals. As in the PFC, removing the evoked potentials had virtually no effect outside of the lowest frequencies.

Learning-related changes in HPC network dynamics were also different from that in the PFC. As in the PFC, HPC evoked potentials also decreased with learning [Fig. 10A,D,G; cue epoch d′: −0.30; 95% CI (−0.33, −0.27); p ≤ 10⁻⁴; choice epoch d′: −0.32; 95% CI (−0.36, −0.28); p ≤ 10⁻⁴, bootstrap test; cue epoch r: −0.25, p ≤ 10⁻⁴; choice epoch r: −0.19; p ≤ 10⁻⁴, permutation test], though with a significantly stronger change than in the PFC (p ≤ 10⁻⁴ for both time periods, two-sided permutation test]. Oscillatory power in the HPC also increased with learning like the PFC [Fig. 10B,E,H; beta-band ROI d′: 0.10; 95% CI (0.06, 0.14); p ≤ 10⁻⁴, bootstrap test; beta-band ROI r: 0.19; p ≤ 10⁻⁴, permutation test], with a comparable change in beta-band power between the two areas (difference in d′: p = 0.15; difference in correlation with behavior: p = 0.08). However, the learning-related increases were less frequency-specific in the HPC (sparseness across frequency of positive d′ values: 0.37) than in the PFC (0.68, p = 0.016), despite the similar bandwidths of their overall power (compare Figs. 6B, 9B; frequency sparseness of power: 0.47 in the HPC; 0.45 in the PFC, p = 0.54). Finally, HPC beta-band synchrony, while overall stronger than that in the PFC (Figs. 6C, 9C), showed little to no consistent change with learning [Fig. 10C,F,I; beta-band d′: −0.005; 95% CI (−0.014, 0.004), p = 0.24; significantly smaller than the PFC changes: p ≤ 10⁻⁴]. The HPC did show a broadband (>∼20 Hz) decrease with learning that was nearly constant throughout the extent of the trial (Fig. 10F,I) and, due to its overlap with beta frequencies, induced a significant negative correlation between HPC synchrony and behavior within the beta-band ROI (r: −0.07; p ≤ 10⁻⁴). These results suggest that, while learning-related evoked potential decreases may be widespread across brain regions, band-specific delay-period increases in internally generated power and synchrony may be more restricted in nature, perhaps reflecting network signatures specific to regions supporting the learning.

Figure 10.

HPC networks exhibit primarily local changes with learning. Plotting conventions and color scale ranges are same as for corresponding plots in Figure 7. A–C, Population means of HPC evoked potentials (A), LFP power (B), and intra-HPC LFP–LFP synchrony (C) time courses during the early, middle, and late learning stages (light to dark colors). D–F, Change in HPC evoked potentials (D), LFP power (E), and LFP–LFP synchrony (F) with learning (d′ statistic between late and early learning stage population distributions). G–I, Correlation of HPC evoked potentials (G), LFP power (H), and LFP–LFP synchrony (I) with behavioral performance (Spearman rank correlation between LFP signals and percent correct). Like PFC evoked potentials, HPC evoked potentials exhibit broadband decreases with learning. In contrast to the relatively restricted beta-band increases in PFC power and synchrony, HPC power shows broadband increases, while HPC synchrony primarily shows broadband high-frequency (>∼20 Hz) decreases extending through the entire trial period.

PFC–HPC synchrony exhibits primarily theta-band increases with learning

Finally, we examined cross-area oscillatory synchrony between the PFC and HPC, also computed with evoked potentials removed to isolate internally generated components (though again, results were nearly identical without this preprocessing; data not shown). PFC–HPC synchrony was overall much weaker than that within either the PFC or HPC (compare Figs. 6C, 9C, 11A; p ≤ 10⁻⁴ for both area-pair comparisons), and followed a time course similar to that of intra-PFC synchrony. Changes in beta-band PFC–HPC synchrony with learning (Fig. 11B,C), pooled within the full-trial ROI, were modest and nonsignificant [d′: 0.002; 95% CI (−0.009, −0.014); p = 0.73]. However, this was partially due to a complex mixture of opposing negative and positive changes at different time periods—significant learning-related decreases were observed during the precue fixation period, cue, and the middle of the delay period, while significant increases were observed at the start and end of the delay period (Fig. 11C). The behavioral correlation analysis more strongly emphasized the negative changes, resulting in a significant negative correlation with behavior within the beta-band ROI (r: −0.07; p ≤ 10⁻⁴). Also notable was a relatively robust increase in theta-band (∼3–7 Hz) synchrony with learning, particularly during the memory delay period (Fig. 11C). Although this learning-related theta synchrony increase was significant [d′ pooled within full-trial ROI: 0.13; 95% CI (0.12, 0.15); p ≤ 10⁻⁴], and significantly stronger than the more modest theta-band increases observed within the PFC [0.08; 95% CI (0.07, 0.10); p = 0.002] or the HPC [0.02; 95% CI (0.01, 0.03), p ≤ 10⁻⁴], it was much less prominent in the behavioral correlation analysis (Fig. 11D). These results indicate that, although cross-area synchrony between the PFC and HPC was weaker and showed less consistent changes with learning overall, it did exhibit learning-related increases at theta frequencies, perhaps reflecting the idea that long-range neural communication is mediated by synchrony at lower frequencies (Buzsáki and Draguhn, 2004).

Figure 11.

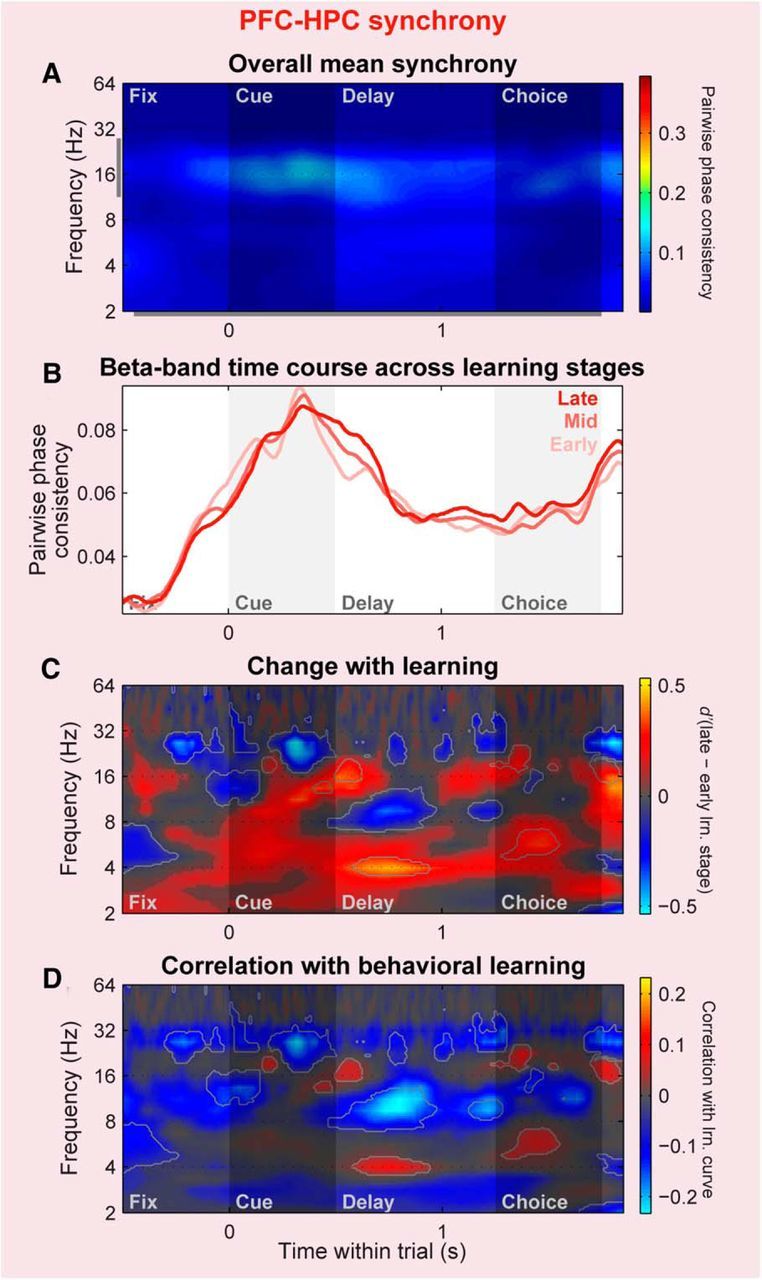
Cross-area PFC–HPC synchrony exhibits less consistent changes with learning. Plotting conventions and color scale ranges are the same as for corresponding within-area plots in Figures 6, 7, 9, and 10. A, Population mean LFP–LFP synchrony across all cross-area (PFC–HPC) pairs of LFP sites, pooled across all trials. B–D, Change in PFC–HPC LFP–LFP synchrony strength with learning, shown in three different ways. B, Beta-band PPC during early, middle, and late learning stages (light to dark colors). C, d′ between late and early learning stages of population distributions of PPC values. D, Correlation between PPC and behavioral performance. Cross-area synchrony exhibits a complex mixture of increases and decreases with learning.

Alternative explanations

We have presented evidence of changes in PFC neural and network-level signals during associative learning. It could be argued, however, that these effects might relate to factors other than learning per se that also change during a learning session. Previously, we (Brincat and Miller, 2015) showed that there is little evidence for changes in global arousal (as indexed by pupil size) or motor function (as indexed by reaction time and saccade endpoint variability) with learning, and thus these factors are unlikely to drive our results. To minimize any influence of changes in familiarity of the novel objects used in the learning task, immediately before each learning session we familiarized the monkeys with the new set of objects by having them perform dozens of passive-viewing and identity match-to-sample trials with them.

To assess whether the effects we observe during the learning task might simply reflect a continuation of signal changes arising during these prelearning control tasks—for example, due to residual object familiarity effects—we compared the across-trial time courses of LFP signals during learning to those observed in the control tasks. For cue object-evoked potentials, the control task responses do fall within the predictions based on their changes during the learning task (Fig. 12A), and we therefore cannot rule out the possibility that this particular result might be due to increasing stimulus familiarity or other effects arising before learning. However, control task values for choice object-evoked potentials (Fig. 12B), beta-band power (Fig. 12C), and beta-band synchrony (Fig. 12D) fell well outside the predictions from the learning-related changes; for choice-evoked potentials and beta power, there was even a clear nonmonotonic relationship between control and learning-task responses. These results argue against the idea that the changes we observe during learning are likely, in general, to be due to familiarity or other passive processes that develop continuously through the entire session.

Discussion

Our results suggest a shift in PFC coding over the course of associative learning, whereby the strength of feedforward sensory signals is downregulated, while the strength of internally generated associative signals is upregulated. At the neuronal level, information in PFC spike rates about the identity of viewed cue and choice objects decreased with learning, while information recalled from memory about learned associate objects increased. At the network level, the evoked potentials elicited by the cue and choice objects diminished with learning, while internally generated oscillations became stronger and more synchronized across distant PFC sites, particularly during the period when the monkeys must map the cue object onto its learned associate.

One might ask whether there is a link between our observed learning-related decrease of sensory information and evoked potentials and the well known decline in spiking responses evoked in the visual cortex by repeated presentations of an object (referred to by different authors as habituation, repetition suppression, or familiarity; Miller et al., 1991; Li et al., 1993; Anderson et al., 2008). However, as mentioned above, to minimize the contribution of such passive memory processes to our results, we presented all novel objects to the monkeys ∼40 times (passive presentations and identity match-to-sample task trials) just before the start of each learning session. By comparison, familiarity effects in inferotemporal spiking responses are reported to asymptote by 6–8 repetitions of an object (Li et al., 1993). We confirmed that our learning effects cannot, in general, be accounted for by a continuation of processes arising during these control tasks before learning (Fig. 12). Further, in contrast to spiking responses, evoked potentials have been observed to increase with stimulus familiarity across a variety of cortical areas and species [mouse primary visual cortex (Cooke and Bear, 2015), monkey inferotemporal cortex (Anderson et al., 2008), human visual cortex and PFC (Gilbert et al., 2010)]. Thus, familiarity-based effects would predict the exact opposite of our evoked potential results, suggesting our results instead reflect explicit associative learning processes.

Internally generated oscillations were strongest—both their overall strength and the magnitude of their learning-related increases in the PFC—in the beta band (∼11–27 Hz). A growing body of evidence (Buschman and Miller, 2007; Buffalo et al., 2011; Schmiedt et al., 2014; van Kerkoerle et al., 2014; Bastos et al., 2015; Fries, 2015) suggests that in the visual cortex, feedback processing from higher-level to lower-level cortical areas is mediated by alpha/beta-band oscillations (∼8–30 Hz), while feedforward processing is mediated by gamma-band oscillations (∼30–80 Hz). This is consistent with our interpretation—based on their sustained, nonphase-locked time course—that our observed beta oscillations originate internally within the cortex and that learning entails an upregulation of top-down signals. It further suggests these beta oscillations could play a role in propagating retrieved associate information from PFC down to lower-level visual cortical areas (Tomita et al., 1999; Barceló et al., 2000), such as the inferotemporal cortex, where signals reflecting learned object associations have also been found (Messinger et al., 2001). In contrast, we observed little evidence for a role for gamma oscillations in our data, in line with previous work suggesting gamma oscillations are less prominent in the frontal cortex (Siegel et al., 2009; Antzoulatos and Miller, 2014) than in the posterior visual cortex (Bastos et al., 2015). We did observe a learning-related decrease in PFC power within the gamma band (Fig. 7E)—though its broadband nature rendered it difficult to unambiguously discriminate from spiking activity (Ray and Maunsell, 2011)—and a negative correlation between intra-PFC gamma-band synchrony and behavioral learning. Both trends are consistent with our interpretation of feedforward signals diminishing with learning. In sum, the increase in nonphase-locked beta-band power and synchrony—and possibly the decrease in gamma-band power and synchrony—suggest a shift from bottom-up to top-down oscillatory signals in the PFC with learning.

Our results suggest the HPC is not explicitly involved in acquiring or representing learned information in our task. The HPC and PFC did share many basic properties: both exhibited spiking and evoked potential responses to, and carried neural information about, the viewed objects; both showed LFP beta-power modulation with a similar stimulus-suppressed temporal profile; and sensory-evoked potentials in both areas decreased with learning. However, in contrast to PFC neurons, HPC neurons carried no information reflecting the learned associations and exhibited no clear change with learning. At the network level, learning-related increases in HPC LFP power were not band-specific and intra-HPC synchrony did not peak during the memory delay or increase with learning. We hypothesize that these network-level signatures may be secondary biomarkers of brain regions with explicit involvement in a learning task. The lack of explicit HPC involvement in our task is in line with the idea that the HPC may not be required for simple within-domain (i.e., object–object) associations (Murray et al., 1993; Bunsey and Eichenbaum, 1996), unless there is a requirement to link items with a spatial location (Wirth et al., 2003; Buffalo, 2015) or other broader context (Bunsey and Eichenbaum, 1996; Eichenbaum et al., 2012).

It was not the case, however, that the HPC was simply not engaged by our task. We have previously shown (Brincat and Miller, 2015) that during the post-trial feedback period, the HPC spiking rate and band-specific HPC–PFC synchrony carry robust information about trial outcome—whether the monkey was rewarded for choosing the correct paired associate or given no reward after choosing the incorrect one. With learning, both the spiking and synchrony signals shifted from a bias in favor of incorrect outcomes to one in favor of correct outcomes. Based on these results, we hypothesized that the HPC may play a modulatory role in this task, guiding plasticity in the PFC and other neocortical regions where the learned information is actually encoded, and the shift from error-preferring to correct-preferring coding might reflect a shift from supporting neocortical acquisition to consolidation. It remains an open question whether other medial temporal lobe areas, such as entorhinal and perirhinal cortex—which are known to have explicit representations of well learned object-pair associations (Sakai and Miyashita, 1991; Erickson and Desimone, 1999; Messinger et al., 2001)—also show a PFC-like explicit representation or play an HPC-like modulatory role during the initial stages of acquisition.

Finally, what might be the functional implications of shifting neural processing from feedforward sensory inputs to internally generated associative signals? Early in associative learning, processing of the constituent items is clearly critical for building their associative links. However, once they are well learned, it may be that an associative cue rapidly and automatically retrieves its learned associate, and therefore requires less neural processing. Further, a recurring theme in cognitive neuroscience is competition for limited neural processing resources—objects are thought to compete for representation in the visual cortex (Desimone and Duncan, 1995), and working memory has a limited capacity to hold only a few items simultaneously (Luck and Vogel, 2013). Our results suggest there may also be competition for representation in higher-level cortical areas between externally generated sensory signals and internally generated associative signals, with the former dominating early in associative learning and the latter taking precedence as learning progresses.