Partial Adaptation of Obtained and Observed Value Signals Preserves Information about Gains and Losses

Abstract

Given that the range of rewarding and punishing outcomes of actions is large but neural coding capacity is limited, efficient processing of outcomes by the brain is necessary. One mechanism to increase efficiency is to rescale neural output to the range of outcomes expected in the current context, and process only experienced deviations from this expectation. However, this mechanism comes at the cost of not being able to discriminate between unexpectedly low losses when times are bad versus unexpectedly high gains when times are good. Thus, too much adaptation would result in disregarding information about the nature and absolute magnitude of outcomes, preventing learning about the longer-term value structure of the environment. Here we investigate the degree of adaptation in outcome coding brain regions in humans, for directly experienced outcomes and observed outcomes. We scanned participants while they performed a social learning task in gain and loss blocks. Multivariate pattern analysis showed two distinct networks of brain regions adapt to the most likely outcomes within a block. Frontostriatal areas adapted to directly experienced outcomes, whereas lateral frontal and temporoparietal regions adapted to observed social outcomes. Critically, in both cases, adaptation was incomplete and information about whether the outcomes arose in a gain block or a loss block was retained. Univariate analysis confirmed incomplete adaptive coding in these regions but also detected nonadapting outcome signals. Thus, although neural areas rescale their responses to outcomes for efficient coding, they adapt incompletely and keep track of the longer-term incentives available in the environment.

SIGNIFICANCE STATEMENT Optimal value-based choice requires that the brain precisely and efficiently represents positive and negative outcomes. One way to increase efficiency is to adapt responding to the most likely outcomes in a given context. However, too strong adaptation would result in loss of precise representation (e.g., when the avoidance of a loss in a loss-context is coded the same as receipt of a gain in a gain-context). We investigated an intermediate form of adaptation that is efficient while maintaining information about received gains and avoided losses. We found that frontostriatal areas adapted to directly experienced outcomes, whereas lateral frontal and temporoparietal regions adapted to observed social outcomes. Importantly, adaptation was intermediate, in line with influential models of reference dependence in behavioral economics.

Introduction

Complex environments coupled with broad behavioral repertoires and diets mean that huge quantities of value-related information need to be processed to learn about the world and generate adaptive behavior. A question of central interest in decision neuroscience is how these values are represented in the brain. Given that the firing range of neurons is finite, one idea is that motivationally relevant information is encoded in a relative fashion, adapting to the current value-context (Seymour and McClure, 2008). This mechanism allows neurons to efficiently use their full firing range by encoding the most likely outcomes with highest sensitivity. For example, a foraging animal that finds itself in a nutrition-rich environment without poisonous food may devote most of its value-processing neural machinery to monitoring the nutritional value of the food. By contrast, if the same animal finds itself in an environment with less nutritious but potentially poisonous food, it may rescale value processing and maximize sensitivity for poison content. Such a context-based rescaling of value is efficient because it uses a common neural circuitry to assign motivational value in different contexts, and has been documented in various outcome processing structures of the brain (Tremblay and Schultz, 1999; Breiter et al., 2001; Akitsuki et al., 2003; Tobler et al., 2005; Nieuwenhuis et al., 2005; Elliott et al., 2008; Fujiwara et al., 2009; Kobayashi et al., 2010).

One critical issue facing any organism that engages in the adaptive coding of outcomes concerns the extent of rescaling. Consider an animal that fully rescales its neural representation of outcomes to the new contexts. For such an animal, it would be difficult to distinguish between tasty berries in a nutrition-rich environment and the absence of poisonous berries in a nutrition-sparse environment, as both of these good outcomes would be represented in the same way and elicit the same level of activation in value coding regions. However, the absence of a bad outcome is clearly not the same thing as the presence of a good outcome, and failure to distinguish between the two could lead to suboptimal behavior. For example, if contextually dependent learned values are recalled in new contexts, it could be that animals remain indifferent between gaining a reward and avoiding a punishment (Pompilio and Kacelnik, 2010). On the other hand, simply coding absolute values independent of context would be inefficient because of reduced sensitivity to the most likely outcomes in a given context, thereby reducing the discriminability of fine-grained differences between food items.

Under partial neural adaptation, the neural response would represent the worst and best outcomes available at the extremes but efficiently rescale its responses to intermediate values according to the current context. As such, the full range of neural activity is used to represent outcomes, satisfying efficient coding concerns while allowing for absence of bad outcomes in bad contexts to be coded differently from the presence of good outcomes in good contexts, allowing motivational drive to be maintained in environments where punishments need to be avoided. Although recent computational and neuroscientific work has highlighted the importance of relative value coding when learning to avoid negative outcomes to promote neural efficiency (Palminteri et al., 2015), the extent of neural adaptation between gain and loss contexts has not been investigated. Accordingly, we hypothesized that partial neural adaptation to outcome values would be optimal, allowing for both adaptive use of the current context while nevertheless tracking the fundamental nature of outcome information within the same neural architecture.

We assessed this prediction for outcomes received by the individual in the scanner. Moreover, we tested for the generality of our findings by also investigating the neural coding of outcomes received by somebody else in a social observational learning context. Given that previous reports have identified substantial neural representations of social outcomes (e.g., Sul et al., 2015), we hypothesized that social outcomes would also be coded in a partially adaptive manner, in line with the notion that the tension between efficiency and information is a general feature of neural outcome representation.

Materials and Methods

Predictions.

We used a social version of the 2-armed bandit task (Fig. 1A) which alternated between gain and loss blocks (Burke et al., 2010). In gain blocks, the available outcomes for both a confederate and the participant were 10 points and 0 points, whereas in loss blocks the available outcomes were 0 and −10 points. In this task, the extent of adaptive coding can be assessed with multivariate methods for both observed and actually received outcomes. For example, in fully adapting regions, activity patterns differentiating between 0 points in a loss block (i.e., a good outcome) and 0 points in a gain block (i.e., a bad outcome) should be identical to patterns differentiating between 10 points in a gain block (i.e., a good outcome) and −10 points in a loss block (i.e., a bad outcome), as the activity patterns adapt to simply code good and bad outcomes across the blocks (Fig. 1B). Thus, significant decoding accuracy of a classifier trained to discriminate 0 points in a loss block from 0 points in a gain block and tested on its ability to predict the difference between 10 points in a gain block and −10 points in a loss block would reveal similarities in the neural patterns and constitute evidence for full adaptation.

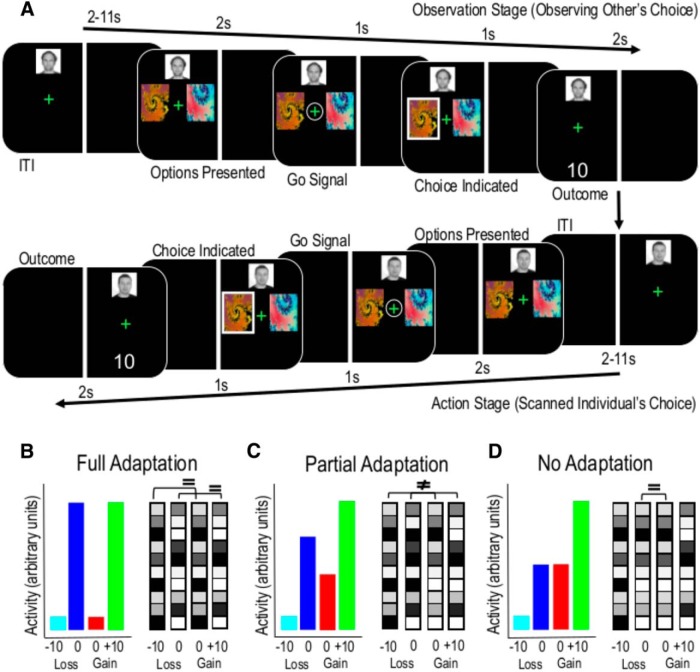
Figure 1.

Behavioral task and context-based coding schemes. A, After a variable ITI, participants were first given the opportunity to observe the confederate player making a choice and receiving an outcome (observation stage). After another variable interval, participants were then presented with the same stimuli and the trial proceeded in the same manner (action stage). Reprinted with permission from Burke et al. (2010). B, Under full adaptation (Model 3), the neural activity rescales completely so that good and bad outcomes share the same representation within their separate contexts. C, Under partial adaptation (Model 4), the neural representation rescales to an intermediate degree, to reflect the best and worse alternatives within a context. For example, an absence of a punishment in a loss block is represented as similar to a reward in a gain block; but because rescaling is not complete, it is still possible to discriminate between good outcomes or bad outcomes received in different contexts. D, Under an absolute value coding scheme (Model 5), neural activity is associated with nominal numerical values regardless of the loss or gain context.

By contrast, under partial adaptation (Fig. 1C), significant decoding would not be observed in this situation because the neural representation of good and bad outcomes is no longer similar across the blocks (patterns associated with L⁰ and G⁰ will be more similar than patterns associated with G¹⁰ and L⁻¹⁰ yielding lower classification accuracies). However, the relative difference between patterns associated with G¹⁰ and L⁰ should be the same as those between G⁰ and L⁻¹⁰ (Fig. 1C). Finally, under an absolute value coding scheme (Fig. 1D), three distinct patterns of neural activity should be associated with G¹⁰, L⁻¹⁰, and (G⁰ = L⁰) outcomes.

Participants.

Twenty-three participants were recruited from the graduate and undergraduate student population of the University of Cambridge. Two participants were excluded for excessive head motion in the scanner. Of those scanned and retained, 11 were female and the mean age of participants was 25.3 years (range 18–38 years). All were fluent speakers of English, right-handed, and had normal or corrected-to-normal vision in the scanner. Participants were preassessed to exclude those with a history of neurological or psychiatric illness. All participants gave informed consent, and the Local Research Ethics Committee of the Cambridgeshire Health Authority approved the study. To minimize the number of missed trials during scanning, participants learned the timings and sequence of task events for 20 training trials no more than 7 d before scanning. Data from this study were previously analyzed in a model-based fashion to identify the neural correlates of prediction errors during observational learning (Burke et al., 2010). The analysis in this paper differs in both the methods (multivariate pattern analysis) and the questions asked (the degree of adaptive coding of outcomes for self and others).

Behavioral task.

Participants performed a social 2-armed bandit task while undergoing fMRI. During scanning, the participants observed the behavior of a confederate performing the same task. Thus, participants could learn from both the confederate's outcomes, and their own outcomes. During training, participants were instructed that they would be taking part in a social experiment with two players. In particular, they would be able to observe the behavior of another player, but the other player would not be able to observe them. When participants arrived at the scanner, an experimental confederate (previously unknown to the participant) arrived a little later. The confederate was gender-matched to the participant. Confederates and participants sat together in the waiting area of the MR facility and went through the same procedures, filling in forms, reading task instructions, and undergoing MR-safety screening. After these preliminary procedures, one research team member led the confederate into a separate room, where a computer was present. Another member of the research team led the to-be-scanned participant into the scanner. After scanning, the exit of the confederate from the facility was timed to coincide with the debriefing of the participant (who was seated in the waiting area). The confederates never actually performed the task (except to familiarize themselves with the experiment), and the confederate behavior displayed to the participant was controlled by a computer and kept constant across participants. Participants were explicitly instructed that the task was not a competition, and outcomes received by the confederate in no way affected the points received by the participant.

In each trial, participants were required to choose one of two abstract fractal stimuli. The better stimulus was associated with p = 0.8 of delivering a good outcome and p = 0.2 of delivering a bad outcome. For the alternative stimulus, the contingencies were reversed. Participants learned by trial and error which stimulus was better with 10 trials of individual learning and 10 trials of observational learning per block. They performed 6 blocks of the task: 3 gain blocks and 3 loss blocks. The gain and loss blocks were interleaved, and participants were made aware of what block would come next. In gain blocks, the potential outcomes were 10 points (good outcome) and 0 points (bad outcome). In loss blocks, the potential outcomes were 0 points (good outcome) and −10 points (bad outcome). All outcomes were displayed numerically on the screen during the outcome phase. Total points accumulated over the course of the experiment were not shown to the participant.

The task screen was split vertically, with one side of the screen assigned to the confederate and the other assigned to the participant. Each trial started with a variable intertrial interval (ITI) with the fixation cross presented on the confederate's side of the screen (Fig. 1A). The ITI varied according to a truncated Poisson distribution between 2 and 11 s and during this time the confederate's photograph was displayed to indicate to the scanned participant that it was the confederate's turn. The fixation cross was followed by the presentation of two fractal stimuli for 2 s. The fixation cross was then circled for 1 s. Participants were instructed that this was the “go” instruction for the confederate to make their choice, but the participants were required to press the third finger button on the response box to demonstrate they were attending to the choice of the confederate. Failure to make an “attend” response at this stage was registered as an error; and in these cases, the trial was repeated. If an attend response was made within the 1 s window, then the choice of the confederate was indicated for 1 s by a white box surrounding the chosen stimulus. Next, the outcome of the confederate was displayed below the fixation cross. The participant's turn then commenced with the display of a fixation cross on their side of the screen. Additional conditions with reduced information (where confederate outcomes and actions were not shown to participants) did not feature in the present analysis but have been described and analyzed in detail previously (Burke et al., 2010).

Following the observation of the confederate's choice and outcome, at the “go” signal the participant was required to choose between the same two stimuli by pressing the first button on the response box for the stimulus on the left and the second for the stimulus on the right. The left/right location of the stimuli randomly varied between trials and player turns to prevent direction imitation. The side of the screen devoted to the participant and confederate was counterbalanced across participants, removing side-bias and laterality confounds. Participants were required to complete 40 error-free trials per block and were instructed to maximize the number of points earned (in gain blocks) and minimize the number of points deducted (in loss blocks).

Participant payment.

Participants were paid according to the total points accumulated during all blocks of the task, which were converted to GBP at a rate of 30 points to £1. Participants also received a £20 show-up payment regardless of task performance. The average participant payment was £52. Participants were instructed that any losses outweighing their gains would be subtracted from the £20 show-up payment.

Behavioral analysis.

To test whether participants learned in a manner consistent with adaptive coding of outcome information, we fitted two model-free reinforcement learning algorithms to the behavioral choice data. The two models were adapted from Palminteri et al. (2015). The first model (absolute value learning) was identical to a standard Q-learning algorithm, which updates the value (Q) of the chosen option based on what the participant received. At trial t, the chosen (c) option value in the current block context (b) is updated with the δ rule as follows:

And

Where R is the outcome received on trial t.

We contrasted this absolute model with the relative model of Palminteri et al. (2015), where in addition to standard Q-learning, prediction errors are adjusted according to the learned value (V) of the current block as follows:

and V is learned in a separate updating algorithm

In both models, decision making was modeled using the softmax function (where P is the probability of choice and x and y represent the options):

Model paramters (α and β for the absolute model, and α, α₂, and β for the relative model) were optimized by minimizing the negative log likelihood of the data given the parameters using MATLAB's fmincon function (The MathWorks). To compare models, we computed the Bayesian information criterion (BIC) for each model for each participant:

In addition, we calculated the exceedance probabilities (XP) for each model using the mbb-vb-toolbox (http://mbb-team.github.io/VBA-toolbox/).

Data acquisition.

Scanning took place at the Medical Research Council Cognition and Brain Sciences Unit, Cambridge. The task was projected on a display, which participants viewed through a mirror fitted on top of the head coil. We acquired gradient echo T2*-weighted EPIs with BOLD contrast on a Siemens Trio 3 tesla scanner (slices/volume, 33; repetition time, 2 s). The experiment was split into six blocks, each lasting ∼10 min. Depending on the performance of participants, 280–350 volumes were collected in each block of the experiment, together with five “dummy” volumes at the start and end of each scanning run. Scan onset times varied randomly relative to stimulus onset times. A T1-weighted MP-RAGE structural image was also acquired for each participant. Signal dropout in basal frontal and medial temporal structures resulting from susceptibility artifact was reduced by using a tilted plane of acquisition (30° to the anterior commissure-posterior commissure line, rostral > caudal). Imaging parameters were the following: echo time, 50 ms; FOV, 192 mm. The in-plane resolution was 3 × 3 mm, with a slice thickness of 2 mm and an interslice gap of 1 mm. High-resolution T1-weighted structural scans were coregistered to mean EPIs and averaged together to permit anatomical localization of the functional activations at the group level.

Imaging analysis.

Statistical Parametric Mapping (SPM8; Functional Imaging Laboratory, UCL) served to spatially realign functional data. For univariate analysis, the images were then normalized to a standard EPI template and smoothed using an isometric Gaussian kernel with a FWHM of 8 mm. We used a standard rapid event-related fMRI approach in which evoked hemodynamic responses to each event type are estimated separately by convolving a canonical hemodynamic response function with the onsets for each event and regressing these against the measured fMRI signal. For gain blocks we modeled 10 point outcomes (G¹⁰) and 0 point outcomes (G⁰) for both observed and received outcomes separately. Loss blocks were modeled in an analogous fashion for observed and received 0 and −10 point outcomes (L⁰, L⁻¹⁰) separately. Additional conditions with reduced information where no outcome was shown to the participant (see Burke et al., 2010) were modeled as separate regressors of no interest, along with participant-specific movement parameters. For random-effects analysis, first level contrast images of G¹⁰, G⁰, L⁰, and L⁻¹⁰ events were entered into a 2 × 2 ANOVA with gain and loss as factors and good (G¹⁰, L⁰) and bad (G⁰, L⁻¹⁰) as levels.

Multivariate analysis.

We performed whole-brain searchlight decoding (Kriegeskorte et al., 2006; Haynes et al., 2007) to assess the degree of outcome adaptation (and evidence for absolute value coding) in local fMRI patterns surrounding each voxel (radius 12 mm) for each participant using the realigned but not normalized or smoothed imaging data. A GLM was constructed that modeled 10 point outcomes (G¹⁰) and 0 point outcomes (G⁰) for both observed and received outcomes separately. Loss blocks were modeled in an analogous fashion for observed and received 0 and −10 point outcomes (L⁰, L⁻¹⁰). Error trials were modeled separately, along with participant-specific movement parameters as regressors of no interest. G¹⁰ and G⁰ events (in gain blocks) and L⁰ and L⁻¹⁰ events (in loss blocks) served as inputs for the classifiers and were labeled according to the model. Analysis was performed using the Decoding Toolbox (Hebart et al., 2015) and SPM8. Data were then split into different training and testing subsets depending on the model. We trained a linear support vector classifier to separate fMRI patterns corresponding to different outcomes. The support vector classifier was tested by classifying fMRI patterns corresponding to outcomes in the independent testing data subset. For this, we used the Library for Support Vector Machines implementation (www.csie.ntu.edu.tw/∼cjlin/libsvm/) with a linear support vector classifier that had a cost function of 1. To account for potential classifier biases across the partial and fully adaptive coding models, we also computed area under the ROC curve (AUC) images and compared these images at the whole brain level. AUC images account for the specificity versus sensitivity of the classifier and remove any bias the classifier has for decoding each specific class. Accuracy and AUC images (corresponding to observed prediction accuracy minus chance prediction for each voxel) for each analysis were normalized and smoothed with an 8 mm kernel and entered into second level t tests for group-level analysis on a voxel-by-voxel basis.

To identify value coding regions (whether nonadaptive, partially adaptive, or fully adaptive), we first identified voxels that differentiated between good and bad outcomes regardless of whether block type was gain or loss (Model 1; for a description of the models, see Model 1: decoding good versus bad outcomes). Depending on the decoding analysis, we trained classifiers to differentiate between outcomes on a subset of the data (training subset). Classifier accuracy was then tested by assessing how well the trained support vector machine could decode these outcomes on the remaining data (testing subset). By using classifiers to distinguish between different outcomes in the training and testing subsets, it is possible to test the similarity in neural patterns across different outcomes and thus the extent of adaptive coding.

Model 1: decoding good versus bad outcomes.

The first decoding analysis identified voxels that encoded outcome information, regardless of whether this information was adaptive or absolute. Under such a model, there would be one pattern of activity for good outcomes and another for bad outcomes. We trained a classifier to distinguish between good and bad outcomes in a subset of the data and tested whether it could decode this difference in a different subset of the data. In regions coding outcome information, the classifier should perform better than chance. Specifically, we trained the classifier on G¹⁰ and G⁰ outcomes in blocks 1, 3, and 5 (gain blocks) and then tested the accuracy of this classifier to decode L⁰ and L⁻¹⁰ outcomes in blocks 2, 4, and 6 (loss blocks) in three independent decoding runs. We then performed the reverse analysis (training the classifier to distinguish between L⁰ and L⁻¹⁰ outcomes in blocks 2, 4, and 6 and testing the accuracy of decoding G¹⁰ and G⁰ outcomes in blocks 1, 3, and 5 in three decoding runs). In this manner, training and test data were kept independent during each decoding run and cross-validated in a train 3, leave 1 run out procedure. For each decoding run, the average accuracy (minus chance) within the searchlight cluster was then assigned to the central voxel in the cluster, to create an accuracy-chance image, and the six images were averaged to assess overall predictive power of the classifier across gain and loss blocks. The goal of this classifier was to identify regions where good outcomes elicit different neural patterns than bad outcomes regardless of whether or not the regions exhibit adaptive coding. Only voxels that surpassed the conservative threshold of p < 0.05 whole-brain corrected (peak level) were then used as an inclusive mask to test for partial and full adaptive coding and absolute value coding.

Model 2: decoding block information.

Because the models designed to decode the degree of adaptive coding feature across-block designs, block-specific effects (such as differences in physiological arousal or motivation between gain and loss blocks) may be present in such analyses. For this reason, we next removed any voxels encoding such information from the outcome encoding mask from Model 1 at the threshold of p = 0.05 uncorrected. To do this, we trained a classifier to distinguish between any gain block (e.g., G¹⁰ and G⁰ outcomes) from any loss block (L⁰ and L⁻¹⁰ outcomes) on blocks 1, 2, 3, and 4 and tested the classifier's accuracy at decoding gain from loss blocks in blocks 5 and 6. A further 2 decoding runs were performed (first training on blocks 1, 2, 5, and 6, then testing on 3 and 4; second training on 3, 4, 5, and 6 and testing on 1 and 2) in a train 4-leave 2 blocks out-cross validation procedure (maintaining independence of training and test data for each decoding run). Accuracy minus chance images were averaged over the three decoding runs. Voxels showing significant decoding in this model suggest that activity patterns differ nonspecifically between gain and loss blocks rather than reflecting outcome related information. Any voxels encoding block information were therefore removed from the mask identified in Model 1, and the resulting mask of outcome-related, but not block-related, voxels was used for further investigation.

Model 3: full adaptive coding.

Under full adaptation, patterns associated with good and bad outcomes should be identical in both gain and loss blocks. In our task, this would mean the brain responds similarly to both reward G¹⁰ and absence of punishment L⁰ on the one hand, versus both punishment L⁻¹⁰ and absence of reward G⁰ on the other hand. To identify patterns that displayed fully adaptive coding (Fig. 1B), we therefore trained a classifier to distinguish G¹⁰ and L⁻¹⁰ outcomes and tested its accuracy at decoding L⁰ and G⁰ outcomes and vice versa. We used a full cross validation design keeping training and testing data independent. Six decoding runs were performed for all combinations of training and testing data subsets. Significant decoding accuracy of a classifier trained to distinguish between G¹⁰ and L⁻¹⁰ and tested on L⁰ vs G⁰ outcomes (and vice versa) reflects fully adaptive multivariate patterns in the brain.

Model 4: partial adaptive coding (or absolute value coding).

If activity patterns are consistent with partially adaptive (Fig. 1C) or absolute value coding, one would expect to see different patterns between the good outcomes in gain and loss blocks, suggesting an ability to differentiate between rewards received and punishments avoided as well as between punishments received and rewards missed. Model 4 was designed to detect regions consistent with this by identifying pattern differences between bad outcomes (e.g., G⁰ and L⁻¹⁰) that can be used to decode pattern differences between good outcomes (e.g., G¹⁰ and L⁰), and vice versa. If outcome patterns display full adaptation, then no difference in patterns should be discernible between G¹⁰ and L⁰ outcomes (and equally between G⁰ and L⁻¹⁰ outcomes, as in Fig. 1B) and the classifier should perform at chance level. In contrast, for both partial adaptive coding and absolute outcome coding, classification accuracy would be significantly higher than chance because responses to good and bad outcomes across blocks are not identical (Fig. 1D). Accordingly, we trained a classifier to distinguish G⁰ and L⁻¹⁰ outcomes and then test its accuracy at decoding G¹⁰ and L⁰ outcomes, and vice versa, using a full cross validation design that kept training and testing data independent. For example, this consisted of training the classifier to distinguish between G¹⁰ and L⁰ outcomes in a training subset, and testing how accurately it would decode G⁰ and L⁻¹⁰ outcomes in three decoding runs. We averaged the resulting decoding accuracy with the accuracy of a classifier trained to distinguish G⁰ and L⁻¹⁰ outcomes in all blocks and tested on G¹⁰ and L⁰ outcomes in three decoding runs. This classifier should have no predictive power to localize fully adaptive coding regions, as it specifies differences in patterns between G⁰ and L⁻¹⁰ outcomes (and G¹⁰ and L⁰ outcomes). Such differences are excluded under a fully adaptive coding scheme where good outcomes (and bad outcomes) should be encoded in similar multivoxel patterns regardless of the context. Because voxels that demonstrate significant predictive power in this analysis would be consistent with both partially adaptive and absolute value coding schemes, it is necessary to test absolute value encoding (Model 5) and remove these voxels to identify partially adaptive regions.

Model 5: absolute value coding.

If absolute coding is reflected in multivariate activity, then there should be differential patterns associated with 10, 0, and −10 outcomes regardless of the block in which they occur. Crucially, the patterns for G⁰ and L⁰ outcomes should be similar. To test for this, we used a searchlight multivariate support vector regression (testing for unique pattern differences between G¹⁰, (G⁰ = L⁰) and L⁻¹⁰ outcomes) within the outcome-coding mask identified in Model 1, subtracting unspecific voxels from Model 2. A leave one run out full cross validation design was used in six decoding runs to keep training and test data independent. Because of the use of a linear regression, this analysis identifies patterns where L⁰ and G⁰ outcomes are similar, but different from G¹⁰ and L⁻¹⁰ outcomes in a manner consistent with the absolute coding of value in Figure 1D.

Univariate analysis.

Value coding regardless of adaptation requires stronger activation for good outcomes than bad outcomes (i.e., G¹⁰ > G⁰, L⁰ > L⁻¹⁰, and G¹⁰ > L⁻¹⁰). Full adaptation corresponds to equivalent activation for the good outcomes on the one hand and the bad outcomes on the other hand, regardless of their absolute values. To test for full adaptation of value coding regions, we performed a conjunction analysis of G¹⁰ > G⁰ and L⁰ > L⁻¹⁰, exclusively masked by voxels where G¹⁰ and L⁰ and/or G⁰ and L⁻¹⁰ significantly differed from each other (p < 0.05, uncorrected). The first two contrasts fulfill the requirement of value coding, whereas the exclusive masking ensures that full adaptation holds. Partial value adaptation also requires stronger activation by good outcomes than bad outcomes but allows for differences within good outcomes and within bad outcomes. Crucially, adaptation requires for a good outcome in a loss context to elicit significantly more activation than a bad outcome of the same magnitude in a gain context. To test for partial adaptation of value coding regions, we used G¹⁰ > L⁻¹⁰ (satisfying the value requirement), which was inclusively masked by L⁰ > G⁰ (satisfying the adaptation requirement). Finally, in addition to stronger activation by good than bad outcomes, absolute value coding requires equivalent activation by outcomes with the same magnitude, reflecting absence of adaptation. To test for absolute value coding, a t test between G¹⁰ > G⁰ ∼ L⁰ >L⁻¹⁰ was performed (satisfying the value requirement), exclusively masked by voxels where L⁰ and G⁰ significantly differed from each other (ensuring absence of adaptation) and voxels that differed between gain and loss blocks. Regions of interest were identified neuroanatomically with the Pickatlas Toolbox (Maldjian et al., 2003). Reported voxels conform to MNI coordinate space, with the right side of the image corresponding to the right side of the brain. Images were thresholded at p < 0.001 uncorrected or p < 0.05 peak-level whole brain corrected.

Results

Behavioral results

To test whether participants learned about outcomes in a context-dependent fashion compatible with partial adaptive coding, we fitted the behavioral choices in the nonsocial learning conditions with a standard Q-learning model (consistent with the learning of absolute values) and a relative model that assumed that values are learned in a context-dependent fashion (for details, see Palminteri et al., 2015). The relative model specifies that outcomes are evaluated in relation to the specific value context that the decision maker finds themselves in (in our case, whether outcomes are obtained in a gain or loss session). Decision making in both models was implemented using a standard softmax rule. Model parameters (learning rate and softmax temperature for standard Q learning and an additional contextual learning rate for the relative model) were optimized by minimizing the negative log likelihood of the data given different parameter combinations using MATLAB's fmincon function. Model performance was compared using the Bayesian information criterion. We found that the relative model best explained our data, even when accounting for the number of free parameters (two-tailed t test, T = 3.05, p < 0.01), suggesting that participants learned in a manner consistent with partial adaptation coding. In an additional comparison, we calculated the exceedance probabilities (XP) for each model based on an approximate posterior probability of the model, and found the relative model outperformed the absolute model (XP = 1.0). For trials where outcomes were shown and adaptation could occur, there were no significant changes in reaction time across blocks (one-way ANOVA, F = 1.63, p = 0.15), the percentage of correct choices across blocks (one-way ANOVA; F = 0.59, p = 0.70), or learning rates across blocks (one-way ANOVA; F = 0.56, p = 0.71).

Context-dependent encoding of obtained outcomes

We first trained a classifier (Model 1) to distinguish between good and bad outcomes in gain blocks and then tested its ability to decode good and bad outcomes in loss blocks (and vice versa), a requirement for processing outcomes that applies regardless of the degree of adaptive coding: Figure 1B–D. We used voxels with significant predictive power in this analysis as a conservative inclusive mask (at p < 0.05 whole-brain corrected) for further interrogation of the degree of adaptive coding. We next identified voxels that encoded block-specific changes that were not related to outcome encoding by training a classifier to distinguish between gain and loss blocks regardless of the outcome received (Model 2). Voxels that encoded block-specific effects were then removed from the outcome-encoding mask at a lenient threshold of p < 0.05 uncorrected, to ensure that the remaining voxels were related to outcome encoding independent of unspecific differences between gain and loss blocks. Within the remaining areas, we performed three additional decoding analyses (Models 3–5) to distinguish between the three possible coding schemes depicted in Figure 1B–D.

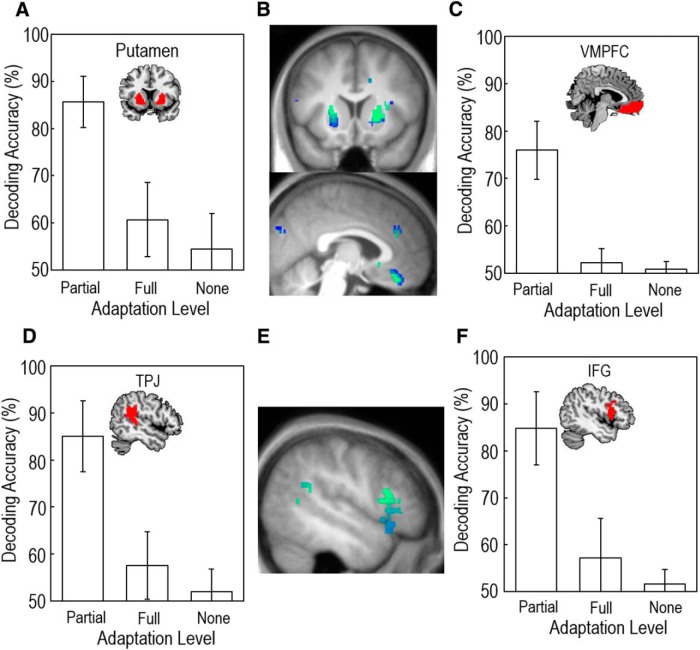
We found significant support for partial adaptive coding of outcomes in the putamen (Fig. 2A; peak at 24, 8, 14; p < 0.05 whole brain corrected) and ventromedial prefrontal cortex (vmPFC) (Fig. 2B; peak at 4, 34, −22; p < 0.05 whole brain corrected). Classifier accuracies were 85% and 75%, respectively (AUC range = 0.48–0.95 for putamen; range = 0.66–0.95 for vmPFC; Fig. 2C). This result is consistent with the hypothesis that neural activity patterns in the brain show intermediate adaptation to gain and loss contexts, ostensibly allowing it to differentiate the overall reward structure of the environment. This would permit flexible responses to new contexts (e.g., being able to differentiate a true reward from an absence of a punishment) while also satisfying the computational demands for efficient coding and punishment-avoidance learning.

Figure 2.

Decoding accuracies for classifiers consistent with partial adaptation to obtained outcomes (Model 4) were significantly higher than for classifiers based on full adaptation (Model 3) or absolute value coding (Model 5) in the bilateral putamen (A, B) and the vmPFC (B, C). Multivariate analysis of activity in the left TPJ (D, E) and IFG (E, F) showed patterns consistent with partially adaptive coding of observed outcomes (Model 4). Voxels with lower decoding accuracies are blue and voxels with higher accuracies are green. Error bars indicate standard error of the mean.

To test for evidence of fully adaptive coding (Fig. 1B), we trained a classifier to distinguish between G¹⁰ and L⁻¹⁰ outcomes and tested its accuracy at decoding L⁰ and G⁰ outcomes (and vice versa). This model tests for equivalent neural patterns for the good (G¹⁰ and L⁰) and bad (G⁰ and L⁻¹⁰) outcomes across both gain and loss blocks, as specified by a system that adapts completely. There were no regions that showed full adaptation, even at an uncorrected threshold of p < 0.001. We next aimed to identify regions consistent with an absolute value encoding scheme, by looking for multivariate patterns that were different between 10 point (G¹⁰), 0 point (G⁰ and L⁰ together), and −10 point outcomes (L⁻¹⁰). This analysis revealed no evidence for absolute value coding in multivariate activity patterns at the p < 0.05 peak-corrected threshold (Fig. 2D). To test whether decoding accuracies were significantly higher for partial adaptation than full adaptation or absolute value coding, we performed a one-way ANOVA on the mean decoding accuracies in the putamen and vmPFC. There was a significant main effect of model in both regions (F = 75.97, p < 0.001 for vmPFC; F = 72.41, p < 0.001 for putamen). Post hoc tests (Tukey's HSD) confirmed that the partial adaptation classifier had significantly better performance than the full and absolute models (p < 0.001 for both regions of interest). AUC values in the regions of interest, which account for potential classifier bias, were significantly higher for the partial adaptation model for the vmPFC (two-tailed t test; p < 0.001) and putamen (two-tailed t test; p < 0.001).

One possible interpretation of this data is that increasing levels of adaptation as learning proceeds (from little or no adaptation at the start of the experiment to full adaptation at the end) results overall in partial adaptation. To address this possibility, we split the data from each block in half and ran the identical decoding analysis on the first half and second half separately. A repeated-measures ANOVA confirmed that there was no main effect of time (F = 0.343; p = 0.34 for putamen; F = 0.27; p = 0.45 for vmPFC) and post hoc tests revealed that partial adaptation had significantly better classification performance in both the first and second half for both vmPFC (p < 0.001) and putamen (p < 0.001). Thus, patterns of brain activity do not appear to encode outcome value in a manner consistent with the two most extreme (fully adaptive and absolute) coding schemes shown in Figure 1B, D.

Context-dependent encoding of observed outcomes

For observed outcomes, we performed the exact same stepwise decoding analysis in the same order as for obtained outcomes. Our first-pass classifier to identify outcome-related information showed that for activity patterns in the left inferior frontal gyrus (IFG), left insula, and bilateral temporoparietal junction/posterior superior temporal sulcus (TPJ/pSTS), we were able to decode L⁰ and L⁻¹⁰ outcomes from G¹⁰ and G⁰ training data (and vice versa). We then removed voxels encoding block-specific information at the lenient threshold of p < 0.05 uncorrected, leaving us with voxels related to observed outcomes but not to blocks. We next performed the identical three additional decoding analyses to distinguish between the three possible coding schemes depicted in Figure 1B–D for observed outcomes.

The left TPJ/pSTS (peak at −54, −44, 6, p < 0.05 whole-brain corrected) and left IFG (peak at −44, 20, 14, p < 0.05 whole-brain corrected) showed partially adaptive activation patterns coding observed outcome information (Fig. 3A), with classification accuracies significantly above chance level (85%, AUC range = 0.62–0.93 for TPJ/pSTS; 84%, AUC range = 0.56–0.90 for IFG; Fig. 3B). In contrast, no regions within the outcome mask showed significant decoding accuracies consistent with fully adaptive coding or absolute coding of reward levels at a cluster corrected threshold of p < 0.05 (Fig. 3C). To test whether decoding accuracies were significantly better for the partial adaptation model as opposed to full adaptation and absolute value coding, we performed a one-way ANOVA on the mean decoding accuracies for the TPJ and IFG. There was a significant main effect of model for both the TPJ (F = 66.4, p < 0.001) and IFG (F = 57.3, p < 0.001). Post hoc tests (Tukey's HSD) revealed that partial adaptation classifier performance was significantly better than full adaptation or no adaptation cases (p < 0.001 for both TPJ and IFG). AUC values in the regions of interest were significantly higher for the partial adaptation model versus the full adaptation model for the TPJ (two-tailed t test; p < 0.001) and IFG (two-tailed t test; p < 0.001). A repeated-measures ANOVA on the first and second half of each block confirmed that there was no main effect of time (F = 1.68; p = 0.18 for IFG; F = 1.81; p = 0.17 for TPJ), and post hoc tests revealed that partial adaptation decoding accuracy was significantly higher than full adaptation and absolute value coding in both the first and second half of each block in the TPJ (p < 0.001) and IFG (p < 0.001). These results demonstrate that the coding of observed outcomes in brain activity patterns is entirely consistent with the coding of outcomes actually received, suggesting that partially adaptive outcome coding extends from the individual into the social domain.

Figure 3.

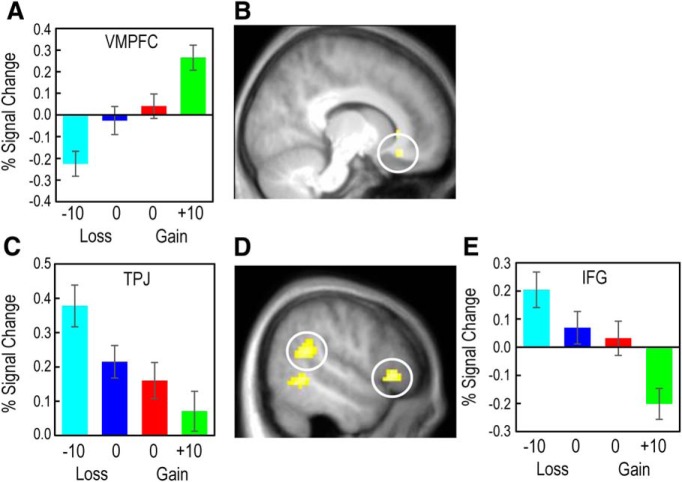
Univariate activity in response to received and observed outcomes reflecting partially adaptive coding. A, Ventral striatum showed a positive increase in activity as received outcome value increased, although the absence of punishment elicited higher activation than the absence of reward, consistent with partial adaptive coding. B, The BOLD response in ventral striatum reflects partial adaptation to received outcomes. C, Activity levels in the pSTS/TPJ and IFG showed evidence for partial adaptive coding of observed outcomes. D, The BOLD response in these regions decreased with increasing value of observed outcomes, with G⁰ outcomes showing significantly higher activity than L⁰ outcomes. Images are displayed at the p < 0.001 uncorrected threshold. Error bars indicate standard error of the mean.

Univariate analysis of obtained and observed outcome adaptive coding

We also used univariate methods to assess the degree of adaptive coding in outcome-sensitive regions. To test for partially adaptive coding, we identified regions that showed increased activity to G¹⁰ outcomes relative to L⁻¹⁰ outcomes, in conjunction with voxels that showed a significant increase in activation for L⁰ relative to G⁰ outcomes (Fig. 1C). Activity in the ventral striatum revealed partial adaptation to the local context in response to obtained outcomes (Fig. 4A; peak at 12, 6, −9; p < 0.05 whole-brain corrected), with a significant difference in the activation levels between G⁰ and L⁻¹⁰ outcomes (t test, p < 0.05; Fig. 4B). The identical analysis searching for full and partial adaptive coding of outcomes received by the confederate revealed partial adaptive responses in the IFG and STS (Fig. 4C) for bad outcomes (i.e., G⁰ > G¹⁰ and L⁻¹⁰ > L⁰), with significant differences observed between G⁰ and L⁻¹⁰ outcomes (p < 0.05, t test; Fig. 4D). There was no evidence for fully adaptive coding in the response to the confederate's outcomes at an uncorrected threshold of p < 0.001, suggesting that also observed outcome coding does not fully adapt.

Figure 4.

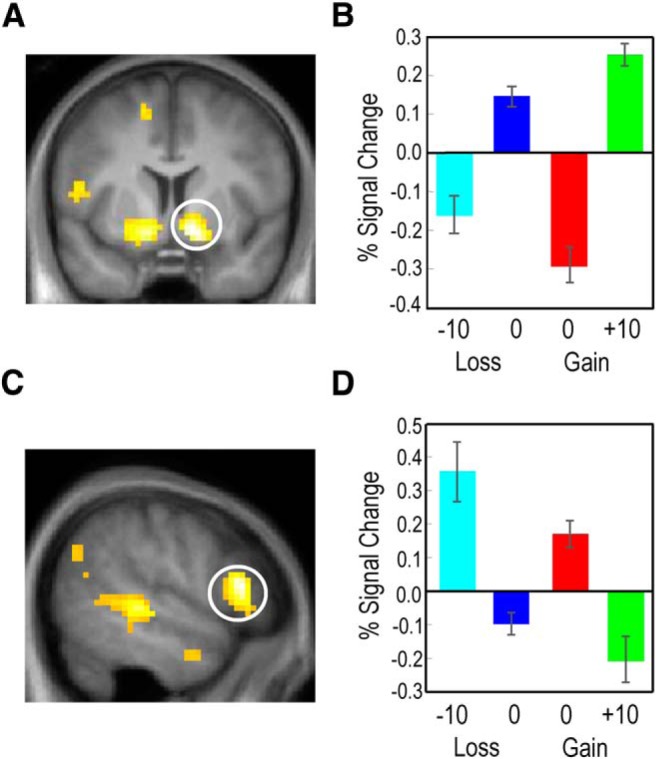
Univariate activity to received and observed outcomes showing evidence of absolute value coding. A, B, vmPFC activity increased significantly in response to received rewards with no significant difference in activity levels between L⁰ and G⁰ outcomes, consistent with absolute value coding of received outcomes. C, D, pSTS/TPJ and IFG showed absolute value coding for observed outcomes. Activity in both pSTS/TPJ (C) and IFG (E) decreased as observed outcomes increased, with no significant difference in the activity levels associated with observed L⁰ and G⁰ outcomes. Images are displayed at the p < 0.001 uncorrected threshold.

Next, we tested whether any regions displayed overall activity levels that corresponded to absolute value encoding by looking at the G¹⁰ > L⁻¹⁰ contrast and exclusively masking any voxels that showed differential activity between G⁰ and L⁰ outcomes, and differences between gain and loss blocks. In contrast with the lack of evidence for multivariate encoding of absolute outcome value, we found that more posterior regions of vmPFC (peak at 9, 30, −9, p < 0.05 cluster-level corrected, peak p < 0.001 at the voxel level; Fig. 4A,B) showed absolute coding of outcome values actually received by the participant. The equivalent test for observed outcomes revealed that a more ventral region of the IFG and the TPJ encoded the absolute outcome value (Fig. 4C,D,E), but in an inverse fashion (i.e., increased activity for punishment rather than reward events; Fig. 4C). Thus, for both received and observed outcomes, univariate analysis of overall activity levels demonstrated the presence of both absolute value coding and partial adaptive coding.

Finally, to test whether overall activity reflected fully adaptive value coding (Fig. 1B), we conducted a conjunction analysis of obtained good versus bad outcomes in gain and loss blocks, and removed any voxels that showed differential activation between G¹⁰ and L⁰ outcomes and between G⁰ and L⁻¹⁰ outcomes. There were no regions that showed fully adaptive value coding at the uncorrected threshold of p < 0.001. Thus, the univariate analysis converged with the multivariate analysis in failing to find full adaptive coding. The fact that no evidence for full adaptation was found suggests that the brain at least partially keeps track of the overall (absolute) reward structure across blocks through absolute activity levels, which constrain the degree of adaptation in regions involved with sensitively representing within-block outcomes.

Discussion

Our results identify two previously unexplored aspects in the context-dependent processing of outcome information. First, there were substantial differences in the degree of adaptation and how each type was encoded in the brain; whereas outcome information encoded in a multivariate manner displayed only partial adaptive coding, univariate activity levels showed both partial adaptive coding and absolute outcome encoding in neighboring frontal areas (Figs. 2–4). Perhaps surprisingly, we found no evidence for full adaptive coding of outcomes, suggesting that the brain keeps track of overall outcome values, possibly to stabilize behavior and responses to rewards and punishments. Second, our results extend previous research by showing differential adaptive coding for received and observed outcomes. While the striatum and vmPFC encoded obtained outcomes, the IFG, TPJ, and STS showed preferential sensitivity to observed outcomes.

By using a stepwise multivariate searchlight analysis, we were able to test the degree of outcome adaptation for the first time. The use of multivariate analysis methods was important because interspersed value coding neurons in these regions show either increasing or decreasing activity with increasing value (Tremblay and Schultz, 1999), potentially cancelling each other out in univariate analyses. Our data build on previous studies that have demonstrated that the vmPFC encodes values across categories in multivoxel patterns (McNamee et al., 2013) by investigating the extent of adaptation in value coding. Whether the neural encoding of outcome value completely rescales to the range of outcomes available, or retains some context-independent information about the nature of outcomes, has important implications for theories that predict how value is represented in the brain. Theories that predict fully adaptive coding have been advanced on the basis that this might be an efficient way to encode wide ranges of values due to the limited firing range of neurons (Laughlin, 1981; Louie and Glimcher, 2012). These theories can explain when economic decisions violate axioms of rational choice, and cause apparent preference reversals depending on choice context.

Evidence for adaptive coding is pervasive, and investigations have shown adaptive univariate activity reflecting outcome value in the ventral striatum and vmPFC (Breiter et al., 2001; Nieuwenhuis et al., 2005, Kim et al., 2006; Elliott et al., 2008; Park et al., 2012). These studies have shown similar neural responses to the best available outcome within a given context, regardless of the objective outcome value. Evidence suggests that the vmPFC plays a central part in the valuation of options and integrating various sources of value information (Rangel and Hare, 2010; Rushworth et al., 2011), and orbital parts of ventral prefrontal cortex have been shown to adapt to the local reward environment by rescaling neural responses to outcomes (Kobayashi et al., 2010). Subjective value responses in the vmPFC in humans have been shown to rescale depending on the range of available values (Cox and Kable, 2014), with BOLD sensitivity to value increasing as the range of potential rewards becomes narrower. Single-unit recording studies have suggested that orbitofrontal neurons show value-related responses that are independent of the availability of other items in a behavioral context (Padoa-Schioppa and Assad, 2008). However, their sensitivity to incremental increases in value is inversely proportional to the available value range (Padoa-Schioppa, 2009), information that can be provided by contexts.

Adaptation might be particularly useful for punishment avoidance, which, exactly because of adaptation, acquires positive rather than neutral values (Kim et al., 2006) and therefore would be facilitated in aversive contexts (Moutoussis et al., 2008; Maia, 2010). Previous work has posited that two separate neural mechanisms govern reward approach and punishment avoidance (Bartra et al., 2013) and that standard reinforcement learning mechanisms struggle to explain punishment avoidance because instrumental avoidance responses are no longer explicitly reinforced (Gray, 1987). A recent investigation into adaptive value learning solved this issue by modifying established reinforcement learning models to account for different contexts (Palminteri et al., 2015). In this manner, under an adaptive coding framework, successfully avoiding a punishment becomes reinforcing in itself, suggesting that the need for two neural and computational systems for reward and punishment may arise primarily in mixed contexts. One possible interpretation of the fact that we found no evidence for fully adaptive coding could relate to how neural adaptation develops over time or throughout the course of a task. For example, one possibility is that, given enough time, the neural representations of outcomes might be consistent with full adaptation (with no adaptation at the start of the task). Although we found no evidence for this effect in our data, the time-frame over which adaptation occurs remains unknown and may be dependent on a number of external factors. In our study, participants received training on the task on a separate day before the experiment, which could have facilitated steady-state levels of (partial) adaptation.

Adaptive coding of outcomes is closely related to economic theories of reference dependence, where the utilities of outcomes are assessed relative to an internal reference point and not on an absolute scale. Behavioral (and by extension neural) sensitivity is thought to be highest around the reference point and to rescale as reference points change. Reference dependence is a prominent feature of prospect theory (Kahneman and Tversky, 1979) and was developed to explain behavior seemingly at odds with the standard economic theories based on absolute value (Bernoulli, 1954; Von Neumann and Morgenstern, 1947). However, recent models of reference dependence have incorporated both absolute and relative measures in the assessment of outcomes to explain apparent discrepancies in both theories (Kőszegi and Rabin, 2006) by assuming a dynamic reference point. This allows for the representations of gains and losses to change over time while still remaining sensitive to extreme outcomes. The presence of partially adaptive and absolute outcome coding schemes would prevent confusion between good outcomes and bad outcomes, and absolute outcome encoding would allow for scalar operations to take place on outcome information. Our finding of both absolute value coding and partial adaptive coding fits this view, allowing much more flexible behavior in the environment than that predicted by fully adaptive or absolute value models.

Our observational learning paradigm allowed us to test whether simultaneous partial adaptive and absolute value coding arises also in the social domain. The STS, TPJ, and IFG showed partial adaptation to observed bad outcomes, suggesting that this dual value encoding scheme is a general feature of the brain, consistent with previously reported parallels between social and nonsocial learning and decision making processes (Burke et al., 2010; Seid-Fatemi and Tobler, 2015; Sul et al., 2015). Both TPJ and IFG have been implicated in social functions. The TPJ in particular has been noted for its crucial role in processing self-other distinctions and in tasks that require theory of mind (Saxe and Kanwisher, 2003). The IFG forms part of the action observation/execution mirror network (Kilner et al., 2009; Centelles et al., 2011), which has been closely associated with certain aspects of observational learning (Burke et al., 2010; Gariépy et al., 2014).

The lateral temporoparietal and frontal regions responding to observed outcomes displayed an inverse pattern to the more medial frontostriatal areas responding to received outcomes, in that partial adaptation took place for bad outcomes, and higher overall activity levels were associated with progressively worse outcomes. One potential explanation for this difference is that negative outcomes may be more important to attend to during observational learning (Olsson et al., 2007). Accordingly, it has been suggested that negative outcomes may be more fundamental in driving social learning than positive outcomes (Lindström and Olsson, 2015). Indeed, previous fMRI research has demonstrated that valuation regions show increased sensitivity when participants observe bad outcomes being delivered to another agent, suggesting preferential tuning for detecting negative outcomes affecting others (Nicolle et al., 2012). Context-based adaptation to these negative outcomes in the social domain could increase the encoding efficiency and detection of potential punishments for an organism with observational learning becoming a preferred strategy when learning is costly (Laland, 2004). An alternative possibility is that social comparison effects influence the way observed outcomes are processed by the brain, with negative outcomes delivered to a perceived competitor encoded as positive reward value (Takahashi et al., 2009). Although our task instructions explicitly stated that outcomes delivered to the observed player would not affect the earnings of the scanned player, we cannot rule out that observing punishments was rewarding to participants.

In conclusion, we found two sets of regions that preferentially processed outcomes actually received by participants or observed outcomes received by a confederate. Within these areas, there was local context-based adaptation of the coding of outcomes represented in both overall activity level changes, as well as spatial patterns as analyzed using multivariate searchlight decoding. The finding of concurrent absolute and partial adaptation in value encoding regions supports ideas from behavioral economics that advocate flexible reference dependence and illustrate how neural processing reconciles efficiency with precision of information. By demonstrating that these mechanisms also extend into the processing of observed outcomes, our results suggest common neural principles for value representation during both nonsocial and social decision making.