Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Aug 31;56(9):1762–1775. doi: 10.1021/acs.jcim.6b00211

Building Graphs To Describe Dynamics, Kinetics, and Energetics in the d-ALa:d-Lac Ligase VanA

Nathalie Duclert-Savatier 1, Guillaume Bouvier 1, Michael Nilges 1, Thérèse E Malliavin 1,*
PMCID: PMC5039762  PMID: 27579990

Abstract

graphic file with name ci-2016-00211r_0010.jpg

The d-Ala:d-Lac ligase, VanA, plays a critical role in the resistance of vancomycin. Indeed, it is involved in the synthesis of a peptidoglycan precursor, to which vancomycin cannot bind. The reaction catalyzed by VanA requires the opening of the so-called “ω-loop”, so that the substrates can enter the active site. Here, the conformational landscape of VanA is explored by an enhanced sampling approach: the temperature-accelerated molecular dynamics (TAMD). Analysis of the molecular dynamics (MD) and TAMD trajectories recorded on VanA permits a graphical description of the structural and kinetics aspects of the conformational space of VanA, where the internal mobility and various opening modes of the ω-loop play a major role. The other important feature is the correlation of the ω-loop motion with the movements of the opposite domain, defined as containing the residues A149–Q208. Conformational and kinetic clusters have been determined and a path describing the ω-loop opening was extracted from these clusters. The determination of this opening path, as well as the relative importance of hydrogen bonds along the path, permit one to propose some key residue interactions for the kinetics of the ω-loop opening.

1. Introduction

The development of bioinformatics has been initially driven not only by the enormous quantity of data that the biologist community was able to produce during the last decades, but also by the necessity of finding approaches to organize and better analyze these huge datasets. Although the protein structures constitute small datasets with respect to many other data encountered in biology, they nevertheless represent a challenge for the data analysis, as the relative positions of atomic coordinates in a protein structure take values in the continuous three-dimensional (3D) space. The large variability of protein features is obvious from the variety of physicochemical properties among a given family of proteins.1 Furthermore, the full understanding of a protein function requires, in addition of the knowledge of its structure, the knowledge of the internal dynamics and thus of the conformational landscape of the protein, which correspond to large datasets.

Graphs are traditionally used for modeling biological datasets, as for the analysis of protein–protein and molecular interaction networks,2−9 for description of drug function,10−16 for the description of interactions within a protein,17−19 for the description of the hierarchy of local minima in the conformational space.20−22 In the description of protein conformational space, the determination of such a graph is hampered by the need to (i) simplify the protein local geometry without loss of information and (ii) find a generic approach for graph determination, while preserving the specificity of each protein. In contrast, the description of protein structure and dynamics through graphs would allow one to (i) relate structure description, conformational variability, and protein function; (ii) unify the structural and dynamical representations; and (iii) obtain, for a given protein, a model that could be interfaced with the graphs described at the cellular level, as the interactome network.23

In order to investigate the points quoted above, we have been using several processing tools to describe the graphs underlying the structural and dynamical features of the d-Ala:d-Lac (VanA) ligase:

  • (i)

    the self-organizing maps,24 to convert the conformational space in a two-dimensional (2D) map;

  • (ii)

    the Louvain greedy algorithm,25 to determine kinetic clusters in the conformational space;

  • (iii)

    the Girvan–Newmann algorithm, to determine contact communities within the protein structure, which was already used in other structural objects;26,27 and

  • (iv)

    the analysis of hydrogen bonds within the protein structure, using a machine-learning approach (Random Forest28).

The conformational space has been explored using an enhanced sampling approach: the temperature-accelerated molecular dynamics (TAMD).29−41

The d-Ala:d-Lac ligase (VanA) is present in cases of resistance to the glycopeptide antibiotic vancomycin in Enterococcus faetium and Staphylococcus aureus.42,43 VanA synthesizes a modified precursor d-Ala-d-Lac instead of the usual d-Ala-d-Ala, synthesized by using a d-Ala:d-Ala ligase.44 This depsipeptide is then fixed at the end of the N-acetyl-muramyl-l-Ala-d-Glu-l-Lys-d-Ala-d-Lac monomers involved in the building of the peptidoglycan, giving rise to a fully efficient cell wall while preventing the binding of vancomycin.

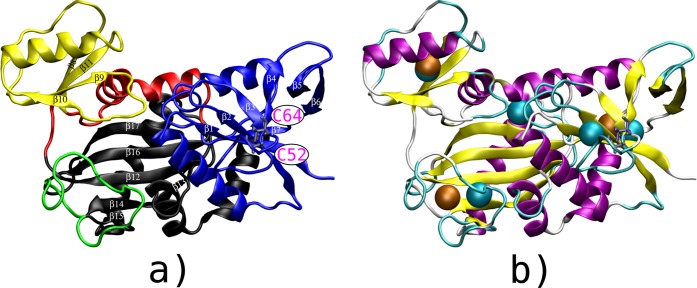
The X-ray crystallographic structure of VanA45 (Figure 1a) includes the domains N-terminal (residues A2–G121 shown in blue), central (residues C122–S211 shown in red and yellow), and C-terminal (residues G212–A342 shown in black and green). The ω-loop (shown in green in Figure 1a, residues L236–A256) is part of the C-terminal domain and closes the binding site where the ligase enzymatic reaction occurs. The two-layer β-sandwich (residues A149–Q208) is a region opposite to the ω-loop in the structure and colored yellow in Figure 1a. It was called “opposite domain” in a previous work.46 The binding site is located at the interface between N-terminal, central, and C-terminal domains. Concerted motions of the opposite domain and of the ω-loop allow the opening of the binding cavity to release the product of the catalytic reaction and accept new ligands.46

Figure 1.

Figure 1

Open in a new tab

(a) Three-dimensional (3D) view of the X-ray crystallographic structure of VanA, colored according to its domains: the N-terminal [A2–G121] shown in blue, the C-terminal [G212–A342] shown in black, which includes the ω-loop [L236–A256] shown in green, and the central domain [C122–S211] shown in red, which includes the opposite domain [A149–Q208] shown in yellow. The disulfide bridge C52–C64, located in the N-terminal domain, is shown with magenta labels (bottom right). (b) Localization of the collective variables (CV) used for the different TAMD calculations on a cartoon view of VanA extracted at the end of a 10 ns MD trajectory. The three structural CV are shown in orange and the five CV obtained from contact communities calculations are shown in cyan.

The bioinformatics approaches described above have been applied to MD and TAMD trajectories recorded on VanA. Several graph models describing the structural architecture, internal dynamics, and the opening of the ω-loop, have been established. These models give an extended view of the structural and dynamical features of VanA and agree with the experimental knowledge available for the protein function.

2. Materials and Methods

2.1. Molecular Dynamics Simulation

The starting point of the simulations was the X-ray crystallographic structure of the d-Ala:d-Lac ligase (VanA) from Enterococcus faecium BM4147 VanA (PDB ID: 1E4E).45 The co-crystallized ligands, ADP and phosphinate (1(S)-aminoethyl-(2-carboxypropyl)phosphoryl-phosphinic acid), located in the active site were removed. The C52–C64 disulfide bridge, observed in the crystal was disrupted to be as close as possible to the physiological state of the d-Ala:d-Ala ligase.47

The force field CHARMM22 including the correction map (CMAP)48,49 was used. The system was neutralized with five Na+ counterions. Explicit TIP3P50 solvent water molecules were added to the systems using a cutoff of 10 Å. The solvated system includes 13585 water molecules. The molecular dynamics (MD) and the temperature-accelerated molecular dynamics (TAMD) trajectories were recorded using NAMD 2.7b2.51 A cutoff of 12 Å and a switching distance of 10 Å were defined for nonbonded interactions. Long-range electrostatic interactions were calculated with the Particule Mesh Ewald (PME) protocol.52

Before starting the initial MD trajectories, the system was initialized in the following way. It was first minimized using 1000 steps, then thermalized by heating the system from 0 to 300 K over 30 ps, with a time step of 1 fs. The system then is equilibrated in the NPT ensemble for 100 ps with a time step of 2 fs before a 40 ns MD simulation.

The analyzed trajectories were recorded in the NPT ensemble with periodic boundary conditions. The temperature was maintained at 300 K using a Langevin thermostat,53 and the 1 atm pressure was regulated using the Langevin piston Nose–Hoover method.54,55 The SHAKE algorithm56 kept all covalent bonds involving hydrogens rigid, so an integration time step of 2 fs was used for all MD simulations. Atomic coordinates were saved every picosecond.

2.2. TAMD Simulations

At the end of the first 10 ns of the MD trajectory, five independent 30-ns temperature-accelerated molecular dynamics (TAMD) simulations were launched (Table S2 in the Supporting Information). The TAMD approach is an enhanced sampling approach, based on the parallel evolution of the protein coordinates x in a classical MD simulation and of the target values z for the collective variables θα(x):

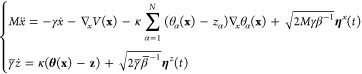2.2. 1

where x are the physical variables (atomic coordinates) of the system, θ(x) are the collective variables, and z the instantaneous target values of the collective variables. M is the mass matrix, V(x) is the empirical classical potential of the system, ηx,z(t) denotes white noise (i.e., Gaussian processes with mean 0 and covariance of ⟨ηαp(t)ηα′(t′)⟩ = δαα′δ(t – t′), with p = x,z), κ > 0 is the so-called spring force constant, γ and γ̅ > 0 are friction coefficients of the Langevin thermostats, β–1 = kBT, and β̅–1 = kBT̅, where kB is the Boltzmann constant and T and T̅ represent the temperatures.

Equation 1 describes the motion of x and z under the extended potential

2.2. 2

It was shown in ref (29) that, by adjusting the parameter κ, so that z(t) ≈ θ(x(t)), and the friction coefficient γ̅ so that the value of z moves slower than that of x, one can generate a trajectory z(t) in z-space that effectively moves at the artificial temperature T̅ on the free-energy hyper-surface F(z), which is defined at the physical temperature T. Hence, by construction, the limiting equation for z(t) in eq 1 samples the distribution e–β̅F(z). Then, using T̅ > T in eq 1) accelerates the exploration of the free-energy landscape by the z(t) trajectory, as energy barriers can be crossed more easily.

The value for the artificial friction γ̅ on the z variables can be determined following the principle that the separation of time scales between x and z must be such that the x have time to equilibrate before the z values move substantially. In practice, we proceeded as suggested in ref (57), i.e., we ran short standard MD trajectories with the collective variables restrained at θ(x) = z fixed, and monitored the mean force estimators Gj(N) defined for each collective variable j as

2.2. 3

where θj(x(ti)) is the instantaneous value at time ti of the collective variable. The time required for Gj(N) to reach a plateau (see Figure S1 in the Supporting Information) allows one to extract the characteristic time of relaxation of the Cartesian variables to a fixed value of the variables z, and hence an estimate of γ̅ to ensure the time-scales separation γ̅/γ. As the estimator (described in eq 3) converges in 5000 simulation time steps (0.002 ps), a friction γ of 50 ps–1, corresponding to a characteristic time of 0.02 ps, is sufficient to allow system relaxation.

The TAMD approach was implemented in NAMD using a tcl script.39,57 In TAMD, the evolution of the usual MD equation, at 300 K, was coupled to the evolution of collective variables at a much higher temperature. Several sets of collective variables were used, which were all geometric centers located in different protein regions.

The friction coefficient, γ = 0.5 ps–1, and the physical thermal energy, β–1 = 0.6 kcal/mol, are the parameters of the conventional Langevin thermostat, which allow one to obtain a simulation temperature of 300 K. The restraint force constant is set to κ = 100 kcal/(mol Å2).

TAMD trajectories were run using a value of 20 kcal mol–1 for the artificial thermal energy β̅–1 of the Langevin thermostat attached to the collective variables. This thermal energy corresponds to an artificial temperature T̅ of 10 060 K. Despite the high temperature values used for the Langevin thermostat attached to the collective variables, it is not expected that the folded structure of VanA would be destabilized, as a large friction (γ̅ = 50 ps–1) is used for this thermostat, along with the high force constant (κ = 100 kcal/(mol Å2) to restraint the collective variable coordinates to the collective variables. In that way, we reduce the risk of system instability due to large deviation of the collective variables θ(x) from their target values z.

2.3. Determination of Contact Communities

The following method has been used to determine the contact communities of VanA along each recorded trajectory. At each trajectory frame, a contact is set up for all α-carbon pairs closer than 12 Å,58 and the frequency of contacts is calculated along the trajectory. The protein structure is then considered as a graph, where the residues Cα constitute the vertices and the edges are weighted by the frequency of contacts between Cα atoms along the trajectories. An absence of contact is modeled as a nonexisting edge. The Girvan–Newman algorithm,59 as implemented in the program Python, allows one to divide, in an iterative way, the graph into contact communities. First, all possible shortest paths are calculated between the Cα and the betweenness of each edge, which is defined as the number of shortest paths crossing this edge, is computed. The algorithm then removes the edge exhibiting the most important betweenness and includes the two edge vertices into the same community. The betweenness of all edges affected by the removal is recalculated. Several runs of the algorithm are performed to remove the edge of highest betweenness until no edges remain. At the end of the process, the initial dynamic map of frequency of contacts has been split into contact communities of amino acids that are strongly connected.

2.4. Conformational Analysis of the Simulations Using SOM

The Self-Organizing Maps (SOM) approach24,60,61 was used to cluster the conformations generated along MD and TAMD trajectories. The SOM algorithm allows the mapping of the conformational space on a periodic subspace of reduced dimensions: a 50 × 50 map. 341 × 341 pairwise square Euclidean distance matrices D were calculated for the 341 Cα atoms of VanA, for each frame of the trajectory. To compress the data, a covariance matrix C was computed from each D. Its four eigenvectors, corresponding to the first four significant eigenvalues Ni were kept. For each trajectory frame t, the resulting compressed 4 × 341 matrix D · Vi=1,...,4, stored as a vector Vt, contains the conformational descriptors and is used to cluster the protein conformations.61

The SOM was trained in two phases with the following parameters: (i) a map size of 50 × 50 with periodic boundaries, initialized randomly with a constant learning rate of 0.5 and a radius of 6.250 for the first phase (180 000 iterations), and (ii) an exponential decrease of learning rate (starting at 0.25) and radius (starting at 3.125) for the second phase (360 000 iterations). After the random initialization of the map, vectors of conformational descriptors Vt described above, were presented to the map in random order,46 and the neuron closest to the presented Vt was updated, as well as the neighbor neurons to preserve the coherence of the clustering. At the end of the calculation, each neuron of the SOM contains a average vector ⟨Vt⟩ corresponding to a mixture of clustered protein conformations.

The Unified distance matrix (U-matrix) representation was computed to display the SOM topology on a bidimensional matrix. In the U-matrix, each node shows the local similarity between the corresponding neighboring SOM neurons, i.e., the mean distance between the node and its eight neighbors. A flooding algorithm was then used to aggregate the U-matrix basins, and to reject outside the regions corresponding to nonsimilar neurones, leading to a continuous map representation while preserving the inherent SOM topology.61

2.5. Graph Processing of the Self-Organizing Maps

The SOM were additionally processed in two ways in order to determine graphs describing (i) the kinetics of the conformational space sampled and (ii) the opening path between the closed and open conformations of VanA.

The graph related to the kinetics of the conformational space sampled was determined in the following way. A transition matrix is built from the SOM map. The SOM neurons define the microstates, and each structure along a given MD or TAMD trajectory is assigned to a given neuron. The element Tij of the transition matrix, depicting the transition between neurons i and j, is defined as the number of i → j transitions divided by the number of starts from neuron i. The transition matrix can be represented as a weighted graph, with the weight of the vertex ij being given by Tij.

The obtained graph is then partitioned using the greedy algorithm of Louvain,25 in order to maximize the graph modularity. The modularity is a value between −1 and +1, measuring the density of edges inside the partitions, compared to the density of edges outside the partitions. The greedy algorithm of Louvain optimizes the modularity in two phases.

In the first phase, each SOM neuron is assigned to distinct kinetic clusters. Then, for each SOM neuron u, the variation of modularity is evaluated when u is removed from its cluster and placed to the cluster of each of its neighbors. If no gain of modularity is possible, u remains in its cluster. In the second phase, a new graph is built by merging the SOM neurons belonging to the same cluster. The weights of the resulting graph are computed by summing the weights of the links between nodes in the corresponding two clusters.

The opening path between the VanA states displaying open and closed ω-loops was determined in the following way. Edges between SOM neurons were weighted by the value of the corresponding element of the U-matrix, which measures the local similarity between protein conformations. The starting point was the SOM node u corresponding to the starting point of all trajectories, with closed ω-loop. The final point of the path was chosen as the medoid of the SOM kinetic cluster 15 which will be described in section 3.3. The medoid is the neuron whose average distance to all the neurons in the cluster is minimal.

The shortest path is computed using the Dijkstra algorithm,62 using the similarity between neurons as a distance. Finally, the path defined from SOM neurons was converted to a series of VanA conformations by replacing each neuron by the VanA conformation exhibiting the smallest Euclidean distance between its vector of conformational descriptors Vt and the average of the neuron vector ⟨Vt⟩.

2.6. Analysis of Hydrogen Bonds within VanA

The path describing the ω opening has been analyzed to detect the most critical hydrogen bonds for the conformational change. For that purpose, along the opening path, a representative conformation was extracted from each kinetic cluster obtained above using the Louvain greedy algorithm.25 This representative conformation was chosen as the medoid of the path conformations belonging to this kinetic cluster.

On each of these VanA conformations, hydrogen bonds have been detected using criteria based on a survey of small-molecule crystal structures.63 This analysis was performed using the UCSF Chimera package,64 producing 1623 hydrogen bonds. A hydrogen bond is supposed to be established if the donor–acceptor and the hydrogen–acceptor distances are respectively smaller than 4.0 and 3.0 Å.

A Random Forest (RF)28 machine learning approach was used to calculate the importance of each hydrogen bond for predicting to which kinetic cluster the representative conformation belongs. The information on established and disrupted hydrogen bonds was encoded as a Boolean vector for each conformation populating the path. The hydrogen bonds were indexed by protein residue numbers. The Boolean vectors were used as descriptors to train the RF. The predicted value for each vector was the identifier of the kinetic cluster.

The RF calculation was performed using the Python package scikit-learn (scikit-learn.org). The number of trees in the forest was set to 10, with a Gini criterion28 to measure the quality of a split. The number of features used when searching for the best split was set to 40, which is approximately the square root of the length of the Boolean vectors (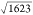Inline graphic ≈ 40). The trees are expanded until all leaves are pure. Once the training done, the importance of each hydrogen bond to define a kinetic cluster has been computed.

2.7. Ligand Docking Procedure and GBSA Scoring

The substrates, ATP, d-Ala, d-Lac, d-alanyl-phosphate (d-Ala(P)), the transition-state analogue phosphinate or PHY, the product of the reaction, d-Ala-d-Lac, and the allosteric binder,65 were formatted in mol2 with Chimera 1.464 and MarvinSketch 5.1 (www.chemaxon.com/products/marvin/marvinsketch) for docking.

UCSF DOCK 6.566−68 was used to perform ligand docking VanA conformations along the opening path obtained as described at the end of the section 2.5.

Chimera64 was used to add hydrogens, check atom assignment, and assign partial charges consistent with the AMBER-ff99SB force field.69 Chimera was also used to produce mol2 format files for the ligands and the selected conformations of the receptor. The DMS software program70,71 generated the molecular surface of the receptor, using a radius probe of 1.4 Å. Spheres then were calculated around the receptor with the DOCK 6.5 command “sphgen” with radius probe values varying between 1.4 Å and 4 Å.72 Spheres were selected within a radius of 10 Å around the geometric center defined by the residues E15, K170, R289, N303, E304, N306, which are close to positions observed for the ligands (ADP, phosphinate) in 1E4E. The grid encoding van der Waals and electrostatic interactions was precalculated with the “grid” tool72 in a box containing the selected spheres. The DOCK program builds up to 500 flexible ligand docking orientations, on the precalculated “grid” interaction map. The ligand poses were then re-scored with the implementation of the Hawkins Molecular Mechanics Generalized Born Surface Area (MM-GBSA) score,73−77 implemented in UCSF DOCK 6.5. The best scoring solution was kept for each protein–ligand pair.

3. Results

3.1. Choice of Collective Variables from the Structural and Community Domains of VanA

The use of the enhanced sampling approach TAMD requires the definition of collective variables. In the present work, these variables were chosen as geometric centers of α-carbons located in various VanA regions. These regions were detected (Table 1) from an analysis of the X-ray crystallographic structure of VanA (PDB ID: 1E4E) or from the contact communities determined by the Girvan–Newman algorithm, as described in section 2. Starting from these regions, two sets of geometric centers were determined (see Table S1 in the Supporting Information): structural collective variables (CVN-Xr, CVO-Xr, and CVω-Xr) and dynamical collective variables (CVω-Com, CVE0-Com, CVE1-Com, CVM-Com, and CVO-Com). Five independent 30-ns temperature-accelerated molecular dynamics (TAMD) simulations were launched using various combinations of both sets of collective variables (see Table S2 in the Supporting Information).

Table 1. Definition of the Different Domains of Protein VanAa.

domain residues determination method
N-terminal-Xr 2–121 structural
C-terminal-Xr 212–342 structural
Central-Xr 122–211 structural
Opposite-Xr 149–208 structural
Omega-Xr 236–256 structural
Ends_0-Com 2–7, 30–39, 69–78, 88–95, 108–120, 330–342 communities
Ends_1-Com 8–29, 40–68, 79–87, 96–103, 310–313 communities
Middle-Com 104–107, 121–147, 220–226, 277–289, 303–309 communities
Opposite-Com 148–210 communities
ω-Com 211–219, 227–276, 290–302, 314–329 communities
Open in a new tab
a

The first five domain definitions are derived from the analysis of the X-ray (Xr) crystallographic structure451E4E. The last five domain definitions are the communities obtained using the Girvan–Newman algorithm on the 30-ns MD trajectory.

The structural collective variables CVN-Xr, CVO-Xr, and CVω-Xr (Table S1 and Figure 1) were respectively defined on the N-terminal domain, opposite domain, and ω-loop, chosen from a direct observation of the PDB structure 1E4E. This choice is supported by several observations on X-ray crystallographic structures and MD trajectories.45−47 First, the ω-loop, containing CVω-Xr, displays diverse orientations in X-ray crystallographic structures of d-Ala:d-Ala ligases.45 Second, the opposite region (residues 149–208) was chosen to define CVO-Xr, as this region moves apart from the protein core, as published in a previous work.46

The dynamical collectives variables were derived from the contact communities calculated using the Girvan–Newman algorithm along a 30-ns MD trajectory: these communities are described in more detail below. The corresponding geometric centers are located in the ω-loop (CVω-Com), in the N-terminal and C-terminal domains (CVE0-Com, CVE1-Com), and in the middle (CVM-Com) and opposite (CVO-Com) domains (see Table S1 and Figure 1).

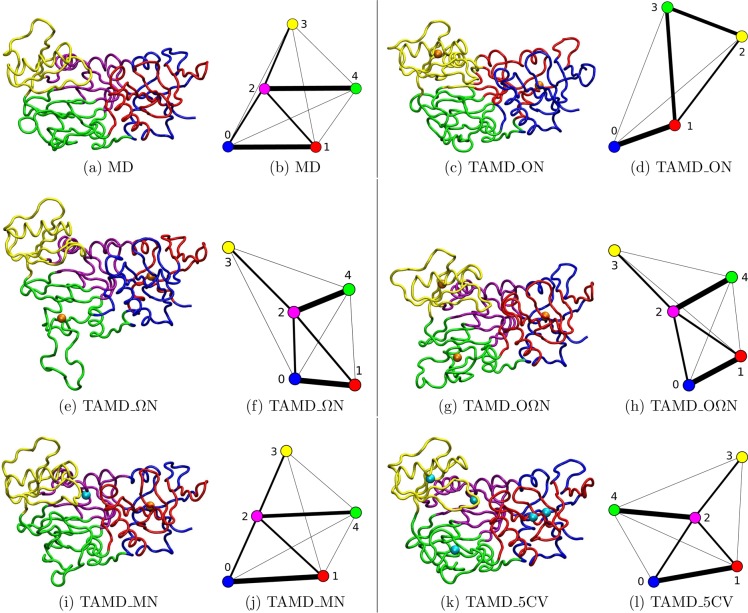
The contact community analysis based on the Girvan–Newman algorithm allowed one to divide VanA in five communities either in MD or in TAMD simulations, except in TAMD_ON, where four communities were observed (see Figure 2). These communities are variable from one simulation to another, but involve similar protein regions for all trajectories (see Table S3 in the Supporting Information), even though different sets of collective variables were used during each TAMD trajectory. The two Ends_0-Com and Ends_1-Com communities are interlaced in the protein sequence, and contain residues from the structural definition of the N- and C-terminal regions. The Opposite-Com community is located in the opposite domain, while the ω-Com community corresponds to the ω-loop and part of the C-terminal. The last community, Middle-Com (see Table S3), located in the middle of the protein and partially superimposed with the central structural domain Central-Xr (Table 1), is detected in all trajectories except TAMD_ON. The definition of contact communities are slightly different from the definitions of structural domains, except Opposite-Com, almost superimposed to the domain Opposite-Xr (Table 1). The good fit of Opposite-Com to Opposite-Xr is expected as the opposite domain was previously detected from an analysis of MD trajectories.46

Figure 2.

Figure 2

Open in a new tab

Communities determined by the Girvan–Newman algorithm59 along the MD and TAMD trajectories recorded on VanA. The same color code was kept for the communities both on the 3D structures and on the graphs: the communities mainly located in the N-terminal region (numbers 0 and 1) are shown in blue and red; the Middle (number 2) community is shown in magenta, if it exists; the Opposite region is shown in yellow (number 3); the ω-loop and the main part of the C-terminal are shown in green (number 4). Projection of the communities calculated on a 30-ns trajectory of VanA for (a) MD, (c) TAMD_ON, (e) TAMD_ωN, (g) TAMD_OωN, (i) TAMD_MD, and (k) TAMD_5CV. Also shown is a graph of the interconnectivity calculated between the different communities for (b) MD, (d) TAMD_ON, (f) TAMD_ωN, (h) TAMD_OωN, (j) TAMD_MD, and (l) TAMD_5CV. The collective variables (CV) used for TAMD trajectories are represented by orange balls when they were derived from structural calculations and cyan balls if they were obtained from the communities calculations.

The contact communities graph is connected by edges (Figure 2), which depict the frequency of contact between α-carbons belonging to two different communities. The larger the frequency, the thicker the edge.26,27 Thus, the edge thickness gives a qualitative indication of the relative influences that the communities have on each other. Overall, the same pattern of influences between communities is observed in all trajectories (Figure 2). The community corresponding to the ω-loop is always strongly linked with the opposite community, as reflected by the high betweenness. This communication is mostly mediated by the middle community (in purple). The opposite domain is itself connected to the Ends communities detected into the N- and C-terminal domains (shown in red and blue in Figure 2).

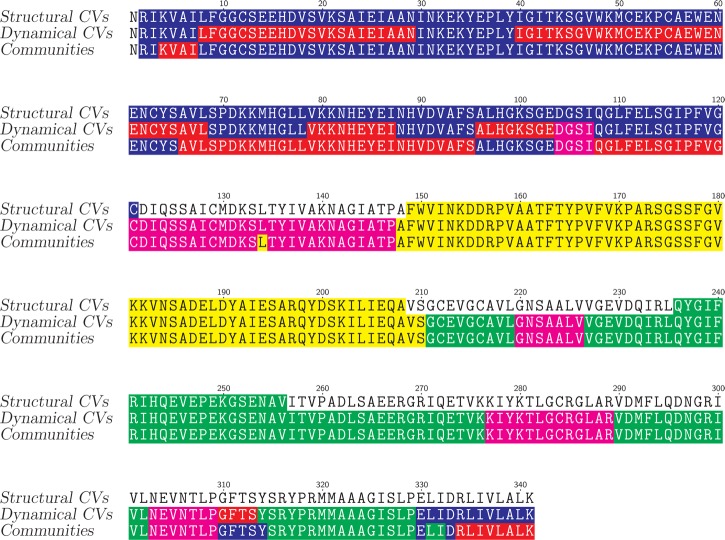
The definitions of structural, dynamical collective variables and of contact communities determined on the trajectory TAMD_ωN are depicted (Figure 3) using a color code. The definitions corresponding to the opposite domain (yellow) and to the ω-loop (green) are similar for the three sets of definition. Also, similar middle or central domains (magenta) are detected between dynamical collective variables and contact communities.

Figure 3.

Figure 3

Open in a new tab

Definition of collective variables (CV) and of contact communities displayed on the VanA sequence. The first line contains the definition of structural collective variables (CVN-Xr, CVO-Xr, CVω-Xr: see Table S1) determined from an analysis of the structure 1E4E. The second line contains the definition of dynamical collective variables (CVE0-Com, CVE1-Com, CVM-Com, CVO-Com, CVω-Com: Table S1) determined from a community analysis using the Girvan–Newman algorithm over the 30-ns MD trajectory. The third line contains the definition of communities (Ends_Oc, Ends_1c, Middle_c, Opposite_c, ω_c: see Table S3) determined by the Girvan–Newman algorithm on the trajectory TAMD_ωN. The following color code is used. For the structural CV: CVN-Xr (blue), CVO-Xr (yellow), and CVω-Xr (green). For the dynamical CV: CVE0-Com (blue), CVE1-Com (red), CVM-Com (magenta), CVO-Com (yellow), and CVω-Com (green). For the TAMD_ωN communities: Ends_Oc (blue), Ends_1c (red), Middle_c (magenta), Opposite_c (yellow), and ω_c (green).

3.2. Conformational Clustering of the Conformational Landscape

The existence of α helices and β strands has been monitored along the MD and TAMD trajectories (see Table S4 in the Supporting Information). Most of the secondary structure elements are present more than 80% of the time, at the exception of 5 β-strands, which are destabilized in the MD as well as in the TAMD trajectories. Thus, the folded structure of VanA is not specifically altered by the use of the TAMD, as has been already noticed in section section 2.2.

The 180 000 frames of VanA generated either along the MD or TAMD trajectories were subjected to a SOM clustering.46,61 The analysis of SOM permits one to determine six clusters of conformations (see Figure 4). For each cluster, the average VanA conformation has been drawn in tube representation, where the tube width and color depend on the conformational local variability (root-mean-square fluctuation (RMSF), Å) within the cluster. The color varies from blue (RMSF close to 1 Å) to red, corresponding to the maximal fluctuation in a given cluster (e.g., cluster 1, 13 Å; cluster 2, 13.3 Å; cluster 3, 15.7 Å; cluster 4, 7.9 Å; cluster 5, 8.0 Å; cluster 6, 8.4 Å). A permanent feature of the entire conformational landscape of VanA is the large internal mobility of the ω-loop. This agrees with the apo form of VanA simulated: the ω-loop tendency to open is expected to play an important role in the substrate processing.

Figure 4.

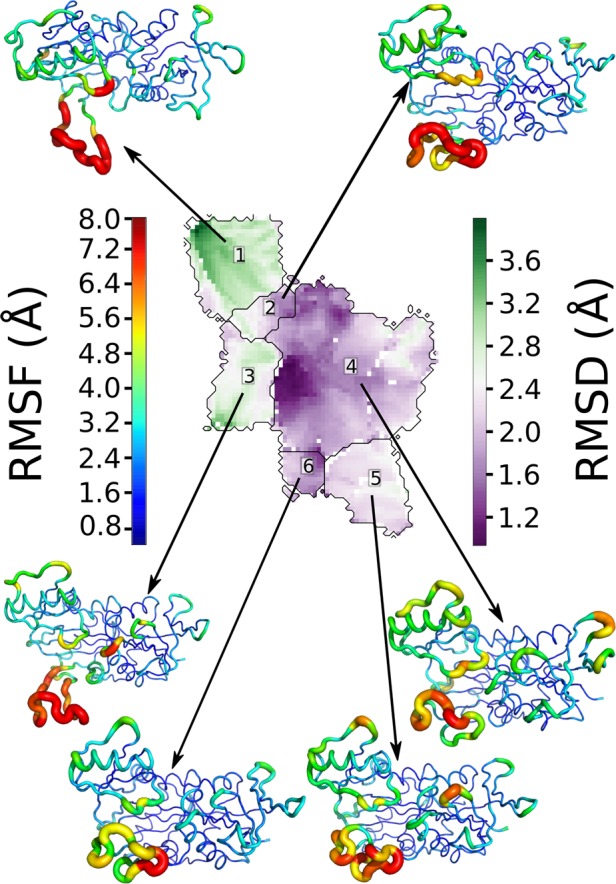
Figure 4

Open in a new tab

Clustering of VanA conformations sampled along MD and TAMD trajectories, using SOM. The root mean square deviation (RMSD) from the starting conformation of the trajectories is shown in a prune-green heat map (in Å). The conformation sets associated with the medoid of each cluster are depicted in putty cartoons. On the cartoons, the root-mean-square fluctuation (RMSF) of the backbone is represented by the width of the main chain and by a blue–green–red color scale corresponding to the RMSF values within the corresponding SOM cluster.

Cluster 4 contains the starting point of MD and TAMD trajectories. The average conformation of this cluster is characterized by three regions displaying large local RMSF: the ω-loop, the opposite domain, and three loops [residues I43–V48], [residues P71–H76], [residues N83–H84].

A first series of clusters, represented by clusters 1, 2, and 3, displays significant opening of the ω-loop, with the loop being the most open in clusters 1 and 3. In all of these clusters, the protein internal mobility remains concentrated on the ω-loop (with maximal RMSF values of 13 Å in cluster 1 and 15.7 Å in cluster 3) and the other regions are much less mobile, except the opposite domain (maximal RMSF value of 8.0 Å), the other maxima remaining ∼4–5 Å. Thus, after only 30 ns of simulation, the TAMD trajectories have been able to reach conformations displaying a wide opening of the ω-loop. These conformations are similar to the X-ray crystallographic structures published on the TtDdl d-Ala:d-Ala ligase (PDB ID: 2YZG).47

The second series of clusters, which is represented by clusters 5 and 6, displays conformations with semiopen or semiclosed ω-loop, similar to the X-ray crystallographic structure of the d-Ala:d-Ala ligase in ref (47) (PDB ID: 2ZDG). The averaged conformations of clusters 5 and 6 display large mobility of the ω-loop, as well as that of a few regions of the protein: the opposite domain and the three loops previously detected in cluster 4: [residues I43–V48], [residues P71–H76], [residues N83–H84].

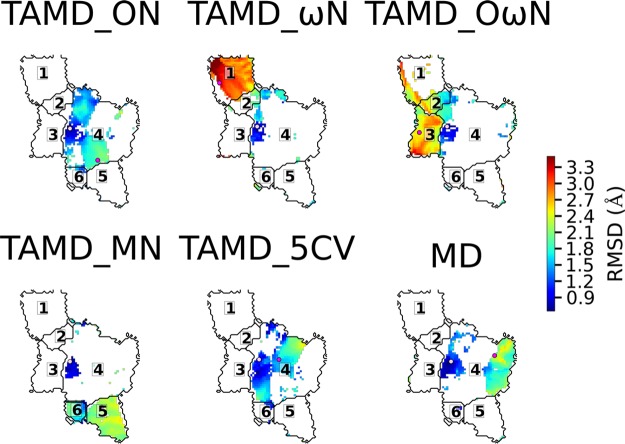
The various trajectories explored the U-matrix differently (see Figure 5). The larger cluster, cluster 4, was sampled by the different trajectories, but each one sampled distinct areas. The MD trajectory explored mainly cluster 4, keeping the coordinate RMSD value as low as 2.5 Å, with respect to the starting point (Figure 4), and performing few incursions into cluster 6. This result agrees with the previously recorded MD trajectories in the absence of the disulfide bridge C52–C64.46

Figure 5.

Figure 5

Open in a new tab

Detailed exploration of the SOM map by each trajectory. The starting points are shown in pink and the ending ones are shown in magenta. The blue–green–red color scale represents the local root-mean-square deviation (RMSD), from the starting structure for each structure (values shown are given in Å).

Although all TAMD trajectories started from the same conformation, the different choices for the collective variables, as well as the random evolution of MD simulations, induced distinct explorations of the conformational space. In that respect, three main behaviors were observed. The trajectories TAMD_ON and TAMD_5CV visited mainly cluster 4, containing the starting conformation. The trajectories TAMD_ωN and TAMD_OωN explored clusters 1, 2, and 3, corresponding to the opening of the ω-loop. The trajectory TAMD_MN explored regions 5 and 6. Therefore, it seems that the geometric center of the ω-loop is a required collective variable to obtain the loop opening. Frames extracted from TAMD_ΩN are plotted in Figure S2 in the Supporting Information, and reveals that, before the full opening, the ω-loop undergoes a sideways movement.

Overall, the cluster analysis of MD and TAMD trajectories provides an exploration of several possible models for ω-loop mobility. Indeed, protein conformations with fully open loop are obtained along with conformations displaying mobile closed ω-loop, corresponding to several conformational states explored by apo VanA.

3.3. Kinetic Clustering of the VanA Conformational Space

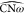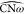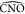The opening of the VanA binding cavity was monitored by following the values of the angles Inline graphic and Inline graphic between the centers of mass of the entire protein VanA (C), of the opposite domain (O), of the N-terminal (N), and of ω-loop (ω) (Figure 6a). The values of Inline graphic and Inline graphic angles were projected on the U-matrix (see Figures 6b and 6c). An increased value for Inline graphic corresponds to an opening of the ω-loop, while an increased value for Inline graphic corresponds to a displacement of the opposite domain apart from the VanA structure core.

Figure 6.

Figure 6

Open in a new tab

(a) Tube representation of VanA with the ω-loop in green and the opposite domain in yellow. Their own centers of mass is marked with a ball of the same color and respectively called ω and O. The center of mass of the entire protein VanA is called C (shown in red) and the center of mass of the N-terminal region, called N (shown in blue). 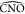(b, c) Projections of the angles on the SOM using a prune-green heat map: Inline graphic (panel (b)) and Inline graphic (panel (c)). The angles are expressed in degrees.

Some of the structural clusters previously determined from the SOM analysis (Figure 4) display homogeneous angle values while other clusters show much more heterogeneous values (see Figures 6b and 6c).

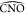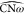Cluster 3, which contains some of the most open conformations of VanA (Figure 4) is very homogeneous. It exhibits the widest opening (∼55°) for the angle Inline graphic (Figure 6c), while Inline graphic (Figure 6b) is shrunk with a value of ∼52°, showing the opposite domain moving apart, with respect to the protein core, while the ω-loop is still closed. Unlike cluster 3, clusters 1 and 2, containing open ω-loops, display quite heterogeneous angle values. 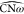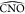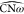The Inline graphic and Inline graphic are mostly mirrored, with large Inline graphic values (green regions in Figure 6c) corresponding to small Inline graphic values (violet regions in Figure 6b) and vice versa. This is the sign of an anticorrelation between the ω-loop and opposite domain displacements. Nevertheless, some regions of Figures 6b and 6c in clusters 1 and 2 display the same color, corresponding to simultaneous shrinkage or expansion of the two protein domains. 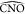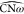For the conformations displaying the most closed ω-loop, sampled in clusters 4, 5, and 6, there is mainly little opening of the angles Inline graphic and Inline graphic.

To analyze the kinetics of the conformational exchange in VanA, the protein conformations were clustered by the Louvain greedy algorithm, taking into account the time order of the dynamic simulations, as described in section 2. In that way, 15 individual kinetic clusters were determined (see Figure 7). The conformations populating each kinetic cluster were sampled along the same trajectory, which is a sign that the different TAMD trajectories explored various aspects of the conformational kinetics. The division of SOM according to the kinetic clusters (Figure 7) display patterns quite similar to the ones observed for the projection of the angle Inline graphic or Inline graphic on the SOM (see Figures 6b and 6c), which proves that the overall system kinetics is mainly determined by these angle variations. However, the kinetics clustering brings additional information, with respect to the conformational clustering performed by SOM. 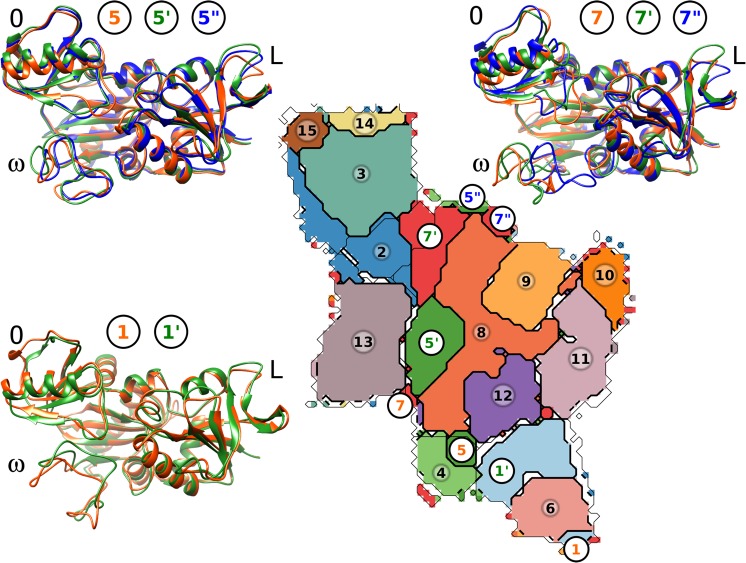Indeed, three clusters (1, 5, and 7) display nonconnected regions on the SOM, respectively labeled 1 and 1′, 5, 5′, and 5″, and 7, 7′, and 7″ on Figure 7, putting in evidence fast conformational equilibrium between distinct conformational regions. The representative conformations extracted from the nonconnected regions of each of three clusters, display conformational variability in precise regions of VanA, as the L and ω loops and the opposite domain (O). Different types of movements for these regions are observed within the three clusters, as shown by the superimposed representative conformations (Figure 7).

Figure 7.

Figure 7

Open in a new tab

Kinetic clustering of the VanA conformation using the Louvain greedy algorithm on the SOM neurones. A given color is associated with each of the 15 obtained clusters. For the three clusters, including nonconnected regions (1, 5, and 7), the disconnected regions are labeled, respectively, as 1 and 1′, 5 to 5″, and 7 to 7′′. The representative conformations corresponding to each disconnected region are drawn superimposed in cartoons.

3.4. A Path Describing the ω-Loop Opening

Starting from the kinetic clustering of SOM map and using a procedure described in section 2, a path relating the conformations of VanA with closed and open ω-loop has been traced on the U-matrix (see Figure 8a). The opening path starts from the kinetic cluster 5′ (Figure 7), passes through clusters 7′, 2, and 3, and ends up in cluster 15. The conformations sampled along this path correspond to a slight translational move of the ω-loop (conformational cluster 2 in Figure 4) and then to a rotation of the loop on the side (conformational cluster 1 in Figure 4). Note that the path through conformational clusters 2 and 1 presents the advantage of permitting a large opening, which allows the substrates to easily enter into the active site.

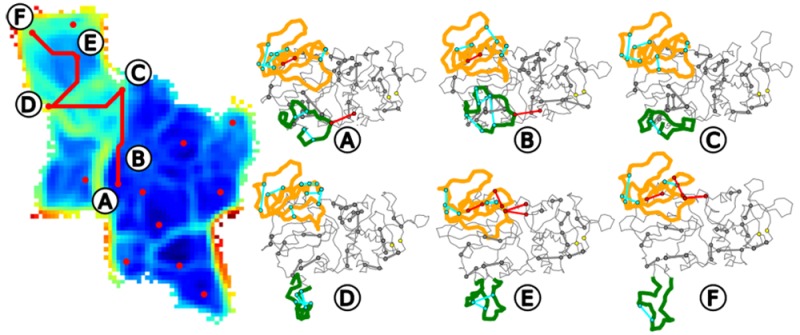
Figure 8.

Figure 8

Open in a new tab

(a) Opening path traced on the U-matrix. The medoids of each clusters, labeled from A to F, are shown in red and their minimum spanning link is shown in red. (b) GBSA score (in kcal/mol) for the molecules involved in the enzymatic reaction: the substrates d-Ala, d-Ala-(P), d-Lac; the reaction intermediate homologous, PHY; the product of the enzymatic reaction d-Ala-d-Lac; and an allosteric inhibitor.65 The GBSA score is plotted along the conformations labeled from 0 to 60, extracted from the opening path.

Since the opening of the VanA binding site is directly related to the protein function, we analyzed the path with respect to the interaction of VanA with the substrates, inhibitors, and reaction intermediate. The relative importance of hydrogen bonds within VanA along the path then was statistically evaluated, and connected to experimental observations.

Several ligands (d-Ala, d-Ala(P)), d-Lac, PHY, d-Ala-d-Lac, and an allosteric inhibitor65) were docked into the VanA conformations extracted from the path and the poses scored using the GBSA interaction energy (Figure 8b),75,76 according to the procedure described in section 2. The score profile displayed by the allosteric inhibitor (green curve in Figure 8b) is quite negative and constant. Similarly, the score profile of d-Ala (red curve in Figure 8b) is also negative and does not display much variation along the path, which is in agreement with the fact that d-Ala is not specific of VanA, but rather binds to all proteins of the d-Ala:d-Lac ligase family. In contrast, the other ligands—d-Ala(P), d-Lac, PHY, and d-Ala-d-Lac—all display profiles, becoming mostly negative in cluster E of the path, after the ω-loop opening (see Figure 8b). Before this opening, the reaction product d-Ala-d-Lac (orange curve in Figure 8b) displays repulsion for VanA, which agrees with the release of the product after reaction. The intermediate of reaction, PHY, displays a behavior similar to that of the other compounds.

Six conformations, labeled A to F, were picked up in each of the kinetic clusters crossed by the path (Figure 8a). On these conformations, a Random Forest approach, described in section 2, was used to determine the relative importance of hydrogen bonds for the kinetic cluster prediction (Figure 9). The most important hydrogen bonds are mainly located in the N-terminal domain, in the opposite domain, and in the ω-loop, which reflects the displacements of these domains described above. In addition, some important hydrogen bonds are observed in the C-terminal region.

Figure 9.

Figure 9

Open in a new tab

Most important hydrogen bonds for the prediction of the kinetic cluster along the opening path. The protein structure is displayed in trace, with the Opposite domain (residues [149–208]) colored orange and the ω-loop (residues [236–256]) colored green. The hydrogen bonds within the ω-loop and the opposite domain are colored cyan, and the hydrogen bonds between these protein domains and other protein regions are colored red. The other hydrogen bonds are gray.

The hydrogen bonds connecting residues from different regions have been colored red in Figure 9. From this outline, the breaking of interactions between protein domains can be followed along the opening path in order to give a description of the kinetic events. The two interactions E250–K22 (between ω-loop and N-terminal region) and E207-Y137 (between the opposite domain and the N-terminal region) are broken in the protein conformation labeled C (Figure 9). On the other hand, hydrogen bonds E207–Y137, K203–D132, R174–D105, and, to a lesser extent, R174–E104 are formed in the two conformations E and F at the end of the path. The change from the first set of hydrogen bonds to the second set gives a description of the opening, involving only few residues, and can be compared to the patterns of experimental mutations observed for VanA.

The E250A mutation induces a slight decrease in experimental catalytic efficiency,78 which would agree with the importance of the E250–K22 interaction along the opening of the ω-loop. The only limited decrease experimentally observed could arise from a possible reorganization of the VanA structure, which would be due to the presence of residues compensating for the mutation effect. Besides, in the X-ray crystallographic structure of VanA,45 it was observed that the residues E15, S177, and H244 are involved in a network of hydrogen bonds preventing the entrance of water molecules that could impair the catalytic reaction by hydrolyzing the ligands. The residues K22 and E250 detected in the present analysis, are located, respectively, in the vicinity of E15 and H244, and could play a similar role.

The analysis of the trajectories in the frame of graph theory has permitted the determination of an opening path of VanA, allowing the entrance of substrates in the binding site. The path found agrees with the interaction energy profiles observed for various VanA ligands. The relative importance of hydrogen bonds is supported by some experimental observations.

4. Discussion

The d-Ala:d-Lac ligase VanA was analyzed by molecular modeling and various algorithmic tools, in order to obtain a phenomenological description of the protein internal dynamics and conformational landscape, based on graph models.

The comparison of MD and TAMD trajectories reveals the efficiency of TAMD to perform enhanced sampling of the protein conformational space. As expected, the regions of conformational space explored during TAMD trajectories are closely dependent on the collective variables used. In particular, the opening of the ω-loop seems to be favored if a geometric center of the ω-loop is included into the collective variables. The exploration of the conformational landscape has permitted us to describe two different modes of ω-loop opening: in one mode, ω opens through a translation, whereas in the other, a translation of ω is followed by a rotation.

The partial opening of the ω-loop has been previously46 observed spontaneously in MD trajectories in the presence of the crystallographic disulfide bridge C52–C64.45 The moving of the opposite domain, closely related to the opening of the active site, was also observed in these MD trajectories. One should notice that Roper et al.45 mentioned that this disulfide bridge was unexpected, because VanA is a bacterial intracellular enzyme that should behave in a reducing environment incompatible with the formation of the bridge. The enhanced sampling approach taken here made it possible to observe the opening in the absence of disulfide bridge. The dynamics features observed along the opening path, as the mobility of the opposite domain, are similar to the observations previously made46 in the presence of the disulfide bridge.

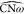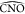The protein internal dynamics along the opening of the active site seems to be closely related to the relative mobility of the ω-loop and of the opposite domain, as shown by the conformational clustering (Figure 4), by the importance of the angles Inline graphic and Inline graphic (Figure 6), to describe the protein kinetics (Figure 7), and by the analysis of hydrogen bonds along the opening path (Figures 8 and 9).

MD and TAMD trajectories of d-Ala:d-Lac ligase VanA have been analyzed using various algorithms. Graph models describe the protein architecture and behavior in the conformational landscape, as well as along the conformational change related to the opening of the ω-loop.

The contact communities detected by analysis of the contacts along the trajectories display a pattern of connections relating the ω-loop to the middle domain, which acts as a hub to establish connection to the opposite and the N- and C-terminal domains. This pattern is conserved in most of the trajectories, whereas contrasted internal dynamics are observed in these protein regions over the conformational space (Figure 4). Indeed, the ω-loop is always quite mobile whereas other protein regions display large (clusters 5 and 6) to small (clusters 1, 2 and 3) internal mobility (Figure 4).

The various graphs obtained on the contact communities, or on the SOM, display characteristics similar to those observed in other bioinformatics graphs obtained in different contexts, for example, in hub, Middle-Com, observed in the graph of contact communities (Figure 2). Such hubs have been also observed in protein–protein interaction networks.79 The graph of hydrogen bonds along the opening path reveals that all residues establishing discriminating hydrogen bonds are connected to <4 other residues (Figure 9), a property of ”small world” also encountered in chemo-informatics networks based on the ligand-set similarities.80

Several approaches have been proposed in the literature to describe the conformational space of proteins as graph of local minima. The analysis performed in ref (22) is based on Principal Component Analysis (PCA) of protein motion. However, the PCA-based analysis detects only linear correlation, whereas SOM can capture nonlinear correlations. The method proposed here is related to the Conformational Space Network (CSN), which was proposed by Yin et al.21 However, these authors used discrete structural class to cluster conformations. Similarly, in ref (20), the structures were clustered using an all-atom RMSD cutoff of 2.0 Å. In the present paper, we defined the so-called microstates as the elements of the SOM grid. This avoids having to define arbitrary structural classes to cluster the conformations. In addition, from an analysis of conformational transitions between SOM neurons, a method to detect the kinetics cluster is proposed, and put in evidence fast conformational exchange.

The graphs proposed here could be used in a systematic way in proteins for which structural information can be obtained, in order to insert these protein structural graphs into larger graphs as the ones observed in protein–protein interaction networks. Such model stacking would permit to relate directly phenotypic information to physicochemical interactions at the atomic level.

In the case of VanA, the graphs provide a model of the open/closed motion of the ω-loop, allowing one to perform the synthesis between various information. The influence of specific residues and/or conformations in such graphs provides candidates for directed mutagenesis studies.

The MD and TAMD trajectories allows an exploration of the VanA conformational space, which induces the observation of the ω-loop opening. As the closed loop blocks the entrance of the active site, understanding the way the loop is opening gives a qualitative view of the kinetics of the VanA enzymatic function. In the enhanced sampling approach, the time scale of opening events observed along TAMD trajectories is biased and cannot be used to give quantitative information on the opening kinetics. However, on the other hand, the conformations extracted along the opening path of the ω-loop, can be used for docking purposes. Indeed, during the ω-loop opening, the entire architecture of the VanA structure, as well as the active site geometry change. Docking ligands on the active site pocket modified by the ω-loop opening would block this site into an inactive conformation and would orient the docking prediction toward effective inhibitors of the VanA function. The protein conformations sampled during the opening path are available from the authors upon request.

5. Conclusion

The d-Ala:d-Lac ligase VanA have been exhaustively investigated by molecular dynamics and enhanced sampling simulations, in order to propose outlines of (i) protein architecture and (ii) protein conformational landscape. These two types of analyses have been conducted in parallel and give consistent results. The conformational landscape of VanA is characterized by a large mobility of the ω-loop, which displays different translational and rotational motions, with respect to the remaining part of the protein. This conformational view of the landscape is completed by a slightly different kinetic view, which fully agrees with an angular description of the relative mobility of the opposite domain and ω-loop. The importance of the relative motions of the opposite domain and ω-loop is further enforced by the contact communities analysis of the protein structure, showing a large influence between these two regions. Overall, the numerical and statistical tools used here provide parallel descriptions of the protein structure and of the protein conformational landscape, which are in global agreement.

Acknowledgments

This work was funded by the European Union (No. FP7-IDEAS-ERC 294809 to M.N.). CNRS and Institut Pasteur are acknowledged for funding.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jcim.6b00211.

  • Variation of the mean force estimator Gj(N), used to determine the characteristic time of relaxation of the Cartesian variable, and hence to give an estimate of γ̅ in TAMD to ensure the time-scales separation γ̅/γ (Figure S1); conformations of VanA extracted along the trajectory TAMD_ΩN and displaying an opening of the loop ω (Figure S2); definition of the collectives variables used during the TAMD trajectories (Table S1); list of TAMD trajectories along with their corresponding sets of collective variables (Table S2); definition of the different communities calculated using the Girvan–Newman algorithm over the MD and TAMD trajectories (Table S3); and time percentage formation of the α helices and β strands along MD and TAMD trajectories (Table S4) (PDF)

Author Contributions

† These authors contributed equally to the work.

The authors declare no competing financial interest.

Supplementary Material

ci6b00211_si_001.pdf (1,018.6KB, pdf)

References

  1. Tóth-Petróczy Á; Tawfik D. S. The Robustness and Innovability of Protein Folds. Curr. Opin. Struct. Biol. 2014, 26, 131–138. 10.1016/j.sbi.2014.06.007. [DOI] [PubMed] [Google Scholar]
  2. Winterbach W.; Van Mieghem P.; Reinders M.; Wang H.; de Ridder D. Topology of Molecular Interaction Networks. BMC Syst. Biol. 2013, 7, 90. 10.1186/1752-0509-7-90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Zhang Y.; Gao P.; Yuan J. S. Plant Protein–Protein Interaction Network and Interactome. Curr. Genomics 2010, 11, 40. 10.2174/138920210790218016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Rual J.-F.; Venkatesan K.; Hao T.; Hirozane-Kishikawa T.; Dricot A.; Li N.; Berriz G. F.; Gibbons F. D.; Dreze M.; Ayivi-Guedehoussou N.; Klitgord N.; Simon C.; Boxem M.; Milstein S.; Rosenberg J.; Goldberg D. S.; Zhang L. V.; Wong S. L.; Franklin G.; Li S.; Albala J. S.; Lim J.; Fraughton C.; Llamosas E.; Cevik S.; Bex C.; Lamesch P.; Sikorski R. S.; Vandenhaute J.; Zoghbi H. Y.; Smolyar A.; Bosak S.; Sequerra R.; Doucette-Stamm L.; Cusick M. E.; Hill D. E.; Roth F. P.; Vidal M. Towards a Proteome-Scale Map of the Human Protein–Protein Interaction Network. Nature 2005, 437, 1173–1178. 10.1038/nature04209. [DOI] [PubMed] [Google Scholar]
  5. Li S.; Armstrong C. M.; Bertin N.; Ge H.; Milstein S.; Boxem M.; Vidalain P.-O.; Han J.-D. J.; Chesneau A.; Hao T.; Goldberg D. S.; Li N.; Martinez M.; Rual J.-F.; Lamesch P.; Xu L.; Tewari M.; Wong S. L.; Zhang L. V.; Berriz G. F.; Jacotot L.; Vaglio P.; Reboul J.; Hirozane-Kishikawa T.; Li Q.; Gabel H. W.; Elewa A.; Baumgartner B.; Rose D. J.; Yu H.; Bosak S.; Sequerra R.; Fraser A.; Mango S. E.; Saxton W. M.; Strome S.; van den Heuvel S.; Piano F.; Vandenhaute J.; Sardet C.; Gerstein M.; Doucette-Stamm L.; Gunsalus K. C.; Harper J. W.; Cusick M. E.; Roth F. P.; Hill D. E.; Vidal M. A Map of the Interactome Network of the Metazoan C. Elegans. Science 2004, 303, 540–543. 10.1126/science.1091403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ho Y.; Gruhler A.; Heilbut A.; Bader G. D.; Moore L.; Adams S.-L.; Millar A.; Taylor P.; Bennett K.; Boutilier K.; Yang L.; Wolting C.; Donaldson I.; Schandorff S.; Shewnarane J.; Vo M.; Taggart J.; Goudreault M.; Muskat B.; Alfarano C.; Dewar D.; Lin Z.; Michalickova K.; Willems A. R.; Sassi H.; Nielsen P. A.; Rasmussen K. J.; Andersen J. R.; Johansen L. E.; Hansen L. H.; Jespersen H.; Podtelejnikov A.; Nielsen E.; Crawford J.; Poulsen V.; Sørensen B. D.; Matthiesen J.; Hendrickson R. C.; Gleeson F.; Pawson T.; Moran M. F.; Durocher D.; Mann M.; Hogue C. W. V.; Figeys D.; Tyers M. Systematic Identification of Protein Complexes in Saccharomyces Cerevisiae by Mass Spectrometry. Nature 2002, 415, 180–183. 10.1038/415180a. [DOI] [PubMed] [Google Scholar]
  7. Rain J.-C.; Selig L.; De Reuse H.; Battaglia V.; Reverdy C.; Simon S.; Lenzen G.; Petel F.; Wojcik J.; Schächter V.; Chemama Y.; Labigne A.; Legrain P. The Protein–Protein Interaction Map of Helicobacter Pylori. Nature 2001, 409, 211–215. 10.1038/35051615. [DOI] [PubMed] [Google Scholar]
  8. Shen R.; Guda C. Applied Graph-Mining Algorithms to study Biomolecular Interaction Networks. BioMed Res. Int. 2014, 2014, 1. 10.1155/2014/439476. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Han J.-D. J.; Bertin N.; Hao T.; Goldberg D. S.; Berriz G. F.; Zhang L. V.; Dupuy D.; Walhout A. J.; Cusick M. E.; Roth F. P.; Vidal M. Evidence for Dynamically Organized Modularity in the Yeast Protein-Protein Interaction Network. Nature 2004, 430, 88–93. 10.1038/nature02555. [DOI] [PubMed] [Google Scholar]
  10. Fliri A. F.; Loging W. T.; Volkmann R. A. Cause-Effect Relationships in Medicine: A Protein Network Perspective. Trends Pharmacol. Sci. 2010, 31, 547–555. 10.1016/j.tips.2010.07.005. [DOI] [PubMed] [Google Scholar]
  11. Ma X.; Gao L. Biological Network Analysis: Insights into Structure and Functions. Briefings Funct. Genomics 2012, 11, 434–442. 10.1093/bfgp/els045. [DOI] [PubMed] [Google Scholar]
  12. Zhou T.-T. Network Systems Biology for Targeted Cancer Therapies. Aizheng 2012, 31, 134. 10.5732/cjc.011.10282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Sukumar N.; Krein M. P. Graphs and Networks in Chemical and Biological Informatics: Past, Present and Future. Future Med. Chem. 2012, 4, 2039–2047. 10.4155/fmc.12.128. [DOI] [PubMed] [Google Scholar]
  14. Yim K.; Cunningham D. Targeted Drug Therapies and Cancer. Recent Results Cancer Res. 2011, 185, 159–171. 10.1007/978-3-642-03503-6_10. [DOI] [PubMed] [Google Scholar]
  15. Lee S.; Park K.; Kim D. Building a Drug-Target Network and its Applications. Expert Opin. Drug Discovery 2009, 4, 1177–1189. 10.1517/17460440903322234. [DOI] [PubMed] [Google Scholar]
  16. Riccione K. A.; Smith R. P.; Lee A. J.; You L. A Synthetic Biology Approach to Understanding Cellular Information Processing. ACS Synth. Biol. 2012, 1, 389–402. 10.1021/sb300044r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Das A.; Gur M.; Cheng M. H.; Jo S.; Bahar I.; Roux B. Exploring the Conformational Transitions of Biomolecular Systems using a Simple Two-State Anisotropic Network Model. PLoS Comput. Biol. 2014, 10, e1003521. 10.1371/journal.pcbi.1003521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Chennubhotla C.; Bahar I. Signal Propagation in Proteins and Relation to Equilibrium Fluctuations. PLoS Comput. Biol. 2007, 3, 1716–1726. 10.1371/journal.pcbi.0030172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Maragakis P.; Karplus M. Large Amplitude Conformational Change in Proteins Explored with a Plastic Network Model: Adenylate Kinase. J. Mol. Biol. 2005, 352, 807–822. 10.1016/j.jmb.2005.07.031. [DOI] [PubMed] [Google Scholar]
  20. Krivov S. V.; Karplus M. Hidden Complexity of Free Energy Surfaces for Peptide (Protein) Folding. Proc. Natl. Acad. Sci. U. S. A. 2004, 101, 14766–14770. 10.1073/pnas.0406234101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Yin Y.; Maisuradze G.; Liwo A.; Scheraga H. Hidden Protein Folding Pathways in Free-Energy Landscapes Uncovered by Network Analysis. J. Chem. Theory Comput. 2012, 8, 1176–1189. 10.1021/ct200806n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Golas E.; Czaplewski C.; Scheraga H.; Liwo A. Common functionally Important Motions of the Nucleotide-binding Domain of Hsp70. Proteins: Struct., Funct., Genet. 2015, 83, 282–299. 10.1002/prot.24731. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Porras P.; Duesbury M.; Fabregat A.; Ueffing M.; Orchard S.; Gloeckner C. J.; Hermjakob H. A Visual Review of the Interactome of LRRK2: Using Deep-Curated Molecular Interaction Data to Represent Biology. Proteomics 2015, 15, 1390–1404. 10.1002/pmic.201400390. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kohonen T. Self-Organized Formation of Topologically Correct Feature Maps. Biol. Cybern. 1982, 43, 59–69. 10.1007/BF00337288. [DOI] [Google Scholar]
  25. Blondel V. D.; Guillaume J.-L.; Lambiotte R.; Lefebvre E. Fast Unfolding of Communities in Large Networks. J. Stat. Mech.: Theory Exp. 2008, 2008, P10008. 10.1088/1742-5468/2008/10/P10008. [DOI] [Google Scholar]
  26. Sethi A.; Eargle J.; Black A. A.; Luthey-Schulten Z. Dynamical Networks in tRNA: Protein Complexes. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 6620–6625. 10.1073/pnas.0810961106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Fuglestad B.; Gasper P. M.; McCammon J. A.; Markwick P. R.; Komives E. A. Correlated Motions and Residual Frustration in Thrombin. J. Phys. Chem. B 2013, 117, 12857–12863. 10.1021/jp402107u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Breiman L. Random Forests. Mach. Learn. 2001, 45, 5–32. 10.1023/A:1010933404324. [DOI] [Google Scholar]
  29. Maragliano L.; Vanden-Eijnden E. A Temperature Accelerated Method for sampling Free Energy and determining Reaction Pathways in Rare Events Simulations. Chem. Phys. Lett. 2006, 426, 168–175. 10.1016/j.cplett.2006.05.062. [DOI] [Google Scholar]
  30. Maragliano L.; Cottone G.; Ciccotti G.; Vanden-Eijnden E. Mapping the Network of Pathways of CO Diffusion in Myoglobin. J. Am. Chem. Soc. 2010, 132, 1010–1017. 10.1021/ja905671x. [DOI] [PubMed] [Google Scholar]
  31. Abrams C.; Vanden-Eijnden E. Large-scale conformational sampling of proteins using temperature-accelerated molecular dynamics. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 4961–4966. 10.1073/pnas.0914540107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Vashisth H.; Maragliano L.; Abrams C. ”DFG-flip” in the Insulin Receptor Kinase is facilitated by a Helical Intermediate State of the Activation Loop. Biophys. J. 2012, 102, 1979–1987. 10.1016/j.bpj.2012.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Vashisth H.; Brooks C. Conformational Sampling of Maltose-transporter Components in Cartesian Collective Variables is governed by the Low-frequency Normal Modes. J. Phys. Chem. Lett. 2012, 3, 3379–3384. 10.1021/jz301650q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Nygaard R.; Zou Y.; Dror R.; Mildorf T.; Arlow D.; Manglik A.; Pan A.; Liu C.; Fung J.; Bokoch M.; Thian F.; Kobilka T.; Shaw D.; Mueller L.; Prosser R.; Kobilka B. The Dynamic Process of β(2)-adrenergic Receptor Activation. Cell 2013, 152, 532–542. 10.1016/j.cell.2013.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Lapelosa M.; Abrams C. A Computational Study of Water and CO Migration Sites and Channels Inside Myoglobin. J. Chem. Theory Comput. 2013, 9, 1265–1271. 10.1021/ct300862j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Vashisth H.; Abrams C. All-atom Structural Models of Insulin Binding to the Insulin Receptor in the presence of a Tandem Hormone-binding Element. Proteins: Struct., Funct., Genet. 2013, 81, 1017–1030. 10.1002/prot.24255. [DOI] [PubMed] [Google Scholar]
  37. Scarpazza D.; Ierardi D.; Lerer A.; Mackenzie K.; Pan A.; Bank J. A.; Chow E.; Dror R.; Grossman J.; Killebrew D.; Moraes M.; Predescu C.; Salmon J.; Shaw D.. Extending the Generality of Molecular Dynamics Simulations on a Special-Purpose Machine. In Proceedings of the 27th IEEE International Parallel and Distributed Processing Symposium, 2013; pp 933–945 10.1109/IPDPS.2013.93. [DOI] [Google Scholar]
  38. Vashisth H.; Storaska A.; Neubig R.; Brooks C. Conformational Dynamics of a Regulator of G-protein Signaling Protein reveals a Mechanism of Allosteric Inhibition by a small Molecule. ACS Chem. Biol. 2013, 8, 2778–2784. 10.1021/cb400568g. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Selwa E.; Huynh T.; Ciccotti G.; Maragliano L.; Malliavin T. Temperature-accelerated Molecular Dynamics gives Insights into Globular Conformations Sampled in the Free State of the AC Catalytic Domain. Proteins: Struct., Funct., Genet. 2014, 82, 2483–2496. 10.1002/prot.24612. [DOI] [PubMed] [Google Scholar]
  40. Hosseini-Naveh Z. M.; Malliavin T.; Maragliano L.; Cottone G.; Ciccotti G. Conformational changes in Acetylcholine binding protein Investigated by Temperature accelerated Molecular Dynamics. PLoS One 2014, 9, e88555. 10.1371/journal.pone.0088555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Cortes-Ciriano I.; Bouvier G.; Nilges M.; Maragliano L.; Malliavin T. Temperature Accelerated Molecular Dynamics with Soft-ratcheting Criterion orients Enhanced Sampling by Low-resolution Information. J. Chem. Theory Comput. 2015, 11, 3446–3454. 10.1021/acs.jctc.5b00153. [DOI] [PubMed] [Google Scholar]
  42. Arthur M.; Reynolds P.; Courvalin P. Glycopeptide Resistance in Enterococci. Trends Microbiol. 1996, 4, 401–407. 10.1016/0966-842X(96)10063-9. [DOI] [PubMed] [Google Scholar]
  43. Courvalin P. Vancomycin Resistance in Gram-Positive Cocci. Clin. Infect. Dis. 2006, 42, 25–34. 10.1086/491711. [DOI] [PubMed] [Google Scholar]
  44. Arthur M.; Molinas C.; Bugg T.; Wright G.; Walsh C.; Courvalin P. Evidence for in vivo Incorporation of d-lactate into Peptidoglycan Precursors of Vancomycin-Resistant Enterococci. Antimicrob. Agents Chemother. 1992, 36, 867–869. 10.1128/AAC.36.4.867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Roper D.; Huyton T.; Vagin A.; Dodson G. The Molecular Basis of Vancomycin Resistance in clinically relevant Enterococci: Crystal Structure of d-alanyl–d-lactate Ligase (VanA). Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 8921–8925. 10.1073/pnas.150116497. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Bouvier G.; Duclert-Savatier N.; Desdouits N.; Meziane-Cherif D.; Blondel A.; Courvalin P.; Nilges M.; Malliavin T. E. Functional Motions Modulating VanA Ligand Binding unraveled by Self-organizing maps. J. Chem. Inf. Model. 2014, 54, 289–301. 10.1021/ci400354b. [DOI] [PubMed] [Google Scholar]
  47. Kitamura Y.; Ebihara A.; Agari Y.; Shinkai A.; Hirotsu K.; Kuramitsu S. Structure of d-alanine–d-alanine Ligase from Thermus Thermophilus HB8: Cumulative Conformational Change and Enzyme-ligand Interactions. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2009, 65, 1098–1106. 10.1107/S0907444909029710. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. MacKerell A.; Bashford D.; Bellott M.; Dunbrack R.; Evanseck J.; Field M.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Kuchnir L.; Kuczera K.; Lau F.; Mattos C.; Michnick S.; Ngo T.; Nguyen D.; Prodhom B.; Reiher W.; Roux B.; Schlenkrich M.; Smith J.; Stote R.; Straub J.; Watanabe M.; Wiórkiewicz-Kuczera J.; Yin D.; Karplus M. All-atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  49. MacKerell A. D.; Feig M.; Brooks C. L. Extending the Treatment of Backbone Energetics in Protein Force Fields: Limitations of gas-phase Quantum Mechanics in reproducing Protein Conformational Distributions in Molecular Dynamics Simulations. J. Comput. Chem. 2004, 25, 1400–1415. 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
  50. Jorgensen W. Quantum and Statistical Mechanical Studies of Liquids. 10. Transferable Intermolecular Potential Functions for Water, Alcohols, and Ethers. Application to Liquid Water. J. Am. Chem. Soc. 1981, 103, 335–340. 10.1021/ja00392a016. [DOI] [Google Scholar]
  51. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kale L.; Schulten K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Nam K.; Gao J.; York D. M. An efficient Linear-scaling Ewald Method for Long-range Electrostatic Interactions in Combined QM/MM Calculations. J. Chem. Theory Comput. 2005, 1, 2–13. 10.1021/ct049941i. [DOI] [PubMed] [Google Scholar]
  53. Frenkel D.; Smit B.. Understanding Molecular Simulation: from Algorithms to Applications, Vol. 1; Academic Press: New York, 2001. [Google Scholar]
  54. Martyna G. J.; Tobias D. J.; Klein M. L. Constant Pressure Molecular Dynamics Algorithms. J. Chem. Phys. 1994, 101, 4177–4189. 10.1063/1.467468. [DOI] [Google Scholar]
  55. Feller S. E.; Zhang Y.; Pastor R. W.; Brooks B. R. Constant Pressure Molecular Dynamics Simulation: the Langevin Piston Method. J. Chem. Phys. 1995, 103, 4613–4621. 10.1063/1.470648. [DOI] [Google Scholar]
  56. Ryckaert J.; Ciccotti G.; Berendsen H. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  57. Abrams C. F.; Vanden-Eijnden E. Large-scale Conformational Sampling of Proteins using Temperature-Accelerated Molecular Dynamics. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 4961–4966. 10.1073/pnas.0914540107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Vassura M.; Margara L.; Medri F.; di Lena P.; Fariselli P.; Casadio R.. Reconstruction of 3D Structures from Protein Contact Maps. In Bioinformatics Research and Applications; Springer: Berlin, Germany, 2007; pp 578–589. [Google Scholar]
  59. Girvan M.; Newman M. E. Community Structure in Social and Biological Networks. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 7821–7826. 10.1073/pnas.122653799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Kohonen T.Self-Organizing Maps; Springer Series in Information Sciences: Heidelberg, Germany, 2001. [Google Scholar]
  61. Bouvier G.; Desdouits N.; Ferber M.; Blondel A.; Nilges M. An Automatic Tool to Analyze and Cluster Macromolecular Conformations Based on Self-Organizing Maps. Bioinformatics 2015, 31, 1490–1492. 10.1093/bioinformatics/btu849. [DOI] [PubMed] [Google Scholar]
  62. Dijkstra E. A Note on Two Problems in Connexion with Graphs. Numer. Math 1959, 1, 269–271. 10.1007/BF01386390. [DOI] [Google Scholar]
  63. Mills J.; Dean P. M. Three-dimensional Hydrogen-bond Geometry and Probability Information from a Crystal Survey. J. Comput.-Aided Mol. Des. 1996, 10, 607–622. 10.1007/BF00134183. [DOI] [PubMed] [Google Scholar]
  64. Pettersen E.; Goddard T.; Huang C.; Couch G.; Greenblatt D.; Meng E.; Ferrin T. UCSF Chimera—A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 2004, 25, 1605–1612. 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
  65. Liu S.; Chang J. S.; Herberg J. T.; Horng M.-M.; Tomich P. K.; Lin A. H.; Marotti K. R. Allosteric Inhibition of Staphylococcus Aureus d-Alanine:d-Alanine Ligase revealed by Crystallographic Studies. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 15178–15183. 10.1073/pnas.0604905103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Shoichet B.; Bodian D.; Kuntz I. Molecular Docking using Shape Descriptors. J. Comput. Chem. 1992, 13, 380–397. 10.1002/jcc.540130311. [DOI] [Google Scholar]
  67. Meng E.; Shoichet B.; Kuntz I. Automated Docking with Grid-Based Energy Evaluation. J. Comput. Chem. 1992, 13, 505–524. 10.1002/jcc.540130412. [DOI] [Google Scholar]
  68. Lang P.; Brozell S.; Mukherjee S.; Pettersen E.; Meng E.; Thomas V.; Rizzo R.; Case D.; James T.; Kuntz I. DOCK 6: Combining Techniques to Model RNA-Small Molecule Complexes. RNA 2009, 15, 1219–1230. 10.1261/rna.1563609. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins: Struct., Funct., Genet. 2006, 65, 712–725. 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Richards F. Areas, Volumes, Packing and Protein Structure. Annu. Rev. Biophys. Bioeng. 1977, 6, 151–176. 10.1146/annurev.bb.06.060177.001055. [DOI] [PubMed] [Google Scholar]
  71. Connolly M. Solvent-Accessible Surfaces of Proteins and Nucleic Acids. Science 1983, 221, 709–713. 10.1126/science.6879170. [DOI] [PubMed] [Google Scholar]
  72. Kuntz I. D.; Blaney J. M.; Oatley S. J.; Langridge R.; Ferrin T. E. A Geometric Approach to Macromolecule-Ligand Interactions. J. Mol. Biol. 1982, 161, 269–288. 10.1016/0022-2836(82)90153-X. [DOI] [PubMed] [Google Scholar]
  73. Srinivasan J.; Cheatham T.; Cieplak P.; Kollman P.; Case D. A. Continuum Solvent Studies of the Stability of DNA, RNA, and Phosphoramidate-DNA Helices. J. Am. Chem. Soc. 1998, 120, 9401–9409. 10.1021/ja981844+. [DOI] [Google Scholar]
  74. Kollman P.; Massova I.; Reyes C.; Kuhn B.; Huo S.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini G.; Cieplak P.; Srinivasan J.; Case D.; Cheatham T. Calculating Structures and Free Energies of Complex Molecules: Combining Molecular Mechanics and Continuum Models. Acc. Chem. Res. 2000, 33, 889–897. 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
  75. Hawkins G. D.; Cramer C. J.; Truhlar D. G. Pairwise Solute Descreening of Solute Charges from a Dielectric Medium. Chem. Phys. Lett. 1995, 246, 122–129. 10.1016/0009-2614(95)01082-K. [DOI] [Google Scholar]
  76. Hawkins G. D.; Cramer C. J.; Truhlar D. G. Parametrized Models of Aqueous Free Energies of Solvation Based on Pairwise Descreening of Solute Atomic Charges from a Dielectric Medium. J. Phys. Chem. 1996, 100, 19824–19839. 10.1021/jp961710n. [DOI] [Google Scholar]
  77. Rizzo R.; Aynechi T.; Case D. A.; Kuntz I. Estimation of Absolute Free Energies of Hydration using Continuum Methods: Accuracy of Partial Charge Models and Optimization of Nonpolar Contributions. J. Chem. Theory Comput. 2006, 2, 128–139. 10.1021/ct050097l. [DOI] [PubMed] [Google Scholar]
  78. Lessard I. A.; Healy V. L.; Park I.-S.; Walsh C. T. Determinants for Differential Effects on d-Ala-d-lactate vs d-Ala-d-Ala Formation by the VanA Ligase from Vancomycin-resistant Enterococci. Biochemistry 1999, 38, 14006–14022. 10.1021/bi991384c. [DOI] [PubMed] [Google Scholar]
  79. Song J.; Singh M. From Hub Proteins to Hub Modules: the Relationship between Essentiality and Centrality in the Yeast Interactome at Different Scales of Organization. PLoS Comput. Biol. 2013, 9, e1002910. 10.1371/journal.pcbi.1002910. [DOI] [PMC free article] [PubMed] [Google Scholar]
  80. Hert J.; Keiser M. J.; Irwin J. J.; Oprea T. I.; Shoichet B. K. Quantifying the Relationships among Drug Classes. J. Chem. Inf. Model. 2008, 48, 755–765. 10.1021/ci8000259. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ci6b00211_si_001.pdf (1,018.6KB, pdf)

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES