STRUM: structure-based prediction of protein stability changes upon single-point mutation

Abstract

Motivation: Mutations in human genome are mainly through single nucleotide polymorphism, some of which can affect stability and function of proteins, causing human diseases. Several methods have been proposed to predict the effect of mutations on protein stability; but most require features from experimental structure. Given the fast progress in protein structure prediction, this work explores the possibility to improve the mutation-induced stability change prediction using low-resolution structure modeling.

Results: We developed a new method (STRUM) for predicting stability change caused by single-point mutations. Starting from wild-type sequences, 3D models are constructed by the iterative threading assembly refinement (I-TASSER) simulations, where physics- and knowledge-based energy functions are derived on the I-TASSER models and used to train STRUM models through gradient boosting regression. STRUM was assessed by 5-fold cross validation on 3421 experimentally determined mutations from 150 proteins. The Pearson correlation coefficient (PCC) between predicted and measured changes of Gibbs free-energy gap, ΔΔG, upon mutation reaches 0.79 with a root-mean-square error 1.2 kcal/mol in the mutation-based cross-validations. The PCC reduces if separating training and test mutations from non-homologous proteins, which reflects inherent correlations in the current mutation sample. Nevertheless, the results significantly outperform other state-of-the-art methods, including those built on experimental protein structures. Detailed analyses show that the most sensitive features in STRUM are the physics-based energy terms on I-TASSER models and the conservation scores from multiple-threading template alignments. However, the ΔΔG prediction accuracy has only a marginal dependence on the accuracy of protein structure models as long as the global fold is correct. These data demonstrate the feasibility to use low-resolution structure modeling for high-accuracy stability change prediction upon point mutations.

Availability and Implementation: http://zhanglab.ccmb.med.umich.edu/STRUM/

Contact: qiang@suda.edu.cn and zhng@umich.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Mutation and evolution in the human genome are mainly through single nucleotide polymorphisms (SNPs). With the developments of high-throughput array-based genotyping methods and the next generation sequencing technologies, a large volume of SNP data has been recently accumulated. It is estimated that around 58% of the exonic SNPs in the human genome can result in change in protein amino acid sequences, called ‘non-synonymous’ SNP or nsSNP (Tennessen et al., 2012). In many cases, the nsSNP mutations have little or no discernible effect on protein functions, but others are known to be responsible for many human diseases (Yates and Sternberg, 2013). Experimental measurements showed that nearly one-third of nsSNP mutations are deleterious to human health (Tokuriki and Tawfik, 2009). Recognizing such deleterious nsSNP mutations is of critical importance to both protein function annotation and disease diagnosis.

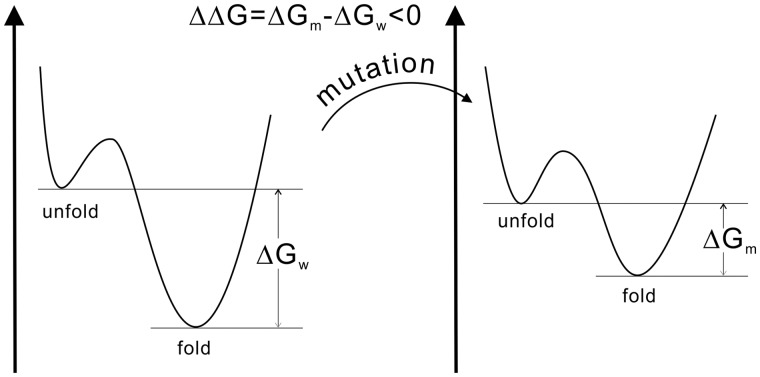
In the viewpoint of thermodynamics, the effects of the mutations can be assessed through changes on the thermal stability of protein systems. The stability of proteins can be quantitatively characterized by a simple two-state model (folded and unfolded, Fig. 1), where the difference in Gibbs free energy between the unfolded ($G_{\mathrm{u}}$) and the folded ($G_{\mathrm{f}}$) states, $\Delta \mathrm{G}=G_{\mathrm{u}}-G_{\mathrm{f}}$, is used to specify the fold stability. The higher and more positive $\Delta \mathrm{G}$ is, the more stable the protein is against denaturation. When a mutation occurs, the free energy landscape and the stability can change, where the free energy gap difference between wild type ($\Delta G_{\mathrm{m}}$) and mutant protein ($\Delta G_{\mathrm{w}}$), $\Delta \Delta \mathrm{G}=\Delta G_{\mathrm{m}}-\Delta G_{\mathrm{w}}$, is a measure of how mutation affects protein stability. Figure 1 illustrates an example where the mutation destabilized the protein by reducing the free energy gap between folded and unfolded states. In general, a ΔΔG below zero means that the mutation causes destabilization; otherwise, it induces stabilization.

Fig. 1.

Definition of stability change upon mutation in a two-state model

Although mutagenesis studies are important approach to experimentally characterizing the thermodynamic and physiological effects of nsSNPs, it is often too expensive and time-consuming for large-scale mutation studies. Computational mutation prediction becomes increasingly important with the rapid accumulation of sequence mutation data. Current computational approaches can be generally categorized into sequence-based and structure-based methods. One of the most popularly used sequenced-based methods is SIFT, which predicts whether an amino acid substitution affects protein function based on the degree of conservation of amino acid residues in multiple sequence alignments (MSAs) that are derived from closely related sequences. A Pearson correlation coefficient (PCC) of 0.55 was obtained by SIFT between the residue conservation and the number of experimentally determined deleterious mutations (Kumar et al., 2009; Ng and Henikoff, 2001). INPS (Fariselli et al., 2015) is another sequence-based method recently developed on SVM regression. By appropriate combination of evolutionary information, a PCC of 0.52 was obtained by INSP when tested in the protein-level cross-validations.

Recent studies have demonstrated considerable advantages in exploiting information of protein 3D structures in the mutation-induced stability change prediction. For instance, FoldX used a full atomic description of protein structure to estimate the importance of the interactions contributing to the stability of proteins and protein complexes, which generated $\Delta \Delta G$ predictions with a correlation 0.73 to the experimental data for 625 single point mutations (Guerois et al., 2002). FoldX was recently exploited by BindProf (Brender and Zhang, 2015), which shows that it can improve the prediction accuracy of mutation effects on protein binding interactions when combined with structure-based interface profiles. I-Mutant trained the stability models on the neighboring residue types within a 9 Å radius sphere and achieved an increase in the correlation of predicted and measured $\Delta \Delta G$ by 14% compared with the model based on sequence features alone (Capriotti et al., 2005). PoPMuSiC went further to take the spatial descriptors from the native structure of the wild-type protein and had the $\Delta \Delta G$ calculated by a linear combination of 13 knowledge-based terms on the protein structure, which resulted in a correlation of 0.8 between predicted and measured stability changes after exclusion of 10% outliers (Dehouck et al., 2009, 2011). ProMaya considered a meta-server approach to combine the structure features with $\Delta \Delta G$ predicted from different programs, which resulted in improved correlation of 0.79 on the validation datasets (Wainreb et al., 2011). More recently, NeEMO used residue connection networks in 3D structure to assess residue stability, achieving a PCC of 0.77 (Giollo et al., 2014). mCSM considered a similar idea of distance maps of vicinity atoms from the wild-type protein structure, which was combined with the pharmacophore counts to estimate the impact of mutations and achieved improved correlation over several competing methods (Pires et al., 2014).

Despite the advantage of the structure-based prediction, the majority of the methods were trained and benchmarked on the experimental structure of the target proteins. Some methods, e.g. ProMaya (Wainreb et al., 2011), require specifically the X-ray crystal structures as crystallography features such as B-factor are used. However, experimental structures are often not available for proteins; in fact, only <0.2% of proteins in the UniProt have a 3D structure in the PDB library. The lack of experimental structures renders many of the structure-based methods unfeasible for the practical application. Given the fast progress in protein structure prediction as witnessed by the community-wide CASP experiment (Moult et al., 2014), here we explore the possibility to use low-resolution models from non-homologous structure prediction to improve the mutation-induced stability change predictions. A new structure modeling approach, STRUM, is developed to combine various physics-based and knowledge-based energy terms, built on the I-TASSER predicted models, with the various sequence and template-based conversation scores to generate the stability change predictions. To examine the strength and weakness of the proposed method, multiple datasets are collected from experimental mutation databases, which will be used to carefully benchmark STRUM with other state of the art methods. The on-line server and standalone package of STRUM are freely available at http://zhanglab.ccmb.med.umich.edu/STRUM/.

2 Methods

2.1 Dataset construction

ProTherm (Kumar et al., 2006) is a protein mutation database that documents experimentally determined thermodynamic parameters published in the literature. To facilitate the training and testing of our methods, as well as the comparison to other methods that are most trained on experimental protein structures, we collected a representative dataset from ProTherm (updated on February 22, 2013). This set contains records from single-point mutations and having the protein structure experimentally solved in the PDB; it constitutes 3421 mutations involving 150 proteins, called Q3421 set. The WT sequences of the 150 proteins are listed at http://zhanglab.ccmb.med.umich.edu/STRUM/benchmark/Sequence.

Because the stability change $\Delta \Delta \mathrm{G}$ can be obtained from multiple measurements at different experimental conditions, we calculated the average $\Delta \Delta \mathrm{G}$ value for each mutation, using a weight scheme similar to Dehouck et al (2009), in which a higher weight is given to the $\Delta \Delta \mathrm{G}$ value measured at the pH close to 7, temperature close to 25°C, and with less additives, i.e.

$$\Delta \Delta G=\frac{{\sum }_{i=1}^n{w}_i^{pH}{w}_i^T{w}_i^{\mathrm{a}\mathrm{d}\mathrm{d}}\Delta \Delta G_i}{{\sum }_{i=1}^n{w}_i^{pH}{w}_i^T{w}_i^{\mathrm{a}\mathrm{d}\mathrm{d}}}\mathrm{ }\left(1\right)$$

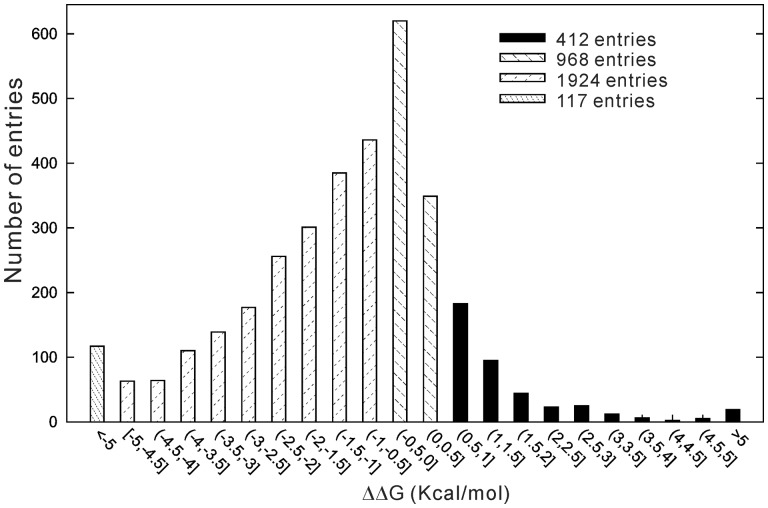
where n is the number of experiments on the same mutation, $\Delta \Delta G_i$ is the value by the ith experiments. $w_i^{pH}[=1-|p{H}_i-7|/7$], $w_i^T[=\mathrm{m}\mathrm{a}\mathrm{x}(0,\mathrm{ }1-|T_i-25|/25\left)\right]$ and $w_i^{\mathrm{a}\mathrm{d}\mathrm{d}}[={\Pi }_{j=1}^{k_i}(1-C_{ij}/C_j^{\mathrm{m}\mathrm{a}\mathrm{x}})$, if $k_i\ge 1$; or =1, if $k_i=0$] are weighting parameters, where $p{H}_i$, $T_i$, $k_i$ are the pH value, temperature, number of additives of ith experiment, $C_{ij}$ is the concentration of jth additive in the ith experiment, and $C_j^{\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{ }}$ is the maximum concentration for the jth additive. Figure 2 shows the histogram distribution of $\Delta \Delta G$ in the Q3421 dataset, where 2618 (or 77%) mutations have $\Delta \Delta G <0$ and 763 (or 22%) have $\Delta \Delta G \mathrm{ }>0$, which means that the majority of mutations have destabilized the protein fold.

Fig. 2.

The histogram distribution of $\Delta \Delta G$ in the dataset Q3421

Two other datasets (Dehouck et al., 2009) collected from the old versions of ProTherm were used as well. The first is S2648 that contains 2648 single-point mutations involved in 131 proteins; the second one, S350, contains 350 mutations in 67 proteins that is a randomly selected subset of the S2648 database. These two datasets have often been used in the previous studies, the use of which can facilitate comparison with other methods.

Since many studies used S2648 as training set, we constructed a new set, Q306, for more stringent tests, which contains 306 point mutations from 32 proteins that have a sequence identity < 60% to any proteins in the S2648. A detailed list of the Q3421 and Q306 datasets with mutation sites, $\Delta \Delta G$, temperature, and pH values are downloadable at http://zhanglab.ccmb.med.umich.edu/STRUM/benchmark/benchmark.tar.bz2.

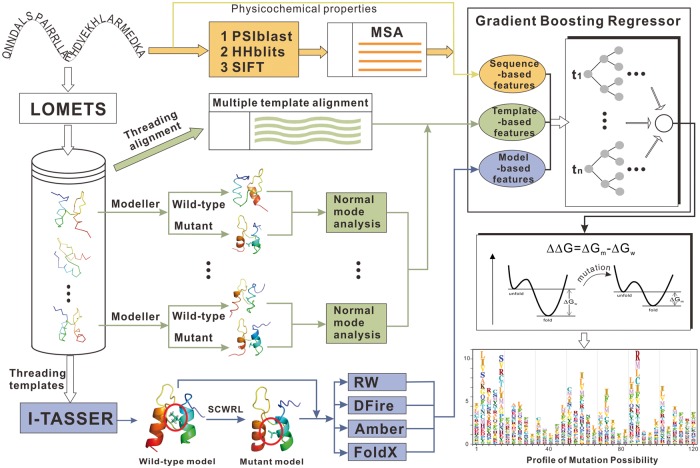
2.2 STRUM pipeline and feature design

STRUM is a machine learning-based mutation stability change predictor that was trained through gradient boosting regression on three groups of features (see Fig. 3). The first group of 37 features is derived from sequence composition and MSAs (called ‘sequence-based’); the second group of five features is from threading template alignments (or ‘threading-based’); and the last group of 78 features is built on the I-TASSER full-length structure prediction (or ‘I-TASSER-based’). A detailed list of all the 120 features is given in Supplementary Table S1. We first outline the feature extraction below.

Fig. 3.

Flowchart of STRUM for mutation-induced stability change prediction. Three sources of features from sequences (orange lines), threading alignments (green), and I-TASSER models (blue) are trained by gradient boosting regression for $\Delta \Delta G$ prediction. The final output is an all-to-all $\Delta \Delta G$ table and a visible mutation profile specifying the mutation probability to different amino acids at each position

2.2.1 Sequence-based features

Three types of the sequence-based features were derived. The first type contains 10 physicochemical properties of the wild type and mutant residues, including the amino acid identity, volume, weight, hydrophobicity scale and isoelectric point (Supplementary Table S1).

The second type of sequence-based features is a position specific conservation score derived from MSAs. Three tools are used to collect the MSA matrices. The first is from PSI-BLAST (Altschul et al., 1997) search through the NCBI non-redundant sequence database with three iterations and E-value cutoff 0.001; the second is from HHblits (Remmert et al., 2012) which generates MSAs by iterative profile-profile based hidden Markov model alignments through the UniProt sequence database (Bairoch et al., 2008); the third is from SIFT (Ng and Henikoff, 2001) that first uses PSI-BLAST to search through UniProt database and then has the MSAs reconstructed by iteratively adding conserved motifs from consensus sequence pairs.

The three MSAs from PSI-BLAST, HHblits and SIFT are combined into a unified matrix according to their alignment on the query sequence. A position specific scoring matrix (PSSM) is then constructed by (Altschul et al., 1997; Ng and Henikoff, 2001)

$$S_{ia}=\frac{N}{N+B_i}{f}_{ia}+\frac{B_i}{N+B_i}{c}_{ia}\mathrm{ }\left(2\right)$$

where N is the number of sequences in the composite MSAs. $f_{ia}$ is the weighted frequency counts of the amino acid a at ith position of MSAs using the Henikoff-Henikoff scheme (Henikoff and Henikoff, 1994), i.e.

$$\{\begin{array}{l}{f}_{ia}={\displaystyle \sum _{j=1}^N{w}_j\delta }(A_{ij}\in a)+\frac{1}{20}{\displaystyle \sum _{j=1}^N{w}_j\delta }(A_{ij}\in \text{gap})\\ w_{ij}=\frac{{\displaystyle {\sum }_{i=1}^L\frac{1}{n_i}\cdot \frac{1}{q_{ij}}}}{{\displaystyle {\sum }_{t=1}^N{\displaystyle {\sum }_{i=1}^L\frac{1}{n_i}\cdot \frac{1}{q_{it}}}}}\end{array}$$ (3)

where A_ij is the amino acid type at ith position of jth sequence, L is the length of query, n_i is the number of the distinct amino acid types at the ith position, q_ij is the number of times of A_ij appearing at the ith position. c_ia in Equation (2) is the pseudo-count designed to offset the deficiency of statistics by

$$c_{\mathrm{i}\mathrm{a}}=\frac{{\sum }_{t=1}^{20}\left(f_{it}\times \frac{B\left(t,a\right)}{\frac{1}{20}{\sum }_{d=1}^{20}B\left(t,d\right)}\right)}{{\sum }_{u=1}^{20}{\sum }_{t=1}^{20}\left(f_{it}\times \frac{B\left(t,u\right)}{\frac{1}{20}{\sum }_{d=1}^{20}B\left(t,d\right)}\right)}\mathrm{ }\left(4\right)$$

where B(t, a) is the mutation probability from amino acid t to a in BLOSUM62 (Henikoff and Henikoff, 1992). The total number of pseudo-count B_i is calculated by $B_i=\exp \left({\sum }_{a=1}^{20}{r}_a{f}_{ia}\right)$, where r_a is the rank of amino acid a in an ordered list from the highest to lowest score from the substitution matrix BLOSUM62 for the reference amino acid with the highest frequency at the ith position.

At each position i, the 20 PSSM scores are used as the training feature of STRUM. In addition, the overall conservation score

$$R_i={\log }_{2}20+{\displaystyle \sum _{a=1}^{20}{S}_{ia}{\log }_2{S}_{ia}}$$ (5)

is also used as the training feature (see Table S1).

The third type of sequence-based features is the local structure features derived from the target sequence. These include secondary structure prediction by PSSpred (Yan et al., 2013), specified by three states of coil, helix and strand; solvent accessibility by MUSTER (Wu and Zhang, 2008 b), and the backbone torsional angle ($\varphi , \psi$) by ANGLOR (Wu and Zhang, 2008a).

2.2.2 Threading template-based features

Starting from the wild-type sequence, multiple template structures are identified from the PDB library by LOMETS, a meta-server threading program that consists of 9 locally installed threading algorithms (Wu and Zhang, 2007). To filter out homologous contaminations, all templates with a sequence identity above 30% to the target or detectable by PSI-BLAST with an E-value below 0.05 are excluded from the template library. Based on the LOMET alignments, a set of N top templates is selected to construct the multiple template alignment (MTA) by mapping the template residues onto the query sequence. Here, N = 30 for the Easy targets that have at least one significant template for each threading program; and N = 50 for the rest of the Hard targets that have fewer or no significant hits.

Five different features are derived from the LOMETS based on MTA. The first two features describing residue conservations in threading alignments (listed as wBLSUM and mBLSUM in Supplementary Table S1) are calculated by

$$\left\{\begin{array}{c}S\left(A_i\right)=\frac{1}{N}\sum _{j=1}^N{T}_j\times B(A_i,A_{ij})\\ S\left(A_i^{\mathrm{\text{'}}}\right)=\frac{1}{N}\sum _{j=1}^N{T}_j\times B(A_i^{\mathrm{\text{'}}},A_{ij})\end{array}\right.$$ (6)

where A_i and $A_i^{\text{'}}$ are the wild-type and mutant amino acids at ith position of the query, respectively; A_ij is the amino acid type at ith position of jth template at MTA; and B(A_i, A_ij) is the BLOSUM62 mutation matrix as defined in Equation (4). T_j is the weighting factor of jth template based on the consensus TM-score by

$$T_j=\frac{1}{N-1}{\displaystyle \sum _{k=1}^{N-1}\text{TM}(j,k)}$$ (7)

where TM(j, k) is the TM-score between jth and kth LOMETS templates that is normalized by the length of the query protein (Zhang and Skolnick, 2004).

The third to fifth features are derived from the normal mode analysis (NMA) of the LOMETS template structures with the assumption that the mutations with sensitive stability changes can affect the motion and fluctuation of the target residues. First, full-length backbone models are quickly constructed by MODELLER (Sali and Blundell, 1993) from each LOMETS template for both wild-type and mutant sequences. The structure models are submitted to Bio3D (Skjaerven et al., 2014) for NMA based on a ‘C-alpha force field’ derived from fitting to the Amber94 all-atom potential. Features from NMA adopted by STURM include

$$\left\{\begin{array}{l}F\left(A_i\right)=\frac{1}{N}\sum _{j=1}^{N}T{}_j^w\times f_{ij}\left(S_w^j\right)\\ F\left(A_i^{\mathrm{\text{'}}}\right)=\frac{1}{N}\sum _{j=1}^N{T}_j^m\times f_{ij}\left(S_m^j\right)\\ R=\frac{1}{\mathit{N}}\sum _{j=1}^N\frac{T_j^w+T_j^m}{2}\times r_j(S_w^j,S_m^j)\end{array}\right.$$ (8)

where $f_{ij}\left(S_w^j\right)$ and $f_{ij}\left(S_m^j\right)$ are the conformational fluctuations relative to the equilibrium state for ith residues on jth MODELLER models from wild-type ($S_w^j$) and mutant ($S_m^j$) sequences, respectively. $r_j(S_w^j,S_m^j)$ is the root mean square inner product of the 10 lowest normal modes between $S_w^j$ and $S_m^j$. $T_j^{w,m}$ is similar to what was defined by Equation (7) but with TM-score calculated between the MODELLER models.

2.2.3 I-TASSER model-based features

I-TASSER is a hierarchical approach to protein structure prediction, which constructs full-length models by iteratively reassembling the structure fragments excised from the threading templates (Roy et al., 2010; Yang et al., 2015). We use the I-TASSER program to generate atomic structure models for the wild-type protein sequence. The structural model for the mutant sequence is reconstructed by SCWRL4 (Dunbrack and Cohen, 1997) by replacing the side-chain rotamers according to the mutated amino acids, followed by atomic-level FG-MD refinement simulations (Zhang et al., 2011). Again, all homologous templates with sequence identity >30% to the target or detectable by PSI-BLAST are excluded from the template library to avoid homology contaminates.

Three groups of energy potentials are used to evaluate the atomic interactions based on the wild-type and mutation I-TASSER models. The first group of energy potentials is the knowledge-based atomic contact potentials by RW/RWplus (Zhang and Zhang, 2010) and Dfire/dDfire (Yang and Zhou, 2008; Zhou and Zhou, 2002). Both potentials are based on the statistics on the PDB structures but with different reference states. RW/RWplus derives the non-interaction reference state from an ensemble of random-walk chain conformations, while Dfire/dDfire does it from ideal gas states. Meanwhile, RWplus and dDfire consider the orientations of local structures involved in contacts while RW and Dfire are orientation independent. In addition, dDfire specified the interactions between hydrogen-bonded atoms (dDfire1), polar-nonpolar atoms (dDfire2), polar-polar atoms (dDfire3), and the total energy (dDfire) (Yang and Zhou, 2008).

The second group of energy potential is physics-based from AMBER force field (Duan et al., 2003). It contains 18 energy terms counting for bond-length, bond-angle, dihedral, van der Waals, electrostatic, 1–4 van der Waals, 1–4 electrostatic, polar solvation, non-polar solvation, total gas phase free energy, total solvation free energy, and the total energy.

The third group is an empirical force field from FoldX (Guerois et al., 2002), which consists of 14 empirical terms from the van der Waals contribution of all atoms, solvation energy for apolar and polar groups, water bridge hydrogen bonding between water and protein, intra-molecule hydrogen-bonding, electrostatic contribution of interactions between charged groups, entropy costs for fixing main-chain and side-chain atoms in a particular conformation, and the penalty from atomic steric overlaps.

Each of the energy terms from the three groups is calculated for both wild-type and mutant proteins, which are used as training features in STRUM. These constitute 78 training features used by STRUM (see bottom of Supplementary Table S1)

2.2.4 Model training through gradient boosting regression

Given the 120 features describe above, the predictive model in STRUM is built using the Gradient Boosted Regression Trees (GBRT), which has shown to have the advantage to overcome the over-fitting effect compared with many other machine learning methods (Friedman, 2001). The Scikit-learn toolkit (Pedregosa et al., 2011) is used to implement the GBRT training, with the hyper parameters tuned through grid-based search. To further reduce over-fitting, we control the tree size, and set both the maximum depth (max_depth) and the minimum required number of samples at a leaf (min_samples_leaf) as 3 for each tree, with the total number of regression trees (n_estimators) being 3000. When looking for the best split at each stage, the number of randomly selected features to consider is set as equal to the square root of the total number of training features, which aims to enhance the robustness of training against the overcapacity of the base learner. The least square function is selected as the loss function of regression due to its superior computational properties.

Training features often do not contribute equally to the prediction of the target response. Since individual decision trees intrinsically perform feature selection by selecting appropriate split points, the Scikit-learn program uses the number of times of a specific feature appearing at the split points as the importance, i.e. the more often a feature is used at the split points of a tree, the more important that feature is. For decision tree ensembles, the importance of a specific feature is calculated by the average of the importance scores of the feature through all the trees (Pedregosa et al., 2011).

It is worth mentioning that GBRT builds the prediction model in the form of an ensemble of weak decision trees, in which an interior node represents one feature with edges to the child nodes corresponding to the possible values of the input features. This protocol allows STRUM to specify the energy terms from wild-type or mutant as the input features, where the GBRT training can automatically identify the relationship of the difference between the wild-type and mutant energy terms. We have examined the training process using the separated energy terms or energy terms from mutation only. It was found that, based on the same datasets, the model using separated energy training outperforms that trained on the mutant energy, with PCC/root mean sequence error being 0.54/1.25 and 0.45/1.58, respectively, for these two models (definitions seen below).

2.3 Evaluation criterions

The performance of the stability change prediction upon single point mutation is evaluated by

$$\left\{\begin{array}{l}\mathrm{\gamma }=\frac{n\sum _{i=1}^n{x}_i{y}_i-\sum _{i=1}^n{x}_i\sum _{i=1}^n{y}_i}{\sqrt{n\sum _{i=1}^n{x}_i^2-{\left(\sum _{i=1}^n{x}_i\right)}^2}\sqrt{n\sum _{i=1}^n{y}_i^2-{\left(\sum _{i=1}^n{y}_i\right)}^2}}\\ \mathrm{\sigma }=\sqrt{\frac{\sum _{i=1}^n{\left(x_i-y_i\right)}^2}{n}\mathrm{ }}\end{array}\right.\mathrm{ }\left(9\right)$$

where n is the number of single-point mutations in the test set; x_i and y_i represent the predicted and experimental values of $\Delta \Delta G$ for the ith mutation, respectively. γ and σ thus measure the PCC and the root mean square error (RMSE) between the model prediction and experiment.

STRUM is tested mainly through a 5-fold cross validation procedure in which the experimental mutation sample is randomly divided into 5 subsets of equal size. Four subsets are used to train the prediction model by GBRT and the remaining subset is used as validation of the model. For each sample, such test is repeated five times each with a different selection of the training and testing subsets. Since the results often have small fluctuation between the random sample splits, the training/testing process was repeated 50 times, with the average values of γ and σ finally reported.

Three types of sample divisions are conducted: the first divides the mutations regardless what protein they are from, which is called ‘mutation-level’ cross-validation; the second is called ‘protein-level’ that splits the samples based on proteins; the third is ‘position-level’ that divides the samples based on the position of mutation along the sequence. One purpose for the multiple-level sample divisions is to eliminate possible bias caused by the correlation between training and testing samples. In this study, we have confirmed that identical proteins with different PDB IDs were filtered out in all the datasets. For protein-level validation, in particular, a sequence identity cutoff at 60% was applied on Q306 to filter out possible homologies associated with the training set (S2648).

3 Results

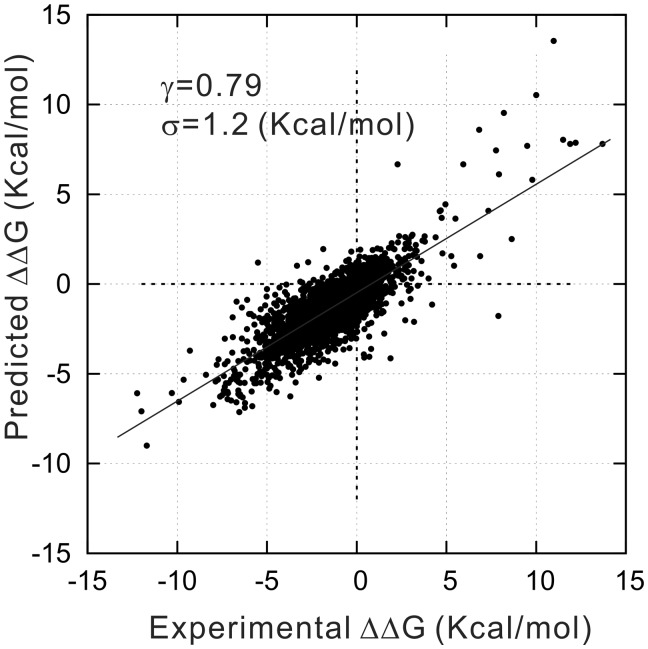
3.1 Testing STRUM on the Q3421 dataset

STRUM was first tested on the Q3421 dataset that contains 3421 experimental mutations from 150 proteins. In Figure 4, we present the predicted versus experimental $\Delta \Delta G$ in the testing dataset, which shows a strong correlation with γ equal to 0.79. The RMSE of the prediction is 1.2 kcal/mol.

Fig. 4.

Regression result of STRUM on the mutation-level cross-validation test using the Q3421 dataset

STRUM has used three groups of 120 individual features to discriminate the stability changes on single-mutations. To examine the sensitivity of different features to the mutation stability, we listed in Column 4–7 of Supplementary Table S1 the distributions of the feature values on mutations that stabilize ($\Delta \Delta G>0$) and destabilize ($\Delta \Delta G<0$) protein folds in dataset Q3421. Column 8 lists the P-value of the difference between stabilizing and destabilizing mutations in the Mann-Whitney test. It is shown that most of the features (78 out of 120) have the P-value below 0.05, meaning that we can safely reject the hypothesis that the distributions of the two datasets are drawn from the same distribution, partly validated the efficiency of feature selections.

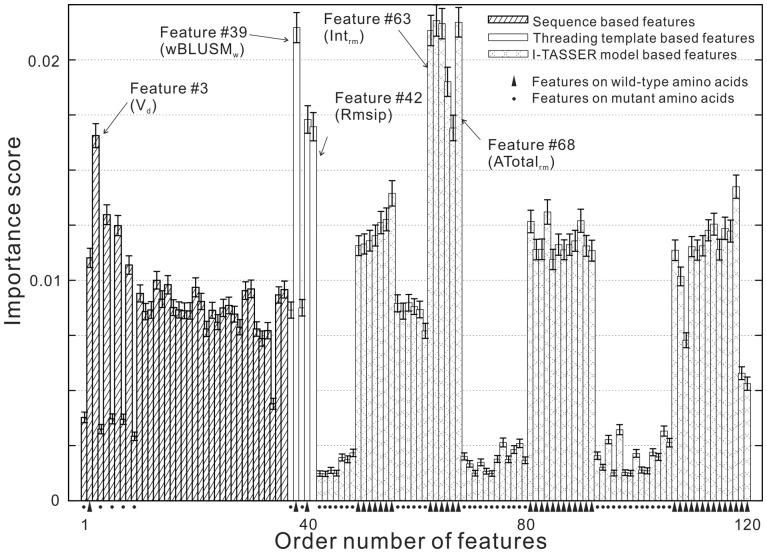
In Figure 5, we show the average importance of the 120 features and the standard errors that are inferred from the Scikit-learn gradient boosting regression program. Here the importance of the individual features is defined by the average number of the times that the features are used in the split points of the regression tree. The most predictive features are the four AMBER energy items, including internal potential (Feature no. 63), van der Waals energy (no. 64), electrostatic energy (no. 65) and the total energy (68), on the I-TASSER models. Meanwhile, the weighted conservation score from threading template alignments (no. 39) also achieves a similar importance index. These data demonstrated the relevance of structure modeling based features on the stability prediction.

Fig. 5.

The importance score of 120 individual features to the regression predictive model in cross validation. The error bars denote the standard deviation in the 5-fold mutation-level cross validation. Triangles and dots at the bottom of the histograms label the source of features on wild-type and mutant amino acids, respectively; the unlabeled histograms are for combined mutant and wild-type residues

The highest importance score in the sequence-based features is from the volume difference between wild-type and mutant amino acids (no. 3). All the features have a non-zero contribution to the final modeling. Interestingly, the importance of the features on the wild-type amino acids is generally lower than that of the features on the mutant amino acids. In fact, the average importance score for the mutant amino acid based features is 0.013, which is 433% higher than the average importance score of the wild-type amino acid based features (0.003). The P-value of the difference in the Student’s t-test is 9.5*10⁻²⁴, which indicates that the difference is statistically significant. This observation highlights the importance for the construction of specific features, including sequence profiles and structural models, from the mutant sequences.

3.2 Comparison of STRUM with other methods on the S2648, S350 and Q306 datasets

To examine STRUM in control with other methods in the field, we compare the performance of STRUM with that by four recently developed, state-of-the-art programs from I-Mutent3.0 (Capriotti et al., 2008), PoPMuSiC (Dehouck et al., 2011), mCSM (Pires et al., 2014) and INPS (Fariselli et al., 2015). The test is mainly on three datasets of S2648, S350 and Q306, in which S2648 and S350 have been widely used in the literature but Q306 is a testing dataset newly constructed. To generate STRUM prediction, we conducted various multi-fold cross-validations in each of the datasets. The predictions on other programs are generated by submitting the sequences and mutations to the webservers provided by the authors. It should be mentioned that since the server results are not from cross-validation, part of the testing data might have been included in training sample of the server models.

3.2.1 Testing result on S2648

Table 1 presents the average results of PCC (γ) and RMSE (σ) between predicted and experimental $\Delta \Delta G$ by different programs (Columns 3–4). Since some servers failed to generate predictions for specific mutations, we listed in Columns 6–7 the results on the 2484 common mutations that have data by all programs. The 5-fold mutation-level cross-validation with 50 loops by STRUM has the average correlation coefficient γ = 0.77, which is the highest among all the programs. Accordingly, the RMSE value of the $\Delta \Delta G$ by STRUM (0.92 Kcal/mol) is also lower than other predictions. The P-values in the Wilcoxon test, when comparing the RMSEs of STRUM with that by different programs, are all below 10⁻¹⁵, meaning that the difference is statistically significant.

Table 1.

Comparison of different methods on the S2648 dataset

Method	All mutations			Common mutations			P-valued
	na	γb	σc	na	γb	σc
I-Mutent3.0	2636	0.60	1.19	2484	0.60	1.19	7.2E-28
INPS	2648	0.56	1.26	2484	0.56	1.26	5.3E-46
mCSM	2643	0.69	1.07	2484	0.70	1.07	1.4E-18
PoPMuSiC	2647	0.61	1.17	2484	0.61	1.17	1.6E-25
STRUM	2647	0.77	0.94	2484	0.78	0.92

^an, number of mutations obtained from the programs.

^aγ, PCC between predicted and experiment $\Delta \Delta G.$

^aσ, RMSE of $\Delta \Delta G$ prediction in Kcal/mol.

^aP-value, P-value in Wilcoxon test between the RMSE of STRUM and that by the control methods on the common mutations.

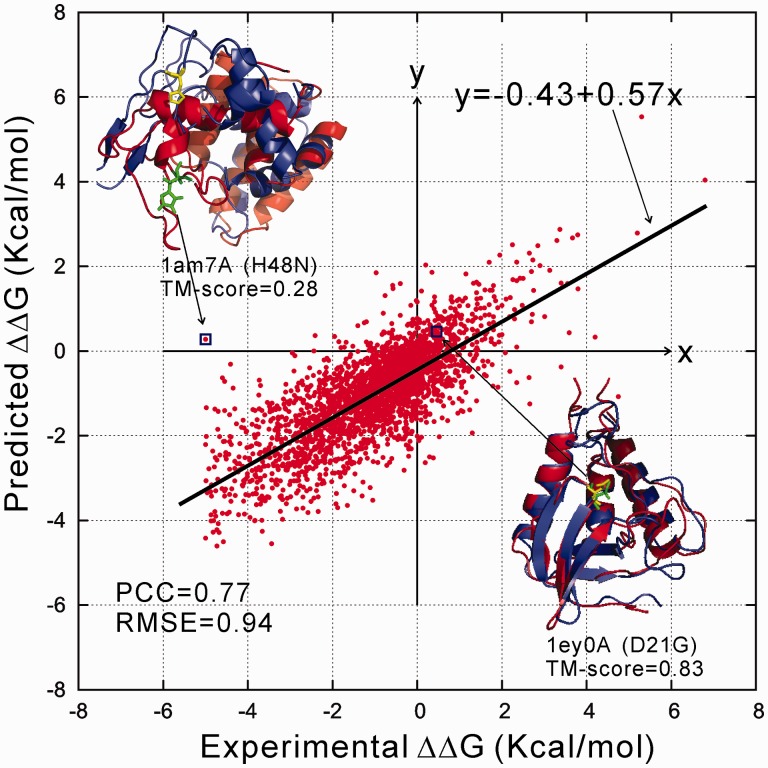
Figure 6 presented the regression result on the S2648 dataset from the 5-fold mutation-level cross validations, where the majority of the points (75.4%) have the $\Delta \Delta G$ error with in 1.0 Kcal/mol. However, there are several mutations that have the $\Delta \Delta G$ error larger than 2 Kcal/mol. The largest error comes from the mutation of H48N in Lysozyme of bacteriophage lambda (PDB ID: 1am7A). A closer look at the examples shows that the I-TASSER model of the target protein has an incorrect fold with a poor TM-score = 0.28. The structure superposition shows that the mutated residue is completely mis-located on the 3D fold. The target residue is buried in the native structure, which results in the destabilized mutation in the native state ($\Delta \Delta G<0$). However, the I-TASSER model misplaced the residue in the surface, which result in a stabilized mutation prediction with $\Delta \Delta G>0$ (see upper-left panel of Fig. 6). In this figure (lower-right panel), we also present an example of I-TASSER model with correct fold (TM-score = 0.83) from the staphylococcal nuclease (PDB ID: 1eyoA), where the predicted $\Delta \Delta G$ is almost identical to the experimental value. These examples seem to imply a correlation of I-TASSER models accuracy on the mutation stability predictions.

Fig. 6.

Regression results of STRUM on Dataset S2648. The red and blue cartoons in two examples represent the protein structure from the PDB and the I-TASSER prediction, respectively

The above tests are based on the mutation-level cross validation in which mutations in training and test sets can come from the same protein or even the same residue. To have a more comprehensive test on the impact of protein and residue separations, we conduct two additional ‘protein-level’ and ‘position-level’ cross-validations, in which proteins and mutation positions are exclusively either in the training or testing set. The results are summarized in Table 2, together with the data taken from two publications that performed the same tests. It is shown that although STRUM still outperforms the control methods in these stringent tests, the overall performance is generally lower than that from the mutation-level validation experiment. More specifically, PCC/RMSE (0.77/0.94) in mutation-level cross validation are reduced to 0.64/1.14 and 0.54/1.25, respectively, in the position-level and protein-level validations. This reduction is probably due to the unique distribution of the current mutation samples, whereas hundreds of mutations can come from a single protein and the mutation-level cross validation could result in some level of bias in the testing results, a phenomenon that was also noted recently by Pires et al. (2014).

Table 2.

Summary of protein-level and position-level cross validation on the S2648 dataset

Method	Protein-levela		Position-levelb
	γd	σe	γd	σe
INPSc	0.52	1.26	0.54	1.28
mCSMc	0.51	1.26	0.54	1.23
STRUM	0.54	1.25	0.64	1.14

^aProtein-level, mutation samples are divided based on their protein origin.

^aPosition-level, mutation samples are divided based on their positions.

^aINPS, mCSM, data taken from authors’ publications.

^aγ, PCC between predicted and experimental $\mathrm{\Delta }\mathrm{\Delta }G.$

^aσ, RMSE of $\mathrm{\Delta }\mathrm{\Delta }\mathrm{G}$ prediction in Kcal/mol.

3.2.2 Testing result on S350

The S350 may provide a convenient comparison of STRUM with other methods, since most of publications have used this dataset as their testing set. Similarly, we trained STRUM on the 2298 (=2648-350) mutations and use the S350 as the testing set. Columns 2–3 of Table 3 present the γ and σ values that we copied from the original publications; and Columns 4–9 are that obtained from the on-line servers. The results from most servers are consistent with (or slightly worse than) the published data. Again, STRUM outperforms the results on the S350 test set with the Wilcoxon test P-values listed in Column 10, which indicates that the differences are statistically significant. It is notable that the P-value here is generally higher than that in Table 1, which is mainly due to the reduced sample size that decreases the degree of freedom and therefore the magnitude of P-values.

Table 3.

Comparison of different methods on the S350 dataset

Method	γa	σa	All mutations			Common mutations			P-valued
			nb	γc	σc	nb	γc	σc
I-Mutent3.0	0.53	1.35	349	0.53	1.32	343	0.52	1.33	2.4E-10
INPS	0.68	1.26	350	0.59	1.28	343	0.59	1.28	3.4E-07
mCSM	0.73	1.08	349	0.70	1.13	343	0.69	1.13	4.2E-05
PoPMuSiC	0.67	1.16	350	0.67	1.17	343	0.66	1.18	5.1E-05
STRUM	0.79	0.98	350	0.79	0.98	343	0.80	0.95

^aγ,σ, Data obtained from corresponding publications

^an, Number of mutations obtained for each method

^aγ,σ, Data obtained from on-line servers

^aP-value, P-value in Wilcoxon test between the RMSE of STRUM and that by the control methods on the common mutations

3.2.3 Testing result on Q306

Although mutations in S350 were excluded from the training set, training and testing samples may come from the same proteins. In Table 4, we report the results on the Q306 that contains 306 mutations from 32 proteins that have a sequence identity < 60% to any proteins in S2648, which STRUM was trained on.

Table 4.

Comparison of different methods on the Q306 dataset

Method	γa	σb	P-valuec
I-Mutent3.0	0.12	2.04	3.7E-4
INPS	0.27	1.96	7.9E-4
mCSM	0.18	2.09	7.0E-2
STRUM	0.40	1.91

^aγ, PCC between predicted and experiment $\Delta \Delta G.$

^aσ, RMSE of $\Delta \Delta G$ prediction in Kcal/mol.

^aP-value, P-value in Wilcoxon test between the RMSE of STRUM and that by the control methods on the mutations.

The results on Q306 become worse than the S350 set with average PCC/RMSE =0.40/1.91 compared with 0.79/0.98, which is probably due to the fact that the mixture of the training and test mutations from homologous proteins is now filtered out completely. We also listed the results from web server of the three control methods (-results from PoPMuSiC were not shown because the server failed to generate a prediction for nearly half of the mutations in Q306). Although STRUM is in general worse than the S350 set, it outperforms the control methods again in this new Q306 dataset. However, the P-value of the difference between STRUM and the control methods becomes less significant compared with that in other datasets. One reason is that the sample is relatively smaller, which can result in fluctuation in performance. Second, the proteins in Q306 are non-homologous to the STRUM’s training set, which may not be the case for the control methods.

3.3 Blind test on p53 protein

Cells in human often face dangers. The normal controls on cell growth may be blocked and the cell will rapidly multiply and grow into a tumor when the key regulatory elements are damaged. P53 is probably the most important tumor suppressor protein that regulates cell growth by binding DNA and activating the expression of a number of down-stream cell-cycle regulation genes. Mutations on the p53 protein-coding genes can result in unnatural growth, which contributed to nearly half of the human cancers. Most of these mutations are missense that can result in amino acid substitution on protein sequence. There are 42 single mutations extracted from the IARC TP53 Database that have been experimentally determined, none of which appear in the STRUM training dataset. Since this dataset was collected after STRUM development, we can consider it as a blind test of the STRUM algorithm.

Table S2 shows the results of $\Delta \Delta G$ predictions by 5 different methods where STRUM uses the I-TASSER model and the rest of the methods use the published crystal structure 2OCJ, except for INPS that is from sequence. It was shown that the stability changes by STRUM has the second strongest correlation with the experimentally values ($\mathrm{\gamma }\hspace{0.17em}=\hspace{0.17em}0.69$), compared with that of other methods, including INPS ($\mathrm{\gamma }\hspace{0.17em}=\hspace{0.17em}0.71$), mCSM ($\mathrm{\gamma }\hspace{0.17em}=\hspace{0.17em}0.67$), I-Mutent3.0 ($\mathrm{\gamma }\hspace{0.17em}=\hspace{0.17em}0.57$), and PoPMuSiC ($\mathrm{\gamma }\hspace{0.17em}=\hspace{0.17em}0.56$). The RMSE of STRUM is the lowest with $\mathrm{\sigma }\hspace{0.17em}=\hspace{0.17em}1.34$ Kcal/mol.

3.4 Further examinations on STRUM

STRUM’s performance is partly attributed to the employment of protein structure prediction and the large-scale feature design collected from multiple resources. Here we examine several relevant issues related to these attributes.

3.4.1 Are 120 features all needed?

To answer this question, we classify the 120 features into 3 groups. The first group is sequence-based containing physicochemical properties plus MSA and local structure predictions; the second includes physicochemical properties plus threading template-based features; and the third consists of physicochemical properties plus I-TASSER model based features (Supplementary Table S3). A protein-level 5-fold cross-validation test is then performed on each of the feature groups. The results show a modest level of variations on the final performance among different feature groups, where the third group based on I-TASSER models shows slightly better PCC/RMSE (0.49/1.31) than the other two groups (0.47/1.34 and 0.41/1.41).

Next, we trained the predictor on the top 5, 10, 20, 50 features selected from each group based on their importance score listed in Figure 5. In all the groups, the performance gradually increases when more features are included, demonstrating the necessity of including more features. Finally, we tried to merge different number of top features from the three groups for STRUM training. The result shows again that the performance increases when including more features (Supplementary Table S4). With the number of features increasing to 86, the PCC/RMSE values increase to 0.51/1.27, which are close but still not equal to the level of using the entire 120-feature set (0.54/1.25), suggesting that the most features used in STRUM are complementary to each other and the inclusion of a comprehensive feature set is needed to achieve the optimal performance.

3.4.2 Impact of protein structure quality on STRUM

Examples in Figure 6 have indicated some correlation between I-TASSER model accuracy and STRUM performance. To have a quantitative assessment on the impact of protein structure prediction, we re-trained STRUM on the experimental structure from the PDB. The data in Supplementary Table S5 shows, however, that the PCC/RMSE values are only marginally improved, from 0.77/0.94 to 0.78/0.92, compared using I-TASSER models. One reason on the small difference can be attributed to the overall quality of the I-TASSER modeling. As shown in Figure S1, although homologous templates were excluded, the majority of the I-TASSER models (83%) have the correct fold with a TM-score above 0.5 (Xu and Zhang, 2010).

If we split the protein sample into two subsets with TM-score >0.5 (109 proteins) and TM-score <0.5 (23 proteins) respectively, it is shown that there is almost no difference on the performance of STRUM between using the native and using the I-TASSER model in the subset of TM-score >0.5, suggesting that a model accuracy of TM-score >0.5 seems sufficient to provide correct spatial environments for STRUM prediction. However, for the subset with TM-score <0.5, the incorrect I-TASSER model reduced γ by 7.5% and increase σ by 6.5%, compared with that using the native structure (Supplementary Table S5), indicating that further improvement on structure prediction may help improve the stability predictions for these targets. For the example of mutation of H48N in the Lysozyme of bacteriophage lambda, STRUM can correctly classify the case into the destabilized mutation with predicted $\Delta \Delta G=-0.39$, if the native structure is used.

In Supplementary Table S6, we present a comparison of the two sets of proteins trained on the I-TASSER models, where a ‘good prediction’ is defined as those with predicted and experimental ΔΔG having the same sign (i.e. both >0 or both <0) and the difference between the predicted and experimental ΔΔG below 0.1; and a ‘bad prediction’ as those with ΔΔG having opposite sign and the difference above 1.0. The portion of good predictions (10%) in the proteins of TM-score >0.5 is slightly higher than that in the protein set of TM-score <0.5 (7%). Meanwhile, the portion of bad prediction in the protein set of TM-score >0.5 (6%) is slightly lower than the set of TM-score < 0.5 (9%). This consensus tendency confirms the observation seen in Supplementary Tables S5, i.e. protein models of better quality tends to positively impact the performance of STRUM prediction.

Since all above tests have the training and test on the same set of structure models (i.e. native or predicted), here we performed a new experiment, in which we first trained STRUM on the native structures but then compared the test results on the native and I-TASSER models separately. The training set contains 2225 mutations from 109 proteins with TM-score >0.5 in the S2648, while the testing set consists of the rest of the 423 mutations from the 23 proteins with TM-score <0.5. The PCC/RMSE based on the native testing dataset (0.47/1.22) is only slightly better than that on the I-TASSER testing dataset (0.43/1.27); but the difference is statistically significant (P-value = 5E-12), consistent with the observation that the correctness of the protein fold can impact the $\Delta \Delta G$ prediction results. Meanwhile, it is observed again that the separation of training and testing data sets on proteins in this experiment considerably reduce the performance on the test results, compared with the cross-validation data shown in Table S5, which confirms the observation by Pires et al (2014).

3.4.3 Impact of NMA features from threading template variations

In STRUM, three normal mode features, defined by Equation (8), are derived from multiple LOMET threading templates (i.e. 30 for Easy and 50 for Hard targets). To examine the effect of the NMA features on STRUM produced by template variations, we tested five different template sets, including (i) the first template; (ii) 10th template; (iii) the last template; (iv) the first 10 templates; (v) the last 10 templates. Supplementary Table S7 lists the correlation coefficients between the experimental $\Delta \Delta G$ and the NMA features built from the different template selections. Although the correlations are all relatively weak (<0.1), there is however an obvious trend that the higher-rank templates have a better TM-score and tend to have a slightly higher correlation.

In Supplementary Table S8, we show the performance of STRUM when replacing the current NMA features with each of the five sets of template selections. Due to the weak correlation of individual features with the $\Delta \Delta G$ data, there is almost no change on the overall performance of STRUM. However, they are all slightly worse than the full version STRUM that exploits the entire set of LOMETS templates (see Table 2).

3.5 Visualization of mutant stability profile and application on staphylococcal nuclease

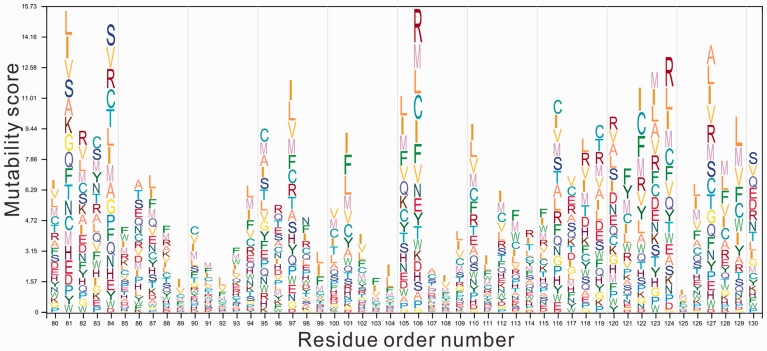
If we consider the protein folding and mutation as a thermodynamic system, the possibility of the occurrence of the mutations should be proportional to $\mathrm{e}\mathrm{x}\mathrm{p}\left(\Delta \Delta G\right)$ (Tokuriki and Tawfik, 2009). Here we define a mutability score $F_i$ that describes the total possibility of mutations of the current residue to all other amino acids by

$$F_i={\displaystyle \sum _{a=1}^{19}{e}^{\Delta \Delta G_{w_i}\to m_a}}$$ 10

where w_i is the wild-type amino acid at ith position of the sequence, m_a is one of the 19 possible amino acids mutated from w_i, and ${\Delta \Delta G}_{w_i\to m_a}$ is the predicted free-energy change on the mutation. Thus, we can introduce a stability profile against mutation that can be conveniently used for visualizations.

Figure 7 showed an example of the mutability score F_i calculated for the staphylococcal nuclease (SNase) that is a widely used model system for mutant study (Carra and Privalov, 1996). There are currently in total 553 experimentally determined mutations from this enzyme. The STRUM model using the I-TASSER model generated $\Delta \Delta G$ prediction with a correlation $\mathrm{\gamma }\hspace{0.17em}=\hspace{0.17em}0.72$ and RMSE $\mathrm{\sigma }\hspace{0.17em}=\hspace{0.17em}1.17$ Kcal/mol compared with the experimental measurements.

Fig. 7.

Visualized mutability profile by STRUM for the staphylococcal nuclease protein. The characters are colored on the polarization property of amino acids, i.e. polar residues are brightly colored and non-polar ones are in darker color. The height of the characters is proportional to the possibility of mutation into the amino acid type from wild-type residue (Color version of this figure is available at Bioinformatics online.)

In this profile, the height of each character is proportional to the possibility of mutation into a corresponding amino acid type from wild-type residue. If the height of the amino acid is greater than 1, it means this mutation is favorable which should stabilize the wild-type protein. Otherwise, the mutation will destabilize the wild-type protein. The higher the mutation score $F_i$ is for a residue, the greater the likelihood of a mutation will be produced. This mutation profile has been integrated into the automated I-TASSER server for assisting visualized stability analysis.

4 Conclusion

Prediction on the SNP mutation-induced stability changes ($\Delta \Delta G$) is of critical importance to protein function annotation and human disease diagnosis. Recent studies have showed advantage for the methods that use experimental protein structure information to improve the $\Delta \Delta G$ prediction accuracy over the sequence-based approaches. However, the experimental structure is often unavailable to protein sequences, which compromises the usefulness of the structure-based prediction methods in practical applications.

We developed a new algorithm, STRUM, to explore the possibility to improve the $\Delta \Delta G$ prediction based on low-resolution models from the iterative assembly refinement (I-TASSER) simulations, in which three groups of features from sequence profile, multiple template threading, and I-TASSER atomic models are combined through the gradient boosting regression tree training. The algorithm was tested on a set of 3421 experimentally characterized mutations from 150 proteins. After homologous templates with sequence identity >30% to the target or detectable by PSI-BLAST with E-value <0.05 were excluded, I-TASSER was able to build structure model of correct fold with a TM-score >0.5 for 109 (83%) proteins. Using the I-TASSER model, STRUM generated $\Delta \Delta G$ prediction for all proteins with a PCC 0.79 and RMSE 1.2 Kcal/mol in the mutation-level 5-fold cross-validation, compared with the experimental mutation data. But the performance can be reduced when tested on the protein-level cross-validation, probably due to the correlation among mutation samples that are from the same proteins.

The detailed data analysis showed that the most predictive features are those from the physics-based energy terms on the I-TASSER structural models and the conservation score based on multiple threading alignments, demonstrating the importance and usefulness of the low-resolution structure predictions in the $\Delta \Delta G$ predictions. Interestingly, features built on the mutated amino acids are generally more sensitive to the $\Delta \Delta G$ prediction accuracy than those on the wild-type amino acids. This is understandable considering the fact that the wild-type amino acids are usually more stable and adoptable to the protein environments due to the long-term evolution than the new mutations. Thus, compared with the relatively uniform stability from the wide-type amino acids, the identity of the mutated amino acids should provide more information with regard to the stability changes upon new mutations. This insight that the wild-type amino acids have a uniformly higher stability than the mutant ones is partly supported by the fact that the majority of the mutations in the database destabilize the protein fold (see Fig. 2).

STRUM was also examined in four other datasets (S2648, S350, Q306 and p35) in control with four state of the art algorithms, including I-Mutent, INPS, mCSM and PoPMuSiC, which have the web server available for exacting on-line $\Delta \Delta G$ predictions. The results showed that STRUM based on predicted structural protein models are comparable with or outperform most of the methods that are built on the experimental structures. One reason for the advanced performance by STRUM is probably due to the combination of multiple complimentary features extracted from a wide range of resources. The gradient boosting regression training also helps to improve the robustness of the training procedure by the reduction of the over-fitting effect.

Finally, the data results show that the $\Delta \Delta G$ prediction is not sensitive to the accuracy of protein structural models as long as the global fold is correct (i.e. with TM-score >0.5). However, when the target structure model has an incorrect fold, the structure-based $\Delta \Delta G$ prediction can be obviously degraded, which highlights the importance of further improvement of protein structure prediction for mutation change modeling, especially for the targets in the ‘twilight zone’ where the creation of correct fold remains a challenge to most structure prediction algorithms (Zhang, 2008).

Funding

The work was supported in part by the National Institute of General Medical Sciences (GM083107, GM116960), the China Scholarship Council Award (No. 201406920033), and the National Natural Science Foundation of China (No. 61170125).

Conflict of Interest: none declared.