Network-based inference of protein activity helps functionalize the genetic landscape of cancer

Abstract

Identifying the multiple dysregulated oncoproteins that contribute to tumorigenesis in a given patient is crucial for developing personalized treatment plans. However, accurate inference of aberrant protein activity in biological samples is still challenging as genetic alterations are only partially predictive and direct measurements of protein activity are generally not feasible. To address this problem we introduce and experimentally validate a new algorithm, VIPER (Virtual Inference of Protein-activity by Enriched Regulon analysis), for the accurate assessment of protein activity from gene expression data. We use VIPER to evaluate the functional relevance of genetic alterations in regulatory proteins across all TCGA samples. In addition to accurately inferring aberrant protein activity induced by established mutations, we also identify a significant fraction of tumors with aberrant activity of druggable oncoproteins—despite a lack of mutations, and vice-versa. In vitro assays confirmed that VIPER-inferred protein activity outperforms mutational analysis in predicting sensitivity to targeted inhibitors.

INTRODUCTION

Cancer initiation and progression are driven by aberrant activity of oncoproteins working in concert to regulate critical tumor hallmark programs¹. Pharmacological inhibition of aberrantly activated oncoproteins can elicit oncogene dependency², which motivates the development and use of targeted inhibitors in precision cancer medicine. Activating genetic alterations have thus emerged as important candidate drug targets. Yet, activating mutations represent only one of many possible ways to dysregulate the activity of an oncoprotein. Genetic and epigenetic events in cognate binding partners³, competitive endogenous RNAs⁴, and upstream regulators⁵ can all contribute to aberrant activity of oncoproteins. Thus, while cells with activating mutations in a specific oncogene are generally more sensitive to corresponding targeted inhibitors, cells lacking these mutations may also present equivalent sensitivity^6,7. Conversely, an activating mutation is not guaranteed to induce aberrant protein activity, due to autoregulatory mechanisms and epigenetic allele silencing. A more universal and systematic methodology for the accurate and reproducible assessment of protein activity would significantly complement our ability to identify targeted therapy responders based on mutational analysis, especially since most cancer patients have no actionable oncogene mutations⁸.

While gene expression data are ubiquitous in cancer research^9–12, methods for the genome-wide assessment of protein activity are still elusive. Existing methods to measure protein abundance—based on arrays¹³ or mass spectrometry¹⁴ technologies—are still labor intensive, costly, and either cover a small fraction of the proteomic landscape or require large amounts of tissue. More importantly, these methods provide only an indirect measure of protein activity, because the latter is determined by a complex cascade of events, including protein synthesis, degradation, post-translational modification, complex formation, and subcellular localization¹⁵ (Fig. 1a). It is ultimately unclear whether protein activity may be directly and systematically assessed by any individual assay.

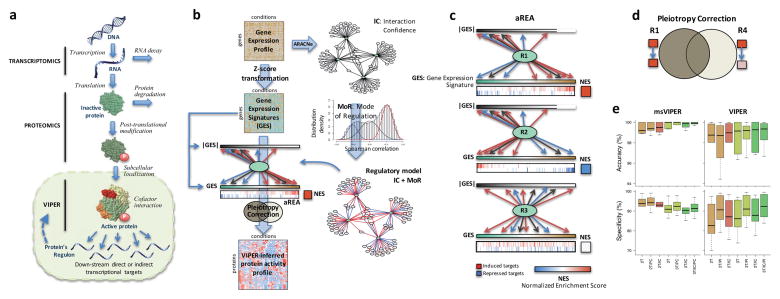
Figure 1. Schematic overview of the VIPER algorithm.

(a) Molecular layers profiled by different technologies. Transcriptomics measures steady-state mRNA levels; Proteomics quantifies protein levels, including some defined post-translational isoforms; VIPER infers protein activity based on the protein’s regulon, reflecting the abundance of the active protein isoform, including post-translational modifications, proper subcellular localization and interaction with co-factors. (b) Representation of VIPER workflow. A regulatory model is generated from ARACNe-inferred context-specific interactome and Mode of Regulation computed from the correlation between regulator and target genes. Single-sample gene expression signatures are computed from genome-wide expression data, and transformed into regulatory protein activity profiles by the aREA algorithm. (c) Three possible scenarios for the aREA analysis, including increased, decreased or no change in protein activity. The gene expression signature and its absolute value (|GES|) are indicated by color scale bars, induced and repressed target genes according to the regulatory model are indicated by blue and red vertical lines. (d) Pleiotropy Correction is performed by evaluating whether the enrichment of a given regulon (R₄) is driven by genes co-regulated by a second regulator (R₄∩R₁). (e) Benchmark results for VIPER analysis based on multiple-samples gene expression signatures (msVIPER) and single-sample gene expression signatures (VIPER). Boxplots show the accuracy (relative rank for the silenced protein), and the specificity (fraction of proteins inferred as differentially active at p < 0.05) for the 6 benchmark experiments (see Table 2). Different colors indicate different implementations of the aREA algorithm, including 2-tail (2T) and 3-tail (3T), Interaction Confidence (IC) and Pleiotropy Correction (PC).

We propose that the expression of the transcriptional targets of a protein, collectively referred to as its regulon, represent an optimal multiplexed reporter of its activity (Fig. 1a). While this concept is not new—it was initially proposed for transcription factors (TFs)¹⁶—it has not been successfully demonstrated in mammalian cells. There are currently no experimentally validated methods to accurately assess the activity of arbitrary proteins in individual samples based on the expression of their regulon genes. Reasons for this include lack of accurate and context-specific protein regulon models, the largely pleiotropic nature of transcriptional regulation, and a lack of methodologies to assess statistical significance from single samples. This severely limits the ability to understand the functional effect of mutations on protein activity and to identify candidate responders to targeted inhibitors based on aberrant protein activity rather than mutations.

We have previously shown that regulon analysis, using the master regulator inference algorithm (MARINa), can help identify aberrantly activated tumor drivers^17–21. However, this requires multiple samples representing the same tumor phenotype and cannot assess aberrant protein activity from individual samples. To address this challenge, we introduce a new regulatory-network based approach for the Virtual Inference of Protein-activity by Enriched Regulon analysis (VIPER) from single gene expression profiles (see Supplementary Table 1 for the list of acronyms used in this manuscript). VIPER can systematically assess aberrant activity of oncoproteins for which high-affinity inhibitors are available, independent of their mutational state, thus establishing them as valuable therapeutic targets on an individual patient basis. The analysis is fully general and may be trivially extended to study the role of germline variants in dysregulating protein activity. We have implemented VIPER as an R-system package available through Bioconductor.

RESULTS

We first discuss development, optimization, and validation of VIPER. We then introduce a statistical framework to allow single sample analysis, without loss of robustness or generality. Finally, we use VIPER to evaluate all non-silent somatic mutations in The Cancer Genome Atlas (TCGA) samples and report the aberrant activity of all oncogenes listed in the Catalogue Of Somatic Mutations In Cancer (COSMIC)²² on an individual sample basis.

The algorithm

VIPER infers protein activity by systematically analyzing expression of the protein’s regulon, which is strongly tumor-context dependent²³ (see Fig. 1b for a schematic overview of the approach). We used the ARACNe algorithm²⁴ (Methods) to systematically infer regulons from tissue-specific gene expression data (Fig. 1b and Table 1). While any algorithm or experimental assay providing accurate, tissue-specific assessments of protein regulons should be equally effective, we found that ARACNe outperformed competing algorithms that derive regulons from genome-wide ChIP databases, including ChEA²⁵ and ENCODE²⁶, and literature curated Ingenuity networks²⁷ (see below). We extended ARACNe to detect maximum information path targets (Methods), as originally proposed in²¹, to allow identification of regulons that report on the activity of proteins representing indirect regulators of transcriptional target expression, such as signaling proteins.

Table 1.

Interactomes and the datasets used to reverse engineer them

Dataset				Interactome
Tissue type	Samples	Platform	Reference	Regulator	Targets	Interactions
B-cell	254	HG-U95Av2	24	633(TFs)	6,403	173,539
B-cell	264	HG-U133plus2	34	1,223(TFs)	13,007	327,837
Glioblastoma	176	HG-U133A	48	835(TFs)	8,263	256,965
Bladder carcinoma	241	RNAseq	TCGA	1,813(TFs)	20,006	245,871
				666(coTFs)	18,739	181,730
				3,455(Sig)	20,441	317,127
Breast carcinoma	1,037	RNAseq	TCGA	1,813(TFs)	20,428	249,501
				666(coTFs)	20,220	217,916
				3,455(Sig)	20,515	366,924
Colon adenocarcinoma	434	RNAseq	TCGA	1,813(TFs)	20,462	294,725
				666(coTFs)	19,742	204,682
				3,456(Sig)	20,492	369,870
Head and neck squamous cell carcinoma	424	RNAseq	TCGA	1,813(TFs)	20,452	319,799
				666(coTFs)	19,874	212,214
				3,456(Sig)	20,520	395,966
Kidney renal clear cell carcinoma	506	RNAseq	TCGA	1,813(TFs)	20,474	355,932
				666(coTFs)	20,080	259,151
				3,456(Sig)	20,522	429,651
Lung adenocarcinoma	488	RNAseq	TCGA	1,813(TFs)	20,405	341,285
				666(coTFs)	19,832	214,048
				3,456(Sig)	20,528	472,933
Lung squamous cell carcinoma	482	RNAseq	TCGA	1,813(TFs)	20,426	342,737
				666(coTFs)	19,948	221,178
				3,453(Sig)	20,498	397,774
Ovarian serous cystadenocarcinoma	262	RNAseq	TCGA	1,813(TFs)	20,261	247,063
				666(coTFs)	19,082	150,949
				3,456(Sig)	20,459	334,906
Prostate adenocarcinoma	297	RNAseq	TCGA	1,813(TFs)	20,215	228,977
				666(coTFs)	19,599	180,315
				3,456(Sig)	20,466	315,155
Rectum adenocarcinoma	163	RNAseq	TCGA	1,810(TFs)	18,506	236,899
				666(coTFs)	16,939	173,579
				3,455(Sig)	19,773	332,088
Stomach adenocarcinoma	238	RNAseq	TCGA	1,808(TFs)	22,017	267,138
				661(coTFs)	20,984	194,782
				3,442(Sig)	22,458	438,054
Thyroid carcinoma	498	RNAseq	TCGA	1,813(TFs)	20,478	333,725
				666(coTFs)	20,038	225,544
				3,369(sig)	20,511	408,356
Uterine corpus endometrial carcinoma	517	RNAseq	TCGA	1,813(TFs)	20,471	350,994
				666(coTFs)	20,190	237,518
				3,456(Sig)	20,527	501,212
Glioblastoma multiforme	154	RNAseq	TCGA	1,811(TFs)	18,354	259,025
				660(coTFs)	16,655	157,230
				3,455(Sig)	19,616	393,595
Low grade glioma	370	RNAseq	TCGA	1,813(TFs)	20,357	328,373
				666(coTFs)	19,558	228,634
				3,455(Sig)	20,463	372,802
Skin cutaneous melanoma	374	RNAseq	TCGA	1,813(TFs)	20,475	281,486
				666(coTFs)	19,656	177,388
				3,453(Sig)	20,501	418,136
Sarcoma	105	RNAseq	TCGA	1,715(TFs)	14,262	142,041
				620(coTFs)	10,920	72,486
				3,024(Sig)	15,552	177,063

VIPER is based on a probabilistic framework that directly integrates target Mode of Regulation, that is, whether targets are activated or repressed (Fig. 1b and Supplementary Fig. 1 and 2), statistical confidence in regulator-target interactions (Fig. 1b), and target overlap between different regulators (pleiotropy) (Fig. 1d) to compute the enrichment of a protein’s regulon in differentially expressed genes (Methods). Several methods exist for gene enrichment analysis, including the Fisher’s exact test²⁸, T-profiler²⁹ and Gene Set Enrichment Analysis (GSEA)^28,30–32. In all these methods, the contribution of individual genes to signature enrichment is binary (i.e., 0 or 1). In contrast, VIPER uses a fully probabilistic, yet efficient enrichment analysis framework, supporting seamless integration of genes with different likelihoods of representing activated, repressed, or undetermined targets and probabilistic weighting of low vs. high-likelihood protein targets. To achieve this, we introduce aREA (analytic Rank-based Enrichment Analysis) a statistical analysis based on the mean of ranks (Fig. 1c and Methods). Differential protein activity is quantitatively inferred as the normalized enrichment score computed by aREA.

Systematic assessment of VIPER’s performance

We first tested VIPER’s ability to correctly infer loss of protein activity following RNAi-mediated silencing of a gene. Specifically, MEF2B³³, FOXM1¹⁷, MYB¹⁷, and BCL6, were silenced in lymphoma cells and STAT3¹⁸ in glioblastoma cells by RNAi mediated silencing (Table 2). Multiple cell lines and distinct RNAi silencing protocols and profiling platforms were included to avoid bias associated with these variables. We used these data to benchmark different regulatory model attributes and enrichment methods.

Table 2.

Benchmark experiments

Cell line	Knock-down gene	Technology	Replicates	Profile platform	DEGa at p < 0.01
P3HR1 (Lymphoma)	MEF2B	shRNA	5	HG-U95Av2	960
ST486 (Lymphoma)	FOXM1 MYB	shRNA shRNA	3 3	HG-U95Av2 HG-U95Av2	276 469
OCI-Ly7 (Lymphoma)	BCL6	siRNA	3	HG-U133p2	646
Pfeiffer (Lymphoma)	BCL6	siRNA	3	HG-U133p2	1,311
SNB19 (Glioma)	STAT3	siRNA	6	Illumina HT12v3	501

^aDifferentially Expressed Genes

We assessed three metrics: (1) the p-value-based rank of the silenced gene (accuracy), (2) the total number of statistically significant regulators inferred by VIPER (specificity), and (3) the overall p-value of the silenced gene. The enrichment analysis methods tested were aREA, Fisher Exact Test (1-tail FET)¹⁸ and 1-tail GSEA. We also tested extensions of FET and GSEA to account for the mode of regulation of a target gene (2-tail FET and 2-tail GSEA), which were previously implemented in our MARINa algorithm^17,18,20. Use of a 3-tail aREA (aREA-3T), accounting for target mode of regulation, confidence and pleiotropic regulation, systematically outperformed all other approaches (Fig. 1e, Supplementary Fig. 3a, Supplementary Fig. 4, Supplementary Table 2 and Supplementary Note). Thus, the aREA-3T method was selected as the methodology of choice for the VIPER algorithm. The experimentally silenced proteins, MYB, BCL6, STAT3, FOXM1, MEF2B and BCL6, were ranked as the 1^st, 1^st, 1^st, 2^nd, 3^rd, and 3^rd most significantly inactivated proteins among all those tested, respectively (Supplementary Fig. 3a and Supplementary Table 2). The small number of additional TFs inferred by aREA was enriched in differentially expressed genes and thus likely represents downstream targets of the silenced regulators or RNAi off-target effects (Supplementary Fig. 5).

To evaluate suitability of ARACNe-inferred regulons for use in VIPER analysis, we benchmarked VIPER performance with non-context specific regulons, as assembled from ChIP-Seq data in ChEA²⁵ and in ENCODE²⁶. We also benchmarked VIPER against the upstream regulator module of Ingenuity Pathway Analysis²⁷. ARACNe-based VIPER outperformed these approaches (Supplementary Fig. 3c and Supplementary Note). Interestingly, the alternative methods/models correctly assessed protein activity decrease only for FOXM1, following its silencing. Among the 5 tested TFs, FOXM1 is the only one representing a core cell cycle regulator, whose regulon is strongly conserved across multiple tissue contexts (Supplementary Fig. 3d), thus not requiring use of context-specific regulatory models.

Signatures were generated from each experiment using the control sample-based Z-transformation (Methods) to allow analysis of individual samples (Table 2). Results from single-sample analyses were virtually identical to those obtained with the multi-sample version of VIPER (Fig. 1e, Supplementary Fig. 3b and Supplementary Table 3), suggesting that single-sample analysis produces robust and highly reproducible results. We then performed several additional benchmarks to assess the specific improvements due to the aREA probabilistic analysis, compared to GSEA, and to assess the overall ability of the algorithm to correctly identify proteins whose activity was modulated by RNAi and small molecule perturbations, or whose abundance was quantified by reverse phase protein arrays (Supplementary Figs. 6–9, Supplementary Tables 4–6 and Supplementary Note). Based on our benchmarking results, we generated a comprehensive map of protein activity dysregulation in response to short term pharmacologic perturbations. We selected 166 compounds in CMAP that induced reproducible perturbation profiles across replicates (FDR<0.05, see Supplementary Note for details) and report their effect on the activity of 2,956 regulatory proteins in Supplementary Table 7.

Algorithm robustness

Poor reproducibility across biological replicates is a critical reason why gene expression analysis has not been broadly adopted in clinical tests. We thus rigorously assessed the reproducibility of the VIPER inferences as a result of multiple sources of technical and biological noise.

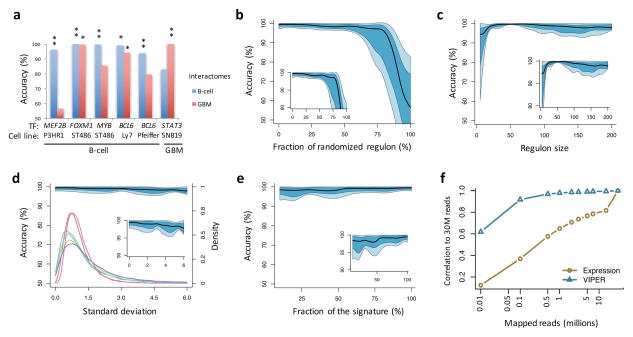
Regulons were degraded by progressively randomizing regulatory interactions while maintaining network topology. While VIPER’s performance depends on availability of tissue-specific regulons (Fig. 2a), it tolerates a high fraction of false-positive interactions, with significant performance degradation observed only when >60% of regulon interactions were randomized (Fig. 2b). Assuming ~30% false positive rate by ARACNe^34,35, this suggests that as long as >28% of genes in a regulon represents bona fide regulatory interactions, protein differential activity can be accurately inferred.

Figure 2. Effect of network and signature quality on VIPER results.

(a–c) Effect of network quality on VIPER accuracy (rank position of the silenced gene), including using a non tissue-matched interactome (a), network degradation by partially randomizing the regulons (b), or reducing the regulon size (c). (a) Barplot showing VIPER accuracy when computing protein activity with a B-cell interactome (blue) or glioma interactome (red). (b–c) Plots summarizing the accuracy across the six benchmark experiments by the median (black line), IQR (blue area), and the lowest and highest data points still inside 1.5 times the IQR away from the quartiles (light-blue area), resembling a box-and-whiskers plots (continuous boxplot). (d–f) Effect of gene expression signature quality on VIPER accuracy. (d) Signature degradation by addition of different levels of Gaussian noise (x-axis). VIPER accuracy (left y-axis) is shown by the continuous boxplot. The probability density plots show the distribution of gene expression variance for the six benchmark datasets (right y-axis). (e) Reduction of the signature coverage by randomly removing genes. VIPER accuracy is summarized by the continuous boxplot. (f) Robust response of VIPER-inferred protein activity signatures to low depth RNAseq data. Shown is the average correlation between 30 million (30M) mapped reads-based gene expression (yellow circles) or VIPER-inferred protein activity (cyan triangles) signatures, and the corresponding signatures computed from lower-depth RNAseq (indicated in the x-axis). The signatures were obtained from 100 breast carcinoma samples profiled by TCGA.

VIPER assessment of protein activity was robust to reduced regulon representation, as confirmed by the analysis of LINCS data (Supplementary Fig. 7 and Supplementary Note). Progressive target removal—starting with those with lowest mutual information—further increased accuracy, with optimal accuracy achieved at n = 50 targets and only modest degradation down to n = 25 (Fig. 2c). Regulons of fewer than 25 targets showed a dramatic decrease in accuracy (Fig. 2c).

VIPER was also highly insensitive to gene expression signature degradation, as seen by adding zero-centered Gaussian noise with increasing variance (comparable to benchmark datasets variance) (Fig. 2d). This makes it well-suited to assessing protein activity from noisy single sample gene expression profiles, where the variance of VIPER inferred activity is much smaller than the variance of gene expression (Fig. 3a–b and Supplementary Fig. 10). For instance, considering a B cell phenotype, VIPER-based protein activity signatures were significantly more correlated than gene expression signatures (p < 10⁻¹⁵, Wilcoxon signed-rank test; Fig. 3a and Supplementary Fig. 10a). Addition of Gaussian noise decreased expression-based sample-sample correlation while having only a minimal effect on VIPER-inferred activity correlation (Supplementary Fig. 10b). VIPER activity was highly resilient to reduced transcriptome representation, showing minimal accuracy decrease when up to 90% of the genes in the signature were removed from the analysis (Fig. 2e) or when RNA-Seq profiles where sub-sampled from 30M reads to 0.5M reads (Fig. 2f), making VIPER appropriate for the analysis of low-depth RNAseq profiles. This was further evidenced when comparing protein activity profiles inferred from fresh frozen vs. matched formalin fixed paraffin embedded (FFPE) samples (Fig. 3c and Supplementary Fig. 10c). The reproducibility of the results from FFPE samples represents a critical pre-requisite for precision medicine applications.

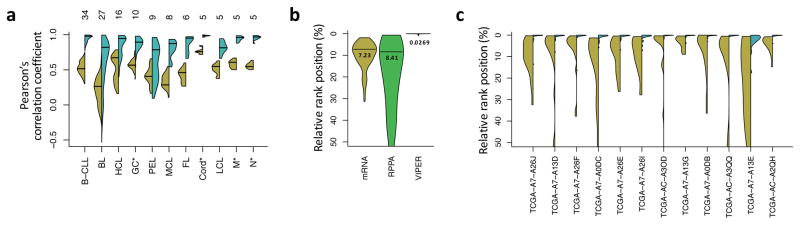
Figure 3. Reproducibility of VIPER results.

(a) Violin plot showing the distribution of correlation coefficients computed between all possible pairs of gene expression signatures (yellow) or VIPER protein activity signatures (cyan) for samples of the same B cell phenotype, including normal (GC, germinal center reaction; M, memmory and N, peripheral blood B cell) and pathologic (B-CLL, B cell chronic lymphocytic leukemia; BL, Burkitt lymphoma; HCL, hairy cell leukemia; PEL, primary effusion lymphoma; MCL, mantle cell lymphoma; FL, follicular lymphoma) phenotypes. The number of samples per phenotype is indicated on top of the figure. (b) Probability density for the relative rank position of the most upregulated gene (mRNA, yellow), relatively abundant protein (RPPA, green) or activated protein (VIPER, cyan), identified in each profiled basal breast carcinoma sample, across all the remaining profiled samples. The horizontal line and number beneath indicates the distribution mode. (c) Probability density for the relative rank position of the top 10 most upregulated genes (yellow) or VIPER-inferred activated proteins (cyan), identified from FF samples on the corresponding FFPE samples.

To assess the effect of biological variability, we computed VIPER activity signatures for 173 TCGA basal breast carcinomas. VIPER-inferred activity signatures were significantly more correlated across samples (p < 10⁻¹⁵ by Wilcoxon signed-rank test for the correlation coefficients, Supplementary Fig. 10d) and top-ranking aberrantly activated proteins were more conserved across samples based on differential activity than on differential expression of the associated gene (Fig. 3b). Overall sample–to–sample variance was reduced more than 250-fold compared to gene expression (Fig. 3b). Thus, VIPER-inferred differentially activated proteins are much more conserved than differentially expressed genes or differentially abundant proteins (based on RPPA measurements) across different samples representing the same tumor subtype (Fig. 3b).

Functionalizing the somatic mutational landscape of cancer

Based on these benchmarks, we used VIPER to systematically test the effect of recurrent mutations on corresponding protein activity. We considered a pan-cancer set of 3,912 TCGA samples, representing 14 tumor types, for which exome data are available (Supplementary Table 8). We first computed the VIPER-inferred activity of each TF and signaling protein in each of the analyzed samples and tested whether samples harboring recurrent mutations were enriched in those with high VIPER-inferred differential activity of the affected protein. From 150 recurrently mutated genes in COSMIC, we selected 89 that were mutated in at least 10 samples in at least one tumor type and for which a matching regulatory model was available (Supplementary Table 8). This identified a total of 342 pairs (e.g., EGFR in GBM) where a specific mutated oncoprotein could be tested in a specific tumor cohort.

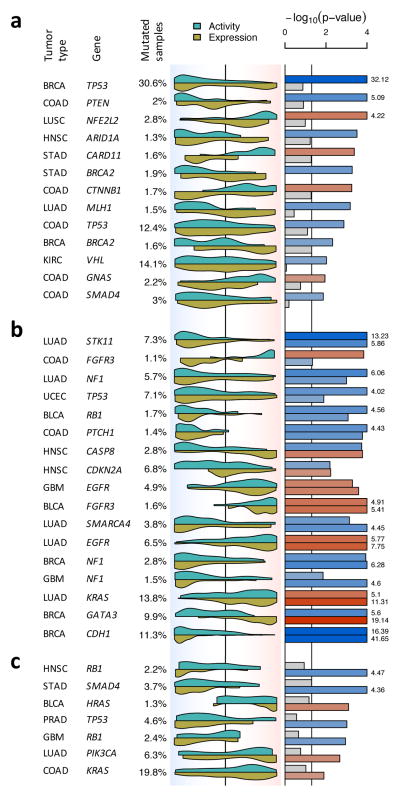
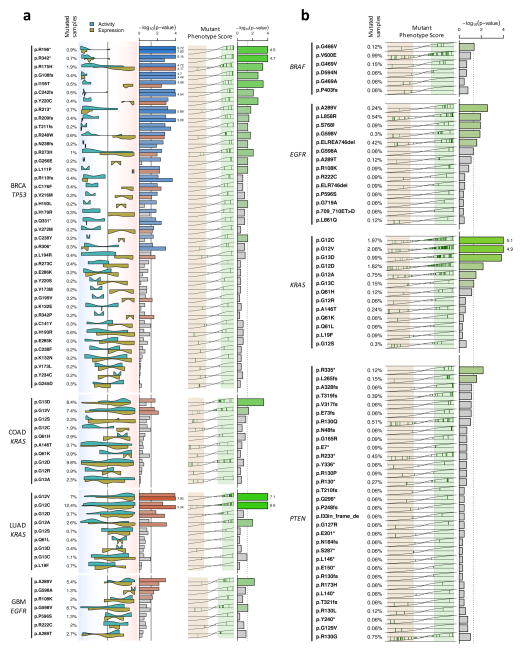
Since protein activity may depend on either total protein abundance or on the abundance of specific, differentially active isoforms, we estimated both global VIPER activity and the residual post-translational (RPT) VIPER activity—the component of activity that cannot be accounted for by differential expression—by removing the transcriptional variance component (Methods). By definition, RPT-activity is statistically independent of gene expression and should account for the purely post-translational contribution to protein activity. Almost 30% of subtype specific mutation-harboring proteins (92/342) were associated with statistically significant differential protein activity, as assessed by VIPER analysis (p < 0.05): 65/342 (19%) by global-activity and 51/342 (15%) by RPT-activity analysis, respectively (Supplementary Fig. 11). This included the vast majority of established oncogenes and tumor suppressors (Fig. 4 and Supplementary Fig. 11a–b), suggesting that this integrative analysis provides an effective mean to capture mutation-dependent dysregulation of oncogene and tumor suppressor activity (Supplementary Fig. 11). VIPER-inferred RPT-activity effectively eliminates the effect of feedback loops on the corresponding gene’s expression, thus identifying mutations with only post-translational effects (Supplementary Fig. 11a–b). We observed that 45% of mutations associated with VIPER-inferred differential activity (41/92) induced no significant differential expression of the corresponding gene (Fig. 4a and Supplementary Fig. 11a), including mutations in established oncogenes and tumor suppressors, such as TP53, PTEN, NFE2L2, ARID1A, CARD11, BRCA2, CTNNB1, MLH1, VHL and SMAD4, among others (Fig. 4a, see complete list in Supplementary Fig. 11a).

Figure 4. Detecting changes in protein activity induced by non-silent somatic mutations.

Shown is the tumor type, gene harboring non-silent somatic mutations and proportion of mutated samples. The violin plot indicates the distribution density for the mutated samples on all samples rank sorted by mRNA expression (yellow) and VIPER-inferred protein activity (cyan). The background color gradient indicates both expression and VIPER-inferred protein activity signatures with down-regulated genes and inactivated proteins to the left (blue), and over-expressed genes and activated proteins to the right (red). The significance level for the association was computed by the aREA algorithm and is shown by the barplot as −log₁₀(p-value). Blue bars indicate enrichment of the mutated samples among low expression or protein activity, while red bars indicate enrichment among high levels of expression or protein activity. The figure displays mutations associated with protein activity only (a), associated with protein activity and mRNA expression (b), and associated with mRNA expression only (c). The complete list of evaluated proteins is shown in Supplementary Fig. 11.

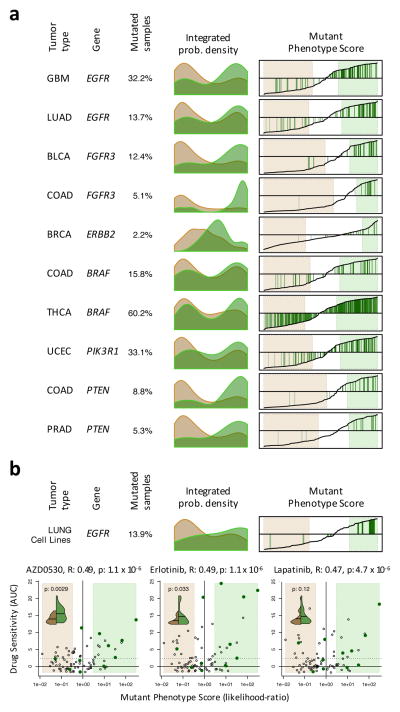
To further assess whether a pharmacologically targetable protein may be aberrantly activated in a tumor sample, independent of the sample’s mutational state, we define a sample’s Mutant Phenotype Score (MPS). This represents the probability of observing mutations in samples with equal or higher total VIPER activity (Supplementary Fig. 12). This is computed as the fraction of mutated vs. wildtype (WT) samples for the specific protein and tumor type. We thus ranked samples based on their MPS for each of the 92 protein/tumor-type pairs for which mutated samples were enriched in differentially activated proteins based on our previous analysis (see Methods for details). While the majority of mutated samples had high MPS, a few had low MPS, comparable to WT samples, suggesting non-functional or subclonal mutations or regulatory compensation of their effect (Fig. 5a and Supplementary Fig. 12), including samples harboring activating mutations in actionable proteins, such as EGFR, ERBB2, BRAF, PI3K, with MPS ≤ −0.5 (i.e., 3-fold more likely to have WT activity) (Fig. 5a), suggesting sub-par response to targeted inhibitors. More important, many WT samples had MPSs ≥ 0.5 (i.e., 3-fold more likely to have mutated activity) (Fig. 5a), suggesting they may respond to targeted inhibitors.

Figure 5. Mutant Phenotype Score and its association with drug sensitivity.

(a) Histograms showing the probability density for the non-mutated (salmon) and mutated (green) samples based on Mutant Phenotype Score (MPS) for 6 actionable mutations (complete list in Supplementary Fig. 12). Right plots show the MPS (y-axis) for all samples rank-sorted by MPS (x-axis) and indicate the mutated samples by green vertical lines. The MPS-defined WT and mutant phenotypes (likelihood-ratio > 3) are highlighted by the light-salmon and light-green boxes. (b) MPS analysis for EGFR on lung carcinoma cell lines. The scatter-plots show the drug sensitivity, quantified by the area under the titration curves (AUC), for EGFR targeting drugs as a function of MPS (expressed as likelihood-ratio). The cell lines resembling an EGFR mutated phenotype are included in the light-green box (likelihood-ratio > 3), while the ones resembling an EGFR WT phenotype are contained in the salmon box. Cell lines harboring non-silent mutations are indicated by dark-green dots. The solid and doted horizontal lines indicate the mean and 2.33 standard deviations over the mean of the chemoresistant cell lines, respectively. The association between drug sensitivity and MPS is shown on top of each plot by the Pearson’s correlation coefficient (R) and associated p-value. The violin plots (inserts) show the probability density for drug sensitivity (AUC) of the cell lines showing an EGFR WT (green) or mutant (brown) phenotype according to MPS. The horizontal line indicates the mean of each of the distributions, which were contrasted by Student t-test (p-value indicated in each insert).

Validating Drug Sensitivity

To assess whether the MPS is a good predictor of drug sensitivity, we performed EGFR-specific MPS analysis of 79 lung adenocarcinoma cell lines, for which gene expression profiles, EGFR status and chemosensitivity to EGFR inhibitors were available from the Cancer Cell Line Encyclopedia⁷, including saracatinib (AZD0530), erlotinib, and lapatinib. Of the cell lines with low EGFR-MPS (< −0.5) that yet harbored EGFR mutations, 0/2, 1/2, and 1/2 were sensitive to AZD0530, erlotinib, and lapatinib, respectively. Conversely, 5/6, 5/6 and 4/6 of those with MPS > 0.5, were sensitive to these drugs (Fig. 5b), suggesting strong association between MPS and chemosensitivity in EGFR-mutated cell lines. Moreover, considering only EGFR-WT cell lines, the fraction responding to EGFR inhibitors was higher among those with MPS > 0.5 (50% vs. 33% for AZD0530, 43% vs. 33% for erlotinib, and 36% vs. 27% for lapatinib, respectively) compared to those with MPS < −0.5 (Fig. 5b). MPS was significantly associated with chemosensitivity, regardless of EGFR mutation status, by Pearson correlation analysis (p < 10⁻⁵ for each of the three drugs, Fig. 5b), and by comparing sensitivity of cells with MPS > 0.5 and MPS < −0.5 by Student’s t-test (p < 0.01 and p < 0.05 for AZD0530 and erlotinib, respectively, Fig. 5b).

Assessing the role of site-specific mutations

In the previous analysis, all mutations in a gene were considered equivalent. We next tested whether VIPER analysis could also assess differential activity associated with mutations at specific protein sites. This could be instrumental in elucidating the functional effect of rare/private mutations. Specifically, we tested whether different mutations within the same gene (e.g., p.Gly12Val vs. p.Gly12Asp mutations in KRAS) may produce quantitatively distinct effects on protein activity. We assessed all mutations affecting COSMIC genes that were detected in at least 2 samples of the same tumor type, based on four quantitative measurements: (a) their VIPER inferred global activity, (b) their VIPER inferred RPT-activity, (c) their differential gene expression, and (d) their MPS (for mutations affecting at least 10 samples). In total, we analyzed 648 locus-specific mutations in 49 distinct genes, across 12 tumor types (Supplementary Fig. 13). Figure 6 summarizes the cases with adequate statistical power. Careful examination shows that functional impact of these mutations is both variant specific (e.g., KRAS p.Gly12Val vs. p.Gly12Asp in COAD, Fig. 6a) and tumor specific (e.g., KRAS p.Gly12Ala in COAD vs. LUAD, Fig. 6a). In addition, while some mutations induce effects equivalent to differential expression, others produce exquisitely post-translational effects that can only be predicted by RTP-activity (e.g., KRAS p.Gly12Val in LUAD vs. p.Gly13Asp in COAD, Fig 6a and Supplementary Fig. 13).

Figure 6. Effect of specific NSSM variants on VIPER-inferred protein activity.

(a) Association of non-silent somatic mutation variants with VIPER-inferred protein activity and mRNA expression. Violin plots indicate the probability density for the mutated samples on all samples rank-sorted by coding gene mRNA levels (yellow) or VIPER-inferred protein activity (cyan). The background color gradient indicates both expression and VIPER-inferred protein activity signatures from decreased (blue) to increased (orange). The statistical level for the association, as estimated by aREA, is shown by the barplot, which color indicates association with increased (red) or decreased (blue) expression or protein activity. The rightmost barplot shows the significance level for the association of mutation variants and the MPS-defined mutant phenotype (likelihood ratio > 3, light-green box). The MPS-defined WT phenotype (likelihood ratio > 3) is indicated by the light-salmon box. Missense mutations are indicated as p.XnY where X stands for 1-letter amoninoacid in position n that was mutated to Y. Nonsense mutations are indicated by ‘*’ while frame shift mutations are indicated as p.Xnfs. The vertical lines crossing the bars indicate the p-value threshold of 0.05. (b) Effect of non-silent variants integrated across different tumor types. MPS was integrated for all 12 tumor types (3,343 samples) and is shown as the x-axis in the left side of the plot, while the enrichment of each variant among the samples with at least 3-fold likelihood of mutation vs. the WT samples (likelihood-ratio > 3), is indicated as −log₁₀(p) by the barplots.

While different mutations may have similar impact on protein activity (for example, all TP53 functional variants were associated with reduction in inferred TP53 protein activity), their effects on gene expression are highly heterogeneous. For instance, nonsense and frame-shift mutations in TP53 invariably reduced mRNA levels (Fig. 6a), likely due to nonsense and nonstop-mediated mRNA decay³⁶. In contrast, missense mutations were consistently associated with increased mRNA levels, likely due to feedback loops attempting to compensate for mutation-induced loss of TP53 protein activity (Fig. 6a)³⁷. Such dichotomy in TP53 somatic variant effect may explain the lack of association between mutations and gene expression, when all variants are considered together (Fig. 4a).

To compensate for lack of statistical power due to the potentially small number of samples harboring locus-specific mutations (Supplementary Fig. 13), we performed integrated analysis across all tumor types. The heterogeneity among tumor types was accounted for by aggregating the samples at the protein activity level, originally inferred using tissue-matched interactomes. This yielded a pan-cancer repertoire of functionally relevant somatic variants, based on the analysis of 3,343 samples across 12 tumor types, for which we report the statistical association between each locus-specific mutation and its MPS, as well as the pan-cancer VIPER activity p-value (Fig. 6b and Supplementary Fig. 14).

DISCUSSION

Precision cancer medicine currently relies on the identification of actionable mutations. These can be reproducibly identified from whole-genome and exome analysis of tumor tissue and have demonstrated clinical relevance. However, only ~25% of adult cancer patients present with potentially actionable mutations⁸. Thus, methodologies, such as VIPER, for inferring aberrant protein activity, independent of mutational state, may complement and greatly extend available genomic approaches. Indeed, genetic mutations are neither necessary nor sufficient to induce aberrant activity and tumor-essentiality of protein isoforms. An increasing catalog of non-oncogene dependencies has emerged in recent years^{5,18,20,21,38,39}, whose aberrant activity depends on indirect genetic alterations, such as those in upstream pathways and cognate binding proteins. Not surprisingly, many tumor cells respond to inhibitors targeting established oncoproteins, such as EGFR, even in the absence of activating mutations, as shown by large scale dose response studies in the cancer cell line encyclopedia^6,7 and by recent analysis of pathways upstream of functional tumor drivers⁵.

VIPER plays three critical roles. First, it helps elucidate aberrant protein activity resulting either from direct or pathway mediated mutations. Second, it can help prioritize the functional relevance of rare and private non-synonymous mutations as hypomorph, hypermorph, or neutral events. Systematic analysis of TCGA cohorts showed that 27% of non-synonymous mutations induce aberrant VIPER-inferred protein activity. This is a substantial fraction, especially considering that not all mutations significantly affect protein activity on canonical targets, including those resulting in entirely novel protein functions (neopmorphs), and that mutation clonality was not accounted for in these studies. Third, VIPER can help distinguish between transcriptionally and post-translationally mediated mutational effects (Figs. 4a–c and 6).

Systematic VIPER analysis of TCGA samples (Fig. 5a) shows that, while genetic alterations strongly co-segregate with aberrant VIPER-inferred oncoprotein activity, many WT samples have VIPER-inferred activity comparable to and even greater than those harboring actionable mutations. This is critically relevant for alterations in pharmacologically actionable oncogenes, such as BRAF, EGFR, ERBB2 and FGFR3, among others, suggesting that VIPER may identify additional patients who may benefit from targeted therapy. Similarly, VIPER identified samples with actionable mutations presenting no aberrant activity of the corresponding oncoprotein. Validation of the predictive value of VIPER-inferred activity to infer targeted inhibitors response, using the cancer cell line encyclopedia, suggests that the algorithm may provide valuable new insight in precision cancer medicine.

Several approaches have been proposed to estimate pathway activity^40,41, co-regulation of gene expression modules⁴², or activity of selected proteins⁴³ from gene expression signatures. These, however, do not predict activity of arbitrary proteins, lack tumor specificity, and cannot be used to analyze individual samples. Other approaches developed for yeast⁴⁴ and other model organisms^44–47 were never extended to mammalian cells. Similarly earlier attempts based on TF targets inferred from promoter sequence analysis¹⁶ or from proprietary, literature based networks²⁷ were not systematically validated. As a result, with the exception of VIPER there are currently no validated methods to systematically predict the activity of all signal transduction and TF proteins in individual samples.

VIPER leverages protein regulons reverse engineered from primary tumor sample data to quantitatively assess differential protein activity in individual samples, without any manual annotation or curated gene sets. Critically, VIPER’s performance is extremely robust and resilient to signature noise, regulon subsampling, and sample quality. Indeed, VIPER accurately inferred protein activity for ~50% of all regulatory proteins using <1,000 genes from LINCS perturbational signatures (Supplementary Fig. 7). Furthermore, inference of differentially active proteins from fresh-frozen or FFPE samples from the same tissue was highly correlated, even though correlation of the corresponding gene expression data was low. VIPER predictions were remarkably reproducible across samples belonging to the same molecular tumor subtype. This is critically important for precision medicine applications.

Tissue specificity of protein-target is a critical element of our analysis. Genes with expression affected by changes in protein activity are highly context-specific³⁵, due to lineage-specific chromatin remodeling, combinatorial regulation by multiple transcription factors, and post-translational modification. This is supported by the fact that inference of protein activity using the incorrect regulatory model produced substantially degraded results (Fig. 2c).

VIPER constitutes only a partial contribution toward the ultimate goal of accurately measuring protein activity in mammalian samples. Yet, our data suggest that improvements in the accuracy and coverage of regulatory models could further increase the quality and breadth of these predictions, thus helping determine which proteins drive key pathophysiological phenotypes. We have illustrated the potential application of VIPER to mine existing datasets, including expression profiles in TCGA and LINCS. Finally, VIPER has the power to infer relative protein activity as an extra layer of information, providing additional evidence over classical genetics and functional genomics data to assess the effect of non-silent mutations.

Online Methods

Regulatory networks

The regulatory networks were reverse engineered by ARACNe⁴⁹ from 20 different datasets: two B-cell context datasets profiled on Affymetrix HG-U95Av2 and HG-U133plus2 platforms, respectively; a high-grade glioma dataset profiled on Affymetrix HG-U133A arrays; and 17 human cancer tissue datasets profiled by RNASeq from TCGA (Table 1). The Affymetrix platform datasets were summarized by MAS5 (affy R-package^50,51) using probe-clusters generated by the “cleaner” algorithm⁵². Cleaner generates ‘informative’ probe-clusters by analyzing the correlation structure between probes mapping to the same gene and discarding non-correlated probes, which might represent poorly hybridizing or cross-hybridizing probes⁵². The RNASeq level 3 data were downloaded from TCGA data portal, raw counts were normalized to account for different library size and the variance was stabilized by fitting the dispersion to a negative-binomial distribution as implemented in the DESeq R-package⁵³ (Bioconductor⁵⁴). ARACNe was run with 100 bootstrap iterations using all probe-clusters mapping to a set of 1,813 transcription factors (genes annotated in Gene Ontology Molecular Function database (GO)⁵⁵ as GO:0003700—‘transcription factor activity’, or as GO:0004677—‘DNA binding’ and GO:0030528—‘Transcription regulator activity’, or as GO:0004677 and GO: 0045449—‘Regulation of transcription’), 969 transcriptional co-factors (a manually curated list, not overlapping with the transcritpion factor list, built upon genes annotated as GO:0003712—‘transcription cofactor activity’ or GO:0030528 or GO:0045449) or 3,370 signaling pathway related genes (annotated in GO Biological Process database as GO:0007165—‘signal transduction’ and in GO Cellular Component database as GO:0005622—‘intracellular’ or GO:0005886—‘plasma membrane’) as candidate regulators. Parameters were set to 0 DPI (Data Processing Inequality) tolerance and MI (Mutual Information) p-value threshold of 10⁻⁸. The regulatory networks based on ChIP experimental evidence were assembled from ChEA and ENCODE data. The mode of regulation was computed based on the correlation between TF and target gene expression as described below.

Benchmarking experiments

We used gene expression profile data after MEF2B³³, FOXM1¹⁷, MYB¹⁷ (GSE17172) and BCL6 (GSE45838) silencing in human B-cells, and STAT3 silencing in the human glioma cell line SNB19¹⁸ (GSE19114, Table 2). BCL6 knock down experiments were performed in OCI-Ly7 and Pfeiffer GCB-DLBCL cell lines. Both cell lines were maintained in 10% FBS supplemented IMDM medium and transiently transfected with either a BCL6-specific or a non-target control siRNA oligo in triplicate as described previously⁵⁶. Total RNA was isolated 48h after transfection, time at which a significant knock-down of BCL6 protein was observed (Supplementary Fig. 15a), and gene expression was profiled on H-GU133plus2 Affymetrix gene chips following the manufacturer protocol (Affymetrix Inc.). All experiments showed a significant reduction at the mRNA level for the silenced gene as quantified by expression profile (Supplementary Fig. 15b). Gene expression signatures were obtained by Student’s t-test analysis of the gene expression profiles; see Table 2.

VIPER

The VIPER algorithm tests for regulon enrichment on gene expression signatures. The gene expression signature is first obtained by comparing two groups of samples representing distinctive phenotypes or treatments. Any method that generates a quantitative measurement of difference between the groups can be used (fold change, Student’s t-test, Mann-Whitney u-test, etc). Alternatively, single sample-based gene expression signatures can be obtained by comparing the expression levels of each feature in each sample against a set of reference samples by any suitable method, including for example Student’s t-test, z-score transformation or fold change; or relative to the average expression level across all samples when clear reference samples are not available. Then we compute the enrichment of each regulon on the gene expression signature using different implementations of the analytic Rank-based Enrichment Analysis algorithm (aREA, see below for details). Finally, we estimate the statistical significance, including p-value and normalized enrichment score, by comparing each regulon enrichment score to a null model generated by randomly and uniformly permuting the samples 1,000 times. Alternatively, when the number of samples is not enough to support permutation with reposition (at least 5 samples per group is required), permutation of the genes in the gene expression signature or its analytic approximation can be used (see Analytic Rank-based Enrichment Analysis below for further details).

Fisher Exact Test

We tested whether the overlap between the subset of genes that were differentially expressed following RNAi mediated silencing of each gene (p < 0.01) and the genes in its regulon was statistically significant by Fisher’s exact test (FET). The classical FET method considers equally all differentially expressed genes, regardless of whether they are up- or down-regulated and hence, FET cannot infer whether the regulator activity is increased or decreased by the perturbation. To address this issue, we modified the FET approach to compute independently the enrichment of activated and repressed targets of a regulator (positive and negative parts of its regulon) on up- and down-regulated genes, respectively. Specifically, the genes in each regulon were divided into two subsets: (a) transcriptionally activated (R⁺) and (b) transcriptionally repressed (R⁻) targets. We used the sign of the Spearman’s correlation between the mRNA expression level for the regulator and each of the genes in its regulon to classify them as part of R⁺ or R⁻. This correlation analysis was performed on the same dataset used to infer the network by ARACNe. Then, FET analysis was performed independently for R⁺ and R⁻ on the two tails of each gene expression signature. Regulators with an increase in activity would thus show enrichment of R⁺ targets in over-expressed genes and of R⁻ targets in under-expressed genes, respectively. The opposite would be the case for regulators with a decrease in activity. The use of discrete gene lists by FET produces enrichments that are often not robust with respect to threshold selection (Supplementary Fig. 16).

Gene Set Enrichment Analysis

1-tail GSEA was implemented as described by Subramanian et. al.³⁰. For 2-tail GSEA, we divided the query regulon into two subsets: a positive subset containing the genes predicted to be transcriptionally activated by the regulator (R⁺), and a negative subset encompassing the target genes predicted to be repressed by the regulator (R⁻). The target genes were classified as being part of the R⁺ or R⁻ subsets depending on whether their mRNA levels were positively or negatively correlated with the regulator mRNA levels (Spearman’s correlation). The gene expression signature was then sorted from the most upregulated to the most downregulated gene (signature A) and the rank positions for R⁺ were computed. The rank positions for R⁻ were then computed from the gene expression signature, but this time sorted from the most downregulated to the most upregulated gene (signature B). The enrichment score was computed as described³⁰, using the computed rank positions for the R⁺ and R⁻ subsets, but taking the weighting score values only from signature A.

Analytic Rank-based Enrichment Analysis (aREA)

aREA tests for a global shift in the positions of each regulon genes when projected on the rank-sorted gene expression signature. Following upon the work of Tian and Kim^57,58, we used the mean of the quantile-transformed rank positions as test statistic (enrichment score). The enrichment score is computed twice: first by a 1-tail approach, based on the absolute value of the gene expression signature (i.e. genes are rank-sorted from the less invariant between groups to the most differentially expressed, regardless of the direction of change); and then by a 2-tail approach, where the positions of the genes whose expression is repressed by the regulator (R⁻) are inverted in the gene expression signature before computing the enrichment score. The 1- and 2-tail enrichment score estimates are integrated while weighting their contribution based on the estimated Mode of Regulation through a procedure we call ‘3-tail’ approach (see below for details). The contribution of each target gene from a given regulon to the enrichment score is also weighted based on the regulator-target gene interaction confidence (see below for details). Finally, the statistical significance for the enrichment score is estimated by comparison to a null model generated by permuting the samples uniformly at random or by an analytic approach equivalent to shuffle the genes in the signatures uniformly at random. The arithmetic mean-based enrichment score has several desirable properties, both at the algebraic level, by making the weighted contribution of the targets to the enrichment score trivial to formulate, as well as at the computational level. Regarding this last point, given the linear nature of the mean-based enrichment score, its computation across the elevated number of permutations required to generate the null model can be performed very efficiently by matrix operations. Moreover, the use of the arithmetic mean as enrichment score allows for analytical approaches to estimate its statistical significance, which is equivalent to shuffle the genes in the signatures uniformly at random. We have to note, however, that the null hypotheses tested by these two alternative approaches are not equivalent. In the case of sample shuffling, we test whether the calculated enrichment score for a given gene expression signature (i.e. for gene expression profiles associated with the phenotypes) is significantly higher than the one we can obtain when there is no association between the phenotype and the gene expression profile. Conversely, gene shuffling (or its analytic approximation) tests whether the enrichment score is higher than the one we can obtain when the set of genes to test is uniformly distributed in the gene expression signature. Gene shuffling can be approximated analytically as follows: according to the central limit theorem, the mean of a sufficiently large number of independent random variables will be approximately normally distributed. The enrichment score of our null hypothesis fulfill this condition, and we ensure a mean of zero and variance equal to one for the enrichment score under the null hypothesis by applying a quantile transformation based on the normal distribution to the rank-transformed gene expression signature before computing the enrichment score. Then, under the null hypothesis, the enrichment score will be normally distributed with mean equals zero and variance n⁻¹, where n is the regulon size. This definition can be generalized when the weighted mean is used by ${\sigma }^2={\sum }_{i=1}^n{w}_i^2$, where w_i is the weight for target i.

Mode of Regulation (MoR)

The MoR is determined based on the Spearman’s Correlation coefficient (SCC) between the regulator and the target expression, computed from the dataset used to reverse engineer the network. However, for complex non-monotonic dependencies (e.g., for context-specific rewiring^59–61), assessing the MoR may not be trivial. To address this issue, we first model the SCC probability density for all regulator-target interactions in the network using a three-Gaussian mixture (Supplementary Fig. 2), representing (a) clearly repressed targets (MoR−, blue curve in Supplementary Fig. 2a and b), (b) clearly activated targets (MoR+, red curve in Supplementary Fig. 2a and d), and (c) non-monotonically regulated targets for which the MoR cannot be reliably estimated (MoR^NM, green curve in Supplementary Fig. 2a and c). The parameters for the three-Gaussian mixture model were estimated with the ‘mixtools’ R-package⁶². Then, rather than defining MoR+ or MoR− targets based on the sign of the SCC, we associate each target with three weights (p_A, p_R, p_NM), representing the probability that, given its SCC, it may be activated, repressed, or non-monotonically regulated. These probabilities are computed as the relative likelihood of a given regulator-target interaction to be described by any of these three models and computed as the difference between the cumulative distribution for activation (CDF(G₂)) and the CDF for repression (CDF(G₁)), divided by the total CDF: CDF(G₁ upper-tail) + CDF(G₂ lower-tail) + CDF(G₀ lower-tail for Rho < 0 or G₀ upper-tail for Rho > 0) (Supplementary Fig. 3a–f).

The, 3-tail aREA approach implemented in VIPER uses MoR to weight the contribution of the 1-tail and 2-tail based enrichment scores as: ES = |MoR| ES₂ + (1-|MoR|) ES₁, where ES₁ and ES₂ are the 1-tail aREA and 2-tail aREA estimations of the enrichment score (Fig. 1c). Such probabilistic formulation avoids selection of arbitrary thresholds for determining target MoR, reducing parameter choices and thus risk of data overfitting.

3-tail aREA behaves remarkable robust to changes in the parameter estimates for the 3-Gaussian mixed model. We scanned the ‘mean’ parameter space on a wide range, from −0.3 to −0.6 for G₁ and from 0.3 to 0.6 for G₂; and found a uniform response of 3-tail aREA on the estimated normalized enrichment score and p-values across all benchmarking experiments, with only the rank positions being slightly affected (Supplementary Fig. 3g–h).

Regulator-target confidence

We used the mutual information (MI) between regulator and target gene mRNA levels as inference of regulator-target interaction confidence. To compute a regulator-target interaction confidence score, we first generated a null set of interactions for each regulator by selecting target genes at random from all the profiled genes while excluding those in the actual regulon (i.e. ARACNe inferred). The number of target genes for the null regulon was chosen to match those in the actual regulon. Then we computed a CDF for the MI in the ARACNe regulons (CDF₁) and null regulons (CDF₂), and estimated the confidence score for a given regulator-target interaction (“Interaction Confidence” or IC) as the ratio: IC = CDF₁/(CDF₁ + CDF₂). IC was used to weight the contribution of each target gene to the enrichment score (Supplementary Fig. 17).

Pleiotropy

Pleiotropic regulation of gene expression (genes regulated by several different transcription factors) can lead to false positive results if a non-active regulator shares a significant proportion of its regulon with a bona fide active regulator (Fig. 1d and Supplementary Table 9). To account for this effect, we extended the shadow analysis procedure originally described in¹⁷ to take full advantage of the probabilistic framework used by VIPER. Briefly, we first generate all possible pairs of regulators AB satisfying two conditions: a) both A and B regulons are significantly enriched in the gene expression signature (p < 0.05), and b) they co-regulate (A ∩ B) at least 10 genes. Then we evaluate whether the regulons in each pair are enriched in the gene expression signature mostly due to the co-regulated genes. This is performed by computing the enrichment of the co-regulated genes (A ∩ B) on a subset of the gene expression signature representing only the genes in A (pA) and in B (pB), where pA and pB represent the estimated p-values for the enrichment computed by aREA. Then we compute the pleiotropy differential score as PDE = log₁₀(pB) - log₁₀(pA). If pA < pB we penalize the co-regulated genes for A by PDE ^PI/NT, where PI (for pleiotropy index) is a constant and NT is the number of test pairs involving the regulon A. Conversely, if pA > pB we penalize the co-regulated genes for B by |PDE|^PI/NT. VIPER results showed in general to be robust to different values for the pleiotropy index (Supplementary Fig. 18). We set PI = 20 based on the benchmark data (Table 2), because it was a reasonable compromise between accuracy and specificity (Supplementary Fig. 18).

Availability

The viper algorithm is available as an R-system package from Bioconductor. A detailed description of the package functionality and use-case examples can be found in the viper package vignette.

Residual post-translational RPT-activity

We found a strong association between VIPER-inferred protein activity and the coding gene mRNA level (Supplementary Fig. 19). We estimated the variance in VIPER-inferred protein activity due to the expression level of the coding gene by fitting a lineal model to the rank transformed data. Then, the residuals of such fit constitute the remaining variance in protein activity after removing the expression effect. By definition, this residual post-translational protein activity (RPT-activity) and the expression level of the coding genes are decoupled

Association of somatic mutations with protein activity

We estimated the association between NSSMs and three quantitative traits: (1) mutated gene mRNA levels, (2) VIPER-inferred global protein activity (G-activity), and (3) VIPER-inferred residual post-translational RPT-activity, by computing the enrichment of the mutated samples on each of the traits using the aREA algorithm. An integrated association was obtained by taking the maximum association (minimum p-value) among these traits.

The Mutant Phenotype Score was computed by integrating the relative likelihoods of mutation for a given G- and RPT-activity level. Distribution densities for the mutated and non-mutated (WT) samples, for genes mutated in at least 10 samples, were estimated by a Gaussian kernel, and the probabilities, computed by the derived cumulative distribution functions, were used to compute the relative likelihood for each trait as follows:

$$RL(x)=\frac{p_M(x)-p_{wt}(x)}{p_M(x)-p_{wt}(x)}$$

where p_M and p_wt are the estimated probabilities for mutant and WT phenotypes at a given value x of the evaluated trait, either G- or RPT-activity. MPS is then defined as the maximum deviance from zero of RL among the two evaluated traits.