The present study demonstrates, for the first time, that kinesthetic information of visual and tactile origins are optimally integrated (Bayesian modeling) to improve velocity discrimination for self-hand movement. We used an original paradigm consisting of similar illusory hand movements induced through visual and tactile stimulation. By testing the role of other sources of information favoring nonmoving hand perception, we also highlight the key contribution of the omnipresent muscle proprioceptive information and its overweighting for kinesthesia.
Keywords: illusions, Bayesian modeling, kinesthesia, multisensory integration, muscle proprioception
Abstract
Illusory hand movements can be elicited by a textured disk or a visual pattern rotating under one's hand, while proprioceptive inputs convey immobility information (Blanchard C, Roll R, Roll JP, Kavounoudias A. PLoS One 8: e62475, 2013). Here, we investigated whether visuotactile integration can optimize velocity discrimination of illusory hand movements in line with Bayesian predictions. We induced illusory movements in 15 volunteers by visual and/or tactile stimulation delivered at six angular velocities. Participants had to compare hand illusion velocities with a 5°/s hand reference movement in an alternative forced choice paradigm. Results showed that the discrimination threshold decreased in the visuotactile condition compared with unimodal (visual or tactile) conditions, reflecting better bimodal discrimination. The perceptual strength (gain) of the illusions also increased: the stimulation required to give rise to a 5°/s illusory movement was slower in the visuotactile condition compared with each of the two unimodal conditions. The maximum likelihood estimation model satisfactorily predicted the improved discrimination threshold but not the increase in gain. When we added a zero-centered prior, reflecting immobility information, the Bayesian model did actually predict the gain increase but systematically overestimated it. Interestingly, the predicted gains better fit the visuotactile performances when a proprioceptive noise was generated by covibrating antagonist wrist muscles. These findings show that kinesthetic information of visual and tactile origins is optimally integrated to improve velocity discrimination of self-hand movements. However, a Bayesian model alone could not fully describe the illusory phenomenon pointing to the crucial importance of the omnipresent muscle proprioceptive cues with respect to other sensory cues for kinesthesia.
NEW & NOTEWORTHY
The present study demonstrates, for the first time, that kinesthetic information of visual and tactile origins are optimally integrated (Bayesian modeling) to improve velocity discrimination for self-hand movement. We used an original paradigm consisting of similar illusory hand movements induced through visual and tactile stimulation. By testing the role of other sources of information favoring nonmoving hand perception, we also highlight the key contribution of the omnipresent muscle proprioceptive information and its overweighting for kinesthesia.
to perceive our body movement in space, we can rely on several sensory inputs. Among them, the involvement of muscle proprioception in kinesthesia has been widely investigated (for reviews, see McClosckey 1978; Proske and Gandevia 2012; Roll et al. 1990). The visual system also contributes to the sense of movement, as evidenced by vection phenomenon, i.e., a kinesthetic percept elicited by a visual moving scene scrolling in front of a participant (Brandt and Dichgans 1972; Guerraz and Bronstein 2008) or under one's limb (Blanchard et al. 2013). Touch, like vision, also conveys kinesthetic information with cutaneous receptors sensitive to the velocity of superficial brushing applied to their receptive fields (Breugnot et al. 2006). Illusions of self-body movements can thus be induced using a tactile stimulus rotating under the palm of the hand (Blanchard et al. 2011, 2013).
However, less is known about how these two sensory modalities interact to estimate self-body motion. Many studies have highlighted a perceptual benefit when two or more sensory signals are combined, provided they are temporally and spatially congruent. Based on a probabilistic representation of information and on the assumption that minimizing the variance of the combined perceptual estimate is a primary goal of multisensory integration, the optimal cue combination framework has provided an efficient approach to predict the perceptual enhancement due to multisensory integration (Landy et al. 2011). In particular, the maximum likelihood estimation (MLE) principle postulates that the multisensory estimate of an event is given by the reliability-weighted average of each single-cue estimates (where reliability is defined as the inverse of variance). MLE predictions have been successfully reported for several multisensory tasks but mainly when the object of perception is external to the body (Alais and Burr 2004; Ernst and Banks 2002; Gingras et al. 2009; Gori et al. 2011; Wozny et al. 2008). Whether Bayesian rules can account for multisensory integration subserving self-body perception has been less investigated, especially with regard to the integration of visuotactile kinesthetic cues. Visual and vestibular information were found to be close to optimally integrated in the perception of whole body displacements (Fetsch et al. 2009; Prsa et al. 2012; Vidal and Bülthoff 2009), as were vision and proprioception when evaluating arm movements (Reuschel et al. 2009), positions in space (Tagliabue and McIntyre, 2013; van Beers et al. 2002), and when performing pointing motor tasks (Sober and Sabes 2003, 2005).
The present study aimed to further investigate whether visual and tactile signals are optimally integrated when estimating self-hand movements. During natural movements, muscle proprioceptive afferents are continuously activated, and they cannot be selectively removed without impairing concomitant cutaneous afferents (for instance, an ischemic block affects all large somatosensory fibers, including both cutaneous and proprioceptive fibers) (Diener et al. 1984). Therefore, it is usually impossible to estimate the kinesthetic contribution of visuotactile modalities independently from muscle proprioception. For this reason, we induced illusory movements rather than actual movements using a visual and/or tactile moving background rotating under the hand, i.e., participants felt that their hand was passively rotated even though it remained perfectly still. We estimated the perceptual benefit of visuotactile stimulation compared with each unimodal stimulation in a discriminative test of self-hand movement velocity and then compared it with MLE predictions.
However, in our experiment, participants were aware that their hand was not actually moving, and this cognitive component was further strengthened by a proprioceptive feedback from the wrist muscles conveying static information. This prior knowledge combined with static muscle proprioceptive cues might explain why the perceived velocity of the illusory movements was about six times less than the actual velocity of the stimulation (Blanchard et al. 2013). In the Bayesian framework, sensory illusions have been successfully explained as the result of an optimal combination between noisy sensory information and stimulus-independent prior knowledge. For example, a prior favoring low-speed motion can account for several visual illusory phenomena observed in motion vision (Montagnini et al. 2007; Weiss et al. 2002). Studies about self-body perception used a Gaussian low-speed prior distribution to account for top-down expectations that influence perceptual performance (Clemens et al. 2011; Dokka et al. 2010; Jürgens and Becker 2006; Laurens and Droulez 2006).
Therefore, we tested a Bayesian model including a Gaussian prior distribution as well as a proprioceptive likelihood, both centered on zero, to account for the strong belief in favor of immobility and for the omnipresent static information from muscle spindle endings. The combination of these two Gaussian distributions centered on zero should provide a theoretical ground for the very low gain of the illusory hand motion perception. For the sake of simplicity, we will refer to this combined information as zero-centered prior. We also manipulated this prior static information by disturbing proprioceptive feedback. To this end, we equally applied a covibration onto the participants' antagonist wrist muscles (noisy condition). We expected to make the muscle proprioceptive inputs less reliable and, consequently, to lower the weight of the static information taken into account in the prior distribution and to increase the gain of illusory perception.
METHODS
Participants
Twenty right-handed volunteers (14 women and 6 men) with no history of neurological disease agreed to participate to this study. They all gave their informed consent, conforming to the Helsinki declaration, and the experiment was approved by the local Ethics Committee (CCP Marseille Sud 1 no. RCB 2010-A00359-30). Five of them did not experience any illusory perception during the tactile stimulation and were therefore not included in the complete series of experiments and analysis.
Stimuli
Tactile stimulation was delivered by a motorized disk (40 cm in diameter) covered with cotton twill (8.5 ribs/cm), which is a material known to efficiently activate cutaneous receptors (Breugnot et al. 2006). The disk rotated under the participant's right hand in a counterclockwise direction with a constant angular velocity ranging from 10 to 45°/s (Fig. 1B).
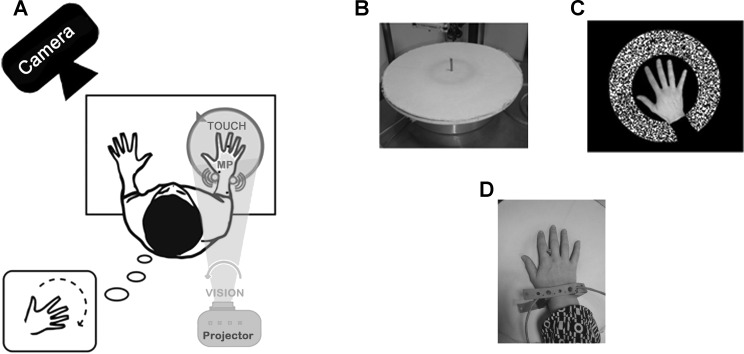
Fig. 1.
Experimental set-up and stimulation devices. A: experimental setup including stimulation devices and motion capture system (CODAmotion) to record actual right hand movements in the reference movement condition. B: the textured disk used as tactile stimulation. C: visual pattern displayed by a video projector (see A). D: mechanical vibrators applied onto two antagonist wrist muscles (pollicis longus and extensor carpi ulnaris) to disturb muscle proprioceptive inputs (MP) in the noisy condition. Participants exposed to a counterclockwise rotation of the tactile and/or visual stimuli had to report whether the induced clockwise illusion of hand rotation they perceived was faster or slower than the velocity of the reference movement they actively executed before or after each stimulation.
Visual stimulation consisted of a projection of a black and white pattern on the disk. To give the participant the feeling that the pattern was moving in the background, i.e., under his/her hand, a black mask adjusted to the size of each participant's hand was included in the video and prevented the pattern from being projected onto his/her hand. The pattern rotated around the participant's right hand with a constant counterclockwise angular velocity ranging from 10 to 45°/s (Fig. 1C).
These two types of stimulation were delivered for 6 s either separately (unimodal conditions) or simultaneously (bimodal condition) at six different velocities (10, 20, 25, 30, 35, and 45°/s). These stimulation velocities were chosen based on a previous study (Blanchard et al. 2013) to induce efficient illusory movements with a perceived velocity well distributed around 5°/s [reference velocity (Vref)].
In the noisy conditions, muscle proprioception was disturbed using low-amplitude mechanical vibration (0.5 mm peak to peak) set at a constant low frequency (20 Hz). We used two vibrators each made of a biaxial direct current motor with eccentric masses forming a 5-cm-long and 2-cm-diameter cylinder. As shown in Fig. 1D, they were fixed on both sides of the participant's right wrist to stimulate equally and simultaneously two antagonist muscle groups: the longus pollicis and extensor carpi ulnaris muscles. Indeed, microneurographic studies have shown that such low-amplitude vibration preferentially activates muscle spindle primary endings. Roll et al. (1989) have shown that in the vibration range of 10–100 Hz, primary muscle spindle endings respond with a frequency of discharge equal to the vibration frequency (with a 1:1 mode of response), resulting in a masking effect of spontaneous natural discharges, usually ranging between 3 and 15 Hz in the absence of vibratory stimulation. When applied onto a single muscle group, vibration stimulation can elicit an illusory sensation of limb movement, but any illusion is cancelled when a concomitant vibration is equally applied onto antagonist muscles (Calvin-Figuière et al. 1999). Therefore, by equally costimulating wrist antagonist muscles, we expected to disturb proprioceptive afferents without inducing any illusory sensation of movement. The stimuli were delivered using a National Instruments card (NI PCI-6229) and specifically designed software implemented in LabView (version 2010).
Procedures
Participants sat on an adjustable chair in front of a fixed table with arm rests immobilizing their forearms, their left hand resting on the table, and their right hand on the motorized disk. A small abutment in the disk center placed between their index and middle finger kept their hand from moving with the disk when it rotated. Head movements were limited thanks to a chin and chest rest, allowing participants to relax and sit comfortably. The experiment took place in the dark, and participants wore headphones to block external noise as well as shutter glasses partially occluding their visual field and reducing it to the disk surface only.
Training Phase
Before the experimental session, each participant underwent two training sessions. First, there was a 15-min session consisting of 150 trials of separate tactile and visual stimulation applied at medium velocity (25°/s). To be included in the experiment, participants had to feel illusory hand rotations in at least 80% of the trials.
Participants were then trained to perform a reproducible 5°/s clockwise hand rotation. During this second 15-min session, with their middle fingers, they had to follow a red line moving at 5°/s that was repeatedly projected onto the disk every 7.5 s. Participants were asked to memorize the movement using all the available information (tactile, visual, and proprioceptive feedback plus efferent motor command). This 5°/s movement was chosen as the reference to which participants would have to compare their perception during the discrimination test phase.
Discrimination Test Phase
The experimental test consisted of a two-alternative forced choice discrimination task with constant stimuli. A stimulation condition (visual, tactile, or combined) and the reference movement were presented by pairs in random order. Participants were instructed to say out loud whether the illusory movement they perceived was faster or slower than the reference movement.
The reference movement executed during the experimental test was similar to that performed during the training phase except that the red line appeared only during the first and the last of the 6 s of the movement duration to prevent the participants from using only visual feedback.
Three stimulation conditions were randomly intermixed within the experimental sessions: two unimodal conditions [tactile (T) and visual (V)] and one bimodal condition [visuotactile (VT)]. For each stimulation condition, six intensities were tested and presented immediately before or after the reference movement. All stimuli lasted 6 s (as the reference movement), and the interstimulus intervals ranged between 1.7 and 2.3 s. Before each reference/stimulation pair, a white line was projected to make sure that participants always positioned their hand in the same orientation. Participants were instructed to focus on their hand to estimate as accurately as possible whether the illusory movement they perceived was faster or slower than the reference movement they executed just before or just after each stimulus. They had to keep their eyes open except if a green screen appeared, signaling them to close their eyes before a tactile-only stimulus. At the end of each pair (reference/stimulation) presentation, participants had 2 s to answer (“faster” or “slower”) and 3 s (±300 ms) before a new pair was presented. The presentation order of the 18 stimulation conditions was counterbalanced for each subject.
During the standard condition test, participants were asked to compare 270 reference/stimulation pairs (3 conditions × 6 intensities × 15 trials) divided into 4 sessions of 10 min each performed on 2 different days (at the same time during the day). Thirteen of fifteen participants were tested in four additional noisy condition sessions of 10 min, during which the same block of 270 pairs of reference/stimulation was presented while participants underwent covibrations of their antagonist wrist muscles.
Movement Acquisition and Kinematic Analysis
Participants were asked to compare the velocity of each illusory movement they experienced during the unimodal and bimodal stimulation conditions with the velocity of the same reference movement, consisting of a clockwise rotation of the right hand at 5°/s that they actively performed just before or just after every stimulus. All reference movements were recorded using an optical motion capture system (CODAmotion, Charnwood Dynamics, Rothley, UK) composed of three infrared “active” markers and one camera to track the three-dimensional marker positions (sampling frequency: 10 Hz). Markers were attached to the participants' middle finger, on the top of their hand back, and on the last third of their forearm to capture the angular rotation of their wrist during the reference movement execution.
For each participant, the mean angular velocity of hand movements was extracted with Codamotion Analysis software (version 6.78.2). Reproducibility of the reference movement across the 270 trials during the standard experiment was further tested by one-way ANOVA for each participant with the session (4 sessions) as experimental factor for the standard condition (without vibration) and the noisy condition (with covibration stimulation). As expected, no significant difference in the mean velocity of the reference movement was found between sessions by any participants in either in standard or noisy condition. Note that individual variability estimated from the four sessions ranged between 0.22 and 0.37°/s. We further verified the precision of estimation of the reference movement in a complementary experiment performed on 10 naïve participants consisting of a discrimination task between several self-hand rotations actively executed. Participants were asked to compare the velocity of the fixed reference movement set at 5°/s (like in the main experiments) with eight other hand movement velocities (3.5, 4, 4.5, 4.75, 5.25, 5.5, 6, or 6.5°/s). Again, the estimated variability was found to be small (ranging from 0.33 to 0.79°/s).
One-way ANOVA was also performed to ensure that reference movement was not significantly different between participants [standard condition: F(3, 42) = 1.05, P = 0.38; noisy condition: F(3, 36) = 0.21, P = 0.89]. Finally, a Student's paired t-test was used to ensure the reproducibility of the reference movement between the standard condition and the noisy condition. There was no significant difference between these conditions (meanstandard: 4.6 ± 0.08°/s and meannoisy: 4.7 ± 0.07°/s, P = 0.34), suggesting that participants referred on average to the same velocity of reference movement in both conditions.
Data Analysis
To evaluate and compare participants' perceptual performance across the three stimulation conditions (T, V, and VT), the psychometric data (i.e., the proportion of “faster than the reference” answers at different stimulation intensities) were fitted by the following cumulative Gaussian function:
where P is probability, x is the stimulus velocity (in °/s), μΨ is the mean of the Gaussian, i.e., the point of subjective equality (PSE) that corresponds to the stimulation intensity leading the participant to perceive an illusory movement on average as fast as the reference set at 5°/s; and σΨ is the SD of the curve, or discrimination threshold, which is inversely related to the participant's discrimination sensitivity. In other words, a smaller σΨ value corresponds with a higher sensitivity in the discrimination task. The two indexes, PSE and σΨ, characterize the participant's performance. λ accounts for stimulus-independent errors due to participant's lapses and was restricted to small values [0 < λ < 0.06 (Wichmann and Hill 2001)]. This parameter is not informative about the perceptual decision; thus, we disregarded it for the following analyses. Psignifit toolbox implemented on Matlab software (The MathWorks) was used to fit the psychometric curves (Wichmann and Hill 2001).
To compare discrimination sensitivity across the three stimulation conditions (T, V and VT), we performed one-way repeated-measures ANOVA with Tukey post hoc tests on σΨ values. In addition, for each participant, the enhancement of the visuotactile discrimination sensitivity over the best unisensory condition was assessed using the multisensory index (MSI) as defined by Stein et al. (2009). Since an improvement of discrimination sensitivity corresponded to a decrease in the σ value, the MSI was computed as follows:
To quantify the perceptual strength of the illusions, the gain of the responses in the different stimulation conditions was assessed as follow (in %):
with Vref set at 5°/s.
For the 15 participants, we compared the response gains between the three sensory stimuli (T, V, and VT) using one-way repeated-measures ANOVA with Tukey post hoc tests. For the 13 participants that underwent the noisy condition, two-way repeated-measures ANOVA was also performed on the illusion gains to test the effect of the sensory stimulation (T, V, and VT) and the experimental condition (standard vs. noisy).
The enhancement or depression of the visuotactile response gain over the best unisensory response gain was computed using the MSI, as defined by Stein et al. (2009):
Models
The MLE model used to predict optimal multimodal discrimination performance.
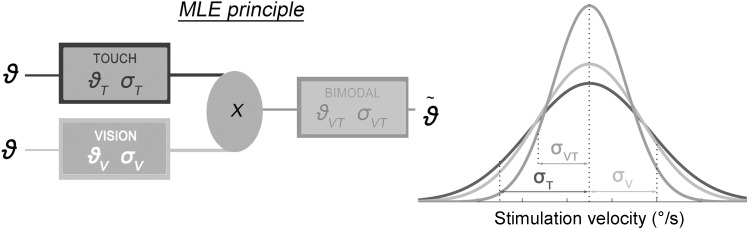
As shown in Fig. 2, the minimum-variance linear combination model (often referred to as the MLE model) predicts how an “optimal observer” would combine two unbiased sensory signals to optimize the resulting perception (in the sense of minimizing its variance) relative to the two unimodal representations. According to MLE rules (which are just one particular instantiation of the more general Bayesian framework; see Landy et al. 2011), the optimal perceptual estimate in visuotactile stimulation can be described by the normalized product of the unimodal Likelihood distributions P(ϑT | ϑ) and P(ϑv | ϑ) with the underlying assumption that visual and tactile sources are conditionally independent variables affected by Gaussian noise:
| (1) |
where ϑT, ϑV, and ϑVT are the tactile, visual, and visuotactile estimates of hand velocity for a given value of stimulation velocity (ϑ).
Fig. 2.
Schematic representation of the maximum likelihood estimation (MLE) principle. To estimate self-hand movement velocity, the central nervous system is supposed to proceed as an inference machine: following MLE rules, unisensory cues (noisy, normally distributed representations of the stimulation velocity ϑT and ϑV on the basis of each sensory modality, touch and vision) are optimally combined to determine the minimum-variance visuotactile perceptual estimate (ϑVT). Right: MLE prediction for the visuotactile (VT) likelihood (with variance σVT2, black curve) resulting from the optimal combination of unimodal [visual (V) and tactile (T)] likelihoods (σT2 and σV2, dark gray and light gray curves, respectively).
The visuotactile likelihood resulting from the normalized multiplication of the two unimodal Gaussians is a Gaussian distribution itself, with a variance (σVT2) related to the unimodal variances through the following equation:
| (2) |
Therefore, Eq. 2 implies that if the two sensory signals are optimally integrated, the visuotactile variance is smaller than the variance of either modality in isolation, thus leading to a sensitivity enhancement.
The MLE model and its predictions can easily be tested on the behavioral data of a multisensory discrimination experiment. It can be shown that the same relation presented in Eq. 2 for the variance of the sensory likelihood does actually apply to the standard deviation (σΨ) of the estimated cumulative-Gaussian psychometric curve (i.e., its discrimination threshold). In particular, in the present study, the predicted and observed visuotactile discrimination thresholds were compared to determine if the integration of vision and touch was optimal with regard to the discriminative sensitivity of the participants.
It should be noticed that in the present experimental context, the uncertainty related to the reference movement velocity estimation could account for a portion of the estimated discrimination threshold σΨ. We will address this issue below.
A Bayesian model to account for the low-perceptual gain of movement illusions.
In the present study, kinesthetic illusions of hand movements were induced while participants were aware that their hand was actually not moving. This prior knowledge was also supported by muscle proprioceptive feedback from their stationary wrist. The conflict between this static information and the moving tactile or visual information may account for the extremely low gain of the velocity illusions with respect to the actual velocity of the moving stimuli (Blanchard et al. 2013).
To account for the low gain of the unimodal and multimodal illusions, a more complex Bayesian model was elaborated including a zero-centered Gaussian likelihood accounting for muscle proprioceptive cues and a Gaussian prior distribution centered on zero as well. The combination of those two distributions is also a zero-centered Gaussian distribution. Therefore, to preserve the model parsimony, we will treat these distinct contributions as a single probability distribution and we will refer to it as “prior” throughout the present report.
The sensory likelihood and prior distributions were combined according to Bayes' rule to obtain the following posterior distribution:
| (3) |
where P(ϑ) is the prior probability distribution of hand velocity, P(ϑi | ϑ) is the sensory Likelihood for modality i, and i is T, V, or VT.
The parameters (mean and variance) of the Bayesian Gaussian distributions are linked by the following relations:
| (4) |
where i is T, V, or VT, μprior equals 0°/s, σprior2 is the unknown variance of the prior (assumed to be constant throughout the different experimental conditions), μi is the mean of the likelihood, σi2 is the unknown variance of the likelihood, and μposti and σposti2 are the mean and variance of the posterior distribution. In line with most Bayesian models, we assumed that the likelihood mean exactly matches the velocity stimulation (μi = ϑi), as it represents the first stage of (presumably unbiased) sensory encoding of global motion information. We also assumed that σi2 does not depend on velocity in the considered range. Although this last assumption is probably not true in general (e.g., Stocker and Simoncelli 2006), it seems to be a reasonable approximation for the relatively small range of stimulation velocities considered here.
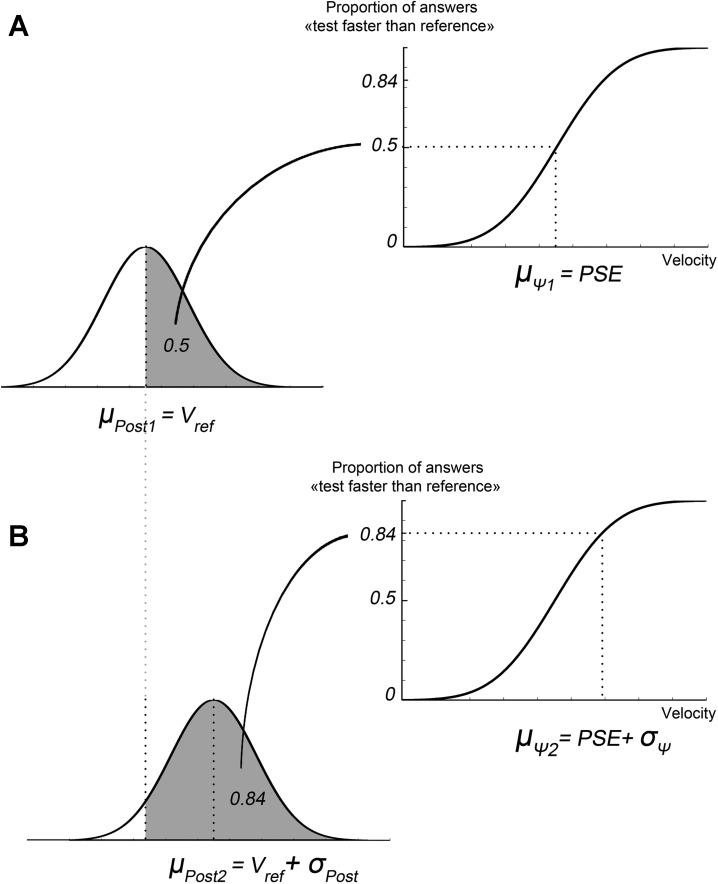
Given all the above-mentioned assumptions, the estimated parameters of the psychometric function can be put in relation to the parameters of the hidden Bayesian distributions. A Bayesian ideal observer uses the information provided by the posterior distribution to formulate a perceptual judgment, such as the velocity discrimination in our study. As shown in Fig. 3, the proportion of judgments of the type “test faster than reference” is equal to the integral of the Posterior distribution over the interval (Vref:+∞).
Fig. 3.
Relationship between Bayesian and psychometric functions. A and B: the two different relevant conditions of stimulations (1 and 2) used to determine the discriminative threshold: the point of subjective equality (PSE; A) and the intensity leading to 84.13% of the “faster than the reference velocity” answer (B). Vref is the velocity of the reference movement (5°/s). σpost, μpost, and μi are parameters of the Bayesian functions: the SD and mean of the posterior distribution and the mean of the likelihood function (assumed equal to the stimulation velocity), respectively. σΨ and PSE are the psychophysical, measured parameters: the variance and mean of the psychometric function, respectively. The PSE is defined as the point of subjective equality, i.e., the stimulation intensity eliciting an illusory movement faster than the reference 50% of the time. These relations allow to estimate all the parameters of the hidden Bayesian functions as a function of the psychometric parameters (see Models).
Let us consider two values of the stimulation velocity that correspond to the critical parameters of the psychometric curve, namely, the PSE and the value at which Ψ = 0.84, which corresponds by definition to (PSE + σΨ).
When the test velocity ϑi = PSE, the ideal observer perceives on average by definition a velocity equivalent to Vref. Thus the mean (and most likely value) of the Posterior pistribution μpost is equal to Vref.
On the other hand, when the test velocity is ϑi = PSE + σΨ, the integral under the posterior is 0.84, which, on the ground of the assumption of normality, implies that its mean μpost is equal to (Vref + σpost).
By substituting these equalities in the system of Eq. 4, we obtained the expression of the variance of the three Bayesian distributions as a function of the parameters of the psychometric curve (PSEi and σi) and of Vref:
| (5) |
| (6) |
| (7) |
Note that these equations hold for each type of stimulation (T, V, or VT). The variance of the prior distribution was thus estimated (through Eq. 6) for each of the unimodal conditions (V and T). Consistent with our assumption of a constant Gaussian prior noise across experimental conditions, we verified that σprior estimated by the “tactile” and “visual” equations (6) did not differ significantly (P = 0.063 by Student's paired t-test). We used the mean of the prior variance estimated from the visual and tactile psychometric parameters (Eq. 6) for the later steps (see also Fig. 4, step 1).
Fig. 4.
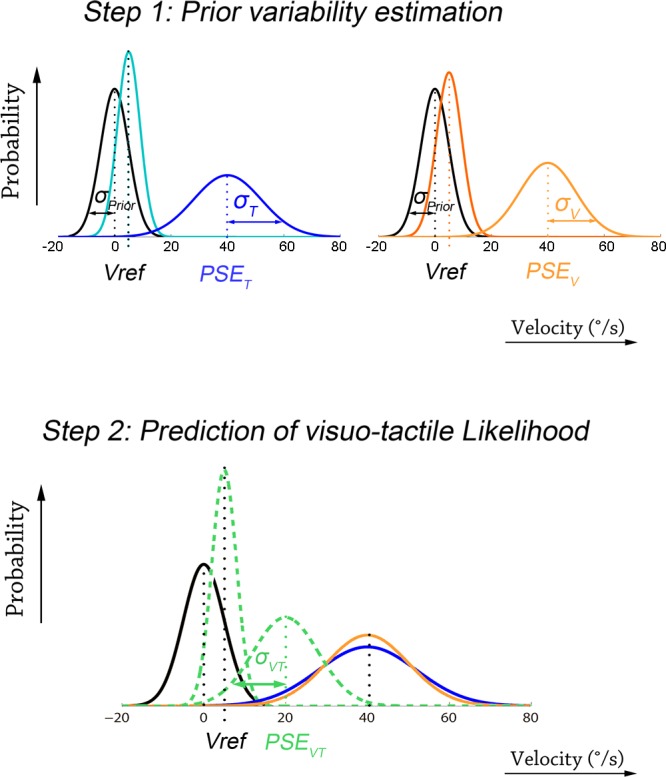
Schematic representation of the key steps for predicting visuo-tactile gain on the basis of a prior-equipped Bayesian model. Step 1: prior variability estimation. The SD (σprior) of the prior distribution (black curve, centered on the null velocity) is estimated for each participant using (through Eq. 6) the psychometric parameters estimated in unimodal visual (orange curves) and tactile (blue curves) conditions. Step 2: prediction of the visuo-tactile gain. The expected PSE in the visuotactile stimulation (mean of the visuotactile likelihood depicted by the dashed green curve) is predicted on the basis of the estimate of the prior variance (step 1), the MLE-estimate for σVT2, and Eq. 7. The visuotactile gain is simply derived from the PSE (see definition in methods).
We then applied the MLE predictions for the estimate of the likelihood variance in the condition of visuotactile stimulation (Eq. 2) and then inverted Eqs. 5–7, relating the Bayesian to the psychometric parameters, to predict the bimodal point of subjective equality PSEVT (Fig. 4, step 2):
| (8) |
where both σVT2 and σprior2 can be expressed as functions of the unimodal psychometric parameters. For all participants, the predicted gain (GVT) of the visuotactile illusion in the standard condition could finally be compared with the observed visuotactile gain.
As previously pointed out, the uncertainty related to the estimation of the reference movement velocity could account for a portion of the perceptual variability in our hand-velocity discrimination task, whatever the sensory stimulation. Therefore, we assessed its influence by including the individual variability of the reference movement reproduction (see methods) in the estimation of the global uncertainty for the velocity discrimination task. However, doing so increased the complexity of the model without improving the predictions or changing the core results. For the sake of parsimony, we will only briefly present the impact of this additional component of perceptual uncertainty on the predictions at the end of the results.
In addition, the same analysis was performed on perceptual responses elicited in the noisy condition, where covibration was applied onto antagonist wrist muscles to disturb static muscle proprioceptive feedback. The variance of the prior σprior2 in the noisy condition was estimated and GVT was predicted.
The relative contribution of the prior in the final perception was also assessed by computing the relative weight of the prior with respect to the visual and tactile weights, as follows:
The relative weights of the prior obtained in standard and noisy conditions were compared using a Student's paired t-test.
Finally, to test whether the model better fit the visuotactile performances in the noisy condition compared with the standard condition, the differences between predicted and observed gains in the two conditions were compared using a Student's paired t-test.
RESULTS
Discriminative Ability for Hand Movement Velocity Based on Visual and/or Tactile Inputs
As expected, for all participants included in the study, the counterclockwise rotation of the visual and/or tactile stimulation gave rise to an illusory sensation of rotation of their stimulated hand, which was always oriented in the opposite direction, i.e., clockwise. For each stimulation condition (T, V, and VT) randomly applied at six different velocities, participants reported whether the illusion was faster or slower than the 5°/s clockwise reference rotation they actively performed just before or just after the stimulation delivery. To compare the participants' performance in the velocity discrimination task between tactile, visual, and visuotactile stimulation, the probability of perceiving the illusion as faster than the reference movement was fitted by a cumulative Gaussian function for the tested stimulus velocities to obtain three individual psychometric curves.
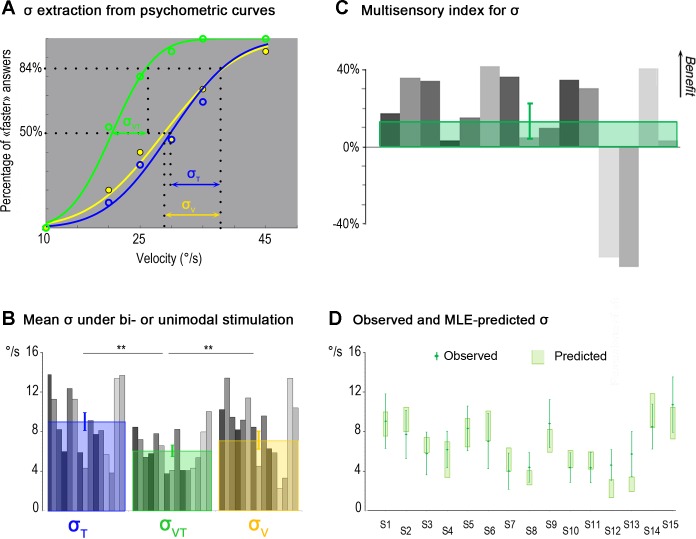
As shown in the examples in Fig. 5A, the participant experienced an illusory movement with a velocity close to the 5°/s reference when the tactile or the visual stimulation was rotating around 29.8 and 28.8°/s, respectively. The participant's ability to discriminate the velocity of his/her hand movement improved in the visuotactile condition compared with the unimodal conditions, as attested by an increased slope of the visuotactile psychometric curve. More precisely, the discrimination threshold σ (i.e., the increase in stimulation velocity required to induce an illusory movement faster than the reference movement in 84% of the trials with respect to 50% of the trials) was lower in the visuotactile condition (mean σVT: 6.02 ± 2.19°/s) than in the unimodal conditions (mean σT: 8.67 ± 3.6°/s and mean σV: 7.68 ± 3.5°/s). In other words, the decrease in the σ value reflected the fact that the velocity discrimination ability of this participant increased in the visuotactile condition.
Fig. 5.
Comparison of velocity discrimination thresholds during tactile, visual, and visuotactile stimulation. A: extraction of σ from psychometric curves. Psychometric curves of one representative participant obtained by fitting the probabilities of perceiving the illusion as faster than the reference movement with a cumulative Gaussian distribution for the tactile stimulation (T; blue curve), visual stimulation (V; yellow curve), and visuotactile stimulation (VT; green curve) are shown. The discrimination threshold (σ) is the difference between the stimulation velocities leading to the faster answer 84.13% of the times and 50% of the times, and it is inversely related to the slope of the psychometric function. B: mean σ in bi- or unimodal stimulation. Mean individual values of σ (gray bars) and mean (±SD) values of σ extracted from the whole population data (N = 15) for tactile (blue square), visual (yellow square), and visuotactile (green square) stimulation are shown. For the mean σ values, significant differences were found between the bimodal and each of the two unimodal conditions (*P < 0.05; **P < 0.01). C: multisensory index for σ. Individual (gray bars) and mean multisensory index (green square) for σ (N = 15 participants) are shown. Positive and negative values correspond, respectively, to a multisensory benefit or loss in the discrimination performance of the participants with respect to their most efficient unimodal performance. D: comparison between observed and MLE-predicted σ. A comparison between observed σ in visuotactile stimulation and σ predicted by the MLE model for the 15 participants (S1 to S15) is shown. The green diamonds correspond to the observed data, and error bars are SDs. No significant difference was found between predictions and observations of σ (P = 0.55; not significant). Light green rectangles represent 95% confidence intervals (CIs) computed using the following bootstrap procedure. Choice data were resampled across repetitions (with replacement) and refitted 1,000 times to create sample distributions of the threshold for each psychometric function and for the predicted visuotactile parameters. CIs were directly estimated from these bootstrap samples (percentile method).
These individual results were confirmed at the group level (Fig. 5B). Performances in velocity discrimination changed according to the stimulation condition [F(2, 28) = 12.375, P = 0.00014]. Mean σ decreased significantly in the visuotactile condition compared with the tactile (P < 0.001 by post hoc test) and visual conditions (P = 0.0025 by post hoc test). Discrimination thresholds for the velocity discrimination task did not significantly differ between the two unimodal conditions (P = 0.58).
To quantify the benefit resulting from visuotactile stimulation, the MSI was calculated individually for the σ values. This index (in %) reveals, for each participant, the enhancement (or depression) of the multisensory sensitivity over the best unisensory response (Stein et al. 2009). For eleven of thirteen participants, the multisensory response showed a positive benefit on the discriminative threshold σ. Quantitatively, visuotactile σ values for those 11 participants were lower than the lowest of the unimodal σ, with an MSI ranging between 3% and 40% (Fig. 5C). Only 2 of 15 participants did not show an improvement of their discriminative sensibility in the visuotactile condition.
As shown in Fig. 2, the MLE model predicted an improved discrimination performance in the multimodal condition. MLE-predicted visuotactile σ values were estimated for each participant on the basis of his/her performances in the two unimodal conditions. As shown in Fig. 5D, a comparison of these estimates with the experimental observations during the visuotactile condition showed that the data estimates did not differ significantly from the observed σ values (P = 0.55 by Student's paired t-test). Note that including the variability of the reference reproduction task in the model did not change the predictions of the discriminative thresholds in any appreciable way (0.9% of difference in the worst case).
A Low-Perceptual Gain for Movement Illusions
Standard condition.
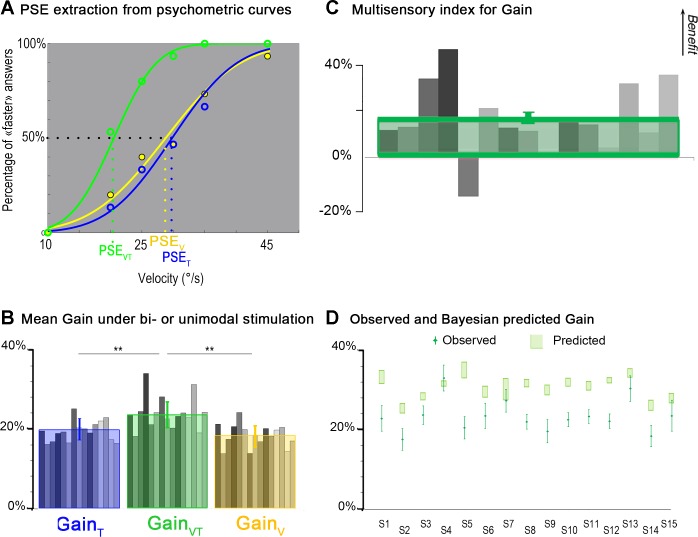
In the individual results shown in Fig. 6A, illusory movement was perceived at a velocity close to the 5°/s reference when the tactile or visual stimulation was rotating at about 29°/s, with a PSE estimated at 28.8 and 29.8°/s, respectively. When the two kinds of stimulation were combined, the velocity of the stimulation required to evoke an illusion close to the 5°/s reference dropped to 20.5°/s (Fig. 6A). The decrease in PSE reflected the fact that the participant perceived a faster illusory movement with combined visual and tactile stimulation compared with only one kind of stimulation. These results can also be expressed in terms of response gain, classically defined as the ratio between the perceived illusion velocity and the actual velocity of the stimulus (see methods). A value of 100% would indicate that the participant perceived a hand movement at the same velocity as the actual stimulation velocity. In our experimental paradigm, the gains of the illusions were always much lower than 100%. They were on average about 19.9% (±2.7% SD) and 18.4% (±2.9% SD) for the tactile and visual stimulation, respectively. During visuotactile stimulation, the gain significantly increased, up to 23.7% (±3.5% SD) compared with unimodal tactile (P = 0.0004 by post hoc test) and visual (P < 0.0001 by post hoc test) stimulations: illusion velocity got closer to the actual stimulation velocity in the visuotactile condition (Fig. 6B). A more detailed analysis showed that the multimodal gain increased for all participants except one (Fig. 6C). This increase was also attested by positive MSI values, ranging from 1% to 40% for 14 of 15 participants (mean MSI: 14 ± 13%).
Fig. 6.
Comparison of the gains of the perceptual responses during tactile, visual, and visuo-tactile stimulation. A: extraction of the PSE from psychometric curves. Psychometric curves of one participant obtained by fitting the probability of perceiving the illusion as “faster than the reference” movement with a cumulative Gaussian distribution for the tactile stimulation (T; blue curve), visual stimulation (V; yellow curve), and visuotactile stimulation (VT; green curve) is shown. The PSE corresponds to the stimulation velocity leading to the faster than the reference answer 50% of the time. B: mean gain in bi- or unimodal stimulation. Mean individual values of gain (gray bars) and mean (±SD) values of gain calculated as the ratio between Vref and the actual velocity of the visual (yellow bars), tactile (blue bars), and visuotactile (green bars) stimulation at the PSE are shown. For the mean gain values, significant differences were found between the bimodal and each of the two unimodal conditions (*P < 0.05; **P < 0.01). C: multisensory index for gain. Individual (gray bars) and mean multisensory index (green square) of illusion gains (N = 15 participants) are shown. Positive and negative values correspond, respectively, to a multisensory increase or decrease in the gain of the perceptual illusions of the participants with respect to the best unimodal performance. D: comparison between observed and Bayesian-predicted gain. A comparison between observed gain in visuotactile stimulation and gain predicted by the Bayesian model with a zero-centered prior for the 15 participants (S1 to S15) is shown. The green diamonds correspond to the observed data, and error bars are SDs. The increase of the bimodal gain was predicted but overestimated by the model. Light green rectangles represent 95% CIs computed using the following bootstrap procedure. Choice data were resampled across repetitions (with replacement) and refitted 1,000 times to create sample distributions of the threshold for each psychometric function and for the predicted visuotactile parameters. The CIs were directly estimated from these bootstrap samples (percentile method).
To account for these low-perceptual gains, we then considered a more complex model than the MLE, including the influence of the “nonmoving hand information” a priori present in our experimental paradigm. Indeed, in addition to the omnipresent proprioceptive static cue, participants were always aware that their hands were not actually moving. By modeling the nonmoving hand information as a Gaussian distribution centered on zero, the variance of this prior was first estimated through the observed data obtained in the two unimodal conditions (Figs. 3 and 4, step 1). In line with our assumption that the prior distribution should be constant over the various sensory conditions, we found that the variance estimates based on each single sensory performance did not differ significantly (P = 0.18).
The visuotactile likelihood was then predicted by combining the estimated prior distribution with the estimated unisensory likelihoods (see Figs. 3 and 4, step 2).
This model predicted that the gain of the illusion in the visuotactile condition would improve compared with the unimodal conditions. However, the observed increase in gain was less than that predicted by the model (Fig. 6D). By taking into account the variability of the reference movement perception in the model, predictions were not improved (they became actually worse; in the worst case, discrepancies between observations and predictions of the gain went from 3.9% to 9.8%) but the discrepancy between data and model predictions did not qualitatively change, highlighting in all cases an overestimation of the gain increase by the Bayesian complete model.
Noisy condition.
To further explore the influence of the nonmoving hand cues in our paradigm, the same experiment was performed while muscle proprioception was disturbed by equivalent vibrations applied on antagonist wrist muscles involved in left-right hand movement: the right pollicis longus and carpi ulnaris extensor muscles. Applied on antagonist muscles with the same low frequency, mechanical vibration equally activates muscle spindle endings, masking natural muscle spindle afferents without giving rise to any relevant movement information (Calvin-Figuière et al. 1999; Roll et al. 1989). Before the beginning of each experimental session, we ensured that muscle covibration did not induce any movement sensation.
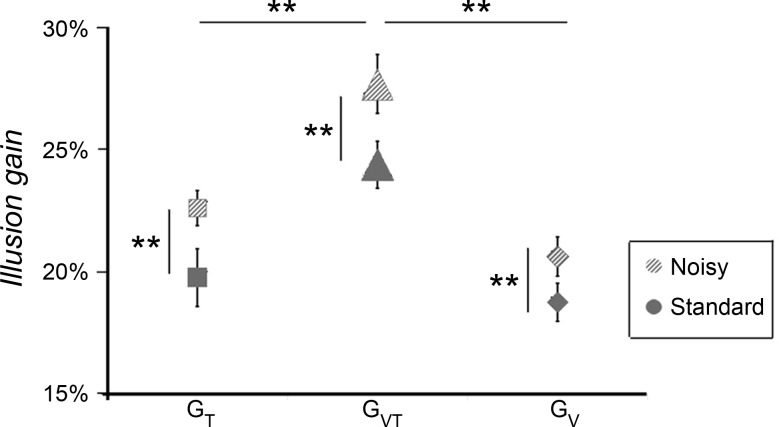
During covibration, all participants were still able to experience the illusory movement elicited by the tactile and/or visual stimulation. In the noisy condition, the stimulus velocity required for the illusory movement to reach a velocity close to the reference value was lower than that previously observed in the standard condition, where no vibration was applied. Two-way ANOVA showed that the gains of the perceptual illusions increased significantly in the noisy conditions compared with the standard conditions [main effect of condition: F(1, 12) = 26.003, P = 0.00026]. When the two noisy and standard conditions were confounded, the gain observed in the visuotactile conditions was significantly higher than those observed in the tactile and visual conditions [F(2, 24) = 25.37, P < 0.0001; Fig. 7]. No significant interactions were found between the condition (noisy vs. standard) and stimulation (T, V, and VT) factors.
Fig. 7.
Comparison of illusion gains between standard and noisy conditions. The mean gain (±SE) of the discrimination responses induced by tactile (T; squares), visual (V; diamonds), and visuotactile (VT; triangles) stimulation for the standard (gray) and noisy (hatched gray) conditions is shown. Note that illusion gains observed in the noisy conditions, in which muscle proprioception afferents were masked by an agoantagonist covibration, were significantly higher than those in the standard conditions whatever the stimulation (T, V, or VT). *P < 0.05; **P < 0.01.
As in the previous standard experiment, we estimated the variance of the prior based on unimodal responses collected during covibration. With degraded muscle proprioceptive information, the influence of the nonmoving hand information modeled by the prior was supposed to be reduced in the noisy conditions. As expected, for the 13 participants tested, the relative weight of the prior (compared with the tactile and visual relative weight) was lower in the noisy experiment (0.89 ± 0.03) than in the standard experiment (0.95 ± 0.017, P = 0.011 by Student's paired t-test).
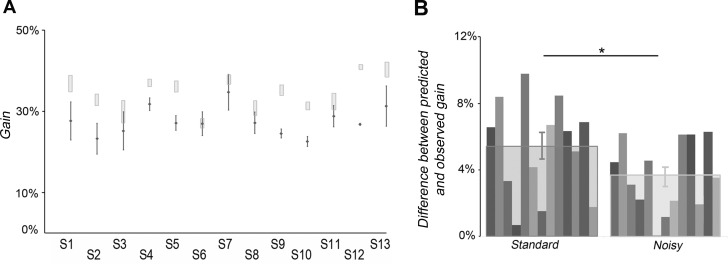
In addition, the predicted gains of the visuotactile responses were estimated on the basis of the unimodal and prior distributions obtained with concomitant covibration. Although the predicted gains were still higher than those observed experimentally, the discrepancy between data and model predictions was reduced in the noisy experiment with respect to the standard experiment (P = 0.019 by Student's paired t-test; see Fig. 8).
Fig. 8.
Comparison of the Bayesian predictions for the standard and noisy conditions. A: Bayesian prediction versus observation in the noisy condition. A comparison between observed gains in visuotactile stimulation and gains predicted by the Bayesian model in the noisy condition for the 13 participants (S1 to S13) is shown. The dots correspond to individual observed data, and error bars are SDs. 95% CIs were computed using the following bootstrap procedure. Choice data were resampled across repetitions (with replacement) and refitted 1,000 times to create sample distributions of the threshold for each psychometric function and for the predicted visuotactile parameters. The CIs were directly estimated from these bootstrap samples (percentile method). Increase of the visuotactile gain was better predicted than in the standard condition but remained overestimated by the model. B: difference between predicted and observed gain. The quantitative difference between model predictions and empirically obtained values of visuotactile gain was significantly smaller in the noisy condition compared with the standard condition (P < 0.05).
DISCUSSION
Optimal Visuotactile Integration in Velocity Discrimination of Self-Hand Movements
The present study shows that visual and tactile motion cues can be equivalently used by the central nervous system (CNS) to discriminate the velocity of self-hand movements. By combining both types of stimulation at the same velocity, one can assume that we generated congruent multisensory signals, as during actual hand movements. As expected, we observed a multimodal benefit provided by the combination of visual and tactile motion cues when participants evaluated the velocity of self-hand illusion rotation. This behavioral improvement was first of all attested by a better discrimination ability (a lower discrimination threshold) in the bimodal condition than in unimodal conditions.
The perceptual benefit of combined vision and touch had mainly been estimated when one has to assess properties of an external object, like its size (Ernst and Banks 2002) or its speed (Bensmaia et al. 2006; Gori et al. 2011). In those studies, as in the present study, the multimodal benefit was well predicted by the MLE principle, suggesting that vision and touch are combined in an optimal way when discriminating perceived self-hand velocity.
Moreover, participants' ability to discriminate the velocity of an illusory hand movement was equivalent when based on the rotation of either the tactile disk or the visual background with a discrimination threshold of about 8°/s for both conditions. This is consistent with the study by Gori et al. (2011) showing equal sensitivities to discriminate the velocity of external motion signals of tactile or visual origin. One can thus hypothesize that common inferential processes take place in situations of visuotactile integration in the context of velocity discrimination, whether the perceived object is the self or an external object.
Influence of the Nonmoving Hand Prior in the Low-Perceptual Gain of Movement Illusions
A strong difference emerges for the absolute estimation of the velocity depending on whether visual and tactile motion signals are related to an external object or to self-body. Whereas velocity estimation of a tactile stream on a fingertip is close to the actual velocity of the moving object (Bensmaia et al. 2006), velocity of the perceived self-hand movement in the present experiment was drastically underestimated with a perceived movement speed always lower than 30% of the actual visual or tactile stimulation velocity. One plausible explanation is that since proprioceptive afferents from participants' wrist muscles informed the CNS that the hand was not actually moving, the sensory conflict might have resulted in a slower perception of hand rotation. To account for this unavoidable proprioceptive feedback together with the fact that participants knew that their hand was actually not moving, we developed a Bayesian model including a prior term defined as the product of two Gaussian distributions (the proprioceptive static sensory likelihood and the cognitive prior) centered on zero. We postulated that, when visual or tactile stimulation was applied, the final perception of illusory hand movement resulted from the combination of the visual, tactile, or visuotactile motion cues with this zero-centered prior. Our parameter-free Bayesian model successfully predicted a gain increase in visuotactile illusions compared with unimodal illusions. In the Bayesian framework, this effect is explained by the stronger weight of the sensory information when two modalities are optimally combined and hence reliability is increased. In a self-angular displacement estimation task, Jürgens and Becker (2006) had postulated a prior favoring a particular rotation speed to account for the velocity-dependent bias observed in the participants' judgments. Although that study did not test a quantitative prediction on the observed bias reduction in multisensory stimulation, the authors' conclusions are consistent with ours and point to a probabilistic integration of sensory representations with a prior knowledge as postulated by Bayes theory. However, the observed gain increase in the present experiment did not match the predicted values, which were overestimated. We discuss some possible explanations below.
Suboptimal Multisensory Integration: Insights Into the Underlying Mechanisms
Deviations from optimal integration predictions have already been reported in cases of sensory conflicts, when sensory information is strongly noncoherent across different modalities. Suboptimal cue weights have been reported in conflictual situations where visual and vestibular inputs are manipulated to give incongruent spatial information relative to passively imposed body rotations (Prsa et al. 2012). In the latter case, participants overweighted the visual cues to discriminate the angle of imposed rotations. Conversely, vestibular cues were found excessively preponderant to visual cues in a heading perception task (Fetsch et al. 2009).
In the present experiment, several explanations may account for the suboptimal benefit on the perceptual gain for visuotactile stimulation.
First, it has been shown that in case of extreme conflict, integration can be prevented, favoring segregation of the multisensory information (Bresciani et al. 2004; Körding et al. 2007; Roach et al 2006; van Dam et al. 2014). Accordingly, causal inference models predict a variable degree of multisensory integration according to the probability of the incoming signals to be causally related to a common origin in the world (Körding et al. 2007). In the present study, one can speculate that, if the statistical inference process assigns high weight to a single cause (proprioception, vision and touch all originating from the same true source), then one would indeed find a strengthening of the illusion when a second moving cue is added to the first one. On the other hand, having two moving sensory cues instead of one may increase the conflict between static and movement information, thus leading to a lower weight for the common origin hypothesis. In the latter case, this conflict increase may have degraded multisensory integration and may then have led the participants to partly attribute the visual and tactile motion cues to a different origin in the environment rather than their own body. However, a change in causal attribution does not seem to fully explain the present results since it is not consistent with the observation of an increased (although suboptimal) gain in the visuotactile condition and also the fact that all participants reported more salient illusory hand movements in bimodal compared with unimodal conditions. Finally, segregation is more likely to occur for large discrepancies between cues. Therefore, future studies should be conducted to test whether increasing the conflict between static and motion information (using higher velocity stimulation) results in a greater deviation from optimality.
Regardless of the conflict between static and motion cues, a second explanation for the overestimation of the bimodal gain improvement can be considered. One can speculate that there is an illusory percept that is being used for a behavioral report and simultaneously a nonreported judgment of background motion and those may interact. In this context, combining visual and tactile cues leads to a decrease in the variability of the velocity estimate, both for self-body movements (as suggested by our psychophysical results) and for external object motions (Gori et al. 2011). As a consequence, if participants have a more coherent percept of the rotation of the environment under their hand, this should in turn facilitate the attribution of the movement to the environment rather than to the hand during the bimodal condition compared with the unimodal conditions and finally result in suboptimal performances compared with Bayesian predictions. Nevertheless, this argument alone fails to explain the observed improvement of gain predictions in the noisy condition. Indeed, muscle proprioceptive noise should not have affected the way external object motion was perceived.
Finally, taking into account the crucial role of muscle proprioception in kinesthesia, the suboptimality in the present study can be interpreted as a weighting bias in favor of this modality. Biases toward one sensory cue in multisensory conflicting situations that cannot be explained by a Bayesian weighting process can rather be attributed to a recalibration mechanism (Adams et al. 2001; Block and Bastian 2011; Prsa et al. 2012 Wozny and Shams 2011). To solve the discrepancy between two sensory estimates, the brain may choose to realign all the sensory estimates with respect to the most appropriate one. This interpretation is consistent with the appropriateness principle (Welch et al. 1980): discrepancies between senses tend to be resolved in favor of the modality not only generally more reliable but also more appropriate to the task at hand. Recently, Block and Bastian (2011) demonstrated that the weighting and realigning strategies are two independent processes that might occur in conjunction.
In the present experiment, the conflict increase between static and movement information may lead to an apparent suboptimal estimation of the illusion velocity due to a recalibration of the visuotactile estimation with respect to the static proprioceptive information. Indeed, the CNS may rely more on less ambiguous information, which is muscle proprioceptive information, rather than on visual or tactile information, which can both relate to either self-body or environmental changes. Such a recalibration mechanism could thus explain why the perceptual benefit of the bimodal situation was lower than predicted.
To test this hypothesis, we degraded muscle proprioceptive signals to reduce the reliability of the static information. Natural messages from muscle spindles were masked thanks to a concomitant vibration applied onto the wrist antagonist muscles (Roll et al. 1989). Such vibration efficiently degraded the information of hand immobility: the velocity required to give rise to an illusory movement with a velocity close to the reference value was lower than previously observed in the standard condition (with no vibration). In other words, the same visual or tactile stimulation gave rise to faster illusory movements when muscle proprioception was masked by the vibration. Using the mirror paradigm, Guerraz et al. (2012) consistently reported that the illusory movement sensation of one arm evoked by the reflection on a mirror of the contralateral moving arm increased with a proprioceptive masking of the arm subjected to kinesthetic illusion.
As expected, the proprioceptive noise enabled our model to better fit the observed illusion gains. However, the model predictions still overestimated the visuotactile benefit on gain, suggesting that attenuating muscle proprioceptive feedback was not sufficient. This quantitative discrepancy may be due to incomplete masking of proprioceptive afferents through our noninvasive stimulation. In addition, static information cannot be completely cancelled, since the participants were always aware that no actual hand movement was occurring during the experiment. This cognitive component might have pushed toward a sensory realignment in conjunction with a greater muscular proprioception reweighting in the visuotactile estimation of illusory hand movements.
Physiological Evidence for Visuotactile Integration and Bayesian Inferences
A large number of studies performed in animals and humans have recently provided compelling evidence for the neural substrates of multisensory integrative processing, including in the early stages of sensory information processing (for reviews, see Cappe et al. 2009; Klemen and Chambers 2012). Bimodal neurons sensitive to both visual and tactile stimuli applied on the hand have been found in the premotor and parietal areas of the monkey (Graziano and Gross 1998; Grefkes and Fink 2005) when spatially congruent stimuli from different origins are simultaneously presented to the animal. Neuroimaging studies further support that heteromodal brain regions are specifically activated in the presence of different sensory inputs (Calvert 2001; Downar et al. 2000; Gentile et al. 2011; Kavounoudias et al. 2008; Macaluso and Driver 2001). By applying coincident visual and tactile stimuli on human hands, Gentile et al. (2011) used fMRI to show the involvement of the premotor cortex and intraparietal sulcus in visuotactile integration processing, supporting observations previously reported in monkeys. More generally, the inferior parietal cortex has been found to subserve visuotactile integrative processing for object motion coding in peripersonal space (Bremmer et al. 2001; Grefkes and Fink 2005) as well as for coding self-body awareness (Kammers et al. 2009; Tsakiris 2010).
Interestingly, direct or indirect interactions between primary sensory areas have been recently evidenced (Cappe et al. 2009; Ghazanfar and Schroeder 2006). Recently, using an elegant design inspired by the Bayesian framework, Helbig et al. (2012) showed that during a task of shape identification, activation of the primary somatosensory cortex can be modulated by the reliability of visual information within congruent visuotactile inputs. The more reliable the visual information, the less activity in S1 increased.
Meanwhile, computational modeling approaches have demonstrated that a simple linear summation of neural population activity may account for optimal Bayesian computations (Fetsch et al. 2013; Knill and Pouget 2004; Ma et al. 2006). By recording single neurones sensitive to both vestibular and visual stimuli within the dorsal medial superior temporal area (MSTd) in monkeys, a brain region activated during self-body motion, Morgan et al. (2008) provided evidence for the neural basis of Bayesian computations in kinesthesia. During the presentation of multisensory stimulation, MSTd neurones displayed responses that were well fit by a weighted linear sum of vestibular and visual unimodal responses.
Taken together, these observations support the assumption that the level of activation of primary sensory regions may reflect the relative weight of the sensory cues and that the perceptual enhancement due to convergent multisensory information might be achieved through a multistage integration processing involving dedicated heteromodal brain regions as well as direct interactions between primary sensory areas. Although the cerebral networks responsible for visuotactile integration involved in self-body movement perception remain to be identified, neural recordings from visuovestibular cortical regions support the assumption of a Bayesian-like multisensory integration at the cortical level, bridging the gap between neurophysiological, computational, and behavioral approaches.
Conclusions
The present findings show, for the first time, that kinesthetic information from visual and tactile origins is optimally integrated to improve speed discriminative ability for self-hand movement perception. In addition, by inducing illusory movement sensations, we created an artificial conflict between static muscle proprioceptive information and moving tactile and/or visual information. Such sensory conflict might explain the low-perceptual gains of the observed illusions, as attested by the increase in illusion gain when muscle proprioception was masked. However, we observed an overweighting in favor of the nonmoving hand cues that cannot be fully predicted by a Bayesian optimal weighting process including a prior favoring hand immobility. An additional recalibration strategy favoring the less ambiguous information in conflictual situations might explain such bias toward the static proprioceptive cues that are omnipresent and play a crucial rule for kinesthesia.
GRANTS
This work was supported by Agence Nationale de la Recherche Grant ANR12-JSH2-0005-01.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
M.C., C.B., M.G., A.M., and A.K. conception and design of research; M.C. and C.B. performed experiments; M.C. analyzed data; M.C., C.B., A.M., and A.K. interpreted results of experiments; M.C. prepared figures; M.C., A.M., and A.K. drafted manuscript; M.C., C.B., M.G., A.M., and A.K. edited and revised manuscript; M.C., C.B., M.G., A.M., and A.K. approved final version of manuscript.
ACKNOWLEDGMENTS
The authors are thankful to Laurent Perrinet for insightful theoretical contributions on earlier versions of the manuscript and Isabelle Virard and Rochelle Ackerley for critical remarks and for revising the English manuscript. The authors also thank Ali Gharbi for technical assistance.
REFERENCES
- Adams WJ, Banks MS, van Ee R. Adaptation to three-dimensional distortions in human vision. Nat Neurosci 4: 1063–1064, 2001. [DOI] [PubMed] [Google Scholar]
- Alais D, Burr D. The ventriloquist effect results from near-optimal bimodal integration. Curr Biol 14: 257–262, 2004. [DOI] [PubMed] [Google Scholar]
- Bensmaia SJ, Killebrew JH, Craig JC. Influence of visual motion on tactile motion perception. J Neurophysiol 96: 1625–1637, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanchard C, Roll R, Roll JP, Kavounoudias A. Combined contribution of tactile and proprioceptive feedback to hand movement perception. Brain Res 1382: 219–229, 2011. [DOI] [PubMed] [Google Scholar]
- Blanchard C, Roll R, Roll JP, Kavounoudias A. Differential contributions of vision, touch and muscle proprioception to the coding of hand movements. PLos One 8: e62475, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Block HJ, Bastian AJ. Sensory weighting and realignment: independent compensatory processes. J Neurophysiol 106: 59–70, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandt T, Dichgans J. Circular vection, visually induced pseudocoriolis effects, optokinetic afternystagmus–comparative study of subjective and objective optokinetic aftereffects. Albrecht Von Graefes Arch Klin Exp Ophthalmol 184: 42–57, 1972. [DOI] [PubMed] [Google Scholar]
- Bremmer F, Schlack A, Shah NJ, Zafiris O, Kubischik M, Hoffmann KP, Zilles K, Fink GR. Polymodal motion processing in posterior parietal and promotor cortex: a human fMRI study strongly implies equivalencies between humans and monkeys. Neuron 29: 287–296, 2001. [DOI] [PubMed] [Google Scholar]
- Bresciani JP, Ernst MO, Drewing K, Bouyer G, Maury V, Kheddar A. Feeling what you hear: auditory signals can modulate tactile tap perception. Exp Brain Res 162: 172–180, 2004. [DOI] [PubMed] [Google Scholar]
- Breugnot C, Bueno MA, Renner M, Ribot-Ciscar E, Aimonetti JM, Roll JP. Mechanical discrimination of hairy fabrics from neurosensorial criteria. Text Res J 76: 835–846, 2006. [Google Scholar]
- Calvert GA. Crossmodal processing in the human brain: Insights from functional neuroimaging studies. Cereb Cortex 11: 1110–1123, 2001. [DOI] [PubMed] [Google Scholar]
- Calvin-Figuière S, Romaiguère P, Gilhodes JC, Roll JP. Antagonist motor responses correlate with kinesthetic illusions induced by tendon vibration. Exp Brain Res 124: 342–350, 1999. [DOI] [PubMed] [Google Scholar]
- Cappe C, Rouiller EM, Barone P. Multisensory anatomical pathways. Hear Res 258: 28–36, 2009. [DOI] [PubMed] [Google Scholar]
- Clemens IA, Vrijer MD, Selen LP, Gisbergen JA, Medendorp WP. Multisensory processing in spatial orientation: an inverse probabilistic approach. J Neurosci 31: 5365–5377, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diener HC, Dichgans J, Guschlbauer B, Mau H. The significance of proprioception on postural stabilization as assessed by ischemia. Brain Res 296: 103–109, 1984. [DOI] [PubMed] [Google Scholar]
- Dokka K, Kenyon RV, Keshner EA, Kording KP. Self versus environment motion in postural control. Plos Comput Biol 6: e1000680, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downar J, Crawley AP, Mikulis DJ, Davis KD. A multimodal cortical network for the detection of changes in the sensory environment. Nat Neurosci 3: 277–283, 2000. [DOI] [PubMed] [Google Scholar]
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415: 429–433, 2002. [DOI] [PubMed] [Google Scholar]
- Fetsch CR, Turner AH, DeAngelis GC, Angelaki DE. Dynamic reweighting of visual and vestibular cues during self-motion perception. J Neurosci 29: 15601–15612, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetsch CR, DeAngelis GC, Angelaki DE. Bridging the gap between theories of sensory cue integration and the physiology of multisensory neurons. Nat Rev Neurosci 14: 429–442, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentile G, Petkova VI, Ehrsson HH. Integration of visual and tactile signals from the hand in the human brain: an fMRI study. J Neurophysiol 105: 910–922, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghazanfar AA, Schroeder CE. Is neocortex essentially multisensory? Trends Cogn Sci 10: 278–285, 2006. [DOI] [PubMed] [Google Scholar]
- Gingras G, Rowland BA, Stein BE. The differing impact of multisensory and unisensory integration on behavior. J Neurosci 29: 4897–4902, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gori M, Mazzilli G, Sandini G, Burr D. Cross-sensory facilitation reveals neural interactions between visual and tactile motion in humans. Percept Sci 2: 55, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graziano MSA, Gross CG. Spatial maps for the control of movement. Curr Opin Neurobiol 8: 195–201, 1998. [DOI] [PubMed] [Google Scholar]
- Grefkes C, Fink GR. The functional organization of the intraparietal sulcus in humans and monkeys. J Anat 207: 3–17, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guerraz M, Bronstein AM. Mechanisms underlying visually induced body sway. Neurosci Lett 443: 12–16, 2008. [DOI] [PubMed] [Google Scholar]
- Guerraz M, Provost S, Narison R, Brugnon A, Virolle S, Bresciani JP. Integration of visual and proprioceptive afferents in kinesthesia. Neuroscience 223: 258–268, 2012. [DOI] [PubMed] [Google Scholar]
- Helbig HB, Ernst MO, Ricciardi E, Pietrini P, Thielscher A, Mayer KM, Schultz J, Noppeney U. The neural mechanisms of reliability weighted integration of shape information from vision and touch. Neuroimage 60: 1063–1072, 2012. [DOI] [PubMed] [Google Scholar]
- Jürgens R, Becker W. Perception of angular displacement without landmarks: evidence for Bayesian fusion of vestibular, optokinetic, podokinesthetic, and cognitive information. Exp Brain Res 174: 528–543, 2006. [DOI] [PubMed] [Google Scholar]
- Kammers MP, Verhagen L, Dijkerman HC, Hogendoorn H, De Vignemont F, Schutter DJ. Is this hand for real? Attenuation of the rubber hand illusion by transcranial magnetic stimulation over the inferior parietal lobule. J Cogn Neurosci 21: 1311–1320, 2009. [DOI] [PubMed] [Google Scholar]
- Kavounoudias A, Roll JP, Anton JL, Nazarian B, Roth M, Roll R. Proprio-tactile integration for kinesthetic perception: an fMRI study. Neuropsychologia 46: 567–575, 2008. [DOI] [PubMed] [Google Scholar]
- Klemen J, Chambers CD. Current perspectives and methods in studying neural mechanisms of multisensory interactions. Neurosci Biobehav Rev 36: 111–133, 2012. [DOI] [PubMed] [Google Scholar]
- Knill DC, Pouget A. The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci 27: 712–719, 2004. [DOI] [PubMed] [Google Scholar]
- Körding KP, Beierholm U, Ma WJ, Quartz S, Tenenbaum JB, Shams L. Causal inference in multisensory perception. PLos One 2: e943, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landy MS, Banks MS, Knill DC. Ideal-observer models of cue integration. In: Sensory Cue Integration, edited by Trommershauser J, Kording K, Landy MS. Oxford, UK: Oxford Univ; Press, 2011, p. 5–29. [Google Scholar]
- Laurens J, Droulez J. Bayesian processing of vestibular information. Biol Cybern 96: 389–404, 2006. [DOI] [PubMed] [Google Scholar]
- Ma WJ, Beck JM, Latham PE, Pouget A. Bayesian inference with probabilistic population codes. Nat Neurosci 9: 1432–1438, 2006. [DOI] [PubMed] [Google Scholar]
- Macaluso E, Driver J. Spatial attention and crossmodal interactions between vision and touch. Neuropsychologia 39: 1304–1316, 2001. [DOI] [PubMed] [Google Scholar]
- McCloskey D. Kinesthetic sensibility. Physiol Rev 58: 763–820, 1978. [DOI] [PubMed] [Google Scholar]
- Montagnini A, Mamassian P, Perrinet L, Castet E, Masson GS. Bayesian modeling of dynamic motion integration. J Physiol 101: 64–77, 2007. [DOI] [PubMed] [Google Scholar]
- Morgan ML, DeAngelis GC, Angelaki DE. Multisensory integration in macaque visual cortex depends on cue reliability. Neuron 59: 662–673, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proske U, Gandevia SC. The proprioceptive senses: their roles in signaling body shape, body position and movement, and muscle force. Physiol Rev 92: 1651–1697, 2012. [DOI] [PubMed] [Google Scholar]
- Prsa M, Gale S, Blanke O. Self-motion leads to mandatory cue fusion across sensory modalities. J Neurophysiol 108: 2282–2291, 2012. [DOI] [PubMed] [Google Scholar]
- Reuschel J, Drewing K, Henriques DY, Rösler F, Fiehler K. Optimal integration of visual and proprioceptive movement information for the perception of trajectory geometry. Exp Brain Res 201: 853–862, 2009. [DOI] [PubMed] [Google Scholar]
- Roach NW, Heron J, McGraw PV. Resolving multisensory conflict: a strategy for balancing the costs and benefits of audio-visual integration. Proc R Soc Lond B Biol Sci 273: 2159–2168, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roll J, Vedel J, Ribot E. Alteration of proprioceptive messages induced by tendon vibration in man-a microneurographic study. Exp Brain Res 76: 213–222, 1989. [DOI] [PubMed] [Google Scholar]
- Roll J, Gilhodes J, Roll R, Velay J. Contribution of skeletal and extraocular proprioception to kinesthetic representation. Atten Perform 13: 549–566, 1990. [Google Scholar]
- Sober SJ, Sabes PN. Multisensory integration during motor planning. J Neurosci 23: 6982–6992, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sober SJ, Sabes PN. Flexible strategies for sensory integration during motor planning. Nat Neurosci 8: 490–497, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein BE, Stanford TR, Ramachandran R, Perrault TJ, Rowland BA. Challenges in quantifying multisensory integration: alternative criteria, models, and inverse effectiveness. Exp Brain Res 198: 113–126, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stocker AA, Simoncelli EP. Noise characteristics and prior expectations in human visual speed perception. Nat Neurosci 9: 578–585, 2006. [DOI] [PubMed] [Google Scholar]
- Tagliabue M, McIntyre J. When kinesthesia becomes visual: a theoretical justification for executing motor tasks in visual space. PLos One 8: e68438, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsakiris M. My body in the brain: a neurocognitive model of body-ownership. Neuropsychologia 48: 703–712, 2010. [DOI] [PubMed] [Google Scholar]
- van Beers RJ, Wolpert DM, Haggard P. When feeling is more important than seeing in sensorimotor adaptation. Curr Biol 12: 834–837, 2002. [DOI] [PubMed] [Google Scholar]
- van Dam LC, Parise CV, Ernst MO. Modeling multisensory integration. In: Sensory Integration and the Unity of Consciousness, edited by Bennett D, Hill C. Cambridge, MA: MIT Press, 2014, p. 209–229. [Google Scholar]
- Vidal M, Bülthoff HH. Storing upright turns: how visual and vestibular cues interact during the encoding and recalling process. Exp Brain Res 200: 37–49, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss Y, Simoncelli EP, Adelson EH. Motion illusions as optimal percepts. Nat Neurosci 5: 598–604, 2002. [DOI] [PubMed] [Google Scholar]
- Welch R, Warren D, With R, Wait J. Visual capture-the effects of compellingness and the assumption of unity. Bull Psychon Soc 16: 168–168, 1980. [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: II. Bootstrap-based confidence intervals and sampling. Percept Psychophys 63: 1314–1329, 2001. [DOI] [PubMed] [Google Scholar]
- Wozny DR, Beierholm UR, Shams L. Human trimodal perception follows optimal statistical inference. J Vis 8: 24, 2008. [DOI] [PubMed] [Google Scholar]
- Wozny DR, Shams L. Computational characterization of visually induced auditory spatial adaptation. Front Integr Neurosci 5: 75, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]