Nonlinear computations shaping temporal processing of precortical vision

This work describes how nonlinear processing of the visual stimulus evolves across successive stages of neural processing: the retina and lateral geniculate nucleus (LGN), using paired recordings of LGN neurons and their primary retinal input. Nonlinear modeling is used to demonstrate that temporal patterning of LGN spikes is largely established in the retina and amplified in the LGN by temporal integration and thresholding. We also detected smaller inputs added at the level of the LGN.

Abstract

Computations performed by the visual pathway are constructed by neural circuits distributed over multiple stages of processing, and thus it is challenging to determine how different stages contribute on the basis of recordings from single areas. In the current article, we address this problem in the lateral geniculate nucleus (LGN), using experiments combined with nonlinear modeling capable of isolating various circuit contributions. We recorded cat LGN neurons presented with temporally modulated spots of various sizes, which drove temporally precise LGN responses. We utilized simultaneously recorded S-potentials, corresponding to the primary retinal ganglion cell (RGC) input to each LGN cell, to distinguish the computations underlying temporal precision in the retina from those in the LGN. Nonlinear models with excitatory and delayed suppressive terms were sufficient to explain temporal precision in the LGN, and we found that models of the S-potentials were nearly identical, although with a lower threshold. To determine whether additional influences shaped the response at the level of the LGN, we extended this model to use the S-potential input in combination with stimulus-driven terms to predict the LGN response. We found that the S-potential input “explained away” the major excitatory and delayed suppressive terms responsible for temporal patterning of LGN spike trains but revealed additional contributions, largely PULL suppression, to the LGN response. Using this novel combination of recordings and modeling, we were thus able to dissect multiple circuit contributions to LGN temporal responses across retina and LGN, and set the foundation for targeted study of each stage.

NEW & NOTEWORTHY

This work describes how nonlinear processing of the visual stimulus evolves across successive stages of neural processing: the retina and lateral geniculate nucleus (LGN), using paired recordings of LGN neurons and their primary retinal input. Nonlinear modeling is used to demonstrate that temporal patterning of LGN spikes is largely established in the retina and amplified in the LGN by temporal integration and thresholding. We also detected smaller inputs added at the level of the LGN.

the function of most sensory neurons is commonly described using the concept of a receptive field (Spillmann 2014). The simple intuition underlying receptive field function is that the response of the neuron is proportional to how closely the stimulus resembles the receptive field, both in space and in time. This description is particularly useful for modeling neurons at early stages of visual processing, including retinal ganglion cells (RGCs) and relay cells in the lateral geniculate nucleus (LGN), where quantitative models based on linear receptive fields have been quite successful (Carandini et al. 2005; Shapley 2009). Furthermore, the ease of receptive field estimation, for example, via the spike-triggered average (Chichilnisky 2001; Reid et al. 1997) or, more recently, with a generalized linear model (GLM; Paninski 2004; Truccolo et al. 2005), in addition to its easy interpretation, has led to the near ubiquitous use of linear receptive fields in characterizing retinogeniculate neuron function.

However, it is clear that nonlinear models are necessary to explain many aspects of the RGC and LGN neuron responses to visual stimuli (Butts et al. 2011; Sincich et al. 2009), in particular, the high temporal precision of RGC and LGN responses (Berry and Meister 1998; Butts et al. 2007; Keat et al. 2001; Liu et al. 2001; Uzzell and Chichilnisky 2004). The presence of clear nonlinear processing provides an opportunity to gain further insight into the roles of different components of the underlying circuitry in shaping the response. Indeed, the interplay of excitatory and delayed inhibitory inputs is a common mechanistic explanation for temporal precision (Gabernet et al. 2005; Levy et al. 2013; Wehr and Zador 2003) and had previously been proposed to explain precision in the LGN (Butts et al. 2011). In this regard, a major limitation of linear models is that they implicitly average the different inputs shaping a given neuron's response, combining what might be anatomically distinct inputs into a single term (the receptive field). However, in situations where distinct inputs do not contribute linearly to the response, a nonlinear modeling approach can detect these separate contributions and quantify their relative influence on the observed spike trains.

The existence of nonlinear processing in retina and LGN is consistent with known physiology. Nonlinear rectification of excitation has been observed at bipolar-to-ganglion cell synapses within the retina (Demb et al. 2001) and also implicitly occurs due to the spiking of RGCs. Likewise, inhibition is present via interneurons in both the retina (Baccus 2007; Grimes 2012; Masland 2012) and LGN (Blitz and Regehr 2005; Dubin and Cleland 1977; Hirsch et al. 2015; Wang et al. 2007), from the perigeniculate nucleus (Vaingankar et al. 2012; Wang et al. 2011b), and through feedback from visual cortex to LGN (Guillery and Sherman 2002; Sillito et al. 2006). Other physiological mechanisms, such as spike refractoriness (Berry and Meister 1998; Gaudry and Reinagel 2007; Paninski 2004) and synaptic depression (Ozuysal and Baccus 2012), have been proposed to contribute to nonlinear processing within the retinogeniculate circuit.

However, it has been a challenge to use nonlinear modeling approaches to understand how these different circuit mechanisms contribute to precision. On the one hand, the most common nonlinear approaches, such as spike-triggered covariance (Fairhall et al. 2006; Liu and Gollisch 2015; Samengo and Gollisch 2013) and maximally informative dimensions (Sharpee et al. 2004; Sincich et al. 2009), result in mathematical terms that have no ready interpretation regarding the underlying physiology. On the other hand, approaches that explicitly consider cellular and circuit mechanisms are usually limited to consider only one mechanism at a time, since models that incorporate multiple mechanisms involve a proliferation of parameters that are hard to constrain with data and that even when adequately constrained are difficult to optimize. As a result, previous explanations of the generation of temporal precision have relied on single mechanisms evaluated at only a single stage of processing.

In the present work, we use a nonlinear modeling approach designed to isolate different nonlinear contributions to neuron responses, the nonlinear input model (NIM; McFarland et al. 2013), combined with paired recordings of LGN relay cells and their primary retinal input, to gain insight into the circuit components that shape LGN responses. This model was originally used to demonstrate that precision in the LGN could be generated through the interplay of excitation and a delayed suppression (Butts et al. 2011). However, it was not clear what the source of such delayed suppression is, or whether there are other contributions to LGN responses. To untangle the contributions from each stage of processing, we used extracellular recordings in the LGN that simultaneously capture the dominant retinal input, in the form of S-potentials (Bishop 1953; Kaplan and Shapley 1984), in addition to the output LGN relay cell spikes.

We first demonstrate that the dominant computations responsible for precise firing in the LGN are also present in the S-potential inputs, suggesting that temporal processing in the LGN is largely inherited from the dominant RGC input. We then show how the interplay of excitation and suppression in the retina can explain the dependence of response timescales on the spatial scale of the visual stimulus. Finally, using a model of LGN response that uses the S-potential input combined with stimulus processing terms, we show that the NIM can detect other inputs that shape the LGN response, some of which have nonlinear characteristics, such as PULL inhibition (Wang et al. 2007), as well as a diversity of other inputs.

Together, this work demonstrates how the LGN response to visual stimuli is shaped through multiple stages of visual processing, which sets the foundation for cortical processing of vision. More generally, the combination of detailed recordings and appropriately targeted nonlinear modeling presented demonstrates how a physiologically motivated nonlinear model can be used to tie visual neuron function to its underlying circuit elements.

METHODS

Neural recordings.

Extracellular recordings of relay cells in the LGN were collected with high-impedance (5–10 MΩ) tungsten-in-glass electrodes placed in dorsal layers A and A1 of the LGN. A total of 19 paired recordings of retinal and relay cell activity (described below) from 11 anesthetized and paralyzed adult cats were used for this study. Details of the surgical preparation are the same as described in previous studies (Casti et al. 2008). All surgical and experimental procedures were performed in accordance with the Institutional Animal Care and Use Committee at the Mount Sinai School of Medicine (New York, NY). Voltage traces were sampled at 40 kHz with a CED Power 1401 data acquisition device (Cambridge Electronic Design, Cambridge, UK).

When an electrode tip is moved sufficiently close to the cell body of a thalamic neuron, it is possible to record simultaneously the output spikes of an LGN cell and its primary excitatory postsynaptic potential (EPSP) inputs from the retina. These retinal EPSPs are called S-potentials because of their relatively slow temporal waveform compared with spikes (Kaplan and Shapley 1984) and in extracellular recordings manifest themselves as small-amplitude events (∼10–20% of peak spike amplitude) that either fail to evoke a relay cell spike within ∼1 ms or succeed in triggering a spike. Spike-evoking retinal S-potentials typically precede the LGN spike within a window of ∼1 ms and are often fused within the spike to varying degrees (Sincich et al. 2007; Weyand 2007). LGN spikes without an obvious S-potential antecedent were rare in our data (<5% of spikes in the most extreme cases). In our definition of the RGC input spike times for those events, we assumed that an S-potential was present but invisibly buried within the spike, with the event time defined as the onset of the relay cell spike.

In this study, we focused on X cells, of which ∼60–80% are reported to have their dominant retinal input provided by a single ganglion cell in the cat (Cleland and Lee 1985; Mastronarde 1987). In this respect, cat LGN is similar to monkey LGN, for which the connectivity between retinal and thalamic cells is predominantly one to one, whereas Y cells in cat invariably receive multiple ganglion cell inputs (Weyand 2016; Yeh et al. 2009). We thus focused on X cells in this study to minimize the confounding influence of multiple undetected RGC inputs to recorded LGN neurons.

In each of these paired RGC-LGN X cell recordings, the detected S-potential events did not overlap in time and had inter-event intervals exceeding ∼2 ms, suggesting that the primary extracellularly detectable retinal inputs to these thalamic neurons derived from a single RGC. We note that although it is possible that the timing of retinal spikes could be jittered at the retinogeniculate synapse, previous studies of simultaneously recorded ganglion cell spikes and their associated S-potentials have shown that the variability between the time of a ganglion cell action potential and the emergence of the S-potential is only about one-tenth of a millisecond (Levick et al. 1972). It is therefore reasonable to expect that the S-potentials accurately reflect the precision of retinal spiking. S-potentials and relay cell spikes were all carefully sorted offline with principal components analysis (Spike2 software; Cambridge Electronic Design).

Visual stimuli.

Visual stimuli were presented monocularly on a cathode ray tube (CRT) monitor with a screen refresh rate of 160 Hz. Once an LGN neuron with discriminable S-potential inputs was encountered, a contrast-reversing or drifting sine wave grating was presented to determine whether it was an X or Y cell (Hochstein and Shapley 1976), and only X cells were used for this study (see above). We first estimated the receptive field center size using spatially homogeneous circular spots modulated at a temporal frequency that drove the strongest F1 response component, and we estimated the center size as the spot size that maximized the firing rate. We used this spot size to determine the ranges of spot size to be presented during the rest of the experiment, as described below. In most cells, we also presented a 16 × 16 checkerboard stimulus in which each pixel is modulated in time by spatially and temporally uncorrelated binary m-sequences (Reid et al. 1997). In these cases, a circularly symmetric difference-of-Gaussians model (Enroth-Cugell and Robson 1966) was fit to the recorded data with the use of a spatiotemporal GLM as described by Butts et al. (2011), with the spatial extent of the center fit taken as the center size. In cells where we could use both methods, the resulting measurements were in close agreement. In the figures, we report spot sizes normalized by this measured center size.

The visual stimuli for the modeled data consisted of spatially homogeneous circular spots centered on the receptive field (RF) of each cell, which were modulated in time either by a binary m-sequence (Sutter 1987) or temporally independent samples of naturalistic luminance sequences (van Hateren 1997). The spot size was varied over a range spanning about one-half the receptive field center size to two to five times the center size. For a few cells there were only two spot sizes recorded, a “small” spot (RF center size) and a “large” spot (full field effectively), but this still allowed a comparison of the effects of small and large stimuli.

For any fixed spot size, a full stimulus run consisted of 128 “frozen-noise” repeat trials interleaved with either 128 or 32 “unique” trials that were distinct temporal sequences sampled from the stimulus intensity distribution. The repeat stimulus was identical across spot sizes so that the firing rate response to the same temporal sequence could be compared at various spot sizes (see Fig. 1A). Each trial had a duration of either 6.39 s (m-sequence modulation) or 8 s (van Hateren stimulus), corresponding to a recording time of ∼27 min (m-sequence) or ∼34 min (van Hateren) for each fixed spot size. The stability of the recording was assessed from the repeat trials: we restricted our analysis to data for which the repeat trial responses had stationary statistics (i.e., there was no eye drift or sudden changes in the cat's physiology). Before the spot size was changed, the RF center was quickly mapped again with the spatiotemporal checkerboard stimulus to ensure that the eye position had not shifted. In the rare instances when the eye did shift, we remapped the RF and recentered subsequent stimuli.

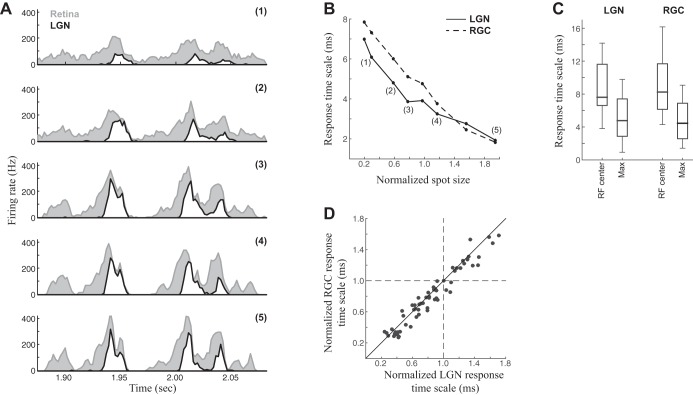
Fig. 1.

Changing response timescales with spot size in retina and LGN. A: peristimulus time histograms (PSTHs) for the response of an example LGN neuron (white) and its associated RGC input (gray) to repeated presentations of a temporally modulated spot. Responses to the smallest spot size (1) were relatively slow and unmodulated over time, but the features of the PSTH became sharper and sparser as spot size was increased (2–5). B: we estimated the response timescale from the autocorrelation of each PSTH (see methods), demonstrating a clear trend in this example neuron to finer response timescales as spot size is increased. The trends in the RGC and LGN neuron closely followed one another. The size of the spot is normalized relative to the LGN neuron's measured center size, with unity corresponding to a spot that just covers the center. C: distribution of response timescales across all neurons in the study (n = 19) measured for the spot size matching each neuron's receptive field center (RF center) compared with the maximum spot size used for that neuron (Max). D: comparisons of the timescales of RGC and LGN neurons closely match. Each point represents the response timescales measured for each spot size (retina vs. LGN), normalized by each neuron's average timescale across spot size.

Measurements of precision.

As described in previous work (Butts et al. 2007, 2010; Desbordes et al. 2008), we associate response “precision” with characteristic temporal widths of firing rate “events” in the peristimulus time histogram (PSTH; Butts et al. 2010). Specifically, the response timescale is derived from the autocorrelation of the PSTH by fitting a Gaussian to the central peak of the response autocorrelation function (ignoring a 3-ms window around zero time lag). The response timescale is then given by √2 times the standard deviation of the Gaussian fit (Butts et al. 2007).

Because the data in this study were generally less sparse (with fewer gaps in the PSTH and smaller magnitude of firing rate fluctuations) than the LGN data for which these methods were originally derived, we modified the measurement of response timescale to calculate a clean central peak of the autocorrelation. To do this for a given spot size, we began with the LGN spike train responses to the repeated stimulus and used the PSTH to associate each spike with a response “event,” where each event corresponded to a period of high firing rate (greater than one-fourth of the peak firing rate) surrounded by zero firing for ≥8 ms (Butts et al. 2010). The resulting events were further broken up if there were two distinct peaks in its smoothed PSTH, with the firing rate in between the peaks less than half the height of the lower peak. In these cases, we used a Gaussian mixture model to split up the spikes between the two smaller events. Once the LGN events were labeled, we used their timing to guide a similar parsing of the S-potentials into corresponding events, which often had more ambiguous boundaries due to their less sparse firing. Using these event structures, we calculated the autocorrelation of the response on each event separately and computed the total autocorrelation assembled as a weighted average over each event. This allowed for unambiguous identification of the central peak of the autocorrelation as well as its width, because the autocorrelation function was not confounded by the additional correlations between spikes in different events. This method robustly identified the response timescales of RGC and LGN, and was consistent with the application of earlier methods (Butts et al. 2007, 2010; Desbordes et al. 2008) applied to the data in this study.

The nonlinear input model framework.

The nonlinear input model (NIM) was previously described in detail (McFarland et al. 2013), with an early version initially applied to LGN data (Butts et al. 2011). Briefly, the model is of the form of an LNLN cascade (see Fig. 2A; Eq. 5), with model parameters representing excitatory and suppressive filters {k₁, k₂}, corresponding upstream nonlinearities f₁(·) and f₂(·), a spike history term h, and parameters of the spiking nonlinearity F[·]. The NIM in principle can incorporate many separate excitatory and suppressive components, but we found that models with more than two components (one excitatory and one suppressive) did not have significantly better performance. Likewise, although the upstream nonlinearities can be directly estimated in the NIM framework, we found that their forms could be accurately captured by constraining f₁(·) to be linear and f₂(·) to be threshold-linear with a threshold θ₂. These parametric nonlinearities often led to better model performance because they had fewer parameters and made the optimization less prone to settling into suboptimal local maxima of the likelihood function. The spike history term h was constrained to be negative such that it only captured suppressive effects of previous spikes (positive values for h effectively allow previous spikes to predict futures ones, independent of stimulus input). This negative constraint had negligible (if any) effects on model predictions.

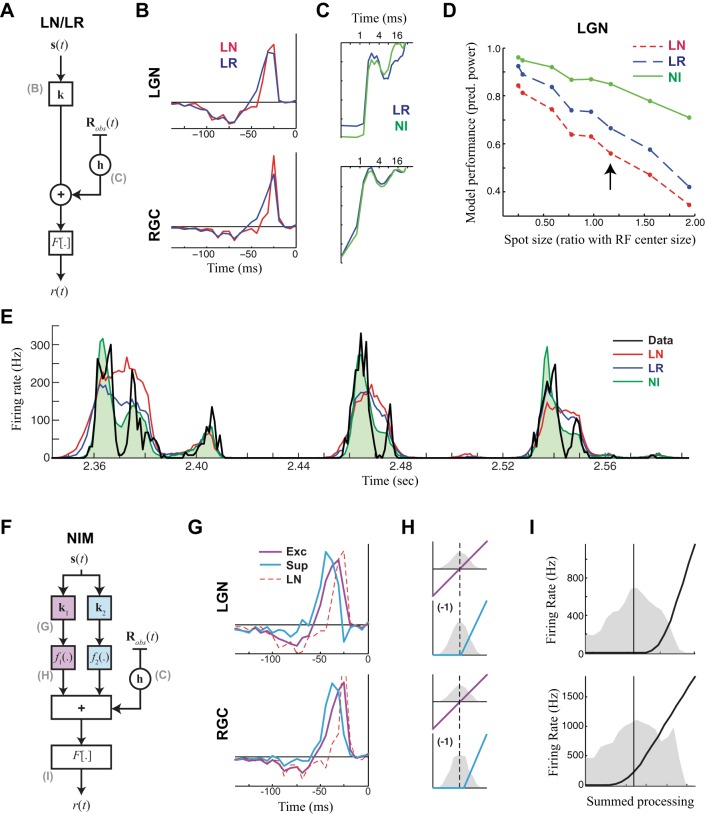
Fig. 2.

Computation in the LGN seems largely inherited from the retina. A: model schematic for the linear-nonlinear (LN) and linear-refractory (LR) models, both based on the generalized linear model (GLM). Both models have a linear receptive field k that filters the stimulus, whose output is then scaled into a firing rate by the spiking nonlinearity F[·]. For the LR model, a spike history term h processes the previous history of spiking R_obs(t), whose output is added to the output of the receptive field before going through the spiking nonlinearity. B: LN and LR model receptive fields for an example LGN neuron at an intermediate spot size (top) and for that of its RGC pair (bottom). Note the filters are slightly different between the models of the same neuron but are more different from LGN to RGC. C: the spike history terms of the LR model and the nonlinear input (NI) model (see below) for the LGN (top) and RGC (bottom). D: model performance, measured as the predictive power (“pred. power”; or fraction of explainable variance that the models capture), measured at 1-ms resolution on the cross-validation repeats for each spot size for the example LGN neuron. Performance of the LN and LR models decreases dramatically with spot size because of their inability to capture the increasingly high timescales, whereas the NIM fares better. The arrow indicates the spot size that the models are shown in B, C, E, and G–I. E: the model predictions (colors) compared with the measured PSTH (black) for the repeated trials (not used for model fitting). The NIM (green) is able to largely reproduce the precision of the true response, whereas the other models are less precise. F: model schematic for the NIM, which has 2 nonlinear inputs comprising a linear temporal filter k_i and upstream nonlinearities f_i(·). The output of these filters is summed with a spike history term h and passed through a spiking nonlinearity F[·]. G: the temporal filters of the NIM compared with those of the LN model (from B) for the LGN example neuron (top) and its RGC input (bottom). H: the upstream nonlinearities were fixed to be linear for the excitatory term (Exc; magenta) and threshold-linear with a single parameter for the threshold that is fit (Sup; cyan), shown for the LGN (top) and RGC (bottom), relative to the filter output of the corresponding temporal filter (distribution shown in gray). I: the spiking nonlinearity (black) relative to the distribution of the generator potential (i.e., its summed input). The main difference between the NIMs of RGC and LGN is a shift in the spiking nonlinearity such that it is lower threshold in the RGC.

For the spiking nonlinearity, we fit a logistic function

$$F[g]=\frac{1}{1+\exp [-\beta (g-\Theta )]},$$ (1)

where Θ is a measure of the effective spiking threshold and β controls the response gain near threshold.

Parameter optimization was performed using maximum a posteriori (MAP) likelihood maximization (McFarland et al. 2013). In this case, we maximized the Bernoulli log-likelihood (Haslinger et al. 2012) instead of the more common Poisson likelihood (Paninski 2004; Truccolo et al. 2005), because the time bins used for analysis (Δt = 0.5 ms) can contain only zero or one spike. For a set of observed spike times {t_s}, the Bernoulli log-likelihood with regularization penalty is given by

$$\mathit{L}\mathit{L}={\displaystyle \sum _{\mathit{t}={\mathit{t}}_{\mathrm{s}}}\log \hspace{0.17em}\mathit{r}(\mathit{t})+{\displaystyle \sum _{\mathit{t}\ne {\mathit{t}}_{\mathrm{s}}}\log [1-\mathit{r}(\mathit{t})]}}-\mathit{P}[\left\{{\mathbf{k}}_{\mathit{i}}\right\};\left\{{\lambda }_{\mathit{i}}\right\}],$$ (2)

where P[.] is a positive penalty determined by the filters of the model and choice of regularization meta-parameters {λ_i} (see below).

We then maximized the different parameters of the model using gradient ascent from chosen initializations of the parameters. Analytic computation of the LL and its gradient with respect to the model parameters (i.e., ∂LL/∂k_i) allowed for efficient gradient ascent. Although the dependence of the LL on model parameters was not convex (unlike models with only linear terms such as the GLM; e.g., Paninski 2004), in practice the NIM parameters robustly converged to the same solution given particular strategies for initializing the model.

For the NIM applied to RGC and LGN data (e.g., Figs. 2 and 3), we initially fit the linear-nonlinear (LN) model and linear-refractory (LR) models, which are special cases of the general mathematical form of the NIM (Eq. 5) that are guaranteed to converge to the optimal model regardless of initialization (Paninski 2004; Truccolo et al. 2005). We then added a delayed suppression term, using the previously computed linear filter of the LR model as an initialization of the excitatory filter, and a delayed version of this filter to initialize the suppressive filter. These initializations lead to robust estimation of the NIM for RGC and LGN models (Butts et al. 2011). The code we used to implement the NIM is available for download (see endnote at the end of this article).

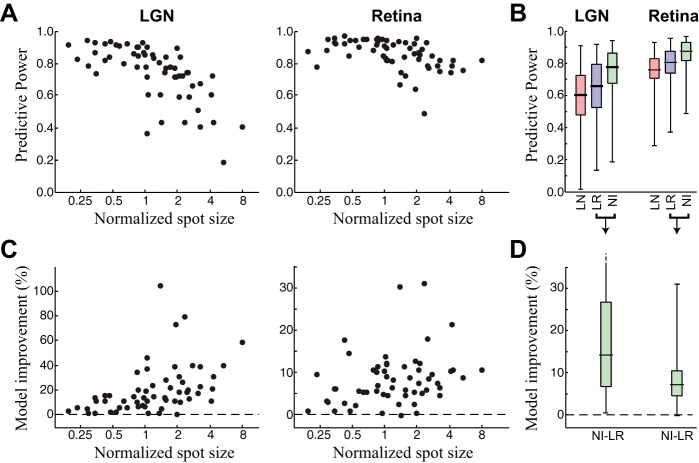
Fig. 3.

Model performance across spot size. A: predictive power of the NIM fit separately to each spot size and neuron for the retina and LGN. Note that performance is high (generally >80%) across all neurons but decreases more for the LGN than for RGCs. B: box plots showing the distributions of model performances for the LN, LR, and NI models across all neurons and spot sizes. C and D: percent model improvement between the NI and LR models for the same data shown in A and B, respectively. All increases are highly significant.

Extensions of the NIM to S-potential recordings.

We extended the NIM to incorporate information from S-potential recordings, resulting in the “postsynaptic current” nonlinear input model (PSC-NIM). This was done by adding a linear temporal filter p, the PSC term, which operates directly on the binned S-potential data. The model-predicted firing rate (Eq. 5) thus becomes

$$r(t)=F\left[p\cdot R_{\mathrm{s}}(t)+{\displaystyle \sum _i{\mathrm{f}}_i[k_i\cdot s(t)]+h\cdot R_{\mathrm{L}\mathrm{G}\mathrm{N}}(t)}\right],$$ (3)

where R_S(t) is the binned history of S-potentials at time t, and R_LGN(t) is the binned LGN spike history. The PSC term was implemented in the same way as the spike history term h, except that p was not constrained to be negative, as h was. This additional linear filter p was simultaneously optimized with the rest of the model parameters.

Regularization and cross-validation.

We added a penalty term to the log-likelihood (Eq. 2) to enforce smoothness in the filters and avoid overfitting. As with earlier work (McFarland et al. 2013), we penalized the squared magnitude of the discrete Laplacian $\mathrm{ℒ}$ acting on each filter, i.e.,

$$P\left[\left\{k_i\right\};\left\{{\mathrm{\lambda }}_i\right\}\right]={\displaystyle \sum _i{\mathrm{\lambda }}_i{\left|ℒk_i\right|}^2}\mathrm{.}$$ (4)

We used nested cross-validation to determine {λ_i}: 85% of the unique stimulus sequence data was used to fit the model parameters for a given choice of each λ_i, and the remaining 15% was used to measure a cross-validated log-likelihood. We then systematically varied each λ_i to maximize this cross-validated log-likelihood. Once the appropriate regularization meta-parameters were determined, we used the responses to repeated stimuli, which were not used for in the parameter optimization, for assessing the model performance.

Unified model across spot size.

We pooled data from the same neuron across spot size to fit unified models, where only the temporal filters were allowed to vary. Specifically, we started with independent fits for each spot size, and then used each temporal filter k_i from the n-th spot size to process the stimulus into a single filtered stimulus g_ni(t) = k_i·s(t). We then concatenated each filtered stimulus sequentially across spot size [g_n1(t), g_n2(t), g_n3(t), …], in register with the corresponding response, and used these data to fit the spike history term h, the upstream nonlinearity thresholds θ_j, and, for the PSC-based models, the PSC filter p. We then fit models for each spot size with these shared parameter values fixed, optimizing the filters for each spot size separately. Next, we alternated between fitting the shared parameters and separate filters until the likelihood no longer improved (generally 2–3 iterations). Because we often found slow shifts in the threshold of the spiking nonlinearity (as can happen with anesthetized data; Butts et al. 2011; Goris et al. 2014), the offset in the overall generating function was allowed to vary across spot size.

Model performance.

We gauged model performance using both the cross-validated log-likelihood LL_x and the predictive power (Sahani and Linden 2003), which is defined as the fraction of explainable variance that the model captures. The predictive power is similar to the standard R² measure (i.e., fraction of explained variance) but uses the variability in response to repeated stimuli to estimate how much of the variance is unexplainable and adjusts for this. Both measures are highly correlated, and thus we usually just report predictive power for measuring model performance in all but the PSC-NIM. Because the firing rate of the PSC-NIM depends on the S-potential input, performance measures relying on repeated presentations are not reliable, and we report the LL_x to measure performance for this model.

For the NIMs of RGCs, we reported the predictive power of models fit to single spot sizes (see Fig. 3), as well as comparisons between these single-spot-size models and unified models for single neurons fit across spot sizes (see Fig. 4C). For the PSC-NIMs of LGN, we made the assumption that the PSC term should not change with spot size, and thus restricted all models of a given neuron to share the PSC, spike history, and upstream nonlinear terms for the purpose of measuring cross-validated model performance (see Fig. 7).

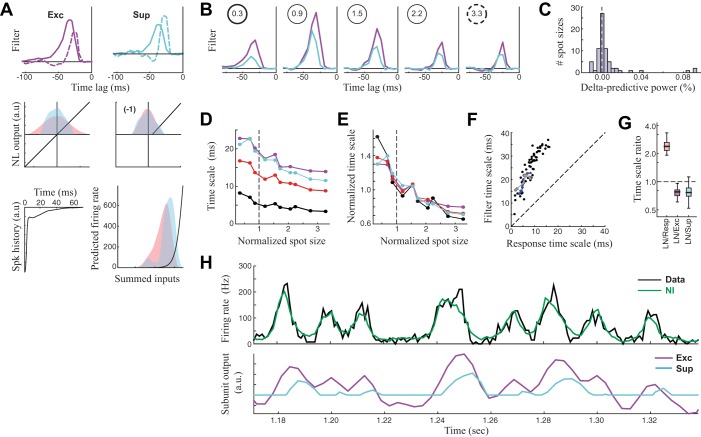
Fig. 4.

Explaining the response timescales with the RGC model. A and B: unified NIMs were fit across all spot sizes for each RGC, where only the temporal filters were allowed to vary across spot size. A, top: the excitatory and suppressive filters for the smallest (solid) and largest spot size (dashed), demonstrating the changing temporal scales of both filters with spot size. Bottom, other model parameters that are held fixed across spot size (NL, nonlinear; Spk, spike; a.u., arbitrary units; firing rate is in Hz). Note that the distributions of generating function change with the filters, shown as shaded red and blue for the smallest and largest spot sizes, respectively. B: the filters for 5 of 10 spot sizes recorded for this neuron, demonstrating both the temporal filtering change and the change in amplitude. C: the distribution of performance decreases of the unified model (with shared parameters across spot size), compared with models fit to each spot size independently. Performance is more than 2% worse in only 5/70 cases. This suggests that only the temporal filters change across spot size. D: the timescale of model filters (Exc, magenta; Sup, cyan) compared with timescale of the LN filter (red) and that of the response (black) for the example RGC neuron. Note that the response timescale is still much smaller than those of the filters. E: the trend in timescale changes is similar between the filters and response, as shown by normalizing the curves in D by the mean timescale of each curve. F: comparisons between response timescale and excitatory filter timescale for all neurons and spot sizes, demonstrating a roughly constant ratio, suggesting that filter timescales are predictive of response timescales. G: box plots showing the distribution of ratios between the various timescales. H: the NIM prediction compared with the observed PSTH for the largest spot size (top) demonstrates how the NIM predicts precision through the interplay of excitation and suppression (bottom). Specifically, the output of the suppression (cyan) is driven by the same stimuli as excitation (purple) but is delayed, and so it cancels the latter part of the slow-varying excitation, reducing the response timescale.

Fig. 7.

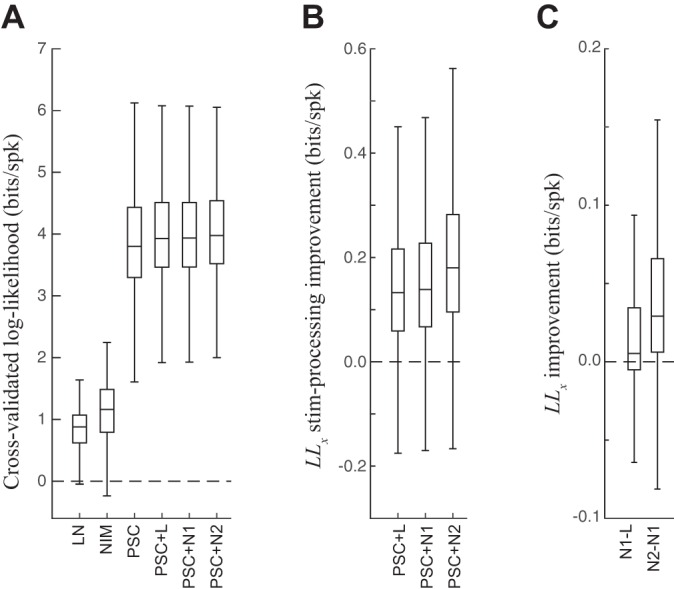
PSC model performance. A: cross-validated log-likelihood (LL_x) for all LGN neurons and spot sizes, across all the models considered for the LGN neuron. The LN and NI models do not use S-potential input (e.g., Fig. 2); the PSC models are as follows: PSC alone is without any stimulus processing terms, +L is with a linear stimulus processing term, +N1 is with PULL suppression, and +N2 is with PULL and PUSH suppression. Notably, the PSC-based models all have much larger LL_x because of their ability to predict the precise timing of the LGN spikes due to the S-potential inputs. Relatively speaking, the additional enhancements of the stimulus-processing terms to the PSC models were small but statistically significant (see below). B: the difference in LL_x (“stim-processing improvement” in bits/spike; equivalent to the logarithm of the likelihood ratio) between the PSC models with stimulus terms and the baseline PSC model. All comparisons are statistically significant (t-test), both when each neuron is considered separately and when all neurons are considered together. C, left: LL_x difference between PSC+N1 and PSC+L across neurons (all significant for all neurons, t-test). Right, the difference between PSC+N2 and PSC+N1. Comparisons were significant for all but 4 neurons (and otherwise P < 10⁻⁶).

Temporal resolution of all analyses.

We binned all data (LGN spike times, S-potential times, stimulus values) at the resolution of one-twelfth the stimulus refresh (∼0.5 ms). To model the stimulus input at this resolution, we assumed the stimulus was a delta function with its value at the recorded stimulus-onset trigger time, and then zero for the other 11 time bins, which approximated the temporal luminance profile of the CRT. Alternatives, such as assuming the stimulus was constant across the 12 bins, led to artifacts in the filter estimation.

We fit the temporal filters at one-half the frame resolution (i.e., 6 time bins) using tent basis functions (Ahrens et al. 2008; McFarland et al. 2013) with 60 time lags for each filter, corresponding to a total filter duration of ∼180 ms. We used 20 parameters for the spike history term, which represented the spike history amplitude at logarithmic spacing that initially started at 0.5 ms and doubled every 5 values, encompassing a total duration of ∼40 ms. For the extended PSC-NIM that used S-potential recordings, the PSC term was fit at 0.5-ms resolution and had 40 equally spaced time lags, encompassing an ∼20-ms duration.

RESULTS

Precision and nonlinearity in the LGN increase with surround stimulation.

We recorded LGN spike trains driven by a temporally modulated spot centered on each neuron's receptive field (RF). We presented each neuron with a range of spot sizes. As spot size increased, LGN neuron responses became more finely structured in time (Fig. 1A), with larger, faster fluctuations in the firing rate that reflected more precise spike timing across trials. As a result, the timescale of the response, based on the autocorrelation time of the PSTH (Butts et al. 2007, 2010; Desbordes et al. 2008), gradually decreased with increasing spot size (Fig. 1B). For the example neuron, the response timescale at the smallest spot size (7.8 ms) was nearly four times larger than at the largest spot size (2.0 ms). This trend was observed in 18/19 LGN neurons recorded, with a median 2.4-fold decrease in response timescale from smallest to largest spot size.

To understand how the temporal precision of LGN responses is generated, we made use of the simultaneously recorded retinal S-potentials. Because the S-potentials represent the dominant RGC input to each LGN X cell that we recorded from (Cleland and Lee 1985; Mastronarde 1987; Weyand 2016), this allowed us to make direct comparisons between LGN and RGC spike trains to determine how precision is shaped at each stage of the circuit. Comparisons between the two PSTHs suggest that the RGC response, although much less sparse than the LGN response, develops finer temporal structure with increasing spot size in parallel to the LGN PSTHs (Fig. 1A). We similarly measured the RGC response timescale and found similar reductions to that of the LGN, both for the example shown (Fig. 1B) and across all neurons in the study (Fig. 1C). The close correspondence between the two across spot sizes of all neurons (Fig. 1D) suggests that the temporal patterning of LGN responses have their source in the retina.

Comparisons between nonlinear models of LGN and RGCs.

The circuit components that shape LGN response features such as precision (Fig. 1A) are potentially distributed across the retinogeniculate pathway, so we took a modeling approach that is capable of inferring these mechanistic properties and locations within the circuit. To establish a baseline of model performance, we first modeled the LGN responses using a linear-nonlinear (LN) cascade model (Chichilnisky 2001; Simoncelli et al. 2004), which predicts a response on the basis of how closely the stimulus s(t) at a given time t matches a linear receptive field k (Fig. 2A). The first stage of processing in the LN model is a linear comparison between the stimulus and temporal filter k, denoted by the dot product k·s(t), where we use bold type to denote a vector (i.e., s(t) = [s₁(t), s₂(t), s₃(t), …]). Note that with this notation, the different components of the time-binned stimulus s_i(t) correspond to different time lags, and the receptive field is a temporal filter (Fig. 2B). The output of this linear comparison is followed by a spiking nonlinearity F[·], which maps the projection of the stimulus onto the receptive field into a firing rate: r(t) = F[k·s(t)].

We then augmented the LN model to include spike history effects, such as a refractory period (Paninski 2004; Pillow et al. 2005; Truccolo et al. 2005), which has previously been suggested to explain the millisecond timescale precision in the responses of RGC and LGN neurons (Berry and Meister 1998; Keat et al. 2001; Pillow et al. 2005). The spike history term can be similarly modeled as the projection of a vector of “spike history” weights h (Fig. 2C) onto the observed spike history, R_obs(t), where R_obs(t) is a vector of the most recent spike counts before time t (not including the current time bin labeled by t). The filtered spike history h·R_obs(t) is added to the output of the receptive field so that the firing rate is given by r(t) = F[k·s(t) + h·R_obs(t)] (Paninski et al. 2007; Truccolo et al. 2005). We refer to this as the “linear-refractory” (LR) model, highlighting that it still processes the stimulus linearly but also is influenced by spike refractoriness. Neither the LN nor LR model accurately predicts LGN responses at high time resolution (∼1 ms) (Butts et al. 2007, 2011), as gauged by the predictive power (Fig. 2D), which quantifies the differences between the model-predicted PSTH and the observed PSTH (Fig. 2E). Notably, the LN and LR models often did not perform as badly at small spot sizes (Fig. 2D), where the LGN response had slower temporal scales.

We then added a nonlinear suppressive component to the LR model, which has previously been shown to predict the fine timescales of the LGN response (Butts et al. 2011). The resulting nonlinear input model (NIM; McFarland et al. 2013) has the form of an LNLN cascade (Korenberg and Hunter 1986) where each “input” to the model is itself an LN model with its own receptive field k_i and upstream nonlinearity f_i(·). These nonlinear inputs are summed together with the output of the spike history term before being passed through a spiking nonlinearity (Fig. 2F):

$$r(t)=F\left[{\displaystyle \sum _i{f}_i[k_i\cdot s(t)]+h\cdot R_{\mathrm{o}\mathrm{b}\mathrm{s}}(t)}\right]\mathrm{.}$$ (5)

This model implicitly encompasses the LN and LR models, since the best fit f_i(·) functions can in principle be linear (reducing to the LR model), and likewise the spike history term can vanish, reducing to the LN model. As with the LN and LR models, which are both in the category of GLMs (Paninski 2004; Truccolo et al. 2005), the NIM can be fit using maximum-likelihood estimation (McFarland et al. 2013; see methods), resulting in nonlinear models that predict the observed LGN spike trains with much higher fidelity (Butts et al. 2011; McFarland et al. 2013), as we shall show.

For LGN neuron responses, we found that most parsimonious model had two inputs (Butts et al. 2011): a linear excitatory term and a nonlinear suppressive term (Fig. 2, G and H). The suppressive temporal filter was always delayed relative to the excitatory filter, and the suppressive output (but not that of the excitation) was rectified using a parametric threshold-linear functional form (see Fig. 2H). The resulting NIM outperformed the LN and LR model across spot sizes (Figs. 2D and 3), with a particularly substantial differential improvement at large spot sizes, where the LGN response was more precise.

Given the similarity of response timescales between retina and LGN (Fig. 1), we expected an optimized NIM to produce a similar model when applied to the RGC output (measured by the S-potentials; see methods). Indeed, fitting the RGC data with the NIM yielded nearly identical models, with the same paired excitatory and suppressive filters (Fig. 2F, bottom). In contrast, the LN and LR models were often much less similar between the retina and LGN (Fig. 2B; also see Rathbun et al. 2010; Wang et al. 2010), likely indicating a difference in processing between the two areas that could not be captured without nonlinear stimulus processing. The main difference in the NIMs between the two areas was a change in the spiking nonlinearity F[·] (Fig. 2I), which had a higher threshold in the LGN. This reflects that spikes in the LGN are more selective to the stimulus (Rathbun et al. 2010) and will likewise contain more information per spike (Sincich et al. 2009; Uglesich et al. 2009; Wang et al. 2010).

The trends illustrated in the example cell from Fig. 2 were consistent across the 19 RGC-LGN paired recordings used in this study. In particular, the NIM performed well across spot sizes for both RGC and LGN (Fig. 3, A and B) but showed larger improvements over the LR model at larger spot sizes (Fig. 3, C and D). Notably, the NIM performance fell less at large spot sizes in the retina than in LGN, suggesting its nonlinear structure was more effective at capturing the RGC responses.

Filter changes underlie response timescales in the retina.

Because of the similarity of the nonlinear models for the LGN and retina, we hypothesized that the changes in LGN response timescales are inherited from the retina and thus might be explained by studying the models of RGCs across spot size. To determine what aspects of RGC computation changed across spot size, we fit a single model to all the data for a given neuron, allowing only certain model parameters to change with spot size (see methods). In doing so, we found that nearly all changes across spot size could be captured by a change in the excitatory and suppressive filters alone (Fig. 4, A and B). The performance of this “unified” model for each spot size was not significantly worse than a model fit separately to each spot size on a neuron-by-neuron basis (t-test, P > 0.05), and there were only 5/70 spot sizes (distributed across the 12 neurons recorded with ≥3 spot sizes) where the individually fit model had a >2% improvement in predictive power over the unified model (Fig. 4C).

The filter changes followed the same trend for all neurons: filters became narrower at larger spot sizes and had a peak amplitude around the size of the RF center (e.g., Fig. 4B). Such filter changes are consistent with the well-known center-surround organization of RGC receptive fields (Cai et al. 1997; Kuffler 1953). For spot sizes smaller than the RF center size (e.g., Fig. 4B, left), increases in spot size produced increases in the amplitude of both excitatory and suppressive filters, consistent with more stimulation of the RF center. As the spot size increased past the measured RF center size, filter amplitudes became smaller (Fig. 4B, right), presumably because stimulation of their opposite-sign surround increasingly canceled the center response. Throughout, the temporal scale of the filters became sharper, likely due to the partial cancellation of the later part of the center response by the delayed surround (Cai et al. 1997). Note that whereas this trend was previously reported for linear receptive fields (Butts et al. 2007, 2011; Cai et al. 1997), this is the first report that it applies to both the excitatory and suppressive RF components, suggesting that the suppressive term has similar center-surround organization to the excitation.

As a result, the models for the smallest and largest spot sizes had dramatically different temporal filtering associated with them (Fig. 4A, top). This suggests the possibility that changes in the filter timescales underlie the changes in response timescales. To further investigate this, we characterized the timescales of these filters in a way analogous to that of the response timescale (see methods). In agreement with this intuition, the timescale of linear filtering decreased with increasing spot size (Fig. 4D, left), both for the LN model (red) and for the excitatory (purple) and suppressive (cyan) filters of the NIM. The similarity in these trends can be demonstrated by normalizing each curve by its mean timescale (Fig. 4E). Similarly, plotting the timescales of the linear filter with that of the response timescale across spot sizes and neurons (Fig. 4F) revealed a roughly consistent ratio between these timescales.

It is also clear, however, that the timescale of filtering is still significantly larger than the response timescale. Across neurons, the filter timescales were on average 2.5 times larger than the response timescales (Fig. 4G). As previously described (Butts et al. 2011), the response timescales emerge in the NIM due to the interplay of excitation and suppression, because the delayed suppression will subtract from the latter parts of excitatory events (Fig. 4H), resulting in more transient responses than can be predicted by linear filtering.

Direct model of LGN processing.

The presence of excitatory and suppressive inputs in the RGC model suggests that the analogous elements of the LGN neuron models (Fig. 2; Butts et al. 2011) are at least partially inherited. To determine whether this was the case, as well as to resolve other contributions to LGN responses distinct from its dominant RGC input (Guillery and Sherman 2002; Sillito and Jones 2002), we constructed a model to explain the LGN response using paired S-potential–relay cell recordings (Babadi et al. 2010; Carandini et al. 2007; Casti et al. 2008) in combination with additional stimulus processing terms (e.g., Babadi et al. 2010). In this modeling framework, the stimulus-processing terms that are inherited from the retina would presumably be represented in the S-potential inputs, and thus this direct S-potential input will “explain away” the presence of analogous stimulus-processing terms determined by the NIM. As a result, additional terms detected by the model that incorporated the S-potentials will result in better model performance only to the degree that they capture the effects of additional inputs to the LGN neuron.

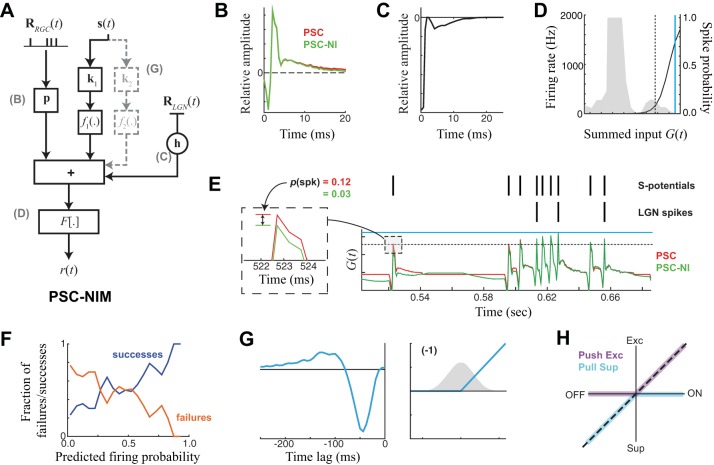
In the PSC-NIM (Fig. 5A), the S-potential input is processed through a linear temporal filter that we call the “postsynaptic current” (PSC) term p (Fig. 5B), which weighs the effect of the S-potential input history on the LGN neuron's response, p·R_S(t). The output of the PSC term is combined with the previously elaborated terms of the NIM, including a spike history term acting on observed LGN spikes (Fig. 5C), and potentially one or more independent LN “stimulus-processing” components acting directly on the stimulus as in previous NIMs. The summed input is then passed through a spiking nonlinearity (Fig. 5D). The PSC-NIM is fit in the same way as the NIM described above, with the PSC term simultaneously optimized with the other model components.

Fig. 5.

Model of LGN spikes based on input S-potentials and the stimulus. A: model schematic for the NIM with an added “postsynaptic current” (PSC) term p, which linearly processes the S-potential history R_RGC(t) and adds to the other terms of the NIM to predict the firing rate. B: the PSC term for an example ON LGN neuron. Adding additional NIM components to the PSC term alone does influence its shape (compare red vs. green). C and D: the spike history term (C) and spiking nonlinearity (D) relative to the distribution of generating function G(t) for this neuron. Solid cyan and black dashed lines are shown to reference the magnitudes of the generator signal shown in E. E: the generator signal [summed model components for this example neuron, with (PSC-NIM, green) and without (PSC, red) an additional stimulus-processing term]. Observed S-potentials and LGN spikes are shown above the resulting model predictions. Although the effect of the additional stimulus-processing term is small relative to the fast component of the PSC term (green vs. red), it has an effect on spike probability at S-potential times and tends to decrease the probability that an S-potential will be relayed where no spikes are observed (see inset). F: the measured probability of successful S-potential transmission (blue) vs. failures (orange) for the model. G: the additional stimulus-processing term in the model of this example neuron is a suppressive OFF filter. H: OFF suppression is known as “PULL” suppression in this case, because for this neuron the S-potentials had ON selectivity but their output was also implicitly rectified. Together, this is a PUSH-PULL arrangement that approximates a full linear response.

The PSC-NIM was far superior in its prediction of LGN spiking compared with the stimulus-based models of the LGN (Fig. 2), as evidenced by the much larger magnitude of the output of the spiking nonlinearity (Fig. 5D) and the cross-validated performance measure described below. This was primarily due to the fact that the summed contributions of the model components [the generating signal G(t); Fig. 5E] were dominated by the fast component of the PSC term, which had a large, often biphasic, transient component lasting 1–2 ms (Fig. 5B). The role of this sharp transient in the model was simply to ensure that the timing of each LGN spike is associated with an S-potential (Sincich et al. 2007). In this sense, the PSC model ensures the precise timing of LGN spikes automatically, and the other parts of the model serve to influence the probability that a given S-potential will evoke an LGN spike.

Without this additional modulation from both the slow component of the PSC filter and other terms (Fig. 5A), each S-potential would predict the same probability of transmission. Instead, the model predicts higher probability of firing for conditions where the S-potential triggered an LGN spike (S-potential “successes”) compared with when it was not associated with an LGN spike (“failures”; Fig. 5F). LGN responses are sparser because not all transmissions are successful, and transmission failures are nonrandom (Casti et al. 2008; Rathbun et al. 2010; Sincich et al. 2007; Uglesich et al. 2009). The slower components of the PSC term allow for interactions between closely spaced S-potentials (e.g., Fig. 5E, middle). Note that because we only consider linear interactions in this study, the PSC term is likely capturing more than the effects of the postsynaptic current itself and will implicitly be shaped by nonlinear processes involved in the integration of RGC inputs (Rathbun et al. 2010). We did test more explicit models of nonlinear interactions between closely spaced S-potentials but found we could not significantly improve model performance with more complex models of PSC integration. As a result, we opted to keep the PSC term in this relatively simple linear form and focus on nonlinearities associated with the stimulus-processing terms in the model.

We next considered the nature of additional stimulus-processing terms that contributed to the PSC-NIM. Such stimulus-processing terms would resemble those of the LGN NIM [for example, containing ON excitation and delayed ON inhibition for an ON cell (e.g., Fig. 2G)], if the effects of these terms were not “explained away” by the S-potential input. Indeed, although this approach detected additional stimulus-processing terms that contributed to model performance in every neuron, such terms never resembled the original stimulus-processing filters of the NIM (without the PSC term). The most commonly identified additional processing term was “PULL” suppression (Wang et al. 2007), which for an ON LGN neuron, for example, corresponds to a suppressive term with an OFF filter (Fig. 5G). PULL suppression was detected in every neuron in the study (see below), and in 11/19 recorded pairs it was the only stimulus-processing term detected by the PSC-NIM. Together with ON excitation from the S-potential, such an arrangement is known as PUSH-PULL processing (Fig. 5H) and is prevalent in both LGN and simple cells in primary visual cortex (Hirsch et al. 2015; Martinez et al. 2014; Wang et al. 2007).

Was there any evidence that the stimulus-processing terms resembling the original NIM without the PSC term (e.g., Fig. 2) were still present? We observed that PUSH excitation (e.g., ON excitation associated with an ON neuron) only led to model improvements over a PSC-NIM that already had PULL suppression in 3/19 neurons, leading in these cases to an average model performance improvement of only 1.20%. Likewise, PUSH suppression led to a significant model performance improvement in 11/19 neurons over the PSC-NIM that already had PULL suppression, with an average model performance improvement of 1.19%. Together, this suggests that the excitation-with-delayed-suppression interaction underlying temporal precision in LGN X cells (Butts et al. 2011) is almost entirely due to computations already present in the S-potential input, although there is often a small contribution from PUSH inputs (largely suppressive) added at the level of the LGN.

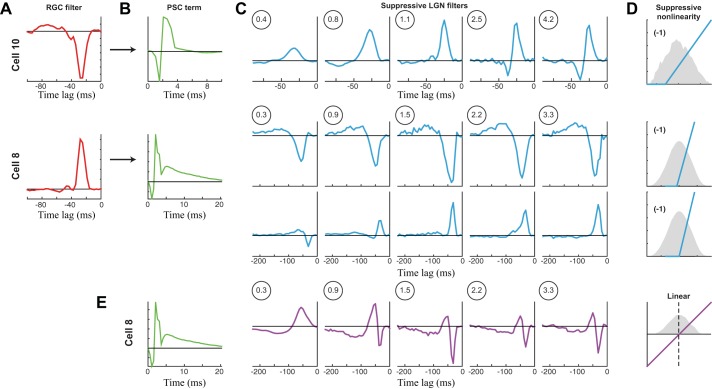
The presence of additional stimulus-processing terms in the PSC-NIM does suggest that LGN X cells are integrating input from more than one RGC, through either direct excitatory inputs or suppressive inputs likely operating through LGN interneurons (Hirsch et al. 2015; Maffei and Fiorentini 1972; Martinez et al. 2014; Wang et al. 2011a). We would thus expect the selectivity of the additional stimulus processing terms to evolve with spot size similar to the RGC example (e.g., Fig. 4). Indeed, for an example neuron with a single PULL suppressive term (Fig. 6, A–D, top), the temporal filter became faster with increasing spot size, and the amplitude had a peak at intermediate spot sizes.

Fig. 6.

PSC models across spot size. A–D: PSC-NIMs for 2 neurons (cells 8 and 10) across spot size, an OFF X cell (top) and an ON X cell (bottom), where only the stimulus-processing filters were allowed to vary with spot size. A: the linear temporal filter of the corresponding S-potential input to the LGN neuron. This is not part of the PSC-NIM but demonstrates the selectivity of the RGC that is input via the PSC term. B: the PSC term that is shared across all spot sizes. C: the temporal filters across spot size for both neurons. Top, the OFF cell only had one discernible filter, which had ON selectivity (and thus was PULL suppression). It evolves with spot size as in the RGC models in Fig. 4. Bottom, the ON cell had two detectable stimulus-processing terms, one with ON selectivity (PUSH) and one with OFF selectivity (PULL). These filters also each independently evolved with spot size as the RGC models did. D: the suppressive nonlinearities that are shared across spot size for each neuron, with a sample of the generating distribution (gray) for the middle spot size. E: we used a simpler linear stimulus-processing model coupled with the PSC term for cell 8. Even though the performance of this model is almost as good as that of the nonlinear models, it has nonintuitive changes in its linear filter with spot size due to the different evolution with spot size of the underlying nonlinear terms.

Such evolution of temporal processing also could be observed in neurons with multiple stimulus-processing terms in the PSC-NIM but required the ability to separate the effects of each term. For example, for a neuron where a clear second PUSH suppressive term, of opposite stimulus selectivity to the PULL suppression, was detected in addition to the PULL suppression, each filter evolved with a similar pattern (Fig. 6, A–D, bottom). By comparison, if one were to only fit a single linear term to these neurons, the selectivity of its filter shifts dramatically with spot size (Fig. 6E), because the two detected inputs evolve differently with spot size (Fig. 6C), resulting in a different balance of PUSH and PULL at a given spot size. Note that the success of separate ON and OFF suppression describing the range of models across spot size offers strong evidence for the presence of both ON and OFF suppressive inputs onto this neuron, which cannot be detected with the use of standard whole cell approaches in the context of sparse noise (e.g., Wang et al. 2007), due to the summation of PUSH suppression with direct RGC input.

In all cases, the addition of stimulus-processing terms to a model with just PSC and spike history terms (the PSC model) improved performance (Fig. 7B). Such models also outperformed PSC models with just a single linear processing term (Fig. 7C; Babadi et al. 2010). For these data, we could not compare model output to an observed firing rate (as above for the RGC models) because the different S-potentials on each trial would predict different firing rates on each trial. As a result, in this case we report the cross-validated log-likelihood (see methods), which can be measured on a trial-by-trial basis, and its values are correlated with more familiar measures of model performance such as R² and predictive power (Butts et al. 2011; Cui et al. 2013).

For these models, the influence of these stimulus-processing terms was subtle because the model performance was dominated by the PSC term (Fig. 7A). Indeed, we found that these additional stimulus-processing terms only slightly influenced the timing of LGN spikes by making some S-potentials less likely to be transmitted. Because the resulting model is better able to predict transmission successes and failures (Fig. 5F), it has a better performance. As expected from direct measurements of timescales between the LGN and its S-potential input (Fig. 2), this had almost no influence on the response timescale from retina to LGN but served to make the LGN response sparser. This is consistent with our earlier conclusion that the elements responsible for the generation of temporal precision reside in the retina. However, this sensitive circuit-inspired analysis did reveal that the RGC spike train is further shaped at the level of LGN by both S-potential integration (Carandini et al. 2007; Casti et al. 2008) and additional inputs (Babadi et al. 2010; Blitz and Regehr 2005; Martinez et al. 2014; Wang et al. 2007).

DISCUSSION

Neural responses in the early stages of visual processing up through primary visual cortex are surprisingly linear (Carandini et al. 2005; Shapley 2009): this is surprising because the anatomy and physiology of retina and LGN are rife with nonlinear processing elements. Specifically, “linearity” in this context refers to the fact that the response of neurons can be well predicted by comparisons between the stimulus and a linear receptive field, or “filter,” with the response roughly proportional to the similarity between the two (Carandini et al. 2005; Chichilnisky 2001). In this sense, it is likely that the visual circuitry is in part geared to construct linear responses from its intrinsically nonlinear elements (Shapley 2009). However, the linearity of visual neuron responses in large part confounds the ability to gain insight into how their responses are shaped by the underlying circuit, since multiple linear filters operating on the same stimulus are equivalent to a single filter, obscuring potentially distinct circuit components.

We used a nonlinear modeling approach, the nonlinear input model (NIM; McFarland et al. 2013), to bridge this gap between circuit and function. We focused on aspects of the response of LGN neurons known to require nonlinear processing, most prominently the stimulus transformations underlying temporal precision (Berry and Meister 1998; Butts et al. 2007; Liu et al. 2001; Passaglia and Troy 2004; Uzzell and Chichilnisky 2004), by specifically analyzing responses at high (0.5 ms) time resolution. At this resolution, models based on linear processing such as the linear-nonlinear (LN) cascade model (Chichilnisky 2001) and the more general class of generalized linear models (Paninski 2004; Truccolo et al. 2005), such as the linear-refractory (LR) model, do a relatively poor job at explaining the response (Butts et al. 2011), providing an opportunity to explain the details of visual responses through nonlinear computations that relate to specific circuit components. Our approach is thus unique in how it combined targeted experiments with tailored nonlinear models to bridge circuit and function. First, the NIM has a mathematical form inspired by the basic nonlinearities intrinsic to all neural circuits: rectification (McFarland et al. 2013). It thus implicitly divides inputs into excitatory and suppressive terms, and can characterize the tuning of each separately. Second, we used recordings at two successive stages of the visual pathway, with extracellular recordings at the LGN revealing the timing of spikes of its main retinal ganglion cell RGC driver in the form of S-potentials (Bishop 1953; Bishop et al. 1958; Cleland et al. 1971; Freygang 1958; Kaplan and Shapley 1984). This allowed us to distinguish whether nonlinear terms detected in the LGN (Butts et al. 2011) have their source in the retina, versus being generated in the LGN de novo. This detailed, circuit-specific model of processing at both retina and LGN produced a description of how multiple mechanisms contribute at each stage of processing, and the contribution of each in the transformation of signals from visual stimulus to RGC response to LGN response.

This contrasts with previous approaches to describing the computations from RGC to LGN in more abstract terms, such as spike-triggered covariance (STC; Fairhall et al. 2006; Liu and Gollisch 2015; Samengo and Gollisch 2013; Wang et al. 2010) and maximally informative dimensions (MID; Sincich et al. 2009). Such approaches can identify multiple components contributing to processing in retina and LGN. However, the interpretation of the STC and MID components is much more challenging (McFarland et al. 2013) and is geared to offer insight into the transformation of the computation (Rathbun et al. 2010; Wang et al. 2010) rather than into the underlying circuit. Other approaches have employed more mechanistic modeling (Carandini et al. 2007; Casti et al. 2008), although neither could explain LGN responses to larger spot sizes (Casti et al. 2008), or have restricted the study to receptive field center-sized stimuli (Carandini et al. 2007), for which responses are less precise and could be explained without the circuit mechanisms presented in this report.

What did we ultimately learn with the NIM about LGN computation and the circuitry behind it? First, our results suggest that the mechanisms underlying temporal precision present in the LGN response (Butts et al. 2007, 2011; Keat et al. 2001) are present in the retina and thus likely inherited. Furthermore, we demonstrated that the observed spot-size dependence of LGN response timescales is predicted from changes in the temporal filtering of both excitation and suppression, in combination with the interplay of excitation with a nonlinear suppression (Butts et al. 2011). We elucidated how these mechanisms worked together with postsynaptic summation of input spikes (Babadi et al. 2010; Carandini et al. 2007; Casti et al. 2008) to achieve a much sparser LGN response, which despite involving fewer spikes produces more information per spike than the retina (Sincich et al. 2009; Uglesich et al. 2009). We also saw that spike refractoriness has a role in shaping the response at the level of both the retina (Berry and Meister 1998; Pillow et al. 2005) and the LGN (Gaudry and Reinagel 2007), although it had little influence on the overall firing rate envelopes (Butts et al. 2011), mainly influencing the patterning of spikes within these envelopes (Pillow et al. 2005).

Our results also suggest that additional suppressive influences are added at the level of the LGN, predominantly PULL inhibition (Hirsch et al. 2015; Martinez et al. 2014; Wang et al. 2007), but in some cases PUSH inhibition as well. The purpose of PULL suppression in LGN processing of vision is difficult to discern in this present study, which used a randomly varying, spatially homogeneous spot that cannot engage the spatial footprint of PULL suppression, as a natural visual stimulus might. Possible roles for PULL inhibition include burst priming in natural contexts (Alitto et al. 2005; Denning and Reinagel 2005; Lesica and Stanley 2004; Wang et al. 2007), the generation of linear response profiles despite half-wave rectified inputs from spiking neurons (Shapley 2009; Werblin 2010), and the enhancement of edge detection (Martinez et al. 2014).

Across relay cells there is variability in the source of inhibitory inputs (Hirsch et al. 2015), some of which may be locked or nonlocked to the arrival times of the synapsing upon interneurons on the feedforward pathway (Blitz and Regehr 2005), whereas others may originate in feedback from primary visual cortex (Briggs and Usrey 2007; Sillito et al. 2006), the reticular nucleus (Mayo 2009; McAlonan et al. 2006), or elsewhere. It is natural, then, to ask if the NIM weighed in with a verdict on the source of the suppression, at least in the context of time-varying but spatially homogeneous stimuli (which are not expected to engage corticothalamic feedback mechanisms as effectively as patterned stimuli; Sillito and Jones 2002). To address this, we can compare the latency of the LGN receptive field term in the NIM (Fig. 2) with the latency of the suppressive nonlinear filters in the PSC-NIM (Fig. 5G). Because both achieve their peak amplitudes ∼35 ms after stimulus onset, this suggests that suppressive nonlinearities come from interneurons on the feedforward pathway. If the source of the suppression was corticogeniculate feedback, by way of the reticular nucleus, for example, then we would expect the latency peak of the suppressive filters to be delayed ∼5–10 ms given the known spike transit times along that pathway (Briggs and Usrey 2007). Furthermore, the timescales of the PUSH inhibition observed are consistent with the “triad” circuitry in which some LGN cells, X cells in particular, are embedded (Koch 1985; Sherman 2004), for which the primary retinal driver synapses directly upon a nearby interneuron along with its target relay cell. The timescale of the PULL inhibition is consistent with the circuit suggested in Wang et al. (2007), in which an opposite-polarity RGC adjacent to the primary RGC driver synapses upon an interneuron connected to the LGN cell, thus providing maximal inhibition for the stimuli least preferred by the relay cell.

In summary, we have presented an integrated picture of processing across the precortical visual pathway and described how multiple circuit mechanisms work together to generate precision in the retina and amplify it in the LGN. Although this study was performed with a relatively simple time-varying but spatially homogeneous stimulus, the resulting structure of the computations we describe sets the foundation for understanding the visual computation for more complex stimuli, for which the nonlinear computations essential to LGN precision are likely to be important to cortical processing (Alonso et al. 1996; Kara et al. 2000; Stanley et al. 2012).

GRANTS

D. A. Butts was supported by National Science Foundation Grant IIS-1350990. A. R. R. Casti was supported by National Institute of Mental Health Grant K25MH67225.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at the institutional website of one of the authors, which at the time of publication they indicate is: http://neurotheory.umd.edu/nimcode. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

AUTHOR CONTRIBUTIONS

D.A.B. and A.R.R.C. conception and design of research; D.A.B., Y.C., and A.R.R.C. analyzed data; D.A.B. and Y.C. interpreted results of experiments; D.A.B. and Y.C. prepared figures; D.A.B. drafted manuscript; D.A.B. and A.R.R.C. edited and revised manuscript; D.A.B., Y.C., and A.R.R.C. approved final version of manuscript; A.R.R.C. performed experiments.