Relating normalization to neuronal populations across cortical areas

Normalization is thought to underlie many sensory, motor, and cognitive processes and likely arises from interactions between neuronal populations. To gain insight into normalization mechanisms, we recorded the activity of populations of neurons in response to combinations of visual stimuli. We found that neurons that show strong normalization shared less trial-to-trial variability with other neurons in the same cortical area and more variability with neurons in other cortical areas than did units with weak normalization.

Abstract

Normalization, which divisively scales neuronal responses to multiple stimuli, is thought to underlie many sensory, motor, and cognitive processes. In every study where it has been investigated, neurons measured in the same brain area under identical conditions exhibit a range of normalization, ranging from suppression by nonpreferred stimuli (strong normalization) to additive responses to combinations of stimuli (no normalization). Normalization has been hypothesized to arise from interactions between neuronal populations, either in the same or different brain areas, but current models of normalization are not mechanistic and focus on trial-averaged responses. To gain insight into the mechanisms underlying normalization, we examined interactions between neurons that exhibit different degrees of normalization. We recorded from multiple neurons in three cortical areas while rhesus monkeys viewed superimposed drifting gratings. We found that neurons showing strong normalization shared less trial-to-trial variability with other neurons in the same cortical area and more variability with neurons in other cortical areas than did units with weak normalization. Furthermore, the cortical organization of normalization was not random: neurons recorded on nearby electrodes tended to exhibit similar amounts of normalization. Together, our results suggest that normalization reflects a neuron's role in its local network and that modulatory factors like normalization share the topographic organization typical of sensory tuning properties.

NEW & NOTEWORTHY

Normalization is thought to underlie many sensory, motor, and cognitive processes and likely arises from interactions between neuronal populations. To gain insight into normalization mechanisms, we recorded the activity of populations of neurons in response to combinations of visual stimuli. We found that neurons that show strong normalization shared less trial-to-trial variability with other neurons in the same cortical area and more variability with neurons in other cortical areas than did units with weak normalization.

normalization, in which a neuron's response is divisively scaled when multiple stimuli are presented, is thought to underlie many sensory, motor, and cognitive properties, ranging from olfaction in fruit flies to attention in primates (Britten and Heuer 1999; Carandini et al. 1997; Heeger 1992; Lee and Maunsell 2009; Ni et al. 2012; Ohshiro et al. 2011; Olsen et al. 2010; Reynolds and Heeger 2009; Simoncelli and Heeger 1998; Tolhurst and Heeger 1997). Because it is so widespread, normalization has been hypothesized to represent a canonical cortical computation (for review see Carandini and Heeger 2012). Despite substantial recent interest from the experimental and theoretical neuroscience communities, the neuronal mechanisms underlying normalization remain poorly understood.

Most models of normalization are descriptive (e.g., Carandini and Heeger 2012), but they appeal to the notion that normalization arises through interactions between groups of neurons (see also Busse et al. 2009; Chance et al. 2002; Rubin et al. 2015; Rust et al. 2006; Sit et al. 2009). Experimentally, even neurons measured in the same brain area under identical experimental conditions exhibit different degrees of normalization, ranging from strong suppression by nonpreferred stimuli to linear summation of responses to combinations of stimuli (strong to weak normalization; for examples, see Fig. 1; Busse et al. 2009; Lee and Maunsell 2009;). We hypothesized that if normalization reflects the activity of populations of neurons, then a signature of this mechanism might be differences in shared variability between neurons that exhibit strong or weak normalization and other neurons that are in the same or in different cortical areas.

Fig. 1.

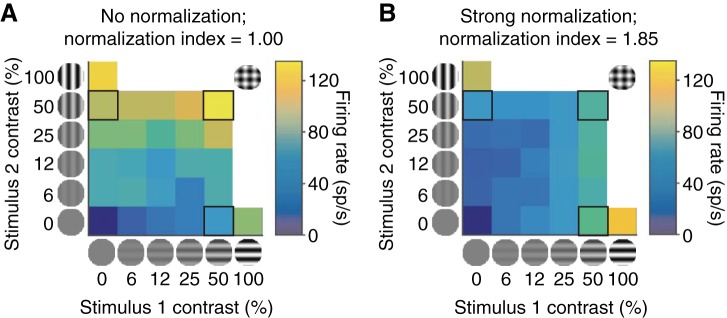
Responses of 2 example V1 units to superimposed orthogonal drifting gratings as a function of the contrast of each grating (x- and y-axes). The neuron in A responds linearly to the 2 stimuli, meaning that its response to 2 superimposed stimuli is approximately equal to the sum of its responses to the 2 stimuli presented alone (compare responses to the outlined stimuli on the x- and y-axes with the response to the combined stimulus along the diagonal). The neuron in B exhibits strong normalization, meaning that its response to the superimposed stimuli is similar to the average of its responses to the 2 stimuli presented alone.

We also hypothesized that we could gain insight into the way that neuron-to-neuron differences in normalization arise by examining the way neurons that exhibit different degrees of normalization are arranged in cortex. Different patterns of interactions with populations of neurons in the same or different cortical areas could arise either through random neuron-to-neuron differences in the strength of direct or indirect connections or through spatially specific inputs to groups of neurons. We reasoned that we could differentiate between these two possibilities by measuring whether neurons that are located near each other in cortex exhibit similar degrees of normalization.

To test these hypotheses, we used an approach with two important components. First, we recorded the responses of neurons in three visual areas to identical stimuli, which allowed us to extract general observations that were not specific to a particular cortical area. Second, we recorded from multiple neurons within each cortical area and sometimes in two areas simultaneously, which allowed us to probe interactions between neurons with different properties and also to measure how normalization is organized across the cortex.

We found strong evidence that the degree of normalization a neuron exhibits is reflected in the pattern of its interactions with neurons both in the same and in different cortical areas. Neurons that showed strong normalization shared less trial-to-trial variability (had lower spike count correlations, also termed r_SC or noise correlations) with other neurons in the same cortical area and shared more variability with neurons in other cortical areas than units that showed weak normalization. We also found that normalization is not randomly organized in the brain, meaning that neurons that are located near each other in the brain tend to exhibit a similar degree of normalization.

Together, our results will constrain future models of the neuronal mechanisms underlying normalization. The relationship between spike count correlations and connectivity is complicated by the facts that spike count correlations can reflect either direct or indirect inputs and can be reduced when a pair of neurons either have fewer common inputs or have both inhibitory and excitatory inputs in common that serve to cancel correlations (Renart et al. 2010). Empirically, however, neurons with higher spike count correlations tend to have more or stronger common inputs than neurons with lower spike count correlations (Hofer et al. 2011; Okun et al. 2015). Our results therefore provide evidence in favor of a model in which normalization is instantiated by inputs that 1) are spatially specific and 2) vary in strength from neuron to neuron such that neurons that receive strong normalization-related inputs from within the same area have weak inputs from other cortical areas, and vice versa. More generally, our study suggests that recordings from groups of neurons in multiple cortical areas can provide insight into the neuronal mechanisms underlying cortical computations.

MATERIALS AND METHODS

Visual stimuli, subjects, and electrophysiological recordings.

We presented visual stimuli on a calibrated CRT monitor (calibrated to linearize intensity, 1,024 × 768 pixels, 90- or 120-Hz refresh rate) placed 57 cm from the animal. We used custom software (written in MATLAB with the Psychophysics Toolbox; Brainard 1997; Pelli 1997) to present stimuli and monitor behavior. We monitored eye position, using an infrared eye tracker (Eyelink 1000, SR Research), and recorded eye position and pupil diameter (1,000 samples/s), neuronal responses (30,000 samples/s), and the signal from a photodiode to align neuronal responses to stimulus presentation times (30,000 samples/s), using hardware from Ripple Microsystems.

We recorded from visual areas V1, MT, and V4 in a total of four adult male rhesus monkeys (Macaca mulatta; monkeys BR, JD, ST, SY, weights 8.8, 10.0, 9.0, and 9.3 kg, respectively). All animal procedures were approved by the Institutional Animal Care and Use Committees of the University of Pittsburgh and Carnegie Mellon University. Before training, we implanted each animal with a titanium head holder. Then, the animal was trained to passively fixate while we presented peripheral visual stimuli. Monkeys BR, JD, and ST were also trained to perform other visually guided tasks that were not used in the present experiments. Once training was complete, we implanted a microelectrode array (Blackrock Microsystems). In monkeys BR and ST, we implanted a 10 × 10 microelectrode array in area V1. In monkeys SY and JD, we implanted a pair of 6 × 8 microelectrode arrays in V4. In monkey SY, both arrays were in V4 in the right hemisphere, and monkey JD received bilateral V4 implants. We identified areas V1 and V4 with stereotactic coordinates and by visually inspecting the sulci. We placed the V1 arrays posterior to the border between V1 and V2 and placed the V4 arrays between the lunate and the superior temporal sulci. The two V4 arrays were connected to a single percutaneous connector. The distance between adjacent electrodes of V1 and V4 arrays was 400 μm, and each electrode was 1 mm long.

In the same surgical procedure, we also implanted recording chambers that allowed access to area MT in monkeys BR and ST. Recordings were made from electrodes inserted into area MT, which was identified based on a combination of stereotaxic coordinates, depth, gray and white matter transitions, and physiological properties. We used 24-channel V-Probes (Plexon) with an interelectrode distance of 50 μm. The contacts had a diameter of 15 μm. We also recorded with 24-channel linear microarrays (Alpha Omega) with an interelectrode distance of 60 μm. The contacts had a diameter of 12.5 μm and were arranged in two rows of 12 electrodes (the 2 rows were on opposite sides of the probe and were therefore separated by ∼300 μm).

We recorded neuronal activity during daily experimental sessions for several weeks in each animal. During each session, the monkeys were rewarded for passively fixating while we presented superimposed orthogonal drifting gratings at a range of contrasts. Superimposed gratings elicit response suppression that has been called cross-orientation suppression and has been shown in previous studies to be well-described by divisive normalization (Busse et al. 2009; Carandini et al. 1997; Heeger 1992; Heuer and Britten 2002). We verified that a normalization model provides a good account of the trial-averaged responses of the neurons we recorded (see below).

The stimuli we used were generally presented for 200 ms and were large enough to cover the classical receptive fields of all of the neurons we recorded (grating diameters depended on receptive field eccentricity; range 2.5–7° of visual angle in V1, 7–13° in MT, and 1–9° in V4). Because V1 receptive fields are substantially smaller than those in MT and V4, the stimuli typically covered a greater proportion of the surrounds in V1 than in the other two areas.

Our data set includes 25 recording sessions in V1 (5 from monkey BR and 20 from monkey ST), 30 recording sessions in MT (21 from monkey BR and 9 from monkey ST), and 16 recording sessions in V4 (4 from monkey JD and 12 from monkey SY). In a subset of experiments (1 in monkey BR and 9 in monkey ST), we were able to record simultaneously from groups of neurons in V1 and MT with overlapping receptive fields.

During recordings from the chronically implanted microelectrode arrays we used in V1 and V4, it is nearly impossible to tell whether we recorded from the same single unit or multiunit clusters on the array across subsequent days. We therefore included analyses of individual example recording sessions (see Fig. 4, A and D). These example days were picked because the animal performed a large number of trials with good psychophysical performance and because recording quality was good. Because we inserted the MT probe each day, each MT unit (and V1-MT pair) is unique.

Fig. 4.

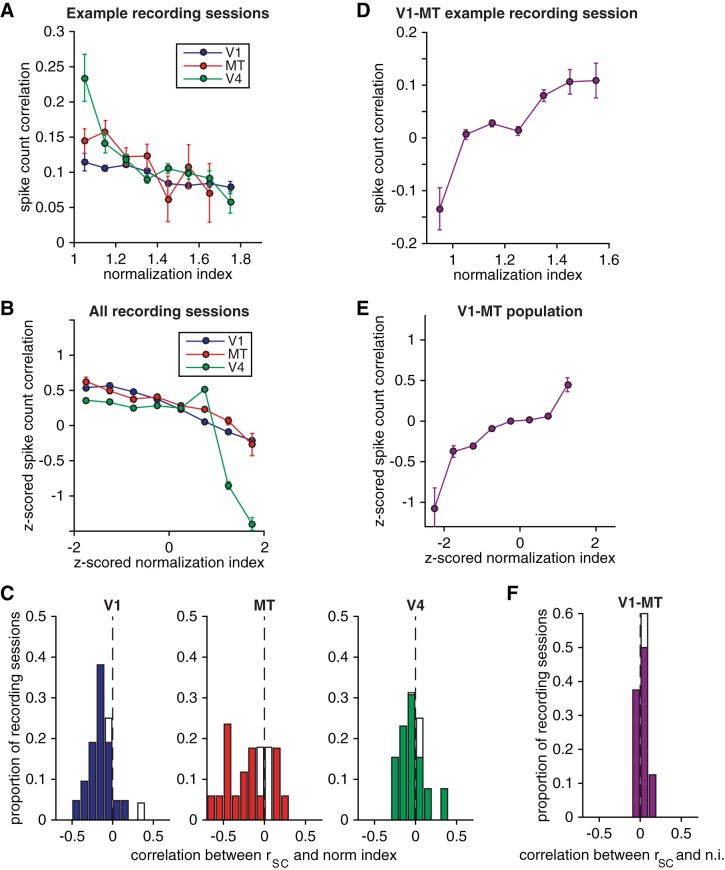
Normalization has opposite relationships with spike count correlations within and across cortical areas. A and B: spike count correlation as a function of the mean normalization index (averaged over stimulus orientations and averaged over the 2 neurons in the pair) for pairs of units that had similar normalization indexes (bin size = z-score of 0.5) recorded during an example recording session from each cortical area (A) and averaged over pairs of simultaneously recorded units that had normalization indexes that had similar normalization indexes (bin size = z-score of 0.5) from all recording sessions (B). Error bars represent SE. C: histograms of the correlation coefficient between spike count correlation and normalization index (n.i.) for the recording sessions in each cortical area. Filled bars represent recording sessions for which this correlation coefficient was significantly different from 0 (P < 0.05). D–F: same as A–C for pairs of simultaneously recorded units in V1 and MT.

Data analysis.

All spike sorting was done manually after the experiment with Plexon's Offline Sorter. We sorted single units as well as multiunit clusters (sorted to remove noise). We included single units or multiunit clusters for analysis if their response to 0% contrast stimuli (a blank screen) was significantly different from the average response to stimuli with at least 50% contrast (t-test, P < 0.01). For many analyses we combined data from single units and multiunits, and we use the term “unit” to refer to either. We recorded a total of 3,835 units in V1 (230 single units and 3,605 multiunits), 976 units in MT (96 single units and 880 multiunits), and 1,550 units in V4 (86 single units and 1,464 multiunits).

To allow for the latency of V1, V4, and MT responses, our analyses are based on spike count responses calculated from 30–230 ms after stimulus onset for V1 and 50–250 ms after stimulus onset for V4 and MT. We quantified spike count correlations (r_SC) as the Pearson's correlation coefficient between spike count responses to repeated presentations of the same stimulus. This measure is extremely sensitive to outliers, so we did not analyze trials for which the response of either unit was more than three standard deviations away from its mean (following the convention of Kohn and Smith 2005). For each pair of units recorded simultaneously from the same hemisphere but not from the same electrode, we computed r_SC separately for each 50% contrast stimulus condition (with single orientations or superimposed orthogonal gratings) and averaged the results. Taking the z-scored responses for each condition and computing a single value of r_SC for each pair (as in Ecker et al. 2010) gave qualitatively similar results.

The distribution matching procedure to control for electrode distance in our analysis of spike count correlations (see Fig. 5) is described in detail elsewhere (Churchland et al. 2010; Ruff and Cohen 2014a). Briefly, the goal of this analysis was to have the same distribution of electrode distances for pairs of neurons with normalization indexes that were below (left bars in Fig. 5) or above (right bars in Fig. 5) the median normalization index. We compared distributions of electrode distances for each half of the data set and selected the greatest common distribution. We then subsampled our pairs of units to match that distribution and analyzed spike count correlations for those subdistributions. There was a large overlap of these distributions of electrode distances. The mean-matched resampling process was repeated 1,000 times, and the bars in Fig. 5 represent the average z-scored r_SC values from these resampled distributions, with error bars that are the standard error of the mean from one representative resampled distribution.

Fig. 5.

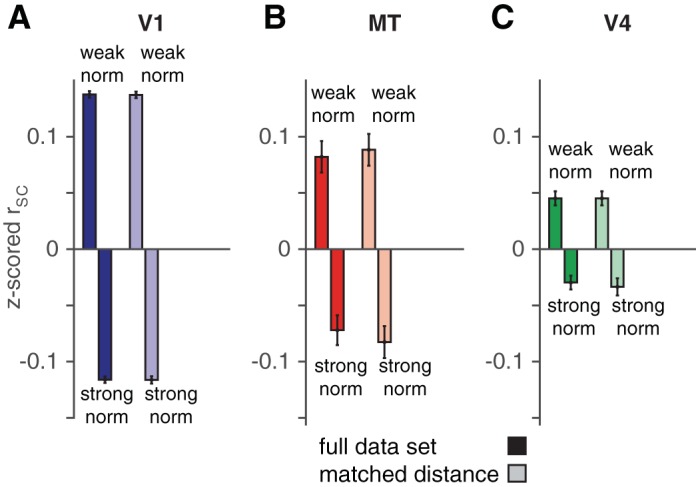
The relationship between normalization index and spike count correlation does not depend on electrode distance. Mean z-scored spike count correlation for pairs of units whose z-scored normalization indexes were < (left bar in each pair) or > (right bar) 0 in V1 (A), MT (B), and V4 (C). Light bars represent the same analysis for pairs of neurons with matched distributions of electrode distance (see materials and methods). Error bars represent SE.

To assess the extent to which we recorded the same cell on multiple contacts of the 24-channel probes we used to record in MT, we calculated zero-lag synchrony with a trial shuffle correction (Smith and Kohn 2008) for all pairs of units collected on different electrodes. The results of our synchrony analyses were qualitatively similar whether we analyzed spikes during all stimulus presentations (see Fig. 7B) or all spikes recorded during the experimental session, regardless of the stimuli or behavior.

Fig. 7.

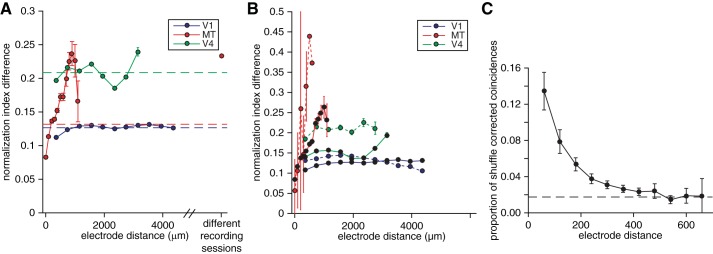
The degree of normalization is topographically organized. A: relationship between difference in normalization indexes and electrode distance for pairs of simultaneously recorded units. Dashed lines indicate the average difference in normalization indexes for pairs of simultaneously recorded units in each cortical area. Error bars represent SE. B: relationship between difference in normalization indexes and electrode distance for pairs of simultaneously recorded single units (dashed lines) and multiunits (solid lines). Conventions as in A. C: average shuffle-corrected millisecond-level synchrony as a function of electrode distance between pairs of MT units during an example recording session using a linear microarray with 2 rows of 12 electrodes. Dashed line indicates the average shuffle-corrected synchrony between pairs of electrodes on opposite sides of the probe (which are separated by several hundred micrometers). Note that the function relating synchrony to distance asymptotes at ∼300 μm, while the relationship between normalization index and electrode distance reaches a peak much later (>1 mm; A and B), suggesting that the topography does not arise from recording the same unit on multiple electrodes. Error bars represent SE.

Normalization model of cross-orientation suppression.

In this study, we used cross-orientation suppression as a proxy for normalization. To quantify the extent to which divisive normalization accounts for the suppression we observed, we fit the trial-averaged responses of the units we recorded to a standard normalization model. There are many published instantiations of normalization models. We selected one that has only four free parameters (Ni et al. 2012), but it is very similar to other published normalization models (Boynton 2009; Carandini and Heeger 2012; Lee and Maunsell 2009; Reynolds and Heeger 2009).

In this instantiation of the model, the mean response of a neuron to a combination of stimuli in its preferred (P) or null orientation (N) is given by

$$R_{\text{P},\text{N}}=\frac{c_{\text{P}}{L}_{\text{P}}+c_{\text{N}}{L}_{\text{N}}}{c_{\text{P}}+\alpha c_{\text{N}}+\sigma }$$ (1)

where R_P,N is the mean response of the neuron under study, c_P and c_N are the contrasts of the preferred and null gratings, L_P and L_N represent the response of the neuron's linear receptive field to a full-contrast stimulus with the preferred or null orientation, α is a tuned normalization parameter, and σ is a semisaturation constant. For each neuron and pair of orientations, we fit the four free parameters of this model (L_P, L_N, α, and σ) to the 27 combinations of contrasts we used.

The numerator of Eq. 1 represents the tuned, linear response of the neuron, and the neuron's preference for the preferred over the null orientation is determined by L_P and L_N. Note that because we did not optimize the orientations of the stimuli under study for the tuning of each unit, responses to the two stimuli were often similar. We therefore designated the “preferred” orientation as the orientation in each pair that elicited the bigger mean response, and the “null” orientation was the opposite orientation. For some units/orientation pairs, L_P and L_N were therefore very similar.

The denominator of Eq. 1 represents divisive normalization. It depends only on the contrasts of the stimuli and on the tuned normalization parameter α and the semisaturation constant σ. These parameters represent tuned normalization from combinations of stimuli and contrast-dependent normalization, respectively (Carandini et al. 1997).

RESULTS

Our results are based on multineuron recordings from visual areas V1, MT, and V4 in a total of four rhesus monkeys. The monkeys were rewarded for passively fixating while we presented superimposed orthogonal drifting gratings that were large enough to cover the receptive fields of the neurons we recorded. This is a standard procedure for measuring cross-orientation normalization (Busse et al. 2009). Figure 1 shows the responses of two representative V1 units to different combinations of contrasts of the two gratings. We calculated a normalization index for each unit we recorded, which we defined as the ratio of the sum of the unit's responses to 50% contrast stimuli at each of two orthogonal orientations to the unit's response to those same two gratings when they were superimposed. Therefore, a normalization index of 1 represents perfect summation (no normalization; Fig. 1A) and a normalization index of 2 means that the response to the superimposed stimulus was the average of the responses to each stimulus alone (strong normalization; Fig. 1B). When we measured normalization using multiple pairs of stimulus orientations, we report the mean normalization index for each unit. This simplification is well-justified because the normalization index we calculated did not depend substantially on the stimulus orientation (see below and Fig. 3).

Fig. 3.

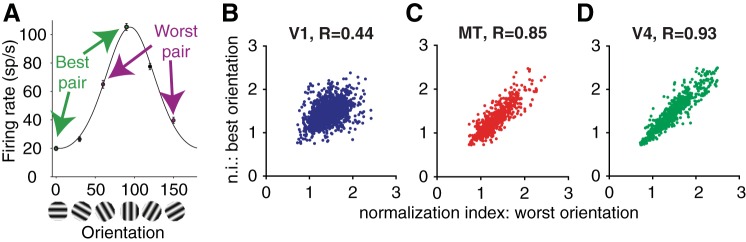
Normalization is largely a property of a cell rather than a response to specific stimuli. A: responses of an example V1 unit to single, full-contrast gratings at different orientations (black line represents the best fit von Mises function). Arrows indicate the pairs of orthogonal gratings that elicit the largest (best orientation pair) and smallest response differences (worst orientation pair) in the example unit. Error bars represent standard error of the mean (SE). B–D: scatterplots of the normalization indexes calculated using the best (y-axis) and worst (x-axis) orientation pairs for each unit recorded in V1, MT, and V4, respectively.

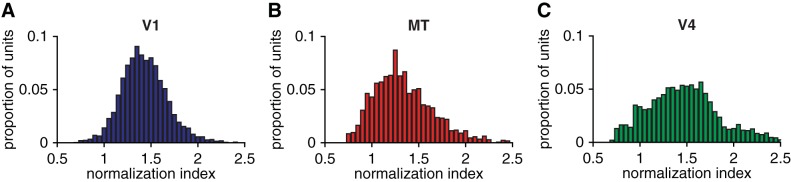
Consistent with previous studies (Lee and Maunsell 2009; Ni et al. 2012; Rust et al. 2006), we found units in V1, MT, and V4 whose normalization indexes spanned a wide range (Fig. 2). This variability did not depend on whether the unit was a well-isolated single unit or a multiunit cluster; the mean normalization index was indistinguishable for single units and multiunits in each area (mean normalization indexes were V1: 1.18 for single units and 1.14 for multiunits, t-test, P = 0.10; MT: 1.08 for single units and 1.04 for multiunits, t-test, P = 0.54; and V4: 1.20 for single units and 1.08 for multiunits, t-test, P = 0.23). The mean normalization index was significantly different for each area (t-tests on each pair of areas, P < 0.01).

Fig. 2.

Normalization indexes span a wide range in 3 cortical areas: histograms of the normalization indexes for all of the recorded units in V1 (A), MT (B), and V4 (C).

Normalization is largely a property of a cell rather than a response to specific sensory stimuli.

Our recording methods allowed us to measure the spiking activity of many units simultaneously. Therefore, we could not optimize the orientations of the gratings for the tuning of each cell (Busse et al. 2009). Because all of our analyses involved comparing the properties of neurons with different normalization indexes, we explored the relationship between normalization indexes and the extent to which the stimuli were optimized for the tuning of the cell.

In many recording sessions, we recorded responses to several pairs of orthogonal gratings. We used responses to full-contrast stimuli presented alone (i.e., with the orthogonal grating at 0% contrast) to construct a tuning curve for each unit. Figure 3A depicts a tuning curve for an example V1 unit. For each unit, we identified the pair of orthogonal gratings that elicited the biggest response difference (“best pair” in Fig. 3A) and the pair of orthogonal gratings that elicited the smallest response difference (“worst pair” in Fig. 3A) and computed a normalization index for each pair.

We found that the degree of normalization a unit exhibited did not depend in a systematic way on whether the normalization index was computed based on responses to the best or worst pair of orientations (Fig. 3, B–D). The normalization indexes computed from responses to the best and worst orientations were significantly correlated in all three cortical areas (r = 0.44 for V1, 0.85 for MT, 0.93 for V4, all of which are significantly different from 0, P < 10⁻²⁰), and the mean normalization indexes for best and worst orientations were indistinguishable (paired t-tests, P > 0.05 in all 3 areas). Similarly, we found a strong correspondence between normalization indexes calculated using 50% contrast stimuli (which we used here) and normalization indexes calculated using lower-contrast stimuli (see below for a discussion of this issue using fits to a normalization model).

Despite these similarities, the strength of the correlation between normalization indexes computed from the best and worst orientations differed across areas. In part, the lower correlation between indexes in V1 and MT compared with V4 could be because of noise; the number of trials per condition was lower in V1 (mean 32 trials per condition) and MT (mean 29 trials per condition) than in V4 (mean 165 trials per condition).

Another possibility is that normalization might depend on the direction or orientation selectivity of the unit, which varies across areas. To determine whether normalization index depended on the extent to which the unit responded differently to the two orthogonal grating orientations, we calculated an orientation selectivity index for each unit and pair of orientations that was equal to the absolute value of the difference in the unit's mean response to single 50% contrast gratings divided by the sum of those responses. The mean orientation selectivity index was 0.15 for V1, 0.16 for MT, and 0.10 for V4 [all significantly greater than 0 (t-test, P < 10⁻⁵) and significantly different from each other (t-tests, P < 0.01 for each pair of areas)]. A large proportion of units/conditions had orientation selectivity indexes that were significantly greater than 0 (78% of units/conditions in V1, 69% of units/conditions in MT, and 54% of units/conditions in V4). However, normalization index was not significantly correlated with orientation selectivity index either for the full data sets or for units/conditions with orientation selectivity indexes that were significantly greater than 0 (P > 0.05 for each cortical area/data subset). Furthermore, the difference in normalization index for the best and worst orientation pairs was uncorrelated with orientation selectivity index in MT and V4 (correlation coefficient = −0.04, P = 0.10 in MT, correlation coefficient = −0.02, P = 0.44 in V4) and only very weakly anticorrelated in V1 (correlation coefficient = −0.06, P = 0.01). Together, these results suggest that normalization index does not depend strongly on the orientation tuning of the cell.

Although the strength of the relationship between normalization indexes for best and worst orientation pairs varied across areas, these observations imply that to a large extent normalization is a fixed property of a cell rather than a response to the specific orthogonal motion directions we tested. This idea is consistent with past results (Busse et al 2009). For the present study, these observations also suggest that the results of our analyses were not substantially affected by the fact that the stimuli were not optimized for the orientation tuning of each unit.

Cells that exhibit normalization have qualitatively different interactions with other neurons within and across cortical areas.

Normalization is thought to arise through suppressive interactions with a large group of other neurons. Current models of normalization do not address response variability (Carandini and Heeger 2012; Rubin et al. 2015). However, we hypothesized that if normalization involves interactions between neurons we might see signatures of these interactions by comparing the extent to which neurons that do or do not exhibit normalization share trial-to-trial variability. We tested this hypothesis by measuring correlations between trial-to-trial fluctuations in the responses of pairs of simultaneously recorded units (termed spike count or noise correlations, or r_SC). The average multiunit spike count correlation varied across recording sessions, animals, and brain areas (presumably because of differences in recording quality or average firing rate or differences in recording methodology between the chronically implanted microarrays in V1 and V4 and the movable probes we used in MT). We also found hints that normalization is topographically organized (see Fig. 7), which meant that individual recording sessions varied in mean normalization index depending on the properties of the cluster of cells located near the probe. To facilitate comparisons across recording sessions, we therefore z-scored the spike count correlations and normalization indexes within each recording session.

We found that within all three cortical areas spike count correlation depended strongly on the extent to which the units in a pair exhibited normalization. We first calculated spike count correlations for pairs of units with similar normalization indexes (bin size = a z score of 0.5). We found that pairs of units that showed similarly strong normalization (high normalization indexes) had lower average spike count correlations than pairs of units that showed similarly weak normalization (low normalization indexes). Figure 4, A and B, depict the average z-scored spike count correlation for pairs of neurons with similar normalization indexes (for example recording sessions and the full data set, respectively). Across all pairs of simultaneously recorded units, the correlation between z-scored r_SC and z-scored normalization index was negative for each of the three cortical areas (P < 10⁻¹⁸ for each cortical area). The correlation between r_SC and normalization index was also significantly less than zero in the majority of individual recording sessions for all three cortical areas (Fig. 4C). In all three areas, the dependence of spike count correlation on normalization index was maintained even when the distributions of strong and weak normalizing pairs were matched for electrode distance (compare left and right sets of bars in Fig. 5).

In a subset of experiments, we were able to record from V1 and MT units with overlapping receptive fields. During these recording sessions, we observed opposite patterns of correlations between units in different cortical areas as we did for pairs within the same area. Units that showed strong normalization had higher average spike count correlations with units that showed a similar degree of normalization in the opposite cortical area than did units that showed weak normalization (Fig. 4, D and E). Across all pairs of simultaneously recorded V1 and MT units, the correlation between z-scored r_SC and z-scored normalization index was significantly greater than zero (P < 10⁻¹⁷). The raw correlation between r_SC and normalization index was on average positive and was significantly different from zero in the majority of individual recording sessions (Fig. 4F). The relationship between cross-area correlation and normalization index was also maintained when the distributions of strong and weak normalizing pairs were matched for electrode distance (compare left and right sets of bars in Fig. 5).

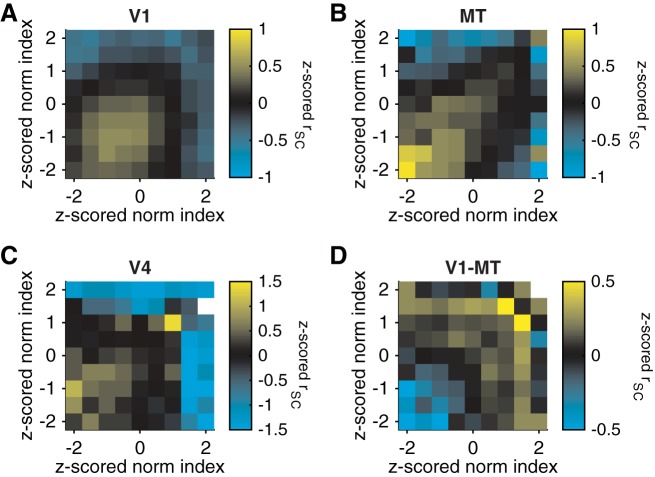
Figures 4 and 5 focus on pairs of units with similar normalization indexes. To visualize the full data set, we plotted z-scored r_SC (represented by colors in Fig. 6) as a function of the normalization index of each unit in the pair. Within each cortical area, units with very different normalization indexes (upper left and lower right portions of Fig. 6, A–C) tended to have very low spike count correlations. An important caveat of these results is that the topographic organization of normalization that we observed (see below) meant that units with dissimilar normalization indexes were often located further apart in the brain than units with more similar normalization indexes. Our data set was not large enough for a distance matching control as in Fig. 5, so some of the trend toward low correlations between pairs of units with dissimilar normalization indexes may be attributable to the known dependence of r_SC on cortical distance for pairs within V1 (Smith and Kohn 2008), MT (Zohary et al. 1994), and V4 (Smith and Sommer 2013).

Fig. 6.

Relationship between z-scored spike count correlation (color) and the z-scored normalization index of each member of each simultaneously recorded pair of units in V1 (A), MT (B), V4 (C), and pairs in which 1 unit was in V1 and 1 in MT (D). For A–C, the x-axis represents the unit in the pair with the lower (worse) orientation selectivity.

The relationship between spike count correlation and normalization index was similar for single units and multiunits both within each cortical area and between V1 and MT. Within each cortical area, the Pearson's correlation between z-scored r_SC and z-scored normalization index was significantly different from zero for both single units and multiunits and for each cortical area/combination of areas (within V1, the Pearson's correlation coefficient was −0.14, P < 0.001 for single units and −0.15, P < 10⁻³⁰ for multiunits; within MT, the Pearson's correlation coefficient was −0.33, P < 10⁻⁷ for single units and −0.12, P < 10⁻²⁸ for multiunits; within V4, the Pearson's correlation coefficient was −0.13, P < 10⁻³ for single units and −0.16, P < 10⁻¹¹ for multiunits; between V1 and MT, the Pearson's correlation coefficient was 0.17, P = 0.03 for single units and 0.21, P < 10⁻¹⁶ for multiunits).

Cortical organization of normalization.

Topography is a hallmark of the organization of neurons in many sensory modalities. Neurons with similar receptive field locations or tuning for orientation or direction are located near each other in V1, MT, and V4. Over the past several decades, topographic organization in sensory cortex has been identified for a wide variety of sensory tuning properties (Hubel 1982; Mountcastle 1997; Yao and Li 2002). However, whether there is functional organization for modulatory factors like normalization remains unknown.

To determine whether normalization strength is topographically organized, we compared normalization indexes for each pair of simultaneously recorded units. Borrowing a convention in a previous study for quantifying topography (DeAngelis and Newsome 1999), we plotted the difference between normalization indexes as a function of the distance between the electrodes for each pair of simultaneously recorded units. In each cortical area, difference in normalization index increases with cortical distance until an interelectrode distance of 1–2 mm (Fig. 7, A and B).

Because our normalization index is effectively bounded (nearly all normalization indexes fell between 0.5 and 2.5; see Fig. 2), the difference in normalization index between two neurons cannot increase monotonically as a function of distance, so the functions in Fig. 7A decrease after 1–2 mm. Put another way, neurons that are very far apart in the brain will have a difference in their normalization indexes that are close to the average difference (dashed lines in Fig. 7A) rather than a maximum, meaning that in the case of perfect topography the functions in Fig. 7, A and B, would oscillate. There are differences between cortical areas (compare the 3 colors in Fig. 7, A and B) and between single units and multiunits (compare the dotted and solid lines in Fig. 7B). The differences between single units and multiunits arise from the fact that that multiunits exhibit a smaller range of normalization indexes than single units. The standard deviations of distributions of normalization indexes were 0.11 for multiunits and 0.16 for single units in V1, 0.13 for multiunits and 0.17 for single units in V4, and 0.15 for multiunits and 0.23 for single units in MT (differences between single and multiunits were different for each area, P < 0.001). Despite this heterogeneity, the plots of difference in normalization index reach a maximum at cortical distances of 1–2 mm in all three cortical areas and for single units and multiunits. This size is on the order of the size of a cortical column (for review see Hubel 1982; Mountcastle 1997). Further experiments, perhaps using imaging techniques, will be necessary to determine whether the organization is truly columnar.

For pairs of units separated by <1 mm, the difference in normalization index was positively correlated with electrode distance in all three areas (Pearson's correlation between raw, unbinned normalization index and raw, unbinned electrode distance = 0.06, 0.22, and 0.04 for V1, MT, and V4, respectively, all significantly greater than 0, P < 10⁻⁴). In addition, when we performed a permutation test by shuffling the electrode distances (destroying the relationship between difference in normalization index and electrode distance), the actual mean difference in normalization indexes was significantly less than the shuffled mean for pairs separated by <400 μm and greater than the shuffled mean for pairs separated by 800-1,200 μm in all three areas (P < 10⁻³). However, the relationship between normalization and distance was much stronger in MT than in the other two areas. Further research will be necessary to determine whether this difference in our data set represents a true difference between these three cortical areas or is attributable to differences in our recording technology between MT and the other two areas. In V1 and V4, we used chronically implanted arrays to record from neurons that were all at a similar depth. In contrast, our electrode penetrations in MT were at a variety of angles. In the future, it will be interesting to find out whether angle of penetration affects the dependence of normalization difference on distance.

One factor unlikely to account for differences in the apparent organization for normalization in the three areas is interelectrode distance. In our MT recordings, where the interelectrode distance was small (50 or 60 μm; see materials and methods), we occasionally detected the same spike on multiple electrodes, as evidenced by synchronous spikes occurring more often than expected from recordings of separable, weakly synchronous spikes. Figure 7C shows the proportion of synchronous spikes as a function of interelectrode distance. The relationship between synchrony and cortical distance is substantially different from the relationship between difference in normalization index and cortical distance. This analysis suggests that the topography we observed cannot be attributed to recording the same cell on multiple electrodes. Together, our observations provide evidence in favor of the idea that normalization has a functional organization reminiscent of that of sensory or motor tuning properties.

Cross-orientation suppression is well-described by a normalization model.

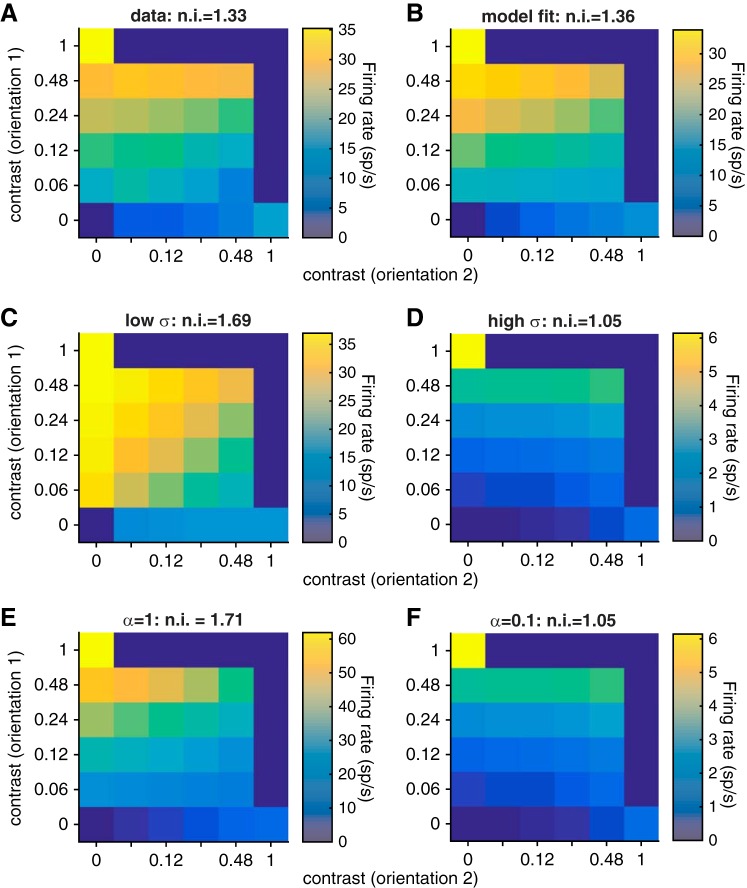
In our study, we used cross-orientation suppression as a proxy for normalization. To quantify the validity of this assumption, we fit a standard normalization model to the trial-averaged responses of the units we recorded (see materials and methods). Consistent with previous studies (Carandini and Heeger 2012; Heeger 1992; Said and Heeger 2013), we found that a normalization model accounted for the majority of the variance in trial-averaged responses in all three visual areas (85%, 69%, and 82% of the variance in V1, MT, and V4, respectively). Figure 8 shows the actual (Fig. 8A) and predicted (Fig. 8B) mean rates for an example V1 unit. Overall, the normalization indexes predicted by the model were robustly correlated with the actual normalization indexes (Pearson's correlation coefficient between the predicted and actual normalization indexes was 0.26 for V1, 0.62 for MT, and 0.46 for V4, all significantly greater than 0, P < 10⁻⁷⁰).

Fig. 8.

Fits of the normalization model for an example V1 single unit. A: actual mean rates of an example V1 unit (with baseline rate subtracted) as a function of the contrast of the grating at orientation 1 (y-axis) and orientation 2 (x-axis). The normalization index (n.i.) is shown at top. B: mean rates predicted by the best-fit normalization model. Conventions as in A. C and D: mean rates predicted by the normalization model with low and high σ, respectively (note the different color scales, which are adjusted for ease of viewing). Other model parameters as in B. The parameter σ scales the contrast response function and also changes the degree of normalization because it is a contrast-independent term in the denominator of the normalization equation. Conventions as in A and B. E and F: mean rates predicted by the normalization model with low and high α, respectively. Other model parameters as in B. The tuned normalization parameter α scales the relative contributions of the preferred and null stimuli to normalization. Conventions as in A–D.

Two of the parameters in the model, α and σ in Eq. 1, are associated with different aspects of normalization. The tuned normalization parameter α affects stimulus interactions in a contrast-dependent way by scaling the relative contributions of the preferred and null stimuli to normalization, while the semisaturation constant σ changes the contrast at which the contrast response curve saturates. The effects of these parameters on the predicted contrast response functions of an example V1 unit are plotted in Fig. 8, C–F. Although both of these processes have been associated with normalization (for review see Carandini and Heeger 2012), in previous studies the tuned normalization parameter α, but not the semisaturation constant σ, was associated with neuron-to-neuron differences in normalization invoked using combinations of stimuli (Ni et al. 2012; Rust et al. 2006) or with changes in attention (Ni et al. 2012).

As expected given the wide range of normalization indexes we observed (Fig. 2), the fitted values of α and σ differed substantially from unit to unit. The tuned normalization parameter α was correlated with the normalization index we used for all three areas (correlation coefficient between normalization index and α was 0.17, 0.19, and 0.19 for V1, MT, and V4, respectively; all significantly greater than 0, P < 0.01; not significantly different than each other, P > 0.05), meaning that a strong normalization index is associated with untuned normalization (which is consistent with the results of Ni et al. 2012). In V1 and MT, the semisaturation parameter σ was also correlated with our normalization index (correlation coefficient between normalization index and σ was 0.05, 0.14, and 0.01 for V1, MT, and V4, respectively; P < 0.01 for V1 and MT but P = 0.26 for V4). This difference may stem from the fact that the average value of σ was lower for V4 than for V1 or MT. Therefore, V4 responses saturate at lower contrast on average (see also Sclar et al. 1990), which may imply that the exact contrast saturation point is unrelated to the normalization index we used that was calculated from responses to high-contrast stimuli.

Consistent with the robust correlation between our normalization index and the tuned normalization parameter α, we found that the relationships between α and r_SC for pairs of units in the same or different areas had the same sign as the relationships between normalization index and r_SC depicted in Fig. 4 (all relationships still significantly different from 0, including separately for single units and multiunits). Consistent with the results in Fig. 7, electrode distance was positively correlated with the difference in α between two units. Together, these observations suggest that cross-orientation suppression is a good proxy for normalization and that the relationship between r_SC or electrode distance and normalization holds regardless of whether a simple index or a fitted parameter is used to quantify normalization.

DISCUSSION

Our multineuron, multiarea recordings revealed several new observations about normalization. First, we demonstrated that normalization index was similar for pairs of orientations that elicited large and small differences in firing rate, suggesting that normalization is a general property of a neuron rather than a response to specific stimuli. Second, we found that units that showed strong normalization had qualitatively different patterns of interactions with other neurons within the same cortical area and in different cortical areas. Finally, our data suggest that cells that are located near each other in the brain exhibited similar degrees of normalization. Although there were differences across areas, these observations, along with the distributions of normalization indexes, were present to varying degrees in all three cortical areas, implying that the basic characteristics of normalization are not specific to a particular area.

Our results are therefore consistent with the idea that normalization, and perhaps all processes that divisively scale neuronal responses, is a general cortical computation (Carandini and Heeger 2012). This means either that cross-orientation normalization is computed in an early stage of processing (such as V1) and passed on in an organized way to extrastriate areas or that it is computed in a similar way in each area. Our results also suggest that normalization, and likely other processes that are well-described by normalization models, is instantiated by a mechanism that involves spatially specific inputs from other brain areas. More generally, our results suggest that measuring the responses of neurons in multiple cortical areas can provide insights into the neural mechanisms that underlie modulatory processes like normalization.

Does normalization depend on cortical layer?

We showed that neurons that are located near each other in the brain have similar normalization indexes (Fig. 7) and that neurons that exhibit normalization have patterns of spike count correlations qualitatively different from those that do not (Fig. 4). One interesting possibility is that neurons in different layers exhibit different amounts of normalization, perhaps arising from layer-dependent differences in connectivity that might in turn give rise to different patterns of spike count correlations.

Using our recording methods, it is difficult to determine which cortical layer we are recording from. However, we have two indirect pieces of evidence that our results do not arise from a systematic relationship between cortical layer and normalization. First, during individual recording sessions we often see a range of normalization indexes that change nonmonotonically across each chronically implanted array. Because the electrodes on the arrays are all the same length (1 mm), the recorded neurons are likely all in the same layer (or at least layer should vary smoothly and slowly across the array). The observation that normalization index both increases and decreases across the array suggests that our topography results are not solely driven by differences across cortical layers. Second, a recent study showed that the spike count correlations do not vary substantially across layers in area V2 (Smith et al. 2013), leading the authors to hypothesize that spike count correlations arise from cortico-cortico interactions that should be constant throughout extrastriate cortex. Although the layer dependence of r_SC has not been measured in MT and V4, this hypothesis suggests that the dependence of r_SC on normalization strength did not arise from differences in cortical layer. However, investigating the way that normalization and other modulatory influences depend on cortical layer will be an interesting avenue for further study.

Opposite patterns of correlations within and across cortical areas: a general feature of cortical circuits?

We showed that there is an opposite relationship between normalization and spike count correlations within and across cortical areas (Fig. 4). Neurons that show strong normalization typically had lower correlations with other neurons that exhibited similarly strong normalization within the same area (Fig. 4, A–C) and higher correlations with neurons in other cortical areas that also exhibited strong normalization (Fig. 4, D–F) compared with pairs of neurons that exhibit less normalization.

This result bears some resemblance to recent work showing how other sensory and cognitive processes that divisively scale neuronal responses affect spike count correlations. A variety of modulatory influences including stimulus contrast (Kohn and Smith 2005; Snyder et al. 2014), learning or experience (Ahissar et al. 1992; Gu et al. 2011; Gutnisky and Dragoi 2008; Jeanne et al. 2013), global cognitive factors (Ruff and Cohen 2014a), and visual attention (Cohen and Maunsell 2009, 2011; Gregoriou et al. 2014; Herrero et al. 2013; Mitchell et al. 2009; Ruff and Cohen 2014b; Zénon and Krauzlis 2012) reduce spike count correlations between neurons in the same cortical area. In addition, we recently showed that attention has the opposite effect on correlations between cortical areas: shifting attention toward the joint receptive fields of a pair of V1 and MT neurons increases the spike count correlation (Ruff and Cohen 2016a,b).

Modulatory influences like attention have been hypothesized to utilize the mechanisms underlying normalization (Boynton 2009; Lee and Maunsell 2009; Ni et al. 2012; Reynolds and Heeger 2009), and neurons in MT that show strong normalization have stronger attentional modulation of their mean firing rate than those that do not normalize (Lee and Maunsell 2009; Ni et al. 2012; but see Sanayei et al. 2015). Furthermore, during an attention task with a single stimulus in their receptive field, neurons that showed the greatest attention-related rate modulation also show the biggest attention-related decreases in r_SC with similarly tuned neurons in the same cortical area (Cohen and Maunsell 2009, 2011).

A recent study measured the relationship between the variability of individual neurons and the variability of the average response of simultaneously recorded neurons in the same cortical area (termed population coupling; Okun et al. 2015). The authors found that neurons with strong population coupling had stronger average pairwise spike count correlations with other neurons in the same cortical area. In a separate set of experiments, the authors used in vivo two-photon imaging to calculate population coupling followed by in vivo whole cell recordings. They found that neurons with strong population coupling had a higher probability of receiving synaptic input from their neighbors. Broadly, this result is consistent with the idea that spike count correlations can be considered a proxy for synaptic inputs. Extrapolating this result to our experiment suggests that neurons that exhibit weak normalization, which had higher spike count correlations with other neurons in the same cortical area, also likely receive more synaptic inputs from neighboring cells in the same area than cells that exhibit strong normalization. As multineuron and multiarea recordings become more common, it will be interesting to see whether the opposite patterns of interactions between neurons within and across areas we observed are a general feature of cortical circuits.

Constraints on the neuronal mechanisms underlying normalization.

All current models of normalization (including the one we used here) focus on fitting the way that the trial-averaged responses of neurons depend on stimulus and task conditions. Because no current models incorporate response variability or cortical organization, the relationships between normalization and spike count correlation or cortical distance that we observed have not been predicted.

Our hope is that the patterns of interneuronal correlations and the topography we observed provide insight into the neuronal mechanisms underlying normalization. Our results suggest that normalization arises from patterns of inputs that are spatially segregated and that span cortical areas. Although the relationship between spike count correlations and connectivity is in its early stages of exploration (Hofer et al. 2011; Okun et al. 2015), one possibility is that the cells that show strong normalization have a higher proportion of cross-area inputs than within-area inputs. It will be exciting in the future to try to map the functional properties we observed onto anatomical connectivity.

One advantage of using normalization as a model system to study the neuronal mechanisms underlying modulatory factors (as opposed to using a cognitive factor like attention) is that measuring normalization does not require behavioral training. In animals like mice training spatial attention tasks might be prohibitively difficult, but it might be possible to use genetic techniques to learn more about the circuit-level mechanisms underlying normalization.

The body of work showing similarities in the way that different cognitive factors affect populations of neurons (Carandini and Heeger 2012; Ruff and Cohen 2014a) suggests that what we learn from studying normalization will be applicable to understanding the mechanisms underlying a wide variety of sensory, cognitive, and motor processes that scale neuronal responses. Our results imply that recording from groups of neurons in multiple cortical areas and also exploring the differences between the tuning and modulatory properties of neurons within a population can be powerful ways to gain insight into neuronal mechanisms.

GRANTS

The authors are supported by National Institutes of Health (NIH) Grants 4R00 EY-020844-03 and R01 EY-022930 (M. R. Cohen), a training grant slot on NIH 5T32 NS-7391-14 (D. A. Ruff), a Whitehall Foundation Grant (M. R. Cohen), a Klingenstein-Simons Fellowship (M. R. Cohen), a grant from the Simons Foundation (M. R. Cohen), a Sloan Research Fellowship (M. R. Cohen), and a McKnight Scholar Award (M. R. Cohen). This work was also supported by a core grant from the NIH (P30 EY-008098).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

D.A.R. and M.R.C. conception and design of research; D.A.R. and J.J.A. performed experiments; D.A.R., J.J.A., and M.R.C. analyzed data; D.A.R. and M.R.C. interpreted results of experiments; D.A.R., J.J.A., and M.R.C. prepared figures; D.A.R. and M.R.C. drafted manuscript; D.A.R., J.J.A., and M.R.C. edited and revised manuscript; D.A.R., J.J.A., and M.R.C. approved final version of manuscript.