Compressed Sensing Reconstruction of Ultrafast 2D NMR Data: Principles and Biomolecular Applications

Abstract

A topic of active investigation in 2D NMR relates to the minimum number of scans required for acquiring this kind of spectra, particularly when these are dictated by sampling rather than by sensitivity considerations. Reductions in this minimum number of scans have been achieved by departing from the regular sampling used to monitor the indirect domain, and relying instead on non-uniform sampling and iterative reconstruction algorithms. Alternatively, so-called “ultrafast” methods can compress the minimum number of scans involved in 2D NMR all the way to a minimum number of one, by spatially encoding the indirect domain information and subsequently recovering it via oscillating field gradients. Given ultrafast NMR’s simultaneous recording of the indirect- and direct-domain data, this experiment couples the spectral constraints of these orthogonal domains –often calling for the use of strong acquisition gradients and large filter widths to fulfill the desired bandwidth and resolution demands along all spectral dimensions. This study discusses a way to alleviate these demands, and thereby enhance the method’s performance and applicability, by combining spatial encoding with iterative reconstruction approaches. Examples of these new principles are given based on the compressed-sensed reconstruction of biomolecular 2D HSQC ultrafast NMR data, an approach that we show enables a decrease of the gradient strengths demanded in this type of experiments by up to 80%.

Introduction

Two-dimensional nuclear magnetic resonance (2D NMR) provides valuable information for resolving and identifying the nature of chemical sites in a variety of chemical and biochemical systems. The data acquisition paradigm for 2D spectroscopy originates from the suggestion by Jeener, Ernst and their coworkers [1; 2], to record the signal emitted by a spin system as a function of two independent time variables: t₂, a run-time variable associated with a direct physical measurement; and t₁, a parametric delay that is systematically incremented throughout a series of independent experiments. Spectral information can be retrieved from this 2D time-domain matrix by a fast Fourier Transformation (FT), best implemented when using a uniform sampling of the time variables. A restricting factor, however, is imposed by this choice of sampling: as each of the parametric increments Δt₁ required to suitably map the indirect-domain is associated with an independent scan, the minimum number of experiments that will be needed, N₁, is determined by the indirect domain spectral width (SW₁=1/Δt₁) and by the associated spectral resolution $\left(\Delta v_{\mathit{1}}=1/t_{\mathit{1}}^{\max }=1/N_{\mathit{1}}\Delta t_{\mathit{1}}\right),$ according to N₁ = SW₁ / Δν₁. This is a restriction arising from the numerical demands posed by the fast FT procedure rather than from signal-to-noise ratio (SNR) considerations; therefore, various strategies have been suggested to bypass it, and hence reduce the minimum number N₁ of required scans. One of main routes proposed for this relies on exploiting spectral information available from a priori 1D NMR measurements, and use this for either a selective addressing of the spectral peaks of interest [3; 4], or for "unfolding" these from aliased spectral windows upon post-processing [5]. Another group of methods aims to reconstruct the spectra of interest by departing from traditional Nyquist time-domain sampling criteria altogether, for instance utilizing reduced-dimensionality measurements [6–8] or non-uniformly sampling of the indirect domains whose results are processed using non-fast-FT algorithms [9–13]. Included among the latter algorithms are maximum entropy, maximum likelihood, frequency decomposition, and a number of other algorithms that rely on some form of regularization to stabilize what could otherwise become an ill-conditioned inversion problem. All these approaches are based on the commonly fulfilled premise that sensitivity is sufficiently high, and that the number of spectral lines in the indirect domain is considerably smaller than the number of scans required by the FT paradigm.

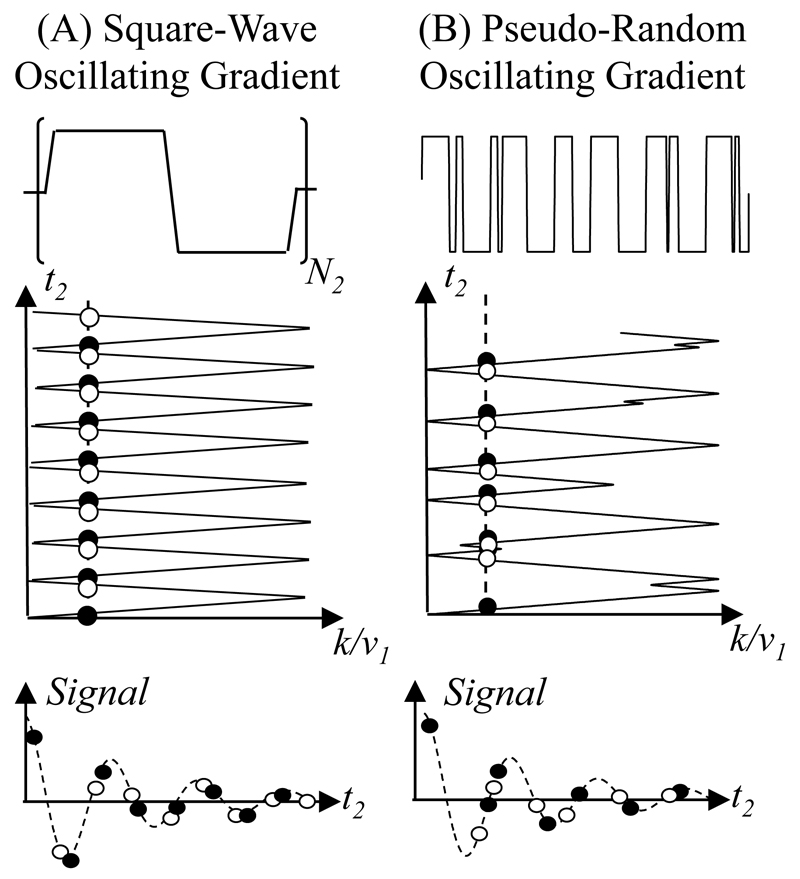
As an alternative to these methods, recent years have witnessed the emergence of “ultrafast” approaches [14–16], capable of reducing the total number of scans required in 2D spectroscopy from a different perspective. These approaches rely on concepts derived from NMR imaging, to parallelize all N₁ experiments involved in a 2D NMR measurement so as to complete it in a single scan. To do so ultrafast 2D NMR endows each voxel within the sample with an indirect domain evolution time that is proportional to its position, i.e. t₁(z) = C·z. The linearly distributed evolution time provides the transverse magnetization of nuclei with a chemical shift of Ω₁ with a phase of ϕ(z) = C·Ω₁ · z. When summed over the entire sample the resulting winding of magnetizations will generate no signal; yet in the presence of a field gradient possessing an appropriate orientation and magnitude, this helical magnetization pattern can be unwound, and bring all the spins into phase to form a macroscopic echo. Defining for this latter gradient a wavenumber $k(t)\equiv {\displaystyle \underset{0}{\overset{t}{\int }}{\gamma }_a{G}_a(\tau )d\tau },$ these echoes will be formed when k=-CΩ₁ establishing, in a one-to-one fashion, a correspondence between the k-variable and the ν₁ indirect-domain frequency axis. To extract the full information contained in a 2D experiment, the ultrafast strategy thus applies a rapid oscillation of the acquisition gradient G_a; this oscillation unravels the indirect domain information multiple times, and monitors it as it evolves as a function of the direct domain time t₂. A typical acquisition trajectory generated by a square-wave oscillation of this decoding gradient in the k/ν₁-t₂ plane, is depicted in Fig. 1A. This Figure evidences how, when the positive and negative gradients used to unravel the spatially encoded magnetization windings have equal magnitudes, every k/ν₁-echo –and therefore every “peak” in the indirect-domain spectrum– is sampled twice during each oscillation period. Moreover, if considering just the positive or negative gradient applications, every k/ν₁-echo is sampled at exactly 2·T_a time intervals along t₂. Either one of these “positive” or “negative” sets can therefore be independently processed by fast FT, and subsequently co-added for improving the overall SNR. (Alternatively, the may be jointly processed in a single transformation leading also to improved SNR by the interlaced FT [17].) Regardless of which route is implemented for doing such FTs, the direct-domains of the resulting spectra will be characterized by similar relations: in both cases their spectral widths SW₂ will inversely proportional to T_a, and their corresponding resolutions Δν₂ be given by the extent of the sampling along the direct-domain time axis, $t_{\mathit{2}}^{\mathit{max}}$. As for the indirect domain, the extent of its spectral characterization will be given by the encoding characteristics and by the range of k/ν₁- space that has been scanned. In particular, for a given indirect-domain target SW₁, the amplitude of the G_a acquisition gradient will become inversely proportional to T_a –that is, proportional to SW₂ [16]. Thus, the fact that this method enables the acquisition of arbitrary 2D spectra within a single scan, also means that spatial encoding will tie together demands on the spectral parameters of the various sampled axes according to

$$\frac{S{W}_{1}S{W}_2}{\Delta {\nu }_1}\sim {\gamma }_a{G}_{a}L,$$ (1)

where as mentioned Δν₁ and SW₁ are the indirect-domain spectral resolution and bandwidth, SW₂ is the direct-domain spectral width, G_a the gradient amplitude (assumed of constant magnitude during the acquisition), and L is the sample's length. Notice that since L is a constant and the maximal gradient strength that can be imparted on G_a may be limited, a tradeoff among the characteristics of the direct- and indirect-domains may end up being unavoidable. Moreover, even if strong enough gradients are available to fulfill all spectral width demands, increasing G_a’s amplitude requires a concomitant opening of the receiver's bandwidth, which in turn increases the noise level in proportion to the square-root of eq. (1)’s right-hand side.

Figure 1.

Strategies explored in this work for ultrafast 2D NMR acquisitions. (A) Traditional scheme based on a constant square-wave modulation of the acquisition gradient G_a. (B) Pseudo-random approach assayed in this study for the sake of an iterative n₂ reconstruction. The upper and middle panels display the G_a waveforms and their corresponding k/ν₁-t₂ trajectories. The bottom row considers a cross section of these trajectories for a given k/ν₁-value (dashed line), and shows the sampled FID points with black and white dots denoting data recorded during positive and negative gradient, respectively. Unlike the regular sampling provided by the square-wave modulation in (A), the random sporadic sign-changes in waveform (B) provide a sampling pattern that is suitable for an iterative reconstruction that exceeds Nyquist criteria.

It follows from these arguments that reducing the maximum gradient's amplitude is always desirable in ultrafast 2D NMR –whether to ease the hardware demands or to improve the method's SNR. Several approaches have been put forward for this purpose, in all cases using a priori information about the indirect-domain to optimize the encoding of its interactions [18–20]. Recently developed spatial/spectral manipulations, for example, uniformly distribute the echoes expected to arise from different chemical sites along the k/ν₁-axis. This in turn transforms Eq. (1) into

$$n_1\cdot S{W}_2\sim {\gamma }_a{G}_{a}L,$$ (2)

where n₁ is the number of peaks known to arise along the indirect domain. Dealing with a sparse indirect domain spectrum can therefore reduce considerably the demands on G_a, while making no compromises on the indirect-domain’s resolution or bandwidth. Notice, however, that this method still relies on reading the indirect-domain echoes using an acquisition whose overall scheme is identical to that of ultrafast 2D NMR, and which is bound by the same fast FT considerations. Therefore, although the k/ν₁-range can be considerably reduced, no departures from Shannon-Nyquist sampling criteria are involved. Still, the current work demonstrates that the coupling of non-linear sampling and of suitable data processing methods can be harnessed for ultrafast methodologies, provided that they focus on alleviating the Nyquist demands of the direct domain. In particular this Communication demonstrates that by departing from the usual, square-wave G_a modulation characteristic of ultrafast acquisitions, and by incorporating iterative algorithms like compressed sensing, it is possible to lift stringent relations of the kind embodied by eqs. (1) or (2), and enable the acquisition of improved ultrafast 2D NMR spectra.

Numerical Methodology

The methods used as basis for this research, share a common approach with those normally used when iterative algorithms are employed to speed up other kinds of NMR or MRI nD data acquisitions [9–13]. Like those counterparts, we will also rely on a non-uniform sampling pattern and a numerical algorithm that frees the spectrum retrieval process from the constraints posed by the fast FT. In conventional nD NMR spectroscopy/imaging this enables the reconstruction of frequency-domain data based on the acquisition of considerably fewer scans than those demanded by the Shannon criterion. In ultrafast NMR/MRI spectroscopy, however, where the number of scans has already been decreased to a minimal value, speed-up goals are no longer relevant. Moreover, given the absence of FT along the spatially encoded domain, extracting the indirect-domain spectrum by numerical means is also not pertinent. Still, the additional flexibility provided by non-FT methods can be harnessed for another purpose: reducing the amplitude of the G_a decoding gradients, and thereby alleviate the technical and sensitivity problems that were alluded to earlier. This will in turn imply applying iterative reconstruction methods along t₂-axis over which these gradients operate. Such procedures have to our knowledge not been applied before to dealing with the direct domain of 2D NMR, as its information comes here nearly “for free” in both time and sensitivity. The coupling of the G_a and SW₂ put forward by eq. (1), however, lead us to consider the consequence of using non-FT methods along ultrafast NMR’s direct-domain.

One of the essential ingredients required for departing from the criteria imposed by fast FT processing, is to abandon the use of equi-spaced data sampling patterns: only in such a way can aliasing be avoided, and genuine frequencies be extracted from a time-domain response over a range that exceeds the Nyquist limit. It follows that the gradient waveform normally used in ultrafast NMR (Fig. 1A) will not serve this purpose: by providing for each k/ν₁ echo a sampling pattern that is uniform along t₂, this periodic G_a square-wave will not deliver a randomized array of time-domain points like the one required by non-FT processing. A non-uniform t₂ pattern, however, can easily be introduced by imposing onto the gradient waveform a pseudo-random sign alteration. This alternation should not be entirely random, as the k/ν₁-axis also needs to probe a predefined indirect-domain range SW₁ of frequencies. Changes imparted on G_a should therefore be tailored so as to fulfill a suitable coverage of a given targeted indirect-domain spectral region. Figure 1B illustrates one route for achieving this, with a potential gradient waveform and its resulting trajectory in the k/ν₁-t₂ space. A proper rearrangement of points sampled during the resulting FID will provide, for each coordinate along the k/ν₁-axis, an individual set of randomly distributed points along t₂ (Fig. 1B, bottom). Iterative algorithms can then be used for each coordinate along k/ν₁, to reconstruct the associated 1D spectrum arising along the direct-domain, and from there the full 2D distribution being sought.

The consequences of following this approach were here explored with the aid of a compressed sensing reconstruction of the expected 2D spectra [13;21–25] –even if other methods [9–12;26] could also have been used. Compressed sensing relies on a number of basic assumptions. One is that the spectral information being sought is sparse; i.e., that most of the frequency coordinates within the targeted range do not contain any information. This premise may seldom be fulfilled for the 1D direct-domain NMR spectrum as a whole, but will often be valid when considering that our problem will only deal with rows of the full 2D interferogram, whereby the data to be reconstructed has already been separated into the numerous k/ν₁ making up the whole 2D distribution. Each of the 1D direct-domain spectra being sought can then, with high probability, be reconstructed by fitting its corresponding FID to a function S, fulfilling the minimization of the so-called ℓ₁ -norm

$$\underset{S}{\min }\parallel S{\parallel }_1\text{under}FID\left(\left\{t_p\right\}\right)=\underset{¯}{\underset{¯}{A}}\cdot S,$$ (3)

where ${\ell }_1(x)\equiv \parallel x{\parallel }_1\equiv {\displaystyle \sum _i\left|x_i\right|}$. The $\underset{¯}{\underset{¯}{{\rm A}}}$ operator in eq. (3) is a Fourier transformation of the spectrum S, which takes into account that its corresponding FID was sampled at a series of arbitrary direct-domain times {t_p}. Several methods have been proposed to solve this numerical fitting problem; this study implements one of the simplest forms based on an Iterative Soft Thresholding [13; 23]. In order to estimate the spectral distribution S this algorithm makes a series of iterations, preserving in each of these only those spectral components that are clearly distinguishable from potential numerical or thermal noises. The algorithm then adds these “peaks” to a reconstructed spectrum, and filters out the residual according to a thresholding operator defined by

$${\left({\delta }_{\lambda }\left(y\right)\right)}_q=e^{i\cdot \angle y_q}{\left(\left|y_q\right|-\lambda \right)}_{+}.$$ (4)

This operation returns zero if the magnitude of the residual’s spectral input for a particular y_q value is below a threshold λ, and reduces its amplitude otherwise while keeping the input’s original phase. The expected FID generated by the reconstructed spectrum is calculated and subtracted from the initial FID; the result is then used as input for a subsequent iteration. The pseudocode of the algorithm used in this study to recover in this manner a full 2D spatially encoded spectrum, is presented in Table 1.

Table 1. Pseudocode for the Iterative Soft Thresholding Processing of Ultrafast 2D NMR Data.

Input:
G(t)- Gradient waveform (N×1); FID (N×1); k/ν1-axis grid (n×1); ν2 – the direct domain frequency vector (1×m), ε , MaxIter – maximal number of iterations
Output:
S(k/ν1, ν2) – 2D spectrum matrix (n-by-m):
Preliminary calculations:
k(t) – wavenumber as a function of acquisition
t2(k) – n vectors containing the t2 points at each wavenumber k
${\underset{¯}{\underset{¯}{A}}}_k=\text{exp}\left(i\cdot 2\pi \cdot {\left(t_2\left(k\right)\right)}^T{v}_2\right)$ - n complex matrices
Initialization:
Residual vectors	r0(k)=FID(k,t2)
Correlation vectors	${\text{c}}_0\left(k\right)={\underset{¯}{\underset{¯}{A}}}_k^{†}{r}_0\left(k\right)$
Global threshold value	λ0=μ·max{|c0(k)|}
Solution	S0=0 of size n×m
while (p<MaxIter) and $\left({\Vert {\text{r}}_{\text{p}}\Vert }_2\ge \epsilon {\Vert \text{FID}\Vert }_2\right):$
Update solution	Sp+1(k) = Sp(k)+δλp (cp (k))
Calculate residual	$r_{p+1}\left(k\right)=FID\left(k\right)-\underset{¯}{\underset{¯}{A_k}}{S}_{p+1}\left(k\right)$
Calculate correlation	$c_{p+1}\left(k\right)=\underset{¯}{\underset{¯}{A_k^{†}}}{r}_{p+1}\left(k\right)$
Update threshold value	λp+1=μ·max{|cp+1(k)|}
end while
Post-processing: Inverse FT for S(k/ν1, ν2) along the direct domain; Exponential, Gaussian or                               Lorentzian Filtering; FT for S(k/ν1, ν2) along the direct domain.

Another requirement for achieving a successful compressed sensing reconstruction, is to secure a sufficient number of t₂ points for every k/ν₁ value. Indeed, a proper characterization of the ν₂ spectrum will only arise if this set of points is substantially larger than the number of inequivalent peaks arising along the direct-domain for every k/ν₁ coordinate. Noting that different k/ν₁ points cannot be measured simultaneously, that the same G_a physical gradient needs to be used to reach sequentially the different k/ν₁ coordinates, and that the strength of the G_a used is finite, it follows that an excessive focusing on one region of the k/ν₁-axis will degrade the performance of the sampling imparted at some other k/ν₁ region. This constraint, taken in unison with the presence of a T₂ relaxation that puts a limit to the maximal acquisition time that can be used, implies that in order to exploit this kind of processing strategy one should choose the continuous gradient waveform that will be used, with an average cycle period <T_a> that is longer than the normal T_a for any of the sampled k/ν₁ coordinates. Accordingly, this study relied on relatively small random factors for imparting these variations, which added or subtracted from the normal square-wave modulation period 2T_a. The chance to switch signs at any point along the gradient waveforms computed in this study, was assumed to be only in the range of 0.1%-0.2%. This lead to the kind of waveforms and k-t₂ space trajectories illustrated in Figure 1B. Naturally, the sparser the spectrum under investigation is, the more flexible one can be in this choice of parameters and the larger a randomness factor can be used. This in turn leads to spectra that can be retrieved using weaker gradients than in the conventional FT-based ultrafast 2D NMR approach, an advantage whose ensuing qualities are illustrated by the experimental results below.

Experimental

In order to demonstrate the potential advantages of compressed sensing reconstruction in ultrafast 2D NMR, a ≈2 mM sample of ¹⁵N-enriched Ubiquitin dissolved in a 90%/10% H₂O/D₂O buffer was analyzed. Constant-time spatially-encoded 2D HSQC NMR experiments were recorded on such sample [16;27], using a 14 T magnet and a Varian VNMRS^© spectrometer equipped with a triple channel probe possessing a single, linear z-gradient. Square-wave acquisition gradients were used for performing the normal ultrafast 2D NMR experiments and taken as reference; custom waveforms were generated and used for the iterative spectral reconstruction experiments. All of these waveforms, their ancillary RF pulses and the data processing algorithms, were written using customized Matlab programs that are available upon request.

Results

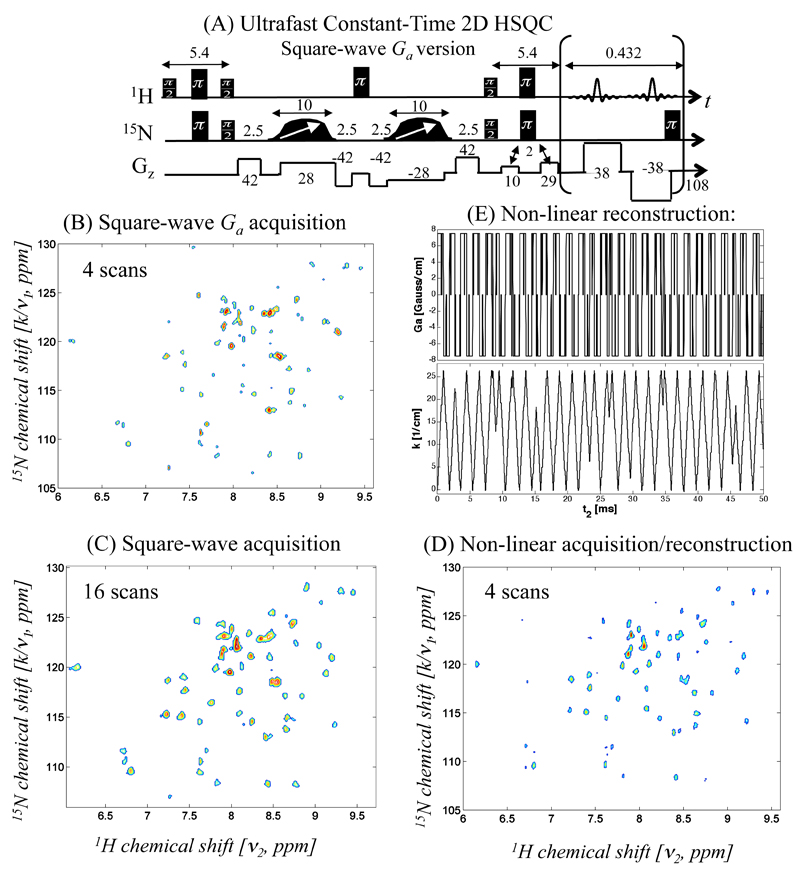
Two sets of compressed-sensing HSQC NMR experiments were carried out on the targeted 8.5 kDalton protein, aimed at demonstrating the sensitivity advantages that could result from exploiting this iterative processing. These sets differed in the duration of the maximum encoding period $t_1^{\mathit{max}}$ utilized: the longer this encoding is the higher the resulting resolution of the indirect spectral domain, but a larger G_a gradient is then needed (cf. eq. (1)), and thereby a lower SNR will result. Figure 2 illustrates how this penalty can be bypassed by the new methods hereby discussed, utilizing as test case a sequence with a relatively long encoding period (20 ms, Fig. 2A). Given this choice of $t_1^{\mathit{max}}$ and the spectral bandwidths to be targeted, a relatively large |G_a| ≈ 38 G/cm square-wave gradient had to be used for fulfilling the sampling criteria of normal ultrafast NMR acquisitions. Most peaks are still discernable in the 2D plot when four scans are used (Fig. 2B), but spectra only exhibits good SNR after averaging signals over 16 scans (Fig. 2C). By comparison, Fig. 2D displays the results obtained upon using only four scans, but with a pseudo-random alternating gradient. A significantly higher SNR is visible upon subjecting these data to a compressed-sensing spectral reconstruction, and comparing it against its conventional counterpart. This reflects the fact that, as it is no longer necessary to rely on a constrained T_a period to sample the full wavenumber range, a five-fold weaker |G_a| value can be used without compromising the indirect-domain’s SW₁ (see the corresponding waveforms used in this experiment in Fig. 2E). These remarkably smaller amplitudes enable one in turn to decrease the receiver’s bandwidth by a similar factor, and arrive at ca. x2 improvements in SNR.

Figure 2.

(A) Scheme of the constant-time, spatially-encoded HSQC sequence assayed. All timing and gradient strength values used are indicated in units of ms and G/cm, respectively; water suppression was implemented by strong purge gradient pulses; acquisition dwell times were set to 2 µs; and following each gradient cycle a hard 66 µs π pulse was used for ¹⁵N decoupling. In order to achieve a high resolution along the indirect domain the experiments used a relatively long 20 ms encoding period. (B) Purely-absorptive 2D spectrum obtained on an aqueous Ubiquitin solution using the conventional ±G_a square-wave acquisition gradient, after signal averaging four scans and displayed at a contour level of 50%. Only the positive gradient data set was processed by zero-filling, exponential apodization with a decay time of 30 ms along t₂, and fast FT. Given the strong acquisition gradients employed, the receiver’s bandwidth was correspondingly set to = 290 kHz (L =1.8 cm). (C) Idem as (B) but after signal averaging sixteen scans, and plotted at a 40% contour level. (D) Idem as (B), but upon subjecting the data to an iterative reconstruction. The gradient waveform used in this acquisition is shown in panel (E), which also shows the non-periodic trajectory resulting in the k/ν₁-t₂ plane. The actual G_a(t₂) waveform incorporated rise/fall times of 16 µs, and a zero-gradient period of 66 µs every 634 µs for performing the ¹⁵N-decoupling via hard π pulses. By lifting the stringent sampling demands of the fast FT, the overall |G_a| strength reduced to 7.5 G/cm. The ensuing reduction in receiver’s bandwidth enabled the reconstruction of a high-quality spectrum using only four scans: data in (D) are shown at a 25% contour level. The iterative reconstruction leading to this spectrum involved an iterative fit according to Table 1 using m=0.9, on a spectral region of ±1.2kHz with a resolution of 6 Hz. These fits were terminated after 250 iterations (increasing the number of iterations did not induce appreciable change in the 2D spectra) and following their implementation the resulting vectors were inversed-FT along the direct domain, weighted with a 30 ms exponential decay, and forward-FT to provide the final spectrum. On a dual core, 2.2GHz CPU, the overall time required to process such data set took under 60 seconds.

It follows from eq. (1) that sensitivity can also be improved by demanding a smaller resolution along the indirect-domain; i.e., by reducing the $t_1^{\mathit{max}}.$ The acquisition gradient can then be decreased, and good SNR obtained for the kind of targeted sample even if using a conventional square-wave acquisition gradient. These features can be appreciated by comparing the data in Fig. 2 with the panels Fig. 3A and Fig. 3B, which show how a reduction of $t_1^{\mathit{max}}$ to 12 ms allows one to reduce |G_a| to 23 G/cm, and thereby get good spectral SNR using the usual ultrafast acquisition mode in only two scans. Yet again, also under such conditions, advantage can be taken from the iterative reconstruction schemes that lead to an even better SNR (Fig. 3C). This once again reflects the nearly five-fold reduction in the |G_a| amplitude (Fig. 3D), that are made possible by combining the use of non-linear data sampling and iterative reconstructions.

Figure 3.

Analog results as shown in Figure 2, but for spatially encoded 2D HSQC acquisitions involving a lower ν₁-resolution, and hence a higher SNR. (A) Schematic pulse sequence used. (B) 2D purely absorptive spectrum obtained using a conventional G_a = ±23 G/cm square-wave modulation (same as in Fig. 2A but with a 40% smaller gradient). The reduced gradient allowed us to use a narrower receiver bandwidth, and hence acquire a spectrum in only two scans. Processing was as for Fig. 2B, and the spectrum is displayed at a 20% contour level. (C) Purely-absorptive HSQC spectrum obtained using a non-periodic sampling and a iterative reconstruction approach, enabling acquisitions with |G_a| ≤ 4.5 G/cm and leading to a x3 SNR improvement. These two-scan data are shown at a 20% contour level, and their processing involved similar characteristics as for Fig. 2D. (D) Non-periodic gradient waveform used in the latter acquisition, and corresponding k/ν₁-t₂ trajectory.

Discussion and Conclusions

The examples shown in Figs. 2 and 3 demonstrate that, even when dealing with moderately complex spectra, sensitivity advantages can be obtained from iterative reconstruction schemes. By allowing one to non-uniformly sample the direct domain, these enable the use of weaker gradient amplitudes than would be normal in ultrafast 2D NMR, bringing about ensuing reductions in noise. This does not mean, however, that one can always benefit from relying on iterative reconstruction algorithms in this kind of experiments. One issue limiting the applicability of these schemes concerns the sparsity criteria, which may not be applicable along every k/ν₁ coordinate of the sampled interferogram. Fulfilling this demand may require, for more complex biomolecules than Ubiquitin, the introduction of additional spectral dimensionalities. Another concern arises from the higher sensitivities that iterative reconstruction protocols like the one here assayed, may have to the level of noise characterizing the sampled data –particularly concerning their numerical stability. Indeed, whereas the fast FT is a stable procedure where output and input noise are always linearly dependent on one another, the faithfulness of non-linear numerical schemes will depend in a complex way on the level of the input noise affecting the fitted FID. Therefore, although iterative processing could in principle always allow one to reduce the acquisition gradient, the SNR will, in general, vary in a complex way with the receiver bandwidth and/or with the number of signal averages. This noise sensitivity was also found to be dependent on the validity of the sparseness assumption: the denser the spectrum to be reconstructed is, the more sensitive it becomes to the input noise. This in turn may end up resulting in counter-intuitive effects. For instance: whereas demanding low resolution along the indirect-domain allows one to weaken the G_a gradient, this loss in resolution will also broaden the ν₁ lines, and endow (on average) every k-coordinate with an effectively denser direct-domain spectrum. This in turn, may increase the numerical noise associated to the reconstruction –rather than decrease it, as could have been expected from purely bandwidth-related arguments. On the other hand, the new flexibility introduced by the iterative processing methods can always be exploited without compromises, to enable the scanning of a considerably larger k/ν₁-range, corresponding to an enlargement of the indirect-domain spectral width SW₁. Compressed sensing methods could also be combined with spatial encoding paradigms other than those involved in the usual ultrafast 2D NMR experiment, for instance with the above-mentioned techniques that optimize the positioning of the peaks in the indirect domain [18–20], and thereby extend even further the applicability of ultrafast spectroscopy to a wider range of systems and setups. Beyond these purely 2D spectroscopy applications, the modifications that were here described could also find uses in other kinds of mixed spectroscopic imaging applications. These subjects will be further developed in upcoming publications.