Abstract
Recent studies have described some of the new opportunities opened within the context of ultrafast 2D imaging, by the advent of spatiotemporal encoding methods. This paper explores the potential of integrating these non-Fourier, single scan 2D MRI principles, with multi-slice and with phase encoding schemes acting along a third dimension. In unison, these combinations enable the acquisition of complete three-dimensional images from volumes-of-interest within a one-second timescale. A number of alternatives are hereby explored for carrying out these very rapid 3D acquisitions, including: (i) the use of two-dimensional slice-selective, spatiotemporal encoding excitation radiofrequency pulses, (ii) driven-equilibrium slice selective schemes, and (iii) phase encoded volumetric approaches. Whenever tested under in vivo conditions, the ‘hybrid’ schemes combining spatiotemporal encoding with k-encoding imaging principles, proved superior to traditional schemes based on EPI. The resulting images were found less affected by field inhomogeneities and by other potential offset-derived distortions, owing to a combination of factors whose origin is discussed. Further features, extensions and applications of these principles are also addressed.
Keywords: 3D fast MRI, spatiotemporal encoding, single scan 2D imaging, super-resolved MRI, Echo Planar Imaging
Introduction
One of the major driving forces in contemporary MRI rests on the development of new schemes for retrieving the best possible images, in the shortest possible acquisition times. Two general approaches underlie the majority of fast two-dimensional (2D) imaging sequences: one is based on executing multiple scans while waiting the shortest possible repetition times (TR) (1–3); the other relies on compressing all the information gathering process into a single continuous scan. The first of these approaches typically probes the multidimensional k-space domain on a “line-by-line” basis, and can produce 2D NMR images in a seconds timescale. Foremost among the second kind of fast-sampling approaches stands Echo Planar Imaging (EPI) (4) and its many different variants (5,6), which by scanning the full 2D k-space in a single transient can reduce the overall data acquisition down to a few tens of milliseconds. Being limited by the amount of information that can be acquired in a single scan, these “ultrafast” methods usually involve tradeoffs between spatial resolution and imaging speed. These tradeoffs may also make the ensuing acquisitions susceptible to a variety of inhomogeneity-derived artifacts. EPI-based methods are therefore usually employed in cases that require high temporal resolution or are inherently long –such as fMRI (7) or diffusion tensor imaging (8).
In a series of recent publications, others and we have explored an alternative approach for acquiring single-scan NMR images based on the spatiotemporal encoding (SPEN) of the magnetic resonance spin interactions. Originally developed as a method for acquiring multidimensional NMR spectra within a single transient (9,10), this general spectroscopic principle endows 2D single-scan MRI with a number of distinct features (11–15). SPEN, which is an approach related to quadratic phase encoding methods first proposed by Kunz and analyzed and exploited in further detail by Pipe (16–18), has as salient property its confinement of the observable signals to contributions arising from limited spatial regions. Its time-domain response is in fact designed so as to be proportional to the spin density’s spatial profile, S(t) ∝ ρ(r), and an image can be produced simply by taking the magnitude of the time-domain signal |S(t)| –without the need for a Fourier transformation. This special type of encoding is imparted during the excitation stage, and thus stands in contrast to a majority of imaging sequences where it is the post-excitation process that actually encodes –via its k-space sampling– the spins’ locations. A main benefit from SPEN vis-à-vis EPI, is a significantly higher robustness to field inhomogeneities and to the presence of multiple chemical shifts (13–15). This reflects the non-Fourier nature of the method, as well as a higher flexibility arising upon setting the gradients amplitudes during the excitation and acquisition process, which allows one to effectively tune these gradients so as to overcome offset-related effects (14). Further robustness arises from the SPEN’s use of chirped radiofrequency (RF) pulses, which sweep over the sample volume in a sequential fashion. By virtue of these, a single spin-echo π pulse applied midpoint between suitably timed excitation and acquisition events, can refocus inhomogeneities at each and every instant of the acquisition process –rather than at a single τ instant as is the case for the classical π/2–τ–π spin echo. The ensuing self-refocusing characteristics can produce images which are fully devoid from T2*-related dephasings (14,15). Initial SPEN implementations, however, materialized all these advantages at the cost of a decreased efficiency in terms of the use of the acquisition time variable; resulting in either decreased intrinsic sensitivities, or increased specific absorption rate penalties. Recent developments based on the use of super-resolution (SR) reconstruction algorithms (19–21) resolved many of these deficiencies, offering a performance that in terms of image faithfulness and correction of inhomogeneity-related pixel miss-registrations, often exceeds that arising from k-based encoding methods (22,23).
Notwithstanding these advantages, a major challenge still appears to affect spatiotemporal encoding vis-à-vis traditional k-domain ultrafast MRI counterparts. This arises from SPEN’s reliance on the use of frequency-swept excitation pulses acting in conjunction with uniaxial gradients, a strategy that is ill-posed to perform slice-selective excitations. This in turn appears to deprive these novel imaging sequences from the possibility of efficiently executing rapid volumetric acquisitions, using for example multi-slice excitations of the kind that underlie a majority of fast 3D MRI techniques. To appreciate this limitation it is worth recalling that, while single-scan Echo-Volume-Imaging experiments of complete 3D objects have been demonstrated (24–27), the main contemporary routes to the very fast scanning of 3D Volumes of Interest (VOIs) involves collecting arrays of single-transient 2D imaging scans. Two major 3D-oriented strategies can be identified with this principle. The first of these approaches acquires a series of 2D EPI images employing slice-selective excitations along a third dimension. Given the different spins addressed by these selective excitation processes, a whole array can be collected using minimal TR delays. In a second approach a series of 2D EPI matrices are collected, this time as a function of an independent phase-encoding variable gradient acting along the third dimension. While requiring longer inter-scan delays due to their bulk excitation of all spins in the VOI during each scan, this latter approach also shows attractive features including the absence of “slice-gaps” and an increase in the signal-to-noise ratio (SNR) due to the additional Fourier processing applied along the third axis.
This work focuses on the issue of fast 3D MRI acquisitions from a SPEN perspective, addressing in particular the issue of how to harmonize an object’s swept RF excitation with the 3D image-retrieval process. Attention is centered on three new pulse sequences, which extend the original 2D single-scan SPEN MRI approach to three dimensions. The first two sequences discussed are based on multi-slice excitation strategies, tailored to enable the rapid, repeated acquisition of series of 2D slice-specific images. The third sequence follows an approach based on a full VOI excitation, combined with phase-encoding along the third dimension. All sequences that are here described rely on the SR-enhanced, hybrid 2D SPEN implementation described in Ref. (14), in which the high-bandwidth dimension is k-encoded, whereas along the second (low-bandwidth) dimension a spatiotemporal encoding replaces the use of a blipped k-space phase-encoding. As will be shown, multi-slice 3D MRI sequences that derive from these principles can yield superior quality images than their purely k-based encoding counterparts. Different challenges were found in the phase encoded 3D SPEN MRI realizations, owing largely to the need to use longer inter-scan delays given these schemes’ excitation of the entire VOI during each scan. In spite of these challenges, it was found that also in this case the 3D SPEN sequence retained the advantages described in Refs. (14,15,23). In fact some versions of these 3D phase-encoded SPEN experiments, constituted the best of all assayed alternatives for extending fast imaging into volumetric acquisitions.
Materials and Methods
All experiments described in this work were performed at 7 T on a 300/89 Varian VNMRS vertical imaging system (Varian Associates, Inc., Palo Alto, CA) using a quadrature-coil probe with a FOV of 30x30x46 mm3. The examined samples included three targets: a plastic cross-shaped phantom filled with tap water, a post mortem mouse fixated in Formaldehyde, and a mouse scanned under in vivo conditions. Mouse experiments and handling were done in accordance with protocols approved by the Weizmann Institute’s Animal Care and Use Committee. All sequences were simulated on MATLAB® (The MathWorks, Inc., Natick, MA) before being implemented on the Varian system. RF pulses were also designed in MATLAB using the SLR algorithm (28), and executed on the spectrometer by clocking out the amplitude and phase waveform components at an appropriate rate (usually given by 2 µs dwells). A similar approach was taken with the ramped gradient waveforms acting over the course of the excitation, encoding and acquisition processes. Post-experimental data processing was implemented using custom-written MATLAB software packages, incorporating Fourier transformation for the k-encoded dimensions, and a super-resolution reconstruction specially designed for processing spatiotemporally encoded data. A detailed description of this SR reconstruction algorithm is given in Ref. (23) and is therefore omitted from this report; suffice it to say that in order to apply this processing, a minor manipulation consisting of suitably pre-aligning the data originating from positive and negative readout echoes, is required. This alignment procedure is analogous, yet less demanding, to the one that we used upon processing the EPI based sequences for decreasing the half-Nyquist ghost patterns associated with this technique. Further details on the rationale of the various sequences assayed and the specific parameters used in each case are given below; all the imaging sequences and post-processing codes used in this study are available upon request.
To evaluate the performance of the new 3D approaches hereby discussed, a matrix-type series of experiments was executed: for each of the three different samples that were analyzed, SPEN-based strategies were compared with similarly structured and timed EPI-based experiments, as well as with multiscan FLASH images taken as reference. A summary of the distinctive features for the various sequences tested, is presented in Table 1.
Table 1.
Summary of the pulse sequences assayed in this work, indicating their respective modes of 3D encoding and the axes notations employed in Figs. 1 and 2
| MULTI-SLICE 3D MRI | PHASE-ENCODED 3D MRI | |||||
|---|---|---|---|---|---|---|
| Encoding direction | Fig 1a* | Fig 1b* | Fig 1c† | Fig 2a* | Fig 2b† | |
| x-axis | Freq. enc (RO) | Freq. enc (RO) | Freq. enc (RO) | Freq. enc (RO) | Freq. enc (RO) | |
| y-axis | SPEN | SPEN | Phase enc. (PE) | SPEN | Phase enc. (PE) | |
| z-axis | Slice-select. (SS) | Slice-select. (SS) | Slice-select. (SS) | Phase enc. (PE) | Phase enc. (PE) | |
New sequences introduced in this report based on SPEN.
Standard sequences based on k-space encoding.
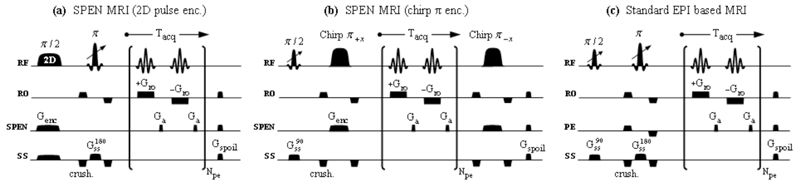
The first kind of 3D-oriented experiments assayed, relied on the multi-slice pulse sequences in Figure 1. These in turn compared two SPEN-based variants (Figs. 1a-b), against a sequence based on spin-echo EPI (Fig. 1c). This latter protocol lends itself to an immediate, fast volumetric scanning, simply by arraying the frequency offsets in its slice-selective excitation and spin-echoing pulses. By contrast, the variants in Figs. 1a and 1b need to address the challenges arising upon relying on SPEN-based sequences, which as pointed out replace the usual slice selective MRI excitation with a volumetric frequency-swept manipulation. This initial frequency-swept π/2 pulse will excite the entire sample; endowing spins with the quadratic phase profile being sought (along an axis, which for consistency with Refs. (14,23) we denote henceforth as the y-axis), but preventing a rapid repetition of this scheme for different slices along a third dimension. Figure 1a shows a potential solution to this problem, with the introduction of what could arguably be considered as the simplest adaptation of the slice-selective concept to a 3D SPEN-based acquisition. The novel component involves replacing the original 1D frequency-chirped pulse, by a 2D RF pulse (29) that simultaneously performs two tasks: one is the slice-selective excitation of the spins along the sample’s z-axis; the other is endowing these excited spins with a quadratic phase along the orthogonal y direction. This is followed by a slice-specific spin-echo pulse, a hybrid 2D SPEN acquisition block that collects the imaging data, and a spoiler gradient dephasing any residual transverse magnetization that might otherwise interfere with the acquisition of 2D images from the remaining slices. From a pulse engineering standpoint, the 2D RF pulse involved in this sequence has to fulfill three independent constraints; including a slab excitation with pre-defined bounds in the yz plane, and the simultaneous imparting of a tailored 1D quadratic phase profile along the sample’s y-axis. Although pulses of such kind are to our knowledge not common, the mathematics that defines them is relatively straightforward –at least in the small excitation angle limit. In fact, analogs of such tailored spatial and phase profiles imparted onto two-dimensional excitation pulses, have been recently discussed within a variety of contexts related to the acquisition of single-scan 2D NMR spectra (30,31). In parallel with what was done in those spectral/spatial instances, one can pose the demands expected from the new pulse arising in Figure 1a in terms of the required post-excitation transverse magnetization pattern
| (1) |
where M0 denotes the relaxation-weighted spin density of the object, ϕexc(y) is the usual quadratic phase pattern imparted by SPEN (14):
| (2) |
and P(y, z − z0) denotes the desired slice-selective excitation profile, centered at a chosen z0 and exciting along predefined y bounds –but with no dependence along the x axis. Within the small tilt angle approximation (32,33) the theory of shaping a B1(t) RF capable of delivering the 2D magnetization distribution of Eq. (1) is known (29,34): it needs to act in conjunction with two suitably chosen Gy(t), Gz(t) gradients, and its waveform is to be tailored to fulfill the condition
| (3) |
where is a suitably designed excitation trajectory. A more comprehensive description on how these profiles were calculated, as well as numerical algorithms for the computation of the resulting 2D RF pulses, is available upon request.
Figure 1.
Three-dimensional multi-slice imaging sequences assayed in this work, based on acquiring series of single-scan 2D images for different z-coordinate values. (a) SPEN-based sequence employing a two-dimensional excitation RF pulse acting to spatiotemporally-encode one of the dimensions, and a slice-selective π pulse with variable offset (indicated by the arrow) to select the orthogonal one. (b) Alternative encoding approach employing a standard 1D π/2 slice-selective excitation and a non-specific spatiotemporal encoding π-pulse (chirped adiabatic passage). Full gradient and RF rewindings are applied following each acquisition block, allowing the use of short inter-scan recycle delays and minimizing the residual T1 weighting of subsequently acquired slices. (c) EPI-based sequence employing slice-selective excitations and spin-echo pulses, followed by a standard k-space 2D encoding block. Spoiler gradients were added to all three sequences in order to dephase any residual transverse magnetizations that may have been left between the acquisitions of consecutive slices. In all cases the 2D data matrices were collected in a single scan per slice-encoding increment. Axes definitions are as summarized in Table 1; additional abbreviations used include exc: excitation, crush: crusher gradients, SPEN: spatiotemporal encoding channel, SS/ss: slice-selective channel, RO/ro: readout channel, PE/pe: phase-encoded channel, acq: acquisition, Npe: number of phase-/SPEN-encoded lines.
In addition to this variant based on the use of quadratic-phase 2D RF pulses, a more conventional approach based on the use of 1D RF pulses acting along orthogonal directions was also tested (Fig. 1b). SPEN was implemented in this case by replacing the slice-selective spin-echo π-pulse with a chirped adiabatic-like counterpart (35), preceded in turn by a variable-offset π/2-pulse like the one used in slice-selective EPI. When followed by a standard 2D hybrid SPEN acquisition block, only the slice that was addressed by the initial π/2 excitation pulse contributes to the final 2D image. As a result of involving a non-selective, chirped π pulse, however, such sequence would not yet be suitable for fast multi-sliced repetitions. Indeed, its adiabatic sweep would also affect (invert) the magnetizations of all the remaining spins in the sample; an undesired byproduct that if accumulated, could lead to a T1 weighting of all subsequently acquired slices. To minimize this feature an additional chirped RF π-pulse plus a pair of gradient rewinding blocks were introduced following the data sampling, which in just a matter of a few milliseconds reversed all the inverted magnetizations back to their equilibrium Boltzmann state. At the conclusion of each transient the state of the spin ensemble was thus akin to that resulting from the application of the two-dimensional RF pulses; with the difference that only two short, robust pulses were needed to achieve this state –rather than the use of longer and in the end more offset-vulnerable (y,z)-tailored 2D pulse.
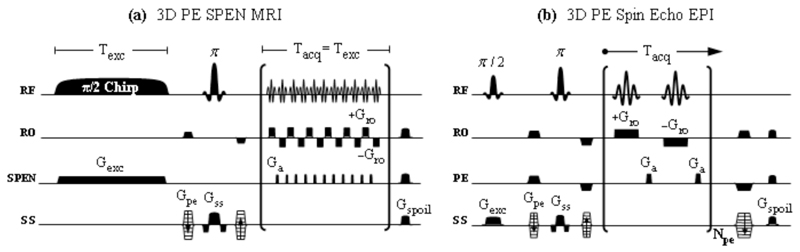
A second set of comparisons between SPEN and EPI spin-echo sequences is schematized in Figure 2. These 3D alternatives differ from the multi-slice counterparts just discussed in that they rely on broadband volumetric excitations, where the single-transient scanning of entire 2D planes is applied in combination with a phase-encoding of the latter’s information along a third axis. From a fast-repetition perspective these two sequences will perform at lower frame rates than their multi-slice counterparts, owing to their repeated need to excite all spins in the sample’s VOI. This drawback can be ameliorated by reducing the effective pulse angle down to the Ernst excitation (36); in exchange for the resulting decrease in the contributing magnetizations stands the SNR enhancement arising from the additional Fourier Transform along the phase-encoded z-axis (27). Further comparisons of these phase-encoded sequences and of their multi-slice counterparts are discussed below.
Figure 2.
Three-dimensional imaging sequences based on acquiring a series of 2D single-scan images which are phase-encoded with respect to a third, slab-selective (SS) dimension. For both sequences in (a) and (b), phase-encoding was implemented by adding a pair of Gpe gradients, symmetrically located around the spin-echo π-pulse. (a) Sequence developed on the basis of a self-refocused 2D SPEN experiment (14) that echoes all T2* relaxation effects due to the symmetric nature of the excitation and acquisition events (total Tacq over the Npe loops = Texc). (b) Standard slab-selective phase-encoded EPI based sequence incorporating rewinding gradients after each acquisition block for the purpose of minimizing the required inter-scan recycle delays. In both cases spoiler gradients were added to dephase any residual transverse magnetization that may have been left in-between acquisitions of consecutive phase encodings.
Results
Fast 3D MRI Using Arrayed Slice-Selective SPEN Acquisitions
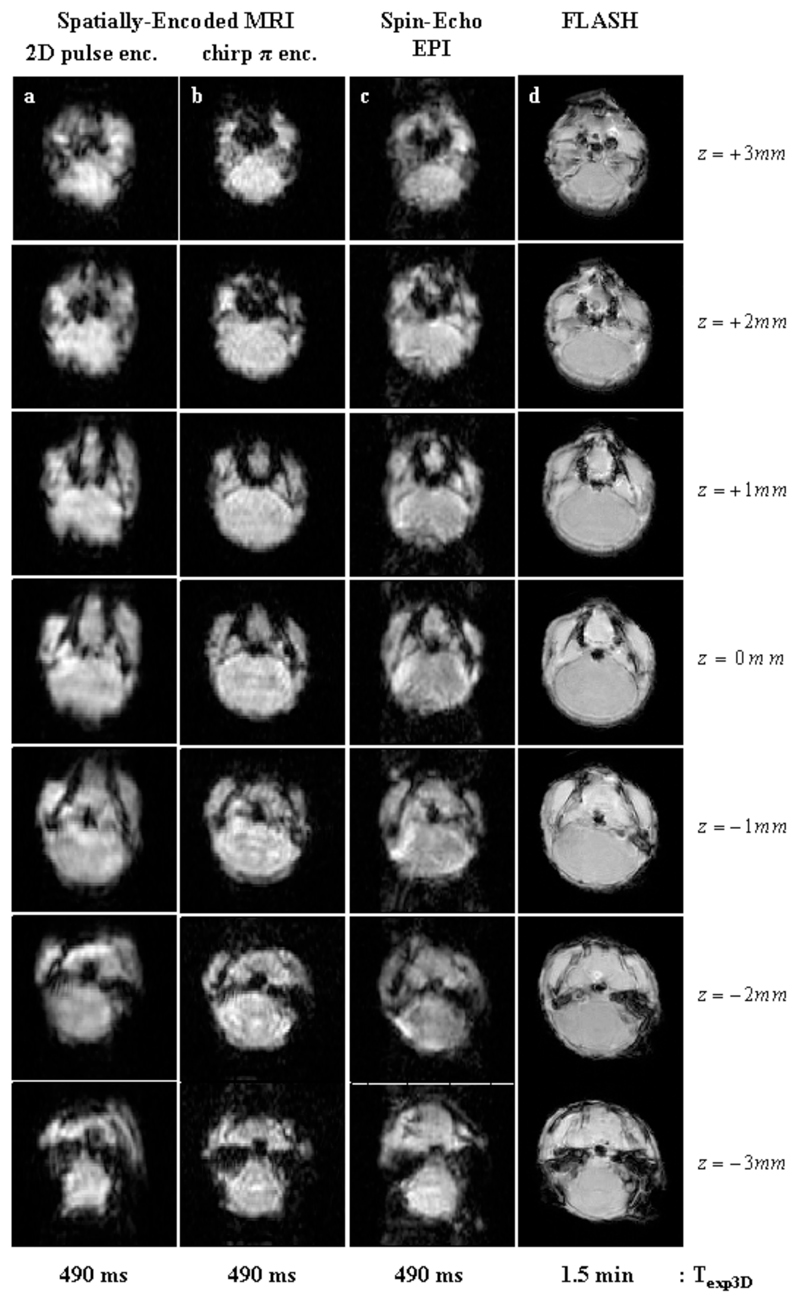
Figures 3–5 summarize the main features that the new sequences introduced in Figure 1 produced for three different kinds of samples. Figure 3 focuses on a water cylinder containing a solid cross-shaped phantom in its centre; multi-slice pulse schemes were used on this system to rapidly scan five 1-mm slices along the z-axis using a zero inter-slice gap. From the data shown in columns 3a-3c, one can appreciate that all ultrafast pulse sequences are capable of reconstructing satisfactorily, and within similar acquisition times, the basic shape of this phantom over its entire VOI. Spatial artifacts were noted upon using 2D pulses (Fig. 3a); small artifacts also characterize the EPI-based multi-slice sets (Fig. 3c), mainly involving characteristic offset-derived distortions and spurious half-FOV ghosting artifacts along the phase-encoded axis. The most reliable 3D reconstruction –i.e., the one most akin to the FLASH image set acquired over a significantly longer time– stems from the slices acquired using the rewinder-based sequence introduced in Figure 1b. Comparing this set with the reference FLASH set (Figures 3b vs. 3d) reveals minimal spatial distortions or intensity heterogeneities. These images are also free from ghosting artifacts, leading to a faithful reconstruction of the actual phantom. A similar conclusion is revealed upon assessing the post mortem results afforded by all sequences (Figure 4), which this time involved the slightly less favorable homogeneity settings arising from a mouse fixated in Formladehyde, and focused on a series of seven adjacent 1 mm slices inside the brain. As before, the most blurred 3D image arises upon using the 2D RF excitation pulse (Fig. 4a); the remaining ultrafast acquisition sets (Figs. 4b, 4c) provide images of similar quality, even if slight ghosting artifacts arise upon using spin-echo EPI. For both examples, we ascribe the relatively poorer performances observed upon relying on the 2D RF excitation, to the challenges that confront these elegant but relatively long pulses in the present context. These demands arise from the simultaneous need to impart sharp quadratic phase profiles along the y-axis, together with a narrow excitation bandwidth along the z-axis for the slice selection. This leads to restrictions that can only be fully met by the use of strong gradients or of relatively long RF pulses, and which in turn result in relatively high sensitivities to either B1 or B0 inhomogeneities. Such problems appear accentuated as the sample’s field homogeneity degrades; in fact, when implemented on the most challenging of all the experimental setups assayed –involving in vivo investigations on mice brains, Figure 5– this multi-slice approach did not yield images of sufficient quality. We ascribe the ultimate factor conspiring in this case against the 2D RF approach, to the relatively poorer shimming and eddy current conditions associated with in vivo experiments in our vertical-bore scanner.
Figure 3.
Multi-slice 2D images arising from a cross-shaped phantom, using the sequences introduced in Figure 1. Five 1 mm slices were excited using a zero inter-slice gap over a 3D FOV of 25x25x5 mm3. Texp3D: total acquisition time for each of the indicated 3D experiments. Left to right columns: (a) SPEN MRI using a 2D slice-selective chirped excitation pulse (sequence in Fig. 1a) and the following parameters: TR=70 ms; TE=[7…28] ms (depending on the precise location along the SPEN axis; idem for Figs. 4, 5); matrix size=115×60×5; pixel size=0.24×0.50×1 mm3. (b) Idem but using a chirped π encoding pulse (sequence in Fig. 1b) using the following parameters: TR=70 ms; TE=[7…28] ms; matrix size=70×70×5; pixel size=0.40×0.40×1 mm3. (c) Spin-Echo EPI (sequence in Fig. 1c) using the following parameters: TR=70 ms; TE=18 ms; matrix size=115×45×5; pixel size=0.40×0.64×1 mm3. (d) Reference FLASH images (pixel size=0.20×0.20×1 mm3). Texp3D: total acquisition time for the 3D experiment.
Figure 5.
Multi-slice 2D images recorded in-vivo on a mouse brain using similar sequences as in Figures 4b-4d. Five 1 mm slices were acquired using a zero inter-slice gap over 3D FOV of 16x16x5 mm3. Left to right columns: (a) SPEN MRI using a chirped encoding π-pulse (sequence in Fig. 1b) and the following parameters: TR=130 ms; TE=[7…28] ms; matrix size=50×50×5; pixel size=0.40×0.30×1 mm3. (b) Spin-Echo EPI (sequence in Fig. 1c) with the following parameters: TR=130 ms; TE=18 ms; matrix size=50×50×5; pixel size= 0.40×0.30×1 mm3. (c) Reference FLASH images (pixel size= 0.20×0.20×1 mm3).
Figure 4.
Multi-slice 2D images produced by the sequences in Figure 1, recorded post-mortem on a fixated mouse. Seven 1 mm slices were acquired on the animal’s brain using a zero inter-slice gap over 3D FOVs of 16x16x7 mm3. Left to right columns: (a) SPEN MRI using a 2D slice-selective chirped excitation pulse (sequence in Fig. 1a) using the following parameters: TR=70 ms; TE=[7…22] ms; matrix size=50×50×7; pixel size=0.40×0.40×1 mm3. (b) Idem but using a chirped π-encoding pulse (sequence in Fig. 1b) and the following parameters: TR=70 ms; TE=[7…22] ms; matrix size=50×50×7; pixel size=0.40×0.40×1 mm3. (c) Spin-Echo EPI (sequence in Fig. 1c) using the following parameters: TR=70 ms; TE=15 ms; matrix size=50×50×7; pixel size=0.40×0.40×1 mm3. (d) Reference FLASH images (pixel size = 0.20×0.20×1 mm3).
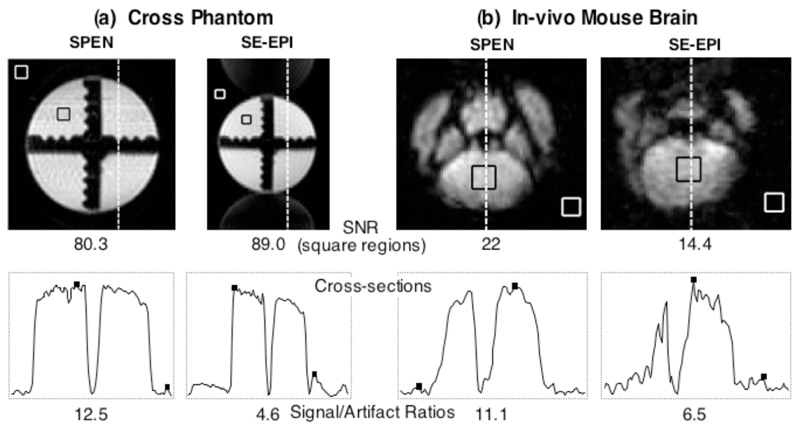
In view of the superior performance obtained from the rewound-based multi-slice SPEN sequence introduced in Fig. 1c, it is pertinent to conclude this discussion by highlighting two features of this sequence. One of these concerns issues of SNR and of image-to-artifact ratios, which characterize this approach vis-à-vis its k-encoded counterparts. In its original, magnitude-mode implementation (11), SPEN MRI was challenged by its non-Fourier character, and by an ensuing inability to bring the multiplexing advantage to bear. This was subsequently solved for both 1D and 2D experiments, by the use of matched filtration and of hybrid SPEN/k-space encoding sequences acting in conjunction with SR algorithms. This point is examined for the present 3D study in further detail in Figure 6, with representative cross-sectional comparisons taken from the water cross-phantom and from the in vivo mouse data sets. The first of these data shows that EPI-based methods are indeed capable of yielding, under the nearly optimal homogeneity conditions arising for the water phantom, a time-domain signal that at its maximum value is ca. 3 times stronger than its SPEN counterpart. Upon applying the FT and SR processing, however, different scenarios are revealed in the corresponding image spaces: maximal pixel intensities that are nearly identical for both sets of phantoms arise, but both SNR as well as signal-to-artifact ratios favor by over 300% the SPEN-derived cross-sections over their EPI counterparts –free as they are of the half-Nyquist artifacts that arise even under these optimal conditions (Fig. 6a). An even more conclusive evidence of this behavior is furnished by the in vivo mouse brain results introduced in Fig. 5, which unambiguously reveal both higher signal intensities and more favorable signal-to-artifact ratios for the SPEN experiments, thanks to this approach’s ability to compensate field inhomogeneity distortions under these challenging conditions (Fig. 6b).
Figure 6.
Comparison between images and corresponding cross-sections arising from the sequences introduced in the multi-slice 2D single-scan sequences of Figs. 1b, 1c, implemented on phantom (a) and in vivo (b) samples. The 1D cross-sections shown at the bottom were extracted at the positions indicated by the dashed lines, and run in both cases along the low-bandwidth PE/SPEN axes. Indicated in the images are the square regions chosen as representative signal and the thermal noise regions for the SNR calculations reported underneath each 2D plot. The square dots in the cross-sections indicate the signal and the characteristic artifact intensities used to compute the Signal/Artifact ratios reported on the bottom.
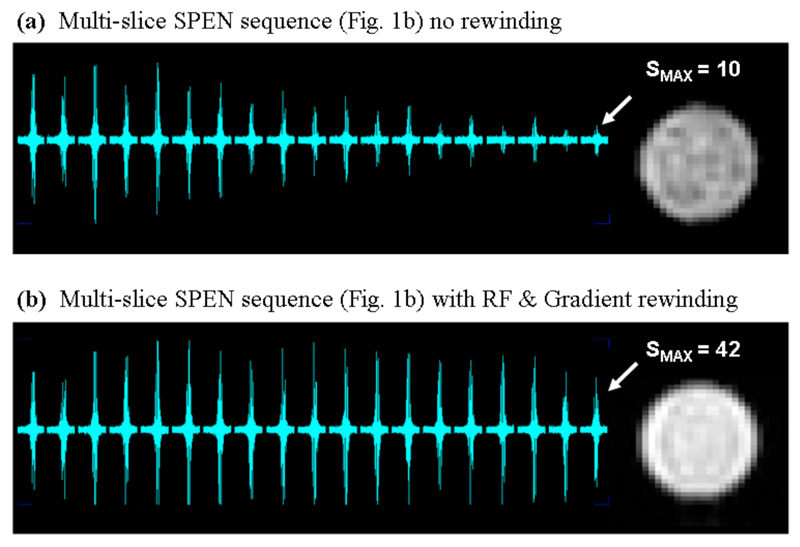
A second, independent feature worth highlighting, concerns the advantages arising from the rewinding procedure implemented at the conclusion of the SPEN pulse sequence (right-hand modules in Figure 1b). When this is not the case, and unused spin magnetizations are not restored back to their longitudinal equilibrium states in-between scans, a progressive saturation rapidly sets in. Figure 7 illustrates this with a comparison of results arising from 19 adjacent slices excited in the absence and in the presence of this driven equilibrium procedure.
Figure 7.
Ability of the rewinding procedure included in the sequence of Fig. 1b to enhance the longitudinal magnetization’s recovery, illustrated with the acquisition of 19 consecutive single-scan images. The targeted slices were adjacent to each other, spread over 19 mm, and collected with a 200 ms TR. The final image intensity for the non-rewound set (a) is ca. 75% smaller than its rewound counterpart (b).
Fast 3D MRI Using Arrayed 2D SPEN Acquisitions and Phase-Encoding Along a Third Dimension
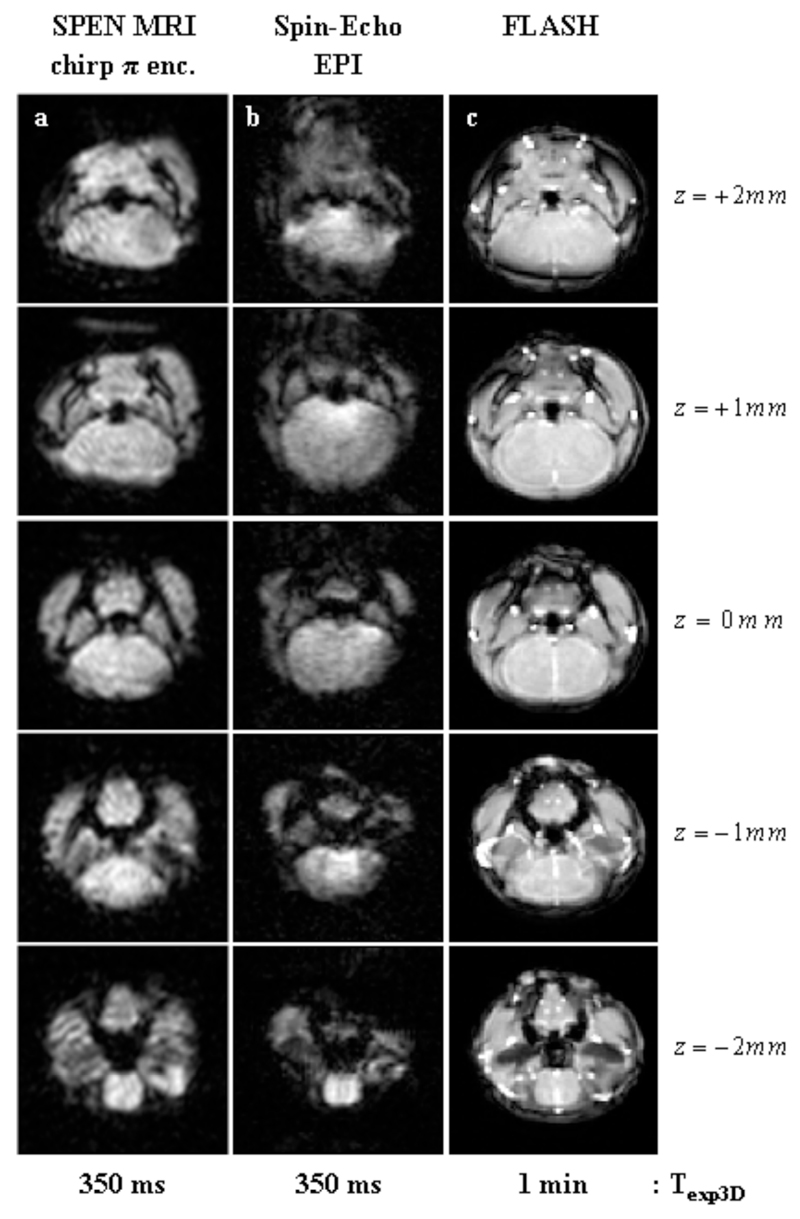
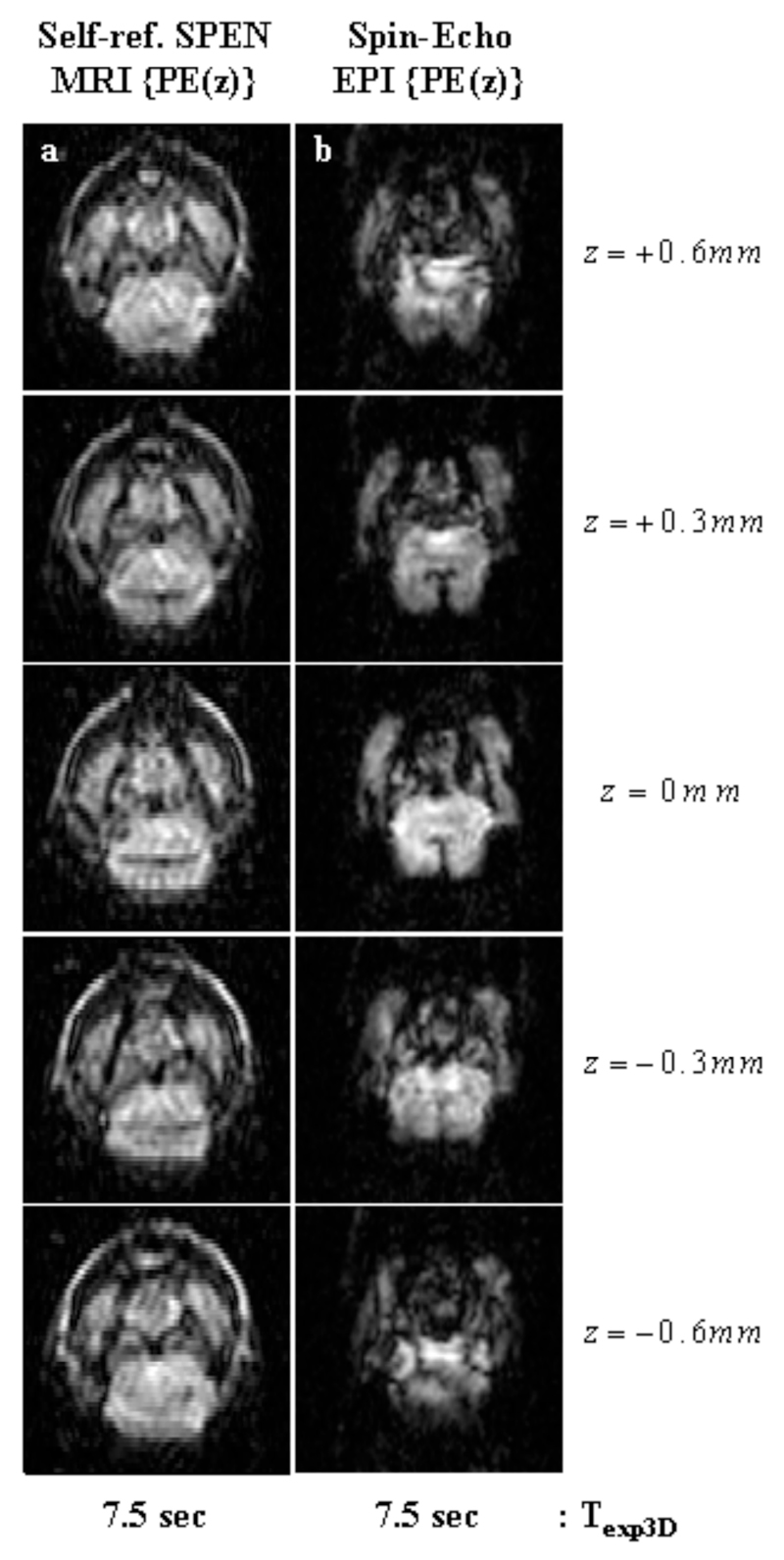
The sequences introduced in Figure 1 deliver volumetric coverage, thanks to their combined use of multi-slice selective excitations along one axis followed by ultrafast read-outs of the perpendicular in-plane information. A different approach to rapid 3D MRI is furnished by the sequences in Figure 2, which deliver volumetric images based on exciting the full VOI, and then phase-encoding 2D single-scan signal matrices arising from either SPEN or EPI using a stepped Gz gradient. Figure 8 illustrates the image qualities that these phase-encoded experiments can yield, with a series of images arising from an in vivo mouse brain. Noticeable in both the SPEN- and the EPI-derived images shown in this Figure, are the higher spatial resolutions that can be attained by phase-encoding the third dimension when compared with what arose from the slice-selective approaches (≈0.3 vs 1 mm respectively). Furthermore, upon comparing the 3D image structures afforded by the two alternatives, a higher quality could once again be appreciated for SPEN- over EPI-based counterpart experiments. As in the previously discussed cases, relatively minor differences were seen for those brain regions characterized by homogeneous B0 distributions; i.e., for VOIs at the center of the xy plane and in the neighborhood of the central z0 ≈ 0 position. By contrast, marked differences in pixel resolution, overall SNR and image-to-artifact ratios, became noticeable for regions suffering from heterogeneous field distributions –particularly for tissues located in the periphery of the xy plane, or for z-slices located beyond ±0.5 mm values. Once again this can be ascribed to SPEN’s non-reliance on Fourier processing along the low-bandwidth dimension; in this particular case it can also be traced to the robust refocusing that the sequence introduced in Fig. 2a can achieve for inhomogeneities over the entire 3D VOI. Indeed, this sequence follows self-refocusing principles whereby each location along the SPEN axis is separately excited, spin-echoed and detected; this provides a full compensation of T2* effects throughout each instant in a scan’s acquisition, and can refocus all internally-derived frequency shifts for each and every readout event throughout the decoding process (14). When combined with the addition of a phase encoding process along the third axis and with the reliable pixel registration provided by the SR reconstruction (23), these advantages transform the approach summarized in Figure 2a into the optimal alternative of all the methods that we tested for the fast recording of 3D MRI data.
Figure 8.
In vivo 3D images of a mouse brain, using the z-axis phase-encoding sequences in Fig. 2 and leading to five slices spread over FOVs of 16x16x1.5 mm3. (a) Self-refocused phase-encoded SPEN MRI with the following parameters: TR=1.5 sec; TE=[7…25] ms; matrix size=50×45×5; pixel size = 0.40×0.45×0.30 mm3. (b) Phase-Encoded Spin-Echo EPI with the following parameters: TR=1.5 sec; TE=16; matrix size=50×45×5; pixel size=0.40×0.45×0.30 mm3.
Discussion and Conclusions
The goal of the present report was to examine the feasibility and competitiveness of SPEN sequences developed for the ultrafast scanning of two-dimensional objects (14,23), when adapted to fast 3D imaging. Driving this search were the challenges put forward by spatiotemporal encoding, which uses frequency-swept rather then slice-selective RF pulses, and is therefore at a handicap against multi-slice fast imaging. A solution to this problem was sought in the use of 2D RF pulses, a suggestion that restored specificity along the third dimension and could easily be incorporated into a conceptual 3D scheme. This approach, however, required longer and more complex RF and gradient waveforms; this robbed the resulting solution from performance –particularly in the challenging case of in vivo imaging, where 2D SPEN actually works best. In terms of potentially improving these results, it is important to note that most of the 2D pulse’s overhead is placed by our demand to achieve a strong, smooth quadratic phase profile along the spatially-encoded y dimension. This demand could be alleviated by trading-off selectivity along the z dimension, lengthening the pulse’s duration, or increasing the spatial-encoding Gy gradient strength. All these options, however, should be considered with care, as a lengthened excitation might result in stronger field inhomogeneity artifacts or result in unacceptable power depositions.
In view of these limitations, the multi-slice alternative presented in Figure 1b was explored. In this case the targeted object was first “sliced” using a selective pulse, while a subsequent chirped RF π-pulse was used to impart both the spatiotemporal encoding of the excited slice and to deliver a spin-echo. A detrimental side effect of this scheme, involving the adiabatic inversion by the swept pulse of all the remaining magnetization in the sample, was resolved by introducing an additional rewinding block bringing all inverted spins back to their original equilibrium following the data acquisition. Experiments carried out using this approach showed a very stable performance over a range of samples and field distributions, allowing full VOI coverage, and minimal TRs limited solely by the gradient’s duty cycle. The experimental results, particularly those shown in Figures 5–7, demonstrate the absence of spurious T1 weighting distortions, as well as SPEN’s ability to deliver faithful images over extended VOIs. Notwithstanding the capabilities offered by these multi-slice principles, the ensuing spatial resolution along the third dimension was still bound by the minimal thickness that can be uniformly excited using selective pulses. A different regime could be accessed by the alternatives depicted in Figure 2, whereby the entire 3D VOI is excited during each scan, and z spatial resolution is determined by a number of executed phase-encoding steps. This approach could deliver z-resolutions that were up to an order of magnitude higher than those afforded by the multi-slice methods. As illustrated by the 3D data presented in Figure 8, better images resulted from SR-enhanced SPEN sets relying on this phase-encoding approach, than from all other counterparts assayed in this study.
An aspect worth mentioning regarding the latter phase-encoded methods is their reliance on a full excitation of the relevant VOI, leading to a need for relatively longer inter-scan delays so as to allow a reasonable degree of longitudinal T1 relaxation to occur. As mentioned, a straightforward solution to this problem could result from using lower effective excitation flip-angles –albeit at a cost of a lowered per scan SNR. An alternative relaxation-enhancing option, consists of introducing additional RF pulses and gradients capable of fully rewinding –and then storing– the employed spin magnetization at the end of each acquisition event. This kind of bulk magnetization storage back towards the Bloch sphere z-axis, forms the basis of “driven-equilibrium” principles (37). These could also be incorporated into spatiotemporal encoding strategies like the one illustrated in Fig, 2a, provided that a suitable sequence of gradients and chirped pulses were applied. While theoretical schemes, confirmed by independent numerical simulations, revealed a number of options capable of fulfilling these conditions, our experimental experience showed that the efficiency of these storage strategies was quite low. On examining the potential source for these losses we focused on a central prerequisite of such methods, which is to have all spin magnetizations aligned in perfect quadrature vis-à-vis the rotating-frame RF field throughout the different positions of the sample at the time of their final storage. It was found that field inhomogeneities and hardware imperfections prevented us from reaching this ideal situation, resulting in turn in amplitude modulations and in SNR compromises which deprived this approach from usefulness as a signal-enhancing aid. Moreover, while field inhomogeneities could be reasonably compensated using additional spin-echo pulses, the 3D eddy-current effects arising in our vertical imaging system posed a challenge which we could not successfully overcome. We are investigating further more robust approaches for compensating non-idealities during these rewinding processes, which might allow us to perform full magnetization storage and thereby help reduce the corresponding inter-scan delay times.
The results in this report attest to the enhancement that can be gained by incorporating 2D spatiotemporal encoding into 3D imaging schemes –either when used to acquire multi-slice sets, or as complement to phase-encodings along a third dimension. Careful consideration should be given to the different regimes and to the imaging conditions that suit best each of these methods. Yet overall we believe that further functionalities and hitherto untapped potential could arise from these 3D SPEN approaches –not only in very fast imaging applications but also in spectroscopic imaging, in the monitoring of diffusion and flow, and in full echo-volume-like 3D acquisitions (24). We trust to report our progress on these and other avenues in upcoming studies.
Acknowledgments
We are grateful to Dr. Yoav Shrot (WIS) for valuable discussions. This research was supported by the Israel Science Foundation (ISF 447/09), the Minerva Foundation (Germany), ERC Advanced Grant #246754, a Helen and Kimmel Award for Innovative Investigation, and the generosity of the Perlman Family Foundation.
Abbreviations
- T1/T2
longitudinal/transverse spin relaxation time
- TR
Repetition Time
- SNR
Signal to Noise Ratio
- EPI
Echo Planar Imaging
- VOI
Volume of Interest
- FOV
Field of View
- SPEN
Spatiotemporal Encoding
- RF
Radiofrequency
- SR
Super Resolution
References
- 1.Haacke EM, Tkach JA. Fast MR imaging techniques and clinical applications. Americal Roentgen Ray Society. 1990;155:951–964. doi: 10.2214/ajr.155.5.2120964. [DOI] [PubMed] [Google Scholar]
- 2.Chavhan GB, Babyn PS, Jankharia BG, Cheng HM, Shroff MM. Steady-State MR Imaging Sequences - Physics, Classification, and Clinical Applications. Radio Graphics. 2008;28(4):1147–1160. doi: 10.1148/rg.284075031. [DOI] [PubMed] [Google Scholar]
- 3.Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. Elsevier Academic Press; 2004. Basic Pulse Sequences. [Google Scholar]
- 4.Mansfield P. Multi-planar image formation using NMR spin echoes. Journal of Physics C. 1977;10:L55–L58. [Google Scholar]
- 5.Schmitt F, Stehling MK, Turner R. Echo-Planar Imaging - theory, technique and applications. Springer-Verlag. 1998 [Google Scholar]
- 6.Bernstein MA, King KF, Zhou XJ. Handbook of MRI pulse sequences. Elsevier Academic Press; 2004. Echo train pulse sequences. [Google Scholar]
- 7.Charms RC. Applications of real-time fMRI. Nature reviews. 2008;9:720–729. doi: 10.1038/nrn2414. [DOI] [PubMed] [Google Scholar]
- 8.Basser PJ, Jones DK. Diffusion-tensor MRI: theory, experimental design and data analysis - a technical review. NMR Biomed. 2002;15:456–467. doi: 10.1002/nbm.783. [DOI] [PubMed] [Google Scholar]
- 9.Frydman L, Scherf T, Lupulescu A. The acquisition of multidimensional NMR spectra within a single scan. ProcNatlAcadSciUSA. 2002;99(25):15858–15862. doi: 10.1073/pnas.252644399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mishkovsky M, Frydman L. Principles and progress in ultrafast multidimensional nuclear magnetic resonance. AnnuRevPhysChem. 2009;60:429–448. doi: 10.1146/annurev.physchem.040808.090420. [DOI] [PubMed] [Google Scholar]
- 11.Shrot Y, Frydman L. Spatially encoded NMR and the acquisition of 2D magnetic resonance images within a single scan. JMagnReson. 2005;172:179–190. doi: 10.1016/j.jmr.2004.09.024. [DOI] [PubMed] [Google Scholar]
- 12.Tal A, Frydman L. Spatial encoding and the acquisition of high definition MR images in inhomogeneous magnetic fields. JMagnReson. 2006;181:179–194. doi: 10.1016/j.jmr.2006.06.022. [DOI] [PubMed] [Google Scholar]
- 13.Tal A, Frydman L. Spectroscopic imaging from spatially-encoded single-scan multidimensional MRI data. JMagnReson. 2007;189:46–58. doi: 10.1016/j.jmr.2007.08.003. [DOI] [PubMed] [Google Scholar]
- 14.Ben-Eliezer N, Shrot Y, Frydman L. High-Definition Single-Scan 2D MRI in Inhomogeneous Fields Using Spatial Encoding Methods. Magn Reson Imag. 2010;28(1):77–86. doi: 10.1016/j.mri.2009.05.026. [DOI] [PubMed] [Google Scholar]
- 15.Chamberlain R, Park JY, Corum C, Yacoub E, Ugurbil K, Jack CRJ, Garwood M. RASER: a new ultrafast magnetic resonance imaging method. MagnResonMed. 2007;58:794–799. doi: 10.1002/mrm.21396. [DOI] [PubMed] [Google Scholar]
- 16.Kunz D. Use of frequency-modulated radiofrequency pulses in MR imaging experiments. MagnResonMed. 1986;3:377–384. doi: 10.1002/mrm.1910030303. [DOI] [PubMed] [Google Scholar]
- 17.Pipe JG. Spatial encoding and reconstruction in MRI with quadratic phase profiles. MagnResonMed. 1995;33:24–33. doi: 10.1002/mrm.1910330105. [DOI] [PubMed] [Google Scholar]
- 18.Pipe JG. Analysis of localized quadratic encoding and reconstruction. MagnResonMed. 1996;36:137–146. doi: 10.1002/mrm.1910360122. [DOI] [PubMed] [Google Scholar]
- 19.Irani M, Peleg S. Improving Resolution by Image Registration. Graphical models and image processing. 1991;53(3):231–239. [Google Scholar]
- 20.Hell SW. Microscopy and its focal switch. Nature methods. 2009;6(1):24–32. doi: 10.1038/nmeth.1291. [DOI] [PubMed] [Google Scholar]
- 21.Shechtman E, Caspi Y, Irani M. Space-Time Super-Resolution. IEEE TransPattern AnalMachine Intell. 2005;27(4):531–545. doi: 10.1109/TPAMI.2005.85. [DOI] [PubMed] [Google Scholar]
- 22.Ben-Eliezer N, Shrot Y, Frydman L. Single-Scan Spatially Encoded MRI - Principles & Applications. ProcIntlSocMagResonMed. 2009:2670. [Google Scholar]
- 23.Ben-Eliezer N, Irani M, Frydman L. Super-Resolved Spatially-Encoded Single-Scan 2D MRI. Magnetic Resonance in Medicine. 2010 doi: 10.1002/mrm.22377. [DOI] [PubMed] [Google Scholar]
- 24.Song AW, Wong EC, Hyde JS. Echo Volume Imaging. Magnetic Resonance in Medicine. 1994;32:668–671. doi: 10.1002/mrm.1910320518. [DOI] [PubMed] [Google Scholar]
- 25.Yang Y, Mattay VS, Weinberger DR, Frank JA, Duyn JH. Localized Echo-Volume Imaging Methods for Functional MRI. Journal of Magnetic Resonance Imaging. 1997;7:371–375. doi: 10.1002/jmri.1880070220. [DOI] [PubMed] [Google Scholar]
- 26.Gunther M, Oshilo K, Feinberg DA. Single-Shot 3D Imaging Techniques Improve Arterial Spin Labeling Perfusion Measurements. Magnetic Resonance in Medicine. 2005;54:491–498. doi: 10.1002/mrm.20580. [DOI] [PubMed] [Google Scholar]
- 27.Poser BA, Koopmans PJ, Witzel T, Wald LL, Barth M. Three dimensional echo-planar imaging at 7 Tesla. Neuro Imag. 2010;51(1):261–266. doi: 10.1016/j.neuroimage.2010.01.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pauly JM, LeRoux P, Nishimura DG, Macovski A. Parameter relations for the Shinnar– LeRoux selective excitation pulse design algorithm. IEEE Transactions on Medical Imaging. 1991;10:53–65. doi: 10.1109/42.75611. [DOI] [PubMed] [Google Scholar]
- 29.Pauly J, Nishimura D, Macovski A. A k-Space Analysis of Small-Tip-Angle Excitation. Journal of Magnetic Resonance. 1989;81:43–56. doi: 10.1016/j.jmr.2011.09.023. [DOI] [PubMed] [Google Scholar]
- 30.Shrot Y, Frydman L. Spatial/spectral encoding of the spin interactions in ultrafast multidimensional NMR. J Chem Phys. 2009;131(22) doi: 10.1063/1.3266422. [DOI] [PubMed] [Google Scholar]
- 31.Tal A, Shapira B, Frydman L. Single-Scan 2D Hadamard NMR Spectroscopy. AngewChemIntEd. 2009;48:2732–2736. doi: 10.1002/anie.200805612. [DOI] [PubMed] [Google Scholar]
- 32.Callaghan Paul T. Principles of Nuclear Magnetic Resonance Microscopy. Clarendon Press; Oxford: 1993. [Google Scholar]
- 33.Freeman R. Spin Choreography - Basic Steps in High Resolution NMR. Oxford University Press; 1999. [Google Scholar]
- 34.Bernstein MA, King KF, Zhou XJ. Handbook of MRI pulse sequences. Elsevier Academic Press; 2004. Spatial Radiofrequency Pulses. [Google Scholar]
- 35.Garwood M, DelaBarre L. The Return of the Frequency Sweep: Designing Adiabatic Pulses for Contemporary NMR. Journal of Magnetic Resonance. 2001;153:155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 36.Freeman R, Hill HDW. Phase and Intensity Anomalies in Fourier Transform NMR. Journal of Magnetic Resonance. 1971;4:366–383. [Google Scholar]
- 37.Van Uijen CMJ, Den Boef JH. Driven-Equilibrium Radiofrequency Pulses in NMR Imaging. Magnetic Resonance in Medicine. 1984;1:502–507. doi: 10.1002/mrm.1910010409. [DOI] [PubMed] [Google Scholar]