Controlling spin-spin network dynamics by repeated projective measurements

Abstract

We show that coupled-spin network manipulations can be made highly effective by repeated “projections” of the evolving quantum states onto diagonal density-matrix states (populations). As opposed to the intricately crafted pulse trains that are often used to fine-tune a complex network’s evolution, the strategy hereby presented derives from the “quantum-Zeno effect” and provides a highly robust route to guide the evolution by destroying all unwanted correlations (coherences). We exploit these effects by showing that a relaxation-like behaviour is endowed to polarization transfers occurring within a N-spin coupled network. Experimental implementations yield coupling constant determinations for complex spin-coupling topologies, as demonstrated within the field of liquid-state nuclear magnetic resonance (NMR).

Introduction

Dynamical control methods set out to affect a system-bath dynamics on time scales that are much shorter than the bath correlation times [1]. On these time scales, the qubit-bath interaction behaves coherently: when control is effected via projective measurements - i.e., by driving the ensemble’s density matrix onto populations - it can move the system away from harmful, dissipative bath modes and approach dynamical decoupling. The resulting destruction of the quantum coherences established between a system and its surroundings can display intriguing characteristics. For qubits coupled to complex spin networks emulating a bath [2], such projections can steer the qubit towards either higher or lower purities, thereby driving the ensemble to asymptotic steady states associated to opposing quantum Zeno or quantum Anti-Zeno effects [3]. We have recently demonstrated examples of these “cooling” and “heating” behaviors with a series of NMR experiments [4], involving polarization exchanges between a carbon atom targeted as “the system”, and a neighboring ensemble of protons acting as the “bath”. Cooling and heating effects were then observed, and associated with a mismatched polarization exchange acting in either quantum Zeno or anti-Zeno regimes. The present study explores yet another use of projective quantum manipulations, this time dealing with a homonuclear network of exchange-coupled spins, where the inequivalent identity between a given targeted spin and its surrounding neighbors is actively erased by the application of a train of radiofrequency (RF) pulses. We find that the complex transfer patterns generated by the many-body network Hamiltonian thus created, can be transformed into simple, relaxation-like spin-polarization transfers, by relying on periodic dephasings of the off-diagonal density matrix elements via projective measurements. This in turn can facilitate the extraction of information on the coupling structure when dealing with complex spin-spin topologies, as is often desirable within the context of liquid-state NMR. Additionally, manipulating spin-coupling network topologies is a prerequisite for quantum information processing, where the Hamiltonian parameters are given by qubit-qubit interactions, which would normally have to be known beforehand to design robust quantum gate operations.

Principles and Methods

The present study explores the use of repeated projections as applied to Total Correlation Spectroscopy (TOCSY), a widespread tool in the arsenal of liquid-state NMR that serves to establish spin-coupling network topologies [5]. This experiment exploits an isotropic J-coupling spin Hamiltonian,

$${\widehat{H}}_J={\displaystyle \sum _{i<j}^N{J}_{ij}{\widehat{I}}_i\cdot {\widehat{I}}_j,}$$ (1)

where J_ij are the scalar coupling constants of the spin coupling terms Î_i · Î_j. While originally the {Î_k} operators are truncated to their Î_k,z components owing to the effect of σ_z-dependent chemical shifts, the TOCSY experiment erases these site-specific resonance frequency effects by the action of a suitable train of refocusing pulses [6]. Under such conditions an effective N-spin Hamiltonian of the form given in Eq. (1), is reinstated. Even when containing a small number of coupling coefficients {J_ij}_1≤i,j≤N such ${\widehat{H}}_J$ can rapidly lead to a complex time evolution on every spin, owing to its many-body nature [5, 6]. In fact, the multi-spin response that originates from ${\widehat{H}}_J$ is exploited in NMR for transferring coherences among all homonuclear spins, and thereby help establish spin-spin connectivities. Figure 1a illustrates the complex kind of polarization transfer patterns that will be promoted by ${\widehat{H}}_J.$ This complexity can eventually become a drawback, as it may demand a systematic scanning of evolution times to ensure that no spin-spin correlations are fortuitously missed. It will also complicate the quantitative determination of the pairwise spin-spin coupling parameters.

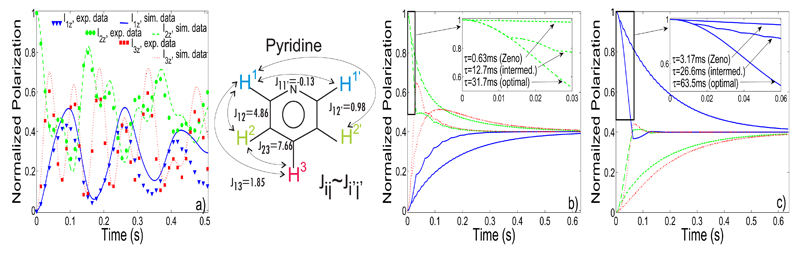
Figure 1.

(Color online) Time evolutions of Pyridine’s spin polarization operators ${\widehat{I}}_{iz}.$ (a) Coherent oscillatory transfer patterns (simulated → solid/dashed lines, experimental data → spin I₁, blue triangles, spin I₂, green circles, spin I₃, red squares) driven by ${\widehat{H}}_J$ between the spin sites in Pyridine (structure shown; J-couplings taken from [7]). A selective initial state concerning the spins ${\widehat{I}}_2$ (a,b) and ${\widehat{I}}_1$ (c) is prepared, followed by an ${\widehat{H}}_J$ evolution. (b,c) Diagrams illustrating the switch of the dynamics shown in (a) to quasi-monotonic polarization transfers, as a result of introducing repeated projective measurements. These calculated curves involved instantaneous erasements of the off-diagonal density matrix terms at intervals τ=31.7ms (optimal transfer), τ=12.7ms (intermed.), τ=0.63ms (Zeno) for panel (b) and τ=63.5ms (optimal transfer), τ=26.6ms (intermed.), τ=3.17ms (Zeno) for panel (c). Points in panel (a) (and all remaining data in this work) were acquired on a 600 MHz NMR spectrometer using 50 mM Pyridine in CDCl₃. The time evolution of Pyridine’s spin polarizations were monitored for each of the molecule’s three chemically inequivalent sites, in a point-by-point fashion. The transfer pattern under a free evolution driven by ${\widehat{H}}_J$ was recreated using pulse sequences capable of efficiently suppressing chemical shift differences, including DIPSI-3 and MLEV-8 [6, 8].

By contrast to this complexity, the use of “projections” involving the repeated erasing of off-diagonal coherences between every spin and its surroundings, can be used to guide the spins’ evolutions to a desired target state in an almost monotonic fashion. This amounts to collapsing the density matrices onto their diagonal elements; an effective switch of the N-qubit’s quantum evolution from a Hilbert space of dimension 2^N, to a much simpler, incoherent form occurring within an N-dimensional space. This imparts a welcome simplification of the complex free-evolution spin-spin transfer patterns, and thereby facilitates the extraction of information on the coupling structure topology as well as on the (often unknown) J_ij values involved. This is illustrated in Figs. 1b, 1c, which show how projective measurements are expected to transform the complex evolutions displayed in Fig 1a, into quasi-monotonic transfer functions. The central parameter defining the nature of this transition to a relaxation-like dynamics is the time delay τ elapsed between projections. As this J-evolution period is reduced, the transfer patterns among the spins change their originally complex oscillations to a smooth polarization sharing. For the limit of short τ a “freezing” of all evolutions (other than for irreversible decays) can be expected, corresponding to the ’Zeno’ cases in Figs. 1b, 1c. It is worthwhile noting that for optimally chosen τ values nearly equal distributions of polarizations - as usually desired in structural NMR measurements - can be rapidly achieved. In the absence of instrumental or relaxation losses these amplitudes converge to the ratio of initially polarized spins to the total number of spins determined (for the example in Fig. 1 this would correspond to $\frac{2}{5}=\mathrm{0.4.}$)

Figure 2a sketches how isotropic mixing sequences driven by ${\widehat{H}}_J$ can be modified to incorporate the projective measurements leading to the kind of behaviors illustrated in Figs. 1b, 1c. In lieu of a full 2D acquisition where every spin is excited and labeled to follow its dynamics, the sequence starts with a selective pulse that excites or depletes an individual spin/chemical site. This continues with a looped evolution incorporating an ${\widehat{H}}_J$ acting over a period τ, concatenated by emulated projective measurements. These projections rely on magnetic field gradients which, although acting over the full sample volume, yield effects that can be understood at a microscopic-level quantum dynamics [4, 9]: at their conclusion all off-diagonal density matrix elements are dephased, and solely spin populations remain untouched. Figs. 2b, 2c illustrate how these gradient-based elements help to erase the off-diagonal coherences created when ${\widehat{H}}_J$ acts on an ensemble. These projective elements will in turn drastically change the multi-spin dynamics - from the complex transfers in Fig. 1a, to the almost monotonic, pseudo-equilibrated transfers illustrated by the experiments in Fig. 3. Notice the close agreement between these results, and the theoretical expectations that had been put forward by the simulations in Figs. 1b, 1c.

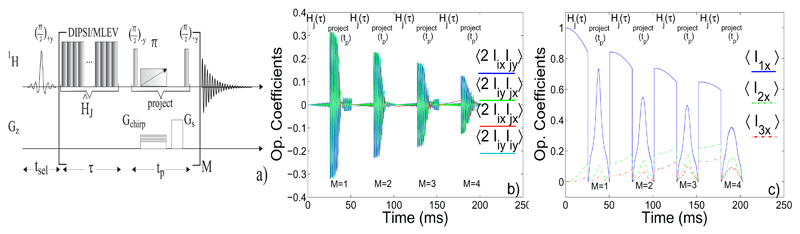
Figure 2.

(Color online) (a) Polarization transfer sequence emulating projective measurements interspersed with segments of isotropic ${\widehat{H}}_J$ evolution. The sequence begins with a t_sel pulse, that excites or depletes a single spin polarization. It continues with a looped evolution incorporating an isotropic ${\widehat{H}}_J$ action of length τ, and an emulated projective measurement. This projection consists of a chirped π pulse acting in combination with a gradient G_chirp for dephasing the zero-quantum off-diagonal elements in the spin density matrix [10], followed by a spoil gradient G_s charged with erasing all remaining higher coherence orders [6]. Commonly used parameters were M = 20 − 40, t_sel=5-10ms, τ=1-60ms, t_p=25-30ms, G_s=20 G/cm, G_chirp=0.5-1 G/cm and a sweep range of the chirped π pulses of ∆ω=20kHz. (b) Transfer characteristics expected during the course of this sequence for the two-spin zero and double quantum spin operators (off-diagonal terms of the density matrix). Notice the predicted suppressions of off-diagonal elements of the density matrix over the full sample volume: G_s is predominantly responsible for eliminating single- and double-quantum coherences, whereas G_chirp erases off-diagonal zero-quantum terms. The amplitudes of all these gradients were varied in a random fashion throughout each loop in order to avoid fortuitous revivals (echoes) of the coherences [4, 9]. (c) The destruction of the correlations between the spins and their surroundings steers the $\langle {\widehat{I}}_{ix}\rangle$ single-quantum elements corresponding to populations in terms of the initial density matrix, towards the desired monotonic evolution.

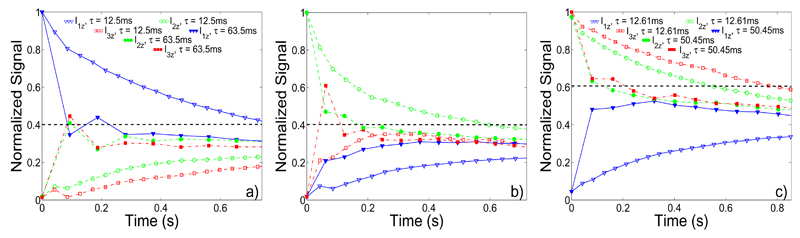
Figure 3.

(Color online) Experimental single spin polarizations, obtained from a sequence of the kind illustrated in figure 2a for Pyridine. (a,b) Transfer characteristics resulting from a “projected” ${\widehat{H}}_J$ evolution, following selective single-spin state preparations of ${\widehat{I}}_1$ (a) and ${\widehat{I}}_2$ (b) for τ=63.5ms (filled symbols) and τ=12.5ms (empty symbols). (c) Time evolution for an analogous repolarization experiment performed after a selective demagnetization of spin ${\widehat{I}}_1$ for τ=50.45ms (filled symbols) and τ=12.61ms (empty symbols). The main discrepancies between the experimental data and the simulated expectation (black dashed line) arise from the fact that the asymptotic polarization distributions are reached at a lower signal amplitude (∼0.35) than ideally expected as determined by the quasi-Boltzmann equilibrium ($\sim 0.35\text{vs}.\frac{2}{5}=0.4$ for Figs. 3a, 3b; $\sim 0.5\text{vs}.\frac{3}{5}=0.6$ for Fig. 3c). RF pulse inaccuracies and/or relaxation-derived losses are probably responsible for this.

It is worth exploring to what extent can the coupling constants effecting these transfers, be extracted from such relaxation-like dynamics. This is facilitated by the short-τ regime leading to the kind of curves illustrated in Fig. 3, where the original 2^N dimensionality defining the coupled spins’ Hilbert space, is projected into the N-dimensional space spanned by the diagonal of the multispin density matrix. The corresponding dynamics can then be represented by a vector $\overrightarrow{P}\left(M\tau \right)$ containing all the single-spin polarization elements, whose time evolution is given by

$$\overrightarrow{P}\left(M\tau \right)={\left[\mathit{p}\left(\tau \right)\right]}^M\overrightarrow{P}\left(0\right),$$ (2)

where M is the number and τ the timing of the projective measurements. The vector $\overrightarrow{P}\left(0\right)$ is the initial polarization of each spin i, and the polarization transfer matrix [p(τ)]^M represents an N × N spectrum whose elements carry the intensities of the self- and the cross-correlations observed at times M · τ. These intensities can be computed from the knowledge, that under the action of a ${\widehat{H}}_J=J{\widehat{I}}_i\cdot {\widehat{I}}_j,$ the two-spin (i, j) evolution will be of the form [5, 6]

$${\widehat{I}}_{iz}\stackrel{{\widehat{H}}_J}{\to }{\widehat{I}}_{iz}\left(\frac{1+\text{cos}\frac{J\tau }{2}}{\text{2}}\right)+{\widehat{I}}_{jz}\left(\frac{1-\text{cos}\frac{J\tau }{2}}{2}\right)+𝒪$$ (3)

where $𝒪$ represents higher-order relayed transfer terms. Considering that short durations τ justify the approximations

$$\frac{1+\text{cos}\frac{J\tau }{2}}{2}\approx 1-\frac{J^2{\tau }^2}{8};\frac{1-\text{cos}\frac{J\tau }{2}}{2}\approx \frac{J^2{\tau }^2}{8},$$ (4)

and that projective measurements only preserve diagonal populations, lead after M projections to a two-spin transfer matrix

$${\left[\mathit{p}\left(\tau \right)\right]}^M\approx \left[\begin{array}{cc}1-\frac{1}{2}M{\left(\frac{J\tau }{2}\right)}^2& \frac{1}{2}M{\left(\frac{J\tau }{2}\right)}^2\\ \frac{1}{2}M{\left(\frac{J\tau }{2}\right)}^2& 1-\frac{1}{2}M{\left(\frac{J\tau }{2}\right)}^2\end{array}\right].$$ (5)

The simple quadratic behaviour evidenced by the off-diagonal build-up in this matrix, can be expanded to the full many-body Hamiltonian of Eq. (1). Assuming then that the condition J_ijτ≪1 still holds for all pairwise couplings, the on- and off-diagonal elements of [p(τ)]^M can be approximated by

$${\left[\mathit{p}\left(\tau \right)\right]}^M\approx \{\begin{array}{c}M\frac{J_{ij}^2{\tau }^2}{8},\text{for}i\ne j\\ 1-{\displaystyle \sum _{j}M\frac{J_{ij}^2{\tau }^2}{8},\text{for}i=j}\end{array}.$$ (6)

for as long as one repeats the projections in the short J_ijτ ≪1 time regime. From this experimentally accessible matrix the absolute values of the involved couplings J_ij can be extracted; either from the initial build-up of crosspeaks observed in a two-dimensional spectral distribution, from the ratio between crosspeak intensities obtained in 1D build-up transfer curves, or from these crosspeak values normalized by the self-peak intensity. For the model system Pyridine, an effective five spin system possessing three inequivalent chemical shifts, this would mean that J₁₃ and an average of J₁₂ and J_1′2 could be extracted from the short-τ slopes of the data obtained after a selective excitation of Î₁ (Fig. 3a), that J₁₃ and J₂₃ can be obtained from an initial excitation of I₃, etc. Alternatively, numerical density matrix calculations could be used to simulate the system’s dynamics under the pulse sequence displayed in figure 2a, so as to ascertain the approach’s theoretical accuracy from the previously known coupling parameters. The resulting comparisons are summarized in Table I, which show a good agreement between short-τ experimental couplings and values found in literature, as well as when the latter are compared against the predictions of numerical simulations. Alternatively, an analogous analysis based on a relaxation-like evolution can be derived if all arguments related to the selective excitation of a particular site, are replaced by a selective demagnetization. The corresponding experimental data (Fig. 3c), illustrates the possibility of repolarizing a depleted magnetization via neighboring J-coupled spins, and of performing a corresponding theoretical modeling.

Table I.

J-values extracted from the short-τ peak ratio approximation (Eq. 6) compared against simulated numerical expectations, and literature values [7].

	J12, J1′ 2	J13	J23
short-τ approx.	3.4±0.1	2.0±0.2	6.6±0.9
simulations	3.50	1.86	7.64
literature	4.86, 0.98	1.85	7.66

Conclusion and Outlook

This study outlined a strategy that uses well-known elements from NMR spectroscopy’s toolbox, like field gradients and RF pulses, to imitate projective measurements. This allowed us to use NMR as a “quantum simulator” for describing the realization and potential advantages derived from novel Zeno-like effects, in exchange-coupled spin networks. These concepts also lead to a new experimental approach with potentially useful applications, whereby complex and a priori unknown polarization transfer patterns are morphed into monotonic, relaxation-like functions. From these it is straightforward to determine the underlying spin-spin coupling constants, to establish unambiguous correlations among spin networks, and/or to redistribute pools of unused polarization among the spins. It is also interesting to relate these projective measurements to Tycko’s recent studies [11] which showed that pseudo-random timings of NMR pulses could be used for switching the coherent character of dipole-dipole dynamics to an incoherent limit. Such strategies can be further extended to additional NMR experiments, including generalizations to other types of scalar, dipolar and quadrupolar multi-spin dynamics. We have also found this approach useful to shorten recycle delays - particularly in heteronuclear polarization transfer experiments [12]. Further synergies between such quantum control concepts and magnetic resonance experiments are being explored.