Time, number and attention in very low birth weight children

Abstract

Premature birth has been associated with damage in many regions of the cerebral cortex, although there is a particularly strong susceptibility for damage within the parieto-occipital lobes (Volpe, 2009). As these areas have been shown to be critical for both visual attention and magnitudes perception (time, space, and number), it is important to investigate the impact of prematurity on both the magnitude and attentional systems, particularly for children without overt white matter injuries, where the lack of obvious injury may cause their difficulties to remain unnoticed. In this study, we investigated the ability to judge time intervals (visual, audio and audio-visual temporal bisection), discriminate between numerical quantities (numerosity comparison), map numbers onto space (numberline task) and to maintain visuo-spatial attention (multiple-object-tracking) in school-age preterm children (N29). The results show that various parietal functions may be more or less robust to prematurity-related difficulties, with strong impairments found on time estimation and attentional task, while numerical discrimination or mapping tasks remained relatively unimpaired. Thus while our study generally supports the hypothesis of a dorsal stream vulnerability in children born preterm relative to other cortical locations, it further suggests that particular cognitive processes, as highlighted by performance on different tasks, are far more susceptible than others.

1. Introduction

The ability of our visual system to estimate the number, time or spatial extent of visual objects in the world has been traditionally thought of as independent and distinct mechanisms. However, recent work has begun to suggest that a common cortical metric is responsible for the processing those features (a theory of magnitude “ATOM”, see Walsh (2003), and proposed that the parietal cortex is the crucial brain area for this goal. As the parietal cortex is particularly vulnerable to early injuries, especially in preterm subjects (Volpe, 2009), it is of great importance whether injury, even sufficiently minor to typically pass undetected, could result in subtle difficulties for individuals with any kind of magnitude judgement.

Even in the absence of evident brain lesions, preterm children show impairments in a variety of different visuo-spatial abilities. This includes performance on tasks designed to investigate selective, sustained, shifting or divided-attention (Anderson et al., 2011; de Kieviet et al., 2013; Potharst et al., 2013) as well as tasks investigating both local and global motion (Guzzetta et al., 2009; MacKay et al., 2005; Taylor et al., 2009). Crucially, the current literature suggests that all these functions occur primarily in the parietal cortex (Bueti and Walsh, 2009). Recently, clinical research investigating parietal functioning and the impact of premature birth has focused on a subgroup of preterm children, characterized by a very low birth-weight (less than 1500 g; VLBW), representing 1–5% of all live-births. These children suffer an exceptionally high risk of death or extensive brain lesions. If they survive, even without major neural deficits, they very often encounter more “subtle” symptoms such as academic underachievement (Rodrigues et al., 2006; Taylor et al., 2009), behavioral problems (Bhutta, et al., 2002; Hack et al., 2004; Saigal et al., 2003) and deficits in higher-order neurocognitive functions such as executive functions (Ni et al., 2011).

Although a large variety of these less direct symptoms have been reported, visuospatial abilities (particularly those related to magnitude) may be common to many of them and represent a root cause. Indeed preterm children often undergo school achievement problems (Rodrigues et al., 2006; Taylor et al., 2009), particularly impacting on the acquisition of mathematical achievements (Taylor et al., 2009). Two different mechanisms have been proposed to underlie number representation (Castronovo and Gobel, 2012), an approximate number system (ANS) and an exact number system (ENS). The first, functional from very early, preverbal age, allows fast and approximate estimations of sets of objects, without requiring serial counting. In contrast the ENS refers to formal school-acquired mathematical education and knowledge of symbolic numbers. ANS precision (often reported as ‘number acuity’) has been shown to greatly improve throughout development (Piazza et al., 2013) and has furthermore been demonstrated to be a good predictor for future (Halberda and Feigenson, 2008) and current formal mathematics achievement in children (Anobile et al., 2013; Chen and Li, 2014; Halberda et al., 2008; Mazzocco et al., 2011).

The neural substrate supporting both the approximate and the exact number systems has been localized predominately within parietal–frontal regions (Butterworth and Walsh, 2011; Dehaene et al., 2003; Eger et al., 2009) with the intraparietal sulcus (IPS) identified as the as the locus for such processes (Kaufmann et al., 2011). The IPS has also been identified as the brain area where number and space interact (Hubbard et al., 2005). Indeed humans have a strong intuition of the spatial representation of numbers, with this spatial relationship often expressed as a mental numberline with numbers increasing from left to right (Hubbard et al., 2005). However, this mental numberline is not static throughout development (Booth and Siegler, 2006; Siegler and Booth, 2004; Siegler and Opfer, 2003). Kindergarten children have been shown to represent numbers in space in a compressed, seemingly logarithmic, scale (placing the number 10 near the midpoint of a 1–100 scale). As children mature (and experience the first three or four years of formal education) this scale becomes progressively more accurate (linear) and the degree of the accuracy has been found to positively correlate with children’s mathematical skills (Halberda and Feigenson, 2008).

Similarly to how numerical estimation has been shown to have strong links to the spatial representation of numbers (numberline), visual attention has also been shown to interact with many aspects of numerosity and numerical cognition (Sathian et al., 1999). Indeed, simply looking at different numbers can cause a shift either to the left or right in covert attention, depending upon the magnitude of the number (Fischer et al., 2003). Furthermore, the capacity to quickly estimate small sets of items (subitizing) employed by the ENS, as well as the ability to map numbers onto space (numberline) have both been shown to require visual attention (Anobile et al., 2012; Railo et al., 2008; Ross and Burr, 2010; Vetter et al., 2008). Anobile et al. (2013) investigated the relationship between formal mathematical skills, the perception of numerosity (discrimination and mapping to numberline) and visual sustained attention in school age children (from eight to 11 years). The results showed that formal math skills correlated with numerosity discrimination precision, number-to-space mapping (numberline task) and with visual attention capacity. Interestingly, attentional performance remained correlated with formal math skills after controlling for age, non-verbal intelligence, gender and reading accuracy.

Walsh (2003) has proposed that numerical and temporal information are processed by partially overlapping magnitude systems. In a recent study, Hayashi et al. (2013) used fMRI in humans to show that the right intra-parietal cortex (IPC) and inferior frontal gyrus (IFG) are jointly activated by duration and numerosity discrimination tasks, with a congruency effect in the right IFG. Using transcranial magnetic stimulation and two different numerosity–time interaction tasks, they demonstrated that the right IFG is specifically involved at the categorical decision stage, whereas interaction of numerosity with perception of time occurs within the IPC. Taken together, there is abundant evidence for a strong connection between the representations of numbers, time, space and attention in children with typical development.

Given that impairments in mathematical and other dorsal-stream-mediated skills have been widely reported in preterm children, especially in those born with VLBW, we believe that preterms represent an interesting population to investigate the perception of magnitude-related features, as well as attention. Surprisingly, to our knowledge, the literature on this topic is limited to few studies: one that investigates basic numerical processes in very preterm children (Guarini et al., 2014) and another about numerosity discrimination in extremely preterm school-aged children (Hellgren et al., 2013) and a very recent paper (Skagerlund and Traff, 2014) showing a general magnitude processing deficit (space, time and number) in children with developmental dyscalculia.

In this study we measured performance on time estimation, visual numerosity perception, number-to-space mapping (numberline) and sustained visual attention in a group of VLBW children and age-matched controls. In brief, our results confirm the vulnerability of the dorsal stream in children born preterm (VLBW), and further show that the degree of vulnerability is specific for particular tasks processed through this neural pathway, rather than applying uniformly to all tasks.

2. Materials and methods

2.1. Participants

This study was conducted under ethical approval from the Stella Maris Scientific Institute Ethics Committee. Preterm children were enrolled from a population based follow-up study and consisted of a group of children born with VLBW. The enrolment was done if they met the following criteria: (1) gestational age at birth below or equal to 32 weeks and birth-weight less than or equal to 1500 g; (2) absence of any major cerebral damage: normal results at postnatal brain ultrasound or periventricular increased echo density persisting less than 14 days and being less than or equal to grade I of De Vries’ classification (de Vries et al., 1992) and/or intraventicular hemorrhage (IVH) grade I according to Papile et al. (1978); (3) absence of motor impairment or other specific disorders at neurological examination; (4) no congenital malformations; (5) absence of major ocular anomalies such as cataracts, optic atrophy and retinopathy of prematurity > II grade, and a binocular visual acuity above 0.4 logMAR (20/50 Snellen acuity); (6) no auditory impairment (a hearing exam was done to all subjects within 1 year of age); and (7) age ranging from 6 to 11 years.

Forty-five families of VLBW children born between January 2001 and December 2003 were contacted by phone. Thirty families gave their consent to the enrolment of their children in the study (i.e. 67%) but only 29 of them (97%) satisfied the inclusion criteria. One subject was eliminated from the study as their attentional span was insufficient to complete the task.

Controls consisted of term-born children with a birth-weight more than 2500 g recruited from the local schools and matched to the preterm group in both gender and age.

2.2. Materials and procedure

For the contrast sensitivity measurements, stimuli were generated using PsychToolbox routines (Brainard, 1997) and displayed on a Barco monitor at 1024 × 768 pixels resolution at 85 Hz framerate, with mean luminance 20 cd/m², viewing distance 57 cm.

Numerosity and attention stimuli were presented in a dimly lit room on a 17-in. LG touch screen monitor with 1280 × 1024 resolution at refresh rate of 60 Hz, viewed binocularly from 57 cm. For the temporal task the subject was positioned in front of a device that could produce visual, auditory or visual–auditory stimuli (see picture in Fig. 1A).

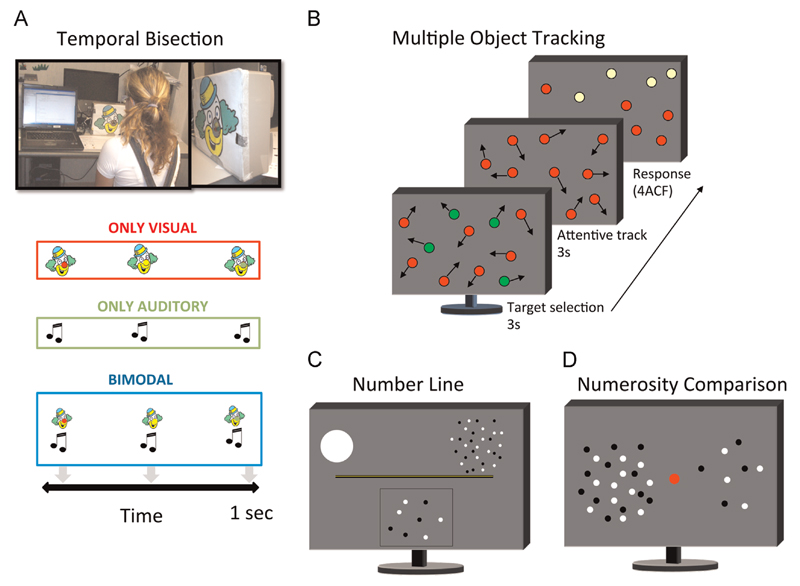
Fig. 1.

Illustration of tasks and stimuli. (A) Temporal Bisection: Three stimuli (visual, auditory, or both) were presented in succession for a total duration of 1000 ms, and observers were required to indicate by button-press whether the middle stimulus appeared closer in time to the first or the third stimulus. In the vision-only task the subject perceived a sequence of three lights: the first always red, the second yellow and the third green. The subject had to respond whether the yellow light appeared closer in time to the first or the last. In the auditory task the subjects perceived a sequence of three sounds and the subject had to respond whether the second was nearest to the first or to the third. In the bimodal task the subject perceived a sequence of three lights associated with three sounds. (B) Multiple Object Tracking: Eleven disks, four green targets and seven red distracters, moved randomly on the screen (4°/s) for a period of 3 s. The green targets then turned red (like the distracters) and subjects track them for 3 s. They then identified (by touching the screen) which of four possible items (highlighted in yellow) was the target (4ACF). (C) Numberline: at the onset of each trial observers view a number line, marked at each end with a single dot to the left and 30 dots to the right. On key press, the dot stimulus appears, after 500 ms a binary pixel random-noise mask was displayed until subjects respond. Subjects touched the screen at the position on the numberline they thought corresponded to the dot cloud. (D) Numerosity Comparison: two patches of dots were briefly (500 ms) presented to both sides of a central fixation point. Subjects are asked to touch the side of the screen with more dots. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.2.1. Contrast sensitivity

To exclude possible low-level visual impairments we also measured contrast sensitivity for motion direction and orientation (2AFC). A single circular grating (2 cpd, 4° diameter) was presented in the fovea. For motion-direction discrimination the grating was vertical, drifting leftward or rightward at 8 Hz, while for orientation discrimination the grating was stationary at ± 45° orientation. The stimulus presentation duration was 150 ms to minimize the possibility of eye-movements toward the stimulus location. Stimuli contrast was varied according to a QUEST adaptive staircase (Watson and Pelli, 1983) that adapted the presented stimuli to best measure each individuals threshold (contrast level yielding 75% of correct responses). Subjects were required to indicate the direction of the motion or the orientation of the gratings and instructed to guess when unsure. On average 80 trials were collected for each subject.

2.2.2. Time perception task

The procedure was modeled on the technique previously used by Gori et al. (2012) and Burr et al. (2009). All subjects performed a unimodal (visual or auditory) and bimodal temporal bisection task. Three stimuli were presented in succession for a total duration of 1000 ms, and observers were required to verbally report whether the middle stimulus appeared closer in time to the first or the third stimulus (time bisection task). In the visual task the subjects were presented with a sequence of three lights: the first one was always red, the second one yellow and the third one green (see Fig. 1A upper panel). In the auditory task, three sequential sounds were presented. At the beginning of the auditory task we confirmed for each subject that they were able to hear all three presented sounds. In the bimodal task, three sequential lights, temporally matched with the three sounds (Fig. 1A, lower panel), were presented. Condition order (visual, auditory or bimodal) was randomized across subjects. The visual stimuli were 1° diameter LEDs displayed for 75 ms, while the auditory stimuli were 75 ms tones (750 Hz). The presentation program waited for a frame-synchronization pulse then launched the visual and auditory signals.

Before collecting data, subjects were familiarized with the task by conducting two training sessions of 10 trials each (one visual and one audio). No feedback was given during the testing sessions and each session comprised 30 trials (90 in total). The timing of the second stimulus was adjusted with Quest algorithm (Watson and Pelli, 1983) with an additional random offset drawn from a Gaussian distribution of time-constant of 15 ms. This procedure ensured that the psychometric function was sufficiently sampled to provide a good estimate both for the PSE and the slope of the functions. Also, as the Gaussian offset was centered at zero, it ensured an equal number of “closer to the first” and “closer to the third” responses. Data for each condition were fitted by cumulative Gaussians, yielding PSE and threshold estimates from the mean and standard deviation of the best-fitting function. In this paper we report only threshold values with their standard errors estimated by bootstrapping (for details see, Gori et al., 2012).

2.2.3. Numberline task

We measured the ability to map numbers onto space using a “non-symbolic numberline” task in which subjects briefly viewed a cloud of dots and were then required to estimate the quantity by tapping onto a numberline flanked by two sample numerosities (Fig. 1C). Each trial started with subjects viewing a 22 cm numberline with sample dot-clouds representing the extremes: one dot on the left of the numberline, and 30 on the right, both of which remained throughout the trial. Dot stimuli were presented for 500 ms, followed by a random-noise mask that remained visible until the subject responded. The dots were half-white, halfblack and positioned on a gray background in pseudorandom positions within a virtual circle of 8° diameter without overlap. Subjects touched the touch-screen at the position of the numberline they thought corresponded to the dot cloud. Subjects performed three blocks consisting 9 different numerosities (2, 3, 4, 6, 10, 14, 18, 20 and 27) that were each presented once in random order. To discourage the subjects from using strategies other than numerosity (such as texture density), on each trial we alternatively kept constant either the total covered area (by varying individual dot size) or individual dot size (by varying total area covered). Thus on average, neither dot size nor total covered area correlated with numerosity. In the sample dot-clouds of the numberline, we kept constant total covered area. We quantified subject’s performance by computing the root mean square error (RMS), an index that takes into account both variance (average standard deviation of trials at a particular numerosity) and bias (average distance of the mean response from the physical numerosity):

$$RMS=\frac{1}{N}\sqrt{{\displaystyle \sum _i^N\frac{{\left(X_i-R_i\right)}^2}{X_i}}}$$ (1)

where X_i is the physical numerosity on the i’th trial, R_i is the response location to that numerosity and N is the number of trials.

2.2.4. Numerosity comparison

Two patches of dots were simultaneously briefly (500 ms) presented on both sides of a central fixation (see Fig. 1D) at a distance of 10°. Children touched the side of the screen that appeared to contain more dots. Standard numerosity was fixed at 24 dots while the probe was adaptively changed along a logarithmic scale depending on subjects’ responses, with probe values determined by the QUEST algorithm (Watson and Pelli, 1983). The side of the standard and probe were counterbalanced. Patches comprised non-overlapping dots (0.27° area), half-white and halfblack, constrained to fall within a virtual circle of 6° visual angle.

Each trial was initiated by the experimenter once sure that the child was maintaining fixation. To ensure that neither the density nor the area was a consistent or reliable cue for numerosity, three different conditions were simultaneously interleaved: equal-area (density and numerosity correlated), equal-density (area and numerosity correlated) or a minimal increase in both. In the equal-area condition, area was kept constant at 6 degrees with density varying accordingly with numerical changes, while in the equal-density condition, density was fixed at 7.3% and area increased with numerosity accordingly. In the minimal-increase condition an increase in number was associated with half the equal density condition increase in area and half the equal-area increase in density. Two blocks of 45 trials were run (90 trials in total). The proportion of “more” trials were plotted against probe numerosity (in log units) and fit with a cumulative Gaussian function such that the 50% point provided an estimate of the point of subjective equality (PSE) and the standard deviation (σ) gave an estimate of the JND in logarithmic units. At the final stage of analyses numerosity ability was expressed as a weber fraction (w is the ratio of threshold to numerosity) through the formula:

$$w={10}^{\sigma }-1$$ (2)

2.2.5. Visual sustained attention

Visual sustained attention was measured using a multiple-object tracking task (Arrighi et al., 2011; Pylyshyn and Storm, 1988). Eleven disks of 0.9° diameter consisting of four green (xyY coordinates=0.25, 0.69, and 39.5) targets and seven red (xyY coordinates=0.61, 0.33, and 39.5) distracters moved randomly across a gray full screen background at 4°/s for a period of 3 s. The green targets were then turned red (like the distracters), and subject were required to attentionally track them for a further 3 s. Afterwards subjects then identified (by touching the screen) which of four possible items (highlighted in orange, xyY coordinates=0.52, 0.44, and 39.4) was one of the previously green targets (4ACF). Each experimental session comprised ten trials, and subjects perform three sessions for a total of 30 trials. No feedback was provided. Performance was measured as proportion correct responses, and converted to d’ as a measure of sensitivity (see Fig.1 B).

2.3. Data analysis

For the time perception task a Two-Way Repeated measures ANOVA was performed in order to test for the effects of group (preterm, control) on the different tested conditions (visual, audio, and audio-visual). Post-hoc t-tests were then performed to test differences between the groups on each of the three tasks. α-Values were corrected for multiple comparisons (Bonferroni method) and as such a difference between groups was interpreted as statistically significant if p < 0.017: 0.05/3 (number of conditions).

Three separate linear regression analyses were performed for the other tasks (weber fraction, number line and attention), with the IQ (PIQ for preterms and Raven’s score for controls) and maternal level of education as covariates. Effect sizes were measured for all the statistics as Cohen’s d index (the size of the difference between groups in standard deviation units). In case of the repeated measures anova and regression analyses we reported both Cohen’s d and η². Here Cohen’s d was measured transforming η² into Cohen’s d (Cohen, 1988).

3. Results

3.1. Participant characteristics

The final cohort consisted of 29 VLBW preterm-born children (10 M) with a mean age of 8 years and 8 months (range: 6 years 6 months – 11 years 1 month). Their mean gestational age at birth was 28.3 weeks (range 24–32 weeks) and mean birth weight 1107 g (range 490–1480 g). There were no significant differences in gestational age and birth-weight between the preterm subjects who participated in the study and those who did not answer to the invitation (mean gestational age 28.8 weeks; mean birth-weight 1180 g).

Only in 4 subjects (14%) was there a ROP stage 1 or 2 during the first week of life without visual complications. In 7 subjects (24%) minor abnormalities at ultrasound were reported. Specifically, Grade I of PVL while in 2 of them also IVH grade 1 was present.

Maternal and paternal levels of education were distributed as follows: 8 mothers (27%) and 16 fathers (55%) had a low educational level (completed basic education), 19 mothers (65%) and 8 fathers (27%) had a medium level (completed high school), 2 mothers (7%) and 5 fathers (17%) had a high level school or higher level (including degree).

We tested two separate samples of control subjects, one group (N=26) performed the numerosity, numberline and the attentional task (sample 1), while the other (N=26) was tested only with the time perception tasks (sample 2). Due to the length of testing two different control groups were required as the period of time required to complete all tasks exceeded the maximal time the children were permitted by the teachers and parents to be taken out of class for testing.

All VLBW subjects were assessed with the revised Wechsler Intelligence Scale for Children-III (Wechsler, 1991) administered in the full version to evaluate their cognitive functioning. WISC-III is based on separate subtests about no verbal tasks and verbal tasks. Finally, the scores can be grouped in a Total IQ, Performance IQ and in a Verbal IQ. Along the paper we will refer to those as TIQ, PIQ and VIQ respectively.

Only in two subjects was a TIQ under 70 found and these subjects were flagged as ‘low-IQ’ in the subsequent analyses. In control subjects (sample 1) IQ was evaluated by Raven’s Matrices (Belacchi et al., 2008) a widely used, high validity non-verbal test that can be administered quickly. In brief, this test it is made of multiple choice questions, listed in order of difficulty. In each test item, the subject has to identify the missing element that completes a figure pattern. No control children had low IQ levels and all had a good understanding of the instructions to perform the perceptual tasks. No evaluation of IQ and socioeconomic status was done in the second control group (sample 2). Subjects of sample 2 (controls for time task) are part of another study by our research group (Gori et al., 2012), where a very large group of subjects aged from 5 years to adult was studied. We have selected from this sample the control cases for the present study, matched for the age of the preterm children.

In that previous study, data on IQ and SE status were not collected. However, none of those children were reported to have special needs at school. Moreover, we believe any influence of general intelligence factors in the performance of the subjects of sample 2 on this test very unlikely, because of an internal control. In fact, subjects with the worst performance on visual time were not the same as those with the worst performance on audio time and audio-visual time.

Table 1 reports mean IQ values for the preterm subjects and mean Raven’s score for controls (sample 1) with the respective ranges and standard deviations.

Table 1.

Mean IQ values of VLBW preterm children and Raven score in controls (sample 1).

Preterms			Controls (sample 1)
Total IQ (WISC-III)	Verbal IQ (WISC-III)	Performance IQ (WISC-III)	Raven
Min 55	Min 48	Min 68	Min 80
Max 120	Max 118	Max 127	Max 125
Mean 93.7	Mean 91.46	Mean 96	Mean 101.2
Std 16.6	Std 18	Std 15	Std 11.2

Since Raven’s matrices are a non-verbal visual and perceptual task we did a comparison of Raven’s score of the control group with the PIQ score at WISC-III scale of preterm children (for concurrent validity between Raven’s Matrices and WISC-R see Blennerhassett et al., 1994). No statistical difference was found in a 2-tailed t-test (t₍₅₁₎=1.387; p=0.174, Cohen’s d=0.39), confirming that we were analyzing two similar groups for this variable.

The comparison between maternal education level in VLBW children and controls (sample 1) showed instead a significant difference (t₍₅₁₎=4.844; p < 0.001, Cohen’s d=1.21).

Table 2 reports mean and standard deviations measured on each task separately for the entire group of preterm children (VLBW) and for the control group.

Table 2.

Results of psychophysical tasks (mean values and standard deviation) for each group (preterm and control samples). In bracket, the number of subjects that complete the task.

	Time				Math		Attention
	Visual time	Audio time	Audio-visual time	Worst time	Number line	Numerosity comparison	Visual sustained attention
Preterms
Mean	252.83 (n=26)	259.39 (n=26)	181.24 (n=26)	358.79 (n=26)	0.4702 (n=25)	0.3199 (n=25)	1.17 (n=24)
SD	(159.08)	(174.08)	(132.45)	(156.12)	(0.159)	(0.083)	(0.54)
Controls
Mean	179.92 (n=26)	125.65 (n=26)	125.45 (n=26)	196.37 (n=26)	0.4028 (n=25)	0.2922 (n=25)	1.72 (n=25)
SD	(92.27)	(93.07)	(65.47)	(91.33)	(0.104)	(0.053)	(0.32)

3.2. Contrast sensitivity

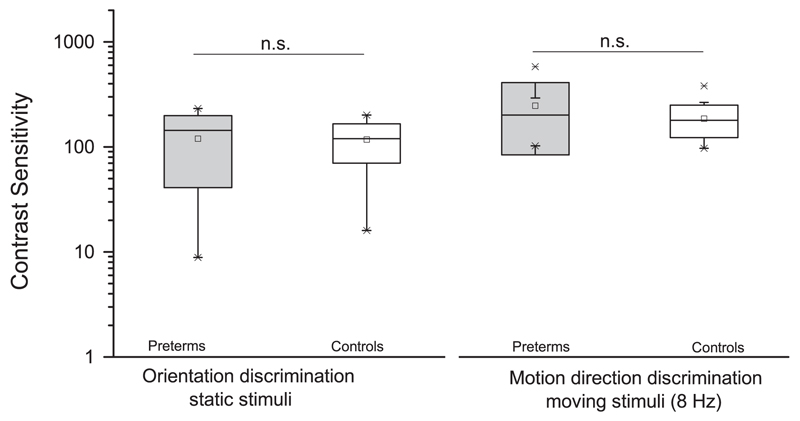
Contrast sensitivity was measured without difficulty for all children in the sample. Fig. 2 shows the contrast sensitivity for orientation and motion discrimination averaged across the control and the VLWB children groups. The average values are close to adult values (Braddick et al., 1978; also unpublished data using identical setup in our lab), and no statistical difference was found between preterm and full-term groups in all the measures of contrast sensitivity: orientation discrimination for static stimuli (t₍₃₁₎=0.08, p=0.93, Cohen’s d=0.03), motion direction discrimination for stimuli drifting at 8 Hz (t₍₃₁₎=1.53, p=0.13, Cohen’s d=0.48).

Fig. 2.

Box plot of contrast sensitivity in two discrimination tasks, for preterm children (gray box) and controls (white box). Both different measures of contrast sensitivity do not differ between groups (n.s.=not significant difference).

3.3. Time perception

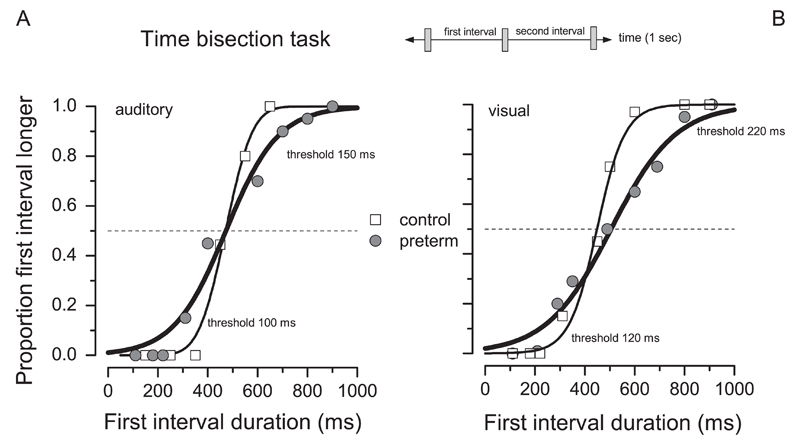
Both groups of children were able to perform the more complex time judgment task and obtained orderly and steep psychometric functions, like those illustrated in Fig. 3. VLBW subjects were also able to perform the task reliably, producing consistent and orderly psychometric functions (see example in Fig. 3). However, the psychometric functions are broader than in the control, indicating a specific deficit. Fig. 4 shows thresholds in the time bisection task for the three sensory conditions (visual, audio and bimodal) for both groups (preterm children and controls). For each subject we also extracted the worst threshold across conditions. As the literature often reports lower IQ in preterm children than controls (Fan et al., 2013; Kormos et al., 2014), we first considered our entire preterm group, including children having a total IQ value under 70 (N=2).

Fig. 3.

Sample psychometric functions for two representative subjects, one preterm (gray circle and line) and one control child (white square, black line), in the unimodal time bisection tasks.

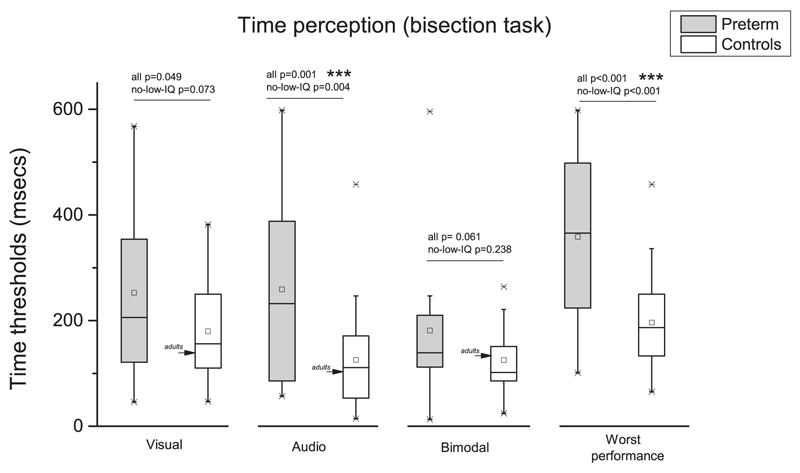
Fig. 4.

Thresholds in temporal bisection tasks for preterm children (gray box) and controls (white box). Arrows indicate adult performance. ***p <=0.001.

Two way repeated measures ANOVA with “conditions” (three levels: visual, audio, and bimodal) and “groups” (two levels: preterm and controls) as factors reveal a significant main effect of group (F_(1,49)=10.418, p=0.002, η²=0.212, Cohen’s d=1.039) and conditions (F_(2,98)=4.738, p=0.01, η²=0.085, Cohen’s d=0.610) with no interaction (F_(2,98)=1.804, p=0.17, η²=0.032, Cohen’s d=0.366).

Post-hoc analysis (Bonferroni corrected alpha-value) reveal that preterm do not differ from controls in case of bimodal condition (t₍₄₉₎=1.918, p=0.061, Cohen’s d=0.534). In the visual condition, the difference between group approach the statistical significance (t₍₅₀₎=2.021, p=0.049, Cohen’s d=0.56), instead in the audio conditions preterm perform clearly poorly then controls (t₍₅₀₎=3.455, p=0.001, Cohen’s d=0.958) as also in the ‘worst performance’ index (F₍₁₅₀₎=26.076, p < 0.001, η²=0.265, Cohen’s d=1.2).

For the control group, the average thresholds both for unimodal and bimodal stimuli were very similar to the adult values, indicating rapid development. To be certain that the effects were robust, we repeated the analysis eliminating children with low IQ (less than 70) from the group analysis. The overall pattern of result remained stable: main effects of factors “group” (F_(1,47)=7.832, p=0.007, η²=0.142, Cohen’s d=0.816) and “conditions” (F_(2,94)=7.115, p=0.001, η²=0.126, Cohen’s d=0.76) with no interaction (F_(2,94)=2.25, p=0.111, η²=0.039, Cohen’s d=0.407). Post-hoc analysis (Bonferroni corrected alpha-value) revealed that preterm performance do not differ from controls in case of visual (t₍₄₈₎=1.833, p=0.073, Cohen’s d=0.522) and bimodal (t₍₄₇₎=1.196, p=0.238, Cohen’s d=0.3423) conditions. Thresholds in the audio (t₍₄₈₎=3.048, p=0.004, Cohen’s d=0.855) condition confirm that preterm scored significantly poorer then controls as also in the ‘worst performance’ (F_(1,48)=14.793, p < 0.001, η²=0.234, Cohen’s d=1.108).

3.4. Numberline and numerosity acuity

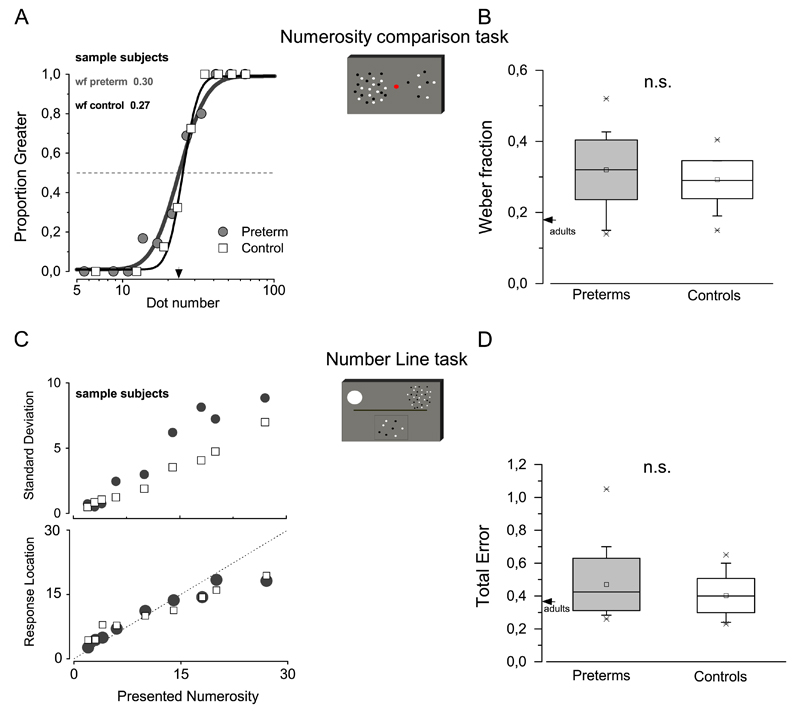
All subjects were very competent in judgments of the numerosity of simultaneous patches of dots. As shown in the example of Fig. 5A, the psychometric functions for reporting which is the more numerous patch straddle the physical equality of 24 dots, and is very steep both for controls and VLBW children. The Weber fraction, given by the JND divided by PSE (see Eq. (2)), averaged across subjects, is reported in Fig. 5B. Regression analysis with non-verbal IQ and maternal level of education as covariates, reveals that mean Weber fraction value for preterm children do not different from controls (F_(3,50)=1.115, p=0.337, η²=0.041, Cohen’s d=0.418).

Fig. 5.

(A) Sample psychometric functions for two representative subjects, one preterm (gray circle and line), and one control child (white square, black line), in the numerosity comparison task. (B) Weber Fraction in the numerosity comparison task in preterm children (gray box,) and controls (white box). (C) Numberline judgment precision (standard deviation) and mean response location for the different numerosities in sample subjects (preterm children represented by gray circles and controls by open squares). (D) Total error in the number line task (preterm: gray box; controls: white box).

We used the numberline task to investigate whether preterm children, compared to controls, are able to spatially represent numerical quantities. Following our previous works (Anobile et al., 2012), we decomposed the overall performance in two components: precision (standard deviation of responses for each tested numerosity) and accuracy (mean response locations for each tested numerosity). Fig. 5C shows that although preterm children (gray circles) perform this task less precisely than controls (opened squares), their average responses location (Fig. 5C, same symbols code) did not substantially differ from that the location indicated by the controls. Fig. 5 D shows total error in the numberline task. This index of performance (Eq. (2)) evaluates both the precision and the accuracy of the performance. As above, regression analysis with non-verbal IQ and maternal level of education as covariates reveal that preterm children performance do not differ from controls F_(3,50)=1.79, p=0.162, η²=0.015, Cohen’s d=0.246).

3.5. Sustained visual attention

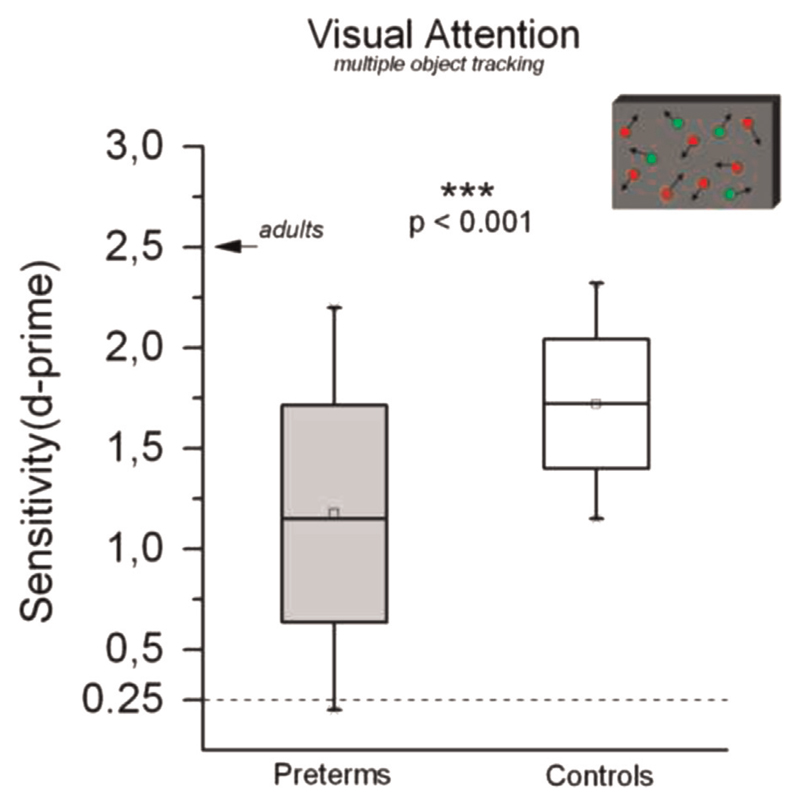
We measured visual sustained attention using a Multiple-Object Tracking task (Pylyshyn and Storm, 1988). For each subject, the proportion of correct responses was converted to D-prime, a measure of sensitivity. Regression analysis with non-verbal IQ and maternal level of education as covariates shows that preterm children perform significantly worse (lower value of sensitivity, Fig. 6) than controls (F_(3,49)=7.424, p < 0.001, η²=0.198, Cohen’s d=0.994).

Fig. 6.

Sensitivity in the multiple object tracking task in preterm children (gray) and controls (white). The box represents ± 1 s.e.m., the whiskers the entire range. The difference in performance is significant ***p < 0.001.

3.6. Correlations between perceptual variables

We also calculated z-scores separately for each task and for each preterm child, in order to examine the relationships between the degrees of impairment shown by preterm children at the various tests, we performed a series of Pearson’s bivariate correlations among the z-scores measured on the perceptual tasks. The only correlation that reached statistical significance was that between worse thresholds on the time bisection task and attentional capacities (r=0.49, p=0.02).

3.7. Correlations between perceptual variables, gestational age and birth weight

Finally, no significant correlations were observed between perceptual variables (z-scores) and either gestational age or birth weight.

4. Discussion

The aim of this study was to evaluate in VLBW school-aged children the impact of prematurity (in the absence of severe brain lesions) on parietal functions. We tested 29 VLBW children and matched controls with a series of psychophysical tasks designed to measure temporal discrimination, estimation and manipulation of numerical quantities, and capacity to focus and maintain visual attention. The tested preterm sample was carefully selected for gestational age (ranging from 24 to 32) and birth-weight (ranging from 490 to 1480 g). All the tested preterm children had normal visual acuity and contrast sensitivity as well as ocular, auditory, language and motor functions. Almost all the key features of the reported preterm sample (IQ level, gestation age, birth weight, socio-economic status) strictly matched those described in many previous studies involving larger samples in the same geographic area of our study (e.g. Guarini et al., 2014; Sansavini et al., 2011).

We observed impairments in some of the parietal functions tested in our subjects, specifically time discrimination and attention. However, we found no significant correlations between gestational age or birth-weight with any of the tasks. It is difficult to draw firm conclusions from the absence of significant correlations. They may reflect, at least in part, the sample size, not large compared with other studies in this field. They could also result from our sample being quite selective (only preterms born earlier than 32 weeks of VLBW), and therefore without large variance in birth-weight or age to facilitate a correlation. Significant correlation may emerge in larger, more variable groups.

4.1. Time estimation

Perceiving and estimating the passage of time is fundamental for most of our sensory and motor activities. This study reveals that time discrimination in our group of VLBW children is compromised. Furthermore, the data show that this deficit is particularly severe when time intervals are demarked by sounds (audio time).

In line with a recent study (Gori et al., 2012) we found that at 9-years-olds typically developing children have a temporal precision similar to that of adults (arrows in Fig. 4). However, VLBW children were considerably worse than what would be expected from their chronological age, indicating delayed development of this function. We also asked whether VLBW children were able to estimate time when the intervals were simultaneously marked by both auditory and visual stimuli, providing redundant congruent information. In this bimodal condition the deficit, although still present, became less evident, suggesting that VLBW children are able to integrate visual and acoustic signals, at least in order to estimate the passage of time. Although the task always required the same judgment (time bisection) across all sensory conditions, the degree of impairment showed by preterm in the three different conditions (visual, auditory, and audio-visual) did not correlate between them.

What could be the cause of impaired time estimation? A recent paper suggested that the ability to perceive temporal rhythm is fundamental for the acquisition of phonological and reading abilities (Flaugnacco et al., 2014). Interestingly, both these abilities have been often reported as impaired in preterm children (Lee et al., 2011).

4.2. Visual sustained attention

Attention has many aspects, but most agree that it acts to select and maintain relevant information while suppressing irrelevant distracters. This ability improves the efficiency with which signals arriving from the environment are acquired, processed, memorized and learned (Posner and Rothbart, 2005). In this study, we focused on visuo-spatial sustained attention, a function that reaches adult-like levels of performance late, and is thought to involve fronto-parietal networks. We measured this ability using a multiple-object tracking task (Pylyshyn and Storm, 1988). In this task subjects must focus and maintain spatial attention on drifting visual targets stimuli embedded in drifting distractors. This task requires many skills, including the initial selection of target stimuli (in this case defined by their color) between the distractors, the ability to divide attentional resources between the 4 targets, inhibiting the interference of the distractors, and the capacity to maintain attentional focus on the targets in space and for the time for 3 s. It is an ecological task, corresponding to natural occasions where we need to track multiple sources of information in time and space.

The brain areas responding to this task are mainly the frontal and parietal cortex, as well as areas dedicated to the processing of visual motion (MT) (Culham et al., 1998). Our work clearly demonstrates that our school-age VLBW children have a compromised visual sustained attentional system. This result fits well with many others showing attentional control deficits in preterm children of both preschool (van de Weijer-Bergsma et al., 2008) and school-age children (Anderson et al., 2011) using different techniques, such as Test of Everyday Attention for Children (TEA-Ch). Recently, visual attentional capacity has been shown to be closely related to the development of academic skills such as reading and math (Anobile et al., 2013; Franceschini et al., 2012; Franceschini et al., 2013). It is reasonable to suggest that a visual attentional deficit could result in a school underachievement, often observed in preterm children (Rodrigues et al., 2006; Taylor et al., 2009).

4.3. Mapping number onto space and numerosity estimation

During typical development, performance on numberline and numerosity estimation tasks has been demonstrated to predict formal math achievement (Anobile et al., 2013; Halberda et al., 2008; Reigosa-Crespo et al., 2012), and many studies report serious difficulties in formal mathematical skills in preterm children (Aarnoudse-Moens et al., 2011; Simms et al., 2013). Furthermore, spatial representation of numbers (numberline), as well as numerical estimation has been reported to rely on parietal brain areas. Here we found that VLBW children performed in the same way of controls in both of these tasks. To our knowledge this is the first study measuring numberline performance in preterm children.

Very few studies have investigated numerosity estimation in preterms, and they have reported partially conflicting results. Guarini et al. (2014), asked 6 years and 8 years old preterms and controls children to indicate which of two clouds of dots was more numerous. Results indicated that preterms accuracy (proportion of correct responses) at both tested ages do not differ from those of controls. Hellgren et al. (2013), with a similar task, reported that 6-year-old preterm children perform less precisely than age-matched control children. In this latter study Weber Fraction was used as the index of precision. Interestingly, both of these studies found slower reaction times on preterm children.

All together, these results suggested that prematurity could have minor negative repercussions on those basic numerical skills supporting the approximate numerical system (ANS), impairing more profoundly the acquisition of formal math skills (ENS).

5. Limitations of the present study

As previously mentioned, interpretation of our results must be tempered by a few some limitations of the study: the small sample size, some inperfections in the selection of the control groups (the use of two groups, instead of one, the lack of WISC or other IQ measures in one group and no match for IQ between groups) and the presence of some VLBW children with minor ultrasound abnormalities, which could affect cognitive functions. In face some recent reports suggest that in very preterm infants microstructural alternation and disorganization of the white matter, detectable by brain MRI and diffusion tensor imaging, may account for neuropsychological disorders, in particular of executive functions, at the age of 7 years (Thompson et al., 2014).

6. General conclusions

Preterm children often show impairment of functions mediated by parietal cortex. In line with other studies, we found that our VLBW preterm children, including subjects with no or minor brain ultrasound abnormalities, suffered from a severe visual attentional deficit. We also demonstrated that their discrimination of time intervals is also profoundly compromised. Interestingly, other parietal functions such as numerosity estimation and mapping number onto space (numberline) are not impaired. These results confirm the vulnerability of the dorsal stream and parietal functions in VLBW children born preterm, and further suggest that certain functions are particularly prone to impairment, with important repercussions in daily life. It is difficult at present to hypothesize about why attention and time perception are both compromised, while the “number sense” seems to be spared. Perhaps attention and time are processed by two connected regions (Culham et al., 1998; Rao et al., 2001). It is also possible that working memory plays an important role in both of these tasks, but is not so fundamental for numerosity.

Further studies, including structural and functional neuroimaging studies, will be necessary in order to confirm the present findings and to identify the specific factors – environmental, genetic, lesional or other – that could account for the impairment of these functions in the preterm infant.