Importance of consensus region of multiple-ligand templates in a virtual screening method

Abstract

We discuss methods and ideas of virtual screening (VS) for drug discovery by examining the performance of VS-APPLE, a recently developed VS method, which extensively utilizes the tendency of single binding pockets to bind diversely different ligands, i.e. promiscuity of binding pockets. In VS-APPLE, multiple ligands bound to a pocket are spatially arranged by maximizing structural overlap of the protein while keeping their relative position and orientation with respect to the pocket surface, which are then combined into a multiple-ligand template for screening test compounds. To greatly reduce the computational cost, comparison of test compound structures are made only with limited regions of the multiple-ligand template. Even when we use the narrow regions with most densely populated atoms for the comparison, VSAPPLE outperforms other conventional VS methods in terms of Area Under the Curve (AUC) measure. This region with densely populated atoms corresponds to the consensus region among multiple ligands. It is typically observed that expansion of the sampled region including more atoms improves screening efficiency. However, for some target proteins, considering only a small consensus region is enough for the effective screening of test compounds. These results suggest that the performance test of VS methods sheds light on the mechanisms of protein-ligand interactions, and elucidation of the protein-ligand interactions should further help improvement of VS methods.

As the structure data of protein-ligand complexes have been accumulated, it has become recognized that many proteins promiscuously bind different ligands at the same binding pockets [1,2]. Such promiscuity of protein pockets is ubiquitous rather than rare, which should provide a clue to developing virtual screening (VS) methods for drug discovery: Molecules having structures similar to the structures of the known multiple ligands that bind to a target protein pocket can be selected as candidate active compounds for that protein. Therefore, much interest has been focused on the way to use multiple ligands to develop VS methods [3–7]. For developing effective VS methods, the structural data of protein-ligand complexes should be further exploited in an efficient and comprehensive way.

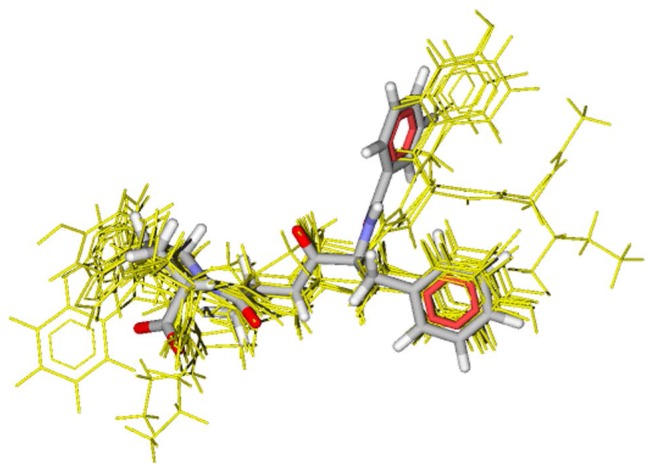
Recently, the present authors developed a VS method, VS-APPLE (Virtual Screening Algorithm using Promiscuous Protein-Ligand complExes) [8] which utilizes the structure data of multiple protein-ligand complexes. In VS-APPLE, structures of protein-ligand complexes are superposed so as to maximize the structural overlap between the target protein and proteins in complexes. Multiple ligands superposed in this way are then combined into a template by keeping their relative position and orientation. Therefore, thus generated multiple-ligand template should represent how the binding pocket of the target protein accommodates various different ligands with flexible pocket surface. Then, a test compound is selected as a candidate active compound when the structural overlap between the test compound and the multiple-ligand template is large while the test compound does not show a strong structural collision against the target protein surface. See Figure 1 for an example of the multiple-ligand template generated in VS-APPLE and an active compound selected by this template.

Figure 1.

An example of multiple-ligand template for ace (yellow thin lines) and an active compound detected by the multiple-ligand template (CPK colored thick lines). The multiple-ligand template comprises ten different ligands. The active compound was superposed so that the structural overlap between the active compound and the multiple-ligand template was maximized.

In Ref. [8], the performance of VS-APPLE was tested by using a filtered, clustered version [9,10] of the Directory of Useful Decoys (DUD) data set [11]. In Area Under the Curve (AUC) analyses [12,13] of this data set, VS-APPLE showed a comparable performance to a VS method Glide [15–17] and outperformed other popular methods such as ROCS [18–20], BABEL [21], DOCK [10,22], and GOLD [22]. Moreover, VS-APPLE successfully identified a hit compound in a compound proposal contest, in which 10 research groups participated and predicted inhibitors of the tyrosine-protein kinase Yes in a blind manner [23].

A further merit of VS-APPLE is its fast computational speed: It was shown that VS-APPLE was about three times faster than Glide by using parameters given in Ref.[8]. Because it is necessary to examine a combinatorially large number of compounds for drug design, which often exceeds 10 millions, the computational speed of VS method is indeed an important subject. Here, the computational speed of VS-APPLE is fast because it does not evaluate the atomic pairwise distances but evaluates the structural overlap between test compound and the template with a method based on geometric hashing [24,25]. Because this evaluation is the speed limiting step, improvement of this calculation greatly accelerates the entire computational process. In VS-APPLE, this acceleration is achieved by imposing a restriction on the number of generated structural overlaps: Only the region where atoms are densely populated within the multiple-ligand template is sampled to evaluate the structural overlap with the test compound.

In the present paper, we examine how the performance of VS-APPLE is affected by this restriction on the sampling. We show that for some target proteins, the region with high atomic density within the multiple-ligand template, which represents the consensus among multiple ligands in the template, is sufficient for effectively finding active compounds with VS-APPLE. In these cases, the binding affinity of a compound to the protein pocket should be largely determined by the consensus region of multiple-ligand template. Also as a general tendency for the other target proteins, enlarging the sampled region within the multiple-ligand template improves the performance of VS-APPLE. Characterization of such differences among target proteins should help improvement of the VS methods based on the multiple-ligand template, and should give insights on the mechanism of protein-ligand interactions.

Methods

In this section, procedures in VS-APPLE are briefly sketched. Please see Ref. [8] for more detailed explanation of the method. Also explained in this section is a subset of DUD data set used for the performance test in the present paper.

A brief sketch of VS-APPLE

The first step in VS-APPLE is to construct a multiple-ligand template for the target protein. To build the multiple-ligand template, protein data bank (PDB) is searched for the structures of the target protein and the structures similar to the target protein. This search is performed by using a structure comparison algorithm MICAN [26,27]. From the structures obtained through this search, structures which contain no ligand are eliminated and those which bind a ligand at the same binding pocket are selected. Thus obtained ith structure-data file C_i of protein-ligand complex comprises a protein P_i and a ligand L_i. The ensemble of ligands {L_i} are clustered according to the Tanimoto coefficient representing the 2D similarity among ligands. Through this clustering, the representative 10 ligands, $L_i^{*}$ with i = 1...10 are selected. Then, the corresponding 10 complexes $C_i^{*}$s are superposed to maximize the TM-score [28], which is one of the most popular measure of protein backbone similarity, between $P_i^{*}$ and the target protein P^t using the structure alignment program MICAN [26]. In this way, we obtain 10 spatially arranged ligands. The ensemble of this spatially arranged ligands, $Q^{\text{multi}}=L_1^{*}+L_2^{*}+\dots +L_{10}^{*}$, is used as a multiple-ligand template.

Using thus defined multiple-ligand template, score of the kth test compound for the target protein P^t is calculated as in the following. Consider that the kth test compound is composed of $N_k^{\text{atom}}$ atoms, which are classified into six types; C, N, O, S, P, and others. For each test compound, various 3D conformers are generated with OMEGA [29] by using the energy threshold value 25 kcal mol⁻¹ [30]. The lth conformer of the kth compound thus generated is denoted by Γ_k(l) with $l=1,\dots ,N_k^{\text{conf}}$, where $N_k^{\text{conf}}\lesssim 100$ is the number of generated conformers. The conformer Γ_k(l) is superposed onto Q^multi by rotating and translating Γ_k(l) with the operator R as RΓ_k(l). Then, the number of atoms in Q^multi which are in proximity to and having the same type as the ith atom in the conformer RΓ_k(l) is counted and stored in N^lig(i, RΓ_k(l), Q^multi). Using this, the measure of match between RΓ_k(l) and Q^multi is given by

$$S^{\text{match}}(R{\mathrm{\Gamma }}_k(l),Q^{\text{multi}})=\sum _{i=1}^{N_k^{\text{atom}}}{N}^{\text{lig}}(i,R{\mathrm{\Gamma }}_k(l),Q^{\text{multi}}).$$ (1)

Then, the degree of how RΓ_k(l) fits to the pocket is estimated by

$$S^{\text{config}}(R{\mathrm{\Gamma }}_k(l),P^t,Q^{\text{multi}})=S^{\text{match}}(R{\mathrm{\Gamma }}_k(l),Q^{\text{multi}})-\mathrm{\omega }{S}^{\text{coll}}(R{\mathrm{\Gamma }}_k(l),P^t),$$ (2)

where S^coll(RΓ_k(l), P^t) represents the degree of collision between the conformer RΓ_k(l) and the surface of the target protein P^t, and ω is the weight parameter to define the balance between the 1st and 2nd terms. We use ω = 2 in the present paper. See Ref. [8] for the discussion of the value of ω and the definition of S^coll(RΓ_k(l), P^t). Finally, the score of kth test compound for the target protein P^t is calculated as

$$S(k,P^t)=\frac{1}{N_k^{\text{conf}}}\sum _{l=1}^{N_k^{\text{conf}}}{\text{max}}_R[S^{\text{config}}(R{\mathrm{\Gamma }}_k(l),P^t,Q^{\text{multi}})],$$ (3)

which is obtained by maximizing S^config(RΓ_k(l), P^t, Q^multi) with respect to the position and orientation R of each conformer. We used this score S(k, P^t) to rank the compounds in the library.

Calculations in Eqs. 1–3 require advance preparation of R, the operator for superposition of a conformer of the test compound to the multiple-ligand template. In VS-APPLE, R is generated with the procedure based on the geometry hashing method [24]. Three atoms are picked up either from the multiple-ligand template or from a conformer of the test compound. For these triplet of atoms, a 3D coordinate system represented as (r₀, e₁, e₂, e₃) is defined as follows: The origin r₀ is defined by the position of one atom in the triplet. A unit vector e₁ is defined by the vector from that atom to another atom. Another unit vector e₂ is defined so that it is vertical to e₁ and the the other atom is also on the plane spanned by (e₁, e₂). e₃ is defined so that the coordinate system (e₁, e₂, e₃) satisfies the right-handed rule. Using the coordinate (r₀, e₁, e₂, e₃)_Γ defined by a triplet of atom in Γ_k(l) and the coordinate (r₀, e₁, e₂, e₃)_T defined by a triplet of atom in Q^multi, R is defined as the superposition of the former to the latter. Here, we denote the number of coordinates defined by a compound and that defined by a multiple-ligand template as N_Γ and N_T, respectively. As explained in Results and Discussion section, the computational time needed to screen compounds for a given target does not much depend on N_Γ but is almost proportional to N_T. Therefore, to reduce the computation time, it is important to reduce N_T by imposing some physically reasonable restrictions on sampling triplets from the template. In Ref. [8], N_T was reduced by two restrictions. One is the restriction which requires that the atoms in a triplet in the template should belong to the same chemical group. To meet this requirement, the triplet is selected only when the atoms were within 2.5 Å and belongs to the same ligand within the multiple-ligand template. With this restriction, N_T was reduced to N_T ≈ 4500–8500 (N_T ≈ 6600 on average) for the 13 targets used in the present paper.

N_T was further reduced by an assumption that the local structure important for binding is densely populated by atoms, corresponding to the consensus among different ligands, within the multiple-ligand template. Accordingly, from the multiple-ligand template, the atom triplet was selected only from the region where atoms are densely populated. The crowdedness of atoms around the coordinate $p={({\mathbf{r}}_0^p,{\mathbf{e}}_1^p,{\mathbf{e}}_2^p,{\mathbf{e}}_3^p)}_T$ was evaluated by

$$D^{\text{crowd}}(p)=\frac{1}{N_T}\sum _{q=1}^{N_T}\text{exp}(-d_{pq}/2\sigma ),$$ (4)

where σ = 1.0 Å and d_pq is distance between the coordinates ${({\mathbf{r}}_0^p,{\mathbf{e}}_1^p,{\mathbf{e}}_2^p,{\mathbf{e}}_3^p)}_T$ and ${({\mathbf{r}}_0^q,{\mathbf{e}}_1^q,{\mathbf{e}}_2^q,{\mathbf{e}}_3^q)}_T$,

$$d_{pq}=\sqrt{{({\mathbf{r}}_0^p-{\mathbf{r}}_0^q)}^2+\sum _{k=1}^3{[{\mathbf{e}}_k^p-{\mathbf{r}}_0^p-({\mathbf{e}}_k^q-{\mathbf{r}}_0^q)]}^2}.$$

N_T coordinates obtained from the multiple-ligand template were sorted in order of D^crowd(p) and top x% coordinates which have most crowded atomic environment in the template was used for generating R. In Ref. [8], x = 10% was used, which dramatically reduced the computation time. Because it is important to find an optimized x satisfying the speed and accuracy of screening, we examine in the present paper how the performance of VS-APPLE is affected by varying x. Here, we refer to this x as the percentage of used coordinate systems.

DUD data set

The performance of VS-APPLE is evaluated by using a test data set which comprises 13 target proteins and the corresponding active and decoy compounds. Here, actives are compounds that can bind to the target protein and decoys have similar structure and chemical features to actives but are presumed to have low binding affinity to the target. The DUD data set has been used for testing VS methods by checking whether the VS methods can discriminate a small number of actives from a large number of decoys [11]. The original DUD data set, however, contained actives which are similar to each other, which hinders the precise evaluation of the performance of VS methods. Using the mutually dissimilar actives selected by filtering and clustering the original DUD data set [9], a subset of the DUD data set was constructed [10]. We use this subset in the present paper, which is summarized in Table 1.

Table 1.

Dataset used for the performance test

Target protein (abbrev.)	PDB code	# of actives	# of decoys
Angiotensin converting enzyme (ace)	1o86	46	1797
Acetylcholinesterase (ache)	1eve	100	3892
Cyclin-dependent kinase 2 (cdk2)	1ckp	47	2074
Cyclooxygenase 2 (cox2)	1cx2	212	13289
Epidermal growth factor receptor (egfr)	1m17	365	15996
Factor Xa (fxa)	1f0r	64	5745
HIV reverse transcriptase (hivrt)	1rt1	34	1519
Enoyl ACP reductase InhA (inha)	1p44	57	3266
p38 mitogen activated protein (p38)	1kv2	137	9141
Phosphodiesterase (pde5)	1xp0	26	1978
Platelet derived growth factor receptor kinase (pdgfrb)	1t46	124	5980
Tyrosine kinase Src (src)	2src	98	6319
Vascular endothelial growth factor receptor (vegfr2)	1fgi	48	2906

Results and Discussion

In the present paper, the performance of VS-APPLE is evaluated by the AUC analyses [12,13]. For a given target protein, the AUC value is calculated as

$$AUC=\frac{1}{N^{\text{active}}}\sum _{n=1}^{N^{\text{active}}}(1-f_n),$$

where f_n is the fraction of decoys that have larger value of score S(k, P^t) than the nth ranked actives and N^active is the number of actives. We have 0 ≤ AUC ≤ 1 by definition, and the larger AUC indicates the better performance of the method examined.

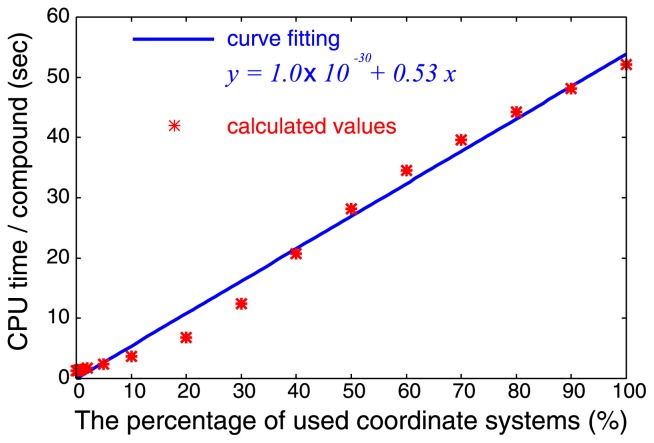
When applying VS-APPLE, we impose a restriction on the number of structural overlaps by focusing on limited part of multiple-ligand template: Only the regions where atoms are densely populated which have top x% value of D^crowd in Eq. 4 are used to define the superposition operator R. We find that the computation time needed for examining data set of Table 1 is almost linearly dependent on x as shown in Figure 2.

Figure 2.

Dependence of computational time on percentage of used coordinate systems for each compound. CPU time was measured on a PC with AMD Opteron 2.4 GHz processor. Calculated values are fitted by a linear function.

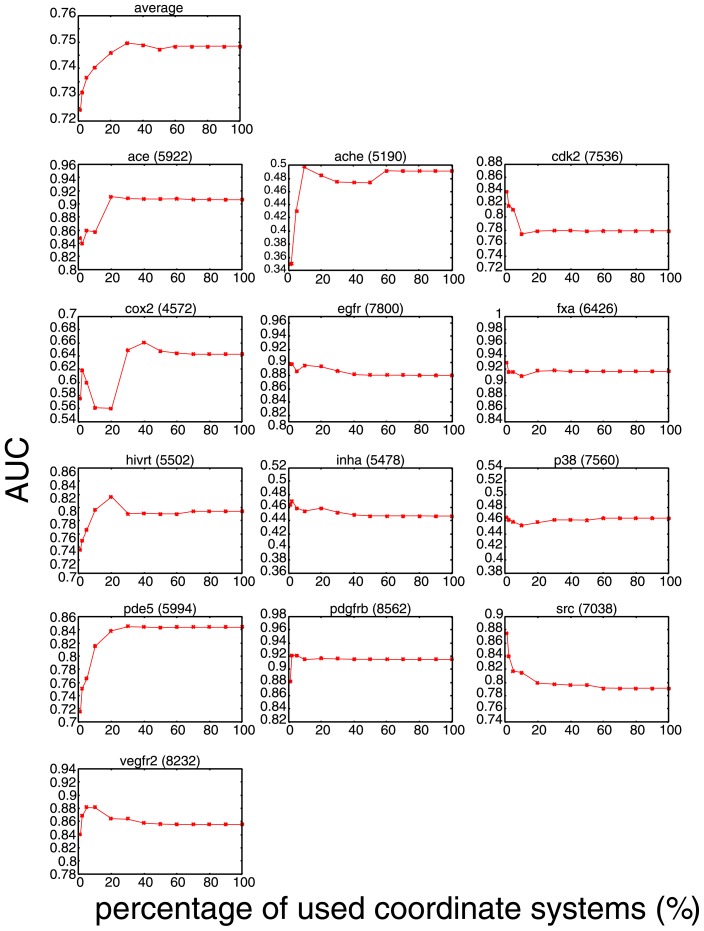
In Figure 3, the x dependence of the AUC value, AUC(x), is shown both for the average over 13 targets and for individual targets. The averaged AUC(x) is an increasing function of x, showing that using wider region in multiple-ligand template leads to better performance, but it saturates at x ≈ 30%. Therefore, the choice of x = 10% adopted in Ref. [8] gives a nearly optimal in terms of balance between speed and accuracy for general target proteins. For individual targets, however, the behavior of AUC(x) differs from target to target. Understanding the mechanism leading to these diverse behaviors is not straightforward, but this can be interpreted by the difference in shape and flexibility of individual binding pockets for some cases. In Figure 4, we show x-dependent changes of the regions with top x% value of D^crowd in Eq. 4 in the multiple-ligand templates for some target proteins.

Figure 3.

Dependence of AUC on the percentage x of most crowded coordinates used in the performance test. The number in a parenthesis shown on the right hand side of each target name represents the total number of the coordinate systems of the multiple-ligand template for each target.

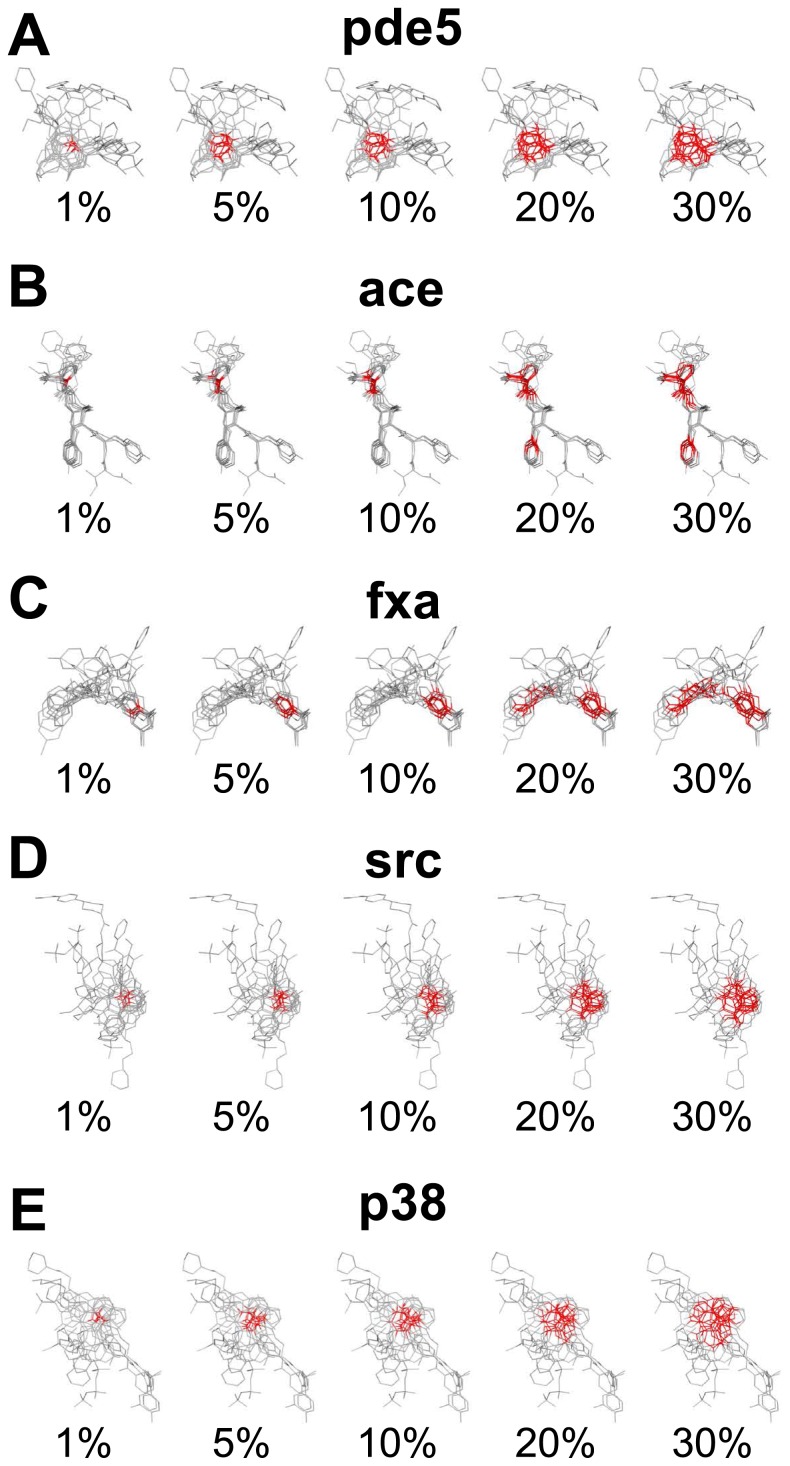
Figure 4.

Dependence of spread of densely populated regions of multiple-ligand templates on the percentage x of used coordinate systems for pde5 (A), ace (B), fxa (C), src (D) and p38 (E). The red colored atoms are ones that are assigned as the origin of reference frame system ranked in top x-percent of the crowdedness defined in Eq. 4.

Consistent with the averaged AUC(x), 5 among 13 targets, ace, ache, cox2, hivrt, and pde5, show increasing AUC(x) as functions of x. A typical example of x-dependent spread of densely populated regions is shown for pde5 in Figure 4(A). In Figure 4(A), we can see that the region of atoms with top x% value of crowdedness is localized for small x and that the region gradually expands with the increase of x to cover the larger part of the template. It is plausible to assume that the atoms in top x_satur percent at which AUC(x) reaches saturation (x_satur ≈ 30% for pde5) represent an important region of ligands for binding. Therefore, the present result with a fairly large x_satur suggests that the important region of ligands for binding is somewhat broadly distributed rather than highly localized within the pocket of pde5. Another example of this class is ace, which shows an interesting behavior. For ace, the steep increase of AUC(x) at x ≈ 10% corresponds to the value of x where the sampled region splits to include the second densely populated region which is distinctively separated from the first densely populated region as shown in Figure 4(B). Comparison of these results shows that the shape and distribution of densely populated regions should reflect the flexibility of the binding pocket of the target protein.

In contrast to the above-mentioned examples, the AUC(x)s for other 6 targets, egfr, fxa, inha, p38, pdgfrb, and vegfr2 are nearly constant for all x: the differences between AUC(1%) and AUC(100%) are less than 0.05. A typical example of this class is fxa and its x-dependent spread of densely populated regions is shown in Figure 4(C). Since the largest AUC(x) was achieved by x = 1% and expanding the sampling region has little effect on AUC(x), it is suggested that the dense region of x < 1% is sufficient for characterizing the important region for binding.

In addition to the two classes discussed above, there is the other class that shows the rapid decrease of AUC(x) is accompanied by the broadening of sampling region. The members of this class are cdk and src. For these cases, the single sampling region simply grows as x increases as shown in Figure 4(D). Though the precise reason for this decrease of AUC(x) is not clear at the present analyses, one possible explanation is that extension of the sampling region leads to the deviation from the important region for binding. However, because the absolute values of AUC(x) are kept large for large x for both cdk and src, we can see that the consensus region, which may not perfectly overlap with the important region in these cases, should reflect the meaningful binding information.

It should be noted that for the average value over 13 targets, AUC(1%) is larger than the AUC value obtained with other methods [8] such as ROCS, DOCK, and GOLD. This superiority of VS-APPLE even for small x also shows the importance of dense atomic region of the multiple-ligand template for screening compounds. Although the performance of VS-APPLE is high on average, there are some targets that show poor performance (AUC is less than 0.5); they are ache, inha, and p38. A plausible reason for the poor performance is that the multiple-ligand templates we used here did not correctly reflect the pocket environments. For example, it is well known that p38 has two largely distinct binding conformations, DFG-in and DFG-out, and that their binding sites to their ligands are spatially largely separated [14]. However, as shown in Figure 4(E), the multiple-ligand template for p38 we used here has only a single densely populated region and thus it should not correctly reflect the highly flexible pocket environment of p38. To improve the performance for these targets, we expect that the appropriate selection of template ligands suited for either one of multiple protein configurations is needed. This is an important subject left for future studies.

The relations between the features of the protein binding pocket and the performance of VS method suggested by the present analyses should help improvement of the VS method. For example, definition of the score function can be modified by putting different weights on S^config(RΓ_k(l), Q^multi) depending on the crowdedness of the coordinates defining R. In addition, investigation of structural features of the binding pockets surrounding the densely populated regions within multiple-ligand template will also help to choose suitable multiple-ligand template and the way to sample its structure. An important avenue of research is to use the analyses with VS-APPLE to investigate the flexibility of the binding pocket: The more detailed analyses of the relation between pocket flexibility and the performance of VS-APPLE should help further understanding of protein-ligand binding mechanisms.

Conclusion

A recently developed VS method, VS-APPLE, in which the structure data of multiple protein-ligand complexes are extensively used, shows high performance when it is tested by using a subset of DUD data set with the AUC analyses. Its performance depends on the way of sampling structure of the multiple-ligand template, and the analyses in the present paper showed that the region with densely populated atoms within the multiple-ligand template plays significant roles to screen test compounds. It has been observed as a general tendency that sampling wider region within the multiple-ligand template improves the performance of VS-APPLE, but the performance saturates at x ≈ 30%. The analyses of the performance of the VS method, therefore, provide clues to understanding protein-ligand interactions and improving VS methods.

Significance.

Virtual Screening (VS) is an important tool in a drug discovery process. Recently, we developed a new VS method, VS-APPLE, which was shown to be one of the best method according to the area under the curve metric. As the likeliness of being active, VS-APPLE uses 3D similarity between a test compound and a multiple-ligand template, which is constructed from multiple known actives. This paper examines what factors of a multiple-ligand template in VS-APPLE are important for accurate screening and shows that consensus region of the multiple-ligand templates is the key for high performance.