Multi-modal Learning-based Pre-operative Targeting in Deep Brain Stimulation Procedures

Abstract

Deep brain stimulation, as a primary surgical treatment for various neurological disorders, involves implanting electrodes to stimulate target nuclei within millimeter accuracy. Accurate pre-operative target selection is challenging due to the poor contrast in its surrounding region in MR images. In this paper, we present a learning-based method to automatically and rapidly localize the target using multi-modal images. A learning-based technique is applied first to spatially normalize the images in a common coordinate space. Given a point in this space, we extract a heterogeneous set of features that capture spatial and intensity contextual patterns at different scales in each image modality. Regression forests are used to learn a displacement vector of this point to the target. The target is predicted as a weighted aggregation of votes from various test samples, leading to a robust and accurate solution. We conduct five-fold cross validation using 100 subjects and compare our method to three indirect targeting methods, a state-of-the-art statistical atlas-based approach, and two variations of our method that use only a single modality image. With an overall error of 2.63±1.37mm, our method improves upon the single modality-based variations and statistically significantly outperforms the indirect targeting ones. Our technique matches state-of-the-art registration methods but operates on completely different principles. Both techniques can be used in tandem in processing pipelines operating on large databases or in the clinical flow for automated error detection.

I. Introduction

Deep brain stimulation (DBS), which sends electrical impulses to specific deep brain nuclei through implanted electrodes, has become a primary surgical treatment for movement disorders such as Parkinson’s disease (PD) [1]. The key to the success of such procedure is the optimal placement of the final implant at millimetric precision level to produce symptomatic relief with minimum or no adverse effects. Traditionally, this is achieved in two stages: a surgical team 1) selects an approximate target location prior to the surgery via visual inspection of anatomic images and 2) adjusts this position based on electrophysiological activities during the surgery. While inaccuracies in pre-operative targeting can be corrected by the intra-operative stage, it may prolong the surgery for hours with the patients awake and increase risk such as intra-cranial hemorrhage [2]. Consequently, accurate pre-operative planning is highly desirable.

Over the past few decades, numerous efforts have been made to optimize the pre-operative target selection. These can be categorized into indirect and direct targeting. Indirect targeting considers the target position as a fixed point in the stereotactic space defined by visible anatomical landmarks, i.e., the anterior commissure (AC), the posterior commissure (PC) and the mid-sagittal plane (MSP). Various approaches have been proposed to facilitate this task [3-4]. Despite being commonly used, this targeting strategy is limited by the lack of consensus on an ideal anatomic point as the target [5], as well as a failure to account for anatomical variations across patients, i.e., variable width of the third ventricle. On the other hand, direct targeting aims at localizing the target without relying on fixed coordinates. Due to limited contrast in regular T1-weighted (T1-w) Magnetic Resonance (MR) images, T2-weighted (T2-w) sequences are often acquired for better visualization of the targets. However, T2-w imaging alone does not provide sufficient or consistent contrast, which may lead to a discrepancy between the target positions identified in T2-w images and the ones localized by means of electrophysiological recordings [6]. Alternatively, direct targeting can be assisted with printed and digitized anatomical brain atlases, histological brain atlases, and probabilistic functional atlases alongside non-rigid registration [7-10]. Once nonlinearly mapped to individual pre-operative brain images, such atlases may provide anatomical or/and functional borders of the target nuclei on standard T1-w images.

A recent validation study shows that, using statistical atlases created from a large population, automatic target prediction exceeds the precision of six manual approaches [11]. Routine target prediction is thus achievable but registration failures, especially when non-rigid registration algorithms are used, happens and are difficult to detect automatically. It is thus desirable to develop robust error detection algorithms. One possible approach is to rely on the analysis of the deformation field but defining quantitative error detection criteria is challenging. Another approach, which is the one proposed herein, is to develop target localization methods that operate on different principles and thus provide another source of information. In this approach agreement between sources would increase confidence in the predictions while disagreement would indicate a possible error.

Recently, discriminative machine learning techniques have gained popularity for anatomy localization and segmentation. Considering targets as functional landmarks localized anatomically consistently across subjects, we can formulate this problem into a supervised learning framework. One challenge is that as targets are localized in homogeneous region, image features extracted from the target may not be discernable enough to distinguish its location from adjacent neighbors. Surrounding structures, however, could be used to infer the target location. In fact, this is the underlying principle employed in indirect targeting, which relates the location of the AC, PC, and MSP to a target point. Castro et al. have also shown that segmentations of the lateral ventricle, third ventricle, and interpeduncular cistern are useful to improve targeting accuracy [12]. Here, we propose to use regression forests to tackle this problem. Multi-variant regression forests, which combine random forests with Hough transform, aim to learn multi-dimensional displacement vectors towards an object through a multitude of decision trees [13]. By aggregating predictions made by various test samples, it allows each sample to contribute to an optimal target position with varying degrees of confidence. This is in direct contrast to indirect targeting or direct targeting as done in [12], which require informative structures to be pre-specified. Recently, this regression forests technique has been applied to detect points to drive an active shape model on 2D radiographs [14], to identify the parasagittal plane in ultrasound images [15], and to initialize a non-rigid deformation field in MR images [16]. These successful applications in medical image analysis show promise for target localization.

In this article, we develop a generic multi-modal learning system using T1-w and T2-w images for pre-operative targeting. We first apply a learning-based technique to spatially normalize the images in the stereotactic space as used by indirect targeting, and then employ regression forests to learn the displacement vectors towards the target as the latent variable. Targets predicted by this model are spatially constrained via the use of spatial features similarly to indirect targeting, while also accounting for variability of surrounding structures with varying confidence levels by incorporating multi-contrast contextual information. This is independent of the atlas-based registrations, thus permitting quality assurance when used together with atlas-based methods.

II. Method

A. Input Data

In this study, we retrospectively examined 100 PD patients with unilateral or bilateral implantations that target the Subthalamic Nucleus (STN) from a data repository that gathers patients’ data acquired over a decade of DBS surgeries. Every subject was consented to participate in this study. For each subject, this repository contains the clinical active contact locations that are automatically extracted from the Medtronic four-contact 3389 lead in the patient post-operative CT image and projected onto the corresponding preoperative MR T1-w image using a standard intensity-based rigid registration. We use these points as the ground truth target positions for training and evaluation.

The input image data for this study include a T1-w image and a T2-w image of each subject, all acquired as part of the normal delivery of care. T1-w MR image volumes with approximately 256×256×170 voxels and 1 mm in each direction, were acquired with the SENSE parallel imaging technique (T1W/3D/TFE) on a 3 Tesla Phillips scanner (TR = 7.92 ms, TE = 3.65 ms). T2-w MR image volumes with approximately 512×512×45 voxels and typical voxel resolution of 0.47×0.47×2 mm³, were acquired with the SENSE parallel imaging technique (T2W/3D/TSE) on the same scanner (TR=3000 ms, TE = 80 ms).

B. Learning-based Landmark / Plane Identification for Image Pre-alignment

Before training or testing, we first spatially normalize the images using a learning-based technique as proposed by Liu et al. [4]. To do this, a different set of 56 subjects were selected from the data repository, each with a T1-w image and manual annotations of the AC, PC, and MSP. Random forests were used as a regressor to learn a nonlinear mapping between the contextual features of a point and the probability of this point being the AC/PC or in the MSP. After identifying the AC, PC, and MSP, we compute a rigid transformation from the original image space to the stereotactic space used in indirect targeting [7]. We rigidly align the T2-w images with their corresponding T1-w images of the same subject using intensity-based techniques. The normalization transformation is applied to both co-registered sequences and these images are resampled at 1mm isotropic resolution for subsequent training and testing.

C. Problem Formulation

We use a voxelwise solution based on regression forests to learn the displacement of a voxel to the target (we train one forest for each side of the brain). As there is substantial shape variability in the cerebral cortex across subjects, it would be difficult for the model to relate a point in this area with diverse appearances to a target. To simplify model training, we define a bounding box that roughly covers the deep brain and constrain the samples to be uniformly drawn from this region.

Each training sample is associated with a heterogeneous high dimensional feature vector and a 3D displacement vector $\overrightarrow{\text{d}}[\text{dx},\text{dy},\text{dz}]$ from its position to the target. Thousands of features are used, which consist of:

• Spatial features, which are the spatial coordinates (x, y, z) of the voxel in the stereotactic space.

• Multi-modal intensity contextual features, which are the mean intensity differences between two cuboids [17]. Those cuboids are randomly displaced by varying amounts to capture multi-scale textural context variations. We compute a number of such features from each image sequence independently.

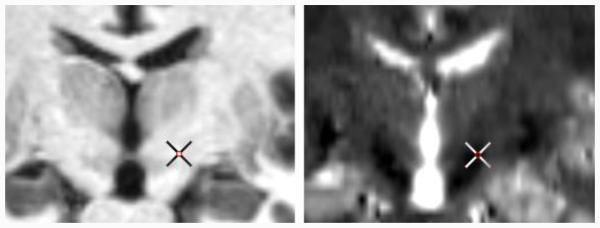
Spatial features cluster training samples according to their distances to the target. Using these features along is equivalent to a simple average of the target points of training volumes. This is similar to an indirect targeting estimation, which can be obtained as a byproduct of the pre-alignment step. Intensity features allow models to capture anatomical variations and adjust target positions accordingly. Moreover, by extracting such features from each sequence, we account for various appearances of different modalities that may complement each other, as shown in Fig. 1.

Figure 1.

Co-registered T1-w (left) and T2-w images (right) of one subject, with the cross indicating the ground truth target point.

D. Regression Forests Training

We use a total of 100 regression trees to construct the forest. To build each tree, a bootstrap of two thirds of training samples is randomly chosen and fed to the root node of the tree. Given the training samples ${\{\overrightarrow{f_n},\overrightarrow{d_n}\}}_{n=1}^{N^{\prime }}$ at a particular node, a feature f^m and a threshold t are selected to split the data, which minimize the mean square error MSE:

$$MSE\left(t\right)=MSE\left(\{\overrightarrow{d_n}:f_n^m<t\}\right)+MSE\left(\{\overrightarrow{d_n}:f_n^m\ge t\}\right)$$ (1)

Node splitting is done recursively, and stops when a certain tree depth is reached or the best split threshold cannot be found. At each leaf node, we obtain a histogram of $\overrightarrow{d}$ of the voxels reaching this node. Assuming uncorrelated univariate Gaussian distribution, we store the mean and variance for each dimension as a compressed representation of the histogram.

E. Regression Forest Testing

During testing, test samples traverse all trees in the forests. Starting from the root node, test samples recursively visit the left or right child based on the binary feature test stored at this split node until a leaf node is reached. To aggregate votes of each test sample from each tree, a range of styles of voting can be used, e.g., casting a single vote per tree as the mean displacement vector, or using multiple votes from the training samples. Cootes et al. compared different voting strategies and showed that a single vote per tree performed the best in terms of accuracy and speed [18]. In this paper, we allow each tree to cast a single vote as the mean displacement vector, and measure the confidence of this vote by the variances $\overrightarrow{\text{v}}:\text{w}=e^{-\alpha \cdot \parallel \overrightarrow{v}\parallel }$. To increase robustness, the final prediction is made using the weighted mean shift method with a Gaussian kernel [19]. This point is then projected back to the original image space using the transformation matrix computed before.

F. Comparison to other methods

Provided with the pre-aligned images in the stereotactic space as done in Section II.B, the indirect targeting strategy can be readily applied. We hereby localize the targets using two widely used indirect targeting methods from the literature. To account for positional variations between our study and the ones published in the literature, we also conduct an experiment that uses training volumes to obtain an indirect estimation. In addition, we compare ours to a state-of-the-art statistical atlas-based method as validated in [11], which was shown to outperform six manual targeting approaches. The following summarizes the experiments we have performed:

• Indirect targeting using the stereotactic coordinates (±12 mm lateral, −3mm anterior, −4 mm superior) as the center of the motor territory of the STN [20] (referred to as IND1).

• Indirect targeting using the stereotactic coordinates (±11.8 mm lateral, −2.4 mm anterior, −3.9mm superior) as a representation of the centroid of active contacts [20] (referred to as IND2).

• Indirect targeting using the stereotactic coordinates of the average active contact position of the training volumes in our dataset (referred to as IND3).

• Statistical atlas-based approach (referred to as SA). Specifically, a statistical atlas is created by performing a series of affine, local affine, and local non-rigid registrations between each training volume and a pre-specified anatomical atlas, and projecting the target locations from the training subject to this reference space. The centroid of all those projections is taken as a robust statistical representation of the target and projected onto a test subject through a series of registrations as the predicted target.

To evaluate the effect of multi-modality images, we refer to our method using T1-w and T2-w images as RF-T1+T2, and compare it to the ones using only a single modality:

• Regression forests-based methods using only T1-w or T2-w images (referred to as RF-T1 and RF-T2 respectively). Specifically, the methodology is the same as described above, except that the intensity contextual features are extracted from only T1-w or T2-w images. The dimensionality of the feature vector remains the same as the one in RF-T1+T2.

III. Results

In this study, we conduct a five-fold cross validation, i.e., using 80 subjects for training and the rest 20 for testing and repeating it five times.

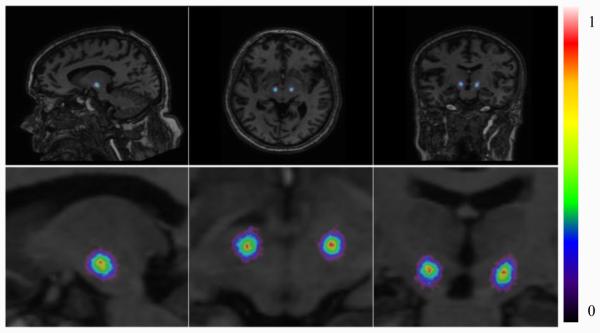
For visualization purpose, we compute a response map as the weighted aggregation of all votes, with predictions at each voxel scaled to the interval [0, 1]. An example for one test subject is shown in Fig. 2. This illustrates the tightness of the predictions made by all test samples.

Figure 2.

Response map for a test subject: a full (top) and a zoomed (bottom) view.

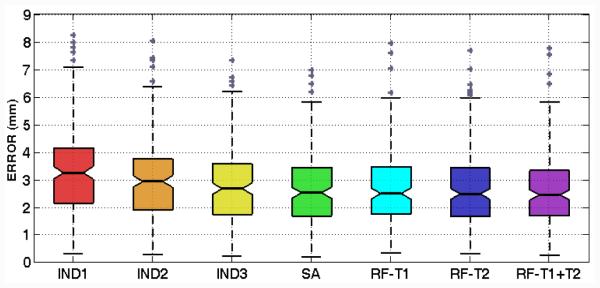
To quantify the targeting accuracy, we define the targeting error as the 3D Euclidean distance between the prediction and the ground truth. A box plot of those errors for all cases is shown in Fig. 3, with their mean and standard deviation reported in Table I. Our method performs better than all indirect targeting methods and comparably to the statistical atlas-based method. Moreover, the use of multi-modal images results in a reduced overall error in contrast to using only T1-w or T2-w images.

Figure 3.

Boxplot of targeting errors using different techniques.

TABLE I.

MEAN AND STANDARD DEVIATION OF TARGETING ERRORSUSING DIFFERENT TECHNIQUES

Error (mm)	IND1	IND2	IND3	SA	RF-T1	RF-T2	RF-T1+T2
Mean	3.26	3.02	2.81	2.68	2.72	2.68	2.63
Std.	1.58	1.53	1.36	1.35	1.37	1.41	1.37

In addition, we perform one-sided paired Wilcoxon signed-rank tests to test whether the medians of errors using our method are smaller than those using the other methods. The p values are shown in Table II, with values lower than the significance level of 0.05 marked in red bold. As shown in Table II, our method significantly reduces the targeting errors compared to all indirect targeting methods, while the difference between our method and the statistical atlas-based method is not found to be significant.

TABLE II.

P VALUES OF WILCOXON TESTS BETWEEN THE TARGETING ERRORS USING OUR METHOD AND THOSE USING OTHER METHODS

P	IND1	IND2	IND3	SA	RF-T1	RF-T2
RF-T1+T2	0.00	0.00	0.00	0.25	0.00	0.13

IV. Conclusion

In this paper, we propose a multi-modal learning-based method using regression forests to automatically localize the target in pre-operative MR brain scans. By taking advantage of a large dataset of past patients, our approach improves upon indirect targeting by tuning this estimate to patient’s individual anatomy, and combines the strength of different direct targeting methods by exploiting the multi-contrast information. Our results show that using both modalities outperforms using either one alone. Our technique also does not require the segmentation of anatomic structures or non-rigid registration. It can be used in tandem with non-rigid registration methods in clinical processing pipelines to develop robust error prediction schemes.

Results from five-fold cross validation have shown that our approach is accurate and robust with 2.63±1.37mm targeting errors, which matches the precision of the state-of-the-art statistical atlas-based methods and exceeds six manual methods as compared in [11]. We have also found a high correlation (ρ=0.83) between targeting errors made by our approach and the ones made by statistical atlas-based method. This is likely because of the discrepancy between imaging and neurophysiology, which causes both imaging-based methods to induce relatively larger errors for some cases. In the future, we will explore electrophysiological data from the past patients to account for this discrepancy.

Our method is also fast. Once the models are trained on the Advanced Center for Computing and Research Education (ACCRE) Linux cluster at Vanderbilt University, the testing pipeline takes approximately 40 seconds on a standard PC with 4 CPU cores and 8GB RAM. This compares favorably to atlas-based registration methods, which may take from several minutes to hours to run.