Fundamental High-Speed Limits in Single-Molecule, Single-Cell, and Nanoscale Force Spectroscopies

Abstract

Force spectroscopy is enhancing our understanding of single-biomolecule, single-cell, and nanoscale mechanics. Force spectroscopy postulates the proportionality between the interaction force and the instantaneous probe deflection. By studying the probe dynamics, we demonstrate that the total force acting on the probe has three different components: the interaction, the hydrodynamic, and the inertial. The amplitudes of those components depend on the ratio between the resonant frequency and the frequency at which the data are measured. A force–distance curve provides a faithful measurement of the interaction force between two molecules when the inertial and hydrodynamic components are negligible. Otherwise, force spectroscopy measurements will underestimate the value of unbinding forces. Neglecting the above force components requires the use of frequency ratios in the 50–500 range. These ratios will limit the use of high-speed methods in force spectroscopy. The theory is supported by numerical simulations.

Force spectroscopy methods are expanding our understanding of the mechanics of biomolecules, cells, polymers, and hybrid materials as well as the interactions between different biomolecules and/or materials. The measurement of a variety of ligand–receptor interactions¹⁻³ and protein unfolding processes⁴ represented key landmarks in the understanding of how single biomolecules respond to external forces. The capability to map mechanical properties with nanoscale spatial resolution of a large variety of surfaces that range from cells to semiconductors represents another major achievement of force spectroscopy.⁵⁻⁷ Nanoscale force spectroscopy measurements are revealing the changes at both the single cell and extra cellular matrix level that accompany the evolution of several diseases.⁸⁻¹⁰

High-speed atomic force microscopy (AFM) has been developed to generate AFM images at video rate.¹¹⁻¹³ An analogous high-speed method has been developed to record force–distance curves.¹⁴ These approaches are based on the miniaturization of the cantilever and the piezoelectric elements that produce the xyz displacements. The miniaturization enables increasing the fundamental resonances of the different mechanical elements, which, in turn, suppress the coupling between the above resonances and the frequencies of the moving elements.¹²

Force spectroscopy is based on the acquisition of force–distance curves (force curves) with an AFM setup (see Figure 1). The tip functionalization method, the biomolecules, or the type of distance modulation used in the experimental setup has led to different force spectroscopy approaches. The most common are single-molecule force spectroscopy,^3,15 single-cell force spectroscopy,¹⁶ force volume,⁵ or peak force tapping.¹⁷ The first two approaches are applied to study biomolecular or cell adhesion processes at the single-biomolecule level. The other two methods are applied to study the nanomechanical response of cells, polymers, and organic and inorganic interfaces. The latter approaches will be called nanoscale force spectroscopy. From the dynamics of the cantilever-tip system, the above approaches are equivalent because they are described by the same equation of motion.

Figure 1.

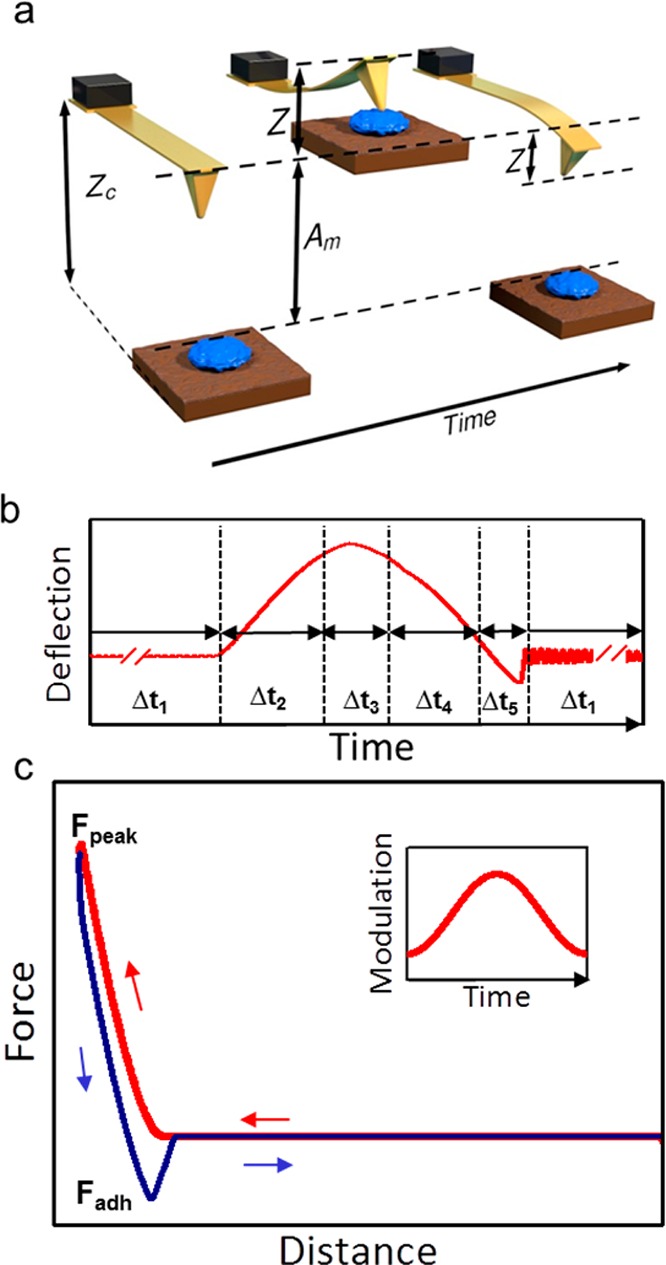
(a) Force spectroscopy. Scheme of the main regions of the tip displacement during the acquisition of a force–distance curve. (b) Instantaneous tip deflection for an interaction force model that considers that adhesion forces are present only once the tip has reached mechanical contact with the sample. Δt₁ is the time interval in the out-of-contact regions (approaching and retracting from the sample). Δt₂ (approaching) and Δt₄ (retraction) are the time intervals suitable for Young’s modulus measurements. Δt₃ is the time interval suitable for establishing a feedback loop on the peak force. Δt₅ is the time interval suitable for unbinding force measurements. The inset shows a sinusoidal tip distance modulation in a force spectroscopy experiment. (c) Force model used to generate the data of (b). The hysteresis in the adhesion force produces the mismatch between the force curve obtained during the approach and retracting sections of the cycle.

We note that a complete theory of single-molecule, single-cell, or nanoscale force spectroscopies involves two independent theoretical elements. First, there is the dynamics of the cantilever-tip system that supports the relationship between the measured force–distance curve and the interaction force between the molecules of interest. The other element is the theory that enables transforming the features measured in a force–distance curve into either unbinding forces or energies (Bell–Evans model)¹⁸⁻²⁰ or into Young’s modulus maps of the sample (contact mechanics models).^5,6 The second element has been the subject of intense scientific activity, while the first element, to our best knowledge, has never been addressed. The development of high-speed AFM methods^{12−14,21−23} motivates the relevance and interest of the theory of the cantilever-tip dynamics in force spectroscopy.

Single-molecule (cell) and nanoscale force spectroscopies postulate the existence of a linear relationship between the interaction force and the cantilever deflection. Here we present the theory of the dynamics of the cantilever-tip system in force spectroscopy. The theory shows the cantilever deflection bears contributions from three different sources: the tip–sample interaction, the hydrodynamic force, and the inertial force. We show that the recorded force–distance curve provides a faithful measurement of the interaction force acting between the tip and the sample when the hydrodynamic and inertial force components are negligible. The proportionality between the cantilever deflection and the interaction force depends on the frequency ratio between the resonant frequency of the cantilever and the frequency at which the distance is modulated. We study the effect of the frequency ratio on three different parameters: the peak-force value for feedback purposes, the stiffness or Young’s modulus values, and unbinding forces. The effect of the frequency ratio is more dramatic on the unbinding force than on the other two parameters. A frequency ratio in the 10–50 range is suitable to perform imaging with a feedback loop in the peak force value. A ratio above 50 is needed to get reliable values of the sample stiffness, while the measurement of unbinding forces with a relative error below 5% requires a ϖ = 300. The use of high ratios would make it hard to combine force spectroscopy with current high-speed AFM operation. Numerical simulations confirm the validity of the theory.

Results and Discussion

Theoretical Model

The theory and considerations reported here apply to all quasistatic force spectroscopy methods such as single-molecule force spectroscopy, single-cell force spectroscopy, force volume, or peak force tapping. These methods are different in terms of the tip functionalization chemistry, tip size, feedback loop, or the type of tip–sample periodic displacement (triangular, trapezoidal or sinusoidal). However, the above factors do not affect the overall dynamics of the tip–sample system.

The theoretical model is developed for a sinusoidal displacement. The use of sinusoidal waves simplifies the mathematical treatment and the interpretation of the measured material properties because they have a single Fourier component. We have simulated the tip–sample displacement by using both sinusoidal and triangular waves. The simulations show that both types of displacements produce the same phenomenology (see below). The conclusions derived in this section are general. They apply for trapezoidal or triangular displacements. In fact, one the latest nanoscale force spectroscopy methods uses sinusoidal displacements.¹⁷

In force spectroscopy, the instantaneous tip–surface interaction force F_ts is postulated as

1

where k is the static force constant and z(t) is the instantaneous cantilever-tip’s deflection. However, neither the above hypothesis nor its applicability range has ever been demonstrated.

In a force spectroscopy experiment the distance between the tip and the sample surface is periodically modulated while the cantilever deflection is measured. This distance modulation is different from the situation in tapping mode AFM. There, the cantilever is directly excited at or near its resonant frequency and the feedback modulates the piezo z to keep the amplitude at a constant value.²⁴

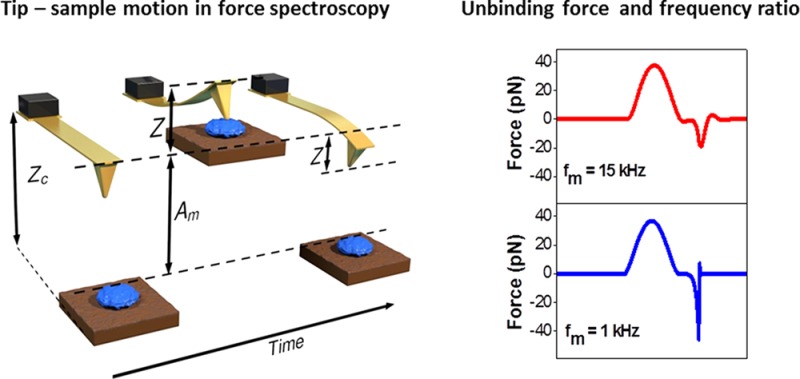
The main control elements of a force spectroscopy experiment operated with a feedback in the maximum value of the force exerted on the sample (peak force) are depicted in Figure 2. The topography feedback processes the instantaneous force and controls the mean cantilever–sample distance to reach a maximum value of the force exerted on the sample. The tip–sample surface separation is modulated by introducing a sinusoidal displacement in the sample support base with respect to the cantilever base (Figure 1a) or vice versa (Figure 1b).

Figure 2.

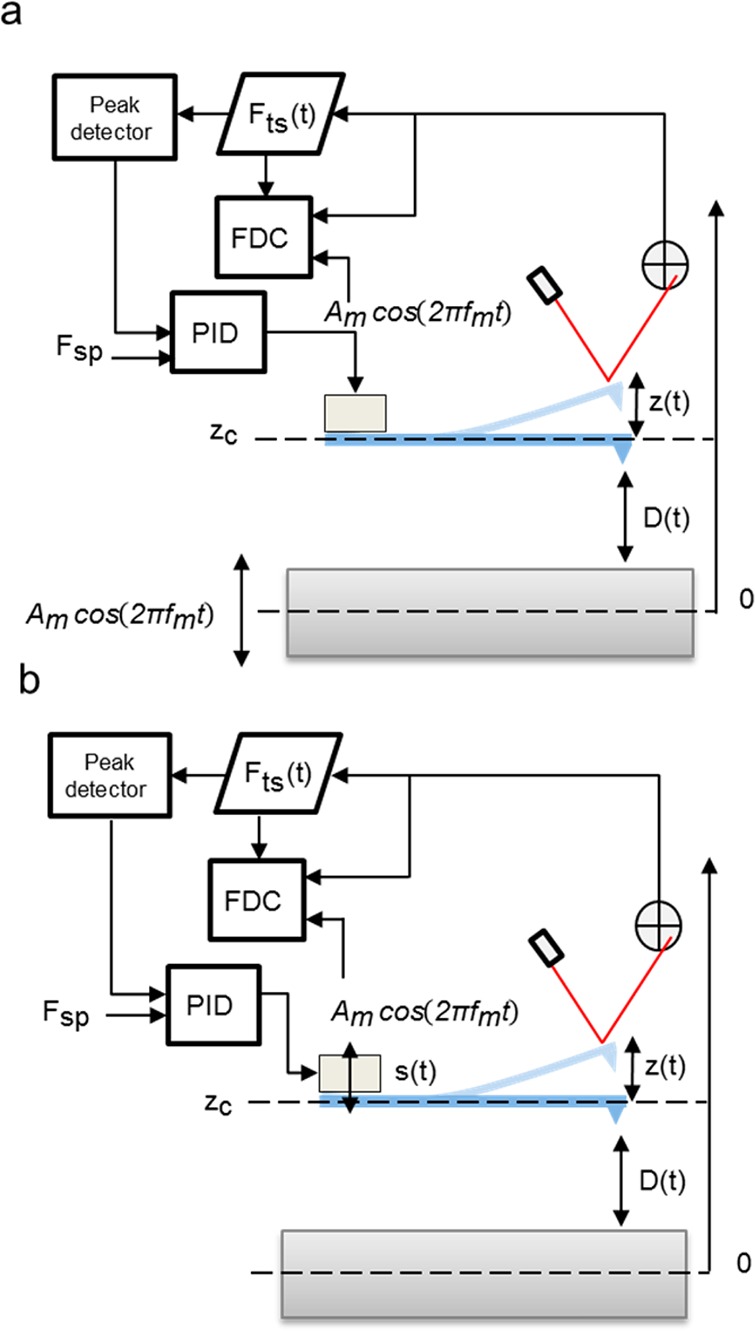
Block diagrams and distances in a force spectroscopy experiment. The tip–sample separation is modulated by a sinusoidal wave. (a) The distance is modulated by moving the sample support with a frequency f_m. (b) The distance is modulated by moving the cantilever base with a frequency f_m. In both cases ω_m = 2πf_m. PID stands for proportional-integral-derivative controller; FDC stands for force–distance curve.

Let us start by proposing the equation of motion when the modulation of the distance is applied to the sample support base. In this case, the tip displacement is given by the projection of the Euler–Bernoulli beam equation at x = L where L is the cantilever length,²⁵

2

where m is the effective cantilever mass, Q the quality factor (fundamental mode), and ω₀ the natural angular resonant frequency (fundamental mode). The instantaneous tip–surface distance D(t) is given by

3

where z_c, A_m, and ω_m are respectively the probe height, the amplitude, and the angular frequency at which the distance is modulated. The sample surface is chosen as the origin for the distance. The cantilever deflection z(t) is measured with respect to its rest (undeflected) position.

The key point expressed in eq 2 is that in a force spectroscopy experiment, the interaction force F_ts has three different force contributions: cantilever restoring, inertia, and hydrodynamic. To emphasize the frequency-dependent character of the z deflection, we introduce a normalized time variable τ:

4

Then eq 2 becomes

5

with

6

Equation 5 expresses the tip motion in terms of the frequency ratio ϖ. If distances and forces are expressed in the MKS unit system, we can estimate the relevance of the different terms in the second right-hand side of eq 5. Force constant values of common AFM cantilevers are in the 0.01 to 100 N/m range; Q values are in the 1 (liquid) to 500 (air) range. For k = 1 N/m, Q = 100, and ϖ = 100, the prefactors in eq 5 (N/m) for the inertial, hydrodynamic, and restoring terms are respectively 10^–4, 10^–2, and 1. We deduce that for ϖ ≫ 1 the inertial and hydrodynamic terms are negligible with respect to the restoring force of the cantilever; then the instantaneous force is well approximated by the restoring force

7

Let us now deduce the equation when the modulation of the distance is applied to the cantilever base. In this case, the inertial and hydrodynamic terms depend explicitly on the distance, while the restoring force depends on the cantilever deflection:

8

9

By introducing the normalized time τ and expressing s in terms of z(t), eq 8 becomes

10

To obtain an asymptotic expression (ϖ ≫ 1) is less obvious than before because of the dependence of the value A_m could be a few hundreds of nm. In general, for high-frequency ratios eq 10 leads to

11

Comparison between Theory and Numerical Simulations

To determine quantitatively the validity of eq 1 to recover the tip–sample interaction force from force–distance curves, we have performed a numerical simulation analysis. The use of numerical simulations is firmly established in dynamic AFM.^24,26−31 First, we introduce a tip–surface force model F_ts; then we solve numerically the nonapproximated equation of motion, respectively, eq 5 and eq 10, to determine z(τ). Finally, the force is reconstructed by using eq 1, and it is compared with the interaction force provided by the model. We have used different models for the tip–surface force such as Hertz and Derjaguin–Muller–Toporov with the inclusion of a van der Waals attraction force. These models and their parameters are fully described in the dynamic AFM simulations code dForce.³¹ We have also simulated the presence of unbinding forces of the ligand–receptor type (see below).

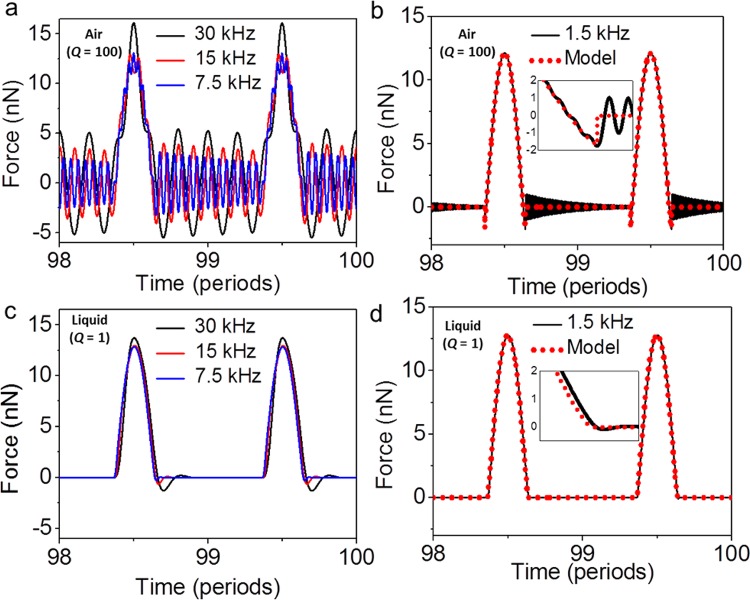
Figure 3 shows a comparison between the interaction force (model) and the force reconstructed by using eq 1 for ϖ ratios of 5, 10, 20, and 100. Figure 3a corresponds to a cantilever with a Q = 100 (air), while Figure 3b describes a cantilever with Q = 1 (liquid). In the simulations, we have used the following parameters: E_eff = 1 GPa, H = 0.5 eV (air) and H = 0 eV (liquid), f₀ = 150 kHz, k = 5 N/m, A_m = 15 nm, z_c = 10 nm. In all cases E_tip = 170 GPa and tip radius R = 5 nm.

Figure 3.

Dependence of the time-varying force reconstructed by using eq 1 on the frequency at which the distance is modulated for air (Q = 100) and liquid (Q = 1). (a) The sample support is displaced at ϖ = 5, 10, 20 (Q = 100). (b) The sample support is displaced at ϖ = 100 (Q = 100). The dashed line shows the model force. (c) The sample support is displaced at ϖ = 5, 10, 20 (Q = 1). (d) The sample support is displaced at ϖ = 100 (Q = 1). The dashed line shows the interaction force (model). The insets show the force in the vicinity of the snap-off region. Simulation parameters: a₀ = 0.2 nm E_eff = 1 GPa, H = 0.5 eV, f₀ = 150 kHz, k = 5 N/m, Q = 100, R = 5 nm, A_m = 15 nm, z_c = 10 nm.

For ϖ = 5 the force reconstructed by using eq 1 oscillates at the actual resonant frequency. The oscillatory behavior comes from the hydrodynamic and inertial terms components of the force. These components give rise to a transient oscillatory behavior. The simulation shows that for relatively small frequency ratios (1–10) the transient component dominates the cantilever deflection. A noticeable ringing is observed in the out-of-contact region. The amplitude of the ringing is about 50% of the peak force value (∼12 nN). The value of the transient term is reduced by increasing the ratio. At ϖ = 20 the amplitude of the ringing in the out-of-contact region amounts to about 25% of the peak force value. The transient term has a dramatic effect in the measurement of the adhesion force. At ϖ = 100, the measured peak and the maximum of the force (model) coincide (Figure 3b). However, the inset shows that the ringing introduces an error in the determination of the adhesion force. We note that the accuracy gained by increasing the frequency ratio comes at the expense of decreasing the imaging speed.

In liquid the ringing in the oscillation associated with the inertial and hydrodynamic terms is attenuated by the low value of the quality factor (Figure 3c and d). In other words, after a few oscillations the cantilever reaches the stationary state. For ϖ = 100 the interaction force (model) shows a good agreement with the time-varying force reconstructed by using eq 1.

A similar trend is obtained when the distance modulation acts on the cantilever base (see Figure S1 in the SI). The simulations show that a sample-based modulation provides a slightly better configuration to achieve the proportionality between cantilever deflection and interaction force in liquid. This is also in agreement with a comparison between the asymptotic limits given by eq 5 and eq 11. However, the numerical differences are very minor. In practice both methods are equivalent to perform a force spectroscopy experiment.

Single-Molecule Force Spectroscopy: Unbinding Force Measurements

It is well established that the unbinding force in single-molecule force spectroscopy depends on the speed at which the tip is retracted from the surface.^15,19,32 The loading rate dependence on the unbinding force incorporates the influence of the thermal energy to overcome the energy barrier of the bond. Here we demonstrate that the apparent value of the unbinding force measured in force spectroscopy also depends on the cantilever dynamics. The hydrodynamic and inertial terms also contribute to the cantilever deflection (eq 5 or eq 11). These terms depend on the frequency ratio between the resonant frequency of the cantilever and the frequency at which the distance is modulated.

To simulate the force measured in a single-molecule force spectroscopy experiment, we have used an interaction force model with the following expression:

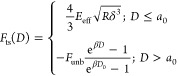12

with F_unb = 50 pN, β = 0.8 nm^–1, D₀ = 10 nm, a₀ = 0.4 nm, and E_eff = 1 MPa. This model simulates a generic unbinding force experiment with a rupture value of −50 pN. The ligand is attached to the AFM tip by a flexible linker with a total length of 10 nm. In the simulation, the tip parameters are k = 0.7 N/m, f₀ = 150 kHz, Q = 1, R = 5 nm, and E_tip = 170 GPa.

Figure 4a shows the time-varying force in the presence of an unbinding event for different modulation frequencies. The profiles indicate that the measured rupture force, minimum in the time-varying force profiles, depends on the modulation frequency. By reducing the modulation frequency (that is, by increasing ϖ), the value of the measured unbinding force increases toward the real value. This effect becomes more noticeable by comparing directly the reconstructed force for two different frequency ratios, ϖ = 5 and 300, with respect to the force model (Figure 4b). For ϖ = 5 the measured unbinding force is −20 pN, that is, 2.5 times smaller in absolute value than the unbinding force of the model (−50 pN). On the other hand, when the modulation frequency is 300 times smaller than the resonant frequency, the unbinding force is −48 pN, that is, 2 pN smaller than the unbinding force of the model.

Figure 4.

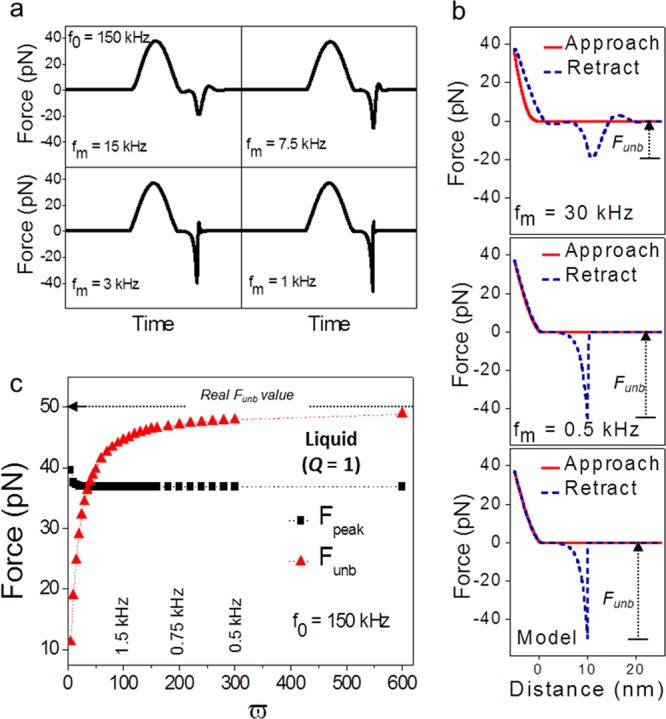
(a) Single-molecule force spectroscopy simulations. Time-varying forces for different distance modulation frequencies in a liquid. (b) Force curve reconstructed by using eq 1 for f_m = 30 kHz (ϖ = 5) and f_m = 0.5 kHz (ϖ = 300) and force curve of the model. (c) Dependence of the unbinding and peak forces on the frequency ratio for f₀ = 150 kHz. Parameters of the interaction force and cantilever dynamics: F_unb = 50 pN, β = 0.8 nm^–1, D₀ = 10 nm, a₀ = 0.4 nm, E_eff = 1 MPa, k = 0.7 N/m, Q = 1, R = 5 nm, A_m = 15 nm, z_c = 10 nm.

Figure 4c shows the unbinding and peak forces as a function of the frequency ratio from 1 to 600. The measured peak force rapidly converges to its value of 37 pN. This happens for a frequency ratio of ϖ = 10. This is in contrast with the behavior of the unbinding force. The unbinding force (absolute value) increases rapidly in the 1 to 200 range. From there it slowly converges to the value of the rupture force (model). To perform the measurements with a relative error below 10% requires a ϖ > 100. A measurement with a relative error below 5% requires a ϖ = 300. These frequency ratios will greatly limit the capability to incorporate high-speed methods into single-molecule force spectroscopy. An estimation of the dependence of the relative error on the frequency ratio could be deduced from the data shown in Figure 4c.

The data shown in Figure 4 have been obtained by using a tip–sample periodic displacement described by a sinusoidal wave. Similar results have been obtained by using triangular waves (see Figure S2 in the SI).

Nanoscale Force Spectroscopy

Nanoscale force spectroscopy, sometimes referred to as multiparametric imaging,³ provides high-resolution images and quantitative mechanical maps of a large variety of materials from cells,³³ to proteins,^34,35 to polymers.³⁶⁻⁴⁰ A distinctive feature of nanoscale force spectroscopy methods with respect to other nanomechanical spectroscopies such as force modulation,⁴¹ pulsed force AFM,⁴² torsional harmonics,^43,44 bimodal,^45,46 and other multifrequency AFM methods^47,48 is that in nanoscale force spectroscopy the force is assumed to be proportional to the cantilever deflection. This hypothesis greatly simplifies the interpretation and processing of the experimental data. However, we have shown for single-molecule force spectroscopy that fulfilling the proportionality hypothesis imposes strong requirements in terms of the frequency ratio.

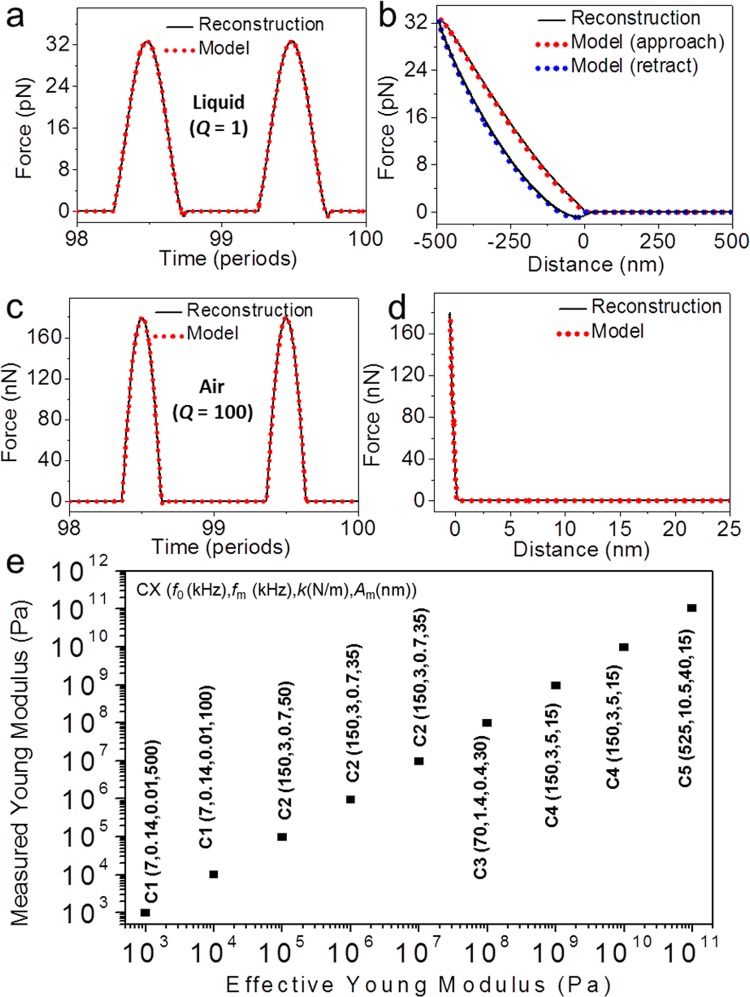
We have performed several simulations to illustrate the transformation of the force versus time curves into force–distance curves, as well as the capability to reconstruct the force for a variety of materials. We simulate the force curves of a very soft material of 1 kPa in liquid Q = 1 (simulations for imaging a living cell) and a very stiff material of 100 GPa in air (Q = 100). In both cases we have used a frequency ratio of ϖ = 100 and a distance modulation applied on the sample support.

Figure 5a,b shows the force curves for the very soft material (1 kPa). In this case the peak force value is close to the sensitivity limit of the instrument (25 pN). The agreement obtained between the interaction force (model) and the force reconstructed by using eq 1 is very satisfactory. The relative numerical difference is always below 1%. A similar agreement is obtained for a material 8 orders of magnitude stiffer (Figure 5c,d). The main difference is that the peak force in this case is about 4 orders of magnitude higher. In the first case (cells) the ringing is not observed because of the low value of the Q factor and the ratio used ϖ = 50. In the second case, the ringing is not observed because the adhesion force is 1 nN, that is, about 2 orders of magnitude smaller than the peak force value.

Figure 5.

Nanoscale force spectroscopy for soft and stiff materials. Force reconstruction by using eq 1 for a high frequency ratio (ϖ = 50). (a) Time varying force for a cell in liquid (E_eff = 1 kPa). (b) Force versus distance curve deduced from (a). The dashed line shows the model. Simulation parameters: H = 0.0 eV, η = 0.1 Pa s, f₀ = 18 kHz, f_m = 0.36 kHz, k = 0.06 N/m, Q = 1, R = 5 nm, A_m = 500 nm, z_c = 10 nm. (c) Time-varying force for a very stiff sample (E_eff = 100 GPa). (d) Force versus distance curve deduced from (c). The dashed line shows the real (model) force. Simulation parameters: H = 0.3 eV, a₀ = 0.2 nm, f₀ = 525 kHz, f_m = 10.5 kHz, k = 40 N/m, Q = 100, R = 5 nm, A_m = 15 nm, z_c = 10 nm. (e) Model and reconstructed Young’s modulus map spanning the whole range of solid materials. We have used the specifications of the following available commercial cantilevers (Bruker, Santa Barbara, CA, USA): C1: MLCT, C2: SCANASYST–LIQ, C3: SCANASYST–AIR, C4: RTESPA–150, C5: RTESP 525. Simulation parameters specified in parentheses (f₀ (kHz), f_m (kHz), k (N/m), A_m (nm)).

Next we studied the capability of nanoscale force spectroscopy to reconstruct the Young’s modulus of a wide range of materials from 1 kPa (living cells) to 100 GPa (steel). Figure 5e shows in a logarithmic scale the comparison obtained between the model and the reconstructed Young’s modulus values. The comparison has been performed by using the most suitable cantilever for each Young’s modulus range. We have used force constant and resonant frequency values from available commercial cantilevers. The agreement is quite satisfactory. Optimum frequency ratios will enable measuring the Young’s modulus over a 10⁹ range, which, in practice, includes all existing solid surfaces.

A more detailed estimation of the theoretical uncertainty is given by calculating the relative error (see Figure S3 in the SI).

Material Property and Frequency Ratio

The above results show that the effect of inertial and hydrodynamic force components on the cantilever deflection affects more the measurement of the unbinding force than the determination of the peak force or the Young’s modulus. This asymmetry arises from the temporal separation that exists between the measurement of those observables, within the period of the modulation signal, and the instant the snap-off of the cantilever from the surface occurs. The hydrodynamic and inertial terms are excited during the snap-off. From then, these terms decay as Q/f₀. Figure 4b shows the measurement of the unbinding force by using eq 1. The temporal interval of the measurement Δt₅ coincides with the snap-off process (Figure 1b). On the other hand, the Young’s modulus is measured at either Δt₂ or Δt₄, and the peak force is measured at Δt₃. These time intervals are far from the influence of the snap-off process. On the basis of the above results, we propose the following rules for quasistatic force microscopy methods. Topography imaging with a feedback on a peak force value could be achieved with high accuracy by using a frequency ratio of ϖ = 10. Young’s modulus measurements require a ratio of ϖ = 50. Unbinding and adhesion forces are very sensitive to the hydrodynamic and inertial terms. Their determination with a relative error less than 5% requires the use of a high frequency ratio, ϖ > 300. This asymmetry has been observed experimentally.⁴⁹

Conclusion

We have developed the theory of the cantilever-tip dynamics as it applies to single-molecule, single-cell, and nanoscale force spectroscopies. These methods postulate that the time-varying tip–sample force is proportional to the instantaneous deflection of the cantilever. The theory shows the cantilever deflection bears contributions from three different sources: the tip–sample, the hydrodynamic, and the inertial forces. We show that a recorded force–distance curve provides a faithful measurement of the interaction force acting between the tip and the sample when the hydrodynamic and inertial force components are negligible. To meet this condition requires the use of data acquisition rates that are 2 to 3 orders of magnitude smaller than the fundamental frequency of the cantilever. We also demonstrate that the influence of these terms depends on the property to be measured. The above asymmetry has its origin in the transient character of the hydrodynamic and inertial terms and the time interval of the modulation period where they are excited. In particular, the hydrodynamic and the inertial forces tend to reduce the value of the unbinding force. To measure unbinding or adhesion forces with a good accuracy might require the use of frequency ratios above 300. For the determination of nanomechanical properties such as the Young’s modulus, the frequency ratio could be lowered to 50, while for controlling the peak force with a 10% accuracy a frequency ratio of 10 could be enough. High-frequency ratios imply limitations to acquire data at high speed. For optimum frequency ratios, nanoscale force spectroscopy can measure the Young’s modulus of any solid surface from 1 kPa to 100 GPa.

Methods

Numerical solutions of eq 5 and eq 10 were obtained using the fourth-order Runge–Kutta algorithm with different tip–sample force models at a given distance z_c. For nanomechanical spectroscopy we use a model that takes into account a repulsive contact regime, a viscous speed-dependent term, and a small adhesion term:

13

where D, E_eff, η, R, δ, H, and a₀ are the tip–sample distance, the effective Young’s modulus, the viscosity, the tip radius, the indentation, the van der Waals constant, and the intermolecular distance, respectively. For stiff contact (η = 0) we set a₀ = 0.2 nm and H = 0.5 eV in air and H = 0 eV in liquid (only the first term remains). For soft contact (η ≠ 0) we consider H = 0 eV and only the first and third terms remain. For unbinding force simulations, we use a different adhesion term during the tip withdrawal (see eq 12), and we set η = 0. We consider a spherical tip with R = 5 nm of negligible mass only for interaction purposes in all cases.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.6b03262.

• Additional figures for time-varying forces when the displacement acts on the cantilever support, unbinding forces for a triangular tip–sample displacement, and error in the determination of Young’s modulus from force–distance curves (PDF)

The authors declare no competing financial interest.